Decadal in situ hydrological observations and empirical modeling of pressure head in a high-alpine, fractured calcareous rock slope

In peri- and paraglacial regions, water plays a critical role in the hydrological cycle and slope stability. However, hydrological models often overlook water infiltration into bedrock due to limited knowledge of groundwater dynamics at high elevations. Although the link between water presence and rock slope failures is evident in many cases, proof of hydrostatic pressure buildup at depth is scarce, highlighting another significant research gap. This study aims to decipher the hydrological dynamics and empirically derive hydrostatic pressures in deep bedrock. We present unique decennial meteorological data, snowmelt modeling, and discharge measurements from two rock fractures in a tunnel located at ≈ 55 m depth under the permafrost-affected Zugspitze ridge (2815–2962 m a.s.l.). We developed an empirical hydraulic model and detected flow anomalies by comparing inputs (i.e., snowmelt and rainfall) and outputs (i.e., discharge from fractures, baseflow, and no-flow events). Results show continuous flow during snowmelt and discontinuous events during summer months. Hydraulic conductivities are in the order of 10⁻⁴ m s⁻¹, with variations according to the saturation. Extreme events are likely to fully saturate the fractures and increase their interconnectivity, producing discharges up to 800 L d⁻¹ and 58 L h⁻¹ from one single fracture. Hydrostatic pressures calculated implementing Darcy's falling-head law are 27 ± 6 m during average snowmelt and 40 ± 10 m for extreme events. These pressure levels can weaken or even destabilize rock slopes in rapidly warming alpine environments. With ongoing climate changes, water relevance is expected to increase, with impacts that have yet to be fully assessed. This study advances the understanding of alpine hydrology and geomorphology by providing new insights into deep groundwater processes and their implications for slope stability.

1 Introduction

High mountain regions are recognized as “global water towers” (Viviroli et al., 2007), significantly contributing to water resources for approximately 1.9 billion people (Immerzeel et al., 2020). During periods of limited recharge, alpine groundwater becomes particularly important, providing up to 50 % of adjacent lowland aquifers (Markovich et al., 2019; Hayashi, 2020). Groundwater flow within mountain bedrock can be categorized into two distinct components. The primary flow occurs at shallow depths and is predominantly driven by topography (Clarke and Burbank, 2011; Welch and Allen, 2014). The secondary flow is deeper and exhibits greater complexity: it is controlled by fracture density, geometry, and connectivity (Banks et al., 2009), as well as a decrease in permeability with depth (Manning and Caine, 2007).

While measurements with lysimeters focus on shallow flow (Courtin and Bliss, 1971; Rist and Phillips, 2005), there is a considerable lack of knowledge about deep groundwater dynamics in alpine slopes and their connection with the cryosphere (van Tiel et al., 2024). Direct measurements of deep groundwater in fractured alpine bedrock using wells are limited to a few studies (Manning and Caine, 2007; Gabrielli et al., 2012) due to the logistical challenges of rugged terrain, harsh weather conditions, and significant spatial variability (Walvoord and Kurylyk, 2016; Arenson et al., 2022). Piezometric measurements in fractures or boreholes are mostly of difficult interpretation (Draebing et al., 2017; Phillips et al., 2023; Bast et al., 2024), while combined geophysical methods can identify liquid water presence (Hauck et al., 2011; Watlet et al., 2018; Pavoni et al., 2023) but cannot measure pressure. So far, studies on high-alpine hydrology have predominantly focused on talus slopes, moraines, or rock glaciers (Hayashi, 2020; Noetzli and Phillips, 2019; Jones et al., 2018; Arenson et al., 2022), and, only recently, Ben-Asher et al. (2023) modeled surface hydrological fluxes in steep bedrock permafrost.

In these environments, water presence also influences slope stability, as shown in numerous failure events (Fischer et al., 2010; Stoffel and Huggel, 2012; Walter et al., 2020; Kristensen et al., 2021), where hydrostatic pressure has been hypothesized as one of the destabilizing factors. In the theoretical model by Krautblatter et al. (2013), hydrostatic pressure can destabilize slopes by increasing lateral shear stress, decreasing frictional strength, and reducing normal stress. Mechanical simulations at slope scale confirm the critical role of water within fractures for stability (Scandroglio et al., 2021; Magnin and Josnin, 2021). From the thermal point of view, water percolating in fractures can quickly thaw bedrock by advection and, therefore, destabilize larger rock masses than heat conduction (Haeberli et al., 1997; Gruber and Haeberli, 2007). Still, so far, direct field evidence of thermal disturbance at depth is only available for one site (Phillips et al., 2016).

Despite the critical role of fracture water in alpine environments, there is a lack of reliable data and modeling efforts, resulting in an inadequate understanding of groundwater flow dynamics and little knowledge of hydrostatic pressures at depth. To address these two gaps, we present a decade-long dataset of high-alpine fracture discharge measurements at significant depths. Firstly, we investigate the spatial and temporal patterns of water flow in deep bedrock fractures in response to snowmelt and rainfall events. Then, we develop an empirical model of fracture water dynamics to constrain catchment characteristics and identify periods of water accumulation. Finally, we provide innovative estimates of hydrostatic pressures in a high-alpine, fractured calcareous rock slope.

2 Study site

Measurements took place on the Zugspitze (2962 m a.s.l.; Fig. 1a), located in the Northern Calcareous Alps at the German–Austrian border. The study site is located southwest of the summit, in a no-longer-used pedestrian tunnel under the east–west-oriented ridge between the Zugspitze and the Zugspitzeck (Fig. 1b). Loggers are placed at approximately 2750 m a.s.l. and are accessible all year round from the research station Scheefernerhaus (UFS).

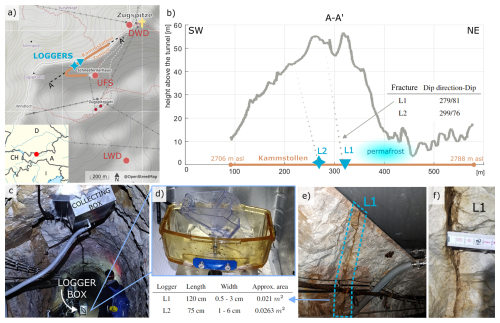
Figure 1 Overview of the study site. (a) Inset map: location of the Zugspitze. Main map: summit in yellow, tunnel in orange. Blue signs represent the two flow loggers, and red circles represent the weather stations: DWD: German Meteorological Service; UFS: Environmental Research Station Schneefernerhaus; LWD: Bavarian Avalanche Warning Service (Lawinenwarndienst Bayern). © OpenStreetMap contributors 2023. Distributed under the Open Data Commons Open Database License (ODbL) v1.0. (b) Section A–A^′ along the tunnel shows the overlaying rock masses. The table and the dotted lines present the dip direction and dip of the two fractures instrumented with loggers. (c) Measuring setup: collecting box, connecting pipe, and logger box. (d) Tipping gauge. (e, f) Fracture L1 and its detail with scale. Table with fracture dimensions: the fracture area covered by the collecting box is length by width.

2.1 Climate and cryosphere

A long-term meteorological record by the German Meteorological Service (DWD) has existed on the summit since 1901 (Fig. S1 in the Supplement). The climate is influenced by the prominent elevation at the northern edge of the Alps and by multiple E–W-oriented ridges, leading to a mean annual precipitation of more than 2500 mm, with no recent changes compared to the reference period. A total of 80 % of precipitation is snowfall from autumn to late spring; most parts of the catchment are snow-free at the end of July; and heavy thunderstorms and intense, long-lasting rainfall events may occur during the summer (Wetzel et al., 2022). The mean temperature in the last decade (2013–2022) was −3.3 °C, which is 1.5 °C warmer than the reference period 1961–1990.

Glacier and permafrost degradation in the area has been extensively documented (Mayer et al., 2021; Gallemann et al., 2017). A permanently frozen lens was detected a few decameters from the water loggers (Krautblatter et al., 2010). Monthly geophysical measurements are conducted to monitor its dynamics and identify potential interaction with infiltrating water.

2.2 Hydrology

The basin south of the summit, also known as the Research Catchment Zugspitze (RCZ; 11.4 km²), with its high-density sensor network, is one of the best instrumented high-alpine catchments for monitoring hydrological processes (Wetzel, 2004; Weber et al., 2021). Hydrochemical investigations by Rappl et al. (2010) and Weishaupt (2023) provided the catchment borders and their hydrogeological characteristics, defining the RCZ as a perfect natural lysimeter. They evidenced a karst water reservoir in the phreatic zone beneath the Zugspitze plateau that can hold around half of the volume of summer precipitation. During the winter season, from the end of October to April, no karst system recharge occurs, and the outflow spring falls dry (Morche et al., 2008). Because of this dynamic, climate-change-induced variations in the snow cover will strongly affect water availability in the RCZ and in the areas downstream (Weber et al., 2016). Furthermore, Voigt et al. (2021) used relative gravity measurements to detect water storage variations in the RCZ at the catchment scale with promising results. Still, the only known measurements of water discharge in shallow bedrock were conducted for measuring persistent organic pollutants in percolated water (Levy et al., 2017), using the same loggers as in this study.

2.3 Geology and fractures

The whole summit area is composed of Triassic Wetterstein limestone, with a thickness of 600–800 m (Hornung and Haas, 2017). Ulrich and King (1993) report brecciated zones up to 1 m thick that dip steeply (60–90°) in the direction of NW–ENE and can be intercalated with ice. A relevant fault zone can be found from above the UFS up to the summit, and karst dissolution is frequent, especially on the plateau. Krautblatter et al. (2010) mapped the fractures in the tunnel, which are newly analyzed here in Fig. S2 of the Supplement. Fractures with a dip of 80–90°are the majority (S1, n=41) but without a predominant direction (SD = 90°). The two fractures where the loggers are installed also belong to this group, as confirmed by punctual measurements conducted by Georg Stockinger in 2023 (personal communication). The indoor mapping agrees only partially with that of Mamot et al. (2021), who conducted scan lines and field mapping from the surface 400 m NW from our site (Fig. S2e). This difference is mainly due to the influence of the fault zone.

3 Data and methods

This section introduces our model's main components, which are water entering the system (fracture inputs) and water leaving the system (fracture output). Definitions and methods used for analyzing water dynamics are then presented in the last part of this section.

3.1 Fracture input: water from rain and snowmelt

Inputs to the model can be rainfall data from the weather stations or snowmelt data from the software Snowpack (SP). The meteorological measurements are conducted at the three locations listed hereafter and in Table 1. For the snowmelt modeling, we use the one-dimensional (1D) open-source software Snowpack, which simulates the evolution of the snow cover based on weather data (Lehning et al., 1999). It reproduces mass and energy exchanges between the atmosphere, snow, and soil and reproduces the evolution of snow microstructure. Simulations are conducted with data from the Bavarian Avalanche Warning Service (LWD, Lawinenwarndienst Bayern) for every hydrological year separately, with 15 min time steps. The inputs provided are incoming and outgoing shortwave radiation, snow height (HS), relative humidity, air temperature (TA), snow surface temperature, and wind speed/direction. The measured snow depth is a proxy for precipitation inputs to force the mass balance. Data gaps are interpolated with the integrated pre-processing library MeteoIO. Ground temperature is set to be constant at 0 °C, and albedo is estimated based on incoming and reflected shortwave radiation. Boundary conditions for snowmelt are adapted each year to fit the melting phase best, but, due to model limitations, discrepancies between modeled and measured snow heights are still possible. The most important output is the amount of meltwater (kg m⁻²) that leaves the snow cover in liquid form and reaches the ground.

Table 1 Meteorological data used in this study. Stations: German Meteorological Service (DWD), located on the summit and often influenced by winds; Environmental Research Station (UFS), located at 2650 m a.s.l. in the middle of the southern slope and protected from the northern winds but exposed to western atmospheric perturbations; Bavarian Avalanche Warning Service (LWD) snow and weather station, located on the plateau at 2420 m a.s.l. in a protected and flat position. The exact locations are visible in Fig. 1a. Parameters: air temperature (TA), precipitation (P), snow height (HS).

3.2 Fracture output: water discharge from fractures

Two water collecting systems, L1 and L2 (Fig. 1c–d and Fig. S3 in the Supplement), were installed in 2010 to collect water from two independent fractures (POPALP Report, 2011; Levy et al., 2017). Each system comprises a collecting box installed on the tunnel's ceiling, a connection pipe, and a logger box. Inside this, a tipping bucket with a resolution of 0.1 L, a reed sensor, and a logger record the discharge hourly. The collecting boxes are located in the unfrozen area, as confirmed by electrical resistivities (Krautblatter et al., 2010), and their vertical distance to the surface is ≈ 55 m. The fractures corresponding to each logger and their measures are shown in Figs. 1e–f and S3. The UFS has provided discharge data since 2013; new loggers were installed in 2020.

3.3 Analysis of fracture water dynamics

Discharge measurements from snowmelt or rainfall events, meteorological data, and Snowpack results are combined in MATLAB at hourly and daily resolution. While snowmelt is analyzed seasonally and daily as water flows uninterrupted for many weeks, rainfall is categorized into events, as dry periods clearly mark the limits. Mixed events are excluded, whereas rain-on-snow cases in spring are included. An output flow event starts with a sudden increase in the discharge, independent of the starting value, and ends when the flow returns to a value smaller than a threshold (typically 1 L h⁻¹). Baseflow is defined here as an almost constant discharge of small magnitude (typically < 1 L h⁻¹) that happens after (or before) a flow event and can last up to some weeks, even without further input. In our model presented in Sect. 5.3, baseflow is closely connected to fracture saturation. By convention, multiple flow events are classified as one if precipitation interruptions are shorter than 24 h and the resulting hydrograph at the gauges does not reach baseflow status between the two rain events. Input–output anomalies in the flow are detected and analyzed. One example is no-flow events when rain generates no relevant flow in the fracture. The rain events are selected manually and present a high heterogeneity of quantities and duration. Analyses are conducted automatically with a dedicated MATLAB function that uses variable parameters provided by the user for each case. All selected events are listed in Fig. S7 in the Supplement, together with the input–output graphics for each event in Figs. S8 and S9. The analysis includes 23 rain events from L1 recorded in the last 10 years, while it was possible to detect a relevant flow in only half of the cases for L2 (Fig. S7 in the Supplement).

4 Results and interpretation

The first two subsections of this section evaluate groundwater dynamics of spring snowmelt and summer rainfall separately. The third section then focuses on no-flow events, baseflow, and extreme events, which are crucial for the empirical model.

4.1 Snowmelt-induced discharge

Daily (Fig. 2a) and hourly (Fig. 2b) snowmelt in spring 2023 is shown in Fig. 2. All seasons are available at daily resolution in Fig. S4. Figure 3 presents snowmelt statistics from 2013 to 2023.

Figure 2 Example of modeled snowmelt rates and measured water discharge for summer 2023, with daily rates in panel (a) and hourly rates in panel (b). The top row of each panel shows the water input into the rock, i.e., melting water and snow height. The bottom rows show the water output, i.e., the discharge measured in gauges L1 and L2 (< 1 L h⁻¹ in the zoom window), and air temperature. In the bottom row of panel (b), two different phases of water flow are highlighted: the main flow in blue and the secondary flow in red.

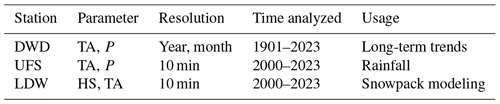
Figure 3 Snowmelt statistics. (a) Violin plot of the flow start. The white points represent the median, and the darker areas represent the 25th and 75th percentiles. (b) Delay between the Snowpack (SP) model and fluid flow loggers. (c) Time of maximum flow for SP compared to L1 and L2. The line represents the same day. (d) Maximum daily discharge for each year for L1, L2, and Snowpack, with probability distribution. (e) Delay between SP and gauge L1 for flow start and maximum discharge. (f) Daily correlation between SP and L1, with the peak at 0 and −1 d. (g) Maximum hourly flow for SP and L1 for each day. (h) Maximum daily melting rate and correlated daily cumulative melting for SP. Excluded exceptions mostly represent rain-on-snow events. (i) Maximum daily fracture flow and correlated daily cumulative flow for L1.

Seasonal and daily analysis – Snowmelt generally starts at the end of April and lasts until the end of June (Fig. 2a). Small events are also possible in summer or autumn, mostly with negligible quantities. Daily values present good temporal agreement between measurements and Snowpack (SP) modeling concerning the start and the interruptions, but discharge stops earlier than in the model (e.g., in 2019, 2021, and 2022). The daily modeled melting rates vary across the season: values increase with time, reaching the maximum at the end. The start time of snowmelt is very similar for the model and for L1, while L2 is delayed to the second half of May (Fig. 3a), with a median delay of 28 d from SP (Fig. 3b). Peak snowmelt for SP is mainly at the end of June, while both loggers reach their peak 2 weeks before or earlier (Fig. 3c). Still, five cases show a very good fitting in time. Yearly peak values reach 80 mm d⁻¹ for SP and 840 L d⁻¹ for L1, but no correlation between variables is evident (Fig. 3d). The variability in L1 and the fact that, on average, its flow is 5 times higher than SP can be explained by increased fracture interconnectivity for periods of high flow, so more surface contributes to these events.

Hourly analysis – Figure 2b shows measured and modeled values at hourly resolution. Some disagreements are evident due to water travel time, storage effects, and model limitations. According to SP, snowmelt occurs from 04:00 to 21:00 local time (LT), with a maximum at 13:00 LT and no flow during the night (Fig. S5a in the Supplement). As expected, melting hours per day increased towards the end of June (Fig. S5b in the Supplement): this explains the maximum daily melting rates of that period. On the contrary, according to L1 and L2, water flows continuously in the tunnel with daily cycles that vary in intensity and timing over the season, which can be divided into two phases (Fig. 2b). The main flow during night hours is marked in blue, and the secondary flow during daily hours is marked in red. The superimposition of hydrographs can explain these two flows: water is coming from at least two paths that have different lengths, fracture apertures, and/or filling compositions. The end of an event corresponds to the start of the next: new events mostly start around 12:00 LT and have a maximum at 22:00 LT (Fig. S5c). The delay between the beginning of SP melting and water flow increase in the tunnel is 13 h, while the delay between peaks is only 11 h (Fig. 3e), but both show substantial variability. Here, we cannot exclude that the actual delay is a multiple of the calculated one. To verify this, we plotted the correlation between SP and L1 for daily values over 5 years (Figs. 3f and S6). A maximum correlation > 0.7 is reached at 0 and 1 d. Therefore, the delay of peaks can be 11 or 11 + 24 h. This variability can be explained by increased fracture interconnectivity or changes in the infill saturation: with high saturation, the hydraulic conductivity increases and water flows faster. The daily maximum for SP is 4.7 mm h⁻¹ on average, with a maximum at 9 mm h⁻¹, while for L1 it is 10 L h⁻¹ on average, with a maximum at 58 L h⁻¹ (Fig. 3g and i). No correlation is evident here. The daily cumulative flow of SP does not fit the hourly maximum flow rates linearly (Fig. 3h), while the daily total flow of L1 is linearly correlated to maximum flow rates (Fig. 3i). This is because the quantity of water that can be released by 1 m² of snow during 1 d is physically limited, but more fractures are connected with higher discharges.

4.2 Rainfall-induced discharge

All possible flow trajectories resulting from a rain event are explained in Fig. 4. The output discharge from L1 and L2 can differ even with the same input; e.g., in Event 2 (yellow area), a flow is recorded only in L2, indicating different pre-saturation levels in the two fractures. For Event 3, discharge is recorded in both loggers; therefore, both fractures are fully saturated.

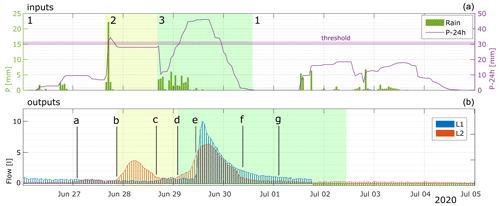
Figure 4 Example of summer precipitation events (i.e., inputs) (a) and the corresponding flow in the fractures (i.e., outputs) (b). Abbreviations are as follows. P: hourly precipitation; P-24h: sum of precipitation in the last 24 h. 1: low-intensity short-duration event with P-24 smaller than the threshold (≈ 30 mm (24 h)⁻¹); 2: high-intensity short duration event around the threshold; 3: low-intensity long-duration events with P-24 above the threshold. L1 in blue and L2 in red. a: no changes for L1 and increase in baseflow for L2; b: start of the event (L2); c: increase in flow (L1); d: start of the second event (L2); e: start of the first event (L1); f: end of the event, only baseflow (L2); g: inflection point, end of the event, only baseflow (L1).

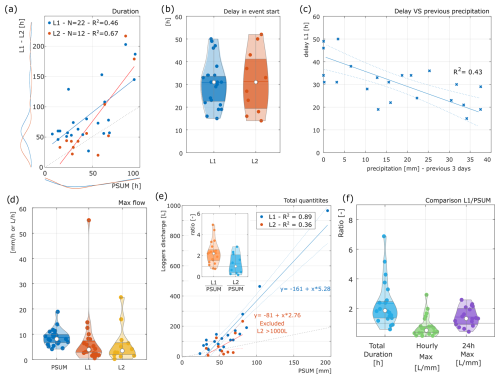
Figure 5 Analysis of rain events. (a) Correlation for event duration: P compared to flow in L1 and L2. (b) Violin plot of the delay between precipitation and flow in L1 and L2. (c) Relation between precipitation in the 3 d before the event and delay for L1. (d) Violin plot with maximum hourly precipitation and flow rate. (e) The main graph shows the correlation analysis for the total quantities, L1 or L2 vs. P. The small graph shows the ratios L1 $/$ P and L2 $/$ P for total quantities. (f) Ratios L1 $/$ P for different quantities: event total duration, maximum flow rate, and 24 h cumulative maximum flow.

Results show that the duration of flow events in the tunnel is mostly longer than precipitation duration (Fig. 5a). Still, the correlation between duration in L1 and L2 is very high (Fig. S10 of the Supplement). Even short rain events (< 10 h) cause discharges that last longer than 2 d. There is a sudden increase in flow duration for more prolonged precipitation (> 80 mm), which also points to an increase in fracture interconnectivity. Flow in the gauge L1 can last up to 7 times longer than the precipitation (Fig. 5f). The delay from precipitation start to flow in the tunnel is 31 h for both loggers (Fig. 5b), but this time can vary ±10 h according to the amount of precipitation occurring in the previous 3 d (Fig. 5c). This value is a good proxy for the pre-saturation level of the fracture: the more rain before the event, the higher the fracture's saturation, so the faster the water flows. Maximum hourly flow rates in L1 (3.9 L h⁻¹) are smaller than precipitation (8 mm h⁻¹) due to slow percolation smoothing the peaks (Fig. 5d), but if we consider the 24 h sums, the discharge in the tunnel becomes proportionally larger than the precipitation (Fig. 5f and Fig. S10). Total quantities confirm this: more than 1 L of water reaches the tunnel for each millimeter of rain falling on the surface: 2.3 L mm⁻¹ of rain in L1 and 1 L mm⁻¹ for L2 (Fig. 5e). These values can be converted into square meters (m²) and express the minimum catchment size for the fractures: considering losses by evaporation and superficial runoff, we can suppose that, in reality, larger areas contribute to each fracture. No events are recorded in the tunnel with less than ≈ 30 mm precipitation (Fig. 5e).

4.3 No-flow and extreme events

No-flow – Rain events that do not produce a relevant water flow in the tunnel are hereafter defined as no-flow events. We selected 49 summer rain events to investigate this anomaly (Table S2, Supplement). No-flow events have maximum precipitation of ≈ 34 mm and last up to 36 h. Still, the 6 h precipitation is very similar to the total precipitation, meaning that the precipitation is mostly concentrated in a few hours. Total precipitation and peak intensity are poorly correlated with duration (Fig 6b), but total precipitation is related to the peak intensity (Fig 6c), confirming the predominance of short high-intensity rainfalls, likely thunderstorms. This is further supported by the absence of no-flow events that exhibit long durations and low intensities.

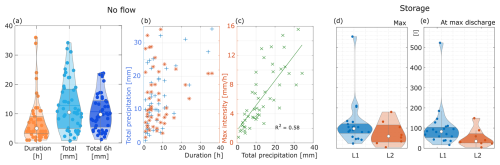
Figure 6 Analysis of no-flow events and storage. (a) Statistics and spread for 49 events. (b) Correlation between duration and total precipitation (blue crosses) or maximum intensity. (c) Correlation between total precipitation and maximum intensity. (d) Maximum storage and (e) storage at maximum discharge.

Extreme events – The logger recorded two special cases with extreme discharges. The first is the snowmelt from 10–12 June 2019, which happened after a record snow depth of more than 6 m in May, coincidently with a sudden increase in air temperature up to +10 °C. This caused extreme tunnel discharges up to 800–750 L d⁻¹ for 3 consecutive days. The second extreme event is the rainfall from 16–18 July 2021, with peak intensities of 160 mm (24 h)⁻¹ and 20 mm h⁻¹, preceded by multiple smaller rain events in the 5 d before, which pre-saturated the fractures. This event was forecasted by the public warning service and generated floods in the valley. In the tunnel, discharges reached values above 800 L d⁻¹ and hourly values up to 55 L h⁻¹, the maximum in the last 10 years. In this case, the delay between peak precipitation and peak flow was only 3 h.

5 Modeling flow and storage in deep bedrock fractures

In the following section, we compute the recession curve and analyze flow anomalies. Afterwards, we explain the anomalies by introducing the empirical model for fracture saturation and quantifying stored quantities. Finally, discharge values are used to estimate hydraulic heads. The following analyses focus solely on rain events because they are distinctly separated by dry periods, and all input/output quantities are directly measured and are therefore highly reliable.

5.1 Recession curve fitting

Recession curves can fully reproduce discharge behavior using empirical coefficients. These aquifer intrinsic parameters provide information on the flow characteristics and on the attributes of the aquifer, e.g., estimation of karstification degree (Malík and Vojtková, 2012; Kirchner, 2009). Boussinesq (1877) was the first to describe aquifer drainage and spring discharge through a porous medium using a diffusion equation. Using simplifying assumptions, he obtained the approximate analytical solution described by Eq. (1), similar to Maillet (1905) for reservoir emptying through a porous plug.

$$\begin{array}{}\text{(1)}& Q_t=Q_{\mathrm{0}}{e}^{-\mathit{\alpha }t}\end{array}$$

Here, Q_t is the discharge at time t, Q₀ is the initial discharge, and α is the recession coefficient. Other equations are available to better fit various shapes of hydrograms, e.g., linear equations. Complex aquifers with mixed laminar–turbulent flow regimes, like karst with multiple conduits, require more equations to fully reproduce their groundwater circulation (e.g., Eq. 2).

$$\begin{array}{}\text{(2)}& Q_t=\sum _{i=\mathrm{1}}^n{Q}_{\mathrm{0}i}{e}^{-a_{i}t}+\sum _{i=\mathrm{1}}^m{Q}_{\mathrm{0}i}(\mathrm{1}-{\mathit{\beta }}_{i}t)\end{array}$$

We first analyzed all events in L1. Normalized curves show a similar pattern (Figs. S11 and S12 of the Supplement) with a discharge peak after only 10 % of the time. Later, at 40 % of the time, discharge decreases back to 30 % of the peak, and the remaining 60 % of the time is required to return to baseflow. For the recession curve fitting, we extracted the discharge part from all events and divided multiple peaks into sub-events, with one curve for each peak. All the curves are first plotted at time t=0 (Fig. 7a), and then, starting from the biggest values, each curve is shifted in time so that its starting value fits the same value of bigger events (Fig. 7b). Finally, we computed the mean of the shifted curves and tested different fitting solutions for it (Fig. 7c), according to Malík (2015). The best results for our spring are obtained using Eq. (2) with n = 2 and m = 0 (Fig. 7d), which reduces the error to an acceptable level (Table S2 in the Supplement). According to the classification suggested by Malík and Vojtková (2012), “the combination of two or more sub-regimes with merely laminar flow (exponential equations) characterized by higher values of α” describes a flow happening in an “irregularly developed fissure network, with the majority of open macrofissures, and with the possible presence of karst conduits of limited extent”.

Figure 7 Modeling of all discharge events with a uniform recession curve. (a) All events are plotted with t₀=0 and semi-logarithmic axes. (b) Discharge curves are shifted in time so that Q₀ fits a similar value from a higher curve. The mean curve is in blue. (c) Recession curve fitting with a single-equation linear flow component (green line) and a single-equation exponential flow (blue line). (d) Recession curve fitting with a two-component exponential flow.

5.2 Flow anomaly detection

Combining input on the surface and output in the tunnel, we observe situations where the presence or absence of water in the tunnel cannot be directly explained. These unforeseen flow behaviors are analyzed in Fig. 8, and all are explainable by water accumulation in the bedrock above the tunnel (“storage”). Possible storage includes (i) karst voids, (ii) pores, and (iii) fractures. (i) Results of the recession curve confirm that the presence is possible but only to a limited extent. Extensive karst voids are present under the plateau (Wetzel, 2004), but their presence in our study area has not been proven yet. Therefore, we exclude this possibility. (ii) An average rock matrix permeability of 5 μD (Krautblatter, 2010) strongly limits the storage possibilities in the matrix. (iii) Fractures are preferred flow paths and can temporarily store water due to their filling with fine material. Therefore, our model will focus on this component.

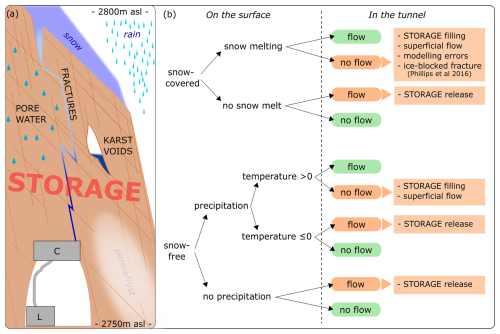
Figure 8 Flow anomaly detection. (a) Simplified model of all hydrological components. Storage includes fractures, karst voids, and pores, i.e., all locations where water can accumulate. In the tunnel, we find the collecting box (C) and the logger (L). (b) Analysis of water presence: green boxes show expected situations, while orange boxes highlight unexpected situations with possible explanations. All these cases can be explained by water accumulation in the bedrock.

5.3 Fracture saturation and storage model

Figure 9 presents the empirical model that explains flow anomalies. The model is composed of four stages and allows a qualitative forecast of the saturation level in the fracture: from unsaturated (S1) through partially saturated (S2a and S2b) to fully saturated (S3). S2a and S2b differentiate for the outflow: in S2a, we have no flow, while, in S2b, we have baseflow. Discharge in the tunnel happens when fractures are fully saturated (S3). S2a/b and S3 can alternate repeatedly when precipitation events happen in quick succession. During dry periods, when S1 resumes and baseflow reduces to zero, we suppose the fracture to be unsaturated, as in Sweetenham et al. (2017).

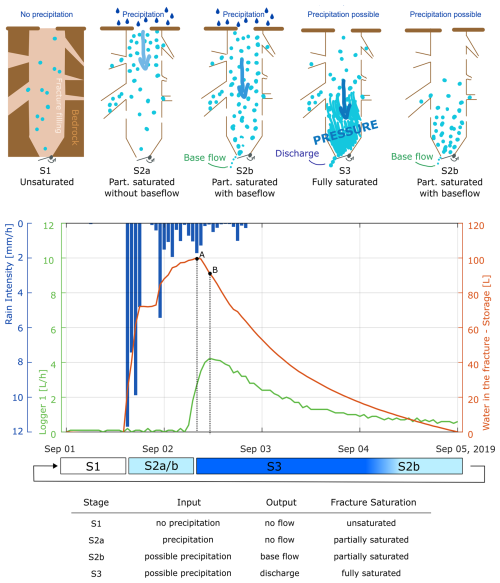
Figure 9 Fracture saturation and storage model. Upper image: graphical representation of the four phases of the model. Central graph: exemplary summer rainfall event. Precipitation (blue bars), fracture discharge (green line), and the corresponding storage level from Eq. (4) (red line). Point A represents the maximum storage in the fracture system, and point B represents the storage at maximum discharge. Lower table: stages of the fracture saturation model as a consequence of input and output.

This model allowed us to estimate the amount of water stored in the fractures at each time step. For this, we calculated the cumulative discharge Q (L) and precipitation P (L m⁻²) at the end of the event. While the first is exactly known, the exact amount of rain infiltrating the fracture is unknown. Therefore, for each event, we calculated the ratio R_end (Eq. 3), which is the surface required to obtain the discharge measured in the tunnel. This value represented only a minimum estimation, since we excluded superficial runoff and evaporation.

$$\begin{array}{}\text{(3)}& R_{\mathrm{end}}=\sum _{t=\mathrm{0}}^{\mathrm{end}}{Q}_t/\sum _{t=\mathrm{0}}^{\mathrm{end}}{P}_t\end{array}$$

R_end was then used in Eq. (4) to determine the difference between cumulative input and output at each time step t, which corresponds to the storage level S_t.

$$\begin{array}{}\text{(4)}& S_t=\sum _{\mathrm{0}}^t{P}_t\times R_{\mathrm{end}}-\sum _{\mathrm{0}}^t{Q}_t\end{array}$$

The Supplement presents the storage curves for all events in Figs. S13 and S14. The average storage in the fracture system is 97 L for L1 and 59 L for L2 (Fig. 6d).

Considering that the timing of the maximum storage is different from the time of maximum discharge in the tunnel (see points A and B in Fig. 9), we expect the maximum pressure in the fracture when the maximum discharge is recorded. Here, we also suppose that all the water in the fracture is concentrated at one point, which is the bottleneck of the fracture. Storage reduces by 15 %–20 % from A to B, and the maximum storage at B reaches 520 L in July 2021 (Fig. 6e).

5.4 Estimating hydrostatic pressures from discharge

Finally, we estimated the resulting hydraulic head using Darcy's law (Eq. 5), the basic equation that describes fluid flow through saturated porous media.

$$\begin{array}{}\text{(5)}& q=-K{\displaystyle \frac{\mathrm{\Delta }h}{\mathrm{\Delta }l}}\end{array}$$

Here, q is the specific discharge (L T⁻¹), K is the hydraulic conductivity (L T⁻¹), h is the head (L), and l is the travel distance (L) (Zha et al., 2019). According to Bernoulli's equation (Eq. 6), the total hydraulic head h_t can be composed of elevation head h_z, pressure head h_p, and velocity head h_v. In this case, h_v can be neglected due to extremely low velocities in porous media, and h_p should be constant within the system. Therefore, the elevation head h_z is the dominant component, and it drives water flow (Freeze and Cherry, 1979).

$$\begin{array}{}\text{(6)}& h_t=h_z+h_v+h_p\approx h_z\end{array}$$

To constrain the hydraulic head, we compared our case to a falling head test with a Darcy cylinder as in Fig. 10a and made the following four assumptions. (i) The only constant head is at the discharge point. (ii) The diameter is constant over the whole length (a=A; Fig. 10b). (iii) L is the “effective path” that offers hydraulic resistance; therefore, a hydraulic head can build up above it. (iv) Lateral flow is neglected.

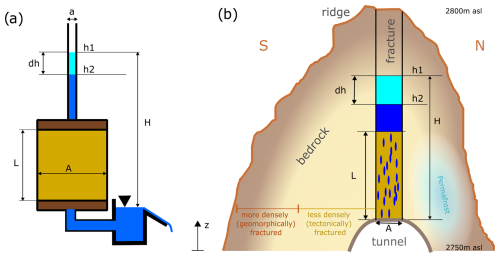
Figure 10 Application of Darcy's law for a falling head. (a) Darcy cylinder with the falling head in the pipe above it and a constant head at the outflow. (b) Illustrative S–N transect of the fracture for water flow with a falling head. Bedrock deeper than 8 m is expected to be less densely fractured (Clarke and Burbank, 2011).

In Fig. 10a, the discharge according to Darcy is $Q=q\cdot A=-K\cdot H/L\cdot A$, and it must be equal to the change in hydraulic head, i.e., the discharge rate above the effective path $Q=a\cdot \mathrm{d}h/\mathrm{d}t$.

$$\begin{array}{}\text{(7)}& a{\displaystyle \frac{\mathrm{d}h}{\mathrm{d}t}}=-KA{\displaystyle \frac{h}{L}}\end{array}$$

Since here a=A, we can simplify, rearrange the terms, and integrate the equation, obtaining

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& \underset{h_{\mathrm{1}}}{\overset{h_{\mathrm{2}}}{\int }}{\displaystyle \frac{\mathrm{d}h}{h}}=-{\displaystyle \frac{K}{L}}\underset{t_{\mathrm{1}}}{\overset{t_{\mathrm{2}}}{\int }}\mathrm{d}t,\\ & \ln \left(h_{\mathrm{2}}\right)-\ln \left(h_{\mathrm{1}}\right)=-{\displaystyle \frac{K}{L}}(t_{\mathrm{2}}-t_{\mathrm{1}}).\end{array}\end{array}$$

Solving for the maximum event length, we suppose t₁=0, and $t_{\mathrm{2}}=t_{max}$ is obtained from the recession curve. Considering baseflow at the end (h₂=0.1 m), we can compute the hydraulic head at the beginning (h₁).

$$\begin{array}{}\text{(9)}& h_{\mathrm{1}}=\mathrm{0.1}\cdot e^{(K\cdot t_{\mathrm{2}}/L)}\end{array}$$

The following boundary conditions apply in this case:

• i.

  The height of the surface above the tunnel should be h₁<55 m.

• ii.

  Bedrock porosity, including matrix and fractures, is estimated at 2.5±1.5 % (Krautblatter, 2010), which gives an average storage capacity of 25±15 L for each cubic meter of rock. Considering the extreme event of July 2021, 520 L must be stored above the tunnel, resulting in $\mathrm{13}<h_{\mathrm{1}}<\mathrm{52}$ m. These numbers might be smaller, since, on the surface, porosity and fractures increase.

• iii.

  The length of the effective path, L, must be realistic: $\mathrm{5}<L<\mathrm{20}$ m. We fix one value for the whole process.

• iv.

  The theoretical length of the maximum event (t₂) can be obtained from the recession curve analysis: t₂=200 h.

• v.

  A plausible range of hydraulic conductivities is obtained from the literature and from the recorded events. According to Freeze and Cherry (1979), K in karst limestone can vary between 10⁻⁶ and 10⁻² m s⁻¹, while estimated field velocities are $\approx \mathrm{5}\times {\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹.

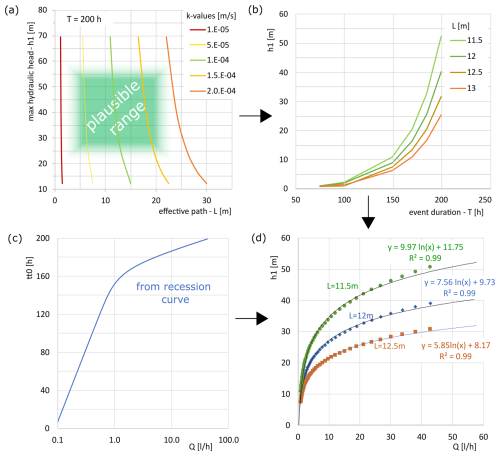
Figure 11 Approximative hydraulic head model. (a) Hydraulic head resulting from different effective path (L) and hydraulic conductivity (K). The area in green highlights physically realistic results. (b) Validation of the results by changing the event duration. (c) Time to 0 flow (tt0) for each discharge Q. (d) Hydraulic head h1 computed using discharge from fracture L1. For this case, we used $K={\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹.

With the given assumptions, these boundary conditions, and Eq. (9), we constrained a realistic range for the hydraulic head at the beginning of an event h₁. Firstly, plausible couples of K and L values were obtained (Fig. 11a and Table S3 of the Supplement). These couples were then validated for different event lengths ($\mathrm{75}<t_{\mathrm{2}}<\mathrm{200}$ h) in Fig. 11b. A realistic value of K appeared to be between $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ and $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹; we chose the median, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹, which requires an effective length L between 11.5 and 12.5 m to produce a maximum hydraulic pressure h1 between 32 and 52 m. The validation of these results for shorter event duration confirmed their feasibility (Fig. 7b). Each discharge requires a specific time to return to baseflow after an event. This was defined as time to 0 flow (tt0) and was obtained for any given discharge Q with Eq. (2) and the parameters in Table S1 (Fig. 7c). The resulting values of tt0 were used in Eq. (9) to compute h1 (Fig. 11d). This way, we connected discharges from the logger and hydraulic heads in the fracture.

Considering the average maximum discharge from the rain events, Q ≈ 4 L h⁻¹, a hydraulic head of 20 ± 4 m is obtained. For snowmelt, we recorded daily Q ≈ 10 L h⁻¹, which generates a hydraulic head of 27 ± 6 m. Extreme snowmelt in June 2019 could generate a hydraulic head of 40 ± 10 m in the fracture, and similar values are also possible for intense rainfall in July 2021.

6 Discussion

This article provides insights into water flow dynamics, reservoir effects, and saturation levels in bedrock fractures. It introduces an empirical method for quantifying hydrostatic pressures generated by snowmelt and rain infiltration. Differently from previous studies (Scandroglio et al., 2021; Magnin and Josnin, 2021), we do not quantify pressures from model results but based on a decade of high-alpine underground discharge measurements. The robustness of these unique flow data indicates the occurrence of periods with high water pressure, allowing the following extensive discussion.

6.1 Snowmelt- and rain-driven water flow dynamics in deep fractures as system input

Average and maximum daily infiltration rates from snowmelt are ≈ 30 and 80 mm d⁻¹, respectively, similar to those measured by Rist and Phillips (2005). The software Snowpack can reproduce the timing of extreme melting events but shows disagreement at the end of the melting phase due to the model's poor performance or to the different locations of the snow station. More snow is available on the flat plateau compared to the 40/50° slopes, and regular avalanche detachments for safety reasons further reduce snow availability. A basal ice layer at the cold interface of rock and snow is supposed to strongly limit snowmelt penetration in rock walls (Phillips et al., 2016; Ben-Asher et al., 2023). Still, Kneisel et al. (2014) documented thermal disturbances in the underground as soon as snowmelt started, while Kristensen et al. (2021) and Roth and Blikra (2009) recorded large increases in rockslide displacements late in the snowmelt season. Our direct flow measurements show that snowmelt infiltrates every year and that the discharge timing for fracture L1 fits with Snowpack modeling from the plateau, which lies southward. This suggests that (i) the catchment of L1 is on the southern slope and that (ii) no basal ice layer is blocking meltwater here. In contrast, a temporary basal ice layer or frozen fractures cannot be excluded for L2, given its delay in some years. A seasonal basal ice layer could also be present on the steep northern slopes, where snowmelt happens later in the season, as observed during fieldwork.

Summer precipitation reaches the tunnel only for events above ≈ 30 mm (24 h)⁻¹. Poulain et al. (2018) confirm that a saturation threshold is necessary to allow vadose connectivity, although values depend from site to site (Sweetenham et al., 2017). High-intensity short-duration events like thunderstorms often happen at the beginning of precipitation, generating no flow or only baseflow. Most of this water drains away as surface flow due to the total absence of a substrate that acts as a buffer. For the same reason, evaporation effects can be neglected at this location. These effects could influence the estimated storage, so we might overestimate it. The amount of precipitation in the period before an event influences the travel time of water in the fracture so that pre-saturated fractures have a higher hydraulic conductivity K. Infiltration rates and fracture conductivity correlate with fracture patterns at the inlet (Zhou et al., 2006). Therefore, detecting the precise inlet location could further improve the understanding of the hydrologic system. Unfortunately, the ridge is very exposed, and access is possible only at high risk.

6.2 Outflow as the summative system output

The response hydrographs of the two fractures are different: L2 presents a symmetrical hydrograph with similar rising and falling limbs (Fig. 4d to f), while for L1 the rising limb is very steep. Still, the falling limb has a slow decay (Fig. 4e to g). The differences could be due to different fracture filling, catchment shapes, isolated karst areas, or higher connectivity. Fracture density also strongly influences the flow at depth: scarcely fractured networks have a slightly faster response to precipitation than a denser network (Sweetenham et al., 2017). The total annual outflow for L1 reached the decennial maximum value in 2019 with 8500 L yr⁻¹, which means a theoretical average of 23 L d⁻¹. However, in that year, one single snowmelt period even recorded a total of 2300 L in 3 d, which is 27 % of the total, showing that extreme events dominate water dynamics. Measured maximum flow rates are 4 to 10 times higher than those computed by Snowpack and measured by Rist and Phillips (2005) because our data are recorded at 50 m depth, where fracture connectivity increases during high discharges (Sweetenham et al., 2017). The highest discharges from snowmelt were recorded at the end of the melting season. For the same period, Weber et al. (2017), Etzelmüller et al. (2022), and Leinauer et al. (2024) demonstrated a clear correlation between snowmelt and the increased displacement of unstable slopes. One single rainfall event produced extreme values similar to snowmelt but for a shorter time. A contribution to flow from the thawing of neighboring permafrost bodies is theoretically possible. The discharges would be small and visible in dry periods at the end of summer, but it is hard to find signs of this in our data.

6.3 Pressurized water inside fractures as an agent driving slope instabilities

The computed hydrostatic pressures strongly depend on the selected parameters, although, according to our premises, only limited pairs of hydraulic conductivity K and effective length L are reasonable. The presented values are computed for $K={\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹ and L=11.5–12–12.5 m, which are the most likely parameters, but the same results could be obtained using, for example, $K=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ m s⁻¹ and L=5.75–6–6.25 m. Still, other K–L couples could lead to different hydraulic pressures. Much higher hydraulic conductivities are measured on the Zugspitzplatt by Rappl et al. (2010) with tracers, but this is due to the well-developed karst system present at that location and not at our site.

In extreme cases, hydrostatic pressures up to 40 ± 10 m can be reached, similarly to the models of Magnin and Josnin (2021). Average values reach 20 m during summer rainfall events and 27 m during spring snowmelt, pressures that can be mechanically critical (Scandroglio et al., 2021). These levels are achieved many times in the summer and every day during snowmelt, generating repeated loading–unloading cycles that have rarely been considered but can be a crucial destabilizing factor for slope instabilities. Leinauer et al. (2024) and Helmstetter and Garambois (2010) reported that every drop of water can accelerate or trigger instabilities. This can be true during snowmelt or only for superficial movements, since our no-flow measurements and the models of Sweetenham et al. (2017) show that minor rain events do not reach depths of 25–50 m.

The proposed model provides qualitative estimates of fracture's saturation level at depth, which is also crucial for rock wall destabilization (Magnin and Josnin, 2021). When fractures are fully saturated, destabilization acts due to the reduction in cohesion and friction of the fracture's filling material and the reduction in shear strength by counteracting the normal stresses (Scandroglio et al., 2021). During snowmelt, water flows uninterrupted for many weeks, and fractures remain saturated for longer periods. In summer, rain events alternate dry periods, so fracture saturation is highly variable, and destabilizing effects last shortly.

6.4 Error sources and uncertainties

Error sources and uncertainties are possible in the components of our fracture flow model: the inputs, the outputs, and the estimation of storage and pressure.

Water flow characteristics along the rock fractures are as follows:

• Inputs. Due to the elevation of the study site, the number of snow events (N>100) is larger than the number of rain events (N=23). Snowpack modeling is computed only in 1D at a different elevation than the ridge: 2D or 3D modeling could improve the fitting of the melting phase. Rainfall events are analyzed only hourly, while a 10 min resolution would provide better insight into high-intensity, short-duration events. Due to their nature, extreme events are rare and statistically less represented.

• Outputs. Both loggers suffered repeated failures due to lightning strikes, battery problems, and maintenance. Therefore, data gaps could be mistaken for no-flow events or for ice sealing the fracture. L1 and L2 do not always behave similarly (e.g., different discharge hydrographs), but the analyses here focus mostly on L1 because only a few events were recorded by L2. In fact, the latter is more prone to failure and shows variations in peak discharge with time that are not clearly explainable.

• Estimation of storage and pressures. Model calibration took place using one extreme rain event that could present higher K and higher fracture interconnectivity than normal events. To include this variability, all events are incorporated in the recession curve. We chose robust estimates and performed sensitivity propagation to check the robustness of the results. Bedrock deeper than 8 m is expected to be less densely fractured (Clarke and Burbank, 2011), and a conductivity reduction up to 65 % is expected close to a tunnel due to stress increase and joint closure (Fernandez and Moon, 2010). These effects can strongly influence pressure locally (Montgomery et al., 2002). K varies in time according to saturation levels (Fig. 5c), while porosity and hydraulic conductivity are very likely not uniform in space. For simplicity, we do not include these variations in our model. Due to the increase in interconnectivity for high discharges, we cannot exclude that, in extreme events other than assumed, water spreads laterally and produces hydraulic heads smaller than suggested here.

6.5 Outlook

Snowmelt is expected to begin up to 1 month earlier by the end of this century (Vorkauf et al., 2021). If so, melting rates will be slower due to the reduced solar radiation early in the year (Musselman et al., 2017), leading to a partial reduction in infiltration rates and consequently lower hydrostatic pressures in fractures during snow-covered periods. Snow-free periods and the number of summer rainfall events might increase. Heavy precipitation will generally become more frequent and more intense with global warming (IPCC, 2023). Accordingly, we expect (i) more events with liquid precipitation and (ii) more frequent and more intense extreme-flow events in fractures, resulting in higher hydrostatic pressures in snow-free periods.

The impact of permafrost bodies on flow paths (Woo, 2012) and water accumulation (Krautblatter et al., 2013) has largely been overlooked. However, climate change is expected to increase active-layer depth, leading to the formation of new horizontal and vertical flow pathways. Consequently, the infiltration depth of water will increase, generating higher hydrostatic pressures (Haeberli and Gruber, 2009). Fracture permeability will also be affected, since unfrozen fractures are up to 3 orders of magnitude more permeable than frozen ones (Pogrebiskiy and Chernyshev, 1977), with significant effects on hydrostatic pressure. Pressurized water in fractures boosts permafrost degradation and could become more important than thermal propagation.

7 Conclusions

This study combines a decade of meteorological data, snowmelt modeling, and discharge measurements, thereby (i) providing novel insights into water dynamics in fractured bedrock and (ii) estimating possible hydrostatic pressures.

• i.

  At this elevation, snowmelt produces, on average and in total, higher discharges than rainfall events, but, due to climate change, more rain is expected by the end of the century. Extreme events can reach up to 800 L d⁻¹ from one single fracture. Rainfall reaches the 55 m deep tunnel with an average delay of 31 h, but this value decreases when the fractures are pre-saturated, e.g., during snowmelt periods. No-flow and baseflow events are indicators of unsaturated and partially saturated fractures, respectively. To fully saturate the fractures, more than 30 mm precipitation within 24 h is required, but high-intensity short-duration rain barely contributes to fracture flow. The discharge curves of summer precipitation fit into a general recession curve composed of two exponential terms for laminar flow, which allows the duration of an event to be forecasted, given its discharge. We detected flow anomalies that can be explained with the help of an empirical fracture flow model, considering saturation changes and water storage. One fracture can store up to 550 L in extreme events, which is expected to fully saturate the fracture and increase its interconnectivity.

• ii.

  The hydraulic head resulting from the water accumulation is computed using the recession curve and Darcy's law for a falling head. On a daily mean, hydrostatic pressures can reach 27 ± 6 m during snowmelt, while rain events generate slightly lower pressures. Snowmelt generates long-lasting pressures with daily cycles that can strongly reduce slope stability. Extreme events produce discharges up to 58 L h⁻¹ in the tunnel, resulting in hydrostatic pressures of 40 ± 10 m (400 kPa). These values are enough to weaken or trigger unstable slopes. Climate change will likely reduce snowmelt pressures and increase summer extreme events.

Here we quantitatively demonstrate the relevance of water flow in deep fractures and prove its relevance for slope stability of degraded bedrock. The estimated hydrostatic pressures can destabilize and/or trigger unstable rock slopes. The combination of climate change and hydrostatic pressures in periglacial areas amplifies permafrost degradation so that, in the near future, water is expected to reach new paths and deeper levels, producing higher pressures, thus increasing the hazard.