Multiple equilibrium configurations in river-dominated deltas

The morphological evolution of river deltas is a complex process influenced by both natural factors and human interventions. The stability and predictability of flow distribution within delta channels are critical for human settlements; however, this requirement conflicts with the natural tendency of deltas to avulse towards the most hydraulically efficient branch. This study examines the existence of alternative equilibrium states within deltaic systems, highlighting key internal feedback mechanisms among delta branches through a novel theoretical model tailored to river-dominated delta channels. In particular, the analysis identifies the total length of delta branches extending toward the downstream end as the primary factor governing the stability of individual bifurcations within the delta. Additionally, the spacing between internal bifurcation nodes plays a secondary role by influencing flow partitioning through feedback mechanisms that modify the free-surface elevation at the bifurcation node. For deltas exhibiting significant asymmetries in either length or width, a threshold condition emerges, reducing the number of possible equilibrium states. Focusing on the Po River Delta, Italy, as a case study, we examine equilibrium variability and identify potential avulsion sites. Our findings provide a valuable framework for predicting future shifts in deltaic morphology and informing management strategies that reconcile natural delta evolution with infrastructural and economic requirements.

1 Introduction

River deltas are dynamic landforms where fluvial and marine environments merge. The continuous evolution of river deltas is governed by a complex interplay of different processes, including the relative balance between sediment supplied by the river and accommodation space. Sediment load depends on upstream conditions such as natural erosion, land use, damming, and vegetation cover. The interplay between sediment supply and hydrodynamic forces, including river discharge, tidal action, sea level changes, and wave energy, determines the morphology and progradation rates of deltas (Galloway, 1975; Nienhuis et al., 2020).

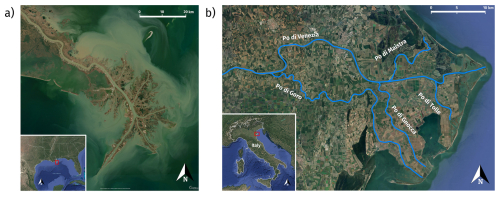
Figure 1 Satellite imagery depicting engineered river-dominated deltas. (a) The Mississippi River Delta, Louisiana, USA (29°10^′ N, 89°15^′ W), showcasing the delta's “bird foot” shape (© Copernicus Sentinel Hub). (b) The Po River Delta, located in northeastern Italy (44°57^′ N, 12°26^′ E), where the primary distributary channel “Po di Venezia” flows into the Adriatic Sea. A sequence of secondary distributary branches diverges from the main channel, comprising the “Po di Goro,” “Po di Gnocca,” “Po di Maistra,” and “Po di Tolle” branches, progressing downstream (© Google Earth 2024).

River deltas hold critical importance for human activities due to their fertile soils, rich biodiversity, and strategic locations. Consequently, they have been often subject to anthropogenic interventions which have significantly impacted their morphological evolution, as shown in Fig. 1. Indeed, large-scale engineering projects, such as dam construction, river channelization, and sand mining, alter sediment transport dynamics, often reducing the sediment load reaching deltas (Nittrouer and Viparelli, 2014).

The Po River Delta and its basin, located in northern Italy (Fig. 1b), provide an example of such a delicate system, being one of the most significant and anthropized deltas in the Mediterranean region. This basin drains the majority of the water and sediment originating from the Italian Alps and the northern Apennines, with an average annual discharge at the delta apex of approximately 1500 m³ s⁻¹ and a total sediment load ranging from approximately 9 to 12×10⁶ tons per year. Similar to most rivers globally, the Po River is affected by extensive dam construction and water management practices throughout its basin, which have led to a reduction in the sediment load reaching the delta, thereby impacting its growth and stability (Syvitski et al., 2005). Moreover, extensive land reclamation projects have progressively transformed wetlands into agricultural and urban areas, altering the natural hydrology and sediment dynamics of the delta. Specifically, one of the measures taken to this end has been the construction of levees along all distributary channels in the delta, resulting in a decreased overflow onto the plains and consequently enhancing local natural subsidence (Syvitski et al., 2009).

Due to their importance for human settlement and their unique characteristics, river deltas have been widely studied from multiple perspectives. Researchers have investigated flow distribution within deltas through field studies (Hiatt and Passalacqua, 2015; Wagner and Mohrig, 2019; Sassi et al., 2012; Dong et al., 2020), laboratory experiments (Paola et al., 2009; Piliouras et al., 2017; Miller et al., 2019), remote sensing techniques (Tejedor et al., 2015, 2017; Hariharan et al., 2022), and hydrodynamic simulations (Maicu et al., 2018; Gao et al., 2024). In recent years, numerous studies have employed numerical models to analyze the effects of tidal currents (Canestrelli et al., 2010; Hoitink et al., 2017), vegetation (Nardin and Edmonds, 2014; Nardin et al., 2016), or permafrost (Lauzon et al., 2019; Overeem et al., 2022) on delta morphology. These investigations are essential to inform active management strategies (Edmonds et al., 2022). To address the long-term evolution of river deltas, morphodynamic numerical simulations have become increasingly prevalent (Overeem et al., 2005; Fagherazzi and Overeem, 2007; Edmonds et al., 2010; Guo et al., 2015; Moodie et al., 2019; Meselhe et al., 2021). However, these models frequently rely on simplified delta configurations due to the substantial computational costs and the numerous assumptions required.

Another branch of the literature models the morphodynamic evolution of deltas in a one-dimensional framework, coupled with a quasi-two-dimensional model for the interactions among delta channels at each bifurcation (Bolla Pittaluga et al., 2003, 2015). Single bifurcation models allow us to isolate the main mechanism affecting the flow partitioning at each bifurcation (Durante et al., 2024) and the chances of avulsion towards secondary branches (Salter et al., 2018; Barile et al., 2024). Despite their simplifications and the assumption that riverbed changes are much slower than the hydrodynamic variations, such models provide useful insights into the temporal evolution of the delta channels. Interestingly, Salter et al. (2020) with a simple delta network model found that two-way coupling between upstream and downstream bifurcations in a network can lead to chaotic dynamics in the network.

Using a similar tree-like structural model, Ragno et al. (2022) examined the long-term equilibrium configuration of idealized tide-influenced deltas characterized by a series of symmetrical bifurcations, where the free-surface elevation is assumed equal between the three branches. This analytical model enables rapid identification of the equilibrium solution by solving a system of equations. This approach allows for isolating and assessing differential variations within the system and their impact on flow distribution at each delta bifurcation.

Here we reformulate the model of Ragno et al. (2022), where river-dominated deltas are solved as a sequence of bifurcations, by relaxing the assumption of free-surface elevation equality at the node and implementing a new energy balance condition at each bifurcation according to the recent work of Durante et al. (2024). The new energy balance condition allows for the detection of intrinsic asymmetries related to downstream effects. This approach demonstrates that the length of the downstream branches plays a crucial role in the stability of the bifurcation. Additionally, the model is formulated in a general form to include possible asymmetries within each bifurcation, allowing for proper application to real-world scenarios.

Furthermore, conceptualizing the delta as a sequence of bifurcations allows for the identification of multiple equilibrium solutions of the system. This framework enables the prediction of how deltaic channels would respond to avulsion events occurring at each bifurcation. The resulting flow reorganization and associated sediment deposition processes would have significant implications for navigability, particularly in large river deltas where navigation has a high economic interest.

In the present study, the model's capability to reproduce real-world scenarios is evaluated through its application to the Po River Delta. Whereas the morphodynamic equilibrium of the Po River upstream of the first bifurcation has been explored within the framework of a one-dimensional model (Lanzoni et al., 2015), no attempts have been made so far to interpret the bed morphology of the Po Delta with a morphodynamic model. The reliability of the obtained equilibrium configurations is assessed by comparing model results with the discharge partitioning among the deltaic branches, provided by flow measurements collected during a series of field campaigns by the Po River Basin Authority from 2002 to 2011 (Zasso and Settin, 2012). Furthermore, model-based estimations of free-surface and bed elevation profiles are validated against cross-sectional measurements taken in 2018. This approach facilitates an assessment of the current equilibrium state of the Po River Delta and allows for the evaluation of potential impacts arising from avulsion events, offering critical insights for effective delta management.

The following sections of the paper are structured as detailed below: Sect. 2 provides a formulation of the analytical procedure employed in this study. Section 3 delineates the main processes involved in a general idealized delta configuration. In Sect. 4 we apply the model to the case of the Po River delta, comparing model results with available measurements. Finally Sect. 5 is dedicated to discussing the results, while Sect. 6 concludes the paper providing a summary of the principal observations and insights.

2 Formulation of the analytical model

From a modeling perspective, a delta can be formally represented as a network of interconnected bifurcations, originating from a single upstream channel referred to as the “delta apex”, as depicted in Fig. 2b. This structure branches progressively from the primary (first) node to the terminal nodes, where the downstream channels discharge into the sea at a defined free-surface elevation.

Figure 2 (a) Schematic representation of a single bifurcation model as proposed by Durante et al. (2024), illustrating the inclusion of multiple asymmetries. (b) Plan view of an idealized river delta, depicted as a network comprising j bifurcations, where j=1, …, N.

Before addressing the problem of the entire delta system, it is essential to first introduce how each of its functional units, specifically a single bifurcation, is approached. As illustrated in Fig. 2a, a single bifurcation consists of an upstream channel a, a node, and two downstream branches b and c. The node is modeled using the two-cell model initially proposed by Bolla Pittaluga et al. (2003) and recently refined by Durante et al. (2024) to account for potential asymmetries. To this end, Durante et al. (2024) introduced the following key parameters: the length ratio between the two downstream branches, denoted as γ_L; the width ratios of each single downstream branch referring to the upstream channel, r_b and r_c; the total downstream enlargement represented by r_a; the kinetic head losses at the bifurcation node, ξ; and the downstream water level differential, Δh^L. More in detail, they read as follows.

• Length ratio: ${\mathit{\gamma }}_L=\frac{L_c^{\ast }}{L_b^{\ast }}$

• Branch width ratios: $r_b=\frac{W_b^{\ast }}{W_a^{\ast }}$, $r_c=\frac{W_c^{\ast }}{W_a^{\ast }}$

• Downstream enlargement: $r_a=\frac{W_b^{\ast }+W_c^{\ast }}{W_a^{\ast }}=r_b+r_c$

• Downstream level asymmetry: $\mathrm{\Delta }{h}^L=h_b^L-h_c^L$

Here $W_i^{\ast }$ and $L_i^{\ast }$ are the width and length of the ith branch, respectively, with $i=\mathit{\{}a,b,c\mathit{\}}$ denoting the channel within the bifurcation, and $h_i^L$, with $i=\mathit{\{}b,c\mathit{\}}$, is the free-surface elevation at the downstream end of the ith branch made dimensionless with the uniform flow depth of the upstream channel.

The model does not consider temporal variations in the geometry, implying no variation in each width and length over time. A uniform grain size $d_{\mathrm{s}}^{\ast }$ is assumed to compose the riverbed. The bifurcation is fed upstream with a constant discharge $Q_a^{\ast }$ and a constant sediment flux $Q{s}_a^{\ast }$ in equilibrium with local hydrodynamics. Furthermore, the model assumes rectangular straight channels, allowing for a unique value for the bed slope s_i for the ith channel. Consequently, the free-surface elevations at the node $h_i^{\ast N}$ can be calculated from the downstream elevation $h_i^{\ast L}$ given the branch length $L_i^{\ast }$.

Note that, for a single bifurcation, the free-surface elevation $h_i^{\ast L}$ at the downstream end of the ith channel branch is imposed as an input parameter and typically set to a fixed value (such as mean sea level).

The model is grounded in a nodal point condition that considers transverse flow and sediment exchange between the two cells in the upstream channel a, influencing the flow partitioning in the downstream branches b and c. The transverse solid exchange is evaluated based on the procedure for describing two-dimensional bed load transport over an inclined bed (Ikeda et al., 1981):

$$\begin{array}{}\text{(1)}& q_{\mathrm{T}s}^{\ast }=q_{as}^{\ast }\left[{\displaystyle \frac{V^{\ast }}{\sqrt{U^{\ast \mathrm{2}}+V^{\ast \mathrm{2}}}}}-{\displaystyle \frac{r}{\sqrt{{\mathit{\vartheta }}_a}}}{\displaystyle \frac{\partial {\mathit{\eta }}^{\ast }}{\partial y^{\ast }}}\right],\end{array}$$

where dimensional variables are denoted with the superscript ^∗. Specifically, $q_{\mathrm{T}s}^{\ast }$ represents the dimensional transverse solid discharge per unit width, and $q_{as}^{\ast }$ denotes the longitudinal solid flow discharge per unit width from upstream. U^∗ and V^∗ are the longitudinal and transverse velocity components, respectively. $\partial {\mathit{\eta }}^{\ast }/\partial y^{\ast }$ denotes the transverse bed slope at the junction of channels b and c. The parameter r is an experimental constant that ranges between 0.3 and 1 (Ikeda et al., 1981; Talmon et al., 1995). The Shields parameter, ϑ_a, associated with the uniform flow is defined as

$$\begin{array}{}\text{(2)}& {\mathit{\vartheta }}_a={\displaystyle \frac{Q_a^{\ast \mathrm{2}}}{\mathrm{\Delta }g{d}_{\mathrm{s}}^{\ast }{C}_a^{\mathrm{2}}{D}_a^{\ast \mathrm{2}}{W}_a^{\ast \mathrm{2}}}},\end{array}$$

where Δ is the submerged sediment density ($\mathrm{\Delta }={\mathit{\rho }}_{\mathrm{s}}/\mathit{\rho }-\mathrm{1}$, with ρ_s and ρ the densities of sediment and water, respectively), g is the gravitational acceleration, C_a is the dimensionless Chézy coefficient, $D_a^{\ast }$ is the flow depth, and $W_a^{\ast }$ is the channel width.

After having appropriately made dimensionless the variables of the problem with respect to the quantities in the upstream channel a, as in Durante et al. (2024), and following algebraic manipulation (details in Appendix A), the nodal point condition is reformulated as

$$\begin{array}{}\text{(3)}& q_{\mathrm{T}s}={\displaystyle \frac{q_T}{D_{abc}{U}_{abc}}}-{\displaystyle \frac{r}{\mathit{\beta }\sqrt{{\mathit{\vartheta }}_a}{r}_a}}\left(h_b^N-h_c^N-D_b+D_c\right),\end{array}$$

where D_abc and U_abc represent the dimensionless average water depth and flow velocity at the node, respectively. Additionally, $h_i^N$ and D_i are the dimensionless free-surface elevation and the water depth at the node in the ith channel, and β is the upstream channel aspect ratio defined as

$$\begin{array}{}\text{(4)}& \mathit{\beta }={\displaystyle \frac{W_a^{\ast }}{\mathrm{2}{D}_a^{\ast }}}.\end{array}$$

To close the problem and find the equilibrium solutions of the bifurcation, we refer to the procedure employed by Durante et al. (2024), where the system of necessary equations to find the equilibrium solutions is determined by five equations and five unknowns (namely, the flow discharge and water depth in every branch and the free-surface elevation at the node). Interestingly, by employing an energy balance approach at the node, the system gains a new degree of freedom, allowing for a slight disparity in water levels at the node, which might allow unequal flow velocities.

As demonstrated by Durante et al. (2024), the key factors influencing bifurcation stability include the dimensionless length of the branches L and the bifurcation parameter R, in line with previous studies (Ragno et al., 2020, 2022; Salter et al., 2018):

$$\begin{array}{}\text{(5)}& L={\displaystyle \frac{L^{\ast }{s}_a}{D_a^{\ast }}}R={\displaystyle \frac{\mathit{\alpha }r}{\mathit{\beta }\sqrt{{\mathit{\vartheta }}_a}}},\end{array}$$

where L is the branch length L^∗ scaled with the backwater length, and α is the dimensionless length of the upstream channel as defined by Bolla Pittaluga et al. (2003).

Let's now extend the formulation to the case of a delta. As previously introduced, a delta can be described as a series of interconnected bifurcations, each considered an individual unit governed by its own set of equations. Unlike the scenario of a single bifurcation, the equations governing each node within the delta are interdependent on those of adjacent bifurcations. This coupling necessitates solving simultaneously the system of equations for all bifurcations to achieve equilibrium for the entire deltaic network.

Assuming that the system is fed upstream with a constant discharge $Q_{\mathrm{up}}^{\ast }$ and a constant sediment flux $Q{s}_{\mathrm{up}}^{\ast }$ in equilibrium with local hydrodynamics, in a similar fashion as Durante et al. (2024), the equations are made dimensionless by scaling the dimensional variables with reference to the dimensions of the “delta apex” channel:

$$\begin{array}{}\text{(6)}& \begin{array}{rl}& (D_{ij},h_{ij})={\displaystyle \frac{(D_{ij}^{\ast },h_{ij}^{\ast })}{D_{\mathrm{up}}^{\ast }}},(q_{ij},q_{Tj})={\displaystyle \frac{(q_{ij}^{\ast },q_{Tj}^{\ast })}{q_{\mathrm{up}}^{\ast }}},\\ & (q_{isj},q_{Tsj})={\displaystyle \frac{(q_{isj}^{\ast },q_{Tsj}^{\ast })}{q_{s_{\mathrm{up}}}^{\ast }}},\end{array}\end{array}$$

where the subscript up denotes the delta apex upstream channel, while the subscript i, with $i=\mathit{\{}a,b,c\mathit{\}}$, denotes the position of the channel within each jth bifurcation: i=a denotes the upstream channel, while i=b and c indicate the two downstream channels, as illustrated in Fig. 2.

The mathematical formulation for each jth bifurcation follows the approach outlined by Durante et al. (2024), which incorporates the necessary system of five equations governing the flow and sediment conservation, the energy balance, and the nodal condition.

1. Flow discharge balance:

   $$\begin{array}{}\text{(7)}& q_{b_j}{r}_{b_j}+q_{c_j}{r}_{c_j}=q_{a_j}\end{array}$$

2. Solid discharge balance:

   $$\begin{array}{}\text{(8)}& q_{b{s}_j}{r}_{b_j}+q_{c{s}_j}{r}_{c_j}=q_{a{s}_j}\end{array}$$

3. Energy balance in cell b:

   $$\begin{array}{}\text{(9)}& h_{b_j}^N+(\mathrm{1}+{\mathit{\xi }}_j){\displaystyle \frac{{\mathit{Fr}}^{\mathrm{2}}}{\mathrm{2}}}{\displaystyle \frac{q_{b_j}^{\mathrm{2}}}{D_{b_j}^{\mathrm{2}}}}=h_{a_j}^N+{\displaystyle \frac{{\mathit{Fr}}^{\mathrm{2}}}{\mathrm{2}}}{\displaystyle \frac{q_{a_j}^{\mathrm{2}}}{D_{a_j}^{\mathrm{2}}}}\end{array}$$

4. Energy balance in cell c:

   $$\begin{array}{}\text{(10)}& h_{c_j}^N+(\mathrm{1}+{\mathit{\xi }}_j){\displaystyle \frac{{\mathit{Fr}}^{\mathrm{2}}}{\mathrm{2}}}{\displaystyle \frac{q_{c_j}^{\mathrm{2}}}{D_{c_j}^{\mathrm{2}}}}=h_{a_j}^N+{\displaystyle \frac{{\mathit{Fr}}^{\mathrm{2}}}{\mathrm{2}}}{\displaystyle \frac{q_{a_j}^{\mathrm{2}}}{D_{a_j}^{\mathrm{2}}}}\end{array}$$

5. Nodal condition:

   $$\begin{array}{}\text{(11)}& \begin{array}{rl}{\displaystyle \frac{q_{b{s}_j}}{q_{a{s}_j}}}{r}_{a_j}-\mathrm{1}& ={\displaystyle \frac{q_{b_j}{r}_{a_j}-q_{a_j}}{D_{ab{c}_j}{U}_{ab{c}_j}}}\\ & +{\displaystyle \frac{R_j}{r_{b_j}}}\left[h_{b_j}^N-h_{c_j}^N-D_{b_j}+D_{c_j}\right]\end{array}\end{array}$$

The Froude number Fr in the upstream channel is defined as

$$\begin{array}{}\text{(12)}& \mathit{Fr}={\displaystyle \frac{q_{\mathrm{up}}^{\ast }}{\sqrt{g{D}_{\mathrm{up}}^{\ast \mathrm{3}}}}}.\end{array}$$

Noteworthy, the local approach adopted here needs a careful definition in each bifurcation of the asymmetry parameters (i.e., ${\mathit{\gamma }}_{L_j}$, $r_{a_j}$, $r_{b_j}$, $r_{c_j}$, and ξ_j), the average water depth and flow velocity at the node ($D_{ab{c}_j}$ and $U_{ab{c}_j}$, respectively), and most importantly the bifurcation parameter R_j (where β and ϑ_a are locally evaluated).

The nodal free-surface elevations for channels b and c are determined by taking advantage of the normal flow equation in a rectangular channel at the equilibrium:

$$\begin{array}{}\text{(13)}& h_{i_j}^N=h_{i_j}^L+L_{i_j}{\displaystyle \frac{q_{i_j}^{\mathrm{2}}{C}_{\mathrm{up}}^{\mathrm{2}}}{D_{i_j}^{\mathrm{3}}{C}_{i_j}^{\mathrm{2}}}}.\end{array}$$

Note that, while for a single bifurcation, the free-surface elevation $h_i^L$ at the downstream end of the ith channel branch is imposed as an input parameter, when extending the analysis to the case of a delta, it still remains known only for the terminal branches (ending order bifurcations). Importantly, in internal bifurcations, the downstream free-surface elevation $h_{i_j}^L$ is a variable of the system, since it is set equal to the nodal level of channel a in the downstream bifurcation $h_{a_{j+\mathrm{1}}}^N$. Therefore, the downstream water level asymmetry Δh^L in each bifurcation is not predetermined and is instead linked to the local length ratio γ_L.

Notably, it is assumed that the flow is confined within the channels – i.e., overbank flow is not considered – in order to isolate the fundamental mechanisms governing the equilibrium of river deltas. However, the principle of flow conservation remains largely applicable to many river deltas worldwide, like the Po River delta, where extensive human interventions, such as the widespread construction of levees, have been implemented to confine the flow within fixed banks.

Given that the delta system consists of multiple interconnected bifurcations, solving the model requires addressing 5N equations, where N is the number of bifurcations. The complexity of the system increases as the number of bifurcations grows, as each bifurcation influences downstream conditions and, conversely, is affected by upstream bifurcation outcomes. Flow partitioning at an upstream bifurcation dictates the flow distribution to subsequent branches, while free-surface elevations at downstream bifurcations feed back into the system, modifying the hydraulic conditions at earlier bifurcations.

The system allows for three potential equilibrium states at each bifurcation: (i) dominance of one branch, (ii) dominance of the other branch, or (iii) symmetric partitioning between branches. Consequently, for a delta system with N bifurcations, there are 3^N possible equilibrium configurations, each representing a unique distribution of flow and sediment throughout the delta.

This exponential growth in the number of possible equilibrium solutions highlights the intricate nature of deltaic bifurcation systems. A comprehensive analytical framework is therefore required to capture all potential equilibrium states and to understand their impact on the delta's long-term morphological and hydrodynamic evolution.

3 Competing effects on the delta equilibrium

Branch length has been identified as a critical factor influencing the stability of river bifurcations. Shorter branches tend to result in more balanced configurations, whereas longer branches can lead to highly unbalanced bifurcations or even increase the likelihood of avulsion (Salter et al., 2018; Barile et al., 2024; Durante et al., 2024).

When considering the entire delta system, the cumulative length of branches downstream of each bifurcation is a key factor in determining the system's equilibrium state. Additionally, the equilibrium of each bifurcation is affected by the distribution of these branch lengths among the downstream bifurcations. This implies that even if the total downstream length remains constant, the specific distribution of lengths among branches can result in slight variations in flow partitioning.

Figure 3 Schematic representation of an idealized river delta debouching into the sea in plan view. The delta structure comprises a primary apex bifurcation (BIF1) followed by secondary bifurcations downstream of each branch (BIF2 and BIF3).

Let's consider a delta with two second-order bifurcations, as sketched in Fig. 3.

We initially focus on the particular sub-case of a second-order bifurcation system, characterized by symmetrical branches. Hence, following notations introduced in Fig. 3, it turns out $L_{b\mathrm{1}}^{\ast }=L_{c\mathrm{1}}^{\ast }$ and $L_{b\mathrm{2}}^{\ast }=L_{c\mathrm{2}}^{\ast }$. For the sake of simplicity we thus denote $L_{\mathrm{up}}^{\ast }$ as the dimensional lengths of the primary branches of the apex bifurcation ($L_{\mathrm{up}}^{\ast }=L_{b\mathrm{1}}^{\ast }=L_{c\mathrm{1}}^{\ast }$) and $L_{\mathrm{down}}^{\ast }$ as the lengths of branches in downstream bifurcations ($L_{\mathrm{down}}^{\ast }=L_{b\mathrm{2}}^{\ast }=L_{c\mathrm{2}}^{\ast }=L_{b\mathrm{3}}^{\ast }=L_{c\mathrm{3}}^{\ast }$). The aggregate length is defined as

$$\begin{array}{}\text{(14)}& L_{\mathrm{tot}}^{\prime }=L_{\mathrm{up}}^{\prime }+L_{\mathrm{down}}^{\prime }=\left(L_{\mathrm{up}}^{\ast }+L_{\mathrm{down}}^{\ast }\right)/W_{\mathrm{up}}^{\ast },\end{array}$$

where the length is made non-dimensional by the upstream channel width of the apex bifurcation $W_{\mathrm{up}}^{\ast }$.

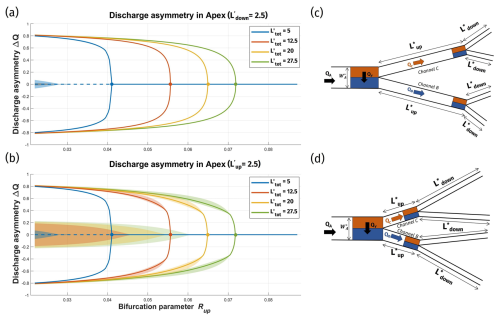
Figure 4 Equilibrium solutions for symmetrical deltas as the aggregate branch length varies. Panels (a) and (b) display the discharge asymmetry ΔQ at the apex bifurcation, plotted against the bifurcation parameter R_up for different total branch lengths $L_{\mathrm{tot}}^{\prime }$. Panel (a) presents solutions varying the primary branch lengths $L_{\mathrm{up}}^{\ast }$ (with $L_{\mathrm{down}}^{\prime }=\mathrm{2.5}$), while panel (b) shows solutions varying the downstream branch lengths $L_{\mathrm{down}}^{\ast }$ (with $L_{\mathrm{up}}^{\prime }=\mathrm{2.5}$). Each line represents the average of all the corresponding solutions for different $L_{\mathrm{tot}}^{\prime }$ values. Filled dots indicate the R_cr value for the corresponding color. The shaded area indicates the range of possible solutions for the corresponding color. Panels (c) and (d) depict the schematic configuration of the delta in the two cases. (Parameters: γ_L=1, r_a=1, r_b=0.5, ξ=0.)

Figure 4 elucidates these dynamics, showing equilibrium solutions for symmetrical deltas as the aggregate branch length varies. Results are reported by varying the upstream bifurcation parameter R_up in terms of discharge asymmetry ΔQ between the branches in the apex bifurcation as follows:

$$\begin{array}{}\text{(15)}& \mathrm{\Delta }Q={\displaystyle \frac{Q_{b\mathrm{1}}-Q_{c\mathrm{1}}}{Q_{\mathrm{up}}}},\end{array}$$

where Q_b1 and Q_c1 are the discharges in the two primary branches, and Q_up is the discharge upstream of the apex bifurcation.

Figure 4a shows the solutions when varying $L_{\mathrm{up}}^{\ast }$ while keeping $L_{\mathrm{down}}^{\ast }$ constant, whereas Fig. 4b shows the solutions when $L_{\mathrm{up}}^{\ast }$ is constant and $L_{\mathrm{down}}^{\ast }$ is varied. Figure 4c and d provide a schematic representation of the delta configurations for elongated branch lengths.

In general, for a given value of $L_{\mathrm{tot}}^{\prime }$, if R_up is higher than a critical threshold, flow is equally distributed at the bifurcation (the system admits just one possible symmetrical solution); on the contrary, when R_up is lower than the critical threshold, the balanced solution becomes unstable and the system attains a stable state where one of the two branches captures most of discharge (the system admits two equivalent solutions depending on which of the two downstream branches dominates).

It is clear that total branch length $L_{\mathrm{tot}}^{\prime }$ is a crucial factor in determining the behavior of the main apex bifurcation. Specifically, a shorter total branch length increases the number of configurations (values of R_up) that achieve equal partitioning of flow between the branches (ΔQ=0). This suggests that, as the total branch length decreases, the system tends toward a more balanced state, reducing the likelihood of unbalanced flow distributions.

An intriguing observation is that, for any given value of $L_{\mathrm{tot}}^{\prime }$, the distribution of branch lengths between the primary and second-order bifurcations does not influence the critical bifurcation parameter R_cr, where unbalanced solutions first appear. This suggests that the onset of flow asymmetry is controlled mainly by the overall length of the channel network (measured from the uppermost node to the outlet) rather than by the specific distances of the secondary bifurcation nodes from the outlet. In other words, it is the total upstream-to-outlet distance that plays a critical role in triggering flow imbalances rather than how it is distributed among the downstream channels through the delta network.

A further significant finding can be drawn from Fig. 4b, highlighting the significance of the shaded areas. When the primary branches ($L_{\mathrm{up}}^{\ast }$) are relatively short, increasing the length of the second-order downstream branches ($L_{\mathrm{down}}^{\ast }$) results in slight deviations among the solutions. Specifically, when the downstream branches remain short, the complete set of 3^N potential solutions effectively collapses to align with the three fundamental solutions, as if the apex bifurcation were solved in isolation (depicted in Fig. 4a). However, as $L_{\mathrm{down}}^{\ast }$ increases, an induced downstream-to-upstream feedback alters the upstream hydraulic conditions, permitting a range of discharge asymmetry values (ΔQ).

This phenomenon occurs because modifications in the lengths of $L_{\mathrm{down}}^{\ast }$ influence the hydraulic conditions at the downstream bifurcation nodes (i.e., nodes 2 and 3), which subsequently impact the water surface elevations. These alterations propagate upstream, affecting the free-surface slopes in the primary bifurcation branches and resulting in a spectrum of possible discharge asymmetry outcomes at the apex.

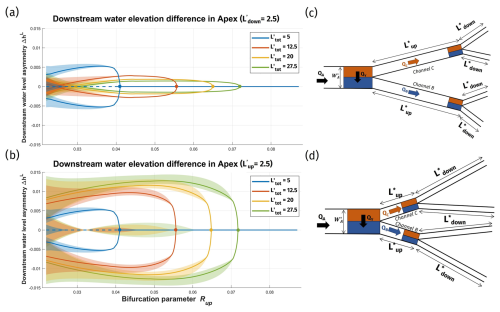
Figure 5 Variations in the parameter Δh^L for symmetrical deltas as the aggregate branch length varies. Panels (a) and (b) show the downstream water level asymmetry parameter Δh^L at the apex bifurcation plotted against the bifurcation parameter R_up for different total branch lengths $L_{\mathrm{tot}}^{\prime }$. Panel (a) presents solutions varying the primary branch lengths $L_{\mathrm{up}}^{\ast }$ (with $L_{\mathrm{down}}^{\prime }=\mathrm{2.5}$), while panel (b) shows solutions varying the downstream branch lengths $L_{\mathrm{down}}^{\ast }$ (with $L_{\mathrm{up}}^{\prime }=\mathrm{2.5}$). Each line represents the values of Δh^L for different $L_{\mathrm{tot}}^{\prime }$ values, with the shaded area indicating the range of possible values for the corresponding color. Filled dots indicate the R_cr value for the corresponding color. Panels (c) and (d) depict the schematic configuration of the delta in the two cases. (Parameters: γ_L=1, r_a=1, r_b=0.5, ξ=0.)

Figure 5 illustrates the downstream water level asymmetry parameter $\mathrm{\Delta }{h}_{\mathrm{1}}^L$ as a function of the bifurcation parameter R_up for different values of the total delta length $L_{\mathrm{tot}}^{\prime }$, corresponding to the equilibrium solution presented in Fig. 4. This parameter, which measures the differences in water elevation between the second-order nodes, is essential for understanding the hydrodynamic interactions within the delta.

In particular, Fig. 5a illustrates the case when the variation in $L_{\mathrm{tot}}^{\prime }$ is achieved by varying the primary branch lengths $L_{\mathrm{up}}^{\ast }$ and keeping $L_{\mathrm{down}}^{\ast }$ constant, while Fig. 5b refers to the opposite case, i.e., varying the downstream branch lengths $L_{\mathrm{down}}^{\ast }$ and keeping $L_{\mathrm{up}}^{\ast }$ constant.

The comparison between Fig. 5a and b shows that lengthening of downstream branches leads to an increase in Δh^L, thereby exerting a greater influence on the discharge partitioning at the upstream bifurcation.

However, river deltas rarely exhibit purely symmetric structures. Complex internal feedback mechanisms during delta formation and evolution typically produce variations in branch lengths and widths (Fagherazzi et al., 2015). These asymmetries are shaped by multiple factors, including planform geometric constraints, vegetation growth, and variations in downstream conditions. Such influences create differential sediment supply across branches, leading to uneven land construction and, consequently, differential channel lengthening and widening.

In Fig. 6, the impact of differential branch length at the apex bifurcation is analyzed by varying the total length ratio γ_L which is thus defined as $L_{c_{\mathrm{tot}}}^{\prime }/L_{b_{\mathrm{tot}}}^{\prime }$. In order to isolate this effect the second-order bifurcations are kept symmetrical and no width enlargement or differential width of primary branches is included.

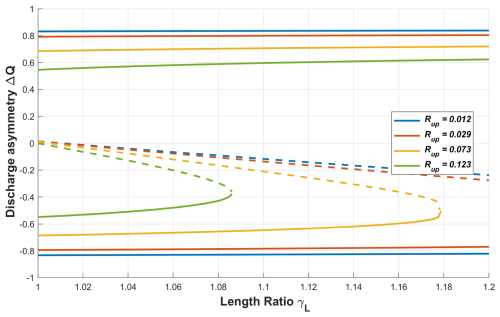
Figure 6 Discharge asymmetry in the apex bifurcation as a function of the total differential branch length ratio γ_L. The plot shows the variation in ΔQ with respect to γ_L for four different values of the upstream bifurcation parameter R_up, depicted with the corresponding color. Solid lines represent stable solutions with dominant flow in one branch, while dashed lines indicate the unstable solution. (Parameters are r_b=0.5, r_a=1, $L_{\mathrm{tot}}^{\prime }=\mathrm{90}$, ξ=0.)

An increase in γ_L results in branch c attaining a greater length relative to branch b, thereby enhancing the flow partition in favor of branch b. Conversely, intermediate solutions and those favoring branch c become less favorable with increasing γ_L. This occurs because longer branches are associated with a lower free-surface gradient, which reduces their sediment transport capacity and promotes sediment accumulation. Moreover, for a given value of R_up, if the length ratio is sufficiently large, the dominance of the shorter branch becomes the only possible solution. Therefore, there are threshold conditions for high values of γ_L and R_up where no switch in dominance can be found.

Another characteristic feature of bifurcations in river deltas is the differential width partition between branches. Typically, the dominant branch in natural deltas exhibits a larger width compared to the branch with lower flow. This geometrical feature is incorporated in the model through the branch width ratio r_b.

For symmetrical lengths and no width enlargement at the apex bifurcation (i.e., γ_L=1 and r_a=1), by defining r_b as $W_{b\mathrm{1}}/W_{\mathrm{up}}$, increasing r_b signifies widening the primary branch b and narrowing the other branch. In Fig. 7, this effect is isolated while maintaining symmetrical bifurcations downstream.

Figure 7 illustrates the variations in r_b from symmetry (i.e., $r_b=r_a/\mathrm{2}=\mathrm{0.5}$) to a highly asymmetrical state where branch b attains 90 % of the upstream width across three different values of the upstream bifurcation parameter R_up. For the dominant branch, the discharge partitioning remains relatively unaffected by variations in r_b. However, the intermediate unstable solution shows an increase in discharge through branch b as r_b increases, eventually achieving almost the same partitioning as the dominant branch solution. More interestingly, for the scenario where the narrower branch is dominant, the system tends towards the complete closure of the larger branch as r_b increases. Beyond a certain threshold value of r_b, the solution that advantages the narrower branch ceases to exist, indicating that for high values of r_b, only solutions where the larger branch is dominant are feasible. The bifurcation parameter R_up does not significantly impact the results, except that higher values of R_up are associated with less unbalanced configurations.

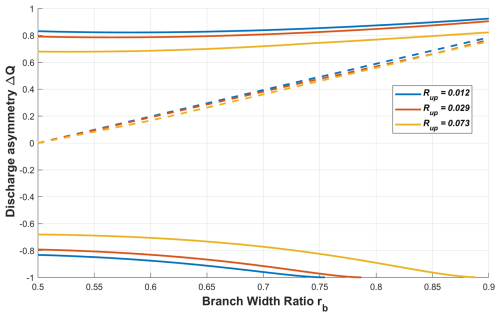
Figure 7 Discharge asymmetry in the apex bifurcation as a function of the branch width ratio r_b. The plot shows the variation in ΔQ with respect to r_b for three different values of the upstream bifurcation parameter R_up, depicted with the corresponding color. Solid lines represent stable solutions with dominant flow in one branch, while dashed lines indicate the unstable solution. (Parameters γ_L=1, r_a=1, $L_{\mathrm{tot}}^{\prime }=\mathrm{50}$, ξ=0.)

4 Equilibrium configurations of the Po River Delta

The Po River is Italy's longest river. It extends over 652 km and drains an area of approximately 71 000 km². Flowing from west to east across northern Italy, the river ultimately discharges into the Adriatic Sea through a delta located several kilometers south of the Venice Lagoon. Within its deltaic system, the Po River's main channel, known as the Po di Venezia, undergoes four morphodynamically active bifurcations, generating four distributary branches as illustrated in Fig. 1b. Specifically, the main channel successively encounters the Po di Goro, Po di Gnocca, Po di Maistra, and Po di Tolle bifurcations as it progresses downstream. Prior to reaching the Adriatic Sea, the primary river channel terminates in three distinct mouths within the Po Delta lagoons, namely Busa di Dritta, Busa di Tramontana, and Busa di Scirocco.

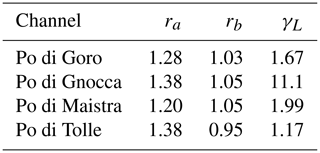
The Po di Venezia carries the majority of the upstream discharge under all flow conditions, and, to accommodate this, it attains a larger width compared to the secondary branches. The average width and length of each channel in the delta are detailed in Table 1, while the average width of the upstream channel at the apex is 370 m.

Table 1 Dimensions of channels in the Po Delta. The upper section lists the secondary branches, while the lower section presents the channels composing the main stem (Po di Venezia).

The local asymmetry parameters for each bifurcation have been quantitatively assessed, with the respective values provided in Table 2. Notably, a downstream enlargement is evident at each bifurcation within the delta, consistent with the data reported by Barile et al. (2023). Furthermore, the branch width ratio r_b exhibits significant asymmetry across all bifurcations, with the most pronounced asymmetry occurring at the Maistra bifurcation.

Table 2 Asymmetry parameters for the bifurcations in the Po Delta.

The delta model employed in this study is calibrated to the current geometric configuration of the Po River Delta down to the Tolle bifurcation. Beyond this point, the model does not reliably capture the morphodynamics of the Po Delta lagoons. As such, downstream of the Tolle bifurcation, the main stem is modeled as debouching primarily through the central mouth, i.e., the Busa di Dritta. Therefore, given the sequence of four bifurcations, the system theoretically offers 81 potential equilibrium solutions.

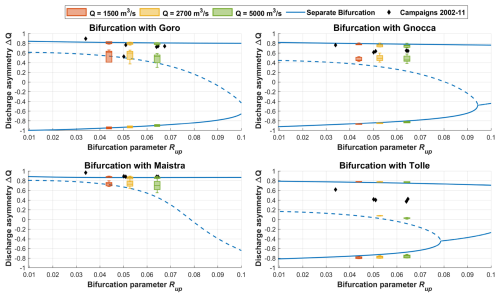
Figure 8 Equilibrium discharge asymmetry ΔQ as a function of bifurcation parameter R_up for each bifurcation in the Po Delta (Goro, Gnocca, Maistra, and Tolle), listed in order from the apex progressing downstream. Boxplots represent model results at upstream discharges of 1500 m³ s⁻¹ (orange), 2700 m³ s⁻¹ (yellow), and 5000 m³ s⁻¹ (green). Solid and dashed blue lines indicate predictions from the separate bifurcation model by Durante et al. (2024). Field data from 2002–2011 are marked by black diamonds.

The equilibrium solutions are reported in Fig. 8 in terms of discharge asymmetry ΔQ displayed for each bifurcation progressing downstream of the apex bifurcation. Model outputs are depicted using boxplots to illustrate the variability in each equilibrium solution due to internal feedback mechanisms within the deltaic system. Results are provided for three distinct upstream discharge values $Q_{\mathrm{up}}^{\ast }$ (or R_up), differentiated by color within the boxplots to represent the flow distribution under conditions representative of formative, reduced, and elevated discharges of the delta (2700, 1500, and 5000 m³ s⁻¹, respectively).

Additionally, leveraging the prior finding that the overall branch length serves as a primary determinant of equilibrium configurations across delta bifurcations, results from this study are compared with those of the single-bifurcation model proposed by Durante et al. (2024). To facilitate this comparison, internal feedback mechanisms are disregarded, and the branches are assumed to discharge directly into the sea. Therefore, the length of each bifurcation's branches is calculated by adding the average length of the downstream branches to the corresponding length of the Po di Venezia reported in the lower section of Table 1. Despite the necessary simplifications, both models demonstrate good alignment with observed discharge partitioning data for the Po Delta from 2002 to 2011 (Zasso and Settin, 2012).

Interestingly, neither the delta model nor the separate bifurcation model can produce equilibrium configurations that exhibit the dominance of the Maistra branch (i.e., ΔQ<0). This result is consistent with the high asymmetry of this bifurcation, as indicated in Table 2 and illustrated by threshold conditions in Fig. 7.

Notably, at the downstream-most bifurcation with Po di Tolle, model results show less agreement with field measurements. This discrepancy is likely due to the model's simplification in representing only one of the three main distributary mouths of the Po di Venezia, omitting the additional discharge redistribution across these channels and the associated delta lagoons. These complex hydro-morphodynamic interactions are not included in the current model formulation.

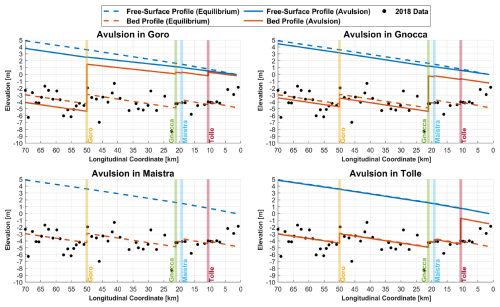
Figure 9 Equilibrium bed and free-surface profiles along the Po Delta main stem (Po di Venezia) under the formative discharge of 2700 m³ s⁻¹, with avulsion scenarios at each bifurcation (Goro, Gnocca, Maistra, and Tolle). Dashed lines indicate equilibrium profiles; solid lines show profiles post-avulsion. Black dots represent cross-sectional bed elevations from 2018. Colored vertical lines mark bifurcation locations.

The model enables delineation of free-surface and bed profiles along all delta channels. Considering the formative discharge upstream of 2700 m³ s⁻¹, it predicts the equilibrium profiles that conform to the current delta geometry. Figure 9 shows the equilibrium profile of the main stem of the Po Delta (Po di Venezia) alongside cross-sectional averaged bed-level data from 2018. Despite variability due to natural channel width fluctuations, the model accurately captures bed slopes in each channel, evaluating the flow discharge diverted into the secondary branches (whose location is represented with colored vertical lines). Notably, the seaward 5 km is not accurately captured, since the flow is dispersed across all the mouths and the hypothesis of constant width channel is certainly not met.

Since the equilibrium analysis includes all configurations with potential dominance shifts at each bifurcation, each subplot of Fig. 9 also shows bed profiles for hypothetical avulsion events at each bifurcation. As previously discussed, the avulsion in the Po di Maistra was never found within this framework.

The switch in dominance towards secondary branches would lead to a substantial deposition in the main stem, thereby affecting navigability downstream. In contrast, significant erosion is anticipated in the secondary branch to accommodate the increased discharge. Furthermore, avulsions in any branch would alter the free-surface slope, consequently impacting the elevation at the upstream boundary. Notably, an avulsion in the Po di Goro branch could lower the free-surface elevation at the bifurcation node by approximately 1 m, with potential upstream consequences resulting from the associated bed erosion.

5 Discussions

River deltas are complex systems subject to a multitude of dynamic and continuously varying forcings. Both upstream discharge and downstream water levels are increasingly influenced by extreme low and high conditions, a trend that is being exacerbated by climate change. In addition, the morphology of river deltas is constantly evolving due to a combination of anthropogenic interventions and natural processes. These include channel widening resulting from bank collapse and modifications in channel length driven by variations in sediment supply. Vegetation also plays a critical role in stabilizing banks and mouth bars within prograding deltas, primarily through root systems and the trapping of suspended sediments.

Therefore, it is important to acknowledge that the proposed model relies on the concept of equilibrium and is not designed to predict the temporal evolution of the system. In order to have an idea of the order of magnitude of the temporal scale over which the system evolves, the morphological timescale T_M can be called upon (Seminara et al., 2024):

$$\begin{array}{}\text{(16)}& T_{\mathrm{M}}=(\mathrm{1}-p){\displaystyle \frac{W_{\mathrm{up}}^{\ast }{D}_{\mathrm{up}}^{\ast }}{q_{s_{\mathrm{up}}}^{\ast }}}.\end{array}$$

Under these dynamic conditions, a state of long-term morphodynamic equilibrium may never be achieved in river deltas. This notwithstanding, models based on the equilibrium concept remain a useful approach for identifying which processes – and usually which negative feedback mechanisms – dominate the system (Zhou et al., 2017).

Nonetheless, the model presented in this study offers simplicity and computational efficiency, facilitating the exploration of key factors that influence flow and sediment distribution at each bifurcation. This model also enables the prediction of evolutionary trends for a given deltaic configuration. Variations in input parameters or planform geometry can be easily incorporated into the model, allowing for an assessment of their impacts on the system's equilibrium. Consequently, the evolutionary trajectory of the delta can be interpreted as a sequence of quasi-equilibrium states.

The analysis of idealized river deltas provides insights into the fundamental mechanisms underlying bifurcation evolution. By isolating specific geometric variations or asymmetries inherent in natural deltas, the model helps identify the key factors controlling discharge partitioning and the potential formation of bed-level differences at each bifurcation.

5.1 Internal bifurcation feedback

As widely recognized in the literature (Salter et al., 2018; Ragno et al., 2020; Barile et al., 2024; Durante et al., 2024), the length of the branches is a critical determinant in establishing the equilibrium solution of riverine bifurcations. However, in the context of river deltas, the sequential nature of bifurcations introduces additional complexities. These complexities complicate the estimation of the equilibrium configuration, which cannot be determined solely based on the overall branch lengths but must also account for internal asymmetries within the delta.

Our findings indicate that the total branch length, $L_{\mathrm{tot}}^{\prime }$, plays a critical role in determining the extent of flow partitioning imbalance between branches. Shorter branches tend to result in a more balanced flow distribution. Intriguingly, regardless of the length distribution in downstream bifurcations, the critical conditions distinguishing between balanced and unbalanced upstream bifurcations are primarily governed by $L_{\mathrm{tot}}^{\prime }$. The fact that the distribution of downstream branch lengths does not affect the critical bifurcation parameter R_cr suggests that computing single bifurcations separately, as if they directly discharge into the sea, may offer a faster yet reliable prediction method.

However, feedback between bifurcations remains significant. As illustrated in Fig. 4b, the possible equilibrium configurations are influenced by differences in downstream water levels at the primary branches. Figure 5 depicts the downstream water level asymmetry parameter, Δh^L, at the apex bifurcation for each equilibrium solution shown in Fig. 4. Notably, when the primary branches are relatively short, an increase in Δh^L directly impacts the upstream bifurcation. In other words, the hydraulic gradient in the primary branches is affected by downstream conditions, leading to slight variations in flow distribution. As also found by Edmonds and Slingerland (2008), the water elevation at the bifurcation can originate a backwater effect that could propagate the perturbation further upstream in the delta.

It is important to note that these considerations are influenced by the assumption of uniform flow in the branches, particularly when width variations are not accounted for. The free-surface profile is significantly affected by flow conditions, leading to potential variations in water elevation at the nodes, especially when branches are short. This factor will be addressed in future research.

5.2 System planimetric effects

Despite the intrinsic internal feedback being intriguing, naturally forced planimetric asymmetries exert a higher influence on the overall evolution of the system. The specific evolutionary dynamics during each bifurcation formation within river deltas are highly influenced by external forcings or planimetric constraints, which lead to asymmetrical branch lengths and widths.

The results presented in Fig. 7 yield significant insights: when the width differential between the downstream branches is constrained, solutions exist where both branches may exhibit dominance. However, as the differential increases (i.e., as r_b approaches r_a), the system converges to a single solution in which the wider branch conveys the majority of the flow. This phenomenon could serve as a foundation for explaining channel abandonment in naturally evolving deltas. In particular, conditions may develop where one branch widens at the expense of the other, which narrows due to sediment deposition. Under steady-state conditions, the model indicates that beyond a critical threshold for r_b, the narrowing branch loses its ability to dominate the flow. Nevertheless, the model does not capture the influence of potential external triggering events that could induce abrupt geometric changes in the system, leading to modified hydrodynamic regimes and alternative flow configurations.

A similar behavior is observed when there is a differential in branch length. Generally, the shorter branch carries more water relative to its longer counterpart due to a higher gradient in the free surface. However, when the length differential is not substantial (i.e., for values of γ_L close to 1), instances where the longer branch dominates may still occur, as depicted in Fig. 6. Nonetheless, above a certain threshold γ_L, based on the characteristic parameters of the system, the only possible solution is one where the shorter branch dominates.

This mechanism underlies river delta avulsion: during the early stages of delta formation and subsequent progradation, as new bifurcations emerge, flow is distributed relatively evenly across the branches, maintaining a radially symmetric deltaic structure. As long as the length differential is limited, both branches of a bifurcation may alternately carry a higher discharge. Even in prograding branches, Salter et al. (2018) observed that internal feedbacks can sustain alternating dominance between branches, a process known as “soft avulsion”. However, as branches elongate, they become less responsive to hydrodynamic variations, amplifying the length differential and leading to the dominance of the shorter branch, potentially culminating in the complete closure of the longer one.

5.3 Po River Delta application

The intriguing observations obtained with the presented delta model lead us to question whether multiple solutions may exist in real-world deltas. The application to the Po River Delta allowed us to estimate the current equilibrium configuration.

The system, characterized by a sequence of four bifurcations, theoretically permits up to 81 possible equilibrium states. However, due to the pronounced geometric asymmetries detailed in Table 2, many of these theoretical states are unattainable within the Po River Delta. This limitation arises from the threshold conditions, as illustrated in Fig. 7, which reduce the number of physically feasible equilibrium solutions. Specifically, because the Po di Maistra branch is substantially narrower than the Po di Venezia, the model does not predict an avulsion event at this bifurcation. This outcome remains reasonable within the model framework, as such a sudden reorganization of the delta would necessitate substantial width adaptation, which is beyond the current model's scope.

Nonetheless, a comparison with field measurements of discharge partitioning under various flow regimes in the Po River Delta, as shown in Fig. 8, indicates that the delta's present state aligns closely with an equilibrium where the primary channel, Po di Venezia, maintains dominance. The further comparison of model-derived bed profiles, established under formative conditions, with 2018 mean bed-level data (Fig. 9) reinforces these findings.

Historical bathymetric data indicate that mean bed levels within the delta branches have, in recent years, reverted to mid-20th century values, following adjustments to accommodate anthropogenic impacts such as upstream dam construction, sediment extraction, and increased subsidence due to groundwater extraction. Evidence of a renovated equilibrium across many reaches of the Po River along its basin supports renewed sediment continuity, resulting in a greater sediment load reaching the delta. Given the aforementioned observations regarding the current equilibrium configuration of the delta, together with the channelization of the delta branches, sediment is transported efficiently to the delta front rather than contributing to natural subsidence compensation within the delta plain. Recent satellite image analyses by Ninfo et al. (2018) further corroborate this trend, showing evidence of progradation along the main stem of the Po Delta.

Historical records show that the Po di Goro has doubled its flow capture over the past century, now accounting for approximately 15 % of the total upstream discharge, likely due to its shorter length relative to the main stem. Given the larger sediment supply along the main stem of the Po River, it is likely that progradation at Po di Venezia will remain at a faster rate than that occurring at the Po di Goro mouth; hence the probability of avulsion at this bifurcation is expected to increase substantially in the coming decades.

Accordingly, the proposed model has also identified alternative equilibrium configurations without accounting for the lengthening of Po di Venezia, which would enable possible avulsion at each bifurcation. Assuming no major changes to delta planform geometry, Fig. 9 suggests that even the free-surface profile would be impacted by an upstream avulsion, particularly near the Po di Goro bifurcation. In such a scenario, the main channel's free-surface slope would be altered, lowering the upstream elevation by approximately 1 m, with significant implications for navigability and downstream infrastructure along the Po di Venezia. Most critically, a resulting backwater effect would influence upstream profiles, severely impacting the bed equilibrium profile, infrastructure stability, and levee integrity.

5.4 Limitations and future perspectives

The model presented in this study is based on a few simplifying assumptions. First, variations in channel width along each branch are not considered. Incorporating this aspect would enhance the accuracy of bed elevation representation at each cross section, as demonstrated for the Po River upstream of the delta apex by Lanzoni et al. (2015). Nevertheless, while the model does not capture riverbed oscillations associated with width variations, its current formulation effectively predicts the average bed slope along each branch. The incorporation of variable river width can be readily implemented in future extensions of the model.

Second, the present configuration of the delta network is based on a series of bifurcations. Future model developments will account for flow exchanges between branches, through either confluences or connecting channels, to better represent real-world delta networks (Ragno et al., 2021; Gao et al., 2024).

Finally, the current model does not consider flow connectivity with the delta floodplain, a characteristic commonly observed in natural deltas (Hiatt and Passalacqua, 2015; Hiatt et al., 2018; Olliver and Edmonds, 2021). The inclusion of lateral flow dispersal would primarily lead to a reduction in flow velocity within the channels, potentially promoting localized sediment deposition. However, the assumption of flow conservation remains valid for many river deltas worldwide, such as the Po River Delta, where flow is predominantly confined within the channels (Correggiari et al., 2005; Syvitski et al., 2005; Simeoni and Corbau, 2009). This assumption becomes less applicable in the seaward reaches of the Po River Delta (notably along the Tolle branch and the main channel), where observed discrepancies in flow partitioning and bed elevation estimations are likely due to overbank flow. To enhance the model's applicability to more natural deltaic systems, lateral outflow from channels to delta islands will be incorporated.

The representation of such complex processes (Passalacqua, 2017; Hiatt and Passalacqua, 2017) must be simplified when addressing the morphodynamic equilibrium of these systems. Consequently, lateral outflow may be modeled as either localized or distributed losses. The latter approach would require explicitly solving for both the bed and free surface within each delta channel. However, implementing such modifications requires careful consideration when addressing the long-term equilibrium of the system. A preliminary assessment of these contributions could be guided by site-specific field studies. Nevertheless, directly integrating such measurements into the model would necessitate assuming their long-term constancy, an assumption that remains highly uncertain, particularly in young and actively prograding deltas.

6 Conclusions

This study advances the understanding of equilibrium dynamics in river-dominated deltas through a novel analytical model that underscores the role of internal feedback mechanisms within each deltaic bifurcation. The model effectively forecasts alternative equilibrium solutions and has identified likely avulsion sites in highly engineered deltas, with major implications for variations in bed-level and free-surface elevation.

The application of the model to the Po River Delta has enabled the identification of a set of equilibrium configurations that best align with the measured flow discharge partitioning and the average bed elevation along the various delta branches. This exercise proved insightful, demonstrating that several alternative equilibrium configurations are possible, each characterized by flow discharge partitioning values significantly different from those currently observed. Furthermore, the study revealed that abrupt shifts from the present configuration to highly asymmetrical states in each bifurcation of the Po River Delta could result in substantial sediment deposition downstream, erosion upstream, and variations in free-surface elevation. Such new equilibrium configurations, which would reduce flow discharge in the current main stem, are likely to have substantial consequences for downstream anthropogenic activities, including navigation, fisheries, and agriculture. Additionally, backwater effects could compromise the stability of upstream infrastructure.

These findings highlight the intricate interplay between fluvial and sedimentary processes, suggesting that future delta management strategies should consider internal feedbacks to enhance resilience against changing environmental pressures.

However, the assumption of cylindrical channels in the model presents limitations when compared to field data on bed levels. To better align with these data and refine insights into delta equilibrium, future work will adapt the model to incorporate variations in channel width.

In extending predictive capabilities, this research lays a foundation for more precise and sustainable approaches to delta conservation and management.

Appendix A: Derivation of the nodal point condition

The transverse solid exchange is evaluated based on the procedure for describing two-dimensional bed load transport over an inclined bed (Ikeda et al., 1981):

$$\begin{array}{}\text{(A1)}& q_{\mathrm{T}s}^{\ast }=q_{as}^{\ast }\left[{\displaystyle \frac{V^{\ast }}{\sqrt{U^{\ast \mathrm{2}}+V^{\ast \mathrm{2}}}}}-{\displaystyle \frac{r}{\sqrt{{\mathit{\vartheta }}_a}}}{\displaystyle \frac{\partial {\mathit{\eta }}^{\ast }}{\partial y^{\ast }}}\right],\end{array}$$

where dimensional variables are denoted with the superscript ^∗. Specifically, $q_{\mathrm{T}s}^{\ast }$ represents the dimensional transverse solid discharge per unit width, and $q_{as}^{\ast }$ denotes the longitudinal solid flow discharge per unit width from upstream. U^∗ and V^∗ are the longitudinal and transverse velocity components, respectively. $\partial {\mathit{\eta }}^{\ast }/\partial y^{\ast }$ denotes the transverse bed slope at the junction of channels b and c. The parameter r is an experimental constant that ranges between 0.3 and 1 (Ikeda et al., 1981; Talmon et al., 1995). The Shields parameter, ϑ_a, associated with the uniform flow is defined as

$$\begin{array}{}\text{(A2)}& {\mathit{\vartheta }}_a={\displaystyle \frac{Q_a^{\ast \mathrm{2}}}{\frac{{\mathit{\rho }}_{\mathrm{s}}-\mathit{\rho }}{\mathit{\rho }}g{d}_{\mathrm{s}}^{\ast }{C}_a^{\mathrm{2}}{D}_a^{\ast \mathrm{2}}{W}_a^{\ast \mathrm{2}}}},\end{array}$$

where $Q_a^{\ast }$ is the upstream flow discharge; ρ_s and ρ are the densities of sediment and water, respectively; g is the gravitational acceleration; $d_{\mathrm{s}}^{\ast }$ is the sediment diameter; C_a is the Chézy coefficient; $D_a^{\ast }$ is the flow depth; and $W_a^{\ast }$ is the channel width.

The velocity magnitude $\sqrt{U^{\ast \mathrm{2}}+V^{\ast \mathrm{2}}}$ is evaluated as the average flow velocity $U_{abc}^{\ast }$ within the cells length $\mathit{\alpha }{W}_a^{\ast }$, while the transverse velocity V^∗ can be computed as

$$\begin{array}{}\text{(A3)}& V^{\ast }={\displaystyle \frac{Q_T^{\ast }}{\mathit{\alpha }{W}_a^{\ast }{D}_{abc}^{\ast }}}.\end{array}$$

Specifically, the average water depth at the bifurcation $D_{abc}^{\ast }$ is defined as

$$\begin{array}{}\text{(A4)}& \begin{array}{rl}{D}_{abc}^{\ast }& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(D_a^{\ast }+{\displaystyle \frac{D_b^{\ast }+D_c^{\ast }}{\mathrm{2}}}\right)\\ & =D_{\mathrm{up}}^{\ast }{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(D_a+{\displaystyle \frac{D_b+D_c}{\mathrm{2}}}\right)=D_{\mathrm{up}}^{\ast }{D}_{abc}.\end{array}\end{array}$$

In a similar fashion, $U_{abc}^{\ast }$ is defined as

$$\begin{array}{}\text{(A5)}& \begin{array}{rl}{U}_{abc}^{\ast }& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(U_a^{\ast }+{\displaystyle \frac{U_b^{\ast }+U_c^{\ast }}{\mathrm{2}}}\right)\\ & =U_{\mathrm{up}}^{\ast }{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(U_a+{\displaystyle \frac{U_b+U_c}{\mathrm{2}}}\right)=U_{\mathrm{up}}^{\ast }{U}_{abc},\end{array}\end{array}$$

where $U_{\mathrm{up}}^{\ast }$ can be rewritten as $\frac{Q_{\mathrm{up}}^{\ast }}{D_{\mathrm{up}}^{\ast }{W}_{\mathrm{up}}^{\ast }}$. Noteworthy, each water depth D_i and flow velocity U_i are retrieved following the scalings introduced in Eq. (6).

Furthermore, the transverse bed slope between the branches $\partial {\mathit{\eta }}^{\ast }/\partial y^{\ast }$ is defined as the bed-level difference at the central point of the inlet of the downstream channels:

$$\begin{array}{}\text{(A6)}& \begin{array}{rl}{\displaystyle \frac{\partial {\mathit{\eta }}^{\ast }}{\partial y^{\ast }}}& ={\displaystyle \frac{{\mathit{\eta }}_b^{\ast }-{\mathit{\eta }}_c^{\ast }}{\frac{W_b^{\ast }}{\mathrm{2}}+\frac{W_c^{\ast }}{\mathrm{2}}}}={\displaystyle \frac{\mathrm{2}{D}_{\mathrm{up}}^{\ast }}{W_a^{\ast }{r}_a}}\left({\mathit{\eta }}_b-{\mathit{\eta }}_c\right)\\ & ={\displaystyle \frac{\mathrm{1}}{\mathit{\beta }{r}_a}}\left(h_b-h_c-D_b+D_c\right),\end{array}\end{array}$$

where the scaling ${\mathit{\eta }}_i=\frac{{\mathit{\eta }}_i^{\ast }}{D_{\mathrm{up}}^{\ast }}$ has been applied and the bed elevation has been derived from ${\mathit{\eta }}_i=h_i-D_i$. Moreover, r_a is the downstream enlargement parameter, and β is the aspect ratio of the upstream channel defined as

$$\begin{array}{}\text{(A7)}& \mathit{\beta }={\displaystyle \frac{W_a^{\ast }}{\mathrm{2}{D}_{\mathrm{up}}^{\ast }}}.\end{array}$$

Therefore, after a few manipulations and recalling the scaling in Eq. (6) the nodal point condition can be written as

$$\begin{array}{}\text{(A8)}& q_{\mathrm{T}s}={\displaystyle \frac{q_T}{D_{abc}{U}_{abc}}}-{\displaystyle \frac{r}{\mathit{\beta }\sqrt{{\mathit{\vartheta }}_a}{r}_a}}\left(h_b-h_c-D_b+D_c\right).\end{array}$$