Short communication: A semiautomated method for bulk fault slip analysis from topographic scarp profiles

Manual approaches for analyzing fault scarps in the field or with existing software can be tedious and time-consuming. Here, we introduce an open-source, semiautomated, Python-based graphical user interface (GUI) called the Monte Carlo Slip Statistics Toolkit (MCSST) for estimating dip slip on individual or bulk fault datasets that (1) makes the analysis of a large number of profiles much faster, (2) allows users with little or no coding skills to implement the necessary statistical techniques, (3) and provides geologists with a platform to incorporate their observations or expertise into the process. Using this toolkit, profiles are defined across fault scarps in high-resolution digital elevation models (DEMs), and then relevant fault scarp components are interactively identified (e.g., footwall, hanging wall, and scarp). Displacement statistics are calculated automatically using Monte Carlo simulation and can be conveniently visualized in geographic information systems (GISs) for spatial analysis. Fault slip rates can also be calculated when ages of footwall and hanging wall surfaces are known, allowing for temporal analysis. This method allows for the analysis of tens to hundreds of faults in rapid succession within GIS and a Python coding environment. Application of this method may contribute to a wide range of regional and local earthquake geology studies with adequate high-resolution DEM coverage, enabling both regional fault source characterization for seismic hazard and/or estimating geologic slip and strain rates, including creating long-term deformation maps. ArcGIS versions of these functions are available, as well as ones that utilize free, open-source Quantum GIS (QGIS) and Jupyter Notebook Python software.

1 Introduction

The field of tectonic geomorphology is increasingly employing computer-based algorithms for displaying and analyzing digital topographic data (Whittaker et al., 2008; Kirby and Whipple, 2012; Zhou et al., 2015; Whipple et al., 2016). As a result, broad-scale tectonic geomorphology toolboxes for automated high-level stream channel analysis and landscape evolution have been rapidly evolving (e.g., TopoToolbox, Topographic Analysis Kit (TAK), Stream Channel, and Floodplain Metric Toolbox) (Whipple et al., 2007; Schwanghart and Scherler, 2014; Hopkins et al., 2018; Forte and Whipple, 2019). Several relatively complete and distinct sets of computational tools and libraries also exist for completing an array of complex topographic and fault zone analysis at the fault zone and outcrop scale (e.g., SPARTA, Structure-from-Motion) (Westoby et al., 2012; Bemis et al., 2014; Hodge et al., 2019), including those that attempt to resolve the full 3-D slip vector (Mackenzie and Elliot, 2017).

These toolboxes are important because fault zones can be extraordinarily complex and require methods for systematically estimating net slip and slip rates across them (Fossen and Rotevatn, 2016). Where original landform geometries are known or can be inferred, fault scarp profiles from GPS surveys or transects across high-resolution digital elevation models (DEMs) can be used to characterize components of fault slip (DeLong et al., 2010; Spencer, 2010; Klimczak et al., 2018). The deformation within these fault zones can be spatially and temporally variable, thus motivating the analysis of large numbers of faults over broad areas (Wallace, 1977; Avouac, 1993; Villamor and Berryman, 2001; Personius et al., 2017; Pérouse and Wernicke, 2017). In most cases, where along-strike variability in slip and/or slip rate are observed, multiple measurements from the same fault are required to delineate the slip history of one feature.

Light detection and ranging (lidar) can be used to identify submeter-scale geomorphic features (Dong, 2015). Currently, this is done by analyzing individual profiles across fault scarps, manually picking fault components on distance vs. elevation plots, calculating statistics and regressions for each, and then running unique analyses for each profile, which is both tedious and time-consuming.

In this paper we introduce a new Python-based graphical user interface (GUI), the Monte Carlo Slip Statistics Toolkit (MCSST), that streamlines and improves on the approach for calculating slip statistics from fault scarps present in high-resolution digital elevation models (DEMs). We describe the basic functionality of MCSST and provide a representative example of the potential utility of this approach for selecting and analyzing fault scarps across a 25 km wide transect of distributed normal faulting. Using this approach, hundreds of profiles can be analyzed in a few hours, allowing for the efficient analysis of spatial and temporal patterns of deformation. The methodology also allows for easy visualization of slip statistics on the original fault profiles in geographic information system (GIS) so that spatial patterns of fault slip can be identified and anomalous values quickly identified and interrogated. A detailed user manual that lays out step-by-step usage of these tools and discusses how the underlying functions and algorithms work is included as a Supplement and within the code repository.

2 Background

The concept and mathematics behind using a Monte Carlo approach to calculating dip slips were developed by Thompson et al. (2002). The motivation behind using this approach is that it accounts for uncertainty in key parameters required for calculating slip from structural data and topographic profiles (Fig. 1). Regression statistics are calculated for lines fit to the hanging wall, scarp, and footwall. Each line has a mean value of slope and y intercept, with 95 % confidence intervals for each component, and can thus be modeled as a normal distribution. The fault dip can be modeled as any type of distribution depending on how well constrained the values are (Fig. 1). For example, if fault dips can be measured in adjacent outcrops, it may be most appropriate to model the value as a normal distribution with a mean and 95 % confidence interval; if dip is constrained only by regional fault geometry data, the user may choose a uniform or trapezoidal distribution to reflect the additional epistemic uncertainty (Fig. 1). In the simplest case, the only other parameter required to calculate dip slip is the location of the fault projected up to the scarp.

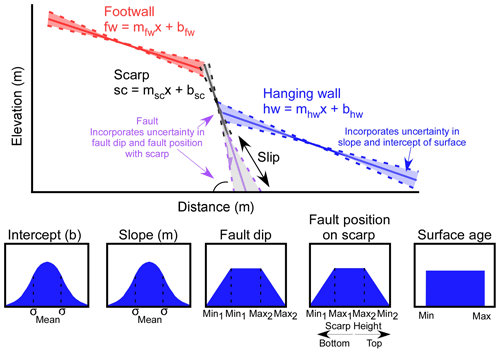
Figure 1 Slip statistics inputs. A schematic of inputs into the Monte Carlo Slip Statistics code, which include uncertainty in intercept, slope, fault dip, fault position on scarp, and the age of the geologic surface in question. For surface age, a uniform distribution is shown; however, the user could define a normal or trapezoidal distribution as well. Symbols used in the figure include slope (m), intercept (b), hanging wall (hw), footwall (fw), and position (x).

This approach has been widely used on dip slip faults around the world (Thompson et al., 2002; Amos et al., 2010; Rood et al., 2011; Stahl et al., 2016; Stahl and Niemi, 2017). Thompson et al. (2002) first used their method to quantify slip rate variability in a transect across the Tian Shan of Kyrgyzstan. Amos et al. (2010) showed that it could be used to identify previously unrecognized offsets along the Kern Canyon fault in eastern central California, highlighting its role in accommodating internal deformation of the southern Sierra Nevada. Rood et al. (2011) analyzed a suite of geomorphic markers along the transition from the Sierra Nevada to the Eastern California Shear Zone–Walker Lane Belt to reveal interactions among multiple faults. Stahl et al. (2016) used manually surveyed GPS profiles along the Fox Peak fault in New Zealand to demarcate segment boundaries based on slip rate. Stahl and Niemi (2017) compared manually surveyed fault scarps to geodetic estimates of strain in the Sevier Desert, Utah, to discern a local magmatic vs. far-field tectonic extension regime along the Wasatch Front. The broad interest in calculating slip statistics from fault scarps around the world, and the increasing access to high-resolution DEMs and powerful coding environments, motivates our development of a semiautomated toolkit for analyzing bulk fault datasets.

The primary goals of creating the MCSST are to (1) lower the barrier to entry for scientists by limiting the required knowledge of coding languages or general programming techniques; (2) allow the user to check for consistency and accuracy in their interpretations of fault components (e.g., fault scarp, hanging wall, and footwall) before proceeding with the slip statistics calculations; (3) optimize the functionality of GIS environments by combining previously created plugins when possible; (4) introduce a methodology for efficiently analyzing numerous fault scarps and delineating distributions of spatial and temporal patterns for slip statistics; and (5) provide open-source software for those who do not have access to commercial products. We reference hanging wall and footwall throughout because this code was developed for use in a rift setting; however, upthrown and downthrown are equally viable terms considering the underlying math should be consistent for reverse faults as well.

MCSST was designed to leverage the power and broad code base of the open-source Quantum GIS (QGIS) plugin environment. It also utilizes the key data manipulation and visualization tools developed for comma-separated value (CSV) file formats analyzed in the Jupyter Notebook Python coding environment. Free, open-source applications, such as QGIS and Jupyter Notebook, provide increased access and functionality for scientific computing and displaying and analyzing spatial datasets. We also provide a version compatible with ArcGIS.

3 Workflow

3.1 Define fault scarp profiles in QGIS or ArcGIS and extract data

The user first defines profiles across fault scarps imaged in high-resolution digital elevation models with UTM coordinates. Profiles are defined on a vertical plane normal to the structural trend of the fault. For each profile, distance and elevation (and optionally, geologic age) data are extracted at a user-defined spacing interval chosen to adequately resolve the vertical offset across the fault.

3.2 Monte Carlo Slip Statistics Toolkit (MCSST)

Automated methods of extracting fault scarp components have shown that mathematically identifying inflection points in a profile is often not adequate (Gallant and Hutchinson, 1997; Hilley et al., 2010; Stewart et al., 2018; Hodge et al., 2019). Therefore, the input of a geologist is needed to analyze each fault scarp, and our methodology makes this as easy as possible.

Within the Jupyter Notebook Python coding environment, the MCSST is used to analyze each profile. Profiles are loaded individually and then interactively displayed continuously to identify relevant fault scarp components (e.g., footwall, hanging wall, and scarp) (Fig. 2). To facilitate visual interaction with the data, a slider has been included to select the distance along the profile each fault scarp component exists at (e.g., in Fig. 2b the red line in Fig. 2a was fit using the data selection shown in Fig. 2b).

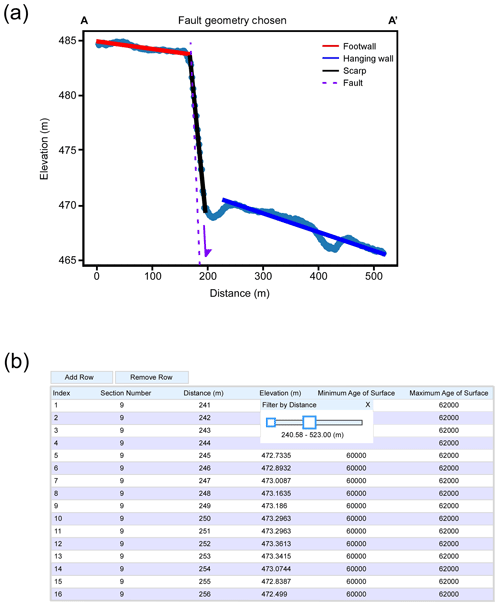
Figure 2 The general workflow. (a) A user-defined profile drawn perpendicular to the strike of a mapped fault. For the location of this feature, see Fig. 4. The red, blue, and black lines represent linear least square fits to the footwall, hanging wall, and scarp of a normal fault, respectively. The purple line is a representation of the geometry of a fault responsible for this scarp. The light blue represents the topographic data. (b) Sliders can be used within the data frame manipulation tool to select data points to represent each relevant component of the fault scarp (e.g., hanging wall, footwall, and scarp). Initially, the red line is fit to all the data in the profile. By using the sliders, you can select a subset of the data as shown in (a) for the generation of the red line. Once data points are selected, the user can visualize the choices for fault component selection before moving forward and calculating slip statistics for the fault in the same Jupyter Notebook environment. The red, blue, and black lines in (a) are generated through this method.

The choices are visualized in real time as a regression line is automatically fit to the values within the modified data frame and displayed in the interactive plot (e.g., red line in Fig. 2a fit to the footwall surface). The least squares linear regressions of these points in an x–y coordinate system determine the mean and standard error of both the slope and the intercept of the lines, which represent the hanging wall and footwall, where the tangent of the surface dip is the slope.

3.3 Visual interpretation and manual editing

Though potentially subject to bias, picking fault scarp components requires human input (Gillespie et al., 1992; Zielke et al., 2015; Middleton et al., 2016; Hodge et al., 2019). Therefore, it is vital that users check each fault scarp component for accuracy. As shown in Fig. 2a, selections are checked for accuracy by the user's visual interpretation and updated, as necessary, by repeating the fault component selection step until a solution that fits the observations is obtained. If the user does not like a specific selection, the user can reselect data from the initial profile, and thus a new best-fit least squares linear regression can be redefined for a surface and that data selection saved instead. Once the user has the desired representation for the fault scarp components, it is saved by running the next code box. The user then loads in the next fault profile and repeats the fault component selection and visual quality check for each new profile. Data selections are saved as a comma-separated file format, where different columns represent the separated data for the hanging wall, footwall, and scarp segments of the profiles. These data are saved together in a separate folder for organization and to be read by the Monte Carlo Slip Statistics calculator.

3.4 Calculate slip statistics

Dip slip (assumed to be net slip in this instance), as well as horizontal and vertical displacement, are calculated automatically in this step (Thompson et al., 2002). The advantage of this step is that multiple transects, faults, and uncertainties in input parameters are analyzed simultaneously. If the hanging wall and footwall strain marker surfaces are not parallel, the dip slip calculation requires knowledge of the position or projection of the fault tip onto the scarp. A line fit to the scarp face contains all possible points for the intersection of the fault tip and scarp. The amount of dip slip is then split into two parts: the distance from the footwall projection up to this point and the distance from the hanging wall down to this point.

Additional input parameters are first defined, including fault dip and intersection with the scarp distributions and geologic age distributions, if available (Fig. 1). Fault dip and uncertainty therein are determined through direct measurement from outcrops, nearby paleoseismic trenches, or by estimating from geomorphic expression. A range of probability density functions (PDFs) can be assigned for fault dip as well as uncertainty of where the fault projects onto the scarp. For example, in our case study below, we chose a trapezoidal distribution for fault dip centered around the most probable dip values and a uniform distribution for the geologic age since only a minimum and maximum age are given for surfaces. Normal distributions for both parameters could have also been chosen. The user would signify this option (see the user manual, which is included as a Supplement to the paper). If the user was interested in defining separate input values for different combinations of fault scarps, the user would manually define these values for each iteration and run the code more than once.

The code calculates the net dip slip component, as well as the vertical separation and horizontal extension, as stated above. Geologic age data can be used to define an age distribution for the geologic surface in question and thus slip rates can be conveniently calculated.

The Monte Carlo approach to calculating slip statistics relies on repeated random samples from the PDFs of the input parameters to obtain numerical results and generate histograms with 95 % confidence intervals for the slip statistics from multiple uncertain estimations.

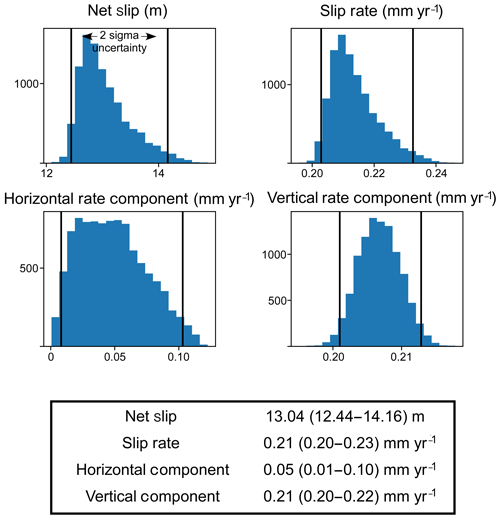
Figure 3 The slip statistics results from the fault scarp visualized in Fig. 2 and with location shown in Fig. 4.

Plots of slip distributions for each fault profile are displayed as output, so the user can easily visually analyze for anomalies in the dataset (Fig. 3). Lastly, the script outputs a CSV file for each group of faults analyzed simultaneously. This can be useful if the user wants to categorize data based on spatial or temporal differences; this was useful in determining displacements on different geologic surfaces, corresponding to different geologic ages, separately. The table also includes a column for cumulative statistics for each group of faults analyzed simultaneously. This was useful for automatically calculating the near-surface horizontal extension rate across the Taupo Volcanic Zone in our case study.

4 Display data in GIS

The data calculated in the previous step can be added to the original shapefile layer to allow for spatial analysis. As outlined in the user manual, the QGIS software allows for seamless “joining” of the CSV file with the original fault scarp profile shapefile layer. When using the ArcGIS software, the ArcGIS tool developed in this study, “attachStats2Profiles”, and its Python stand-alone version can also complete this task.

5 Case study – Taupo Volcanic Zone (TVZ), NZ

The Taupo Volcanic Zone (TVZ), in the central North Island of New Zealand, is a northeast–southwest-trending, 250 km long, 14 to 40 km wide active rift (Wilson et al., 1995; Wallace et al., 2004; Seebeck et al., 2014). Extension across the TVZ over the last 1.6 Myr is expressed primarily as regional volcanism, extensional fractures, and northeast–southwest-trending normal faults (Villamor et al., 2017).

The TVZ represents the ideal case study area to test our methodology because the Quaternary geology of the region has been extensively studied through detailed mapping of geological units and active fault locations. The regional kinematics and near-surface geometry of faults are known and contribute to one of the best paleoseismic datasets in the world, the results from which we can compare our findings (Villamor and Berryman, 2001, 2006). Many fault scarps are clearly imaged to offset a relatively planar geologic horizon which is easily correlated and has been mapped across the relatively narrow tectonic province. Additionally, many high-resolution datasets exist (e.g., the QMAP Geological Map of New Zealand Project, lidar-based DEM of 1 m horizontal resolution, and regional active fault map) (GNS Science, Leonard et al., 2010, Villamor et al., 2010) (Fig. 4).

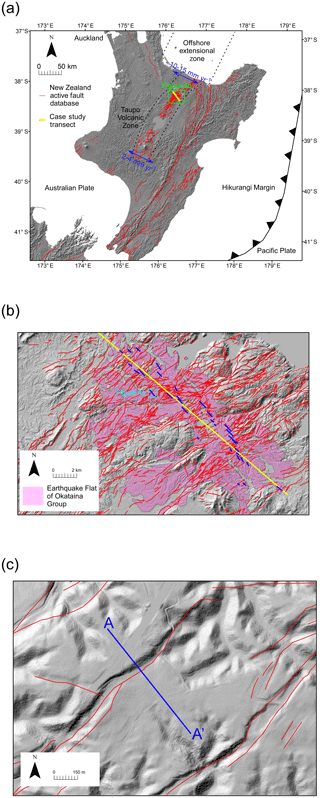
Figure 4 Taupo Volcanic Zone case study. Base images of (a, b, and c) are lidar hillshade maps of the North Island and Taupo Volcanic Zone, New Zealand. (a) Tectonic features of New Zealand where the green box represents the enlarged image in (b). The red fault traces are from the New Zealand Active Faults Database (NZAFD). Active faults have deformed the ground surface of New Zealand within the last 125 000 years. The blue arrow and rate represent geologic extension rates from geodetic and Quaternary fault data (Villamor et al., 2017). The yellow line represents the case study transect. (b) Fault scarp profiles used in this case study are shown in blue and are distributed along the case study transect shown in yellow. Mapped faults in the region are shown in red (NZAFD). For simplicity, only the Earthquake Flat Formation of the Okataina Group outcrops is shown from the Geologic Map of New Zealand Project (GMAP). This is the formation that was analyzed in this study. The light blue box represents the map extent of part (c). (c) Lidar hillshade map of the location of the profile shown in Fig. 2 and analyzed in Fig. 3.

We analyzed fault surface displacements on the Earthquake Flat Formation ignimbrite of the Okataina Group (Nairn, 2002), a volcanic formation of pyroclastic material, lapilli, and ash, which has been dated to 60–62 ka (Wilson et al., 2007). The constructional surface of the ignimbrite is well-preserved and represents a previously continuous, sub-horizontal, planar feature, which has displaced by normal faults in the TVZ.

Here, we applied the methodology for the QGIS-based tool to a transect across the central TVZ. By choosing to analyze fault displacements of a single age surface we can determine spatial patterns of the deformation rates across the region occupied by the surface for the time period represented by the surface chosen. In this case the Earthquake Flat ignimbrite covers practically the entire width of the active rift (only a couple of moderately high scarps on the western margin of the rift do not displace the ignimbrite). We obtained data from as close to the transect line as possible because scarp heights appear to vary along strike of the fault traces due to the complex nature of faulting in the TVZ.

We analyzed 33 faults in a 25 km transect from northwest to southeast in the direction of regional extension. We chose faults with significant offset (>5 m) because smaller faults contribute insignificantly to the overall extension of the region and often represent splays of the larger faults. Thus, because of the filtering small scarps and two missing moderately high-relief scarps on the west of the transect in this study, we report a minimum extension rate for the central TVZ below.

For each fault, we identified the key fault components (e.g., fault scarp, hanging wall, and footwall) and determined slip estimates using MCSST. For our fault geometry distribution, we chose a trapezoidal distribution, centered around 70–80^∘ in dip. This is consistent with data obtained from geological observations in trenches and superficial exposures within 40 m from the ground surface (Grindley 1959; Villamor and Berryman, 2001; Lamarche et al., 2006; Villamor et al., 2010, 2017).

The dip slip values obtained for each fault were in line with reasonable estimates based on extensive experience conducting field campaigns in the region (e.g., altimeter measurements along transects and detailed logging of faults in exploratory trenches) and visual inspection of the digital elevation model (Villamor and Berryman, 2001; Villamor et al., 2010; Villamor et al., 2017). Further, the values plotted in Fig. 3 are consistent with visual inspection of the distance vs. elevation profile (this study). We used recently derived age constraints on the Earthquake Flat Formation to convert these values into dip slip rates.

MCSST automatically converts dip slip rate estimates into horizontal extension rate values by using a trigonometric relationship defined by the fault angle distribution. This resulted in a minimum cumulative near-surface horizontal extension rate of 2.77 mm yr⁻¹ (±0.69 mm yr⁻¹) summed across the mean net slip rate value for all faults along the transect. The minimum cumulative near-surface horizontal extension rate when summed across the median net slip rate values for all faults along the transect is 2.73 mm yr⁻¹ with a 95 % confidence interval of 0.56–5.26 mm yr⁻¹.

This is similar to the values provided by the current best estimate of Quaternary extension rates derived from fault data of 2.4 mm yr⁻¹ (±0.4 mm yr⁻¹) for the central TVZ (Villamor and Berryman, 2001) and only 8 km southwest of this study's transect; 2.9 mm yr⁻¹ (±0.74 mm yr⁻¹) for the northern TVZ immediately offshore (Lamarche et al., 2006); and 2.7 mm yr⁻¹ (±0.3 mm yr⁻¹) for the southern TVZ at the Tongariro Volcano latitude (Gomez-Vasconcelos, 2017).

Note that near-surface fault-derived extension rates along the TVZ have been converted to higher (more realistic) total extension rates (from 4 to 15 mm yr⁻¹ from south to north) in the various studies by applying correction factors that include shallower fault dips and larger fault slips at depth and the contribution from small to moderate earthquakes (small faults that do not rupture the surface) (see Villamor and Berryman, 2001 for method). The differences in fault-derived total extension rate from south to north are mainly dependent on the average “deep” fault dip value chosen (60^∘ for the southern and central TVZ and 45^∘ for the northern TVZ), which remains one of the largest uncertainties for the TVZ faults. Geodetically derived extension rates show a clear extension rate increase from north to south (Wallace et al., 2004).

6 Efficiency of MCSST

The utility of MCSST is best demonstrated by the efficiency with which this study was conducted and the agreement with the current geological understanding of the central TVZ. Once our methodology was defined and the workflow implemented, the analysis of the transect (33 faults across 25 km) was completed in 1 d at a work station. We note that installing and running the Python code packages, navigating the GIS software, and inputting parameters and gaining comfort with the interface for the Jupyter Notebook pose the greatest challenges to employing the MCSST toolkit, so we provide a detailed user manual to accompany the paper to lower the barrier of entry.

7 Limitations of MCSST

Scarp heights appear to vary along strike of the fault traces due to the complex nature of faulting in many geologic settings. This is one limitation of the MCSST. The user must define unique profiles along the fault scarp for each measurement and thus may not choose the position of maximum displacement, a location that can resolve the full 3-D slip vector, or reveal the complex nature of displacement on the fault (Mackenzie and Elliot, 2017). Additionally, the MCSST approach should be used with caution or not used when the fault is located at the base of a concave or complex slope, as it requires markers that were originally parallel and ideally demonstrated to be the same age. However, the approach allows the geologist to incorporate best judgement in selecting fault components and may select far-field, linear features if erosion or diffusion is present at the scarp.

8 Conclusions

The MCSST allows users to quickly and accurately estimate fault slip across several faults imaged in DEMs. This approach improves upon similar studies because it allows for rapid analysis of tens to hundreds of faults simultaneously within GIS, and anomalous values can quickly be identified. The underlying functions are built upon open-source Python code base and are specifically designed to lower the bar of entry for researchers wishing to include robust, quantitative fault scarp analysis in their work or teaching.

Application of this method may contribute to a wide range of regional and local paleoseismic studies with adequate high-resolution DEM coverage, as well as regional fault source characterization for seismic hazard and/or estimating geologic slip and strain rates. In our case study, initial estimates for minimum near-surface extension rates along a northwest to southeast transect (33 faults; 25 km) across the Taupo Volcanic Zone are in line with the current paleoseismological and tephrochronological understanding of the region and provide useful constraints on the uncertainty associated with these values (Villamor and Berryman, 2001).