the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The effect of lithology on the relationship between denudation rate and chemical weathering pathways – evidence from the eastern Tibetan Plateau
Kristen L. Cook
Albert Galy
Hella Wittmann
Niels Hovius
The denudation of rocks in mountain belts exposes a range of fresh minerals to the surface of the Earth that are chemically weathered by acidic and oxygenated fluids. The impact of the resulting coupling between denudation and weathering rates fundamentally depends on the types of minerals that are weathering. Whereas silicate weathering sequesters CO2, the combination of sulfide oxidation and carbonate dissolution emits CO2 to the atmosphere. Here, we combine the concentrations of dissolved major elements in stream waters with 10Be basin-wide denudation rates from 35 small catchments in eastern Tibet to elucidate the importance of lithology in modulating the relationships between denudation rate, chemical weathering pathways, and CO2 consumption or release. Our catchments span 3 orders of magnitude in denudation rate in low-grade flysch, high-grade metapelites, and granitoid rocks. For each stream, we estimate the concentrations of solutes sourced from silicate weathering, carbonate dissolution, and sulfide oxidation using a mixing model. We find that for all lithologies, cation concentrations from silicate weathering are largely independent of denudation rate, but solute concentrations from carbonates and, where present, sulfides increase with increasing denudation rate. With increasing denudation rates, weathering may therefore shift from consuming to releasing CO2 in both (meta)sedimentary and granitoid lithologies. For a given denudation rate, we report dissolved solid concentrations and inferred weathering fluxes in catchments underlain by (meta)sedimentary rock that are 2–10 times higher compared to catchments containing granitoid lithologies, even though climatic and topographic parameters do not vary systematically between these catchments. Thus, varying proportions of exposed (meta)sedimentary and igneous rocks during orogenesis could lead to changes in the sequestration and release of CO2 that are independent of denudation rate.
- Article
(11686 KB) - Full-text XML
-
Supplement
(113 KB) - BibTeX
- EndNote
The relationship between chemical weathering and CO2 drawdown modulates the global carbon cycle and Earth's climate (Walker et al., 1981; Berner et al., 1983). Uplift and denudation of rock control the supply of unweathered minerals to the surface of the Earth and impact the residence time of these minerals in the weathering zone (e.g., Hilley et al., 2010; West et al., 2005; Gabet and Mudd, 2009; Riebe et al., 2001). Thus, increases in denudation rates can boost chemical weathering and ultimately affect Earth's climate (Raymo and Ruddiman, 1992; Hilton and West, 2020; Caves Rugenstein et al., 2019; Kump and Arthur, 1997). The impact of chemical weathering on the attendant emission or drawdown of CO2 depends on the relative importance of different weathering pathways (Torres et al., 2014, 2016; Calmels et al., 2007; Bufe et al., 2021; Hilton and West, 2020; Berner et al., 1983; Hartmann et al., 2009). Weathering of silicate minerals by carbonic acid consumes CO2 from the atmosphere and drives the sequestration of this carbon over timescales longer than marine carbonate compensation (Walker et al., 1981). In turn, sulfuric acid produced by the oxidation of pyrite can drive rapid dissolution of carbonate minerals that releases CO2 into the atmosphere over timescales that exceed the timescale of carbonate compensation in the ocean (Calmels et al., 2007; Das et al., 2012; Torres et al., 2014; Spence and Telmer, 2005), although the impact of that inorganic carbon source and its link to the organic carbon cycle remain debated (Maffre et al., 2021; Torres et al., 2014). Weathering of silicate minerals by sulfuric acid and of carbonate minerals by carbonic acid is carbon-neutral (Calmels et al., 2007; Spence and Telmer, 2005). Importantly, carbonates and sulfides weather several orders of magnitude faster than silicate minerals (Williamson and Rimstidt, 1994; Morse and Arvidson, 2002; Berner, 1978) such that sulfuric-acid-driven carbonate weathering dominates the total solute flux even in lithologies with small fractions of pyrite or carbonate (Anderson et al., 2000; Calmels et al., 2007; Das et al., 2012; Torres et al., 2016; Emberson et al., 2016b; Jacobson and Blum, 2003; Bufe et al., 2021; Kemeny et al., 2021; Relph et al., 2021; Spence and Telmer, 2005).
The dependence of chemical weathering on mineralogy implies a lithologic control on the balance of CO2 drawdown and CO2 release by weathering reactions. Fresh and fine-grained mafic rocks, such as basalts, exhibit some of the fastest silicate weathering rates on the planet and contribute disproportionally to global silicate weathering fluxes (Dessert et al., 2003; Li et al., 2016; Gaillardet et al., 1999; Ibarra et al., 2016). Felsic igneous rocks typically weather more slowly, but silicate weathering in these rocks is also thought to be sensitive to denudation rates (Riebe et al., 2004; West et al., 2005). In contrast, weathering of siliciclastic (meta)sedimentary rocks is often dominated by the dissolution of minor carbonate and sulfides (Anderson et al., 2000; Calmels et al., 2007; Das et al., 2012; Torres et al., 2016; Emberson et al., 2016b; Jacobson and Blum, 2003; Bufe et al., 2021; Blattmann et al., 2019; Spence and Telmer, 2005; Kemeny et al., 2021; Relph et al., 2021), and rapid denudation and exposure of these rocks can drive CO2 release from weathering (Calmels et al., 2007; Torres et al., 2014, 2016; Bufe et al., 2021; Märki et al., 2021; Spence and Telmer, 2005). Carbonate dissolution also dominates weathering of carbonate-rich sediments (Erlanger et al., 2021; Gaillardet et al., 1999, 2018), but the role of sulfide oxidation and therefore the impact of carbonate weathering on the long-term CO2 cycle can be limited in these rocks (Erlanger et al., 2021; Gaillardet et al., 1999, 2018).
Even though lithology exerts a fundamental control on the link between weathering and Earth's carbon cycle, few studies have directly compared and quantified the impact of lithologic variation on the link between physical denudation and chemical weathering and on the importance of different weathering pathways. Such knowledge is important in the context of mountain building, as ongoing exhumation progressively exposes successions of different lithologies to chemical weathering (Hilton and West, 2020). Landscape-scale weathering fluxes are typically estimated by measuring the solute concentration and runoff in rivers that integrate water fluxes across the upstream catchment (Gaillardet et al., 1999; Drever and Clow, 2018; Drever and Zobrist, 1992; White and Blum, 1995). In many settings, denudation gradients coincide with gradients in precipitation, temperature, tectonics, biomass, and/or substrate properties such as fracture density or metamorphic grade (Dixon et al., 2016), which are gradients that affect weathering kinetics independently of denudation rates (Guo et al., 2019; Gaillardet et al., 2018; Ibarra et al., 2016; Godsey et al., 2019; White and Blum, 1995; Drever and Zobrist, 1992; Li et al., 2016; Oeser and von Blanckenburg, 2020; Uhlig and von Blanckenburg, 2019). These co-variations can complicate the interpretation of changes in weathering. Here, we investigate the impact of lithologic variations on chemical weathering across a denudation rate gradient nearly 3 orders of magnitude wide along the eastern margin of the Tibetan Plateau that includes three well-separated groups of lithology (Fig. 1) and relatively small changes in precipitation, elevation, and temperature (Fig. 2, Table S1 in the Supplement).
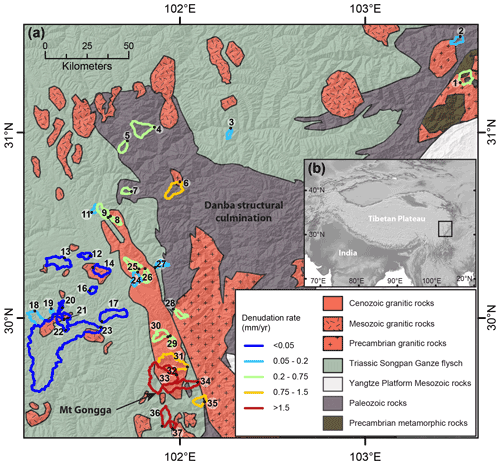
Figure 1Overview of the study area. (a) Simplified geologic map of the study area showing sample locations, sample numbers, and catchment outlines. Outline color indicates the 10Be basin-wide denudation rate from Cook et al. (2018), with two samples from this study (Table S6). (b) Location of the study area along the eastern margin of the Tibetan Plateau.
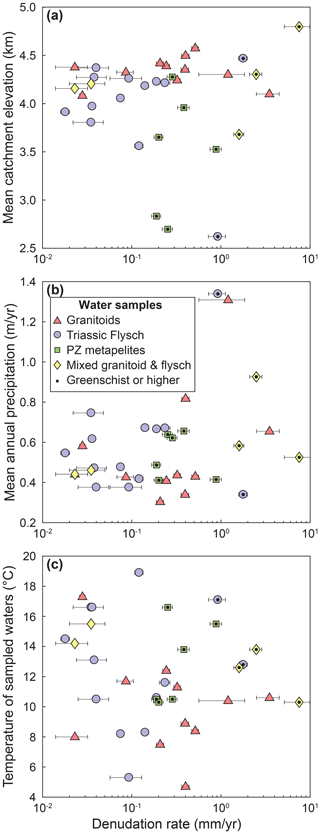
Figure 2Variability of topographic and climatic parameters across the denudation gradient. (a) Catchment-averaged elevation upstream of each sample as a function of denudation rate. (b) TRMM-derived mean annual precipitation in the catchment as a function of denudation rate. (c) Temperature of sampled waters as a function of denudation rate. Catchments underlain by different lithologies are distinguished by symbols and color. Data points with a black dot are metamorphosed to greenschist facies or higher.
On the eastern Tibetan Plateau west of the Sichuan Basin lies the Songpan–Ganze (or Songpan–Garzê) fold belt, which formed during the late Triassic to early Jurassic closure of part of the Paleotethys ocean (Burchfiel et al., 1995; Weller et al., 2013; Chen et al., 2007). The Songpan–Ganze terrane is characterized by a 5–15 km thick sequence of tightly folded Triassic flysch that overlies Paleozoic metasedimentary rocks and Precambrian basement (Roger et al., 2010; Weller et al., 2013) (Fig. 1). These units were intruded by granitoids during both the Mesozoic and Cenozoic. Reactivation of the region during the Cenozoic Indo-Eurasian collision formed zones of rapid uplift and denudation within and at the eastern edge of the slowly eroding Tibetan Plateau. Here, we focus on the southeastern part of the Songpan–Ganze fold belt in the region around the Danba structural culmination and the zone of rapid uplift centered around Gongga Shan (Fig. 1). In this area, in situ 10Be-derived basin-wide denudation rates vary more than 200-fold over a distance of 100–200 km from 0.018 mm yr−1 on the plateau margin (Fig. 1) to 7 mm yr−1 around Mt. Gongga and the Danba structural culmination (Ouimet et al., 2009; Cook et al., 2018) (Fig. 1). This variation of denudation rates is reflected in the topography, with variations of basin-averaged relief between 340 and 5260 m and basin-averaged slopes of 10–37.9∘. The region features three principal lithologic groups. Most of the area exposes the Triassic Songpan–Ganze flysch, a sequence of deep-sea turbidites that is unmetamorphosed or weakly metamorphosed over large areas but can reach greenschist facies close to Gongga Shan and the Danba structural culmination (Burchfiel et al., 1995; Chen et al., 2007). The underlying Paleozoic sequence is exposed in the Danba structural culmination and in the Longmen Shan and consists of a passive margin sequence, which has undergone metamorphism up to amphibolite facies (Huang et al., 2003; Weller et al., 2013). Finally, granitic rocks of a range of ages from Precambrian to Cenozoic are exposed throughout the area (Roger et al., 2004, 2010; Searle et al., 2016) (Fig. 1, Table S1). Rocks within each one of these three broad lithologic groups have varying compositions, but the difference in chemical compositions and mineralogy between these three lithologic groups is greater than the variability within each one of the groups (Jiang et al., 2018; Weller et al., 2013; Chen et al., 2007) (Table S3, Fig. 3). Moreover, minor carbonate and sulfide phases occur in varying proportions in these dominantly silicate lithologies (Jiang et al., 2018; Weller et al., 2013; Chen et al., 2007).
The region is characterized by a cold and humid climate with a pronounced wet monsoon season during the summer months and drier winter months. Mean annual precipitation rates derived by the Tropical Rainfall Measuring Mission (TRMM) vary ∼4–5-fold between 300 and 1340 mm yr−1 (Bookhagen and Burbank, 2010) (Fig. 2b). This range of precipitation values is very similar to the range of runoff values previously estimated for small catchments around the Gongga Shan (Table 1 in Jiang et al., 2018). Our sampled catchments feed the Dadu, Min, and Yalongjiang rivers, which are tributaries to the Yangtze River. They are all headwater catchments that fall within a relatively narrow elevation window, with catchment-averaged elevations of 3500–4800 m with three exceptions at lower mean elevations of 2600–2800 m (Fig. 2a, Table S1). The treeline lies between ∼3500 and 4100 m. Thus, the majority of catchments spans across the treeline and includes forested areas, grasslands, and rocky slopes. Neither the elevation nor the annual precipitation in the studied catchments or the temperature of sampled stream waters correlate strongly with the denudation rate across the area (Fig. 2).
3.1 Sample collection and analysis
We collected water samples from 35 small catchments around the region of Mt. Gongga and the Danba structural culmination (Fig. 1, Table S1). Water samples were collected in mid-May 2018, prior to the rainy season, over a period of 5 d when all catchments were subject to similar hydrological conditions. Most of the sampled catchments drain a single lithologic group: a total of 13 catchments drain the Triassic flysch that is dominantly composed of unmetamorphosed or weakly metamorphosed mixed carbonate–siliciclastic sediments. Only two of the flysch catchments include rocks that have been metamorphosed to garnet-bearing greenschists (S18-35 and S18-36, Fig. 3c). A total of 11 catchments drain granitic rocks, and six catchments drain high-grade Paleozoic and Precambrian metasedimentary rocks, whereas five catchments drain a mix of granitic rocks and Triassic flysch (Fig. 3c, Table S1). Samples were taken as close to sites sampled for cosmogenic-nuclide-derived denudation rates (Cook et al., 2018) as possible and upstream of potential major anthropogenic influences. Water samples were filtered in situ with single-use 0.2 µm filters and collected in high-density polyethylene (HDPE) bottles. Aliquots for cation analysis were acidified on-site to a pH of ∼2 with 3 M ultrapure HNO3. Temperature, pH, and conductivity were measured in the field using a WTW Multi 3430 multimeter.
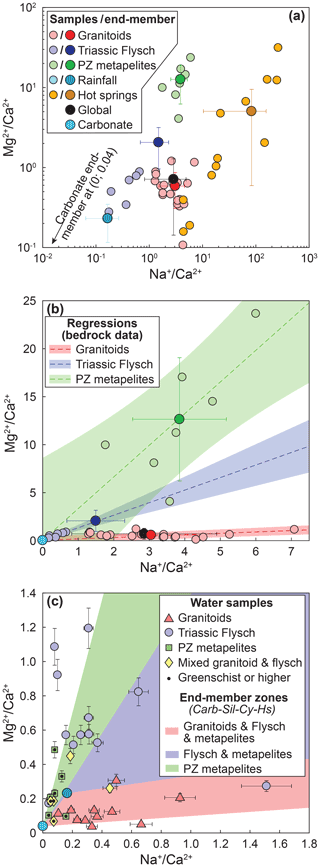
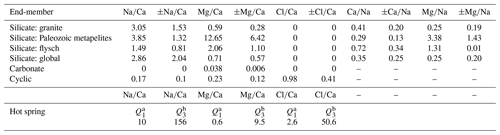
Figure 3End-members and mixing lines in – space. (a) Small points mark individual bedrock, rainwater, and hot spring chemistry (Table S3) (Jiang et al., 2018; Chen et al., 2007; Weller et al., 2013). Large points with error bars mark corresponding end-member estimates (Table 1). Silicate end-members for granitoids and Paleozoic metamorphics as well as for the rainfall end-members are estimated from a mean and standard deviation of individual data points. The flysch silicate end-member was derived from a regression through the bedrock data and estimates of the carbonate content in the bedrock flysch samples (see text). For hot springs, the end-member is the median and interquartile range. The carbonate end-member cannot be shown in logarithmic space. (b) Bedrock chemistry and end-members with regressions through the bedrock data. Colored circles without error bars are lithology data. Colored points with error bars mark the estimate for the silicate end-member for each lithology. The light-blue point marks the carbonate end-member. (c) Individual water samples within the end-member space. Colored areas mark the space between the carbonate, silicate, precipitation, and hot spring end-members for each lithology. Note that spaces are overlapping. Catchments underlain by different lithologies are distinguished by symbols and color. Data points with a black dot are metamorphosed to greenschist facies or higher.
Anion and cation analyses were conducted at the GFZ Potsdam on a Dionex ICS-1100 ion chromatograph and a Varian 720 ICP-OES, respectively, following the procedure described in Bufe et al. (2021). The concentration of bicarbonate was estimated by charge balance. Such estimation is reasonable in active mountain settings where organic acids are scarce, and estimates of bicarbonate from charge balance are within uncertainty of alkalinity values from titrations (Galy and France-Lanord, 1999). Analytical uncertainties for cation analyses were derived from the largest deviation of the calibration standards from the calibration line. For anions, uncertainty estimates were derived from the standard deviation of three repeat measurements (Table S2).
3.2 Unmixing of solute sources
We consider four major sources of cations to rivers in the study area: silicate weathering, carbonate weathering, cyclic contributions (assumed to be dominated by wet precipitation), and hot spring contributions (Table 1). We assume that evaporites are a minor component of the dissolved solids because (i) existing petrologic and geochemical studies do not report evaporite deposits in the upper Triassic flysch or in the Paleozoic metamorphic rocks around the Danba structural culmination (Jiang et al., 2018; Chen et al., 2007), (ii) except for one sample, chloride concentrations range 4–20 µmol L−1 and are thus well within the range of concentrations expected for atmospheric chloride input (Gaillardet et al., 1999), and (iii) the ratios of concentrations are higher than expected for typical evaporite deposits (Gaillardet et al., 1999; Jiang et al., 2018; Chen et al., 2007). Moreover, we assume that secondary precipitation of carbonate minerals is negligible in the area. This assumption is based on the observation that all samples are either undersaturated with respect to calcium carbonate or are within uncertainty of saturation, except for two flysch basins that suggest slightly supersaturated conditions (Fig. A1).
We used a four-end-member inverse model to unmix these contributions based on the relative concentration of the three major soluble cations (Na+, Ca2+, and Mg2+) and chloride (Cl−) (Bufe et al., 2021; Moon et al., 2014; Gaillardet et al., 1999; Torres et al., 2016; Kemeny and Torres, 2021). The mixing model requires that each one of the end-members is unique and therefore occupies a range of compositions that is distinct from the composition of other end-members in the considered space (Fig. 3a and b). In the model, we minimized the following set of equations using the constrained linear least squares solver lsqlin in MATLAB:
with , , and (three equations) under the conditions that
and
Here, is the ratio of concentrations of ion X and calcium, and αCa,Y is the fraction of calcium sourced from end-member Y. The subscript “spl” denotes the sampled ratio in the river water. The end-member subscripts “sil”, “carb”, “cy”, and “hs” denote contributions from silicate, carbonate, cyclic (precipitation), and hot spring sources, respectively.
Equations (1)–(5) were then solved separately for each of the 35 samples based on the input end-member compositions (, see Table 1) and the measured ratios (, see Table S2). Note that one out of three different silicate end-members was chosen for each sample, depending on the lithology in the sampled catchments (Tables 1 and S1). Where catchments contain a mix of different lithologies (for example S18-22 and S18-23, see Table S2), the input silicate end-member was determined by the average between the silicate end-members from the lithologies weighted by the areal coverage of each lithology class in the catchment (see Table S1).
In order to represent the uncertainty of the end-member compositions in the inversion result, we implemented a Monte Carlo approach and ran 100 000 iterations of the inversion for each sample. For each iteration, we randomly picked the end-member from a normal distribution with the mean and standard deviation defined by the end-member estimate and its uncertainty (Table 1). For the hot spring end-member, we instead picked from a uniform distribution defined by a minimum and maximum estimate (see rationale below, Table 1). For each sample (35 samples) and each iteration (100 000 iterations) we used a reduced chi-squared statistic to estimate the goodness of fit of that sample and iteration. The goodness of fit, , was based on (1) , the squared distances between elemental ratios predicted by that particular iteration and the sampled elemental ratios normalized by the uncertainty in the sampled ratio (see Table S2 for data and uncertainties), and (2) , the squared distances between the end-member ratios picked from the normal distribution and the average end-member value normalized by the uncertainty of the end-member values (see Table 1 for end-member values and uncertainties) with
and
where
The superscript “model” refers to quantities that apply to a particular iteration and a particular sample. Note that the end-member misfit ignores the contribution of the hot spring end-member because this end-member was picked from a uniform distribution. Similarly, (see Table 1), and these ratios are not considered in the end-member misfit. The two misfits were then summed and weighted by the number of unique squared distances (three distances for – see Eq. 5 – and six distances for – see Eq. 6) to give equal weight to the summed sample and end-member misfits:
The choice of this weighting is arbitrary, and the absence of any weighting does not change the results substantially. For each sample, the best fit set of end-members and corresponding fractions, αCa, was then chosen from the iteration with the lowest total misfit, . The uncertainty in these parameters was estimated from all Monte Carlo runs that fit the data within a threshold of (on average 9 % of runs). The high number of runs above the threshold of is linked to our approach of picking groups of end-members independently for each Monte Carlo iteration from the entire end-member space (see example in Fig. A2) without an optimization (e.g., Moon et al., 2014).
The most important parameters in the mixing model are the end-member estimates (Table 1). Both silicate and carbonate end-members are based on compiled bedrock compositions around the study area (Jiang et al., 2018; Weller et al., 2013; Chen et al., 2007) (Table S3) as well as the assumption that . Published bulk rock analyses of rocks in the region show substantial variability. Nevertheless, samples from the three individual lithologic groups (granitoids, Paleozoic passive margin metapelites, and Triassic flysch) form distinct trends in – space (Fig. 3a and b). The composition of the granitoids varies around the global silicate end-member estimated from small streams that drain pure silicate lithologies (Gaillardet et al., 1999; Burke et al., 2018). Compared to the granites, the Paleozoic metapelites are substantially enriched in magnesium and the flysch rocks are characterized by high calcium contents (Fig. 3a and b). Major carbonate phases are not reported in the Paleozoic metapelites (Weller et al., 2013) and in the granitoids (Jiang et al., 2018). Even if trace carbonate minerals can strongly affect solutes sourced from chemical weathering (Blum et al., 1998; Jacobson and Blum, 2003; Anderson et al., 2000; Emberson et al., 2016b), the bulk-rock geochemistry measurement should be affected only negligibly. Thus, we assume that the bulk rock compositions are representative of the silicate end-member from these lithologies, and we use the mean and standard deviation of the elemental ratios from individual bedrock samples as an estimate for the silicate end-member of that bedrock group (Table 1). In turn, the flysch samples contain 4 %–80 % carbonate that occurs as both calcite minerals and carbonate cement (Chen et al., 2007). Therefore, these samples represent a mix between a carbonate and a silicate end-member (Fig. 3b). Based on two sediment samples with the highest carbonate content and zero sodium (Table S3), we estimated the magnesium content of carbonates in the area to and , with the subscript “br” denoting data from bedrock samples and the angle brackets denoting the concentration in weight percent rather than in moles. This low ratio is consistent with the absence of reported dolomite in the area (Chen et al., 2007). Based on knowledge of the carbonate end-member, , and the carbonate content of the samples 〈Ca0.96,Mg0.04CO3〉, the and ratios of the flysch can be expressed as
and
where
and uX is the molar mass of component X (Bufe et al., 2021). We estimated both ratios based on the assumption that the carbonate content of the bedrock flysch sample with the lowest carbonate content (farthest away from the origin along the regression in space) has a carbonate content of 〈Ca0.96, Mg0.04CO3〉=4 wt %–10 wt %. The minimum value (4 %) is from the lowest observed carbonate content in the field (Chen et al., 2007), whereas the upper bound is chosen so that the range of resulting values reaches the global end-member value of 2.7. We then used an average of the resulting ratios estimates with an uncertainty based on half of the range (Fig. 3a and b).
For the cyclic end-member, we used a volume-weighted average of rainwater compositions from the eastern flank of Gongga Shan (Jiang et al., 2018) (Tables 1 and S4). The hot spring end-member is also based on hot spring compositions around Mt. Gongga (Jiang et al., 2018) (Table S5). All hot springs are very distinct from rock samples and notably characterized by ratios that are 3–150 times higher than the highest measured stream water samples (Fig. 3a, Table S5). Nevertheless, hot spring compositions are highly variable (Fig. 3a), despite a relatively small area that was sampled. In the inversion, we therefore did not sample the hot spring end-members from a normal distribution around a mean value. Instead, we picked , , and from uniform distributions that span the interquartile range of all hot spring samples. Because of a strong correlation between and in these hot springs, we then picked from the regression between and .
As an alternative to the inverse model, we decomposed the data with a common forward approach (Galy and France-Lanord, 1999; Moon et al., 2014; Bufe et al., 2021; Jacobson and Blum, 2003; Meybeck, 1987). We assumed that all chloride in the river water samples was atmospherically derived and use precipitation-averaged ratios of the measured rainwater (Jiang et al., 2018) (Table S4) to adjust the sample concentrations for rain input. We assumed that our rainwater correction accounts for possible anthropogenic input of SO4 from the industrialized Sichuan Basin through acid rain, and we neglected hot spring contributions. Then, the contributions of silicate and carbonate to the total dissolved Ca2+ and Mg2+ concentrations were estimated as follows.
Equivalent to the inverse model (Eqs. 10 and 11), the silicate end-member ratios for the flysch samples were found by correcting for the carbonate content of the flysch bedrock samples:
and
3.3 Cation sums and fractions
The total sums of cations from silicate and carbonate weathering are the following.
And in charge equivalents they are the following.
The fraction of carbonate weathering is
The fraction of weathering by sulfuric acid (as opposed to carbonic acid) was estimated from sulfate concentrations (Torres et al., 2016; Emberson et al., 2018; Bufe et al., 2021; Galy and France-Lanord, 1999):
where is the sulfate concentration that is sourced from sulfide oxidation given by
Note that this estimate of assumes that contributions of sulfate from evaporites are negligible in the area and that any (likely minor) anthropogenic input as well as minor salts associated with the metasedimentary rocks are captured by the cyclic end-member measured in rainwater samples.
3.4 Estimate of denudation rate
Denudation rates were obtained from existing cosmogenic nuclide concentrations of in situ produced 10Be (Ouimet et al., 2009; Cook et al., 2018). For two sampled catchments (S18.08 and S18.29) without previous denudation rate estimates, we processed two additional samples for analysis of in situ 10Be following the procedure in Cook et al. (2018). Denudation rates were calculated using CRONUS scripts and the Lal–Stone scaling scheme with a sea level low-latitude nucleogenic production rate of 3.7 (Balco et al., 2008) (Table S6). These denudation rates integrate over the time denuding material resides in the first few upper meters of Earth surface. Although this integration time varies between catchments with different denudation rates, it reflects the timescale of mineral supply to the weathering zone and is therefore appropriate for comparison to weathering proxies. Where landslides dominate, their stochastic occurrence may disrupt the relationship between soil formation and chemical weathering (Emberson et al., 2016a, b) and may bias the denudation rate estimates (Niemi et al., 2005; Tofelde et al., 2018; Chen et al., 2020; Yanites et al., 2009). We assume that any such bias is within uncertainty of the denudation rate measurement. Cosmogenic-derived denudation rates incorporate both physical denudation and chemical weathering, but physical denudation rates commonly greatly dominate denudation in active orogens uplifting siliceous rocks with minor carbonates, such as the ones described here (Erlanger et al., 2021; Gaillardet et al., 1999; Dixon and von Blanckenburg, 2012; Riebe et al., 2001; West et al., 2005). Thus, we assume that increasing denudation rates correspond to increasing physical erosion rates. Finally, in situ 10Be-derived denudation rates measure the denudation of quartz-containing bedrock. Based on published bedrock descriptions (Jiang et al., 2018; Weller et al., 2013; Chen et al., 2007; Burchfiel et al., 1995) and observations by the authors (Cook et al., 2018), we assume that carbonate and silicate phases in granitoids and metasediments are mixed to a degree that quartz-derived denudation rates approximate the denudation of the entire rock mass. We acknowledge that unquantified uncertainties may arise where significant weathering occurs below the top few meters of the regolith (Riebe and Granger, 2013) or where significant differences in quartz mineral contribution within the bedrock occur, but these uncertainties are unlikely to change the major trends observed in this work.
In the studied catchments, the concentration of dissolved cations (TDC) generally increases with denudation rates (Fig. 4a). However, the strength of that relationship is greatly influenced by lithology (Fig. 4a). Whereas TDC increases 5–10-fold in the Triassic Songpan–Ganze flysch, the increase in TDC with denudation in the granitic catchments is less than 2-fold and associated with substantial uncertainty (Spearman's p value of 0.19) (Fig. 4a). Mixed flysch–granitic catchments fall between the two trends (Fig. 4a). Catchments with Paleozoic metamorphic lithologies have scattered TDC values, many of which fall within the range of values of the Triassic rocks (Fig. 4a). Magnesium and calcium dominate the solute load and constitute 42 %–96 % (median 84 %) of the TDC. The pattern of increasing TDC is dominated by an increase in calcium concentrations (Fig. 4b), whereas correlations between denudation rate and magnesium, sodium, and potassium concentrations are uncertain (Spearman's p values between 0.1 and 0.9) (Fig. 4c–e). Similarly, no relationship between chloride concentrations and denudation rates is evident (Fig. 4e), but sulfate concentrations show a strong increase with denudation rates in both granites and flysch lithologies (Fig. 4g).
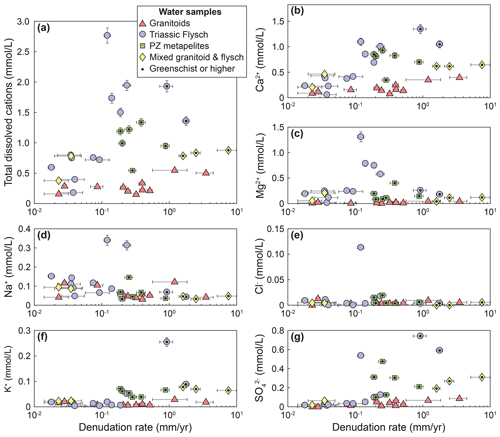
Figure 4Solute concentrations vs. denudation rate. (a) Total dissolved cations. Spearman's rank correlation coefficient and associated p value: , ; , . (b) Ca2+ concentrations , ; , . (c) Mg2+ concentrations. (d) Na+ concentrations. (e) K+ concentrations. (f) Cl− concentrations. (g) concentrations , ; , . Catchments underlain by different lithologies are distinguished by symbols and color. Data points with a black dot are metamorphosed to greenschist facies or higher.
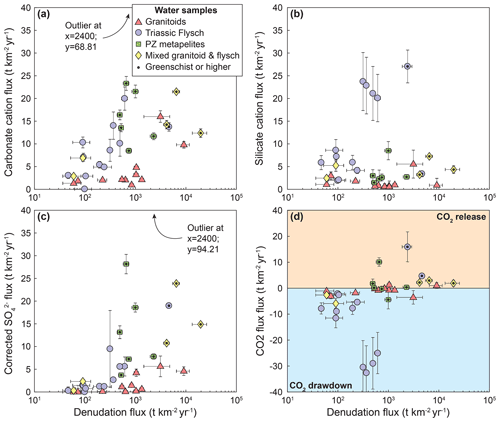
The unmixed cation contributions follow the expectations from the raw data: cation concentrations from carbonate weathering, Ccarb, and sulfate from sulfide oxidation, , display a strong relationship with denudation (Fig. 5a and c). In the flysch and in the Paleozoic metamorphics they increase strongly with denudation rate, whereas the increase in the granitic catchments is weaker, and the mixed catchments are in between (Fig. 5a and c). In contrast, cations from silicate weathering, precipitation sources, and hot springs generally show no relationship to denudation rate for any of the lithologies (Fig. 5b and d–e).
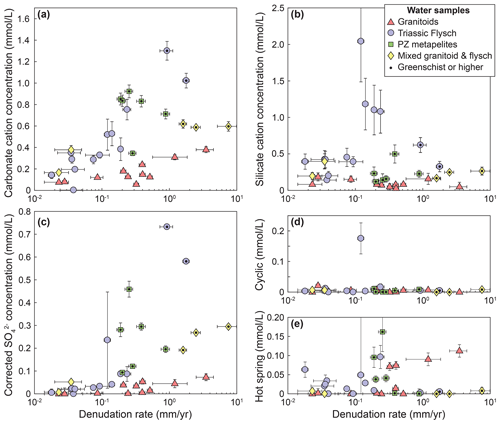
Figure 5Unmixed contributions to the solute load. (a) Cation concentrations from carbonate weathering. (b) Cation concentrations from silicate weathering. (c) Sulfate concentrations corrected for precipitation and inferred to derive from sulfide oxidation. (d) Cation concentrations from cyclic sources. (e) Cation concentrations from hot spring sources. Catchments underlain by different lithologies are distinguished by symbols and color. Data points with a black dot are metamorphosed to greenschist facies or higher.
The contribution of carbonate weathering to the total solute load from weathering, Fcarb, strongly increases with denudation irrespective of rock type (Fig. 6a). Even in granitic catchments carbonate weathering contributes 30 %–89 % (median 65 %) of the cation concentration (Fig. 6a). Thus, both granites and (meta)sedimentary lithologies have comparable fractions of carbonate weathering (Fig. 6a), even if the absolute concentrations differ (Fig. 4). The fraction of weathering by sulfuric acid, Fsulf, also increases with increasing denudation rate, although there is a large amount of scatter at higher denudation rates (Fig. 6b).
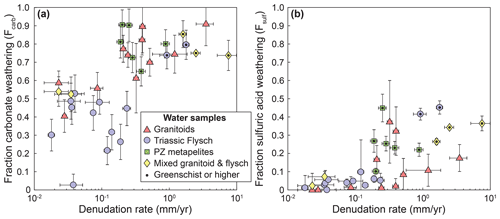
Figure 6Fraction of carbonate weathering and weathering by sulfuric acid. (a) Fraction of carbonate weathering (Eq. 23). (b) Fraction of weathering by sulfuric acid (Eq. 24). Symbols indicate catchment lithology. Catchments underlain by different lithologies are distinguished by symbols and color. Data points with a black dot are metamorphosed to greenschist facies or higher.
In 24 out of 35 samples (67 % of samples), the inferred silicate and/or carbonate cation contributions differ by more than 20% between forward and inverse approaches (Fig. A3). For example, forward-modeled carbonate cation concentrations are more than 20 % higher than results from the inversion in 11 samples (31 % of samples) and more than 50 % higher in three samples (9 % of samples) (Fig. A3). Silicate cation concentrations inferred from the forward approach are lower in these samples. These samples lie outside the zone formed between the silicate, carbonate, hot spring, and precipitation end-members (Fig. 3b), which may explain the offset in the results. Conversely, nine samples (26 %) have more than 20 % higher silicate cation concentrations inferred by the forward model (Fig. A3). In these samples, the inversion predicts 3 %–47 % (median 13 %) cation contributions from hot springs, whereas the median of the cation contributions from hot springs across all samples is 2 %. The hot spring contribution is ignored in the forward approach, and all of the Na+ is attributed to silicate instead, thereby leading to higher silicate cation contributions in the forward model. Despite these differences and resulting outliers, the first-order trends described in this contribution are unaffected by the choice of unmixing method (Figs. A4 and A5).
Our concentration measurements cannot be converted into weathering fluxes because we lack discharge or runoff data for the sampled catchments. However, in comparison to the denudation gradient that is nearly 3 orders of magnitude wide, the mean annual precipitation does not vary widely across the catchments: 82 % of the catchments differ by less than a factor of 2 and 90 % by less than a factor of 3 of precipitation (Table S1). Further, there is no co-variation between precipitation and denudation rate (Fig. 2b, Table S1). The first-order patterns described above do not change substantially when we consider “inferred” weathering fluxes that are obtained by using mean annual precipitation values as a proxy for runoff (Fig. A6). Therefore, it is unlikely that differences in runoff between catchments strongly affect our data, and we interpret the observed patterns as reflecting the response of the weathering system to changes in denudation fluxes.
Our analysis indicates that increasing denudation rates lead to an increase in carbonate weathering and sulfide oxidation in all sampled lithologies (Figs. 5 and 6), likely due to the increased supply of carbonate and sulfide minerals during erosion (Calmels et al., 2007; Torres et al., 2016; Bufe et al., 2021). Conversely, silicate weathering appears to be insensitive to denudation rate and represents a small proportion of the total weathering budget (Figs. 5 and 6). While the granitic catchments have systematically lower cation concentrations from carbonate weathering than the metasedimentary catchments (Fig. 5a), the fraction of carbonate weathering (Fcarb) increases with denudation and is of similar magnitude in all rock types (Fig. 6a). Even in catchments underlain by granitoid rocks, weathering of carbonate phases dominates the solute load at denudation rates above 0.1 mm yr−1 (Fig. 6a). This finding likely arises from the dissolution of trace carbonate minerals disseminated in the crustal granitoids and metapelites that has been described in a number of active mountain ranges (White et al., 1999; Jacobson et al., 2003; Blum et al., 1998; Emberson et al., 2017; Bufe et al., 2021; Torres et al., 2016). In turn, the insensitivity of silicate cation concentrations to denudation (Fig. 5b) is consistent with a kinetic limitation of silicate weathering (West, 2012; West et al., 2005; Gabet and Mudd, 2009). Such kinetic limitation of silicate weathering in conjunction with increasing sulfide oxidation and carbonate weathering across multiple orders of magnitudes of denudation rates (Fig. 5) has recently been documented in the low-grade metasedimentary rocks of southern Taiwan (Bufe et al., 2021). The data presented here suggest that this pattern applies to metasediments in another mountain range, as well as to granitoid rocks. A series of studies on soil formation in metasedimentary and granitic rocks across denudation rates from 10−3 to 2 mm yr−1 has suggested a link between soil denudation rates and soil production rates, and this sensitivity of soil formation rates to denudation has been used to argue for a relationship between orogenesis and silicate weathering (Riebe et al., 2001, 2004; Larsen et al., 2014; Dixon et al., 2012; Dixon and von Blanckenburg, 2012). Spanning a comparable range of denudation rates, our data confirm that these findings from soil profiles may not directly translate to the catchment scale (West et al., 2005; Dixon and von Blanckenburg, 2012). This disconnect is due, most likely, to the dilution of soil waters by fluids that drain parts of the landscape that are not soil-covered or follow deep pathways through bedrock. For example, mass movements, such as landslides, that dominate erosion in parts of the study area are expected to alter weathering fluxes (Emberson et al., 2016a). Thus, in active mountain ranges, landscape-scale silicate weathering may be largely insensitive to denudation rates independently of the major lithologies (Bufe et al., 2021; Gabet and Mudd, 2009; West, 2012).
Even though yearly average precipitation rates do not vary considerably across the denudation rate gradient, monthly precipitation can vary by a factor of ∼5–6 between the high- and low-flow seasons (Jiang et al., 2018). Nevertheless, in small catchments around Mount Gongga, the total dissolved cation concentrations of 80 % of rivers is diluted by less than 2-fold in the high-flow season (median 1.3-fold), and only Cl− and Mg2+ show substantial dilution (Jiang et al., 2018). Thus, the patterns of concentrations that we describe here should broadly mirror the differences in annual weathering fluxes between catchments. Solute concentrations during the high-flow season are expected to carry an elevated proportion of carbonate weathering with respect to the low-flow season (Tipper et al., 2006; Kemeny et al., 2021). Thus, by sampling during the low-flow season and by not accounting for cation exchange with suspended sediment from the clay minerals (Tipper et al., 2021), we might overestimate the proportion of silicate weathering (Tipper et al., 2006, 2021; Kemeny et al., 2021). The dominance of carbonate weathering over silicate weathering in all catchments (Fig. 6) would therefore most likely be strengthened with more data across all seasons and/or with suspended sediment data.
The sulfuric-acid-derived sulfate concentrations and the cation concentrations from silicate weathering allow estimating the concentration of CO2 that is sequestered or emitted during chemical weathering (Torres et al., 2016; Emberson et al., 2018). Beyond the calcium carbonate compensation time of ∼10 kyr (Zeebe and Westbroek, 2003), the moles of CO2 produced (positive [CO2]) or sequestered (negative [CO2]) during chemical weathering per unit volume of weathering fluid can be expressed as
(Torres et al., 2016; Bufe et al., 2021) (Table S7). Note that this formulation is independent of the proportion of sulfuric acid that weathers carbonates or silicates (see Supplement of Torres et al., 2016). The increase in Fcarb and Fsulf with denudation rate (Fig. 6) leads to a clear change from CO2 sequestration to dominantly CO2 release (Fig. 7). These observed trends are most likely explained by the combination of a supply limitation on coupled pyrite oxidation and carbonate weathering as well as a limitation of silicate weathering rates by the slow dissolution kinetics of silicate minerals (Bufe et al., 2021; Torres et al., 2016; Calmels et al., 2007; Gabet and Mudd, 2009). A total of 11 catchments fall into the long-term CO2 release field including all but two of the metamorphic catchments (Paleozoic and Triassic), two of the granitoid catchments, and three mixed granitic–metamorphic catchments (Fig. 7). All of these catchments have denudation rates above 0.19 mm yr−1. Thus, increasing denudation rates lead to decreases in the proportion of weathering that contributes to CO2 drawdown as sulfate concentrations increase, while silicate cation concentrations are invariable (Figs. 4–6).
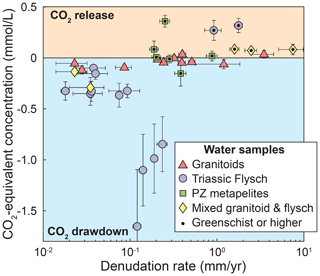
Figure 7Influence of weathering on the carbon cycle. Equivalent concentration of CO2 released or consumed. Symbols indicate catchment lithology. Catchments underlain by different lithologies are distinguished by symbols and color. Data points with a black dot are metamorphosed to greenschist facies or higher.
Compared to the other lithologies, water samples from granite catchments have substantially lower solute concentrations than waters from (meta)sedimentary catchments (Fig. 4a) and weathering in granitoid catchments remains closest to a balance between CO2 release and CO2 consumption across the entire denudation rate gradient (Fig. 7). This contrast persists when we consider “inferred” weathering fluxes that are obtained using mean annual precipitation values as a proxy for runoff (Fig. A6d). In the absence of major differences in climate or topography between granitic and metasedimentary catchments (Fig. 2), this contrast in concentrations is most likely due to low proportions of minor carbonate and sulfide phases in the granitoid lithologies (Fig. 5a and c). In this case, variations in lithology may change the flux of CO2 drawdown or release by a factor of 2–10 at low and high denudation rates, respectively (Figs. 7 and A6d). Hence, even if the relative patterns of silicate, sulfide, and carbonate weathering with denudation are similar across all lithologies, the absolute weathering fluxes are not. As a consequence, our data suggest that changes in the exposed lithologies across an orogenic cycle can substantially alter weathering fluxes (up to a factor of 2–10) independently of variations in denudation rates or runoff.
Water chemistry data from catchments on the eastern margin of the Tibetan Plateau that span across 3 orders of magnitude in denudation rate illustrate the role of lithology in modulating the link between denudation rate and chemical weathering. Perhaps surprisingly, our data show a uniformity in the first-order relationships between weathering and denudation between different lithologies. In particular, in all lithologies, silicate cation concentrations do not increase with increasing denudation rates, whereas concentrations of sulfate and cations from carbonate do show an increase. Whereas granitic and (meta)sedimentary rocks are characterized by similar fractions of carbonate weathering that increase with denudation rate, the (meta)sediments have higher absolute concentrations of sulfate and cations from carbonate weathering, likely due to higher concentrations of these minor phases in the bedrock. In combination, the weathering reactions lead to a transition from CO2 drawdown to dominantly CO2 release at denudation rates higher than 0.2 mm yr−1. In turn, absolute weathering fluxes can vary by a factor of 2–10 between catchments draining granites and (meta)sediments, with implications for the role of changes in the relative exposure of igneous and sedimentary rocks during mountain growth.
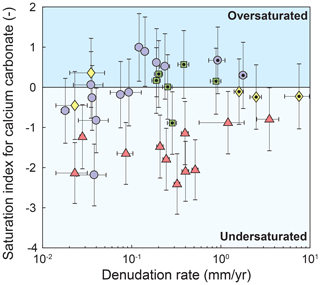
Figure A1Saturation index of samples with respect to calcium carbonate. Catchments underlain by different lithologies are distinguished by symbols and color. Data points with a black dot are metamorphosed to greenschist facies or higher.
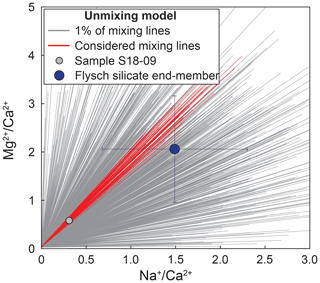
Figure A2Example of mixing lines from Monte Carlo modeling in – space Monte Carlo iterations of the mixing model for sample S18-09 (small light-blue point). Flysch silicate end-member and 1σ uncertainty are in dark blue. 1000 out of 100 000 (1 %) mixing lines from the Monte Carlo modeling are marked as grey lines. Red lines show all runs with among those 1 % of runs.
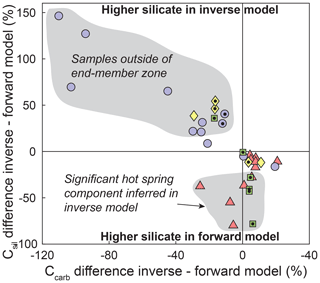
Figure A3Difference between forward and inverse unmixing approaches. Positive values indicate that the inverse approach predicts higher cation ratios than the forward approach. All samples in the upper left quadrant are outside the carbonate–silicate–hot spring–precipitation end-member space in – space (Fig. 3c). Samples with lower inverse silicate cation concentrations are characterized by a 3 %–47 % hot spring contribution that is not accounted for in the forward model (see text). Catchments underlain by different lithologies are distinguished by symbols and color. Data points with a black dot are metamorphosed to greenschist facies or higher.
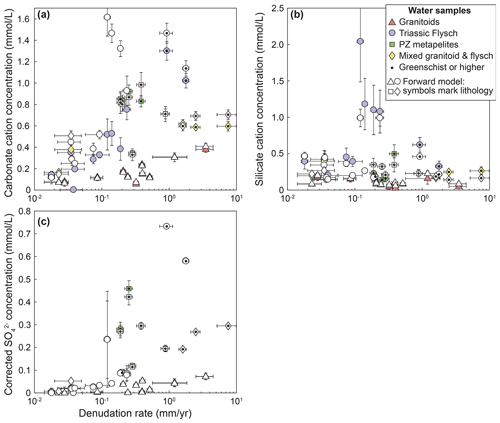
Figure A4Forward model results for silicate, carbonate, and sulfide weathering contributions. Data from Fig. 5 are plotted with results from the forward model (white points). Lithology in the data from the forward model is distinguished by symbology only. Where results from forward and inverse approaches are similar, symbols overlap.
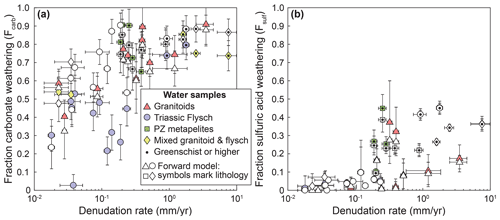
Figure A5Forward model results for the fraction of carbonate weathering and weathering by sulfuric acid. Data from Fig. 6 are plotted with results from the forward model (white points). Lithology in the data from the forward model is distinguished by symbology only. Where results from forward and inverse approaches are similar, symbols overlap.
Codes for the data analysis can be obtained from the first author upon request.
All data used in this paper are included as tables in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-10-513-2022-supplement.
KLC and NH conceived the study and collected samples in the field. AB, HW, and AG contributed to laboratory analyses. KLC and AB led the data analysis and interpretation and wrote the paper with input from all authors.
At least one of the co-authors is a member of the editorial board of Earth Surface Dynamics. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Fan Xuanmei, Dai Lanxin, and Chen Jie for help with fieldwork logistics. Bernhard Zimmermann, Jutta Schlegel, Daniel Frick, Andrea Gottsche, Tanya Goldberg, and the HELGES Lab are thanked for laboratory assistance. We thank J. Jotautas Baronas and an anonymous reviewer for detailed and constructive comments on an earlier version of the paper.
Aaron Bufe has received funding from the European Union's Horizon 2020 research and innovation program under Marie Skłodowska-Curie grant agreement no. 841663. Publication was supported within the funding program “Open Access Publikationskosten” of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – project number 491075472.
The article processing charges for this open-access publication were covered by the Helmholtz Centre Potsdam – GFZ German Research Centre for Geosciences.
This paper was edited by Edward Tipper and reviewed by J. Jotautas Baronas and one anonymous referee.
Anderson, S. P., Drever, J. I., Frost, C. D., and Holden, P.: Chemical weathering in the foreland of a retreating glacier, Geochim. Cosmochim. Ac., 64, 1173–1189, https://doi.org/10.1016/S0016-7037(99)00358-0, 2000.
Balco, G., Stone, J. O., Lifton, N. A., and Dunai, T. J.: A complete and easily accessible means of calculating surface exposure ages or erosion rates from 10Be and 26Al measurements, Quatern. Geochronol., 3, 174–195, https://doi.org/10.1016/j.quageo.2007.12.001, 2008.
Berner, R. A.: Rate control of mineral dissolution under Earth surface conditions, Am. J. Sci., 278, 1235–1252, https://doi.org/10.2475/ajs.278.9.1235, 1978.
Berner, R. A., Lasaga, A. C., and Garrels, R. M.: The carbonate-silicate geochemical cycle and its effect on atmospheric carbon dioxide over the past 100 million years, Am. J. Sci., 283, 641–683, https://doi.org/10.2475/ajs.283.7.641, 1983.
Blattmann, T. M., Wang, S. L., Lupker, M., Märki, L., Haghipour, N., Wacker, L., Chung, L. H., Bernasconi, S. M., Plötze, M., and Eglinton, T. I.: Sulphuric acid-mediated weathering on Taiwan buffers geological atmospheric carbon sinks, Sci. Rep., 9, 2945, https://doi.org/10.1038/s41598-019-39272-5, 2019.
Blum, J. D., Gazis, C. A., Jacobson, A. D., and Page Chamberlain, C.: Carbonate versus silicate weathering in the Raikhot watershed within the High Himalayan Crystalline Series, Geology, 26, 411–414, https://doi.org/10.1130/0091-7613(1998)026<0411:CVSWIT>2.3.CO;2, 1998.
Bookhagen, B. and Burbank, D. W.: Toward a complete Himalayan hydrological budget: Spatiotemporal distribution of snowmelt and rainfall and their impact on river discharge, J. Geophys. Res., 115, F03019, https://doi.org/10.1029/2009JF001426, 2010.
Bufe, A., Hovius, N., Emberson, R., Rugenstein, J. K. C., Galy, A., Hassenruck-Gudipati, H. J., and Chang, J.-M.: Co-variation of silicate, carbonate and sulfide weathering drives CO2 release with erosion, Nat. Geosci., 14, 211-216, https://doi.org/10.1038/s41561-021-00714-3, 2021.
Burchfiel, B. C., Zhiliang, C., Yupinc, L., and Royden, L. H.: Tectonics of the Longmen Shan and Adjacent Regions, Central China, Int. Geol. Rev., 37, 661–735, https://doi.org/10.1080/00206819509465424, 1995.
Burke, A., Present, T. M., Paris, G., Rae, E. C. M., Sandilands, B. H., Gaillardet, J., Peucker-Ehrenbrink, B., Fischer, W. W., McClelland, J. W., Spencer, R. G. M., Voss, B. M., and Adkins, J. F.: Sulfur isotopes in rivers: Insights into global weathering budgets, pyrite oxidation, and the modern sulfur cycle, Earth Planet. Sc. Lett., 496, 168–177, https://doi.org/10.1016/j.epsl.2018.05.022, 2018.
Calmels, D., Gaillardet, J., Brenot, A., and France-Lanord, C.: Sustained sulfide oxidation by physical erosion processes in the Mackenzie River basin: Climatic perspectives, Geology, 35, 1003–1006, https://doi.org/10.1130/g24132a.1, 2007.
Caves Rugenstein, J. K., Ibarra, D. E., and von Blanckenburg, F.: Neogene cooling driven by land surface reactivity rather than increased weathering fluxes, Nature, 571, 99–102, https://doi.org/10.1038/s41586-019-1332-y, 2019.
Chen, C.-Y., Willett, S. D., West, A. J., Dadson, S., Hovius, N., Christl, M., and Shyu, J. B. H.: The impact of storm-triggered landslides on sediment dynamics and catchment-wide denudation rates in the southern Central Range of Taiwan following the extreme rainfall event of Typhoon Morakot, Earth Surf. Proc. Land., 45, 548–564, https://doi.org/10.1002/esp.4753, 2020.
Chen, Y., Liu, F., Zhang, H., Nie, L., and Jiang, L.: Elemental and Sm-Nd isotopic geochemistry on detrital sedimentary rocks in the Ganzi-Songpan block and Longmen Mountains, Front. Earth Sci. China, 1, 60, https://doi.org/10.1007/s11707-007-0009-2, 2007.
Cook, K. L., Hovius, N., Wittmann, H., Heimsath, A. M., and Lee, Y.-H.: Causes of rapid uplift and exceptional topography of Gongga Shan on the eastern margin of the Tibetan Plateau, Earth Planet. Sc. Lett., 481, 328–337, https://doi.org/10.1016/j.epsl.2017.10.043, 2018.
Das, A., Chung, C.-H., and You, C.-F.: Disproportionately high rates of sulfide oxidation from mountainous river basins of Taiwan orogeny: Sulfur isotope evidence, Geophys. Res. Lett., 39, L12404, https://doi.org/10.1029/2012GL051549, 2012.
Dessert, C., Dupré, B., Gaillardet, J., François, L. M., and Allègre, C. J.: Basalt weathering laws and the impact of basalt weathering on the global carbon cycle, Chem. Geol., 202, 257–273, https://doi.org/10.1016/j.chemgeo.2002.10.001, 2003.
Dixon, J. L. and von Blanckenburg, F.: Soils as pacemakers and limiters of global silicate weathering, C. R. Geosci., 344, 597–609, https://doi.org/10.1016/j.crte.2012.10.012, 2012.
Dixon, J. L., Hartshorn, A. S., Heimsath, A. M., DiBiase, R. A., and Whipple, K. X.: Chemical weathering response to tectonic forcing: A soils perspective from the San Gabriel Mountains, California, Earth Planet. Sc. Lett., 323–324, 40–49, https://doi.org/10.1016/j.epsl.2012.01.010, 2012.
Dixon, J. L., Chadwick, O. A., and Vitousek, P. M.: Climate-driven thresholds for chemical weathering in postglacial soils of New Zealand, J. Geophys. Res., 121, 1619–1634, https://doi.org/10.1002/2016JF003864, 2016.
Drever, J. I. and Clow, D. W.: Weathering Rates in Catchments, in: Chemical Weathering Rates of Silicate Minerals, edited by: White, A. F. and Brantley, S. L., De Gruyter, 463–484, https://doi.org/10.1515/9781501509650-012, 2018.
Drever, J. I. and Zobrist, J.: Chemical weathering of silicate rocks as a function of elevation in the southern Swiss Alps, Geochim. Cosmochim. Ac., 56, 3209–3216, https://doi.org/10.1016/0016-7037(92)90298-W, 1992.
Emberson, R., Galy, A., and Hovius, N.: Combined effect of carbonate and biotite dissolution in landslides biases silicate weathering proxies, Geochim. Cosmochim. Ac., 213, 418-434, https://doi.org/10.1016/j.gca.2017.07.014, 2017.
Emberson, R., Hovius, N., Galy, A., and Marc, O.: Chemical weathering in active mountain belts controlled by stochastic bedrock landsliding, Nat. Geosci., 9, 42–45, https://doi.org/10.1038/ngeo2600, 2016a.
Emberson, R., Hovius, N., Galy, A., and Marc, O.: Oxidation of sulfides and rapid weathering in recent landslides, Earth Surf. Dynam., 4, 727–742, https://doi.org/10.5194/esurf-4-727-2016, 2016b.
Emberson, R., Galy, A., and Hovius, N.: Weathering of Reactive Mineral Phases in Landslides Acts as a Source of Carbon Dioxide in Mountain Belts, J. Geophys. Res., 123, 2695–2713, https://doi.org/10.1029/2018JF004672, 2018.
Erlanger, E. D., Rugenstein, J. K. C., Bufe, A., Picotti, V., and Willett, S. D.: Controls on Physical and Chemical Denudation in a Mixed Carbonate-Siliciclastic Orogen, J. Geophys. Res., 126, e2021JF006064, https://doi.org/10.1029/2021JF006064, 2021.
Gabet, E. J. and Mudd, S. M.: A theoretical model coupling chemical weathering rates with denudation rates, Geology, 37, 151–154, https://doi.org/10.1130/g25270a.1, 2009.
Gaillardet, J., Dupré, B., Louvat, P., and Allègre, C. J.: Global silicate weathering and CO2 consumption rates deduced from the chemistry of large rivers, Chem. Geol., 159, 3–30, https://doi.org/10.1016/S0009-2541(99)00031-5, 1999.
Gaillardet, J., Calmels, D., Romero-Mujalli, G., Zakharova, E., and Hartmann, J.: Global climate control on carbonate weathering intensity, Chem. Geol., 527, 118762, https://doi.org/10.1016/j.chemgeo.2018.05.009, 2018.
Galy, A. and France-Lanord, C.: Weathering processes in the Ganges–Brahmaputra basin and the riverine alkalinity budget, Chem. Geol., 159, 31–60, https://doi.org/10.1016/S0009-2541(99)00033-9, 1999.
Godsey, S. E., Hartmann, J., and Kirchner, J. W.: Catchment chemostasis revisited: Water quality responds differently to variations in weather and climate, Hydrol. Process., 33, 3056–3069, https://doi.org/10.1002/hyp.13554, 2019.
Guo, J., Ma, L., Gaillardet, J., Sak, P. B., Pereyra, Y., and Engel, J.: Reconciling chemical weathering rates across scales: Application of uranium-series isotope systematics in volcanic weathering clasts from Basse-Terre Island (French Guadeloupe), Earth Planet. Sc. Lett., 530, 115874, https://doi.org/10.1016/j.epsl.2019.115874, 2019.
Hartmann, J., Jansen, N., Dürr, H. H., Kempe, S., and Köhler, P.: Global CO2-consumption by chemical weathering: What is the contribution of highly active weathering regions?, Global Planet. Change, 69, 185–194, https://doi.org/10.1016/j.gloplacha.2009.07.007, 2009.
Hilley, G. E., Chamberlain, C. P., Moon, S., Porder, S., and Willett, S. D.: Competition between erosion and reaction kinetics in controlling silicate-weathering rates, Earth Planet. Sc. Lett., 293, 191–199, https://doi.org/10.1016/j.epsl.2010.01.008, 2010.
Hilton, R. G. and West, A. J.: Mountains, erosion and the carbon cycle, Nat. Rev. Earth Environ., 1, 284–299, https://doi.org/10.1038/s43017-020-0058-6, 2020.
Huang, M. H., Buick, I. S., and Hou, L. W.: Tectonometamorphic Evolution of the Eastern Tibet Plateau: Evidence from the Central Songpan–Garzê Orogenic Belt, Western China, J. Petrol., 44, 255–278, https://doi.org/10.1093/petrology/44.2.255, 2003.
Ibarra, D. E., Caves, J. K., Moon, S., Thomas, D. L., Hartmann, J., Chamberlain, C. P., and Maher, K.: Differential weathering of basaltic and granitic catchments from concentration–discharge relationships, Geochim. Cosmochim. Ac., 190, 265–293, https://doi.org/10.1016/j.gca.2016.07.006, 2016.
Jacobson, A. D. and Blum, J. D.: Relationship between mechanical erosion and atmospheric CO2 consumption in the New Zealand Southern Alps, Geology, 31, 865–868, https://doi.org/10.1130/g19662.1, 2003.
Jacobson, A. D., Blum, J. D., Chamberlain, C. P., Craw, D., and Koons, P. O.: Climatic and tectonic controls on chemical weathering in the New Zealand Southern Alps, Geochim. Cosmochim. Ac., 67, 29–46, https://doi.org/10.1016/S0016-7037(02)01053-0, 2003.
Jiang, H., Liu, W., Xu, Z., Zhou, X., Zheng, Z., Zhao, T., Zhou, L., Zhang, X., Xu, Y., and Liu, T.: Chemical weathering of small catchments on the Southeastern Tibetan Plateau I: Water sources, solute sources and weathering rates, Chem. Geol., 500, 159–174, https://doi.org/10.1016/j.chemgeo.2018.09.030, 2018.
Kemeny, P. C. and Torres, M. A.: Presentation and applications of mixing elements and dissolved isotopes in rivers (MEANDIR), a customizable MATLAB model for Monte Carlo inversion of dissolved river chemistry, Am. J. Sci., 321, 579–642, https://doi.org/10.2475/05.2021.03, 2021.
Kemeny, P. C., Lopez, G. I., Dalleska, N. F., Torres, M., Burke, A., Bhatt, M. P., West, A. J., Hartmann, J., and Adkins, J. F.: Sulfate sulfur isotopes and major ion chemistry reveal that pyrite oxidation counteracts CO2 drawdown from silicate weathering in the Langtang-Trisuli-Narayani River system, Nepal Himalaya, Geochim. Cosmochim. Ac., 294, 43–69, https://doi.org/10.1016/j.gca.2020.11.009, 2021.
Kump, L. R. and Arthur, M. A.: Global Chemical Erosion during the Cenozoic: Weatherability Balances the Budgets, in: Tectonic Uplift and Climate Change, edited by: Ruddiman, W. F., Springer US, Boston, MA, 399–426, https://doi.org/10.1007/978-1-4615-5935-1_18, 1997.
Larsen, I. J., Almond, P. C., Eger, A., Stone, J. O., Montgomery, D. R., and Malcolm, B.: Rapid Soil Production and Weathering in the Southern Alps, New Zealand, Science, 343, 637–640, https://doi.org/10.1126/science.1244908, 2014.
Li, G., Hartmann, J., Derry, L. A., West, A. J., You, C.-F., Long, X., Zhan, T., Li, L., Li, G., Qiu, W., Li, T., Liu, L., Chen, Y., Ji, J., Zhao, L., and Chen, J.: Temperature dependence of basalt weathering, Earth Planet. Sc. Lett., 443, 59–69, https://doi.org/10.1016/j.epsl.2016.03.015, 2016.
Maffre, P., Swanson-Hysell, N. L., and Goddéris, Y.: Limited Carbon Cycle Response to Increased Sulfide Weathering Due to Oxygen Feedback, Geophys. Res. Lett., 48, e2021GL094589, https://doi.org/10.1029/2021GL094589, 2021.
Märki, L., Lupker, M., France-Lanord, C., Lavé, J., Gallen, S., Gajurel, A. P., Haghipour, N., Leuenberger-West, F., and Eglinton, T.: An unshakable carbon budget for the Himalaya, Nat. Geosci., 14, 745–750, https://doi.org/10.1038/s41561-021-00815-z, 2021.
Meybeck, M.: Global chemical weathering of surficial rocks estimated from river dissolved loads, Am. J. Sci., 287, 401–428, https://doi.org/10.2475/ajs.287.5.401, 1987.
Moon, S., Chamberlain, C. P., and Hilley, G. E.: New estimates of silicate weathering rates and their uncertainties in global rivers, Geochim. Cosmochim. Ac., 134, 257–274, https://doi.org/10.1016/j.gca.2014.02.033, 2014.
Morse, J. W. and Arvidson, R. S.: The dissolution kinetics of major sedimentary carbonate minerals, Earth Sci. Rev., 58, 51–84, https://doi.org/10.1016/S0012-8252(01)00083-6, 2002.
Niemi, N. A., Oskin, M., Burbank, D. W., Heimsath, A. M., and Gabet, E. J.: Effects of bedrock landslides on cosmogenically determined erosion rates, Earth Planet. Sc. Lett., 237, 480–498, https://doi.org/10.1016/j.epsl.2005.07.009, 2005.
Oeser, R. A. and von Blanckenburg, F.: Do degree and rate of silicate weathering depend on plant productivity?, Biogeosciences, 17, 4883–4917, https://doi.org/10.5194/bg-17-4883-2020, 2020.
Ouimet, W. B., Whipple, K. X., and Granger, D. E.: Beyond threshold hillslopes: Channel adjustment to base-level fall in tectonically active mountain ranges, Geology, 37, 579–582, https://doi.org/10.1130/g30013a.1, 2009.
Raymo, M. E. and Ruddiman, W. F.: Tectonic forcing of late Cenozoic climate, Nature, 359, 117–122, https://doi.org/10.1038/359117a0, 1992.
Relph, K. E., Stevenson, E. I., Turchyn, A. V., Antler, G., Bickle, M. J., Baronas, J. J., Darby, S. E., Parsons, D. R., and Tipper, E. T.: Partitioning riverine sulfate sources using oxygen and sulfur isotopes: Implications for carbon budgets of large rivers, Earth Planet. Sc. Lett., 567, 116957, https://doi.org/10.1016/j.epsl.2021.116957, 2021.
Riebe, C. S. and Granger, D. E.: Quantifying effects of deep and near-surface chemical erosion on cosmogenic nuclides in soils, saprolite, and sediment, Earth Surf. Proc. Land., 38, 523–533, https://doi.org/10.1002/esp.3339, 2013.
Riebe, C. S., Kirchner, J. W., Granger, D. E., and Finkel, R. C.: Strong tectonic and weak climatic control of long-term chemical weathering rates, Geology, 29, 511-514, https://doi.org/10.1130/0091-7613(2001)029<0511:stawcc>2.0.co;2, 2001.
Riebe, C. S., Kirchner, J. W., and Finkel, R. C.: Erosional and climatic effects on long-term chemical weathering rates in granitic landscapes spanning diverse climate regimes, Earth Planet. Sc. Lett., 224, 547–562, https://doi.org/10.1016/j.epsl.2004.05.019, 2004.
Roger, F., Malavieille, J., Leloup, P. H., Calassou, S., and Xu, Z.: Timing of granite emplacement and cooling in the Songpan–Garzê Fold Belt (eastern Tibetan Plateau) with tectonic implications, J. Asian Earth Sci., 22, 465–481, https://doi.org/10.1016/S1367-9120(03)00089-0, 2004.
Roger, F., Jolivet, M., and Malavieille, J.: The tectonic evolution of the Songpan-Garzê (North Tibet) and adjacent areas from Proterozoic to Present: A synthesis, J. Asian Earth Sci., 39, 254–269, https://doi.org/10.1016/j.jseaes.2010.03.008, 2010.
Searle, M. P., Roberts, N. M. W., Chung, S.-L., Lee, Y.-H., Cook, K. L., Elliott, J. R., Weller, O. M., St-Onge, M. R., Xu, X.-W., Tan, X.-B., and Li, K.: Age and anatomy of the Gongga Shan batholith, eastern Tibetan Plateau, and its relationship to the active Xianshui-he fault, Geosphere, 12, 948–970, https://doi.org/10.1130/GES01244.1, 2016.
Spence, J. and Telmer, K.: The role of sulfur in chemical weathering and atmospheric CO2 fluxes: Evidence from major ions, ä13CDIC, and ä34SSO4 in rivers of the Canadian Cordillera, Geochim. Cosmochim. Ac., 69, 5441–5458, https://doi.org/10.1016/j.gca.2005.07.011, 2005.
Tipper, E. T., Bickle, M. J., Galy, A., West, A. J., Pomiès, C., and Chapman, H. J.: The short term climatic sensitivity of carbonate and silicate weathering fluxes: Insight from seasonal variations in river chemistry, Geochim. Cosmochim. Ac., 70, 2737–2754, https://doi.org/10.1016/j.gca.2006.03.005, 2006.
Tipper, E. T., Stevenson, E. I., Alcock, V., Knight, A. C. G., Baronas, J. J., Hilton, R. G., Bickle, M. J., Larkin, C. S., Feng, L., Relph, K. E., and Hughes, G.: Global silicate weathering flux overestimated because of sediment–water cation exchange, P. Natl. Acad. Sci. USA, 118, e2016430118, https://doi.org/10.1073/pnas.2016430118, 2021.
Tofelde, S., Duesing, W., Schildgen, T. F., Wickert, A. D., Wittmann, H., Alonso, R. N., and Strecker, M.: Effects of deep-seated versus shallow hillslope processes on cosmogenic 10Be concentrations in fluvial sand and gravel, Earth Surf. Proc. Land., 43, 3086–3098, https://doi.org/10.1002/esp.4471, 2018.
Torres, M. A., West, A. J., and Li, G.: Sulphide oxidation and carbonate dissolution as a source of CO2 over geological timescales, Nature, 507, 346–349, https://doi.org/10.1038/nature13030, 2014.
Torres, M. A., West, A. J., Clark, K. E., Paris, G., Bouchez, J., Ponton, C., Feakins, S. J., Galy, V., and Adkins, J. F.: The acid and alkalinity budgets of weathering in the Andes–Amazon system: Insights into the erosional control of global biogeochemical cycles, Earth Planet. Sc. Lett., 450, 381–391, https://doi.org/10.1016/j.epsl.2016.06.012, 2016.
Uhlig, D. and von Blanckenburg, F.: How Slow Rock Weathering Balances Nutrient Loss During Fast Forest Floor Turnover in Montane, Temperate Forest Ecosystems, Front. Earth Sci., 7, https://doi.org/10.3389/feart.2019.00159, 2019.
Walker, J. C. G., Hays, P. B., and Kasting, J. F.: A negative feedback mechanism for the long-term stabilization of Earth's surface temperature, J. Geophys. Res., 86, 9776–9782, https://doi.org/10.1029/JC086iC10p09776, 1981.
Weller, O. M., St-Onge, M. R., Waters, D. J., Rayner, N., Searle, M. P., Chung, S.-L., Palin, R. M., Lee, Y.-H., and Xu, X.: Quantifying Barrovian metamorphism in the Danba Structural Culmination of eastern Tibet, J. Metamor. Geol., 31, 909–935, https://doi.org/10.1111/jmg.12050, 2013.
West, A. J.: Thickness of the chemical weathering zone and implications for erosional and climatic drivers of weathering and for carbon-cycle feedbacks, Geology, 40, 811–814, https://doi.org/10.1130/g33041.1, 2012.
West, A. J., Galy, A., and Bickle, M.: Tectonic and climatic controls on silicate weathering, Earth Planet. Sc. Lett., 235, 211–228, https://doi.org/10.1016/j.epsl.2005.03.020, 2005.
White, A. F. and Blum, A. E.: Effects of climate on chemical weathering in watersheds, Geochim. Cosmochim. Ac., 59, 1729–1747, https://doi.org/10.1016/0016-7037(95)00078-E, 1995.
White, A. F., Bullen, T. D., Vivit, D. V., Schulz, M. S., and Clow, D. W.: The role of disseminated calcite in the chemical weathering of granitoid rocks, Geochim. Cosmochim. Ac., 63, 1939–1953, https://doi.org/10.1016/S0016-7037(99)00082-4, 1999.
Williamson, M. A. and Rimstidt, J. D.: The kinetics and electrochemical rate-determining step of aqueous pyrite oxidation, Geochim. Cosmochim. Ac., 58, 5443–5454, https://doi.org/10.1016/0016-7037(94)90241-0, 1994.
Yanites, B. J., Tucker, G. E., and Anderson, R. S.: Numerical and analytical models of cosmogenic radionuclide dynamics in landslide-dominated drainage basins, J. Geophys. Res., 114, F01007, https://doi.org/10.1029/2008JF001088, 2009.
Zeebe, R. E. and Westbroek, P.: A simple model for the CaCO3 saturation state of the ocean: The “Strangelove”, the “Neritan”, and the “Cretan” Ocean, Geochem. Geophy. Geosy., 4, 1104, https://doi.org/10.1029/2003gc000538, 2003.