River suspended-sand flux computation with uncertainty estimation using water samples and high-resolution ADCP measurements

Measuring suspended-sand fluxes in rivers remains a scientific challenge due to their high spatial and temporal variability. To capture the vertical and lateral gradients of concentration in the cross-section, measurements with point samples are performed. However, the uncertainty related to these measurements is rarely evaluated, as few studies of the major sources of error exist. Therefore, the aim of this study is to develop a method to determine the cross-sectional sand flux and estimate its uncertainty. This SDC (for sand discharge computing) method combines suspended-sand concentrations from point samples with ADCP (acoustic Doppler current profiler) high-resolution depth and velocity measurements. The MAP (for multitransect averaged profile) method allows obtaining an average of several ADCP transects on a regular grid, including the unmeasured areas. The suspended-sand concentrations are integrated vertically by fitting a theoretical exponential suspended-sand profile to the data using Bayesian modeling. The lateral integration is based on the water depth as a proxy for the local bed shear stress to evaluate the bed concentration and sediment diffusion along the river cross-section. The estimation of uncertainty combines ISO standards and semi-empirical methods with a Bayesian approach to estimate the uncertainty due to the vertical integration. The new method is applied to data collected in four rivers under various hydro-sedimentary conditions: the Colorado, Rhône, Isère, and Amazon rivers, with computed flux uncertainties ranging between 18 % and 32 %. The relative difference between the suspended-sand flux in 21 cases calculated with the proposed SDC method compared to the International Organization for Standardization (ISO) 4363 standard method ranges between −40 % and +23 %. This method that comes with a flexible, open-source code is the first to propose an applicable uncertainty estimation that could be adapted to other flux computation methods.

1 Introduction

The determination of suspended-sediment load is required to estimate sediment dynamics and budgets for river restoration and monitoring, river engineering, and flood risk evaluation (Kondolf et al., 2014). Measuring and monitoring sediment loads and the associated uncertainties within a catchment constitute a major practical issue for hydrologists and river managers (Hoffmann et al., 2010). Even though suspended-sand transport is a key driver of the river evolution (Kondolf, 1997), it remains difficult to measure its concentration due to its temporal and spatial variability in the cross-section, which may account for several orders of magnitude (Armijos et al., 2017). In contrast, fine suspended sediments (< 63 µm) are relatively homogeneous throughout the cross-section, often reaching concentration variations of up to an order of magnitude (Wren et al., 2000).

The total suspended-sediment flux through a cross-section, Φ_total (kg s⁻¹), is defined as the mass of suspended sediment passing through a river cross-section per unit time:

$$\begin{array}{}\text{(1)}& {\mathrm{\Phi }}_{\mathrm{total}}=\underset{y_{\mathrm{lb}}}{\overset{y_{\mathrm{rb}}}{\int }}{q}_{\mathrm{ss}}\left(y\right)\mathrm{d}y=\underset{y_{\mathrm{lb}}}{\overset{y_{\mathrm{rb}}}{\int }}\underset{z_a}{\overset{h}{\int }}c(y,z)v(y,z)\mathrm{d}z\mathrm{d}y,\end{array}$$

where y and z are the lateral and vertical coordinates; q_ss is the suspended-sediment discharge per vertical coordinate; y_lb and y_rb are the left and right boundaries of the cross-section; z_a is the reference level for suspension at the top of the bedload layer, generally assumed to be the riverbed elevation; h is the water elevation; and c(z) and v(z) are the time-averaged suspended-sediment concentration and the water velocity perpendicular to the cross-section, respectively.

Suspended-sediment sampling and computing techniques have been developed over decades (Porterfield, 1972; Starosolsky and Rakoczi, 1981; International Organization for Standardization, 2002). Typically, these methods are based on physical water sampling to determine the suspended-sediment concentration throughout the cross-section using samples taken at different locations throughout the river cross-section. Samples may be taken following the depth-integrating method, where several nearly complete verticals at different distances from the bank are sampled, or the point sampling method, where samples are collected at different discrete water depths and distances from the bank. Different methods were proposed to estimate the suspended-sand flux through the cross-section (Lupker et al., 2011; Shah-Fairbank and Julien, 2015; Santini et al., 2019). The International Organization for Standardization (ISO) standard method (International Organization for Standardization, 2002) consists of computing the velocity-weighted cross-sectional mean concentration by combining physical samples with simultaneous velocity measurements. In this method, the cross-section is divided into N_seg segments and for each increment l, the water discharge Q_l and depth-averaged velocity-weighted concentration C_l are evaluated:

$$\begin{array}{}\text{(2)}& {\mathrm{\Phi }}_{\mathrm{total}}=\sum _{l=\mathrm{1}}^{N_{\mathrm{seg}}}{Q}_l{C}_l.\end{array}$$

This method is derived directly from the velocity–area method for the measurement of water discharge using current meters (International Organization for Standardization, 2009). Even though these classical discrete methods are widely accepted, they are time- and cost-consuming and sometimes difficult to deploy (Camenen et al., 2023). As they are limited to a few points or depth-averaged samples at a limited number of locations, they are characterized by a low spatial and temporal resolution. Also, the method is directly based on depth-integrated sampling with no possibility to interpolate and extrapolate results from sampled verticals to the whole cross-section. Some surrogate technologies (e.g., optical and acoustical methods) have been proposed to measure sediment properties and suspended-sand flux with a better spatial and temporal resolution (Wren et al., 2000; Gray and Gartner, 2010).

Acoustic methods using acoustic Doppler current profilers (ADCPs) have become well-established in streamflow monitoring and provide faster, safer, and more accurate acquisition of stream velocities, discharges, and depths than older current meter methods (Oberg and Mueller, 2007). In a measurement transect, data are acquired on a grid with fixed or variable cell height and many vertical ensembles. For a valid discharge measurement, several cross-sectional transects are typically acquired and processed to obtain information on discharge and velocity. Different post-processing tools have been developed such as the Velocity Mapping Toolbox (VMT) (Parsons et al., 2013) for the analysis and visualization of cross-sectional velocity data collected along multiple ADCP transects. Other examples are the discharge reviews QRev (Mueller, 2016) and QRevInt (Lennermark and Hauet, 2022) developed by an international group, which are applied to ensure discharge measurement reliability and to quantify the uncertainty in the discharge measurement (Despax et al., 2023). While these methods provide temporal averages of each ADCP ensemble, other approaches combine the ADCP measurements spatially close to each other, notably far from the instrument, where the distance between the beams is high (Vermeulen et al., 2014).

In combination with sediment sampling, ADCP measurements of flow velocity and depth can be used to compute the cross-sectional suspended-sand flux (Bouchez et al., 2011; Vauchel et al., 2017). ADCP measurements provide an increased spatial resolution throughout the cross-section compared to point velocity measurements using current meters or rating-curve estimates of the total cross-sectional discharge (Oberg and Mueller, 2007). Moreover, the acoustic backscatter measured by an ADCP, or an acoustic backscattering system (ABS), may be used to improve the spatial integration of the concentration in the cross-section. Indeed, the acoustic backscatter can be inverted and used to measure the suspended-sand concentration (e.g., Topping and Wright, 2016; Venditti et al., 2016; Szupiany et al., 2019; Vergne et al., 2020). Several software tools have been developed to process ADCP data for estimating suspended-sand flux (Boldt, 2015; Dominguez Ruben et al., 2020) or using backscatter inversions. However, acoustic inversion techniques require many physical samples for calibration and are affected by acoustic modeling issues (Vergne et al., 2023).

Informed decisions related to sediment monitoring require reliable estimates of the uncertainty of flux measurements. However, the evaluation of the uncertainty is a difficult task because of the complexity of these measurements, mainly due to the temporal and spatial variations of the sediment concentration. Measurement uncertainty is the expression of the statistical dispersion of the values attributed to a measured quantity (JCGM, 2008). Identifying error sources and estimating uncertainty components for suspended-sand measurements have been addressed in many old reports and papers from the FISP (Federal Inter-Agency Sedimentation Project) (FISP, 1941, 1952; Colby, 1964; Guy and Norman, 1970) and more recently by the U.S. Geological Survey (USGS, Topping et al., 2011; Sabol and Topping, 2013) and others (Gitto et al., 2017). Moreover, the International Organization for Standardization (2002) standard proposes a framework to estimate the errors and uncertainty in the mean cross-sectional suspended-sand concentration determined by a point sampling method. It identifies several sources of error of random and systematic nature. These errors are notably related to the lateral integration of the concentration between the sampling verticals, thus depending on the number of verticals. Another important error source is the vertical integration of the concentration between the sampling points of a vertical, which depends on the number of sampling points along a vertical. Another error is related to the sampling time and consists of the sample's representativity of the natural fluctuations of the concentration due to turbulence. Additional error sources originate from the sampler type and the laboratory analysis. The uncertainty related to each of these error sources is estimated using a high number of samples, the average of which is considered to be the approximate true value. This value is taken as a reference and the uncertainties originating from the different error sources are estimated based on the deviation to the reference. The respective uncertainty is then determined by the difference between the measured value at a given location and the approximate true value. Even though several sources of error are addressed, the International Organization for Standardization (2002) method contains several defects in theoretical and practical respects. First, this standard is not in agreement with the framework proposed in the Guide to the expression of uncertainty in measurement (GUM; JCGM, 2008) defining the uncertainty propagation method, notably concerning the notations and the computation of an approximate true value. Second, the large number of additional samples required for the uncertainty analysis and taken under stable hydro-sedimentary conditions is hardly applicable in most environments due to the quick variability of hydro-sedimentary processes and technical difficulties. For example, to estimate the uncertainty due to the number of verticals (i.e., lateral integration), 15 to 20 verticals with seven point samples each are required for sections less than 100 m wide. The time needed to conduct this kind of survey is practically impossible given the temporal variability of the processes studied. Besides the International Organization for Standardization (2002) method, no other method proposes a framework addressing all commonly identified sources of error. However, some authors tried to evaluate the main sources of uncertainty. Concerning lateral integration, Colby (1964) noticed that the sand flux varies approximately (within a factor k₁) with the third power of the mean velocity $\stackrel{\mathrm{‾}}{v}$ for a constant grain size distribution and temperature, as well as velocities ranging between 0.6 and 1.5 m s⁻¹: ${\mathrm{\Phi }}_{\mathrm{total}}=k_{\mathrm{1}}{\stackrel{\mathrm{‾}}{v}}^{\mathrm{3}}$. Based on these observations and making the required conversions, he stated that the variability of sand concentration at different sampling verticals should be closely related to the variability of ${\stackrel{\mathrm{‾}}{v}}^{\mathrm{2}}/h$, the ratio of the squared mean velocity $\stackrel{\mathrm{‾}}{v}$ to the total sampled depth h. To ensure comparability among different sampling sections and streams, the ${\stackrel{\mathrm{‾}}{v}}^{\mathrm{2}}/h$ index, also called ξ, may be used:

$$\begin{array}{}\text{(3)}& \mathit{\xi }={\displaystyle \frac{\max \left({\stackrel{\mathrm{‾}}{v}}_l^{\mathrm{2}}/h_l\right)}{{\stackrel{\mathrm{‾}}{v}}_z^{\mathrm{2}}/{\stackrel{\mathrm{‾}}{h}}_z}},\end{array}$$

with ${\stackrel{\mathrm{‾}}{v}}_l$ and h_l as the depth-averaged velocity and water depth for each increment l and ${\stackrel{\mathrm{‾}}{v}}_z$ and ${\stackrel{\mathrm{‾}}{h}}_z$ as the depth-averaged velocity and water-depth mean values for the cross-section, respectively. Based on this concept of variability, Guy and Norman (1970) prepared a nomograph that indicates the number of sampling verticals required for a desired maximum acceptable relative standard uncertainty as a function of the percentage of sand p_s and ξ.

The issue of the appropriate sampling time and the associated time averaging has been the subject of several studies. Topping et al. (2011) analyzed the temporal variability in sediment concentration among point samples and estimated the associated uncertainties for depth-integrated measurements. In addition, Gitto et al. (2017) concluded that a 9 to 12 min sampling time was required to get a representative point sample because of the temporal variability in sediment concentration.

Common methods to estimate the mean cross-sectional suspended-sand concentration and its uncertainty are subject to various limitations such as the interpolation and extrapolation of the suspended-sand concentration towards the riverbed and riverbank or the impractical feasibility of the International Organization for Standardization (2002) uncertainty method. Therefore, the first aim of this study is to introduce a method for computing the total suspended-sand flux with a high spatial resolution. That method combines point samples with ADCP measurements using a physically based understanding of suspended-sediment transport processes. A second aim is to provide a method to estimate the uncertainty related to this suspended-sand flux computation. Therefore, the uncertainties related to several sources of error such as discharge, lateral and vertical integration, and determined point concentrations are estimated and combined following the GUM framework.

First, the proposed sand discharge computing (SDC) method to estimate the suspended-sand concentration and the uncertainty in the sand flux is presented (Sect. 2). Then, this method is applied to four rivers across the world with different flow and sediment characteristics (Sect. 3). Finally, the methodology and presented results are discussed and further developments are suggested in Sect. 4.

We use the following notations:

• v is the water velocity perpendicular to the cross-section;

• u is the absolute standard uncertainty – that is, the standard deviation of the probability distribution of errors, “absolute” meaning expressed in the physical unit of the measurement (e.g., in m³ s⁻¹ for discharge);

• u^′ is the relative standard uncertainty, “relative” meaning expressed in percent of the measurement;

• U=ku is the absolute expanded uncertainty, with k a coverage factor taken as k=2, which corresponds to a 95 % probability interval if the distribution of errors is Gaussian;

• U^′ is the relative expanded uncertainty expressed in percent of the measurement result.

2 Method

2.1 General method

The proposed sand discharge computing (SDC) method combines ADCP velocity and discharge measurements performed in multiple transects with suspended-sand concentrations obtained by point samples distributed throughout the cross-section (Fig. 1). The point sand concentrations are interpolated vertically and laterally in the cross-section using a physically based method and Bayesian modeling. In the second part of the SDC method, several sources of error are estimated using novel and literature-based approaches and combined to estimate the uncertainty in suspended-sand flux measurements.

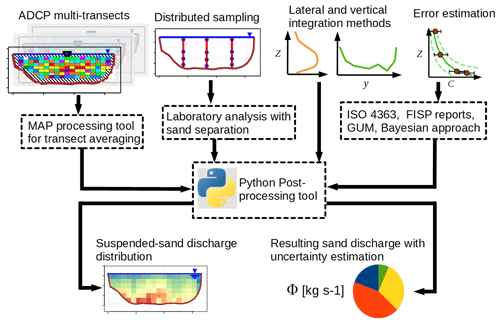
Figure 1 Workflow of the proposed sand discharge computing (SDC) method to estimate the suspended-sand flux distribution and the uncertainty in suspended-sand flux through a cross-section.

The SDC method focuses on suspended-sand flux measurements in simple river cross-sections without tidal effects or strong secondary currents. In the case of strong secondary flow cells causing deviations in the suspended-sand concentration from the dominant flow equilibrium, these deviations should be evaluated separately. Choosing an appropriate measurement site is essential to obtain reliable sand flux and uncertainty estimates (Edwards and Glysson, 1999).

2.2 Physically based method to integrate the concentration in the cross-section

2.2.1 Creating an ADCP multitransect averaged profile (MAP)

The multitransect averaged profile (MAP) method was developed to perform the SDC method proposed in thus study (Fig. 1) and implemented in QRevInt (Lennermark and Hauet, 2022) in 2023 (see the Supplement for a detailed description). A typical ADCP discharge measurement consists of the average of individual discharge measurements from successive ADCP transects. The MAP method includes each ADCP transect to generate an averaged transect profile from the bottom to the water surface including the unmeasured areas. This method developed with Python 3 (Van Rossum and Drake, 2009) is based on the QRevInt measurement output. QRevInt provides quality analysis and quality control, which allows having clean input data. For each ADCP discharge measurement, composed of several transects, one averaged MAP profile is computed with a regular grid for the whole cross-section (including the unmeasured areas). Major differences to similar tools like to the Velocity Mapping Toolbox (VMT) (Parsons et al., 2013) are that the MAP method can compute an average profile in the absence of a GPS positioning and that it allows the extrapolation of areas unmeasured by the ADCP.

First, the MAP method defines a straight average cross-section on the selected transects of the measurement. Then, these transects are projected using an orthogonal translation on the average cross-section. At this point, each transect is interpolated on the cross-section grid (Fig. 2b). The width and height of cells can be defined by the user. Once each transect is defined on the grid, MAP overlays them to average velocity and depth in each cell of the averaged cross-section (Fig. 2c–e). Finally, velocities are extrapolated to unmeasured areas (Fig. 2f). For edge extrapolation, banks are divided into the same shape meshes as the middle streamflow. Mean primary velocity ${\stackrel{\mathrm{‾}}{v}}_{\mathrm{p}}$ (Rozovskii, 1957) on each edge’s vertical is computed according to a power law:

$$\begin{array}{}\text{(4)}& {\stackrel{\mathrm{‾}}{v}}_{\mathrm{p}}={\stackrel{\mathrm{‾}}{v}}_{\mathrm{0}/l}{\left({\displaystyle \frac{x}{L_{\mathrm{edge}}}}\right)}^{\frac{\mathrm{1}}{m_{\mathrm{edge}}}},\end{array}$$

where x is the distance of the vertical from the start of the bank, L_edge is the length of the edge, m_edge is an edge-shape exponent (2.41 for a triangular edge, 10 for a rectangular edge; edge extrapolation is not computed otherwise), and ${\stackrel{\mathrm{‾}}{v}}_{\mathrm{0}/l}$ is the mean primary velocity from the closest measured vertical. Then, primary velocity on each edge's mesh v_p is computed following a power law with the QRevInt extrapolation exponent m_extrap:

$$\begin{array}{}\text{(5)}& v_{\mathrm{p}}={\stackrel{\mathrm{‾}}{v}}_{\mathrm{p}}{\displaystyle \frac{m_{\mathrm{extrap}}+\mathrm{1}}{m_{\mathrm{extrap}}}}{\left({\displaystyle \frac{z_{\mathrm{cell}}}{d}}\right)}^{\frac{\mathrm{1}}{m_{\mathrm{extrap}}}},\end{array}$$

where z_cell is the depth to centerline of mesh and d the depth on the vertical of the edge. Edge extrapolation of secondary velocity uses a linear law between the closest vertical and the edge. Vertical velocity on the edge follows the distribution of vertical velocities on the closest vertical. MAP thus generates a complete averaged profile with homogeneous cell sizes. Each cell contains information on its distance to the left bank and its depth and velocity components. Primary and secondary velocities are then transformed into stream-wise and cross-stream velocities in order to compute discharge.

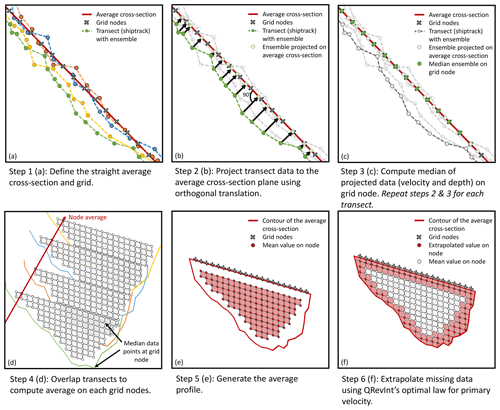
Figure 2 Workflow of the transect averaging procedure deployed by the multitransect averaged profile (MAP) method (based on Parsons et al., 2013).

2.2.2 Point sampling and laboratory analysis

In addition to the ADCP multitransects, point sampling distributed in the cross-section is performed (Fig. 1). Each suspended-sediment measurement follows the point sampling method and contains m verticals (typically three to seven) with N_sam samples per vertical (typically four to five). Two types of samplers, a Niskin water-trap-type sampler (instantaneous non-time-averaged sample; Filizola et al., 2009) and isokinetic samplers (US P-06; Spicer, 2019), were used in different rivers deployed from boats (Colorado, Rhône, and Amazon rivers) or cable cars (Colorado and Isère rivers). The target depth is set with a graduated tag line when deploying from the boat or using the depth information from the reel on the cable car. The sampler is equipped with a pressure sensor for post facto verification (for the Rhône, Isère, and Amazon rivers). An electrical valve allows the US P-06 samplers to collect a sample at the desired depth and for the desired sampling duration. For instantaneous samples, taken with the Niskin sampler, a traveler is sent down the rope to close the sampler. For the analysis of the suspended-sediment concentration of each sample, the standard procedure (option C) of the American Society for Testing and Materials (ASTM) (ASTM D3977, 2007) is applied, which consists of separating fine sediments and sand by wet-sieving prior to filtration of the fine sediments.

2.2.3 Vertical suspended-sand concentration profiles

A physically based method is applied to assign concentrations to individual cells (i,j) in each sampling vertical l (Fig. 1). It uses a theoretical vertical suspended-sand concentration profile estimated using a Bayesian approach to interpolate and extrapolate the sand concentrations vertically from point samples. The exponential vertical concentration profile proposed by Camenen and Larson (2008), based on a constant vertical diffusivity ϵ_v throughout the water column, is defined as

$$\begin{array}{}\text{(6)}& C\left(z\right)=C_{\mathrm{R}}\exp \left(\mathit{\alpha }z\right),\end{array}$$

where C(z) (kg m⁻³ or g L⁻¹) is the sediment concentration at elevation z above the bed, α is the vertical gradient in a logarithmic scale, and C_R is the bottom reference sediment concentration. Prior to the implementation of the Camenen and Larson (2008) profile, we compared empirically fitted Camenen and Larson (2008) and Rouse (1937) profiles. The differences in sand fluxes are lower than the uncertainty in sand flux of the respective measurement (see the Supplement). Moreover, the profile of Camenen and Larson (2008) is of practical interest in that it does not require arbitrarily defining a reference level. Consequently, we used only the Camenen and Larson (2008) profile for the Bayesian modeling in the SDC method. However, other vertical concentration profiles may be used as well and included in the toolbox.

To estimate the concentration profile C(z), the derived depth-averaged concentration, and its uncertainty $u_p^{\prime }$ due to vertical integration (Sect. 2.3.5), the Bayesian Modeling (BaM!) method is applied (Mansanarez et al., 2019). The BaM! method is based on Bayesian inference, which allows the computation of the posterior probability of a model's parameters from their prior probability and from observations. The model can then be applied to predict the distribution of a new, unobserved data point. The posterior distribution of the parameters is computed using Bayes' theorem, and a large number (> 10 000) of realizations are sampled using an adaptive block Metropolis Markov chain Monte Carlo (MCMC) sampler (Renard et al., 2006) varying the parameters α and ln (C(z)). A linear model is applied using logarithmic concentrations in milligrams per liter based on Eq. (6):

$$\begin{array}{}\text{(7)}& \ln \left(C\right(z\left)\right)=\ln \left(C_{\mathrm{R}}\right)-\left|\mathit{\alpha }\right|z.\end{array}$$

The first 5000 realizations are burned as a warm-up period, and then the last 5000 realizations are decimated to decrease the correlation in the results. The MaxPost profile $\ln \left(C_{n_{\mathrm{0}}}\right(z\left)\right)$, the best-fitting profile, is computed with the realization of parameters n₀ that maximizes the posterior distribution and is used for calculating the sand discharge. From this MaxPost profile, the concentration C_i,j in each cell (i,j) along vertical l can be determined. The MaxPost parameters $\ln \left(C_{\mathrm{R},n_{\mathrm{0}}}\right)$ and ${\mathit{\alpha }}_{n_{\mathrm{0}}}$ are retained and used for the lateral interpolation (Sect. 2.2.4).

BaM! requires the definition of the prior distribution of the equation parameters that are ln (C_R) and α here. Both $\left|\mathit{\alpha }\right|$ (to ensure increasing concentrations with depth) and C_R are strictly positive, and therefore they are assumed to follow lognormal distributions with parameters μ and σ. Consequently, ln (C_R) is assumed to follow a Gaussian distribution. The parameters μ_α and σ_α describing the prior distribution of α are the mean and standard deviation of the variable's natural logarithm, respectively. The expected values of α and C_R are evaluated based on local hydro-sedimentary parameters (Camenen and Larson, 2008), which are determined using ADCP depth and velocity, as well as bedload measurements. The expected value of C_R is calculated using the expression of Camenen and Larson (2008), which is a function of the sedimentological diameter D_*, the Shields parameter θ, and the critical bed shear stress θ_cr:

$$\begin{array}{}\text{(8)}& C_{\mathrm{R}}=\mathrm{1.5}{\mathrm{10}}^{\mathrm{3}}\mathit{\theta }\exp (-\mathrm{0.2}{D}_{*})\exp \left(-\mathrm{4.5}{\displaystyle \frac{{\mathit{\theta }}_{\mathrm{cr}}}{\mathit{\theta }}}\right).\end{array}$$

The sedimentological diameter, or dimensionless grain size, D_* is calculated as

$$\begin{array}{}\text{(9)}& D_{*}={\stackrel{\mathrm{‾}}{D}}_{\mathrm{50}}{\left({\displaystyle \frac{(s-\mathrm{1})g}{{\mathit{\nu }}^{\mathrm{2}}}}\right)}^{\mathrm{1}/\mathrm{3}},\end{array}$$

where ${\stackrel{\mathrm{‾}}{D}}_{\mathrm{50}}$ is the median diameter of the sand suspension averaged over the analyzed vertical, s=2.65 is the relative sediment density, g=9.81 m s⁻² is the acceleration due to gravity, and $\mathit{\nu }\approx {\mathrm{10}}^{-\mathrm{6}}$ m² s⁻¹ is the kinematic viscosity of water. The expected value of the prior distribution is then converted to ln (C_R). This reference concentration C_R differs significantly from the reference concentration for a Rouse profile, where the reference concentration is sensitive to the (more or less arbitrary) choice of the reference level, adding some complexity to evaluating the priors. Similarly, the expected value of α can be determined as (Camenen and Larson, 2008)

$$\begin{array}{}\text{(10)}& \mathit{\alpha }=-{\displaystyle \frac{\mathrm{6}{w}_{\mathrm{s}}}{{\mathit{\sigma }}_{\mathrm{t}}\mathit{\kappa }{v}_{*}h}},\end{array}$$

where w_s (m s⁻¹) is the settling velocity estimated following the formula of Soulsby and Whitehouse (1997), σ_t is the turbulent Schmidt number set equal to 1 as a first approximation, κ=0.41 is the von Kármán constant, v_* is the total shear velocity, and h is the water depth determined using ADCP measurements.

Defining the prior of α as lognormal ensures that it remains negative under all hydro-sedimentary conditions. This implies that the concentration decreases as a function of z away from the bed, thereby corresponding to Rouse mechanics for suspended-sediment computing (Rouse, 1937). The concentration of the finest sizes in suspension may increase away from the bed when the concentration of suspended sediment is relatively high due to the “squeezing” effect or density stratification (Hunt, 1969; McLean, 1992), leading to possible positive α values. We neglect these effects since we focus on sand with relatively low concentrations. Grain size information on vertical l is necessary to determine Eq. (8) and the settling velocity w_s and thus to estimate both ln (C_R) and α. In the case that they are not available, no prior parameters are defined and the model is fitted by BaM! on the observations only.

The second parameter σ_α of the lognormal distribution of α can be estimated by uncertainty propagation equations established following the Guide to the expression of Uncertainty in Measurement (GUM; JCGM, 2008). It is estimated based on the relative uncertainty $u_{\mathit{\alpha }}^{\prime }$ of α, supposing ${\mathit{\sigma }}_{\mathit{\alpha }}=u_{\mathit{\alpha }}^{\prime }$. This approximation works well for small values (< 0.5) of σ of the respective lognormal distribution. The parameter ${\mathit{\sigma }}_{\mathit{\alpha }}=u_{\mathit{\alpha }}^{\prime }$ is estimated by propagation from Eq. (10):

$$\begin{array}{}\text{(11)}& {u^{\prime }}_{\mathit{\alpha }}=\sqrt{{u^{\prime }}_{\mathrm{ws}}^{\mathrm{2}}+{u^{\prime }}_{\mathit{\sigma }\mathrm{t}}^{\mathrm{2}}+{u^{\prime }}_{\mathit{\kappa }}^{\mathrm{2}}+{u^{\prime }}_{\mathrm{v}*}^{\mathrm{2}}+{u^{\prime }}_h^{\mathrm{2}}}.\end{array}$$

Only a few studies have evaluated these uncertainties. Since additional experimental measurements are beyond the scope of this article, we define, based on the literature, the uncertainty in the settling velocity $u_{\mathrm{ws}}^{\prime }=\mathrm{5}\mathit{\%}$ (Camenen, 2007), the uncertainty in the turbulent Schmidt number $u_{\mathit{\sigma }\mathrm{t}}^{\prime }=\mathrm{20}\mathit{\%}$ (Gualtieri et al., 2017), $u_{\mathit{\kappa }}^{\prime }=\mathrm{0}$ (theoretical value with negligible variations; Smart, 2022), the uncertainty in the shear velocity $u_{\mathrm{v}*}^{\prime }=\mathrm{5}\mathit{\%}$ (Perret et al., 2023), and the uncertainty in the elevation of the sampled point within the water column $u_h^{\prime }=\mathrm{5}\mathit{\%}$ (Dramais, 2020). With these values, we obtain $u_{\mathit{\alpha }}^{\prime }=\sqrt{\mathrm{0.0475}}\approx \mathrm{21.8}\mathit{\%}$.

The second parameter ${\mathit{\sigma }}_{\ln \left(C_{\mathrm{R}}\right)}$, the standard deviation of ln (C_R), could also be determined by an uncertainty propagation derived from the data reduction equation of C_R (Eq. 8). However, it has been shown that the highest uncertainty is related to the structural uncertainty of the formula of C_R itself, not to its parametric uncertainty (Camenen et al., 2014). Indeed, the dataset used to establish the semi-empirical formula of Camenen and Larson (2008) is characterized by a large scatter, with differences of about 50 % between the measured and predicted concentration (other formulas also come with large structural uncertainty). Consequently, it is assumed that ${\mathit{\sigma }}_{\ln \left(C_{\mathrm{R}}\right)}=u_{C_{\mathrm{R}}}^{\prime }=\mathrm{50}\mathit{\%}$.

2.2.4 Lateral interpolation

The lateral interpolation of the suspended-sand concentration to calculate C_i,j in every cell of the MAP grid is based on a physical approach using the water depth as an index (Fig. 1). Following Camenen and Larson (2008), C_R is set proportional to the local bed shear stress, which can be assumed to be proportional to the water depth h if the friction slope is constant throughout the river cross-section (Khodashenas and Paquier, 1999; Camenen et al., 2011). Thus, the ratio $C_{\mathrm{R},j}/h_j$ of the reference concentration C_R and the water depth h for each column j in the MAP grid is estimated through linear interpolation along the cross-section. As a first approximation, α_j is assumed to be independent of the local bed shear stress, since it is mostly influenced by large-scale turbulence structures (Van Rijn, 1984). α_j varies linearly with horizontal distance between two adjacent sampling verticals (where α was estimated from the concentration profiles fitted to the samples) and remains constant between the first and last sampling vertical and the edge of the cross-section.

2.2.5 Determination of concentration C_i,j in each MAP cell (i,j)

The proposed SDC method is based on the discretization of the river cross-section by a regular grid fitted on the ADCP data (MAP grid) composed of N_j columns and N_i depth cells (Fig. 1). The general idea is to assign a concentration and discharge to each cell so that a flux per cell can be obtained after multiplication. The total cross-sectional sand flux Φ_total is calculated by summing up the suspended-sand fluxes per cell:

$$\begin{array}{}\text{(12)}& {\mathrm{\Phi }}_{\mathrm{total}}=\sum _{i=\mathrm{1}}^{N_i}\sum _{j=\mathrm{1}}^{N_j}{\mathrm{\Phi }}_{i,j},\end{array}$$

where Φ_i,j (kg s⁻¹) is the suspended-sand flux through one MAP cell i,j. The suspended-sand flux Φ_i,j can be calculated as

$$\begin{array}{}\text{(13)}& {\mathrm{\Phi }}_{i,j}=C_{i,j}{Q}_{i,j}=C_{i,j}{u}_{i,j}{w}_j{h}_{\mathrm{cell},i,j},\end{array}$$

where C_i,j (kg m⁻³ or g L⁻¹) and Q_i,j (m³ s⁻¹) are the suspended-sand concentration and liquid discharge through each cell (i,j), respectively; u_i,j (m s⁻¹) is the normal velocity component; w_j (m) is the width; and $h_{\mathrm{cell},i,j}$ (m) is the height of the ith vertical cell in the jth column in the MAP grid. The discharge Q_i,j through each cell is determined using the novel MAP method based on QRevInt (Lennermark and Hauet, 2022) and the suspended-sand concentration C_i,j is determined following the novel physically based SDC method.

The parameters α and C_R are evaluated for each MAP cell (i,j) applying the presented vertical and lateral integration. The suspended-sand concentration in each cell in the MAP grid is thus evaluated as

$$\begin{array}{}\text{(14)}& C_{i,j}={\displaystyle \frac{\mathrm{1}}{h}}\underset{z_{i,j}-h_{\mathrm{cell},i,j}/\mathrm{2}}{\overset{z_{i,j}+h_{\mathrm{cell},i,j}/\mathrm{2}}{\int }}{C}_{\mathrm{R},j}\exp \left({\mathit{\alpha }}_{j}z\right)\mathrm{d}z.\end{array}$$

2.3 Estimation of the uncertainty in measurements of suspended-sand flux through a cross-section

2.3.1 General method

The uncertainty $U_{\mathrm{\Phi }}^{\prime }$ in measurements of the suspended-sand flux through a cross-section is based on the calculation of suspended-sand flux (i.e., Eq. 2, Fig. 1). Therefore, the flux Φ is the product of discharge Q and mean cross-sectional concentration $\stackrel{\mathrm{‾}}{C}$: $\mathrm{\Phi }=Q\times \stackrel{\mathrm{‾}}{C}$. Thus, $U_{\mathrm{\Phi }}^{\prime }$ can be separated into a factor related to discharge $U_Q^{\prime }$ and one related to the concentration $U_{\mathrm{C}}^{\prime }$:

$$\begin{array}{}\text{(15)}& U_{\mathrm{\Phi }}^{\prime }=\sqrt{{U_Q^{\prime }}^{\mathrm{2}}+{U_{\mathrm{C}}^{\prime }}^{\mathrm{2}}}.\end{array}$$

Equation (15) is based on the hypothesis that the errors in discharge and concentration are independent; otherwise, the term has to include the associated covariances. Such an assumption that the errors are independent, however, appears to be reasonable. First, because discharge and concentration are measured independently, the discharge is measured using ADCPs and the concentration is determined using sampling and laboratory analyses. Second, the error sources in discharge and concentration are significantly different. Velocity lateral interpolation errors are negligible due to the high spatial resolution of ADCP measurements, whereas concentration lateral interpolation errors are large. We agree that these two error components are physically correlated, but this is not a problem as the first one is negligible.

To approximate the uncertainty $U_{\mathrm{\Phi }}^{\prime }$ in the suspended-sand flux through a cross-section, uncertainties $U_Q^{\prime }$ and $U_{\mathrm{C}}^{\prime }$ in the discharge and concentration both have to be determined (Fig. 3).

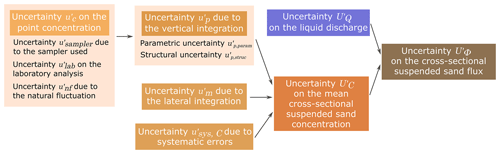
Figure 3 Flow diagram of the developed approach to estimate the uncertainty $U_{\mathrm{\Phi }}^{\prime }$ in the cross-sectional suspended-sand flux.

The uncertainty $U_Q^{\prime }$ in multiple-transect ADCP discharge measurements is calculated following the OURSIN method (Despax et al., 2023) as implemented in the open-source software QRevInt (Lennermark and Hauet, 2022). $U_{\mathrm{C}}^{\prime }$ is the combination of several uncertainty components (see Fig. 3) listed in Table 1 and detailed afterwards.

Guy and Norman (1970)Gordon, 2000

Table 1 Uncertainty components used to compute the uncertainty $U_{\mathrm{C}}^{\prime }$ in the mean cross-sectional suspended-sand concentration.

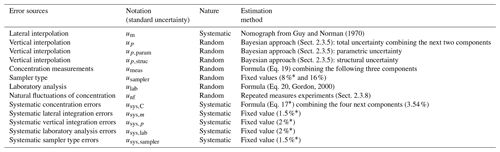
^* Value originating from International Organization for Standardization (2002).

2.3.2 Uncertainty $U_{\mathrm{C}}^{\prime }$ in the mean cross-sectional suspended-sand concentration

The uncertainty ${u^{\prime }}_{\mathrm{C}}^{\mathrm{2}}$ in the mean cross-sectional suspended-sand concentration is calculated as

$$\begin{array}{}\text{(16)}& {u^{\prime }}_{\mathrm{C}}^{\mathrm{2}}={u^{\prime }}_{\mathrm{sys},\mathrm{C}}^{\mathrm{2}}+{u^{\prime }}_m^{\mathrm{2}}+\sum _{l=\mathrm{1}}^m{\displaystyle \frac{{\mathrm{\Phi }}_l^{\mathrm{2}}}{{\mathrm{\Phi }}^{\mathrm{2}}}}{u^{\prime }}_{p,l}^{\mathrm{2}},\end{array}$$

where ${u^{\prime }}_{\mathrm{sys},\mathrm{C}}$ is the uncertainty due to systematic errors in the concentration, $u_m^{\prime }$ is the uncertainty due to the lateral integration based on the number m of verticals, $u_{p,l}^{\prime }$ is the total uncertainty due to the vertical integration estimated for each vertical l (see Fig. 3), and Φ_l is the suspended-sediment flux through vertical l.

2.3.3 Uncertainty due to systematic sources of error $u_{\mathrm{sys},\mathrm{C}}^{\prime }$

Following the International Organization for Standardization (2002) method, the uncertainty due to systematic sources of error u_sys,C is expressed as

$$\begin{array}{}\text{(17)}& {u^{\prime }}_{\mathrm{sys},\mathrm{C}}^{\mathrm{2}}={u^{\prime }}_{\mathrm{sys},m}^{\mathrm{2}}+{u^{\prime }}_{\mathrm{sys},p}^{\mathrm{2}}+{u^{\prime }}_{\mathrm{sys},\mathrm{lab}}^{\mathrm{2}}+{u^{\prime }}_{\mathrm{sys},\mathrm{sampler}}^{\mathrm{2}},\end{array}$$

where ${u^{\prime }}_{\mathrm{sys},m}$ is the uncertainty due to the systematic error of the flux computation scheme, ${u^{\prime }}_{\mathrm{sys},p}$ is the uncertainty due to the systematic error of the vertical integration, ${u^{\prime }}_{\mathrm{sys},\mathrm{lab}}=$ is the uncertainty due to the systematic error of the laboratory analysis, and ${u^{\prime }}_{\mathrm{sys},\mathrm{sampler}}$ is the uncertainty due to the systematic error of the sampler type since the underlying errors are assumed to be systematic. These terms, detailed in International Organization for Standardization (2002), remain constant, independently of the increasing number of sampling points or verticals (see Table 1).

2.3.4 Uncertainty $u_m^{\prime }$ due to lateral integration

To facilitate the application compared to the standardized approach (International Organization for Standardization, 2002), the uncertainty $u_m^{\prime }$ due to lateral integration is estimated based on Eq. (3) and the nomograph published by Guy and Norman (1970):

$$\begin{array}{}\text{(18)}& u_m^{\prime }=\mathrm{0.4}{p}_{\mathrm{s}}(\mathrm{1.43}\mathit{\xi }-\mathrm{1.37})m^{-\mathrm{0.7}},\end{array}$$

with p_s the percentage of sand in the suspension, ξ (see Eq. 3) the ${\stackrel{\mathrm{‾}}{v}}^{\mathrm{2}}/h$ index (Colby, 1964), and m the number of verticals. If only the suspended-sand flux through a cross-section is measured or is of principal interest, as in our study, the percentage of sand in the equation should be assumed to be 100 %, neglecting the influence of the fine sediment flux. This does not signify that no suspended fine sediments are present but allows taking into account the considerable lateral gradients of the sand suspension. It also avoids underestimating the uncertainty due to the lateral integration because the uncertainty $u_m^{\prime }$ for the same sediment discharge measurement (same m and ξ) is higher when assuming p_s=1 than including fine sediments. This approach is applied in our study, although the lateral interpolation applied differs slightly, as it is based on the water depth h and the parameters C_R and α of the vertical profiles. However, this approach is assumed to be consistent with our modified lateral interpolation.

2.3.5 Uncertainty $u_p^{\prime }$ due to vertical integration

The uncertainty ${u^{\prime }}_p$ is determined for each vertical l from the distribution of vertically integrated concentrations computed from the profiles estimated by the Bayesian approach described in Sect. 2.2.3. This uncertainty accounts for the uncertainty ${u^{\prime }}_{\mathrm{meas}}$ (estimated in Sect. 2.3.6) in point concentrations taken as observational data in the Bayesian inference. The integration of the previously obtained vertical concentration profiles ln (C_n(z)) (Sect. 2.2.3) allows the determination of the parametric uncertainty ${u^{\prime }}_{p,\mathrm{param}}$. However, computing the total uncertainty ${u^{\prime }}_p$ due to vertical integration requires the inclusion of structural errors at the elevation of the sampling points prior to the vertical integration. These structural errors are representative of the residuals between the point measurements and the exponential profiles. The structural uncertainty can be estimated from the total uncertainty ${u^{\prime }}_p$ and the parametric uncertainty ${u^{\prime }}_{p,\mathrm{param}}$: $u_{p,\mathrm{struc}}^{\prime }$ as $u{{}^{\prime }}_{p,\mathrm{struc}}^{\mathrm{2}}={u^{\prime }}_p^{\mathrm{2}}-{u^{\prime }}_{p,\mathrm{param}}^{\mathrm{2}}$.

The parametric uncertainty $u_{p,\mathrm{param}}^{\prime }$ can be determined from the distribution of concentration profiles ln (C_n(z)) computed in Sect. 2.2.3 (Fig. 4a). Each of these n profiles is converted to C_n(z) (Fig. 4b) and linearly interpolated by applying a trapezoidal integration to determine its depth-averaged concentration ${\stackrel{\mathrm{‾}}{C}}_n$, which is converted to $\ln \left({\stackrel{\mathrm{‾}}{C}}_n\right)$. Application of the entire procedure for all simulations n then yields a distribution of depth-averaged concentrations $\ln \left({\stackrel{\mathrm{‾}}{C}}_n\right)$. The mean value of this distribution is $\stackrel{\mathrm{‾}}{\ln \left(\stackrel{\mathrm{‾}}{C}\right)}$ and the standard deviation is the uncertainty $u_{p,\mathrm{param}}^{\prime }$ based on the assumption $\mathit{\sigma }=u_{p,\mathrm{param}}^{\prime }$ (Fig. 4c).

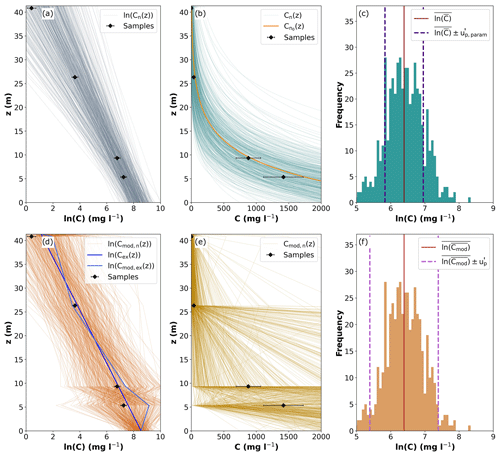
Figure 4 Workflow for the estimation of the uncertainty $u_p^{\prime }$ due to vertical integration, including the estimation of the parametric uncertainty $u_{p,\mathrm{param}}^{\prime }$ in panels (a), (b), and (c) and of the total uncertainty $u_p^{\prime }$ in panels (d), (e), and (f). (a, d) Vertical concentration profiles ln (C_n(z)) and ln (C_mod,n(z)), respectively, sampled through Bayesian interference and including the structural error and two exemplary profiles in (d). (b, e) Vertical concentration profiles C_n(z)=exp (ln (C_n(z))) and $C_{\mathrm{mod},n}\left(z\right)=\exp \left(\ln \right(C_{\mathrm{mod},n}\left(z\right)\left)\right)$, respectively, with the MaxPost profile $C_{n_{\mathrm{0}}}\left(z\right)$ in (b). (c, f) Histograms of depth-averaged concentrations $\ln \left({\stackrel{\mathrm{‾}}{C}}_n\right)$ and $\ln \left({\stackrel{\mathrm{‾}}{C}}_{\mathrm{mod},n}\right)$ with the mean depth-averaged concentrations $\stackrel{\mathrm{‾}}{\ln \left(\stackrel{\mathrm{‾}}{C}\right)}$ and $\stackrel{\mathrm{‾}}{\ln \left({\stackrel{\mathrm{‾}}{C}}_{\mathrm{mod}}\right)}$ as well as the standard deviations $u_{p,\mathrm{param}}^{\prime }$ and $u_p^{\prime }$, respectively.

To determine the structural error, the prior distribution of its standard deviation is defined as lognormally distributed with μ=0 and σ=1 in the BaM! method. For every sampling point at the elevation z, a normally distributed error with mean zero and standard deviation $u_{\mathrm{meas}}^{\prime }$ is defined. An error is then drawn from this distribution and added to the estimated concentration ln (C_n(z)) for every simulation n to obtain a modified vertical profile ln (C_mod,n(z)) (Fig. 4d). In the next step, the same procedure as for the estimation of $u_{p,\mathrm{param}}^{\prime }$ is applied: conversion of ln (C_mod,n(z)) to C_mod,n(z), vertical averaging to obtain ${\stackrel{\mathrm{‾}}{C}}_{\mathrm{mod},n}$, and conversion to $\ln \left({\stackrel{\mathrm{‾}}{C}}_{\mathrm{mod},n}\right)$. The mean value of the resulting distribution is the mean depth-averaged concentration $\stackrel{\mathrm{‾}}{\ln \left({\stackrel{\mathrm{‾}}{C}}_{\mathrm{mod}}\right)}$ and its standard deviation is the total uncertainty $u_p^{\prime }$ due to vertical integration based on the assumption $\mathit{\sigma }=u_p^{\prime }$ (Fig. 4f).

2.3.6 Uncertainty $u_{\mathrm{meas}}^{\prime }$ in point concentrations

As point concentration errors are accounted for in the Bayesian analysis of vertical concentration profiles, the uncertainty $u_{\mathrm{meas}}^{\prime }$ in point concentrations is already included in the uncertainty $u_p^{\prime }$ due to vertical integration. Therefore, in contrast to the International Organization for Standardization (2002) method, $u_{\mathrm{meas}}^{\prime }$ does not explicitly appear in Eq. (16). The uncertainty $u_{\mathrm{meas}}^{\prime }$ is calculated as

$$\begin{array}{}\text{(19)}& u_{\mathrm{meas}}^{\prime }=\sqrt{{u^{\prime }}_{\mathrm{sampler}}^{\mathrm{2}}+{u^{\prime }}_{\mathrm{lab}}^{\mathrm{2}}+{u^{\prime }}_{\mathrm{nf}}^{\mathrm{2}}},\end{array}$$

where $u_{\mathrm{sampler}}^{\prime }$ is the uncertainty due to the sampler type, $u_{\mathrm{lab}}^{\prime }$ is the uncertainty due to the laboratory analysis, and $u_{\mathrm{nf}}^{\prime }$ is the uncertainty due to natural fluctuations in sediment concentration arising from turbulence (Fig. 3).

Uncertainty $u_{\mathrm{sampler}}^{\prime }$ is due to the sampler type. Even though several comparisons have been conducted, the distribution of random errors related to a specific sampler type is difficult to assess. For example, a review of the values of $u_{\mathrm{sampler}}^{\prime }$ used in different studies is provided by Dramais (2020). In this study, the value suggested in the International Organization for Standardization (2002) standard is used for isokinetic samplers such as the US P-06: $u_{\mathrm{sampler}}^{\prime }=\mathrm{8}\mathit{\%}$. To account for the greater uncertainty arising from non-isokinetic sampling, this uncertainty is arbitrarily doubled for non-isokinetic samplers: $u_{\mathrm{sampler}}^{\prime }=\mathrm{16}\mathit{\%}$.

2.3.7 Uncertainty $u_{\mathrm{lab}}^{\prime }$ due to laboratory analysis

Many studies have estimated the random uncertainty related to the measurement of (fine) sediment concentration in the laboratory (e.g., by filtration). The ISO method estimates an uncertainty of 1.5 % due to the random error and an uncertainty of 2 % due to the systematic error (International Organization for Standardization, 2002). Based on an intercomparison study of different laboratories, Gordon et al. (2000) determined a standard uncertainty for the fine and sand fractions separately. We use the approach of Gordon et al. (2000) at the 68 % confidence level and a given sand concentration C (g L⁻¹) in the analyzed sample:

$$\begin{array}{}\text{(20)}& u_{\mathrm{lab}}^{\prime }=\mathrm{1.091}{C}^{-\mathrm{0.5}}.\end{array}$$

2.3.8 Uncertainty $u_{\mathrm{nf}}^{\prime }$ due to natural fluctuations

To approximate the uncertainty $u_{\mathrm{nf}}^{\prime }$ due to the natural fluctuations in concentration and grain size in the point samples arising from turbulence, a simplified method, similar to the ISO method or the “at-a-point error” (APE) (Topping et al., 2011), is applied. To this end, several points are repeated at different hydro-sedimentary conditions with a time difference of less than 1 h between the first and last sample, and the suspended-sand concentration C_i is calculated for each sample. One sampling point is repeated three to nine times and the mean sediment concentration ${\stackrel{\mathrm{‾}}{C}}_{\mathrm{rep}}$ of the respective set of measurements is determined. Based on the nomenclature of the International Organization for Standardization (2002), this mean concentration ${\stackrel{\mathrm{‾}}{C}}_{\mathrm{rep}}$ per set can be understood as the “approximate true value”. The relative standard deviation $u_{\mathrm{rep}}^{\prime }$ for each set of N_rep repetitions is then calculated following International Organization for Standardization (2002):

$$\begin{array}{}\text{(21)}& u_{\mathrm{rep}}^{\prime }=\sqrt{{\displaystyle \frac{{\sum }_{i=\mathrm{1}}^{N_{\mathrm{rep}}}{\left(\frac{C_i}{{\stackrel{\mathrm{‾}}{C}}_{\mathrm{rep}}}-\mathrm{1}\right)}^{\mathrm{2}}}{N_{\mathrm{rep}}-\mathrm{1}}}}.\end{array}$$

Performing this calculation for all repetitions, the relative uncertainty for each set of repetitions $u_{\mathrm{rep}}^{\prime }$ can be plotted versus the mean concentration ${\stackrel{\mathrm{‾}}{C}}_{\mathrm{rep}}$ per set (Fig. 5).

Figure 5 The relative uncertainty $u_{\mathrm{rep}}^{\prime }$ and mean concentration ${\stackrel{\mathrm{‾}}{C}}_{\mathrm{rep}}$ for each set of repetitions (these repetitions include data from the Isère, Colorado, Toutle, and Cowlitz rivers; Spicer, 2019). The relative uncertainty $u_{\mathrm{nf}}^{\prime }$ and the relative expanded uncertainty $U_{\mathrm{nf}}^{\prime }$ due to natural fluctuations correspond to the average and the average multiplied by a coverage factor of k=2 of all tested relative uncertainties $u_{\mathrm{rep}}^{\prime }$.

The number of sets of repetitions and tested hydro-sedimentary conditions within this study is limited compared to the variety of sampling conditions. In the best case, these measurements should be conducted on every sampling campaign; however, in reality, this is hardly possible using the presented measurement techniques. Using the same sampling protocol, the sampling campaign with many additional samples for the uncertainty estimation would take so long that the variation in river discharge would become too great. Therefore, a constant uncertainty $u_{\mathrm{nf}}^{\prime }=\mathrm{14.24}\mathit{\%}$ is determined based on these results and applied to all point measurements, which corresponds to the median of all tested relative uncertainty $u_{\mathrm{rep}}^{\prime }$. The enlarged uncertainty of $U_{\mathrm{nf}}^{\prime }=\mathrm{28.47}\mathit{\%}$ at a 95 % confidence interval roughly corresponds to the estimations made by Gitto et al. (2017) in the Fraser River (they found a 3 % to 33 % uncertainty range for individual 30 s samples). Furthermore, it should be noted that only a small range of hydro-sedimentary conditions at a given sampling location is sampled by this empirical approach. The uncertainties are probably higher than estimated here and may also be grain-size-dependent (Topping et al., 2011).

3 Application

3.1 Survey sites

The proposed SDC method was applied to four datasets from different rivers around the world. Each dataset includes suspended-sediment measurements following the protocol presented above and ADCP data.

3.1.1 Rhône River

The Rhône River is one of the major rivers of Europe, heading from the Rhône Glacier in the Alps and running through western Switzerland and southeastern France. Mostly a gravel-bed river, it is the largest silt and clay contributor to the Mediterranean sea (Delile et al., 2020). The presented measurements were conducted near the gaging station (V3000015) at Lyon Perrache (WGS84 coordinates: 45.742344, 4.826738), France, where the Rhône River drains a catchment of about 20 300 km² with a mean annual discharge of about 600 m³ s⁻¹ (Dramais, 2020).

3.1.2 Isère River

The Isère River is an Alpine river and the largest tributary of the Rhône River by suspended-sediment flux (Poulier et al., 2019). At Grenoble, France (WGS84 coordinates: 45.197747, 5.768566), where the measurements were conducted (gaging station W1410010) (Némery et al., 2013), the mean annual discharge is about 180 m³ s⁻¹ with a catchment area of 5700 km².

3.1.3 Colorado River

The Colorado River is one of the most iconic rivers in the western United States. The measurements took place at the U.S. Geological Survey (USGS) site above the Little Colorado River near the Desert View (WGS84 coordinates: 36.203484, −111.800917), Arizona, gaging station at River Mile 61. This station (number 09383100; U.S. Geological Survey, 2023) has a mean annual discharge of 306 m³ s⁻¹ and a catchment area of 296 000 km². Suspended sediments have been monitored for a long time in this area (Topping et al., 2021).

3.1.4 Amazon River

The Amazon River basin exceeds 6 000 000 km² in area. The Amazon River is the largest river in the world by discharge. The Manacapuru gauging station (14100000) is part of the Critical Zone Observatory HyBAm (Hydrology of the Amazon Basin) and is operated by the French National Research Institute for Sustainable Development (IRD), the Brazilian National Agency (ANA), and the Brazilian Geological Service (CPRM). This station has been used for more than 40 years by the Brazilian national hydrometric network to provide data on the Amazon (Solimões) River (WGS84 coordinates: −3.324377, −60.561183). At this station, the Amazon River watershed is approximately 2 × 10⁶ km² and average water discharge is about 103 000 m³ s⁻¹ (Filizola et al., 2009).

Those four survey sites, with various geomorphological conditions (see Table 2), were sampled according to the above-described ADCP measurement and point sampling procedures. The Isère River was sampled with an isokinetic US P-06 sampler and the other rivers with a water-trap-type sampler (Niskin).

Table 2 Hydraulic and morphological characteristics of the survey sites. Q_w is the total ADCP water discharge including extrapolation areas, Q_Meas. is the ADCP-measured water discharge (excluding extrapolations areas), $\stackrel{\mathrm{‾}}{v}$ is the mean cross-sectional velocity, the aspect ratio is the river width divided by mean depth, D₅₀ is the median diameter of suspended sand, p_s the percentage of sand in the suspension, ξ is an index relating stream velocity and depth, and $U_{\mathrm{\Phi }}^{\prime }$ is the expanded uncertainty in measurements of suspended-sand flux at the 95 % confidence level.

3.2 Vertical suspended-sand concentration and flux profiles

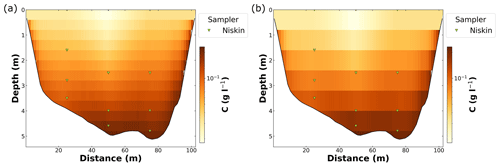
Measured suspended-sand point concentrations are fitted with an exponential profile to extrapolate the concentrations to the unmeasured parts of the water column and also interpolate between points. There is substantial vertical and lateral variability in suspended-sand concentration at all study sites (Fig. 6). Indeed, different vertical gradients α and/or reference concentrations C_R are observed among the measured verticals. The highest sand concentrations and largest gradients, with a difference of up to 3 orders of magnitude between the bottom and surface concentrations, are observed in the Amazon River (see Fig. 6d). This indicates a possible effect of the water depth on the concentration gradient through the vertical diffusion coefficient (inversely proportional to the water depth; Eq. 10) and/or due to dunes (whose height is typically proportional to the water depth and can therefore enhance the shear velocity). In contrast, the concentrations at the other sites range between 0.01 and 0.5 g L⁻¹. In the various surveys, sand concentration gradients are associated with particle size gradients, with coarser particles closer to the riverbed. The measured concentrations vary strongly at some verticals so that they do often not correspond to the fitted vertical concentration profiles, not even when taking the uncertainty $U_{\mathrm{meas}}^{\prime }$ in the point concentrations into account. This uncertainty usually varies for the presented samples between 20 % and 25 % at a 95 % confidence interval.

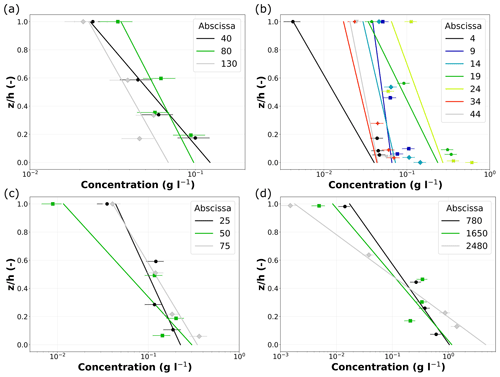
Figure 6 Measured sand concentrations with uncertainty $U_{\mathrm{meas}}^{\prime }$ and exponential fits (represented as colored lines) for each sampling vertical using Bayesian modeling for the (a) Rhône River at Lyon Perrache, (b) Isère River at the Grenoble campus, (c) Colorado River at River Mile 61, and (d) Amazon River at Manacapuru. The colors correspond to the sampling verticals, which are indicated by their distance in meters from the left bank, called abscissa.

Vertical profiles of suspended-sand flux (Fig. 7) are determined by multiplying the suspended-sand concentration in each cell in the MAP grid with the discharge in the same cell. Similarly, the point suspended-sand fluxes are the product of the point concentration and the discharge of the surrounding cell in the MAP grid. Consequently, decreasing fluxes close to the bed, as expected based on theory, are hardly or not at all visible for most verticals sampled in the Isère (Fig. 7b) and the Colorado (Fig. 7c). Large differences between the point fluxes and the profiles notably result from poorly fitted vertical concentration profiles, e.g., vertical 34 in the Isère River and vertical 1650 in the Amazon River. In other words, when the point concentrations do not follow an exponential profile, there are large differences between point fluxes and profiles.

Figure 7 Suspended-sand fluxes interpolated in each MAP cell along the sampling verticals (lines) and measured at the sampling points for the (a) Rhône River at Lyon Perrache, (b) Isère at Grenoble, (c) Colorado River at River Mile 61, and (d) Amazon River at Manacapuru. The colors correspond to the sampling verticals, which are indicated by their distance in meters from the left bank, called abscissa.

3.3 Suspended-sand flux through a cross-section

The suspended-sand concentration in each MAP cell (i,j) is calculated by applying the lateral interpolation and extrapolation of the profile coefficients C_R and α (Sect. 2.2.3). The spatial view of the cross-sections highlights the distribution of the suspended-sand concentration (Fig. 8). Different layers in some measurements appear due to the vertical and horizontal resolution of the ADCP data, i.e., the size of the MAP cells. As the vertical integration is based on the water depth, the lateral interpolation of the profile coefficients produces high concentrations near the bed, especially when there are large water depth variations and when vertical measurements are made on the deepest parts. This is clearly observed in Fig. 8d between the central and right sampling vertical on the Amazon.

Figure 8 Suspended-sand concentrations calculated with the SDC method in each cell of the MAP grid throughout the cross-section and location of the sampling points of the (a) Rhône River at Lyon Perrache, (b) the Isère River at the Grenoble campus, (c) the Colorado at River Mile 61, and (d) the Amazon River at Manacapuru (d).

The mean cross-sectional suspended-sand concentrations ${\stackrel{\mathrm{‾}}{C}}_{\mathrm{SDC}}$ and fluxes Φ_SDC computed with the SDC method are compared to the ISO method (International Organization for Standardization, 2002) using the relative differences ${\mathit{ϵ}}_{\mathrm{C}}=(C_{\mathrm{SDC}}-C_{\mathrm{ISO}})/C_{\mathrm{ISO}}$ and ϵ_Φ, respectively. The results for the suspended-sand concentration are in close agreement between the two methods, with ϵ_C ranging between −2 % and 3.5 % for three examples (Table 3), whereas a significant concentration difference is observed between the two methods for the Colorado computations (−15.8 %). The most likely hypothesis to explain this difference is that the surface sample at the middle of the transect has a relatively low sand concentration (abscissa 50, Fig. 6c). This low concentration heavily influenced the fit of the vertical profile and reduced the flux in this part of the cross-section, which is the place of the most intense flow. This highlights one of the limitations of the method when only a few points are used for suspended-sand flux computation in the cross-section.

Table 3 Mean cross-sectional suspended-sand concentrations and total fluxes for the four presented measurements using the ISO method and SDC method.

3.4 Suspended-sand uncertainty evaluation

The total uncertainty and the contribution of each error source to total variance are evaluated for the four measurements (Fig. 9). The absolute uncertainty at a 95 % confidence interval with a coverage factor of k=2 ranges between 19 % and 31 %. The main uncertainty components are the uncertainty $U_p^{\prime }$ due to vertical integration and the uncertainty $U_m^{\prime }$ due to lateral integration. The uncertainty $U_p^{\prime }$ is displayed as its two components, the parametric uncertainty $u_{p,\mathrm{param}}^{\prime }$ and the structural uncertainty $u_{p,\mathrm{struc}}^{\prime }$. The parametric uncertainty $u_{p,\mathrm{param}}^{\prime }$ is determined by the information from the priors and from the sampling points used to calibrate the model, particularly their number, distribution along the vertical, and uncertainty $u_{\mathrm{meas}}^{\prime }$. Increasing the number of samples and decreasing the uncertainty $u_{\mathrm{meas}}^{\prime }$ would decrease this uncertainty $u_{p,\mathrm{param}}^{\prime }$. In contrast, the structural uncertainty $u_{p,\mathrm{struc}}^{\prime }$ is estimated from the residuals of the fit of the model to the calibration points. The farther they are from the fitted vertical concentration profile and the lower their uncertainty, the greater the uncertainty $u_{p,\mathrm{struc}}^{\prime }$.

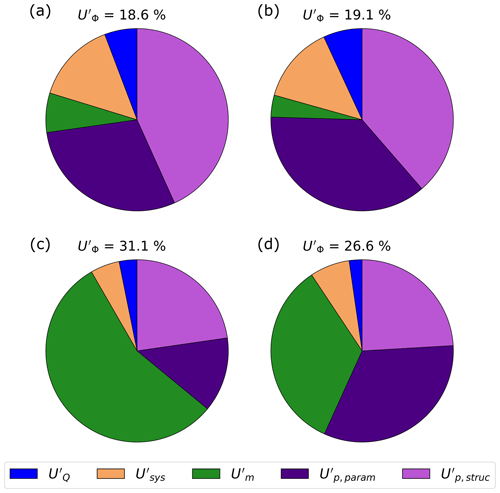
Figure 9 Total expanded uncertainty $U_{\mathrm{\Phi }}^{\prime }$ in suspended-sand flux and the relative contributions of uncertainty components to the total variance on the (a) Rhône River at Lyon Perrache, (b) on the Isère River at Grenoble, (c) on the Colorado at River Mile 61, and (d) on the Amazon River at Manacapuru. The five components are the expanded uncertainty $U_Q^{\prime }$ in the liquid discharge, the expanded uncertainty $U_{\mathrm{sys}}^{\prime }$ due to systematic sources of error, the expanded uncertainty $U_m^{\prime }$ due to the lateral integration of the concentration, the expanded parametric uncertainty $U_{\mathrm{param}}^{\prime }$ due to the vertical integration, and the expanded structural uncertainty $U_{\mathrm{struc}}^{\prime }$ due to the vertical integration.

The uncertainty $U_m^{\prime }$ is estimated from index ξ, representing the lateral homogeneity of the cross-section in terms of depth and discharge with the percentage of sand in the suspension and the number of sampling verticals. However, as only sand concentrations are considered here, the percentage of sand was set equal to 100 %. At relatively high ξ values, such as on the Colorado River, a larger number of verticals would have been required to decrease the uncertainty $U_m^{\prime }$, whereas this uncertainty is relatively low in a more uniform river like the Rhône River with a low ξ value. In that latter case, three verticals are sufficient to describe the lateral distribution of the concentration in the cross-section. The measurements on the Isère and Amazon rivers are both characterized by similar ξ. The large number of sampling verticals in the Isère River (seven) leads to a low uncertainty $U_m^{\prime }$, whereas the uncertainty and small number of sampling verticals in the Amazon River (three) lead to high uncertainty $U_m^{\prime }$. Nevertheless, it has to be taken into account that the lateral integration is based on the water depth, whereas the calculation of the uncertainty $U_m^{\prime }$ is based on ξ. These two different ways to conduct the lateral integration of the suspended-sand concentration and the uncertainty estimation may affect the results. The contributions of the uncertainties $U_Q^{\prime }$ in the liquid discharge and the systematic uncertainties $u_{\mathrm{sys}}^{\prime }$ to the uncertainty $U_{\mathrm{\Phi }}^{\prime }$ in the suspended-sand flux are typically low.

4 Discussion

4.1 A physically based method

The novel SDC method offers a number of advances for cross-sectional sediment flux measurement, especially the physically based integration of concentration.

For the vertical integration of concentration, the first step of the method is based on the fit of an exponential profile. The uncertainty related to the fit of this profile is estimated. As discussed in Camenen and Larson (2007), very similar results would have been obtained by fitting a Rouse profile (see the Supplement). However, another more detailed approach (Hunt, 1969; McLean, 1992) may provide a better fit and thus modify the results. Consequently, various theoretical approaches including the effects of suspended-sediment stratification or size distribution of sediment may be integrated into the toolbox, allowing us to choose the best-fitting semi-empirical model to the sampling conditions. Currently, only the exponential profile and the Rouse profile (not presented here but included in the code) are available in the toolbox.

The goodness of the fit, and thus the structural uncertainty, depends not only on the chosen profile, but also on the number and position of the sampling points. Dramais (2020) applied the same Bayesian approach and showed that the points measured close to the bed have a great influence on the reference concentration C_R value and on the slope α of the fitted exponential profile. In contrast, subsurface samples may in some cases bias the fit of the exponential profile. Interestingly, the best compromise was observed when sampling points are positioned close to the bed and for five samples per profile.

Depth-integrated measurements could be a solution to avoid errors due to the vertical interpolation, which occur with fitting point samples. However, with this protocol, lateral extrapolations and extrapolations in the unmeasured parts of the cross-section are not possible with a physical base. Depth-integrated samples could then be associated with a larger uncertainty.

The lateral integration of the concentration may be improved as well, even though the SDC method presents an advance by using the water depth as a proxy for the shear stress. The current method leads to artifacts of relatively high concentrations close to the riverbed within extrapolated areas (Fig. 8d). Moreover, the use of the parameters of the vertical concentration profile for the lateral integration increases the importance of a well-fitted vertical profile; otherwise, large uncertainties may result.

A major advance in the vertical integration, and particularly the lateral integration, may be made using the acoustic backscatter measured by the ADCP. One option is the use of the backscattered signal intensity as a proxy for suspended-sediment concentration, facilitating the interpolation and extrapolation between the sampling points. Moreover, several studies (Bouchez et al., 2011; Venditti et al., 2016; Szupiany et al., 2019) and some commercial software (e.g., ASET; Dominguez Ruben et al., 2020) focus on the vertical moving-boat backscatter inversion to gain information on suspended sediment. For the inversion of single-frequency applications as the ADCP, strong assumptions or calibrations are necessary to correctly estimate the concentration and grain size of silt–clay and sand-sized sediment (Vergne et al., 2023). Additionally, the issue of unmeasured areas close to the riverbed, surface, and banks persists and requires the extrapolation of the estimated concentrations, e.g., by applying theoretical suspended-sand transport formulas (Dominguez Ruben et al., 2020). However, when using the ADCP backscatter for the calculation of the concentrations, the errors in discharge and concentration would probably not be independent anymore because the same measurement method is used and the uncertainty due to the spatial integration of the concentration, the major error source of the uncertainty in concentration, will decrease. Consequently, the formulation of the uncertainty estimation should be adapted, e.g., by including the covariances.

4.2 A high-resolution ADCP data-based method

Our study proposes a general method which uses high-resolution ADCP data from successive transects. Compared to existing multitransect averaging tools, the newly developed ADCP multitransect averaged profile (MAP) provides an average dataset including the unmeasured areas. MAP uses RDI or SonTek raw binary files and reduces the pre-processing error, as it uses data quality filters from QRevInt. The method may use either the bottom track or the GPS as a reference and the user can customize vertical and lateral dimensions of the resulting grid cells. The obtained regular grid then facilitates the further analysis steps.

One limitation of the SDC method is the vertical and lateral integration of concentrations, which can be limited by the ADCP data resolution. The vertical and lateral integration of concentrations is evaluated on each MAP grid cell. Although this approach allows the estimation of concentrations close to the bed and banks, the size of the grid cells is limited by the size of the ADCP cells. Consequently, if the ADCP spatial resolution is low, the resulting mean concentration may be affected. An example of this problem is provided by the data from the Colorado River (Fig. 10), where cells were set with a height of approximately 0.4 m (Fig. 10a) and 0.8 m (Fig. 10b). In some cases, it could be meaningful to adapt the ADCP cells size to increase the resolution of the measurement and consequently increase the resolution of the resulting cross-sectional estimation of the distribution of the sediment flux (e.g., Vermeulen et al., 2014).

Figure 10 Influence of the vertical cell height on the cross-sectional suspended-sediment measurement in the Colorado River at River Mile 61, (a) with a cell height of 0.4 m and (b) with a cell height of 0.8 m.

4.3 A method open to various sampling protocols

Another advantage of the SDC method is its suitability to different point sampling protocols, with various numbers and locations of sampling points along the verticals and varying numbers of verticals. This flexibility is particularly useful when specific areas or depths are of major interest and require more detailed sampling or if the sampling points are not distributed in the cross-section following the ISO protocols. Also, it provides an estimation of the suspended-sand concentration close to the bed or banks in areas excluded by many methods such as the ISO method.

We evaluate the differences of the suspended-sand flux calculated using the proposed SDC method relative to the flux calculated using the ISO method using a larger dataset for Rhône River and Isère River that encompasses the detailed examples shown above. For these supplementary data, conditions were different but they were at the same locations. The relative difference ϵ_Φ ranges for all four studied rivers between −40 % and +23 % with no clear relationship with the total flux (Fig. 11). These values are lower than the estimated uncertainties, underlining the importance of the errors associated with the sand flux measurement. Similar observations can be made when using an empirically fitted Rouse profile instead of the exponential profile fitted with Bayesian modeling (see the Supplement). In comparison, typical ADCP water discharge measurements are characterized by an uncertainty of 5 %–12 % (results from several repeated experiments performed in France; Despax et al., 2019).

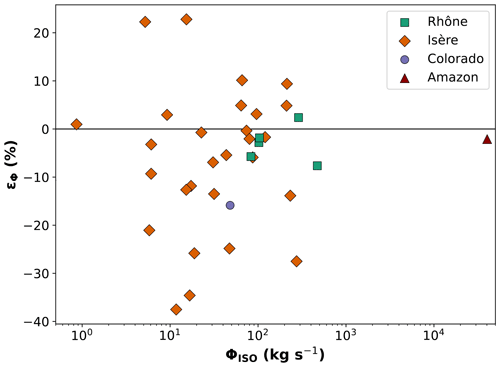
Figure 11 Relative difference ${\mathit{ϵ}}_{\mathrm{\Phi }}=({\mathrm{\Phi }}_{\mathrm{SDC}}-{\mathrm{\Phi }}_{\mathrm{ISO}})/{\mathrm{\Phi }}_{\mathrm{ISO}}$ as a function of the suspended-sand flux Φ_ISO determined using the ISO method for all four studied rivers. Φ_SDC is determined using the SDC method for all four studied rivers.

The relative differences between the sand fluxes calculated following the SDC method compared to the ISO method may reach up to 40 %, but no bias is visible. Extensive field and laboratory measurements under stable and known conditions are required to evaluate the performance of the two methods and determine the best among these two and other existing methods. Divergences may originate from the difference in the sampling protocols. The ISO method is based on a sampling protocol with seven points per vertical, where the samples are taken at precise relative depths, while four samples are typically taken per vertical and at varying relative depths in the present measurements. In addition, the SDC method may be more accurate than the ISO method at high discharges or deep water depths when it is difficult to lower the sampler close to the riverbed. However, accurate flux references are lacking in rivers, so this assumption cannot be verified experimentally.

4.4 A first estimation of the suspended-sand flux uncertainty

This method combines existing and novel approaches to estimate the uncertainty in the suspended-sand flux taking all error sources and their contributions into account in the uncertainty budget, which represents a major advance over the existing ISO method. The method is easy and fast to apply and contains no empirical calculation, except for the uncertainty $u_{\mathrm{nf}}^{\prime }$ in natural concentration fluctuations. Compared to the ISO method, this considerably reduces the required sampling time and effort, facilitating its application even for monitoring purposes. The price of this is additional assumptions on the spatial distribution of concentrations based on a simple physical basis valid for gauging cross-sections with a simple flow. Our method allows interpolating and extrapolating concentrations with a physically based approach. Furthermore, the introduced Bayesian approach to compute $u_p^{\prime }$ appears to be a promising way to analyze vertical concentration profiles and the related uncertainties.

This new approach has advantages, but certain limitations have already been identified. Here are some suggestions for correcting them or improving the code. Concerning the uncertainty estimation, major advances could be made by developing a more robust method for the estimation of the uncertainty $u_m^{\prime }$ due to the lateral integration, the uncertainty $u_{\mathrm{sampler}}^{\prime }$ due to the sampler, and the uncertainty $u_{\mathrm{nf}}^{\prime }$ due to the natural fluctuations. The major issue about the estimation of the uncertainty $u_m^{\prime }$ is its difference to the physical approach followed for the lateral integration of the concentration. The determination of the ${\stackrel{\mathrm{‾}}{v}}^{\mathrm{2}}/h$ index, ξ, accounts for the water depth and the stream velocity, whereas only the water depth is taken into account for the lateral interpolation of the concentration. Developing a consistent method for both uses that is adapted to various channel geometries and lateral concentration gradients is needed, e.g., following approaches developed for index–velocity relations (e.g., Kästner et al., 2018). Similarly, robust methods to estimate the uncertainty $u_{\mathrm{sampler}}^{\prime }$ due to the sampler and the uncertainty $u_{\mathrm{nf}}^{\prime }$ due to natural fluctuations for different settings should be developed. Finally, potentially uncovered error sources such as the uncertainty in the vertical position and the uncertainty related to the total sampling duration (Topping et al., 2011; Gitto et al., 2017) should be estimated and integrated as well. Moreover, the estimation of the prior distributions of α and ln (C_R) to estimate the uncertainty $u_p^{\prime }$ due to the vertical integration could be estimated as well. Other vertical concentration profiles may be included, and the best-fitting formula may be chosen, thereby limiting the uncertainty in the vertical integration.

4.5 An open-source method

A fully operational and open-source toolbox is available. This toolbox includes several options not presented in detail in this article, like the use of an empirically fitted Rouse profile. The code is relatively flexible and suitable for various conditions and protocols commonly applied in point sampling protocols. It allows the computation of suspended sand, but also the silt–clay concentration if available for various sampler types and deployment conditions. If silt–clay concentrations are available, the ratio of silt–clay concentration to sand concentration can be compared at each sampling point and also over the entire cross-section. The vertical position of the sampler may be determined as well as the transit time between the water surface and the final sampling depth if pressure sensor measurements are available. If available, the results of the flux measurements may be related to data from adjacent hydro-sedimentary gauging stations. If grain size data are available for several samples, they are visualized and a mean cross-sectional grain size distribution following International Organization for Standardization (2002) is calculated.

5 Conclusion

The new SDC method presented in this study allows meaningful determination of the suspended-sand flux through a river cross-section with uncertainty. Therefore, this method merges data from ADCP discharge measurements and point suspended-sediment samples. The SDC method includes a method for averaging several ADCP transects with discharge and velocity measurements on a regular grid in the entire cross-section is developed. Suspended-sand concentrations obtained by point sampling are then vertically interpolated by fitting a physically based exponential concentration profile and choosing the best fit using a Bayesian framework (BaM!). The lateral interpolation between the point samples and extrapolation in the unmeasured zones are performed on a physical basis. Both the vertical and lateral integrations allow the computation of the suspended-sand concentration for each ADCP grid cell and consequently the suspended-sand flux.

The toolbox presented in this article proposes a major advance in the estimation of the uncertainty in point suspended-sand sampling. It addresses several sources of error and integrates existing methods with novel approaches to propose an applicable framework. The main error sources are identified as u_m due to lateral integration and u_p due to vertical integration, thereby justifying the SDC method, which seeks to improve spatial integration in the whole cross-section.

The application of the methodology to several cross-sectional suspended-sand measurements conducted following different sampling protocols on four global rivers yields results that slightly differ from the ISO method (−15.9 % to +2.9 % suspended-sand flux difference). This approach can be easily used and is adaptable to different sampling cases; the only requirement is an ADCP discharge measurement including several transects and a point sample dataset. The data processing, analysis, and visualization toolbox are open-access and available online.

Future development may benefit from focusing on the incorporation of the acoustic backscatter measured by the ADCP to guide the vertical and lateral integration and on the development of more robust methods of estimating the uncertainties due to lateral integration, the sampler performance, and the natural fluctuations in concentration arising from turbulence.

Appendix A: Notations

Roman symbols
C	Suspended-sediment concentration (g L−1)
${\stackrel{\mathrm{‾}}{C}}_{\mathrm{ISO}}$	Mean cross-sectional sand concentration calculated using the ISO method (g L−1)
CR	Bottom reference sediment concentration (g L−1)
${\stackrel{\mathrm{‾}}{C}}_{\mathrm{rep}}$	Mean concentration per repetition set (g L−1)
d	Depth of the vertical on the edge (m)
D*	Sedimentological diameter (–)
${\stackrel{\mathrm{‾}}{C}}_{\mathrm{SDC}}$	Mean cross-sectional sand concentration calculated using the SDC method (g L−1)
${\stackrel{\mathrm{‾}}{D}}_{\mathrm{50}}$	Median diameter of the grain size distribution (m−1)
g	Acceleration due to gravity (m s−2)
i	Vertical MAP cell coordinate (–)
j	Lateral MAP cell coordinate (–)
h	Water depth (m)
hcell	Cell height (m)
k	Coverage factor (–)
k1	Coefficient relating the sand flux with the velocity (Colby, 1964) (–)
l	Increment, sampling vertical (–)
Ledge	Length of the edge in ADCP measurements (m)
$\ln \left(C_{n_{\mathrm{0}}}\right(z\left)\right)$	MaxPost best-fitting vertical concentration profile (g L−1)
$\ln \left(C_{\mathrm{R},n_{\mathrm{0}}}\right)$	MaxPost parameter (ln(g L−1)
medge	Edge-shape exponent in ADCP measurements (–)
mextrap	QRevInt extrapolation exponent (–)
n0	Parameters α and ln (CR) used to calculate the $\ln \left(C_{n_{\mathrm{0}}}\right(z\left)\right)$ MaxPost profile (–)
Nrep	Number of repetitions per set (–)
Nsam	Number of samples per vertical (–)
Nseg	Number of segments (–)
m	Number of verticals (–)
u	Absolute standard uncertainty
u′	Relative standard uncertainty (%)
$u_{\mathit{\alpha }}^{\prime }$	Uncertainty in the slope of the exponential profile α
$u_{C_{\mathrm{R}}}^{\prime }$	Uncertainty in the reference concentration CR (%)
$u_{\ln \left(C_{\mathrm{R}}\right)}^{\prime }$	Uncertainty in the logarithmic reference concentration ln(CR) (%)
$u_h^{\prime }$	Uncertainty in the elevation of the sampled point within the water column (%)
$u_{\mathrm{lab}}^{\prime }$	Uncertainty due to laboratory analysis (%)
$u_m^{\prime }$	Random uncertainty due to the lateral integration (%)
$u_{\mathrm{meas}}^{\prime }$	Uncertainty in the point concentration (%)
$u_{\mathrm{nf}}^{\prime }$	Random uncertainty due to natural fluctuations in the suspended-sediment concentration (%)
$u_p^{\prime }$	Total uncertainty due to the vertical integration (%)
$u_{p,\mathrm{param}}^{\prime }$	Parametric uncertainty due to the vertical integration (%)
$u_{p,\mathrm{struc}}^{\prime }$	Structural uncertainty due to the vertical integration (%)
${u^{\prime }}_Q^{\mathrm{2}}$	Uncertainty in the discharge of multiple transects (%)
$u_{\mathrm{rep}}^{\prime }$	Relative standard deviation for each set of Nrep repetitions (%)
$u_{\mathrm{sampler}}^{\prime }$	Uncertainty due to the sampler type (%)
${\stackrel{\mathrm{‾}}{u}}_{\mathrm{sys},\mathrm{C}}^{\prime }$	Uncertainty due to systematic errors in the suspended-sediment concentration (%)
$u_{\mathrm{sys},\mathrm{lab}}^{\prime }$	Uncertainty due to the systematic error of the laboratory analysis (%)
$u_{\mathrm{sys},m}^{\prime }$	Uncertainty due to the systematic error of the flux computation scheme (%)
$u_{\mathrm{sys},p}^{\prime }$	Uncertainty due to the systematic error of the vertical integration (%)
$u_{\mathrm{sys},\mathrm{sampler}}^{\prime }$	Uncertainty due to the systematic error of the used sampler type (%)
$u_{\mathrm{v}*}^{\prime }$	Uncertainty in the total shear velocity v* (%)
$u_{\mathrm{ws}}^{\prime }$	Uncertainty in the settling velocity ws (%)

Roman symbols
$u_{\mathit{\kappa }}^{\prime }$	Uncertainty in the von Kármán constant κ (%)
$u_{\mathit{\sigma }\mathrm{t}}^{\prime }$	Uncertainty in the turbulent Schmidt number σ (%)
U	Absolute expanded uncertainty
U′	Relative expanded uncertainty (%)
$U_{\mathrm{C}}^{\prime }$	Relative expanded uncertainty in measurements of the suspended-sediment concentration (%)
$U_m^{\prime }$	Relative expanded uncertainty due to the lateral integration (%)
$U_p^{\prime }$	Relative expanded uncertainty due to the vertical integration (%)
$U_{\mathrm{\Phi }}^{\prime }$	Relative expanded uncertainty in measurements of the suspended-sediment flux (%)
$U_Q^{\prime }$	Relative expanded uncertainty in measurements of the discharge (%)
${U^{\prime }}_Q^{\mathrm{2}}$	Relative expanded uncertainty in the discharge of multiple transects (%)
$U_{\mathrm{sys}}^{\prime }$	Relative expanded uncertainty arising from systematic sources of error (%)
ps	Percentage of sand in the suspension (%)
Q	Water discharge (m3 s−1)
qss	Suspended-sediment discharge per vertical (kg s−1)
s	Relative sediment density (–)
v	Water velocity perpendicular to the cross-section (m s−1)
$\stackrel{\mathrm{‾}}{v}$	Mean velocity (m s−1)
${\stackrel{\mathrm{‾}}{v}}_{\mathrm{p}}$	Mean primary velocity (m s−1)
${\stackrel{\mathrm{‾}}{v}}_{\mathrm{0}/l}$	Mean primary velocity from the closest measured vertical (m s−1)
v*	Total shear velocity (m s−1)
w	Cell width (m)
ws	Settling velocity (m s−1)
x	Distance of the vertical from the start of the bank (m)
X	East coordinate (MAP)
Xproj	East coordinate on the average cross-section (MAP)
Y	North coordinates (MAP)
Yproj	North coordinate on the average cross-section (MAP)
y	Lateral coordinate
ylb	Left boundary of the cross-section (m)
yrb	Right boundary of the cross-section (m)
z	Vertical coordinate
za	Reference level for suspension at the top of the bedload layer (m)
zcell	Depth to the centerline of the cell (m)

Greek symbols
α	Vertical gradient of the exponential vertical concentration profile (Camenen and Larson, 2008) (–)
${\mathit{\alpha }}_{\mathrm{R},n_{\mathrm{0}}}$	MaxPost parameter (–)
ϵv	Vertical diffusivity (m2 s−1)
ϵC	Relative difference in sand concentration determined by the SDC method compared to the ISO method (%)
ϵΦ	Relative difference in sand flux determined by the SDC method compared to the ISO method (%)
θ	Shields parameter (–)
θcr	Critical Shields parameter or critical bed shear stress (–)
κ	von Kármán constant (–)
μ	Parameter of the lognormal distribution
ν	Kinematic viscosity of water (m2 s−1)
ξ	Ratio of the squared mean velocity to the total sampled depth (Colby, 1964)
σ	Parameter of lognormal distribution, standard deviation of the normal distribution
σt	Turbulent Schmidt number (–)
ΦISO	Total suspended-sand flux through a cross-section calculated using the ISO method (kg s−1)
ΦSDC	Total suspended-sand flux through a cross-section calculated using the SDC method (kg s−1)
Φtotal	Total suspended-sand flux through a cross-section (kg s−1)