Testing floc settling velocity models in rivers and freshwater wetlands

Flocculation controls mud sedimentation and organic carbon burial rates by increasing mud settling velocity. However, calibration and validation of floc settling velocity models in freshwater are lacking. We used a camera, in situ laser diffraction particle sizing, and suspended sediment concentration–depth profiles to measure flocs in Wax Lake Delta, Louisiana. We developed a new workflow that combines our multiple floc data sources to distinguish between flocs and unflocculated sediment and measure floc attributes that were previously difficult to constrain. Sediment finer than ∼10 to 55 µm was flocculated with median floc diameter of 30 to 90 µm, bulk solid fraction of 0.05 to 0.3, fractal dimension of ∼2.1, and floc settling velocity of ∼0.1 to 1 mm s⁻¹, with little variation along water depth. Results are consistent with a semi-empirical model indicating that sediment concentration and mineralogy, organics, water chemistry, and, above all, turbulence control floc settling velocity. Effective primary particle diameter is ∼2 µm, about 2 to 6 times smaller than the median primary particle diameter, and is better described using a fractal theory. Flow through the floc increases settling velocity by an average factor of 2 and up to a factor of 7 and can be described by a modified permeability model that accounts for the effect of many primary particle sizes on flow paths. These findings help explain discrepancies between observations and an explicit settling model based on Stokes' law that depends on floc diameter, permeability, and fractal properties.

1 Introduction

Mud, defined as grains with diameters finer than 62.5 µm, constitutes the bulk of sediment load in large alluvial rivers and deltas (Walling and Fang, 2003; Cohen et al., 2022). Mud deposition can counteract land loss in coastal areas experiencing sea level rise, subsidence, and reduced sediment supply (Blum and Roberts, 2009; Syvitski et al., 2009). Fluvial mud also hosts abundant mineral-bound organic carbon and pollutants and is thus important to the global carbon cycle (Mayer, 1994; Galy et al., 2008; Blair and Aller, 2012) and water quality (Nelson and Lamothe, 1993; Pizzuto, 2014). Flocculation is key for understanding mud sedimentation because flocculation can drastically increase the in situ mud settling velocity (Lamb et al., 2020). Enhanced settling velocity affects mud exchange with the bed and bedform geometry (Partheniades, 1965; Schindler et al., 2015; Tran and Strom, 2019) and can ultimately alter landscape-scale mud transport (Nicholas and Walling, 1996; Craig et al., 2020; Zeichner et al., 2021).

Flocculation is the reversible process in which suspended sediment grains (i.e., primary particles) aggregate into larger and less dense particles called flocs, which can settle orders of magnitude faster than their primary particles (Chase, 1979; Winterwerp, 1998). Many physical, chemical, and biological factors affect flocculation like turbulence, sediment concentration and mineralogy, organics, and water chemistry (Kranck, 1984; Mietta et al., 2009; Nghiem et al., 2022). Researchers have long studied flocculation in estuaries and the ocean where salinity mainly affects flocculation (Kranck and Milligan, 1980; McCave, 1984; Hill et al., 2001). High salinity promotes flocculation because cations compress the electric double layer surrounding grains to the point that van der Waals attraction causes grains to aggregate (i.e., Derjaguin–Landau–Verwey–Overbeek, or DLVO, theory; Derjaguin and Landau, 1941; Verwey, 1947). However, recent studies have found widespread flocculation in rivers (Lamb et al., 2020; Nghiem et al., 2022). Much less is known about flocculation in freshwater where organic matter might instead be the main flocculating agent (Eisma et al., 1982; Lee et al., 2019; Zeichner et al., 2021). Organic matter biopolymers can bind sediment depending on charge interactions and adsorption kinetics (Yu and Somasundaran, 1996; Gregory and Barany, 2011), which classic DLVO theory cannot describe (Deng et al., 2023). Limited direct observations have shown that freshwater flocs are ∼10 to 100 µm in diameter and settle at ∼0.1 to 1 mm s⁻¹ (Droppo and Ongley, 1994; Krishnappan, 2000; Guo and He, 2011; Larsen et al., 2009; Osborn et al., 2021).

Although floc settling velocity is vital for understanding mud transport in rivers and freshwater wetlands, settling velocity models for freshwater flocs are still in their infancy. Many empirical models for estuarine flocs have been proposed (e.g., Gibbs, 1985; Manning and Dyer, 2007; Soulsby et al., 2013) but are not applicable to freshwater flocs because their parameters implicitly depend on sediment and water properties (e.g., Eisma, 1986). Strom and Keyvani (2011) derived a general floc settling velocity model by assuming that flocs are fractal aggregates and modifying the Stokes settling velocity theory to include floc density and permeability. We refer to this model as the “explicit model” because it predicts floc settling velocity from physical principles. The explicit model was validated against a data compilation of floc diameter and settling velocity measurements (Strom and Keyvani, 2011) but is difficult to apply because it relies on floc permeability and primary particle diameter, which are poorly constrained.

Alternatively, floc diameter and settling velocity can be predicted using a flocculation model. In a seminal study, Winterwerp (1998) developed a turbulence-driven flocculation model in which the relative rates of floc aggregation (due to particle collisions) and breakage (due to shear stress) set floc diameter and settling velocity. The Winterwerp model is a function of shear rate and sediment concentration, but the effects of other factors are not explicit. Nghiem et al. (2022) modified the Winterwerp model to include additional factors known to affect flocculation: organic matter, sediment mineralogy, and water chemistry. They fitted the model to a global river compilation. We refer to the Nghiem et al. (2022) model as the “semi-empirical model” because the fitted parameters empirically account for the effects of floc structure, density, and permeability on floc settling velocity. The semi-empirical model was calibrated on floc settling velocity inferred from sediment concentration–depth profiles using Rouse–Vanoni theory (Nghiem et al., 2022) but has yet to be verified against direct measurements.

Here we combined geochemical sampling, camera observations, in situ laser diffraction particle sizing, and Rouse–Vanoni analysis of sediment concentration–depth profiles in the freshwater Wax Lake Delta (WLD), Louisiana, USA, to examine these knowledge gaps: floc permeability and primary particle diameter in the explicit model and validation of the semi-empirical model. First, we review the floc theories (Sect. 2). We introduce the study area in Sect. 3. Next, we describe the field methods and data analysis to calculate floc properties (Sect. 4). Importantly, our complementary data sources provide new constraints on floc properties, allowing us to isolate floc concentration and size distribution and estimate floc permeability and primary particle diameter for the explicit model. These properties, along with floc solid fraction, fractal dimension, and settling velocity distribution, are reported in Sect. 5. In Sect. 6, we discuss the advantages of our data combination, practical considerations for predicting freshwater floc settling velocity, the physical interpretation of primary particle and permeability effects on floc settling velocity, and the leading role of turbulence in setting floc settling velocity.

2 Floc theory

2.1 Explicit model

The explicit model for floc settling velocity, w_s (m s⁻¹), is Stokes' law modified for flocs (Strom and Keyvani, 2011) and hence predicts w_s at the scale of the individual floc:

$$\begin{array}{}\text{(1)}& w_{\mathrm{s}}={\displaystyle \frac{R_{\mathrm{s}}g{D}_{\mathrm{p}}^{\mathrm{2}}}{b_{\mathrm{1}}\mathrm{\Omega }\mathit{\nu }}}{\left({\displaystyle \frac{D_{\mathrm{f}}}{D_{\mathrm{p}}}}\right)}^{n_{\mathrm{f}}-\mathrm{1}},\end{array}$$

where R_s is the submerged specific gravity of sediment (1.65), g is gravitational acceleration (9.81 m s⁻²), D_f (m) is floc diameter, and b₁ (dimensionless) is a shape factor assumed to be 20 (Ferguson and Church, 2004; see Sect. 6.3 for discussion). Equation (1) assumes that flocs are fractal aggregates (Kranenburg, 1994), for which a fractal solid fraction model applies:

$$\begin{array}{}\text{(2)}& \mathit{\phi }={\left({\displaystyle \frac{D_{\mathrm{f}}}{D_{\mathrm{p}}}}\right)}^{n_{\mathrm{f}}-\mathrm{3}},\end{array}$$

where φ (dimensionless) is the solid fraction, the volume fraction of the floc composed of mineral sediment. Although fractal theory is an approximation because floc structure is heterogeneous (e.g., Spencer et al., 2021), it has been well-tested for natural flocs (Kranenburg, 1994; Winterwerp, 1998; Dyer and Manning, 1999). Natural flocs contain many primary particle sizes, so D_p (m) is an effective primary particle diameter that is representative of the primary particle size distribution. Given D_f and D_p, the fractal dimension, $n_{\mathrm{f}}\in [\mathrm{1},\mathrm{3}]$ (dimensionless), quantifies the packing efficiency of primary particles. A compact solid grain has n_f=3, while a linear chain of primary particles has n_f=1. A typical fractal dimension for natural flocs is ∼2 (Kranenburg, 1994; Winterwerp, 1998). All else being equal, Eq. (2) indicates that smaller flocs are denser than larger flocs, and, in turn, the center of a given floc is denser than the edges.

The drag ratio, $\mathrm{\Omega }\in \left(\left.\mathrm{0},\mathrm{1}\right]\right.$ (dimensionless), quantifies floc drag force reduction caused by flow passing through a permeable floc (Neale et al., 1973). Specifically, Ω is the ratio of the drag force of the floc and that of an impermeable particle with the same density and diameter at the same flow velocity (Neale et al., 1973). Equivalently, Ω is the ratio of the settling velocity of the impermeable particle and that of the floc. If Ω=1, then the floc is impermeable. Ω<1 indicates a permeability-induced drag force reduction and settling velocity enhancement. Based on creeping flow theory, Ω decreases with permeability according to

$$\begin{array}{}\text{(3)}& \mathrm{\Omega }={\displaystyle \frac{\mathrm{2}{\mathit{\xi }}^{\mathrm{2}}\left(\mathrm{1}-\frac{\tanh \mathit{\xi }}{\mathit{\xi }}\right)}{\mathrm{2}{\mathit{\xi }}^{\mathrm{2}}+\mathrm{3}\left(\mathrm{1}-\frac{\tanh \mathit{\xi }}{\mathit{\xi }}\right)}},\end{array}$$

where the dimensionless permeability is ${\mathit{\xi }}^{-\mathrm{2}}=\mathrm{4}k{D}_{\mathrm{f}}^{-\mathrm{2}}$, and k (m²) is the floc permeability (Neale et al., 1973). Equation (3) shows that predicting Ω is tantamount to predicting ξ⁻².

The key inputs in the explicit model (Eq. 1) are floc diameter D_f, fractal dimension n_f, effective primary particle diameter D_p, and drag ratio Ω. Of these, D_p and Ω are the outstanding unknowns because prior studies have well-constrained floc diameter and fractal dimension (e.g., Jarvis et al., 2005; Strom and Keyvani, 2011). Cameras are commonly used to measure floc diameter and settling velocity, but these data alone cannot separate the effects of D_p and Ω (Dyer and Manning, 1999; Strom and Keyvani, 2011). As such, D_p and Ω must be estimated from additional relations as follows, but these relations have yet to be tested against observations of natural flocs in freshwater rivers and deltas.

Determining an effective primary particle diameter, D_p, as required for the explicit model (Eq. 1), is uncertain because each floc carries many primary particle sizes. D_p is typically assumed to be the mean or median of the primary particle size distribution (e.g., Syvitski et al., 1995; Strom and Keyvani, 2011). Alternatively, Bushell and Amal (1998) proposed a fractal D_p model:

$$\begin{array}{}\text{(4a)}& {\displaystyle }N{D}_{\mathrm{p}}^{n_{\mathrm{w}}}={\sum }_{i=\mathrm{1}}^N{D}_{\mathrm{p}i}^{n_{\mathrm{w}}},\text{(4b)}& {\displaystyle }N{D}_{\mathrm{p}}^{n_{\mathrm{f}}}={\sum }_{i=\mathrm{1}}^N{D}_{\mathrm{p}i}^{n_{\mathrm{f}}},\text{(4c)}& {\displaystyle }{D}_{\mathrm{p}}={\left({\displaystyle \frac{\sum D_{\mathrm{p}i}^{n_{\mathrm{w}}}}{\sum D_{\mathrm{p}i}^{n_{\mathrm{f}}}}}\right)}^{\frac{\mathrm{1}}{n_{\mathrm{w}}-n_{\mathrm{f}}}},\end{array}$$

where D_pi is the diameter of the ith primary particle in the floc and N is the number of primary particles in the floc. Equation (4a) shows that the effective primary particles of diameter D_p must have the same physical dimension, set by the weighting dimension, n_w (dimensionless), as the original primary particles. For example, n_w=3 means that total primary particle volume is preserved. n_w=0 means that the number of primary particles is preserved. By analogy, Eq. (4b) shows that the effective primary particles must also fill the same n_f-dimensional space as the original primary particles. Bushell and Amal (1998) combined Eq. (4a) and (4b) to obtain a fractal D_p model (Eq. 4c). The mean or median of the primary particle size distribution does not satisfy such conditions and thus might be very different from the fractal D_p. Equation (4c) has been validated using light-scattering experiments on synthetic grains (Bushell and Amal, 2000). Since we could only resolve D_p over floc populations and not at the level of single flocs (Sect. 4.6.2), we followed Gmachowski (2003) and extended Eq. (4c) to average over the primary particle size distribution:

$$\begin{array}{}\text{(5)}& D_{\mathrm{p}}=(\stackrel{\mathrm{‾}}{D_{\mathrm{p}}^{n_{\mathrm{w}}}}/\stackrel{\mathrm{‾}}{D_{\mathrm{p}}^{n_{\mathrm{f}}}}{)}^{\mathrm{1}/(n_{\mathrm{w}}-n_{\mathrm{f}})},\end{array}$$

where the overbars denote calculating the moment using the number-based primary particle size distribution. We evaluate Eq. (5) herein for natural flocs.

Existing analytical permeability models can struggle to predict Ω (Eq. 3) because natural flocs do not fulfill model assumptions of uniformly sized primary particles and uniform porosity (Eq. 2). Several experimental studies observed particularly high floc permeability incompatible with typical permeability models altogether (e.g., Johnson et al., 1996; Li and Logan, 1997). Using a data compilation of field and lab flocs, Strom and Keyvani (2011) found that the classic Brinkman permeability model, which is based on drag theory for a cluster of uniformly sized grains (Brinkman, 1947), vastly overestimated the inferred Ω for flocs with n_f<2. However, their conclusion is uncertain because they calculated Ω using reported primary particle diameters that might not reflect effective primary particle diameters. Kim and Stolzenbach (2002) found that the empirical Davies permeability model (Davies, 1953),

$$\begin{array}{}\text{(6)}& {\mathit{\xi }}^{-\mathrm{2}}={\left({\displaystyle \frac{D_{\mathrm{p}}}{D_{\mathrm{f}}}}\right)}^{\mathrm{2}}{\left[\mathrm{16}{\mathit{\phi }}^{\mathrm{1.5}}\left(\mathrm{1}+\mathrm{56}{\mathit{\phi }}^{\mathrm{3}}\right)\right]}^{-\mathrm{1}},\end{array}$$

predicted the hydrodynamic force on simulated permeable fractal aggregates well. Like the Brinkman model, the Davies model predicts ξ⁻² (and hence Ω through Eq. 3) given φ and n_f because ${\left(D_{\mathrm{p}}/D_{\mathrm{f}}\right)}^{\mathrm{2}}={\mathit{\phi }}^{\mathrm{2}/\left(\mathrm{3}-n_{\mathrm{f}}\right)}$ (Eq. 2). Modified permeability models have been proposed to capture the fact that clustering of primary particles might create macropores that disproportionately set permeability (Li and Logan, 2001; Woodfield and Bickert, 2001). In particular, Li and Logan (2001) replaced D_p with a larger cluster diameter, D_c (m), in any given permeability equation (e.g., Brinkman or Davies model). We tested the abilities of the Brinkman and Davies models and their Li and Logan variants, each coupled with Eq. (3), to describe drag ratio estimates.

2.2 Semi-empirical model

The semi-empirical model is the Winterwerp (1998) model as modified by Nghiem et al. (2022). Unlike the explicit model, the semi-empirical model predicts values representative of a floc population (Winterwerp, 1998) rather than those of individual flocs. At equilibrium between floc growth and breakage, the Winterwerp model predicts floc diameter, $D_{\mathrm{f}}=\left(k_A/k_B\right)C\mathit{\eta }\sqrt{F_y/\left(\mathit{\rho }{\mathit{\nu }}^{\mathrm{2}}\right)}$, in which k_A and k_B (dimensionless) are the floc aggregation and breakage efficiencies, ρ is water density (1000 kg m⁻³), ν is water kinematic viscosity (10⁻⁶ m² s⁻¹), F_y is the floc yield force (N), and C (dimensionless) is the volumetric sediment concentration. The Kolmogorov microscale, η (m), is the length scale of the smallest turbulent eddies in the flow and scales inversely with turbulence intensity (Tennekes and Lumley, 1972).

The semi-empirical model (Nghiem et al., 2022) includes the effects of organic matter, sediment mineralogy, and water chemistry in $k_A/k_B$ using standard geochemical variables measured from river sediment and water samples, which are often more readily available than the floc parameters in the explicit model. The semi-empirical model predicts w_s, D_f, and floc cutoff diameter, D_t (m), which is the threshold grain diameter between significantly flocculated (finer) and unflocculated (coarser) sediment. Using D_t, w_s, and D_f inferred from a global river data compilation of sediment concentration–depth profiles, Nghiem et al. (2022) calibrated the model:

$$\begin{array}{}\text{(7a)}& {\displaystyle }\begin{array}{rl}{D}_{\mathrm{t}}& =\mathrm{0.134}{\left(\mathit{\eta }{\stackrel{\mathrm{̃}}{D}}_{\mathrm{p},\mathrm{50}}\right)}^{\mathrm{1}/\mathrm{2}}{\left(C_{\mathrm{m}}{\mathit{\theta }}^{\mathrm{2}}{\left(\mathrm{1}-\mathit{\theta }\right)}^{\mathrm{2}}\right)}^{\mathrm{0.0734}}\\ & {\left(\mathrm{Al}/\mathrm{Si}\right)}^{-\mathrm{0.774}}{\mathrm{\Phi }}^{-\mathrm{0.180}},\end{array}\text{(7b)}& {\displaystyle }\begin{array}{rl}{w}_{\mathrm{s}}& ={\displaystyle \frac{R_{\mathrm{s}}g{\stackrel{\mathrm{̃}}{D}}_{\mathrm{p},\mathrm{50}}}{\mathrm{20}\mathit{\nu }}}\mathrm{0.306}\mathit{\eta }{\left(C_{\mathrm{m}}{\mathit{\theta }}^{\mathrm{2}}{\left(\mathrm{1}-\mathit{\theta }\right)}^{\mathrm{2}}\right)}^{\mathrm{0.167}}\\ & {\left(\mathrm{Al}/\mathrm{Si}\right)}^{-\mathrm{2.15}}{\mathrm{\Phi }}^{-\mathrm{0.0358}},\end{array}\text{(7c)}& {\displaystyle }\begin{array}{rl}{D}_{\mathrm{f}}& =\mathrm{0.0180}\mathit{\eta }{\left(C_{\mathrm{m}}{\mathit{\theta }}^{\mathrm{2}}{\left(\mathrm{1}-\mathit{\theta }\right)}^{\mathrm{2}}\right)}^{\mathrm{0.147}}{\left(\mathrm{Al}/\mathrm{Si}\right)}^{-\mathrm{1.55}}\\ & {\mathrm{\Phi }}^{-\mathrm{0.360}}.\end{array}\end{array}$$

The variables in the semi-empirical model (Eq. 7) describe the depth-averaged floc population because the floc calibration data are depth-averaged. Accordingly, depth-averaged mud volume concentration, C_m (dimensionless), is the representative sediment concentration for flocculation because, although sand can be incorporated in flocs (Whitehouse et al., 2000; Manning et al., 2010), mud is typically far more abundant (Lamb et al., 2020; Osborn et al., 2021). Depth-averaged median primary particle diameter, ${\stackrel{\mathrm{̃}}{D}}_{\mathrm{p},\mathrm{50}}$ (m), is taken as the primary particle size metric. Sediment Al $/$ Si (molar ratio) represents mineralogy because clay minerals are enriched in Al $/$ Si compared to feldspar and quartz (e.g., Galy et al., 2008; Bouchez et al., 2014). θ (dimensionless) is the organic cover fraction, the fraction of the sediment grain surface covered with organic matter (Smellie and LaMer, 1958). Relative charge density, Φ (dimensionless), quantifies the effect of salinity and sediment mineralogy on flocculation using diffuse double-layer theory (Rommelfanger et al., 2022). Φ is the ratio of net cation charge in solution and that at the surface of sediment grains. Flocculation is expected at higher values of Φ where the cation concentration overcomes the negative charges on the surfaces of clay minerals.

In this study, we combined floc and geochemical measurements in the Wax Lake Delta to constrain explicit model parameters and verify the semi-empirical model. Our objective for the explicit model is to evaluate primary particle diameter and floc permeability theory because these parameters have not been fully tested before for natural flocs. Our objective for the semi-empirical model is to validate it using direct observations of floc diameter and settling velocity.

3 Study site

We conducted fieldwork in the Wax Lake Delta, a river-dominated freshwater delta in the Mississippi River Delta complex (Fig. 1a, b). The lower Mississippi River conveys water and sediment to WLD via the Atchafalaya River and Wax Lake Outlet, which was dredged in 1942 (Fig. 1b; Latimer and Schweizer, 1951). The topset of WLD became subaerial after the 1973 Mississippi River flood and has since been aggrading and prograding into the Gulf of Mexico with little human intervention (Roberts et al., 1980; Jensen et al., 2022). Interactions between the river, tides, wind, and vegetation cause wide variability in delta island inundation, which can expose and submerge many of the levees along island margins (Geleynse et al., 2015). Despite the proximity of WLD to the Gulf of Mexico, the water remains fresh even during low river discharge (Holm and Sasser, 2001).

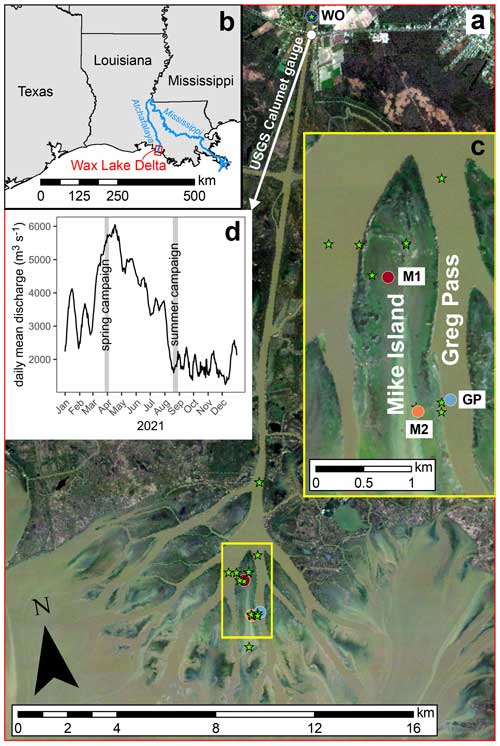
Figure 1 (a) Map of Wax Lake Delta, Louisiana, with sample sites. Circles indicate main sample sites with sediment concentration–depth and LISST profiles. Stars indicate additional sediment concentration–depth profile sites without LISST and floc cam measurements. The satellite image is from January 2021 – Image © 2021 Planet Labs PBC – at relatively low discharge and tide to highlight the full island extents. (b) Map of the Louisiana coast region. (c) Inset map of Mike Island and Greg Pass. The satellite image is the same as that in panel (a) – Image © 2021 Planet Labs PBC. (d) A 2021 hydrograph of Wax Lake Outlet at Calumet, LA (USGS stream gauge 07381590). Gray bands indicate fieldwork periods.

We completed fieldwork in WLD during March and April 2021 (spring campaign) and August 2021 (summer campaign) as part of the NASA Delta-X project. During the spring campaign, the discharge into WLD was ∼5500 m³ s⁻¹, which is near the peak for 2021 (Fig. 1d). During the summer campaign, the discharge was ∼1800 m³ s⁻¹ and is close to the low discharge for the year. We studied four sites: Wax Lake Outlet (WO), Greg Pass (GP), northern Mike Island (M1), and southern Mike Island (M2) (Fig. 1a, c). Site WO is about 20 km upstream of the delta apex. Site GP is near the center of Greg Pass, the distributary channel east of Mike Island. Sites M1 and M2 on Mike Island are in a tidally forced shallow wetland. We sampled all sites during the spring campaign but only sampled site GP during the summer campaign. At each site, we collected vertical profiles of suspended sediment samples (i.e., concentration–depth profiles) and in situ particle size distributions and concentrations with a Sequoia Scientific LISST-200X (LISST) instrument. We collected eight profiles with paired LISST and sample measurements. We took floc images with a camera system (floc cam) for four profiles. We sampled 16 additional concentration–depth profiles distributed throughout WLD without matching LISST or floc cam data, including one profile in October 2019 during a separate field campaign. We also collected water samples to measure major cation and anion concentrations at 20 profile sites and dissolved inorganic carbon (DIC) concentration at 15 profile sites.

4 Methods

Herein we use the terms “grain” or “sediment” to mean the solid disaggregated mineral sediment, which might or might not have been flocculated in situ. As is standard in the flocculation literature, we use “primary particle” to refer to the constituent sediment grains inside flocs. We use “particle” alone (i.e., without “primary”) to refer generically to the in situ suspended material, which includes flocs and unflocculated sediment. This nomenclature is standard throughout the paper and is critical for distinguishing between flocs, unflocculated sediment, and fully dispersed sediment.

We designed our field methods to measure all variables in the explicit and semi-empirical models and test their floc settling velocity predictions. We collected sediment concentration–depth profiles and acoustic Doppler current profiler (ADCP) flow velocity measurements (Sect. 4.1). We measured the major ion concentrations of the water, sediment organic matter concentration, and sediment elemental composition (Sect. 4.2). The primary floc data sources are in situ particle sizing with LISST (Sect. 4.3), a camera (Sect. 4.4), and analysis of suspended sediment concentration–depth profiles (Sect. 4.5), each with different advantages and limitations. In situ particle sizing measures in situ particle size distribution and concentration using laser diffraction (e.g., Agrawal and Pottsmith, 2000; Guo and He, 2011) but cannot distinguish between flocs and unflocculated sediment. Although laser diffraction might be sensitive to primary particles within flocs (Graham et al., 2012), studies have found good agreement between floc size distributions measured by camera and laser diffraction (Mikkelsen and Pejrup, 2001; Mikkelsen et al., 2005). Cameras directly measure floc size and settling velocity (e.g., Mikkelsen et al., 2004; Benson and French, 2007; Osborn et al., 2021). However, camera methods require reliable image processing algorithms, can be limited by the small number of identifiable flocs, and cannot detect flocs finer than the pixel resolution. Depth-averaged floc settling velocity can be inferred from stratification in grain-size-specific sediment concentration–depth profiles (Lamb et al., 2020; Nghiem et al., 2022), but this technique is indirect and does not reveal floc diameter. We combined these data sources in novel ways (Sect. 4.6) to derive the floc variables (floc diameter, floc settling velocity, fractal dimension, effective primary particle diameter, and drag ratio) required to test theory and the floc settling velocity models.

Table 1 Estimated floc variables and their data sources. The variables are listed by order in the data processing workflow. In the column “Data source”, “sediment” refers to sediment grain size distribution, concentration, and/or Rouse–Vanoni equation fitting results. The primary data source (if any) is listed first. In the “Description” column, the data sources are indicated in parentheses next to input variables if there are multiple sources.

4.1 Sediment sampling and hydrodynamic measurements

Nghiem et al. (2021) describe our sediment sampling and lab analysis in full, which are summarized here. For each profile, we collected suspended sediment samples at different heights above the bed from a boat with a Van Dorn sampler. At the channel sites (WO and GP), we collected samples isokinetically by drifting over the target location at the local current speed (Edwards and Glysson, 1999). We sampled while stationary at the wetland sites (M1 and M2) because of the relatively slow flow velocities inside the wetland (∼0.1 m s⁻¹). We also sampled bed sediment with a Ponar grab sampler and shallow sediment cores using a piston core to supplement the samples for X-ray fluorescence (XRF) analysis (Sect. 4.2). We filtered each sample through 0.2 µm pore size polyethersulfone filter paper (Sterlitech) and froze the filtered sediment. In the lab, we dried and weighed samples to measure sediment concentration. We decarbonated, oxidized, and deflocculated an aliquot of each sample for grain size analysis following Douglas et al. (2022) to fully disperse the sediment.

We measured the volume-based grain size distribution using a Malvern Mastersizer 3000E laser diffraction analyzer with the non-spherical scattering model from 0.2 to 2100 µm in 100 logarithmically spaced bins. This method calculates the grain size distribution using Mie theory to model light scattering from particles. Mie theory is sensitive to the refractive index, RI, and absorption index, AI, of the particles. We determined appropriate values of these optical properties for each measurement using the Mastersizer's optical property optimizer, which finds the best values to minimize the difference between measured and modeled light-scattering intensity (Rawle, 2015; Malvern Panalytical, 2024). We limited RI between 1.5 and 1.7, which covers the range of common sedimentary minerals (Özer et al., 2010), and AI between 0.001 and 0.01, which we empirically found to best suit our samples. The median optimized RI and AI across all measurements are 1.57 and 0.01, respectively. For each concentration–depth profile, we calculated the depth-averaged grain size distribution by depth-averaging the concentration in each grain size class with the trapezoidal rule and renormalizing the depth-averaged concentrations. We extrapolated a constant concentration in the unmeasured regions below the deepest measurement and above the shallowest measurement for the integration. We summed the class-specific depth-averaged concentrations to obtain the total depth-averaged sediment concentration. To obtain depth-averaged mud concentration, C_m, for the semi-empirical model, we summed the concentrations in the mud classes only.

We measured flow velocity profiles using a Teledyne RiverPro ADCP instrument concurrent with suspended sediment sampling. We deployed the ADCP near the water surface looking downward. The ADCP measured the flow velocity profile to within 5 to 15 cm of the bed at a frequency of ∼1 Hz. We averaged about 100 to 1000 velocity profiles for the island sites and about 50 for the channel sites to obtain the representative velocity profiles for the concentration–depth profiles. We averaged data within a radius of 1.5 times the flow depth from the concentration–depth profile location and within 10 s of collecting a suspended sediment sample. For the deeper flows (>10 m) in Wax Lake Outlet and the delta apex, the velocity profiles contain about 50 bins in the vertical. The shallow channel profiles (3 to 4 m depth) have about 10 to 30 bins. The island profiles, with depths of 1 m or less, have about five bins. The bin height is about 10 to 20 cm for the deeper flows and about 5 to 10 cm for the shallower flows. We did not observe any clear wind or vegetation signatures in the representative velocity profiles (e.g., Baptist et al., 2007).

We estimated the total boundary shear velocity, u_* (m s⁻¹), by fitting each representative flow velocity profile to the law of the wall (e.g., García, 2008). The law of the wall is reasonable because the representative velocity profiles visually show a clear linear trend between flow velocity and the logarithm of height. However, some data above 50 % of the flow depth deviate from the linear trend, likely due to tide and wake effects (Soulsby and Dyer, 1981; Nezu and Nakagawa, 1993). We excluded these upper data and fitted the law of the wall using a weighted least-squares regression with weights equal to the reciprocal of the square of the velocity standard error. The coefficients of determination have a median of 0.89 and range from 0.06 to 0.99. We used the shear velocity to calculate the near-bed Kolmogorov microscale. The Kolmogorov microscale varies with height above the bed as $\mathit{\eta }\left(z\right)={\left({\mathit{\nu }}^{\mathrm{3}}/\mathit{\epsilon }\right)}^{\mathrm{1}/\mathrm{4}}$, where ε (m² s⁻³) is the dissipation rate of turbulence kinetic energy per unit mass, and $\mathit{\epsilon }=\left(u_{*}^{\mathrm{3}}/\mathit{\kappa }\right)\left(\mathrm{1}/z-\mathrm{1}/h\right)$, where κ (dimensionless) is the von Kármán constant (0.41), z (m) is height above the bed, and h (m) is the water depth (Nezu and Nakagawa, 1993). Following Nghiem et al. (2022), we chose η as the value at 10 % of the flow depth (i.e., the near-bed value; Sect. 4.5).

4.2 Geochemical measurements for the semi-empirical model

We measured sediment Al $/$ Si using X-ray fluorescence (XRF) for 33 suspended, bed, and core sediment samples for the semi-empirical model. Due to sample mass limitations, we measured quantitative Al $/$ Si using glass pellet fusion on a 4 kW Zetium Panalytical XRF analyzer for only seven samples. For the remaining 26 samples, we measured semi-quantitative Al $/$ Si using a Rigaku Primus IV XRF spectrometer. We re-analyzed the samples that had been measured on the Zetium using the Rigaku to calibrate a linear equation (R²=0.91) converting the semi-quantitative Al $/$ Si to quantitative Al $/$ Si. Using the converted quantitative Al $/$ Si, we calibrated a linear equation between Al $/$ Si and a volume fraction finer than a certain grain size threshold so we could predict Al $/$ Si for cases in which grain size distribution is known, but we did not measure Al $/$ Si. We calculated the coefficients of determination for many grain size thresholds and selected the model with the highest R² ($\mathrm{Al}/\mathrm{Si}=\mathrm{0.089}+\mathrm{0.17}\left(\mathrm{volume}\mathrm{fraction}\mathrm{finer}\mathrm{than}\mathrm{23.1}\mathrm{\mu }\mathrm{m}\right)$; R²=0.90). We predicted Al $/$ Si from the depth-averaged grain size distributions (Sect. 4.1) for all concentration–depth profiles using this equation.

We measured the total organic carbon (TOC) concentration of suspended sediment samples to calculate θ in the semi-empirical model. Sediment aliquots were decarbonated by leaching with 2 M HCl at 80 °C and dried. Samples were weighed before and after decarbonation to correct for the fraction of sediment mass lost during decarbonation. The TOC concentration was measured using an Exeter Analytical CHN analyzer with uncertainties determined from repeat measurements of reference materials. We depth-averaged TOC concentrations for each concentration–depth profile using the trapezoidal rule on measured TOC concentrations weighted by sediment concentration. We assumed all organic matter was cellulose to convert depth-averaged TOC concentration to organic matter concentration (Nghiem et al., 2022). We calculated θ using the computed organic matter concentration and depth-averaged median primary particle diameter (Sect. 4.6.1; Nghiem et al., 2022).

We measured the major ion concentrations (cations: Na⁺, K⁺, Ca²⁺, Mg²⁺; anions: Cl⁻, HCO${}_{\mathrm{3}}^{-}$, SO${}_{\mathrm{4}}^{\mathrm{2}-}$) of water samples to calculate Φ for the semi-empirical model (Nghiem et al., 2022; Rommelfanger et al., 2022). We measured dissolved inorganic carbon (DIC) concentrations using a Picarro cavity ring-down spectrometer (G2131-i) and assumed that all DIC was HCO${}_{\mathrm{3}}^{-}$ to calculate HCO${}_{\mathrm{3}}^{-}$ concentrations. For DIC, about 6 mL of filtered river water was injected through a 0.2 µm syringe filter into an evacuated and pre-weighed 12 mL exetainer. Samples were acidified with 10 % phosphoric acid. The resulting CO₂ was carried in a nitrogen stream for total carbon measurements (Dong et al., 2018). The DIC concentration was calibrated against weighed and acidified optical calcite standard reference materials. Concentrations of the rest of the ions were measured by ion chromatography at the Department of Geography, Durham University, and checked by regular measurements of the LETHBRIDGE-03 standard. We solved for the HCO${}_{\mathrm{3}}^{-}$ concentration using charge balance for cases in which we had ion chromatography measurements but did not measure DIC concentration.

4.3 In situ particle size distribution and concentration measurements

We used a LISST instrument to measure in situ particle size distribution and concentration. We assumed that the particles measured by LISST were either flocs or unflocculated sediment. The LISST measures the particle volume concentration, including the pores within flocs, from 1 to 500 µm in 36 logarithmically spaced size bins using laser diffraction at a rate of 1 Hz (Sequoia Scientific, 2022). Unlike the Mastersizer, the LISST does not rely on particle optical properties because it uses an empirical calibration for natural particles to invert the angular light-scattering intensity and calculate the particle size distribution (Agrawal et al., 2008). We deployed the LISST attached to a rope from a boat in drift and measured downcast profiles by lowering the LISST at a rate of about 0.1 m s⁻¹. Optical laser transmission during measurements was within recommended ranges (Sequoia Scientific, 2022). For each LISST cast, we averaged particle size distribution and concentration data into 12 bins uniformly spaced with height above the bed to improve data display in Fig. 5. We calculated the depth-averaged particle size distribution using the trapezoidal rule with the binned concentrations as described in Sect. 4.1. Further LISST methods are documented in Fichot and Harringmeyer (2021).

4.4 Floc imaging

We measured floc diameters and settling velocities with a custom imaging device called the “floc cam” (Fig. 2a). The floc cam is a frame on which we mounted a camera and a modified 2.2 L Van Dorn sampler. We installed a 7 cm diameter window on the side of the sampler through which a backlight illuminates the interior. On the opposite side, we installed a 3 cm diameter window through which a camera takes photos. For each floc cam sample, we followed the same procedure for suspended sediment sampling up until the sample was retrieved from depth. We then mounted the sampler in the floc cam frame and took photos of backlit particles within the sampler using a Nikon D750 camera equipped with an AF-S Micro NIKKOR 60 mm f/2.8G ED lens (Fig. 2a). We programmed the camera to take photos at a rate of 4 Hz. Once the sampler and camera were in place, we covered the frame with a black tarp to shield the floc cam from ambient light. The time between sample collection and the start of image collection was about 1 min. We allowed the camera to take photos for a few minutes, yielding an image time series for each floc cam sample. We measured a resolution of 6 µm per pixel in the focal plane of the camera by photographing a ruler.

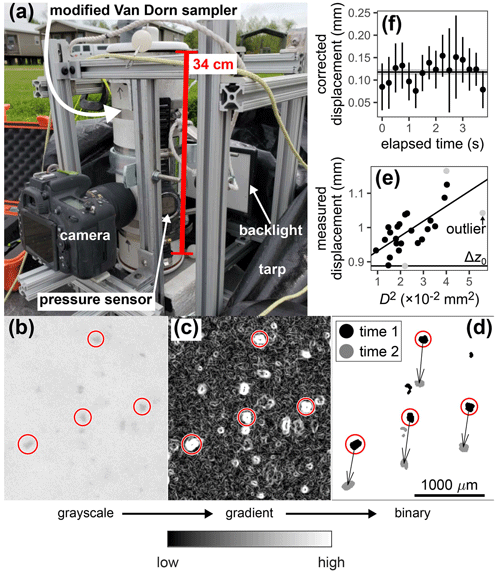
Figure 2 Floc cam data collection and processing. (a) Floc cam setup. During image collection, the black tarp covered the sampler and frame to block external light. (b) Example floc cam grayscale image. (c) 2D gradient of the grayscale image. High-gradient pixels correspond to particle borders. (d) Binarized particles showing particle displacement between an image pair. The scale in panel (d) also applies to panels (b) and (c). (e) Example scatterplot of squared diameter, D², and measured displacement. Δz₀ indicates the fitted background correction. (f) Time series of corrected displacement for a single tracked particle across multiple image pairs. The corrected displacement isolates the displacement due to gravitational settling from that due to background currents.

We detected particles in each image with the MATLAB Image Processing Toolbox following Keyvani and Strom (2013). We converted each image to grayscale and cropped the image to a smaller area of interest. We rescaled the pixel values in the cropped image and applied a Gaussian smoothing filter (Fig. 2b). We took the gradient of the image with a central difference method (Fig. 2c). We binarized the gradient image using a gradient cutoff, determined by trial and error, to exclude any particles where the gradient was too small (i.e., the particle was out of focus; Fig. 2d) but retain a sufficient number of detected particles. We applied morphological erosion and dilation to the binary image to remove noise speckles and connect fragments belonging to the same particle. Finally, we filled any holes within detected particles.

To calculate settling velocity, we tracked particles manually between successive frames in each binary image time series of in-focus particles (Fig. 2d). We identified the same particle across frames according to particle size, shape, and displacement. We tracked 100 unique particles for each time series over an image time span of 10 to 20 s and only recorded particles that could be tracked for at least three consecutive frames. The mean number of frames over which we tracked particles is 7.4. For each tracked particle, we calculated the diameter as the diameter of an equal-area circle using the second-largest measured particle area to exclude outliers. We used a regression method to remove the effect of background currents on observed particle motion and isolate particle displacement due to gravitational settling only. We assumed that background currents perfectly advected particles (Smith and Friedrichs, 2015). The particle displacement between an image pair is $\mathrm{\Delta }\widehat{z}=\mathrm{\Delta }z+\mathrm{\Delta }{z}_{\mathrm{0}}$, where $\mathrm{\Delta }\widehat{z}$ (m) is the observed vertical displacement of the particle, Δz (m) is the displacement due to gravitational settling, and Δz₀ (m) is the displacement due to background currents. For a given time interval, Stokes' law predicts that the gravitational displacement scales with the square of particle diameter, D. We assumed that Δz₀ is independent of particle size because the particles were sufficiently small. Using the data on all tracked particles in an image pair, we regressed $\mathrm{\Delta }\widehat{z}$ against D² according to $\mathrm{\Delta }\widehat{z}=c{D}^{\mathrm{2}}+\mathrm{\Delta }{z}_{\mathrm{0}}$ (Fig. 2e). We recovered Δz₀ as the intercept and solved for Δz (Fig. 2f) for all particles and image pairs. We discarded the data for which $\mathrm{\Delta }\widehat{z}$ fell into the 95 % confidence interval of the estimated Δz₀. This filtering retained 222 out of an initial 400 total tracked particles (56 %). We calculated the settling velocity for each particle as the mean of Δz divided by the time interval (0.25 s).

4.5 Rouse–Vanoni equation analysis of sediment concentration–depth profiles

Rouse–Vanoni equation fits to grain-size-specific concentration–depth profiles provide inferred floc cutoff diameter and depth-averaged floc settling velocity (Lamb et al., 2020; Nghiem et al., 2022). The Rouse–Vanoni equation models the suspended sediment concentration as a function of height from the bed, z, in a flow of depth h assuming a balance of gravitational sediment settling and upward turbulent sediment fluxes (Rouse, 1937):

$$\begin{array}{}\text{(8)}& C_i=C_{\mathrm{b}i}{\left({\displaystyle \frac{\frac{h-z}{z}}{\frac{h-h_{\mathrm{b}}}{h_{\mathrm{b}}}}}\right)}^{p_i},\end{array}$$

where C_i (dimensionless) is the sediment volume concentration, C_bi (dimensionless) is the sediment volume concentration at the near-bed height h_b (m), p_i (dimensionless) is the Rouse number, and the subscript i denotes the ith grain size class. Vertical concentration stratification increases with Rouse number, $p_i=w_{\mathrm{s}i}/\left(\mathit{\kappa }\mathit{\beta }{u}_{*}\right)$, where w_si (m s⁻¹) is the in situ grain-size-specific settling velocity. The diffusivity ratio, β (dimensionless), is the ratio of turbulent sediment diffusivity and turbulent momentum diffusivity and accounts for the fact that sediment does not exactly follow turbulent eddies (e.g., García, 2008). Flux Richardson numbers, calculated using the settling velocities of flocs and unflocculated sediment (Sect. 5.8), have a median of $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ and maximum of $\mathrm{6.6}\times {\mathrm{10}}^{-\mathrm{2}}$, indicating limited sediment-induced turbulence damping effects on flow velocity and concentration–depth profiles (Smith and McLean, 1977; Wright and Parker, 2004).

If β and u_* are known, then w_si can be calculated from the fitted p_i. Past studies using this method interpreted the inferred settling velocity for fine silt and clay grain sizes as the floc settling velocity because it is much faster than the settling velocity theory prediction for individual grains (Lamb et al., 2020; Nghiem et al., 2022). β is an obstacle to calculating w_si because predicting β is still an open question (De Leeuw et al., 2020; Lamb et al., 2020). β is often assumed to be unity. Deviations from unity have been attributed to sediment-induced density stratification (Wright and Parker, 2004; Moodie et al., 2020) and grain-size-dependent momentum effects (Carstens, 1952; Csanady, 1963; Graf and Cellino, 2002). Limited evidence shows that the diffusivity ratio for flocs, β_fl, might follow an existing formulation for solid grains (Izquierdo-Ayala et al., 2021, 2023), but this idea still requires more investigation. For simplicity, we first assumed β=1 for flocs and sediment grains. We re-evaluate β_fl with independent floc settling velocity data in Sect. 5.9.

Following Lamb et al. (2020) and Nghiem et al. (2022), we fitted the log-linearized Rouse–Vanoni equation to grain-size-specific concentration–depth profiles (e.g., profiles of the dispersed grains), an example of which is depicted in Fig. 3a. We converted the sediment mass concentrations to volume concentrations assuming a sediment density of 2650 kg m⁻³ and used h_b=0.1h (De Leeuw et al., 2020). For each grain size class, the grain-size-specific concentration is the total sediment concentration times the volume fraction from the grain size distribution (Sect. 4.1). In order to fit the Rouse–Vanoni equation, we required the grain-size-specific concentration–depth profile to have a nonzero concentration for all suspended sediment samples in the profile. We estimated the grain-size-specific Rouse number, p_i, from the Rouse–Vanoni equation fits. We used shear velocity estimates (Sect. 4.1) and β=1 to calculate w_si. Figure 3b shows grain diameter, D_g (m), and w_si for the concentration–depth profiles with corresponding LISST measurements (Sect. 3). We identified the floc cutoff diameter, D_t, by eye for each concentration–depth profile as the diameter below which the inferred settling velocity begins to depart significantly from conventional settling velocity theory (grain settling velocity, $w_{\mathrm{sg}}=\left(R_{\mathrm{s}}g{D}_{\mathrm{g}}^{\mathrm{2}}\right)/\left(c_{\mathrm{1}}\mathit{\nu }+\sqrt{\mathrm{0.75}{c}_{\mathrm{2}}{R}_{\mathrm{s}}g{D}_{\mathrm{g}}^{\mathrm{3}}}\right)$ for c₁=20, and c₂=1.1; Ferguson and Church, 2004). We calculated the Rouse-estimated floc settling velocity as the median w_si within grain diameters finer than D_t (Nghiem et al., 2022).

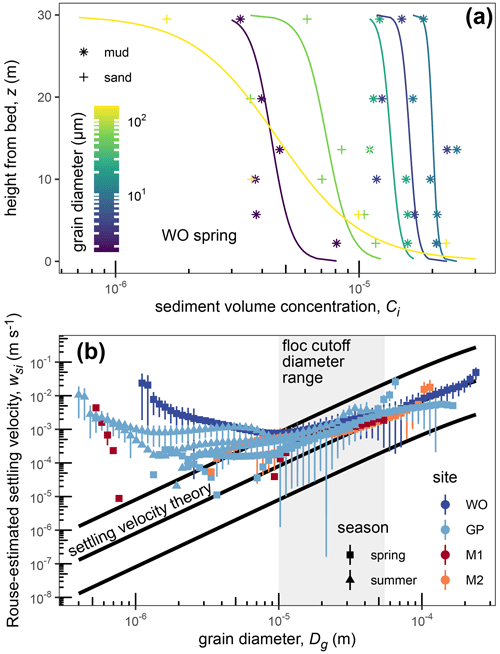
Figure 3 Rouse–Vanoni equation results. (a) Example of sediment volume concentration as a function of height above the bed for profile WO spring. We used the full 100 grain size classes in all calculations but reclassified the data into 6 classes for this panel only to improve readability. Curves represent the best-fit Rouse–Vanoni profiles (Eq. 8). Data scatter likely represents spatiotemporal variations in turbulence, bedforms, and/or other natural sources of variability. (b) Grain diameter and Rouse-estimated in situ settling velocity assuming β=1 for concentration–depth profiles with LISST measurements. Black settling velocity theory curves indicate the Ferguson and Church (2004) model with an order of magnitude above and below. Floc cutoff diameter varies between concentration–depth profiles and ranges between 10 and 55 µm for the displayed profiles. Vertical bars represent the propagated 68 % confidence interval on the Rouse number estimates. Points without vertical bars have confidence intervals that overlap with 0.

4.6 Estimating floc properties

Here we describe how we combined our grain size distributions (Sect. 4.1) and floc data (Sect. 4.3–4.5) to calculate floc properties.

4.6.1 Floc and primary particle size distribution and concentration

Our first goal was to delineate the size distribution and concentration of flocs and primary particles. To do this, we paired LISST and sediment sample data because they record mixtures of different types of particles (Fig. 4). LISST measured the size distribution and concentration of flocs and unflocculated sediment grains together (i.e., in situ particles; Sect. 4.3). The LISST particle volume concentration includes the volumes of mineral sediment and pores between primary particles within flocs (Mikkelsen and Pejrup, 2001; Livsey et al., 2022). On the other hand, suspended sediment data represent the size distribution and concentration of fully dispersed sediment grains, which might have been flocculated in situ. We paired each suspended sediment sample from the concentration–depth profiles with a corresponding set of measurements from the concurrent LISST cast. LISST measurements were assigned when collected within 0.1 m (the sampler radius) of the sample collection depth. If there were no LISST measurements in this range, then we assigned the three measurements closest in depth. We assumed that paired LISST and sediment data statistically represent the same suspended material, allowing direct comparison between the distributions and volume concentrations.

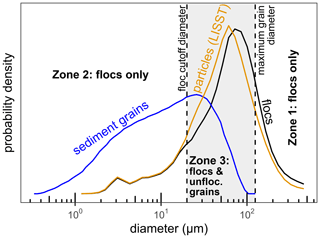
Figure 4 Example of calculating floc size distribution (black) from suspended sediment grain size distribution (blue) and LISST in situ particle size distribution (orange). Particles include flocs and unflocculated grains. Zones describe the particles in the LISST particle size distribution and are demarcated by the floc cutoff and maximum grain diameters. We identified the floc cutoff diameter as the grain diameter at which the Rouse-estimated settling velocity departs from settling velocity theory for single grains (Sect. 4.5; Fig. 3b). The maximum grain diameter is the maximum diameter of sediment grains measured by grain size analysis of fully dispersed sediment (Sect. 4.1). Data correspond to a suspended sediment sample collected at 1.9 m depth out of 3.8 m total depth from the GP spring 1 profile (Table 2).

Figure 4 illustrates how we divided LISST particle sizes into three zones that contain either flocs only or both flocs and unflocculated grains to help isolate the floc and primary particle size distribution and concentration. Zone 1 is defined as particles measured by the LISST that were coarser than the maximum grain diameter of the dispersed sediment. We assumed that all particles in zone 1 are flocs because they are larger than any dispersed sediment grains we measured. Zone 2 is defined as particles measured by the LISST that are finer than the floc cutoff diameter (Sect. 4.5; Fig. 3b). We inferred that particles in zone 2 were also all flocs under the assumption that all sediment finer than the floc cutoff diameter was flocculated (Fig. 3b). In reality, some sediment finer than the floc cutoff diameter might have been unflocculated. However, the enhanced settling velocities inferred from the concentration–depth profiles imply significant flocculation in these sizes (Fig. 3b), making complete flocculation a reasonable assumption. Finally, zone 3 lies between zones 1 and 2 and is defined as particles measured by LISST with sizes between the floc cutoff diameter and maximum grain diameter (Fig. 4). As such, zone 3 likely consists of a mixture of flocs and unflocculated grains.

We calculated the floc size distribution and concentration according to the LISST particle zones (Fig. 4). Floc concentration is the combined volume of primary particles and pores within flocs divided by the total measured volume. We compared sediment and LISST volume concentrations. We calculated the LISST particle volume concentration in each LISST size class by multiplying the particle size fraction and the total particle concentration. We then calculated the corresponding sediment volume concentration by interpolating the grain size fraction to match the LISST size class and multiplying the fraction by the total sediment concentration. According to our assumptions, LISST particle concentrations in zones 1 and 2 already represent floc concentrations and thus do not require any adjustment. This is not true in zone 3, so we calculated the floc concentration in each zone 3 size class by subtracting the particle and sediment volume concentrations. Finally, we renormalized the floc concentrations across size classes to compute the floc size distribution (Fig. 4). We calculated floc size distribution and concentration from each assigned LISST measurement and averaged them to obtain the representative floc size distribution and concentration for each sediment sample. We took the floc diameter for each size class, D_fi, to be the geometric mean of the floc diameter at the lower and upper boundaries of the size class. For each concentration–depth profile, we calculated the depth-averaged floc size distribution using the trapezoidal rule as described in Sect. 4.1.

We computed the primary particle size distribution and concentration by truncating the sediment grain size distribution to the fractions finer than the floc cutoff diameter (Table 1). Median primary particle diameter, D_p,50 (m), is the median of the primary particle size distribution associated with each sediment sample. For the semi-empirical model (Eq. 7), we calculated the depth-averaged median primary particle diameter, ${\stackrel{\mathrm{̃}}{D}}_{\mathrm{p},\mathrm{50}}$, as the median grain size of the depth-averaged grain size distribution (Sect. 4.1) truncated with the floc cutoff diameter. We calculated the floc bulk solid fraction, $\stackrel{\mathrm{‾}}{\mathit{\phi }}$ (dimensionless), as the ratio of the primary particle and floc volume concentrations (e.g., Mikkelsen and Pejrup, 2001; Guo and He, 2011).

4.6.2 Fractal dimension and effective primary particle diameter

Our next goal was to estimate the fractal-related terms in the explicit model: fractal dimension, n_f, and effective primary particle diameter, D_p. Our strategy was to link the explicit model (Eq. 1) and solid fraction theory (Eq. 2), in which n_f and D_p appear, to mean settling velocity and bulk solid fraction estimated from data. As follows, we solved for the n_f and D_p that ensure consistency between the bulk solid fraction and mean settling velocity over the floc size distribution (Sect. 4.6.1).

Estimating n_f and D_p requires two equations to calculate those two unknowns. The first equation is the bulk solid fraction over the floc size distribution using solid fraction theory (Eq. 2):

$$\begin{array}{}\text{(9)}& \stackrel{\mathrm{‾}}{\mathit{\phi }}={\sum }_{i=\mathrm{1}}^n{\mathit{\phi }}_i={\sum }_{i=\mathrm{1}}^n{f}_i{\left({\displaystyle \frac{D_{fi}}{D_{\mathrm{p}}}}\right)}^{n_{\mathrm{f}}-\mathrm{3}},\end{array}$$

where f_i is the volume fraction in the ith floc size class from the floc size distribution and n is the number of floc size classes (36). We assumed that a single D_p applies across the floc size distribution, but primary particle diameter might vary with floc diameter (Nicholas and Walling, 1996). The second equation is the mean settling velocity over the floc size distribution using the explicit model (Eq. 1):

$$\begin{array}{}\text{(10a)}& \stackrel{\mathrm{‾}}{w_{\mathrm{s}}}={\sum }_{i=\mathrm{1}}^n{w}_{\mathrm{s}i}={\sum }_{i=\mathrm{1}}^n{f}_i{\displaystyle \frac{R_{\mathrm{s}}g{D}_{\mathrm{p}}^{\mathrm{2}}}{b_{\mathrm{1}}{\mathrm{\Omega }}_i\mathit{\nu }}}{\left({\displaystyle \frac{D_{fi}}{D_{\mathrm{p}}}}\right)}^{n_{\mathrm{f}}-\mathrm{1}},\end{array}$$

which we set equal to the explicit model settling velocity with mean values of input variables,

$$\begin{array}{}\text{(10b)}& \stackrel{\mathrm{‾}}{w_{\mathrm{s}}}={\displaystyle \frac{R_{\mathrm{s}}g\stackrel{\mathrm{‾}}{\mathit{\phi }}{\stackrel{\mathrm{‾}}{D_{\mathrm{f}}}}^{\mathrm{2}}}{b_{\mathrm{1}}\stackrel{\mathrm{‾}}{\mathrm{\Omega }}\mathit{\nu }}},\end{array}$$

where $\stackrel{\mathrm{‾}}{D_{\mathrm{f}}}$ (m) is the geometric mean floc diameter calculated from the floc size distribution and $\stackrel{\mathrm{‾}}{\mathrm{\Omega }}$ is the mean drag ratio. Although Eqs. (9) and (10a) both use fractal solid fraction theory (Eq. 2), they are distinct constraints because they integrate over different parameters (solid fraction in Eq. 9 and settling velocity in Eq. 10). We substituted $\stackrel{\mathrm{‾}}{\mathit{\phi }}$ in Eq. (10) with Eq. (9), set the resulting $\stackrel{\mathrm{‾}}{w_{\mathrm{s}}}$ equal to Eq. (10a), and rearranged terms to obtain

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{\sum f_i\frac{\stackrel{\mathrm{‾}}{\mathrm{\Omega }}}{{\mathrm{\Omega }}_i}{D}_{fi}^{n_{\mathrm{f}}-\mathrm{1}}}{\sum f_i{D}_{fi}^{n_{\mathrm{f}}-\mathrm{3}}}}={\stackrel{\mathrm{‾}}{D_{\mathrm{f}}}}^{\mathrm{2}}.\end{array}$$

We assumed that the effect of $\stackrel{\mathrm{‾}}{\mathrm{\Omega }}/{\mathrm{\Omega }}_i$ on the summation in Eq. (11) is small and neglected it (i.e., $\sum f_i\left(\stackrel{\mathrm{‾}}{\mathrm{\Omega }}/{\mathrm{\Omega }}_i\right)D_{\mathrm{f}}^{n_{\mathrm{f}}-\mathrm{1}}=\sum f_i{D}_{\mathrm{f}}^{n_{\mathrm{f}}-\mathrm{1}}$). This assumption is justified because n_f estimates align well with typical n_f for natural flocs (Sect. 5.6). As such, n_f remains as the only unknown in Eq. (11) because the rest of the variables, f_i, D_fi, and $\stackrel{\mathrm{‾}}{D_{\mathrm{f}}}$, are all known from the floc size distribution (Sect. 4.6.1). We numerically solved Eq. (11) to calculate n_f for each sediment sample. We then solved Eq. (9) for D_p using f_i, n_f, and the known bulk solid fraction, $\stackrel{\mathrm{‾}}{\mathit{\phi }}$ (Sect. 4.6.1). We estimated uncertainty in the floc concentration, n_f, and D_p as the 95 % bounds on the bootstrap distribution from 1000 bootstrap replicates of resampling the assigned LISST measurements that go into the floc size distribution and concentration (Sect. 4.6.1).

To test the fractal D_p model (Eq. 5), we compared its predictions at different values of the weighting dimension, n_w, to our effective primary particle diameter estimates. We used the number distribution of primary particle size, rather than the volume distribution, to calculate the moments in Eq. (5) because primary particles are added one by one as flocs grow. We constructed the number distribution by dividing the volume fraction in each size class by the cube of the grain diameter and renormalizing the distribution. We also calculated the number-based median primary particle diameter using the number distribution to compare with effective primary particle diameter estimates.

4.6.3 Drag ratio

The remaining parameter in the explicit model is the drag ratio, Ω. We solved the explicit model (Eq. 1) for Ω using n_f, D_p, and the floc-cam-measured floc diameter and settling velocity for each floc cam observation (Sect. 4.4). We used these Ω estimates to test permeability models presented in Sect. 2.1. For each permeability model, we identified the range of all possible Ω predictions as a function of fractal dimension, n_f, to test whether our Ω estimates fall within the range. If D_f=D_p, then the solid fraction is unity (Eq. 2) for all n_f values, leading to a maximum Ω=1 (i.e., impermeable floc). The minimum Ω, Ω_min, at a given n_f occurs at the maximal dimensionless permeability, ${\mathit{\xi }}_{\max }^{-\mathrm{2}}$, because Ω and ξ⁻² are inversely related (Eq. 3). Although ${\mathit{\xi }}_{\max }^{-\mathrm{2}}$ depends on the permeability model, we present the Davies model only because the Brinkman model yielded similar results (Sect. 5.7). We differentiated the Davies model (Eq. 6) with respect to φ to find ${\mathit{\xi }}_{\max }^{-\mathrm{2}}$ and, in turn, ${\mathrm{\Omega }}_{\min }=\mathrm{\Omega }\left({\mathit{\xi }}^{-\mathrm{2}}={\mathit{\xi }}_{\max }^{-\mathrm{2}}\right)$ using Eq. (3):

$$\begin{array}{}\text{(12)}& {\mathit{\xi }}_{\max }^{-\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{16}}}{\left({\displaystyle \frac{\mathrm{1}}{\mathrm{56}}}{\displaystyle \frac{\mathrm{3}{n}_{\mathrm{f}}-\mathrm{5}}{\mathrm{23}-\mathrm{9}{n}_{\mathrm{f}}}}\right)}^{\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{2}}{\mathrm{3}-n_{\mathrm{f}}}-\frac{\mathrm{3}}{\mathrm{2}}\right)}.\end{array}$$

4.6.4 Floc settling velocity distribution

To find the floc settling velocity distribution associated with each sediment sample, we used n_f, D_p, and Ω in the explicit model (Eq. 1) to convert the floc diameters in the floc size distribution into floc settling velocities. In this calculation, we used a best-fit constant drag ratio (Sect. 5.7), Ω=0.48, because we were unable to constrain Ω for concentration–depth profiles that lack floc cam observations. For the bins at the fine tail in which D_fi<D_p, we capped the solid fraction at 1 (Eq. 2). We took the floc settling velocity for each class, w_si, to be the geometric mean of the floc settling velocity at the lower and upper boundaries of the class. For each concentration–depth profile, we calculated the depth-averaged floc settling velocity distribution using the trapezoidal rule as described in Sect. 4.1.

5 Results

First, we describe the basic hydrodynamics, sediment properties, and floc observations from the individual measurement methods (Sect. 5.1–5.4). We then present floc variables derived from combining data sources (Sect. 5.5–5.8). We compare effective primary particle diameter and drag ratio to theory and validate them using floc settling velocity inferred from the Rouse–Vanoni equation fitting (Sect. 5.6–5.9). Finally, we validate the semi-empirical model and use it to examine environmental controls on floc properties (Sect. 5.10).

5.1 Hydrodynamics

The sampled profiles span a wide hydrodynamic range in WLD because of discharge seasonality and environment (Fig. 1d; Table 2). The fastest flow occurred at site WO in the spring (∼1.5 m s⁻¹ depth-averaged) upstream of the delta apex in the Wax Lake Outlet, where the water depth was greatest (30 m) among the sites. Further down the delta, the distributary channel site GP had slower flow velocity (∼0.56 m s⁻¹ depth-averaged in the spring) and shallower depth (∼3.7 m). At site GP, depth-averaged flow velocity in summer was about half (∼0.2 to 0.3 m s⁻¹) of that in spring (Fig. 1d). The island sites were sampled in the spring only. These sites had the slowest flow velocities (0.024 and 0.12 m s⁻¹) of the sampled sites with water depths of ∼0.6 m. Shear velocity generally increased with flow velocity, ranging from ∼0.006 (in the island) to ∼0.1 m s⁻¹ (in Wax Lake Outlet). The near-bed Kolmogorov microscale varied inversely with the shear velocity from 150 to 600 µm. Water chemistry measurements show a median salinity of 0.25 ppt and a maximum of 0.29 ppt, confirming that the water was fresh (<0.5 ppt).

Table 2 Metadata and hydrodynamic data for sediment concentration–depth profiles with paired LISST data (Sect. 3). A bold profile name indicates that we collected floc cam images for the profile. Shear velocity uncertainty indicates the 95 % confidence interval for the law of the wall fit (Sect. 4.1).

5.2 Sediment concentration–depth profiles

Depth-averaged suspended sediment was muddy (∼90 % mud) and more concentrated in the spring ($\sim \mathrm{6}\times {\mathrm{10}}^{-\mathrm{5}}$ volume concentration) than in the summer ($\sim \mathrm{6}\times {\mathrm{10}}^{-\mathrm{6}}$) because of discharge seasonality (Table 2). The grain-size-specific concentration–depth profiles reveal higher concentrations closer to the bed for sand, a pattern consistent with Rouse–Vanoni theory (Eq. 8; Fig. 3a). Mud was also stratified despite the expectation of a uniform concentration–depth profile if mud settled as individual grains (Eq. 8), indicating likely flocculation.

The grain diameter versus in situ settling velocity trend from the Rouse–Vanoni equation fitting shows that sediment finer than 10 to 55 µm (i.e., the floc cutoff diameter) was appreciably flocculated in the eight main sample profiles (Fig. 3b; Table 2). Enhanced settling velocity in the grain sizes finer than the floc cutoff diameter is consistent with Lamb et al. (2020) and Nghiem et al. (2022) and indicates the presence of flocculation. Conversely, in situ settling velocity follows theory well for grain diameters coarser than the floc cutoff diameter and indicates the absence of flocculation. Although the β=1 assumption makes the precise in situ settling velocity values inaccurate, we expect the floc cutoff diameter to be robust because it marks an abrupt change in the settling velocity pattern.

5.3 LISST particle size distribution and concentration

To demonstrate results prior to additional processing (Sect. 4.6.1), Fig. 5 shows the raw LISST-measured in situ particle concentration and size distribution observations. The concentration profiles of flocs and unflocculated sediment (i.e., in situ particles) measured by LISST had little systematic vertical variation except for the site GP profiles in the spring in which the concentration increased slightly closer to the bed (Fig. 5a). In the spring, the particle volume concentration was $\sim \mathrm{3}\times {\mathrm{10}}^{-\mathrm{4}}$ to $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{4}}$ for all sites except for site M1, which had a slightly smaller concentration of $\sim \mathrm{2}\times {\mathrm{10}}^{-\mathrm{4}}$ to $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{4}}$. In the summer, particle volume concentration at site GP was much smaller at $\sim \mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ to $\mathrm{8}\times {\mathrm{10}}^{-\mathrm{5}}$ because of the relatively lower discharge.

Figure 5 LISST results for in situ particles, which include flocs and unflocculated sediment. (a) Profiles of in situ particle volume concentration from LISST, binned into 12 vertical classes (Sect. 4.3). Horizontal bars represent the 95 % bootstrap uncertainty. (b) Profiles of median in situ particle diameter from LISST, binned into 12 vertical classes. Horizontal bars represent the span of the D₁₆ and D₈₄ particle diameters, the diameters for which 16 % and 84 % of particles are finer, respectively. (c) Cumulative distribution functions of depth-averaged particle diameter from LISST. (d) Median depth-averaged grain diameter from sediment samples and median depth-averaged particle diameter from LISST. The legend in panel (c) applies for all panels.

Channel sites (WO and GP) had median particle diameters of ∼50 to 90 µm, while island sites (M1 and M2) had median particle diameters of ∼35 µm, all with minimal vertical variation (Fig. 5b). Depth-averaged particle size distributions were similar across the channel sites for both the spring and summer, while the island distributions were skewed toward finer particles (Fig. 5c). The fraction of particles coarser than the floc cutoff diameter ranged from ∼0.10 to 0.50. The median depth-averaged particle diameter from the LISST ranges from about 3 to 15 times larger than the median grain diameter of the dispersed sediment (Fig. 5d), implying the presence of flocculation.

5.4 Floc cam

Tracked particles imaged by the floc cam had diameters of ∼70 to 200 µm and settling velocities of ∼0.1 to 1 mm s⁻¹ (Fig. 6), but we did not know a priori whether these particles were flocs because the image quality did not permit a visual determination. To test whether tracked particles were flocs, Fig. 6 compares the diameter and settling velocity because, unlike flocs, solid non-cohesive grains follow conventional settling velocity theory (Ferguson and Church, 2004). We concluded that tracked particles were flocs because, for a given diameter, measured settling velocities are slower than settling velocity predictions of solid grains due to the fact that flocs are less dense than sediment grains. Measured settling velocities also are up to 1 order of magnitude faster than the predicted settling velocity of a typical 8 µm mud primary particle, also indicating flocculation.

Figure 6 Diameters and settling velocities of floc-cam-measured particles, which we inferred to be flocs. Vertical bars indicate the propagated mean standard error in the background displacement estimate (Sect. 4.4).

5.5 Floc concentration, size distribution, and bulk solid fraction

As described in Sect. 4.6.1, we paired concentration and size distribution data for sediment and in situ particles to isolate the floc concentration and size distribution (Table 1). Floc volume concentration was $\sim \mathrm{3}\times {\mathrm{10}}^{-\mathrm{4}}$ to $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{4}}$ for the sites in the spring except for site M1, which had a smaller concentration of $\sim \mathrm{2}\times {\mathrm{10}}^{-\mathrm{4}}$ (Fig. 7a). All floc concentrations in the summer were far smaller than those in the spring at $\sim \mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ to $\mathrm{8}\times {\mathrm{10}}^{-\mathrm{5}}$ because of the relatively lower discharge. These concentration trends are similar to those for the particles (Sect. 5.3).

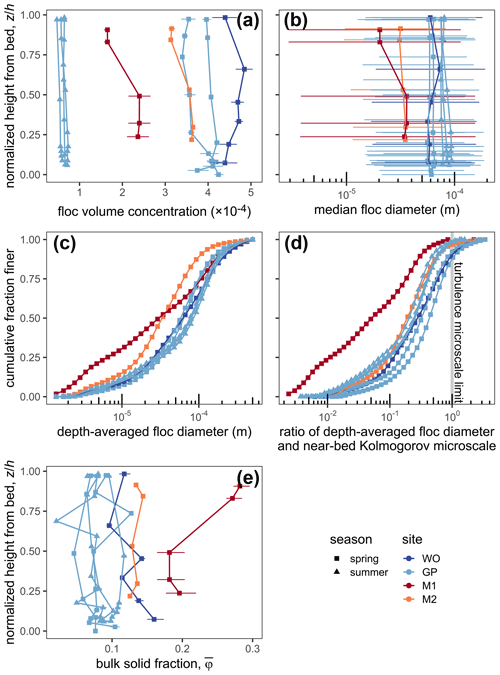
Figure 7 Floc concentration, size, and bulk solid fraction results. (a) Profiles of floc volume concentration. Horizontal bars represent the 95 % bootstrap uncertainty. (b) Profiles of median floc diameter. Horizontal bars represent the span of the D₁₆ and D₈₄ floc diameters. (c) Cumulative distribution functions of depth-averaged floc diameter. (d) Cumulative distribution functions of the ratio of depth-averaged floc diameter to the near-bed Kolmogorov microscale. (e) Profiles of bulk solid fraction. Horizontal bars represent the 95 % bootstrap uncertainty.

Median floc diameter, D_f,50 (m), was ∼50 to 90 µm for channel sites and ∼20 to 30 µm for island sites with little vertical variation (Fig. 7b). Overall, flocs were ∼1 to 100 µm in diameter (Fig. 7c). Depth-averaged floc size distributions at the channel sites were similar for spring and summer (Fig. 7c). In contrast, the floc size distributions at the island sites were enriched in finer flocs. ∼88 to 100 % of flocs by volume were smaller than the near-bed Kolmogorov microscale (Fig. 7d), consistent with the idea that the Kolmogorov microscale sets the maximum floc size (Van Leussen, 1988; Kuprenas et al., 2018). Flocs larger than the near-bed Kolmogorov microscale might either break up once they reach the elevated near-bed shear stress or, if they are sufficiently strong, withstand breakage and deposit on the bed (Mehta and Partheniades, 1975). Floc cam observations yield a median floc Reynolds number of 0.05, indicating minor inertial effects and justifying neglect of the inertial term in the explicit model (Strom and Keyvani, 2011).

After isolating the primary particle and floc volume concentrations (Sect. 4.6.1), we took the ratio of the concentrations as the floc bulk solid fraction. The bulk solid fraction ranged from ∼0.05 to 0.3 and showed little systematic vertical variation (Fig. 7e). The bulk solid fraction in the island was typically higher (>0.1) than that in the channel (<0.1) because flocs in the island were finer (Fig. 7b, c) and hence denser (Eq. 2) than those in the channel. Bulk solid fractions for WO spring were larger than those at GP because faster shear velocity at WO suspended coarser primary particles (Fig. 8; Table 2). Overall, these bulk solid fractions agree with prior floc density measurements (e.g., Van Leussen, 1988).

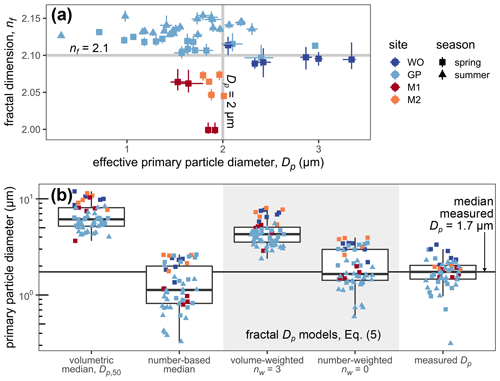
Figure 8 (a) Fractal dimension and effective primary particle diameter. Horizontal and vertical bars represent the 95 % bootstrap uncertainty. Bars are smaller than the points where they are not visible. (b) Effective primary particle diameter, D_p, model comparison. We calculated median primary particle diameters from volumetric (Sect. 4.6.1) and number-based (Sect. 4.6.2) primary particle size distributions. We calculated fractal D_p using Eq. (5) on number-based primary particle size distributions (Sect. 4.6.2) and varied the weighting dimension, n_w, between 0 and 3. Measured D_p values were estimated from data (Sect. 4.6.2).

5.6 Fractal dimension and effective primary particle diameter

Figure 8a displays fractal dimension, n_f, and effective primary particle diameter, D_p, two key explicit model parameters that we derived using the floc size distribution and bulk solid fraction (Sect. 4.6.2; Table 1). n_f is narrowly constrained to ∼2 to 2.15, which is well within the expected range of 1.7 to 2.3 for natural flocs (Tambo and Watanabe, 1979; Winterwerp, 1998). We deemed n_f=2.1 to be representative. Smaller n_f in the island compared to that in the channel might indicate floc response to changes in factors like turbulence, sediment concentration, organic matter, and water chemistry. Effective primary particle diameter, D_p, ranges from ∼1 to 3 µm with a typical value of 2 µm. The range of D_p is similar across sampling sites except for WO spring where all D_p values exceeded 2 µm because of the faster shear velocity. No clear trend is apparent between n_f and D_p.

Figure 8b shows that the median primary particle diameter, D_p,50, and the volume-weighted fractal D_p (Eq. 5 with n_w=3) both overpredict our D_p estimates. Smaller values of n_w improve the comparison between Eq. (5) and measured D_p (not shown) until the best agreement is achieved at n_w=0 (i.e., number weighting). The number-weighted fractal D_p (median = 1.6 µm) best predicts D_p (median = 1.7 µm) within a factor of about 3. Potential error in converting a volume-based size distribution to a number-based distribution might be responsible for the residual misfit between the number-weighted fractal D_p and measured D_p. In contrast, past studies used the median primary particle size diameter as the effective primary particle diameter (e.g., Syvitski et al., 1995; Strom and Keyvani, 2011). The volumetric median is biased by a factor of about 2 to 6 larger than measured D_p. Conversely, the number-based median is biased low compared to measured D_p. These results indicate that the median is a poor representation of D_p.

5.7 Drag ratio

We estimated the final unknown in the explicit model, the drag ratio, Ω, by solving the explicit model (Eq. 1) with n_f, D_p, and floc-cam-measured diameter and settling velocity (Sect. 4.6.3; Table 1). Overall, Ω estimates span a wide range from ∼0.15 to 1 with a mean of 0.48 (Fig. 9a), indicating that permeability enhances floc settling velocity and reduces floc drag force by up to a factor of 7. High variability in Ω exists even within the same floc cam deployment. Although some Ω values exceed 1, ∼91 % of the data fall between 0 and 1, indicating that our estimates are physically reasonable.

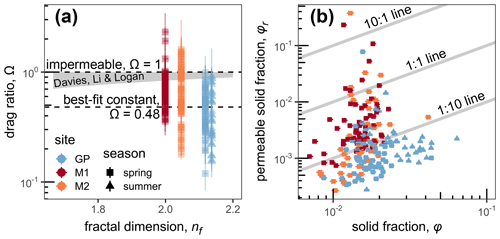
Figure 9 Drag ratio results from combining the explicit model and floc-cam-measured floc settling velocity. (a) Fractal dimension and measured drag ratio. The shaded area indicates the field of all possible drag ratios under the Davies model (Eq. 6) and its Li and Logan modification. Drag ratio bars indicate the propagated mean standard error in the background displacement estimate (Sect. 4.4) and propagated 95 % bootstrap uncertainty in n_f and D_p. (b) Solid fraction and permeable solid fraction according to the permeable solid fraction model based on the Davies model. Horizontal bars represent the propagated 95 % bootstrap uncertainty in n_f and D_p. The legend in panel (a) applies for all panels.

We used our Ω measurements to test the ability of permeability models to predict drag ratio. We first tested four existing models, the Brinkman and Davies models and their Li and Logan variants (Sect. 2.1), but only present the Davies model and its Li and Logan modification because the other models yielded similar results. Figure 9a shows the fractal dimension and drag ratio for each floc cam observation against the field of all possible model predictions defined by the zone between Ω_min (Eq. 12) and 1 for the Davies model and its Li and Logan variant. The zone is the same for the two models because Ω_min only depends on fractal dimension (Eqs. 3, 12). As a result, the Li and Logan strategy, replacing D_p with a larger cluster diameter, D_c, does not affect the range of Ω predictions. Both models are largely incompatible with the data because ∼88 % of the data (excluding Ω>1 data) lie below the zone of possible Ω.

The discordance between our measured values of Ω and the Davies model is probably because natural flocs violate the model assumptions of uniform porosity and a single primary particle size. However, a complete 3D rendering of floc structure is generally impractical, making a full model of nonuniform flow paths difficult to implement. Instead, we explored an empirical approach to modify the Davies model (Eq. 6) by replacing φ with a permeable solid fraction, φ_r, but keeping the same $D_{\mathrm{p}}/D_{\mathrm{f}}$. That is,

$$\begin{array}{}\text{(13)}& {\mathit{\xi }}^{-\mathrm{2}}={\left({\displaystyle \frac{D_{\mathrm{p}}}{D_{\mathrm{f}}}}\right)}^{\mathrm{2}}{\left[\mathrm{16}{\mathit{\phi }}_{\mathrm{r}}^{\mathrm{1.5}}\left(\mathrm{1}+\mathrm{56}{\mathit{\phi }}_{\mathrm{r}}^{\mathrm{3}}\right)\right]}^{-\mathrm{1}},\end{array}$$

where the permeable solid fraction is ${\mathit{\phi }}_{\mathrm{r}}={\left(D_{\mathrm{f}}/D_{\mathrm{p}}\right)}^{n_{\mathrm{r}}-\mathrm{3}}$, and n_r is the permeable fractal dimension (analogous to Eq. 2). This permeable solid fraction model gives another degree of freedom, φ_r or n_r, to capture potential impacts of nonuniform porosity and primary particle size distribution on permeability. Unfortunately, we could not predict φ_r independent of Ω. Instead, we inverted our Ω estimates for values of φ_r and n_r that yield a perfect match between Ω theory (Eqs. 3, 6, and 13) and observations (Fig. 9a). Figure 9b shows these optimal values of φ_r. In most cases, φ_r is smaller than φ (median ${\mathit{\phi }}_{\mathrm{r}}/\mathit{\phi }=\mathrm{0.10}$; $\text{IQR}/\mathrm{2}=\mathrm{0.08}$). We interpreted this result to indicate that φ_r represents the subset of primary particles that set the main throughflow conduits because not all primary particles contribute to throughflow and drag (see Sect. 6.3 for more discussion). n_r estimates range between 1.06 and 2.79 with a median of 1.53. The fact that all n_r values fall within the physically meaningful range of 1 to 3 supports using the permeable solid fraction model (Eq. 13) to overcome the assumptions in the Davies model.

5.8 Floc settling velocity

To calculate floc settling velocity distributions, we used the measured n_f, D_p, and Ω in the explicit model to convert the floc size distributions (Sect. 4.6.4). We used a best-fit constant Ω=0.48 because we only had Ω estimates for the four concentration–depth profiles with paired floc cam measurements (Fig. 9a; Table 2). Median floc settling velocities at the channel sites in spring and summer were ∼0.1 to 0.5 mm s⁻¹ (Fig. 10a). Island sites had median floc settling velocities of about 0.1 mm s⁻¹, with a substantial fraction of floc settling velocity of the order of 0.01 mm s⁻¹. No systematic vertical trends in median settling velocity are apparent. Depth-averaged floc settling velocity broadly ranged from ∼0.1 to 1 mm s⁻¹ (Fig. 10b). Finer floc sizes (Fig. 7c), despite larger bulk solid fractions (Fig. 7e), in the island caused slower floc settling velocity in the island compared to that in the channels (Fig. 10b).

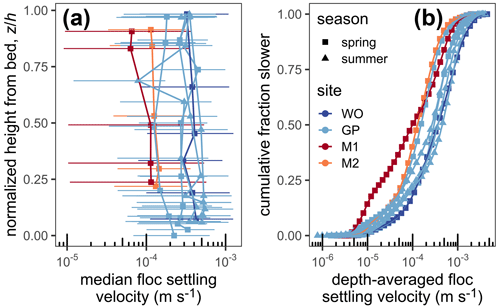
Figure 10 Floc settling velocity results. (a) Profiles of median floc settling velocity. Horizontal bars represent the span of the 0.16 and 0.84 quantile floc settling velocities. (b) Cumulative distribution functions of depth-averaged floc settling velocity. The legend in panel (b) applies for all panels.

5.9 Validating the explicit model

We compared Rouse-estimated floc settling velocities (Sect. 4.5) and explicit model predictions as an integrated test of the estimated n_f, D_p (Sect. 5.6), and Ω (Sect. 5.7) because these settling velocity estimates are independent. Figure 11 shows that Rouse–estimated floc settling velocity displays a linear trend with the median from the explicit model, albeit with some scatter, largely from the non-GP sites. Although we assumed a floc diffusivity ratio, β_fl, of unity to calculate the Rouse-estimated floc settling velocities (Sect. 4.5), the data indicate that β_fl=0.65 optimizes the correlation between the settling velocities. β_fl=0.65 is realistic because it falls within the ranges of previously estimated diffusivity ratios (Nghiem et al., 2022) and diffusivity ratio models (e.g., De Leeuw et al., 2020). As a result, we concluded that the Rouse-estimated settling velocity validates our explicit model parameter estimates well.

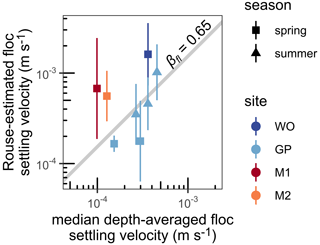
Figure 11 Rouse-estimated floc settling velocity using β_fl=1 and median depth-averaged floc settling velocity computed using estimates of n_f, D_p, and Ω in the explicit model. β_fl=0.65 indicates the best-fit floc diffusivity ratio. Vertical bars indicate the 95 % confidence interval on shear velocity (Sect. 4.1) and standard deviation of Rouse-estimated floc settling velocity (Sect. 4.5).

5.10 Validating the semi-empirical model

Figure 12 shows the validation of the semi-empirical model. We compared the semi-empirical model predictions (Eq. 7; Nghiem et al., 2022) and the observed floc cutoff diameter (sediment concentration–depth profiles, Rouse–Vanoni theory; Sect. 4.5), floc settling velocity (floc cam, Sect. 4.4; LISST combined with sediment sample data, Sect. 4.6.4), and floc diameter (LISST combined with sediment sample data; Sect. 4.6.1). We used the median of the depth-averaged distribution for floc settling velocity and floc diameter in the comparison because the semi-empirical model was calibrated on depth-averaged data (Nghiem et al., 2022). The semi-empirical model predicts the floc cutoff diameter well within a factor of ∼2 of measurements and captures the overall data trend (Fig. 12a). Floc settling velocity predictions of the semi-empirical model agree well within a factor of 2 with the floc cam and LISST-based floc settling velocity measurements (Fig. 12b). Since we used the explicit model to calculate the floc settling velocity distribution (Sect. 4.6.4), Fig. 12b also confirms the consistency between the semi-empirical and explicit models. The floc diameter results indicate that the semi-empirical model predicts adequately within a factor of 2, albeit with a limited number of data points (Fig. 12c). The reasonable performance of the semi-empirical model against direct measurements in WLD validates the model.

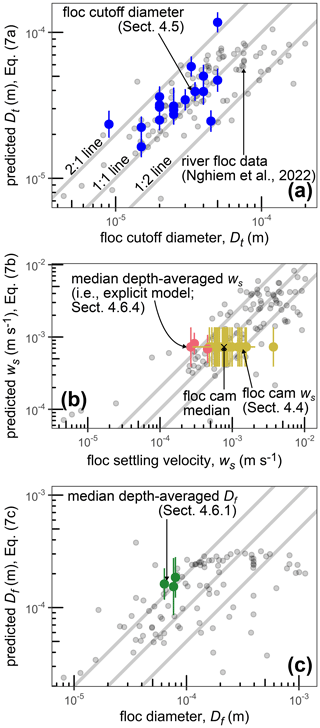
Figure 12 Measured and semi-empirical model predictions of (a) floc cutoff diameter (Eq. 7a), (b) floc settling velocity (Eq. 7b), and (c) floc diameter (Eq. 7c). Gray points are the river floc data that Nghiem et al. (2022) used to calibrate the semi-empirical model. Vertical bars represent the 95 % confidence interval of predictions. The floc cam data have the same predicted floc settling velocity because they represent a single floc cam deployment. Data for which water chemistry was not measured are omitted because they lack semi-empirical model predictions, which explains the absence of floc cam data in panel (c).

To demonstrate environmental effects on flocculation, we followed Nghiem et al. (2022) and plotted the predictors in the semi-empirical model against the floc cutoff diameter (normalized to remove the effects of other variables and by the median) because the floc cutoff diameter model (Eq. 7a) displays the best correlation with measurements (Fig. 12). We expect similar patterns for floc settling velocity and diameter because the floc variables correlate with each other (Nghiem et al., 2022). Turbulence, through the Kolmogorov microscale, limits floc size and settling velocity (Figs. 13a, 7d) because the semi-empirical model assumes that floc growth and breakage rates are balanced (Nghiem et al., 2022). As depth-averaged median primary particle diameter increases, coarser and faster-settling grains can be added to flocs (Fig. 13b). A higher sediment concentration enhances flocculation by increasing the particle collision rate (Fig. 13c). The effect of organic matter, as quantified by the organic cover fraction, θ, promotes flocculation at low values but is predicted to have an opposite effect once θ>0.5 because high organic coverage stabilizes sediment surfaces from aggregation (Fig. 13d). Sediment Al $/$ Si and relative charge density, Φ, vary inversely with floc properties because they might preferentially cause clay flocculation and exclude faster-settling silt grains from flocs (Fig. 13e, f). These trends for WLD are similar to those found for global rivers (Nghiem et al., 2022).

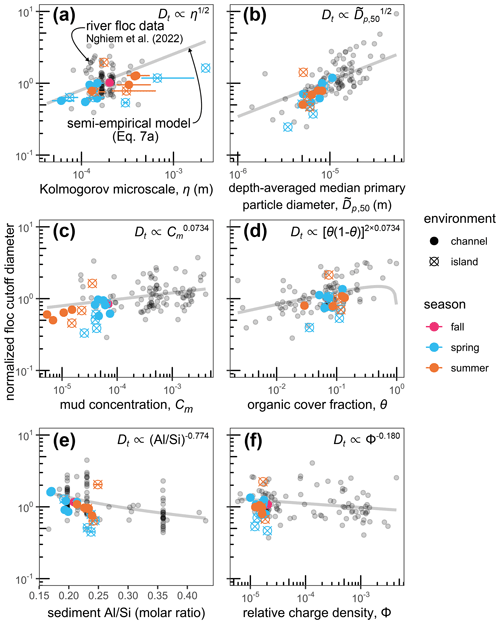
Figure 13 Semi-empirical model predictors plotted against floc cutoff diameter, D_t, normalized by the effects of all other predictors in the floc model (Eq. 7a). Gray curves indicate the model prediction. Horizontal bars indicate the (a) 95 % confidence interval on shear velocity, (d) 1σ error in percent weight organic carbon, or (e) 95 % confidence interval on Al $/$ Si estimates.

6 Discussion

6.1 Leveraging multiple floc data sources

By combining three floc data sources (in situ laser diffraction, camera, sediment concentration–depth profiles), we overcame the limitations of the individual data sources and derived a nearly complete accounting of floc properties, including floc diameter, solid fraction, floc settling velocity, fractal dimension, effective primary particle diameter, and drag ratio. In situ laser diffraction data alone are limited because they record a mixture of flocs and unflocculated sediment grains (e.g., Livsey et al., 2022). We developed a technique to isolate floc concentration and size distribution by separating flocs and unflocculated grains (Fig. 4) using in situ laser diffraction data and sediment concentration–depth profiles (Sect. 4.6.1). From this technique, we also computed the primary particle concentration and size distribution as well as the floc bulk solid fraction (i.e., ratio of primary particle and floc concentrations).

In past studies, a key knowledge gap was the role of effective primary particle diameter and drag ratio in floc settling velocity in the explicit model (e.g., Strom and Keyvani, 2011) because camera-measured floc diameter and settling velocity data alone were insufficient to separate those variables. We leveraged the floc size distribution and bulk solid fraction to compute the fractal dimension and effective primary particle diameter (Sect. 4.6.2). With an independent estimate of the effective primary particle diameter, we could then use the fractal dimension and floc-cam-measured floc diameter and settling velocity to estimate drag ratio (Sect. 4.6.3). Our ability to disentangle the effective primary particle diameter and drag ratio thus paved the way to test theory.

Although our data synthesis proved successful at furnishing many floc properties and holds good potential for future field studies, it still has limitations. We could only estimate a single effective primary particle diameter for each floc size distribution, but the effective primary particle diameter might vary within the floc size distribution, especially at the fine tail where floc and effective primary particle diameters might be on a similar scale. There is some uncertainty in combining LISST and suspended sediment sample data. We assumed that they measured statistically equivalent material because they did not strictly measure the exact same material. We assumed that all sediment finer than the floc cutoff diameter was flocculated across the water column (Sect. 4.5), but some fraction of this sediment could actually be unflocculated. We could not determine this fraction with our data.

6.2 Predicting floc settling velocity

The explicit and semi-empirical floc settling velocity models are consistent with each other (Fig. 12b), indicating that model choice depends on the scale of interest and data availability. The explicit model is at the scale of the individual floc, whereas the semi-empirical model is depth-averaged. We were able to compare the models because the depth-averaged floc settling velocity distributions represent depth averaging of the explicit model, which was used to calculate floc settling velocity distributions (Sect. 4.6.4). The semi-empirical model has the advantage of relying on geochemical data that can be easier to measure compared to the floc parameters in the explicit model.

Although we used joint camera, in situ particle sizing, and suspended sediment concentration and grain size distribution profiles to constrain the effective primary particle diameter and drag ratio in the explicit model, we suggest that the explicit model can still be used to predict floc settling velocity given only suspended sediment grain size distribution and floc diameter (e.g., through camera or in situ particle sizing data). The primary particle size distribution can be obtained from the suspended sediment grain size distribution by choosing a floc cutoff diameter (in the range of ∼10 to 50 µm; Nghiem et al., 2022) and removing coarser sediment from the distribution (Sect. 4.6.1). The fractal dimension of natural flocs can be assumed to be 2 (Winterwerp, 1998). The fractal dimension and primary particle size distribution feed into Eq. (5) with n_w=0 to predict effective primary particle diameter. Predicting the drag ratio remains a challenge because prior analytical permeability models were inconsistent with our drag ratio estimates (Fig. 9a). Ω can be constrained based on additional field measurements, as done here, or left as a tuning parameter.

The semi-empirical model predicts floc cutoff diameter, diameter, and settling velocity as a function of water chemistry, organic matter, sediment mineralogy and concentration, and turbulence in the absence of a purely mechanistic theory to link these factors. The full unsteady form of the semi-empirical model, along with existing dynamic flocculation models (e.g., Xu et al., 2008; Son and Hsu, 2011; Shen et al., 2018), can be used to predict floc settling velocity through time and space in a sediment transport model. However, this approach can be computationally expensive and require parameters that are difficult to constrain. Our analysis suggests that the assumption of local equilibrium is a reasonable simplification to predict floc properties because our observations are consistent with the equilibrium semi-empirical model (Fig. 12). This fact implies that flocs quickly adjust to their local conditions, a behavior that has some experimental evidence (Tran et al., 2018). In fact, we suggest that using a single constant floc settling velocity for the mud settling velocity (Roberts et al., 2000; Braat et al., 2017) might be reasonable in alluvial channels because trade-offs between turbulence, sediment concentration, and primary particle size and mineralogy might offset each other (Sect. 6.4).

6.3 Role of effective primary particle diameter and drag ratio in floc settling velocity

Our results indicate that the effective primary particle diameter best follows the number-weighted fractal D_p model (Eq. 5 with n_w=0; Fig. 8b). In contrast, the volume-weighted fractal D_p (n_w=3) is biased high compared to measured D_p. Regardless of n_w, the fractal D_p model (Eq. 5) ensures that the effective primary particles occupy the same n_f-dimensional space as the original primary particles. The choice of n_w relies on the relevant physical dimension (Bushell and Amal, 2000). The number-weighted version (n_w=0) indicates that the number of effective primary particles matches the number of original primary particles in the floc under fractal theory (Bushell and Amal, 2000). On the other hand, n_w=3 means that the total primary particle volume is conserved. The fact that the number-weighted fractal D_p outperforms the volume-weighted version implies that conserving the number of primary particles, rather than the primary particle volume, is critical for the effective primary particle diameter. This conclusion is counterintuitive because we calculated D_p using fractal theory for the solid fraction (Eq. 9), which is a volume-based metric. However, the number of primary particles might be more important because the fractal solid fraction theory (Eq. 2) assumes that the number of primary particles follows fractal scaling (Kranenburg, 1994). In contrast, past work treated D_p as an average length scale of primary particles (Syvitski et al., 1995; Strom and Keyvani, 2011). If one assumed D_p is the volumetric median, then one would overestimate the solid fraction and floc settling velocity by a factor dependent on the fractal dimension (Eqs. 1 and 2). In our data, this factor ranges from ∼1.7 to 15 and has a median of 3.3.

We used a new permeable solid fraction model to determine the physical reason our drag ratio estimates are incompatible with existing permeability models. Natural flocs are distinct because they have nonuniform porosity (Eq. 2) and a primary particle size distribution. These features probably caused the much smaller drag ratios (higher permeability) than could be predicted by prior permeability models (Fig. 9a). The Li and Logan strategy attempts to account for nonuniform porosity by replacing the effective primary particle diameter with a larger cluster diameter representing the clusters that form the main flow paths through the floc. However, this approach is very limited, as recognized by Kim and Stolzenbach (2002). The increase in permeability caused by the Li and Logan modification is small because an effective increase in the solid fraction partially offsets larger pores caused by primary particle clustering. Kim and Stolzenbach (2002) found that the original Davies model (Eq. 6) performed well at predicting the hydrodynamic drag on fractal aggregates with nonuniform porosity, suggesting that the Davies model is suitable for flocs, in contrast to our findings (Fig. 9a). If nonuniform porosity caused by fractal structure is not the source of the discrepancy between our drag ratio estimates and the Davies model, then it is likely the primary particle size distribution because Kim and Stolzenbach (2002) did not test aggregates containing many primary particle sizes. The permeable solid fraction model offers a physical explanation because the permeable solid fraction is, on average, 10 % of the true solid fraction (Fig. 9b). This result suggests that a subset of the primary particles composes the portion of the floc structure (characterized by the permeable fractal dimension) responsible for conducting flow through the floc. The rest of the primary particles might be shielded from the flow because of their configuration with respect to adjacent larger particles and do not contribute to permeability. The configuration of organic matter within flocs might also affect permeability by controlling flow paths. It is difficult to study all these effects because the complete floc structure must be known, but recent advances in 3D floc imaging might facilitate more detailed studies (Lawrence et al., 2022, 2023).

Although the drag ratio estimates depend on the assumed floc shape, floc shape is not responsible for the inability of existing permeability models to reproduce the drag ratio. Floc shape affects the shape factor, b₁, in the explicit model. Larger values of b₁ cause smaller drag ratio estimates (Sect. 4.6.3). Stokes' law shows that b₁=18 (Stokes, 1851) for an impermeable sphere (Ω=1). Strom and Keyvani (2011) suggested that b₁∼20 is suitable for flocs with n_f<2, but b₁=120 for flocs with n_f≥2.5. Regardless of the precise value of b₁, particle shape effects only cause b₁>18 because shape irregularities induce more drag (McNown and Malaika, 1950; Dietrich, 1982). We used a relatively low value of b₁=20 (Ferguson and Church, 2004) to calculate the drag ratio. Higher b₁ would only further amplify floc permeability and widen the discrepancy with theory.

6.4 Environmental controls on flocculation

The semi-empirical model trends in Fig. 13 show the major environmental controls on flocs in WLD and globally. However, these variables are not independent. We hypothesize that turbulence causes correlation and feedbacks between these factors through sediment entrainment and settling dynamics in alluvial systems. To test this hypothesis, Fig. 14 compares the Kolmogorov microscale, which scales inversely with turbulence intensity, and semi-empirical model parameters. For rivers and WLD channels, the Kolmogorov microscale correlates with a finer primary particle diameter and higher Al $/$ Si because more turbulent flows (smaller microscale and higher shear velocity) entrain and suspend coarser sediment (Fig. 14a, b). Coarser primary particles have a more distinct mineralogy (lower Al $/$ Si) than finer grains. A higher mud concentration corresponds to a smaller Kolmogorov microscale because higher fluid stress entrains more sediment from the bed (Fig. 14c). Flows with higher turbulent energy can also maintain faster-settling flocs, if conditions permit their formation, in the water column (Eq. 8; Dunne et al., 2024). All else being equal, these interactions indicate that higher turbulence intensity correlates with larger floc cutoff diameter, faster floc settling velocity, and larger floc diameter (Eq. 7) in alluvial channels. However, increases in turbulence intensity offset these effects because they cause floc breakage at equilibrium, leading to a negative feedback. These patterns are not evident in the WLD island because variables are poorly correlated with the Kolmogorov microscale (Fig. 14), potentially owing to more complicated two-dimensional and unsteady effects on sediment transport (Geleynse et al., 2015; Bevington et al., 2017).

We argue that turbulence is the overriding variable controlling flocculation in global rivers and the channels of WLD because it not only directly affects particle collisions, floc breakage (Winterwerp, 1998), and flow competence with respect to flocs, but also sets the concentration and primary particle size and mineralogy. The negative feedback demonstrates that flocculation can partially buffer against spatiotemporal changes in turbulence, a mechanism that might explain observations of limited floc settling velocity variation (∼0.2 to 0.6 mm s⁻¹) across seasons in the Mississippi River (Osborn et al., 2023) and, more broadly, the limited global variation of ∼0.1 to 1 mm s⁻¹ (e.g., Hill et al., 2000; Mikkelsen et al., 2007; Nghiem et al., 2022).

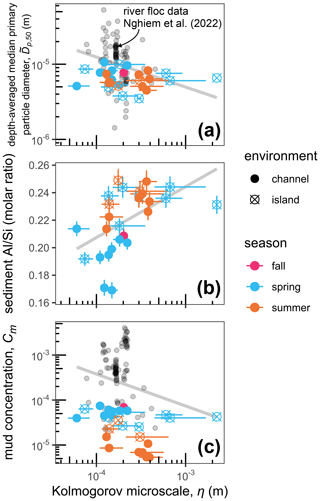
Figure 14 Kolmogorov microscale and (a) depth-averaged median primary particle diameter, (b) sediment Al $/$ Si, and (c) mud volume concentration. In each panel, the gray line indicates the trend line. Horizontal error bars indicate the 95 % confidence interval on shear velocity. In panel (b), vertical error bars indicate the 95 % confidence interval on Al $/$ Si estimates. River floc data are omitted in panel (b) because most Al $/$ Si data compiled by Nghiem et al. (2022) were not concurrent with the sediment concentration–depth profile and hydrodynamic surveys.

In contrast to the other semi-empirical model inputs, the organic cover fraction and relative charge density vary less and are not responsible for the bulk of the variability in floc parameters (Fig. 13). This does not imply that they are unimportant for flocculation. Instead, we propose that they are allogenic catchment-wide controls on flocculation and vary over longer timescales. For example, tectonic activity and climate change can alter biological productivity and chemical weathering intensity on the catchment scale (Geider et al., 2001; West et al., 2005), altering the organic cover fraction and relative charge density through changes in organic carbon loading on sediment and water chemistry (e.g., Galy et al., 2008). These effects are not directly linked to turbulence feedbacks, implying that they can cause persistent changes in floc properties that are not simultaneously offset. In fact, organic matter might modulate turbulence and force a positive feedback that increases floc size and settling velocity because biological cohesion can limit bedform size and hence reduce the turbulent shear (i.e., increase the Kolmogorov microscale) associated with bedforms (Malarkey et al., 2015; Parsons et al., 2016). In contrast, the Kolmogorov microscale, sediment concentration, Al $/$ Si, and primary particle size vary autogenically on shorter flood-to-seasonal discharge timescales because they adjust together in response to discharge and sediment dynamics within the alluvial system (e.g., Phillips et al., 2022).

7 Conclusions

Flocculation controls the transport and distribution of mud across rivers and wetlands by increasing the effective mud settling velocity. To test theory controlling floc settling velocity, we combined multiple floc data sources – a camera, in situ LISST particle size and concentration, and sediment concentration–depth profiles – in the freshwater Wax Lake Delta, LA. We not only calculated commonly constrained floc properties like diameter, settling velocity, and fractal dimension, but also made novel field measurements. Key advances of the data synthesis include isolating floc concentration and size distribution in in situ laser diffraction data and computing hitherto poorly constrained variables: effective primary particle diameter and drag ratio. We observed flocs in WLD with median diameters of 30 to 90 µm, a bulk solid fraction of 0.05 to 0.3, and settling velocities of the order of 0.1 to 1 mm s⁻¹ with little vertical variation. Flocs included grains up to 10 to 55 µm in diameter. Flocs in channels tended to be larger and lighter, while flocs in an island wetland tended to be smaller and denser. On average, floc diameter and settling velocity were an order of magnitude larger than those of primary particles. We used these data to validate and calibrate an explicit floc settling velocity model based on Stokes' law and a semi-empirical model, which relies on hydrodynamic and geochemical data.

Using the new complete dataset of floc attributes, we tested theory for two key unknowns, effective primary particle diameter and drag ratio, in the explicit model. Effective primary particle diameter varied between 1 and 3 µm and had a typical value of 2 µm. We verified a fractal model for effective primary particle diameter that conserves the number and fractal space of the original primary particles (Fig. 8b), demonstrating that the effective primary particle diameter is not a simple characteristic length scale (i.e., median) as previous studies assumed. The volumetric median primary particle diameter systematically overestimates the effective primary particle diameter by an average factor of 2 and up to a factor of 6, leading to overestimates of floc solid fraction and settling velocity. Floc permeability, quantified by the drag ratio, has been under-explored for natural flocs. The mean drag ratio was 0.48, but the drag ratio ranged between 0.15 and 1 (Fig. 9a). These drag ratios indicate enhanced floc settling velocity by a mean factor of 2 and up to a factor of 7. The drag ratio estimates do not conform to prior permeability theory because the theory does not consider a primary particle size distribution. Instead, a new permeable solid fraction model suggests that only some primary particles are relevant for permeability because primary particle size interactions might shield other primary particles from the main flow paths (Fig. 9b).

We tested the semi-empirical model for the first time using direct measurements of flocs. Our data validate the semi-empirical model because it predicts floc cutoff diameter, floc settling velocity, and floc diameter all within a factor of 2 of the measured field data. We also showed that its floc settling velocity predictions are consistent with those of the explicit model. The semi-empirical model reveals that turbulence, sediment concentration and mineralogy, organic matter, and water chemistry control flocculation in WLD and suggests that flocs can be reasonably modeled in local equilibrium. Results indicate that turbulence controls a negative feedback on floc settling velocity because higher turbulence intensity causes a higher sediment concentration, lower Al $/$ Si (a sediment mineralogy proxy), and a higher primary particle diameter through sediment entrainment dynamics (Sect. 6.4). These factors correlate with faster floc settling velocity but are offset by shear breakage of flocs. This feedback might mitigate changes in floc settling velocity in alluvial channels on the flood and seasonal timescales over which flow turbulence typically varies. Organic matter binding and sediment surface charge interactions might affect flocculation at longer timescales because they are set by allogenic catchment- to continental-scale processes like biological productivity and chemical weathering of rock. Overall, the semi-empirical and explicit models are both viable options for predicting floc settling velocity in rivers and freshwater wetlands but require knowledge of different predictors and operate at different scales.

Finally, we emphasize that the workflow of combining multiple floc methods (camera, in situ laser diffraction, sediment concentration–depth profiles) presented in this study is a powerful tool that can provide a more complete description of flocs than previously done with only one or two of the individual methods.

Appendix A: Notation

Al $/$ Si	Sediment Al to Si molar ratio
b1	Settling velocity model constant (20), dimensionless
Cfl	Floc volume concentration, dimensionless
Ci	Sediment volume concentration for ith grain size class, dimensionless
Cbi	Near-bed sediment volume concentration for ith grain size class, dimensionless
Cm	Depth-averaged mud volume concentration, dimensionless
Dc	Cluster diameter, m
Df	Floc diameter, m
Df,50	Median floc diameter, m
Dp	Effective primary particle diameter, m
Dp,50	Median primary particle diameter, m
${\stackrel{\mathrm{̃}}{D}}_{\mathrm{p},\mathrm{50}}$	Depth-averaged median primary particle diameter, m
Dt	Floc cutoff diameter, m
g	Gravitational acceleration (9.81), m s−2
h	Local water depth, m
hb	Near-bed height (0.1 h), m
k	Floc permeability, m2
nf	Floc fractal dimension, dimensionless
nr	Permeable fractal dimension, dimensionless
nw	Weighting dimension, dimensionless
pi	Rouse number for ith grain size class, dimensionless
Rs	Submerged specific gravity of sediment (1.65), dimensionless
u*	Shear velocity, m s−1
ws	Floc settling velocity, m s−1
wsi	In situ particle settling velocity for ith grain size class, m s−1
β	Sediment diffusivity ratio, dimensionless
βfl	Floc diffusivity ratio, dimensionless
η	Kolmogorov microscale, m
θ	Organic cover fraction, dimensionless
κ	Von Kármán constant (0.41), dimensionless
ν	Kinematic viscosity of water (10−6), m2 s−1
ξ−2	Dimensionless floc permeability, dimensionless
ρ	Water density (1000), kg m−3
ρs	Sediment density (2650), kg m−3
Φ	Relative charge density, dimensionless
φ	Floc solid fraction, dimensionless
$\stackrel{\mathrm{‾}}{\mathit{\phi }}$	Bulk floc solid fraction, dimensionless
φr	Permeable solid fraction, dimensionless
Ω	Drag ratio, dimensionless