Dimensionless argument: a narrow grain size range near 2 mm plays a special role in river sediment transport and morphodynamics

The grain size 2 mm is the conventional border between sand and gravel. This size is used extensively, and generally without much physical justification, to discriminate between such features as sedimentary deposit type (clast-supported versus matrix-supported), river type (gravel bed versus sand bed), and sediment transport relation (gravel versus sand). Here we inquire as to whether this 2 mm boundary is simply a social construct upon which the research community has decided to agree or whether there is some underlying physics. We use dimensionless arguments to show the following for typical conditions on Earth, i.e., natural clasts (e.g., granitic or limestone) in 20 ^∘C water. As grain size ranges from 1 to 5 mm (a narrow band including 2 mm), sediment suspension becomes vanishingly small at normal flood conditions in alluvial rivers. We refer to this range as pea gravel. We further show that bedload movement of a clast in the pea gravel range with, for example, a size of 4 mm moving over a bed of 0.4 mm particles has an enhanced relative mobility compared to a clast with a size of 40 mm moving over a bed of the same 4 mm particles. With this in mind, we use 2 mm here as shorthand for the narrow pea gravel range of 1–5 mm over which transport behavior is distinct from both coarser and finer material. The use of viscosity allows the delineation of a generalized dimensionless bed grain size discriminator between “sand-like” and “gravel-like” rivers. The discriminator is applicable to sediment transport on Titan (ice clasts in flowing methane/ethane liquid at reduced gravity) and Mars (mafic clasts in flowing water at reduced gravity), as well as Earth.

1 Introduction

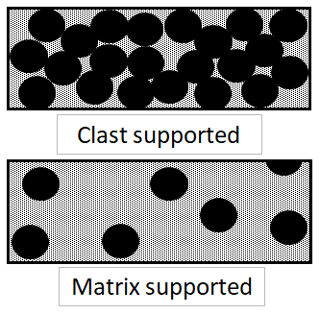
In rivers, the grain size 2 mm is the conventional divider between sand and gravel. This size has been repeatedly used, explicitly or implicitly, as a discriminator of alluvial rivers and their deposits. For example, conglomerate deposits are often classified as clast-supported (pebble-supported) or matrix-supported, depending on whether clasts with a size in excess of 2 mm are in contact with each other (clast-supported) or whether the clasts are “floating” in a finer deposit (sand or silt; matrix-supported) (see, e.g., Tucker, 2003; Frings, 2011; Jutzeler et al., 2015; Li et al., 2017). This classification is illustrated in Fig. 1.

Figure 1 Clast-supported versus matrix-supported deposits. Clasts are > 2 mm, and matrix is < 2 mm.

Gravel bed rivers (characteristic bed material size > 2 mm) and sand bed rivers (characteristic bed material size < 2 mm) have often been treated separately. Communities of researchers have even formed around the distinction. For example, the Gravel Bed Rivers conference series has existed for 40 years, since the early work, summarized in Hey et al. (1982), began. Note that Hey et al. (1982) specifically name their volume Gravel-Bed Rivers. This distinction has continued through at least eight successive conference proceedings (Laronne and Tsutsumi, 2018). Likewise, a large volume of the literature has been devoted exclusively to sand bed rivers (see, e.g., Wright and Parker, 2004; Peng et al., 2022; Venditti and Bradley, 2022). Relations for hydraulic geometry have also been derived separately for gravel bed rivers (e.g., Parker et al., 2007; Khosravi et al., 2021) and sand bed rivers (e.g., Xu, 2004; Wilkerson and Parker, 2011).

Many sediment transport relations have been developed exclusively for sand bed (characteristic bed grain size < 2 mm) or gravel bed (characteristic bed grain size > 2 mm) rivers. For example, the sediment transport relation of Engelund and Hansen (1967) was developed exclusively for sand, based on the flume data of Guy et al. (1966). It was verified by Brownlie (1982), again exclusively for experiments and field data pertaining to the sand bed case. The bedload transport relation of Meyer-Peter and Müller (1948) was originally developed exclusively using experimental results pertaining to gravel. The bedload transport relation for gravel mixtures from Parker (1990) specifies that sand should be removed from the grain size distribution of the bed before the transport rate is calculated. The transport relation for sediment mixtures in Wilcock and Crowe (2003) changes the mobility of gravel (grain size D>2 mm), depending upon the content of sand (D<2 mm) in the bed surface material. (The bedload transport relation of Ashida and Michiue, 1972, however, does include data ranging from 0.3 to 7 mm; i.e., across the 2 mm size.) Experimental studies of sediment transport using size mixtures often have the size 2 mm built into the experimental design, such that sediment fractions finer and coarser than this divider are allowed to interact with each other. Such studies include Hill et al. (2016) and Dingle and Venditti (2023).

Here we pose the following questions. Is the 2 mm divider a social construct based on decades of repetition, convergence, and rearticulation (as viewed from the point of view of social science; Butler, 1997), or does it have a physical basis? Why specifically 2 mm and not 0.6 or 13 mm? And if the size 2 mm has a physical basis, can it be interpreted in a universal, dimensionless way?

2 Empirical evidence for 2 mm as a discriminator in alluvial rivers

There are two lines of evidence that 2 mm, or more specifically the relatively narrow range of 1 to 5 mm, plays a special role in terms of sediment transport and river morphodynamics. Different authors define this range somewhat differently. For example, Church and Hassan (2023) use 1–10 mm, whereas here we follow the lead of Lamb and Venditti (2016) and define it to be 1–5 mm (based on the effect of viscosity described below). The most direct evidence concerns patterns of downstream fining in rivers carrying a mixture of gravel and sand. Many streams show a pattern of downstream fining, such that characteristic bed surface material, e.g., median size D₅₀ of the bed surface material, gradually becomes finer downstream, until a size somewhat coarser than pea gravel is reached, and then abruptly declines to the range of sand. Subreaches of such streams where D₅₀ is in the pea gravel range are either short (∼ 5 widths) or non-existent (e.g., Sambrook Smith and Ferguson, 1995). The first person to document this behavior was Yatsu (1955), who presented numerous abrupt gravel–sand transitions in Japanese rivers. In the Kinu River, for example, characteristic grain size drops from 20 to about 1 mm over a short reach. Yatsu (1955) speculates that this might be due to the abrupt shattering of granitic clasts into their component crystals when the grain size is abraded to about 20 mm. Kodama (1994) provides some support for this view and emphasizes the role of abrasion. Shaw and Kellerhals (1982), however, document the same gravel–sand transition in rivers where non-crystalline sediments such as limestone dominate. Abrasion thus may not play a dominant role in the formation of abrupt gravel–sand transitions. This is further supported by observations in rivers with sharp transitions which have clasts that are highly resistant to abrasion (e.g., Ferguson et al., 1996; Venditti and Church 2014; see the review in Dingle et al., 2021).

Both Fujita et al. (1998) and Lamb and Venditti (2016) use large data sets to illustrate that a substantial number of river reaches have coarse-gravel beds (bed surface D₅₀ or D₆₀>5 mm) and sand beds (bed surface D₅₀ or D₆₀<1 mm), but very few reaches have a characteristic size in the pea gravel range (Fig. 2a, b). Both sets of authors cast this in the context of downstream fining and gravel–sand transitions. Fujita et al. (1996) in particular note that, at least in Japan, the relatively few reaches with a characteristic bed size in the pea gravel pertain to streams with heavy loads of sediment derived from weathered granite.

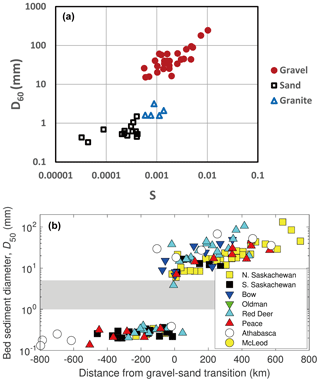
Figure 2 (a) Bed surface size D₆₀ versus bed slope for Japanese streams (adapted from Fujita et al., 1998). (b) Bed surface size D₅₀ versus distance from gravel–sand transition for Canadian streams (Lamb and Venditti, 2016). In panel (a), “granite” is an abbreviation for “rivers that have weathered granitic rock in their catchments”.

Gravel–sand transitions need not be abrupt. Especially in rivers sufficiently wide to develop bedform- and planform-driven variation in local flow conditions (e.g., a bar field), the transition may be rather disperse and elongated (Frings, 2011), with the interleaving of sand and coarse-gravel patches for some distance downstream of the main transition (Venditti et al., 2015; Dong et al., 2016). Paola and Seal (1995) have shown how gravel–sand patchiness can drive such a transition. Frings (2011) shows this elongation of the transition region for the case the Rhine river, western Europe, where the tendency in question might be affected by anthropogenic effects such as river training. Dong et al. (2016) show this behavior for the case of the Selenga river, Siberia, Russia, where anthropogenic effects are negligible. The transitional reaches in question often do not show substantial subreaches where pea gravel is the characteristic bed material size. Instead, that characteristic size is gravel in excess of 10 mm upstream, is below 1 mm downstream, and locally interleaves between coarser gravel and sand in the transitional region, with relatively few locations with a characteristic bed surface size in the pea gravel range. Venditti et al. (2015), for example, describe the Fraser River, British Columbia, Canada, as “an archetypical abrupt gravel–sand transition with a 'diffuse extension' composed of a sand bed with some patches of gravel”. Dingle et al. (2021) provide a thorough review of the gravel–sand transition and grain size gap. This issue is considered in more detail in Sect. 7. Of relevance to the analysis here is the fact that both Lamb and Venditti (2016) and Dingle et al. (2021) suggest a role for viscosity in regard to the grain size gap. This effect is explained in more detail below.

A second line of evidence derives from experiments with mixtures of gravel and sand. Prominent among them is the work of Wilcock and Crowe (2003), who show that in a unimodal mixture of sand and gravel, increasing content of material less than 2 mm in the bed results in an increased transport rate of material greater than 2 mm. Indeed, they modified the basic framework of the Parker (1990) relation to specifically account for this effect, which Lin et al. (2023) have described as gravel transport augmenting sand (GTAS). The results of Wilcock and Crowe (2003) have been verified by others (e.g., Cui et al., 2003a, b; Dingle and Venditti, 2023). They break, however, the completely dimensionless format of Parker (1990) by introducing a parameter with dimensions, namely the 2 mm cutoff between sand and gravel. We show below how this problem can be overcome.

Dingle and Venditti (2023) performed flume experiments using a bimodal mix of pea gravel (∼ 3.8 mm) and sand (∼ 0.57 mm) to show that the addition of sand strongly mobilizes the pea gravel. They suggest that adding sand to a bed consisting of material in the grain size gap produces a “hydraulic smoothing” effect, resulting in mobilization of material in that gap. This same effect was noted when adding sand (∼ 0.57 mm) onto a broader unimodal gravel distribution (2–22 mm; D₅₀=5.5 mm), where the pea gravel fraction became disproportionately mobile relative to the other gravel fractions. The addition of sand was found to increase gravel mobility up to a sand fraction in the bed of about 0.84, beyond which the gravel clasts tend to get buried. Church and Hassan (2023) show experimentally how a continuous, only weakly bimodal mixture of sand and gravel can devolve into a grain size distribution with an autogenically strengthened grain size gap. They note that “Our experiment shows a clear tendency for grains in the range 1–8 mm to outrun both larger and smaller grains in the condition of size-selective transport” (Church and Hassan, 2023).

3 The central problem

So what is so special about the pea gravel range? Consider a thought experiment. Loosely following Dingle and Venditti (2023), we consider Case 1, with 4 mm gravel (in the pea gravel range) moving over a 0.4 mm sand bed (finer than the pea gravel range), and Case 2, where we multiply all the numbers by 10; i.e., 40 mm gravel (coarser than the pea gravel range) moving over a 4 mm gravel bed (in the pea gravel range). Will the finer material of the bed increase the mobility of the coarser material in Case 2 to the same extent in as Case 1? We have a partial answer to this question. Venditti et al. (2010a, b) studied the case where both sizes are in the gravel range. They found that the mobility of coarse-surface layers in gravel-bedded rivers could be enhanced by adding finer gravel as bedload (Case 2). The degree of enhancement, however, is not nearly as strong as Case 1 (as documented by, e.g., Wilcock and Crowe, 2003). Indeed, the extra mobility of Case 2 can be explained solely in terms of the hiding–exposure functions embedded in the relations of Parker (1990) and Wilcock and Crowe (2003), as elaborated in, for example, Parker and Klingeman (1982) and Parker and Toro-Escobar (2002). These relations describe the relative mobility of different sizes in a mixture of gravel in the active (surface) layer of the bed. Relative mobility is mediated by two effects: a weight effect making coarser (and thus heavier) particles harder to move and an exposure (hiding) effect making coarser particles more exposed to the flow and thus easier to move. The residual of the two effects (weight versus hiding–exposure effect) renders finer gravel somewhat more mobile in a sediment mix. Evidently there is something special with regard to the strong enhancement of the mobility of pea gravel moving over a sand bed (Case 1 compared to Case 2). Here we explore two possibilities, one related to sediment suspension and one related to bedload, with both effects mediated by viscosity.

4 Pea gravel corresponds to the finest sizes that do not readily suspend in alluvial rivers

We revisit the relation of Garcia and Parker (1991) for the entrainment of bed sediment into suspension. Although the formulation includes relations for both uniform sediment and sediment size mixtures, we consider the case of uniform sediment here. For equilibrium suspensions, the relation takes the following form:

$$\begin{array}{}\text{(1a)}& c_{\mathrm{b}}={\displaystyle \frac{A{Z}_u^{\mathrm{5}}}{\mathrm{1}+\frac{A}{\mathrm{0.3}}{Z}_u^{\mathrm{5}}}},\end{array}$$

$$\begin{array}{}\text{(1b)}& Z_u={\displaystyle \frac{u_{\ast \mathrm{s}}}{v_{\mathrm{s}}}}{\left(D^{\ast }\right)}^{\mathrm{0.9}},\end{array}$$

$$\begin{array}{}\text{(1c)}& D^{\ast }=D{\displaystyle \frac{{\left(\text{Rg}\right)}^{\mathrm{1}/\mathrm{3}}}{{\mathit{\nu }}^{\mathrm{2}/\mathrm{3}}}},\end{array}$$

Here c_b is the near-bed volume concentration of suspended sediment (evaluated at a point that is 5 % of water depth above the bed); D is the grain size for an equivalent sphere in terms of fall velocity; u_∗s is the bed shear velocity due to skin friction (form drag removed); v_s is the particle fall velocity; g= gravitational acceleration; $R=({\mathit{\rho }}_{\mathrm{s}}-\mathit{\rho })/\mathit{\rho }$ is the submerged specific gravity of sediment, where ρ_s is the sediment density, and ρ is the density of the fluid in which the sediment is immersed (R∼ 1.65 for quartz in water); ν is the kinematic viscosity of fluid in which the sediment is immersed; D^∗ is a dimensionless grain size; and A is a dimensionless constant given as

$$\begin{array}{}\text{(1d)}& A=\mathrm{1.3}\times {\mathrm{10}}^{-\mathrm{7}}.\end{array}$$

(The original formulation of the Garcia–Parker relation (Garcia and Parker, 1991) uses a particle Reynolds number ${\mathit{Re}}_{\mathrm{p}}=(\text{Rg}D{)}^{\mathrm{1}/\mathrm{2}}D/\mathit{\nu }$ but is here recast in terms of the parameter $D^{*}={\left({\mathit{Re}}_{\mathrm{p}}\right)}^{\mathrm{2}/\mathrm{3}}$, which is a more convenient representation, in so far as that dimensionless grain size D^* is linearly proportional to dimensioned grain size D; see van Rijn, 1984.)

The Garcia–Parker relation was developed solely with experimental data on suspensions of quartz sediment in water, using a total of 62 measurements with grain size D varying from 0.093 to 0.44 mm, so that D^* varies from 2.36 to 11.1 for quartz particles immersed in 20 ^∘C water on Earth. The relation was thus not designed to be applied to the suspension of gravel. It is nevertheless illustrative to do so.

In Fig. 3a, the predictions of Eqs. (1a)–(1d) are shown for the sizes D=0.25 and 4.0 mm. Here these are nominal sizes using Earth parameters (g=9.81 m s⁻², R=1.65, and $\mathit{\nu }=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}$ m s⁻²). It can be seen therein that the predictions for near-bed concentration c_b for 4 mm gravel are about half that of the corresponding values for 0.25 mm material. This seems unlikely; however, data for the suspension of any size of gravel seem to be rare in the literature, suggesting that the data are suspended only with difficulty in laboratory flumes and typical alluvial river flood flows (e.g., de Leeuw et al., 2020). That is, the Garcia–Parker relation seems to overestimate the suspension of gravel with a size range which is beyond the range of the experimental data that the relation is based on.

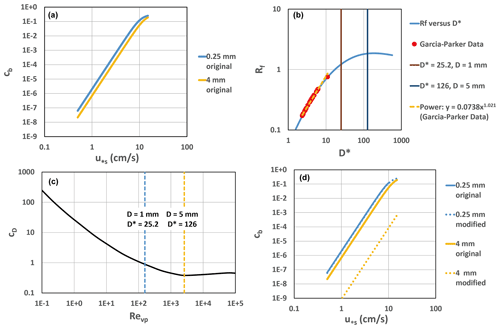
Figure 3 (a) Plot of near-bed concentration of suspended load versus shear velocity due to skin friction for D=0.25 and 4 mm, using the original relation of Garcia and Parker (1991) (i.e., Eqs. 1a, 1b, and 1c). (b) Plot of dimensionless fall velocity $R_{\mathrm{f}}=v_{\mathrm{s}}/(\text{Rg}D{)}^{\mathrm{1}/\mathrm{2}}$ versus dimensionless grain size D^*, using the Dietrich (1982) relation (solid line), including a power regression relation for R_f versus D^* over the original range of the data of Garcia and Parker (1991). (c) Drag curve for spheres illustrating viscous, transitional, and inertial regimes from left to right (adapted from Haljasmaa, 2006). (d) The version of Fig. 3a using both the original (Eqs. 1a, 1b, and 1c) and corrected (Eqs. 4a, 4b, and 4c) relations for Garcia and Parker (1991), showing the near-collapse of the suspension of particles of size 4 mm. In panel (d), the lines “0.25 mm original” and “0.25 mm modified” are on top of each other.

This problem can be explained with the dimensionless fall velocity R_f

$$\begin{array}{}\text{(2)}& R_{\mathrm{f}}={\displaystyle \frac{v_{\mathrm{s}}}{\sqrt{\text{Rg}D}}}.\end{array}$$

The parameter R_f is related to dimensionless grain size D^* according to, e.g., the relation of Dietrich (1982), as shown in Fig. 3b (solid blue line). Also plotted in Fig. 3b are the experimental data of Garcia and Parker (1991) and the dimensionless sizes $D^{*}=$ 25.2 and 126 (nominal sizes D= 1 and 5 mm for quartz particles in water on Earth). The regime to the left of nominal size D= 1 mm is viscous-dependent, i.e., dependent on D^*; the regime to the right of nominal size D= 5 mm is essentially viscous-independent; and the regime of nominal sizes 1–5 mm defines a transitional zone. The relation defined by the solid blue line in Fig. 3b is in turn derived in part from the drag relation for spheres shown in Fig. 3c (e.g., Haljasmaa, 2006), in which $c_{\mathrm{D}}=F_{\mathrm{D}}/\left[(\mathrm{1}/\mathrm{2})\mathit{\rho }\mathit{\pi }(D/\mathrm{2}{)}^{\mathrm{2}}{v}_{\mathrm{s}}^{\mathrm{2}}\right]$ is a drag coefficient, where F_D denotes the drag force on a spherical particle, and ${\mathit{Re}}_{\mathrm{vp}}=(v_{\mathrm{s}}D/\mathit{\nu })$ is a Reynolds number based on fall velocity. It is again seen that the regime to the left of nominal size D= 1 mm is viscous-dependent, the regime to the right of nominal size D= 5 mm is essentially viscous-independent (inertial regime), and the regime of nominal sizes 1–5 mm defines a transitional zone.

Figure 3b and c illustrate an inadequacy of the entrainment relation of Garcia and Parker (1991). The data used to derive it pertain solely to the viscous-dependent region of the relation for fall velocity, so that the relation cannot strictly be extended to coarser sizes. There is, however, a straightforward way to remedy this. Also plotted in Fig. 3b (dashed line) is the following regression relation for R_f versus D^*, fitted specifically over the range of the data used by Garcia and Parker (1991):

$$\begin{array}{}\text{(3)}& R_{\mathrm{f}}=\mathrm{0.0738}{\left(D^{\ast }\right)}^{\mathrm{1.021}}.\end{array}$$

This relation can be substituted into Eqs. (1a), (1b), and (1c) to yield a revised relation in which the constant A is unmodified, as follows:

$$\begin{array}{}\text{(4a)}& {\displaystyle }{c}_{\mathrm{b}}={\displaystyle \frac{A{Z}_u^{\mathrm{5}}}{\mathrm{1}+\frac{A}{\mathrm{0.3}}{Z}_u^{\mathrm{5}}}},\text{(4b)}& {\displaystyle }{Z}_u=\mathrm{9.95}{\displaystyle \frac{u_{\ast \mathrm{s}}}{v_{\mathrm{s}}}}{R}_{\mathrm{f}}^{\mathrm{0.882}}.\end{array}$$

According to Eq. (4b) and Fig. 3b, the modified parameter Z_u does not increase without bound as dimensionless grain size D^* increases. When inertial effects dominate, R_f becomes roughly constant, placing a bound on Z_u and preventing the oversuspension of material in the range of pea gravel and coarser material.

Figure 4 shows that when applied over the range of the original data of Garcia and Parker (1991), the predictive power of the modified formulation of Eqs. (4a) and (4b) is as good as the original formulation of Eqs. (1a), (1b), and (1c). Figure 3d shows that the modified formulation does not change the relation for c_b versus u_∗s for nominal 0.25 mm quartz in water (the two lines overlap) but causes such low values of c_b for nominal 4 mm quartz in water that they are essentially negligible. This negligibility is further reinforced by the Rouse (1937) relation for vertical profile of suspended sediment concentration. This relation contains an exponent proportional to $u_{\ast }/v_{\mathrm{s}}$, where u_∗ is the total bed shear velocity, and so the concentration above the bed collapses as $v_{\mathrm{s}}/u_{\ast }$ becomes sufficiently large.

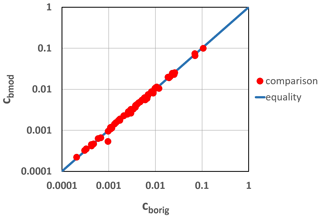
Figure 4 Plot of predicted values of near-bed concentrations c_bmod, using the modified formulation of Garcia and Parker (1991; Eqs. 4a, 4b, and 4c herein) versus those predicted from the original formulation, c_borig (Eqs. 1a, 1b, and 1c). Calculation is conducted over the range of the Garcia–Parker data.

The tendency for suspension to collapse as grain size increases across the pea gravel range can be confirmed in terms of the more recent relation of de Leeuw et al. (2020). Although several relations are presented therein, the one most directly comparable with the above formulation can be expressed in the following form for uniform material:

$$\begin{array}{}\text{(5a)}& {\displaystyle }{c}_{\mathrm{b}}=\left\{\begin{array}{cc}\frac{\mathrm{4.74}\times {\mathrm{10}}^{-\mathrm{0.4}}{X}^{\mathrm{1.18}}}{\mathrm{1}+\mathrm{3}\left(\mathrm{4.74}\times {\mathrm{10}}^{-\mathrm{0.4}}{X}^{\mathrm{1.18}}\right)},& X>\mathrm{0}\\ \mathrm{0},& X\le \mathrm{0}\end{array}\right.,\text{(5b)}& {\displaystyle }X={\left({\displaystyle \frac{u_{\ast \mathrm{s}}}{v_{\mathrm{s}}}}\right)}^{\mathrm{1.5}}\mathit{Fr}-\mathrm{0.015}.\end{array}$$

In the above relation, the Froude number $\mathit{Fr}=U/(gH{)}^{\mathrm{1}/\mathrm{2}}$, where U is depth-averaged flow velocity, and H is depth. A plot of c_b versus u_∗s for the grain sizes D= 0.25, 0.5, 1, 2, and 4 mm (quartz in water at 20 ^∘C) and Froude number Fr= 0.4 is given in Fig. 5. It is again seen that the suspension tends to collapse as the grain size enters the pea gravel range. Similar results are obtained for Fr= 0.2 and 0.6.

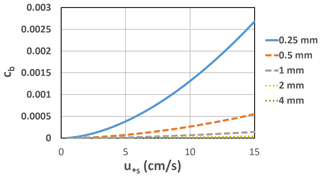
Figure 5 Near-bed concentration c_b versus shear velocity associated with skin friction from Eqs. (6a) and (6b), due to de Leeuw et al. (2020). The grain sizes 0.25, 0.5, 1, 2, and 4 mm are shown. The Froude number Fr is set to 0.4.

The range of the parameter u_∗s used in Figs. 3a and d and 5 is 0 to 15 cm s⁻¹. The higher value of these can be used as a conservative estimate for the total shear velocity u_∗ and thus depth-averaged flow velocity U as follows. Figure 7 in Li et al. (2015) allows estimates of the dimensionless Chézy friction coefficient $\mathit{Cz}=U/u_{\ast }$. The data for gravel bed and sand bed rivers are bracketed for the most part by the range Cz= 7 to 20. This suggests that the modified sediment entrainment relation should be valid for flow velocities up to the range 1–3 m s⁻¹, which are reasonable estimates for bankfull velocity in rivers (Parker, 2014; Birch et al., 2023). The implication is that material in the nominal size range ≥ 1 mm is not subject to significant suspension in typical flood flows of alluvial rivers.

The results presented above do not imply that it is physically impossible to suspend gravel. For example, Larsen and Lamb (2016) infer that gravel could be suspended by the megafloods that sculpted the Channeled Scablands, USA. Recently, Lin et al. (2022) and Song et al. (2022) have modeled sediment transport in the aftermath of a breach of a high landslide dam in the Himalaya mountains. Under such conditions, shear velocity was predicted to reach as high as 2 m s⁻¹, and mean flow velocity was predicted to reach as high as 10 m s⁻¹. Neglecting form drag for the moment, these values applied to the modified Garcia–Parker relation presented here, using a grain size of 4 mm, yield a near-bed concentration taking the maximum possible value of 0.3. This is consistent not only with suspension but also with the formation of a thick grain flow that can be considered transitional to a debris flow (e.g., Hernandez-Moreira et al., 2019). Such a grain flow might be indicated in sedimentary rocks in terms of a massive basal unit (Carling, 2013).

5 Pea gravel is preferentially transported as bedload over sand

The above analysis provides evidence that pea gravel represents the finest range of approximately spherical gravel that cannot easily be suspended by typical alluvial river flood flows (as opposed to megafloods or flows in steep bedrock streams). The bedload transport rate of a given size D tends to be augmented when it moves over a bed of finer material, when compared to a bed of the same size D. This effect, however, is dependent on absolute size and relative size. Here we return to the thought experiment of Sect. 3 and consider an example using 4 mm as a characteristic size within the pea gravel range. We argue that (a) the bedload transport rate of a grain with size 4 mm moving over a bed of 0.4 mm sand (as opposed to a bed of the same 4 mm material) is augmented to a considerably higher extent than (b) the size 40 mm moving over a bed of 4 mm material (as opposed to a bed of the same 40 mm material; Wilcock and Crowe, 2003; Venditti et al., 2010a, b). Wilcock and Crowe (2003) identify 2 mm as a threshold, such that increasing content of material finer than this significantly augments the transport of material coarser than this (GTAS effect).

The problem can again be viewed in the context of viscosity. There is abundant evidence that changes in viscosity, e.g., through temperature change, can significantly affect both the transport rate and bedforms in sand bed streams (e.g., Chen and Nordin, 1976; Southard and Boguchwal, 1990; Nino et al., 2003). Simons and Richardson (1961) have modified a dimensionless bedform regime diagram proposed by Liu (1957), which indicates that the effect of viscosity on the bedform regime becomes negligible as particle grain size passes through the range 1.71–5 mm (quartz particles on Earth in water at 20 ^∘C). Indeed, the effect of viscosity is embedded in the modified Shields relation for the threshold of (significant) bedload transport presented in Garcia (2006). Where ${\mathit{\tau }}_{\mathrm{c}}^{*}$ denotes a critical Shields number, the threshold condition can be represented as

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{\mathit{\tau }}_{\mathrm{c}}^{\ast }& ={\displaystyle \frac{u_{\ast \mathrm{c}}^{\mathrm{2}}}{\text{Rg}D}}\\ & =\mathrm{0.5}\left[\mathrm{0.22}{\left(D^{\ast }\right)}^{-\mathrm{0.9}}+\mathrm{0.06}\times {\mathrm{10}}^{(-\mathrm{7.7}(D^{\ast }{)}^{-\mathrm{0.9}})}\right].\end{array}\end{array}$$

Here u_∗c is the shear velocity at the threshold of (significant) motion. Viscosity enters the problem via the definition of dimensionless grain size D^*. For uniform material over a bed of the same size, assuming quartz and water at 20 ^∘C, the values of ${\mathit{\tau }}_{\mathrm{c}}^{*}$ are 0.029 for 40 mm material, 0.024 for 4 mm material, and 0.017 for 0.4 mm material. Clearly, particles become easier to move as grain size reduces across the pea gravel range. That is, viscosity lubricates a bed that is sufficiently fine, as illustrated analytically in, e.g., Ikeda (1982). The issue is discussed in more detail below, and further elaboration is given in Appendix A.

But the most important effect for the present analysis concerns how a grain of a given size moves over a bed of finer sizes. Turbulent flows over a granular bed are traditionally divided into a turbulent smooth regime, a turbulent rough regime, and a transitional regime (e.g., Streeter, 1971). Julien and Bounvilay (2013) show data indicating that coarse particles moving over a hydraulically smooth bed do not consistently travel at higher velocities than those traveling over a hydraulic rough bed. They are, however, entrained more easily. Novak and Nalluri (1975) provide convincing experimental evidence that the threshold Shields number for the motion of a given grain size is substantially reduced when that particle moves over a hydraulically smooth bed. The viscous sublayer thickness of a turbulent boundary layer can be scaled as (e.g., Garcia, 2006)

$$\begin{array}{}\text{(7)}& {\mathit{\delta }}_{\mathrm{v}}=\mathrm{11.6}{\displaystyle \frac{\mathit{\nu }}{u_{\ast \mathrm{s}}}},\end{array}$$

where δ_v= nominal thickness of the viscous sublayer. Here, the “nominal viscous sublayer thickness”, corresponding to a characteristic length scale for the effect of viscosity, is used in a different sense from “nominal grain size”, the latter of which corresponds to Earth-like conditions. Now let u_∗s be the shear velocity at the threshold of motion u_∗c. Between Eqs. (6) and (7), the ratio $({\mathit{\delta }}_{\mathrm{v}}/D{)}_{\mathrm{c}}$ (i.e., the value of ${\mathit{\delta }}_{\mathrm{v}}/D$ at the threshold of motion) is found to be

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& {\left({\displaystyle \frac{{\mathit{\delta }}_{\mathrm{v}}}{D}}\right)}_{\mathrm{c}}={\displaystyle \frac{\mathrm{11.6}}{{\left(D^{\ast }\right)}^{\mathrm{3}/\mathrm{2}}f\left(D^{\ast }\right)}},\\ & f\left(D^{\ast }\right)=\sqrt{\mathrm{0.5}\left[\mathrm{0.22}{\left(D^{\ast }\right)}^{-\mathrm{0.9}}+\mathrm{0.06}\times {\mathrm{10}}^{\left(-\mathrm{7.7}(D^{\ast }{)}^{-\mathrm{0.9}}\right)}\right]}.\end{array}\end{array}$$

This relation is plotted in Fig. 6. Consider first a nominal 40 mm grain moving over a bed of nominal 4 mm material. The value of $({\mathit{\delta }}_{\mathrm{v}}/D{)}_{\mathrm{c}}$ for either grain size is no larger than 0.074, indicating a turbulent rough bed with no role for viscosity. In the case of a 4 mm grain moving over a 0.4 mm bed $({\mathit{\delta }}_{\mathrm{v}}/D{)}_{\mathrm{c}}$ of the bed is 2.81 for the finer size. This indicates that the 4 mm grain moves over a bed that is transitional to turbulent smooth and thus is subject to increased mobility via lowered threshold Shields number demonstrated experimentally by Novak and Nalluri (1975).

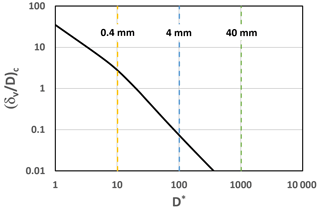
Figure 6 Ratio of the nominal thickness of the viscous sublayer to the grain size at the threshold of motion $({\mathit{\delta }}_{\mathrm{v}}/D{)}_{\mathrm{c}}$ as a function of the dimensionless grain size D^* is denoted by the black monotonically decreasing line. The three solid vertical lines denote, from left to right, $D^{*}=\mathrm{1.01}\times {\mathrm{10}}^{\mathrm{1}}$ (nominal size D=0.4 mm); $D^{*}=\mathrm{1.01}\times {\mathrm{10}}^{\mathrm{2}}$ (nominal size D=4 mm); and $D^{*}=\mathrm{1.01}\times {\mathrm{10}}^{\mathrm{3}}$ (nominal size D=40 mm). The grain sizes D are nominal values for Earth-like conditions.

Novak and Nalluri (1975) offer no explanation for their result that a grain in a turbulent smooth flow has a lower critical Shields number than the same grain in a turbulent rough flow, other than remarking that the result is “to be expected”. In Appendix A, we outline a broad-brush theory as to why this should be true. The key parameter is the ratio $u_{\mathrm{f}}/u_{\ast }$, where u_f is the flow velocity averaged over turbulence acting on the grain. This ratio takes an asymptotic value for the limit of turbulent rough flow but increases monotonically with increasing grain size for turbulent smooth flow, causing the critical Shields number to correspondingly decline monotonically.

The tendencies outlined above are corroborated by the results of Dingle and Venditti (2023), who show, for example, the enhanced mobility of clasts of size 3.8 mm as sand of size 0.57 mm occupies an increasing fractional content in the bed surface layer. It should be noted, however, that were bedforms to be present, they would tend to break up the effect of viscosity, as they set an internally generated roughness (e.g., Lapôtre et al., 2017).

6 “Sand-bed-like” versus “gravel-bed-like” rivers; generalization for Earth, Titan, and Mars

For reference, we here repeat the definition of D^* given in Eq. (1c):

$$\begin{array}{}\text{(1c)}& D^{\ast }=D{\displaystyle \frac{{\left(\text{Rg}\right)}^{\mathrm{1}/\mathrm{3}}}{{\mathit{\nu }}^{\mathrm{2}/\mathrm{3}}}}.\end{array}$$

All specific evaluations of D^* given above have been for a natural (e.g., granitic) particle (e.g., R=1.65 for quartz) on Earth (g=9.81 m s⁻²) and in water at 20 ^∘C ($\mathit{\nu }=\mathrm{1.00}\times {\mathrm{10}}^{-\mathrm{6}}$ m² s⁻¹). These same arguments apply to limestone particles with only a modest modification in the submerged specific gravity R; here we group these together as “natural particles on Earth”. Based on the range 1–5 mm, we can loosely divide river reaches into “sand-bed-like” or “gravel-bed-like”, depending on whether or not characteristic bed surface size (e.g., D₅₀) is less than or greater than 2 mm. For the above conditions, the size D=2 mm yields a value of $D^{*}=\mathrm{51}$. When using this size as an approximate boundary between “sand-like” and “gravel-like” behavior, however, it must be borne mind that the relevant parameter is the dimensionless one. Even on Earth, the kinematic viscosity of water can vary from a low of $\mathrm{2.94}\times {\mathrm{10}}^{-\mathrm{7}}$ m s⁻² at 100 ^∘C to a high of $\mathrm{1.79}\times {\mathrm{10}}^{-\mathrm{6}}$ m s⁻². In addition, Viparelli et al. (2015) have documented the mobility of sediment, with submerged specific gravities R ranging from 0.5 to 3. A discriminating value $D^{*}=\mathrm{51}$ thus corresponds to a range of sizes D from as low as 0.73 mm to as high as 4.42 mm.

We are now able to cast the bedload transport relation of Wilcock and Crowe (2003) in a purely dimensionless form. Generalizing from their 2 mm criterion, as the content of grains in the bed with dimensionless size < $D^{*}=\mathrm{51}$ is increased, the transport of grains with dimensionless size > $D^{*}=\mathrm{51}$ is enhanced. The formulation is now directly applicable to rivers on Mars and Titan, as well as Earth, in so far as it can be applied to a heavenly body with arbitrary gravitational acceleration g, a fluid with arbitrary kinematic viscosity ν, and a sediment particle of arbitrary submerged specific gravity R.

Birch et al. (2023) illustrate how the dimensionless number D^* transforms into dimensioned numbers for Mars, where gravitational acceleration is significantly lower, and Titan, where gravitational acceleration is even lower, the clasts are ice rather than quartz, and the fluid is a mix of methane and ethane. They show that the discriminator $D^{*}=\mathrm{51}$ translates to about 2.66 mm on Mars (mafic sediment in water at 20 ^∘C) and 3.16–4.42 mm on Titan (ice particles in liquid methane/ethane at 84–96 K). Lamb and Venditti (2016) present a similar calculation.

We emphasize here that the nominal dimensioned size 2 mm is used as shorthand for the narrow range 1–5 mm corresponding to natural particles (e.g., granitic or limestone) on Earth in water at 20 ^∘C. The corresponding dimensionless range for D^*, which we argue to be more universal, is 25–126.

7 Discussion

We do not present the above analysis in the context of a specific morphodynamic model. Instead, the analysis bears on the physics underlying what Church and Hassan (2023) describe as a “clear tendency for grains in the range 1–8 mm to outrun both larger and smaller grains in the condition of size-selective transport” via bedload (rather than suspended load) transport. This tendency can in turn be related to the evolution of the pea gravel grain size gap in the bed surface layer of a long profile of a net-depositional river, as expressed in terms of the bed material sizes D₅₀ and D₆₀ (shown in Fig. 2a, b). Pea gravel is not easily suspended but can be preferentially moved as bedload over a coarser bed (weight versus hiding–exposure effect), as well as a finer bed (hydrodynamic smoothing effect). The implication is that even if there is no grain size gap in the feed sediment, the pea gravel tends to become diluted over a long reach, as described in the following thought experiment.

We assume a long river reach undergoing deposition. The grain size distribution of the deposit contains three size ranges: a “sand” range, a “pea gravel range”, and a “coarse-gravel range”. We further specify that the fraction of material in each of the three ranges is equal: one-third sand, one-third pea gravel, and one-third coarse gravel. We divide the reach into upstream and downstream segments of equal length. Let the upstream deposit be two-thirds coarse gravel and one-third pea gravel and the downstream deposit be two-thirds sand and one-third pea gravel. The total amount of the deposit in each size range is equal. Yet the median size D₅₀ of the deposit must abruptly drop from the coarse-gravel size to the sand size halfway down the reach. No paucity of pea gravel is necessary for such behavior. Instead, the pea gravel is diluted due to its preferential mobility as bedload, compared to coarser and finer sediment. A first attempt to incorporate the above ideas into a morphodynamic model is given in An et al. (2020).

In the analysis above, grain size D is interpreted as being an equivalent diameter of a sphere. The analysis would require modification for grain shapes that deviate significantly from spherical. The fall velocity relation of Dietrich (1982) includes a correction factor for grain shape. Particles with a plate-like shape may be significantly easier to suspend than spheres. The arguments above do not rely on the assumption of grain abrasion. Abrasion may, however, play a role in the evolution of some sharp gravel–sand transitions.

The mobilization effect observed when sand is added to a gravel bed, without major change in bed slope, has been verified experimentally by Cui et al. (2003a) and Dingle and Venditti (2023). Lamb et al. (2008) indicate that the critical Shields number of sediment increases with bed slope. In the original experiments of Wilcock and Crowe (2003), where the flow was allowed to reach mobile bed equilibrium, a higher sand content correlated with a lower bed slope. The evolution of this lower slope may also be combined with the tendency for critical Shields stress to be slope-dependent (Lamb et al., 2008). This slope effect is included in the bedload transport relation of Schneider et al. (2015).

The present analysis is focused on the mobility of grains in the pea gravel range. It has been demonstrated above that this grain size range shows little tendency to be suspended even at flood stage in natural alluvial rivers. Thus the present arguments can be posed in the context of bedload transport. The analysis is applicable to, but does not provide a complete explanation of, the formation of gravel–sand transitions for which the transport and deposition of sand must be considered as well (Lamb and Venditti, 2016).

8 Conclusions

The analysis presented here does not specifically identify the size D= 2 mm itself as special. Instead, it serves as shorthand for the dimensionless size $D^{*}=$ 51 and the dimensionless range $D^{*}=$ 25.2–126, corresponding to a nominal size range of pea gravel ranging from 1–5 mm (e.g., granitic or limestone particles on Earth in water at 20 ^∘C). We show that this range corresponds to the finest sizes that cannot be significantly transported in suspension in typical floods (∼ bankfull flow) of alluvial rivers. In addition, we show that pea gravel is preferentially moved as bedload, both over a coarser gravel bed and a sand bed (at least in the absence of bedforms). The physics of the problem is embodied in the dimensionless grain size D^*, which contains kinematic viscosity. These conclusions have bearing on the formation of gravel–sand transitions because they imply that even in the absence of abrasion or a grain size gap in the feed sediment, pea gravel is subject to dilution within any long depositional reach along which downstream fining is observed. That is, pea gravel intrinsically “has trouble finding a home” where it can dominate in the sediment deposit.

The formulation is directly applicable to Mars, where gravitational acceleration is lower than Earth, and Titan, where the gravitational acceleration is even lower, the particles in transport are ice rather than, e.g., quartz, and the fluid is mixture of methane and ethane rather than water.

Appendix A

Novak and Nalluri (1975) use experimental data to show that a grain placed on the bed of a flow in the turbulent smooth range has a substantially lower critical Shields number than the same grain placed on the bed of a flow in the turbulent rough range (their Fig. 2). They do not, however, show a theoretical analysis justifying this conclusion. Here we present a broad-brush analysis to illustrate the general physics behind this behavior. A sphere of size D is placed on the bed of a channel. Where z is an upward normal coordinate from the bed, u is streamwise flow velocity over averaged over turbulence, and k_s is roughness height, the distribution of flow velocity over the bed takes the following form for turbulent rough flow;

$$\begin{array}{}\text{(A1a)}& {\displaystyle \frac{u}{u_{\ast }}}=\mathrm{2.5}\mathrm{\ell }n\left({\displaystyle \frac{z}{k_{\mathrm{s}}}}\right)+\mathrm{8.5}\end{array}$$

(e.g., Schlichting, 1979). Here we crudely estimate k_s as being equal to D. The corresponding form for turbulent smooth flow is

$$\begin{array}{}\text{(A1b)}& {\displaystyle \frac{u}{u_{\ast }}}=\left\{\begin{array}{cc}\frac{u_{\ast }z}{\mathit{\nu }},& \frac{u_{\ast }z}{\mathit{\nu }}\le \mathrm{11.6}\\ \mathrm{2.5}\mathrm{\ell }n\left({\displaystyle \frac{u_{\ast }z}{\mathit{\nu }}}\right)+\mathrm{5.5},& \frac{u_{\ast }z}{\mathit{\nu }}>\mathrm{11.6}\end{array}\right.\end{array}$$

(e.g., Schlichting, 1968). For simplicity, we do not consider flow that is transitional between the turbulent smooth and turbulent rough regimes.

The flow velocity u_f acting on the grain is evaluated at the top of the particle, which is here approximated as z=D. It follows from these definitions and Eq. (A1a) that in the turbulent rough case, the ratio $F_u=u_{\mathrm{f}}/u_{\ast }$ can be estimated as

$$\begin{array}{}\text{(A2a)}& F_u={\displaystyle \frac{u_{\mathrm{f}}}{u_{\ast }}}=\mathrm{8.5}.\end{array}$$

In the turbulent smooth case, from Eq. (A1b) it is found that

$$\begin{array}{}\text{(A2b)}& F_u={\displaystyle \frac{u_{\mathrm{f}}}{u_{\ast }}}=\left\{\begin{array}{cc}\mathrm{11.6}\frac{D}{{\mathit{\delta }}_{\mathrm{v}}},& \frac{D}{{\mathit{\delta }}_{\mathrm{v}}}\le \mathrm{1}\\ \mathrm{2.5}\mathrm{\ell }n\left(\mathrm{11.6}{\displaystyle \frac{D}{{\mathit{\delta }}_{\mathrm{v}}}}\right)+\mathrm{5.5},& \frac{z}{{\mathit{\delta }}_{\mathrm{v}}}>\mathrm{1}\end{array}\right.,\end{array}$$

where δ_v is the nominal viscous sublayer thickness given by Eq. (7).

The drag force F_D and Coulomb resistive force F_R are estimated as follows:

$$\begin{array}{}\text{(A3a)}& {\displaystyle }{F}_{\mathrm{D}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }{c}_{\mathrm{D}}{\left({\displaystyle \frac{D}{\mathrm{2}}}\right)}^{\mathrm{2}}{u}_{\mathrm{f}}^{\mathrm{2}},\text{(A3b)}& {\displaystyle }{F}_{\mathrm{R}}={\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}{\mathit{\mu }}_{\mathrm{c}}\mathit{\rho }\text{Rg}{c}_{\mathrm{D}}{\left({\displaystyle \frac{D}{\mathrm{2}}}\right)}^{\mathrm{3}},\end{array}$$

where c_D is the dimensionless drag coefficient on a sphere, and μ_c is a dimensionless coefficient of Coulomb friction. Again, for simplicity, we neglect any lift force on the particle and express the threshold of motion in terms of the condition

$$\begin{array}{}\text{(A4)}& F_{\mathrm{D}}=F_{\mathrm{R}}.\end{array}$$

Reducing between Eqs. (A3) and (A4), the critical shear velocity u_∗c and critical Shields number ${\mathit{\tau }}_{\mathrm{c}}^{*}=u_{\ast \mathrm{c}}^{\mathrm{2}}/\left(\text{Rg}D\right)$ at the threshold of motion are given as

$$\begin{array}{}\text{(A5)}& {\mathit{\tau }}_{\mathrm{c}}^{\ast }={\displaystyle \frac{u_{\ast \mathrm{c}}^{\mathrm{2}}}{\text{Rg}D}}={\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}{\displaystyle \frac{{\mathit{\mu }}_{\mathrm{c}}}{c_{\mathrm{D}}{F}_u^{\mathrm{2}}}}.\end{array}$$

We evaluate the drag coefficient as a function of the fluid Reynolds number acting on the particle $\mathit{Re}=u_{\mathrm{f}}D/\mathit{\nu }$, using the explicit functional relation of Goldstein (1929), as quoted in Yang et al. (2015).

$$\begin{array}{}\text{(A6)}& c_{\mathrm{D}}={\displaystyle \frac{\mathrm{24}}{\mathit{Re}}}\left[\mathrm{1}+{\displaystyle \frac{\frac{\mathrm{3}}{\mathrm{16}}\mathit{Re}}{\mathrm{1}+\frac{\frac{\mathrm{19}}{\mathrm{240}}\mathit{Re}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{122}}\mathit{Re}}}}\right],\mathit{Re}={\displaystyle \frac{u_{\mathrm{f}}D}{\mathit{\nu }}}\end{array}$$

This relation is accurate from the Stokes range out to $\mathit{Re}=\mathrm{1}\times {\mathrm{10}}^{\mathrm{5}}$.

For the case of a grain on the bed of a turbulent rough flow, we assume an angle of repose of 35^∘ or thus a coefficient of Coulomb friction μ_c=0.7. In the extreme case of turbulent rough flow at a value Re that is large enough for the drag coefficient c_D to asymptote out to the Reynolds-independent value of 0.422 of Eqs. (A6), (A2a), (A5), and (A6), the following simple result is yielded:

$$\begin{array}{}\text{(A7)}& {\mathit{\tau }}_{\mathrm{c}}^{\ast }=\mathrm{0.0306}.\end{array}$$

This value is very close to the asymptotic value 0.030 from Eq. (6) obtained for large D^*.

In principle, the coefficient of Coulomb friction over a smooth bed ought to be less than the value over a rough bed. But this is a geometric rather than a hydrodynamic effect, so we keep μ_c constant in estimating the threshold Shields number for a grain placed on the bed of turbulent smooth flow. Between Eqs. (A1b), (A2b), (A5), and (A6), the critical Shields number ${\mathit{\tau }}_{\mathrm{c}}^{*}$ can be represented in terms of the ratio $D/{\mathit{\delta }}_{\mathrm{v}}$ as shown in Fig. A1 (solid line labelled “present relation”). Also shown therein is the asymptotic result of Eq. (A7) for a sufficiently coarse grain subjected to turbulent rough flow (dashed line labelled “turbulent rough limit”) and the empirical Eq. (13) of Novak and Nalluri (1975) for the threshold of motion over a smooth bed (labelled “Novak–Nalluri”). While the present relation, broad-brush as may be, does not precisely reproduce the empirical result of Novak and Nalluri (1975), it serves to illustrate that (a) a grain on a bed with turbulent smooth flow has a lower threshold Shields number than the same grain on a bed with turbulent rough flow, and (b) that, all other factors being equal, the larger the grain size, the larger the difference between the two becomes.

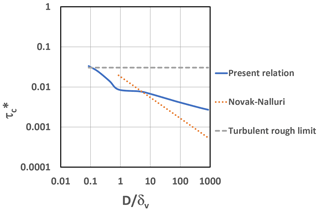
Figure A1 Critical Shields number ${\mathit{\tau }}_{\mathrm{c}}^{*}$ as a function of the ratio $D/{\mathit{\delta }}_{\mathrm{v}}$ (i.e., the ratio of grain size versus the nominal thickness of the viscous sublayer). Shown above are the relation for the limit of turbulent rough flow, the empirical relation of Novak and Nalluri (1975) for turbulent smooth flow, and the relation derived herein (present relation) for turbulent smooth flow.

The reason for this difference in behavior is, for the most part, bound up in the ratio F_u of flow velocity acting on the grain u_f to shear velocity u_∗. For turbulent rough flow, F_u takes the value 8.5 in the present analysis (Eq. A2a). For turbulent smooth flow, F_u increases monotonically with grain size, according to Eq. (A2b). Since the term F_u occurs in the denominator of Eq. (A5) as the grain size increases, the critical Shields number accordingly decreases monotonically in the turbulent smooth case.

It is of some value to note that an analysis similar to the one above, but applied for grain size mixtures solely in the turbulent rough regime, yields the hiding–exposure function of Egiazaroff (1965), which is embedded in a modified form in the bedload transport relation of Ashida and Michiue (1972).

Notation

Here [1] denotes the dimensions of unity (dimensionless).

A	Constant in Eq. (1a) [1]
cb	Near-bed equilibrium volume concentration of suspended sediment [1]
cD	Drag coefficient on a sphere [1]
D	Grain size [L]
D50	Median grain size of bed surface [L]
D60	Grain size, such that 60 % of bed surface material is finer [L]
D*	$=(\text{Rg}{)}^{\mathrm{1}/\mathrm{3}}D/v^{\mathrm{2}/\mathrm{3}}$; dimensionless grain size [1]
FD	Drag force on a sediment grain on a bed [M L T−2]
FR	Coulomb resistive force on a sediment grain on a bed [M L T−2]
Fr	$=U/(gH{)}^{\mathrm{1}/\mathrm{2}}$; Froude number [1]
Fu	$=u_{\mathrm{f}}/u_{\ast }$ [1]
g	Acceleration of gravity [L T−2]
H	Flow depth [L]
ks	Bed roughness height [L]
R	$=({\mathit{\rho }}_{\mathrm{s}}-\mathit{\rho })/\mathit{\rho }$; submerged specific gravity of sediment [1]
Re	$u_{\mathrm{f}}D/\mathit{\nu }$ [1]
Revp	$=v_{\mathrm{s}}D/\mathit{\nu }$ [1]
Rf	Dimensionless fall velocity of sediment [1]
U	Depth-averaged flow velocity [L T−1]
u	Local streamwise flow velocity averaged over turbulence [L T−1]
uf	Local value of u acting on a grain on the bed [L T−1]
u∗	Shear velocity [L T−1]
u∗c	Shear velocity at threshold of motion [L T−1]
u∗s	Shear velocity due to skin friction [L T−1]
vs	Fall velocity of sediment [L T−1]
X	Parameter defined by Eq. (5b) [1]
z	Distance upward normal to the bed [L]
Zu	Parameter defined by Eqs. (1b) and (4b) [1]
δv	Nominal thickness of viscous sublayer [L]
μc	Coulomb coefficient of friction associated with a grain on a bed [1]
ν	Kinematic viscosity of fluid (water or methane–ethane mixture) [L2 T−1]
ρ	Density of fluid (water or methane–ethane mixture) [M L−3]
ρs	Density of sediment (quartz, limestone, ice particles, etc.) [M L−3]
${\mathit{\tau }}_{\mathrm{c}}^{\ast }$	Critical Shields number for the onset of significant sediment transport [1]