Post-glacial reshaping of Alpine topography induced by landsliding

In steep alpine environments, successive glacial-interglacial cycles during the Quaternary led to multiple transient geomorphological phases. In particular, post-glacial periods are key transition phases experiencing rapid geomorphic changes, characterized by intense hillslope processes where ice and permafrost have retreated. Mass wasting is the dominant post-glacial process driving sediment production in steep mountain landscapes. However, its role in shaping topography, particularly in comparison to glacial activity – known for its strong deformational impact – remains poorly understood. By integrating numerical modeling with topographic data, we refine our understanding of how mass wasting shapes an evolving landscape and influences sediment dynamics. In the Ecrins massif (French western Alps), we select three catchments, with particular morphological signatures or inheritance (i.e. from fluvial to glacial), to model their associated topographic evolution driven by mass wasting. Using the landscape evolution model “HyLands”, we quantitatively assess their individual response to landsliding by exploring the role of different internal or external factors (bedrock cohesion and friction, return time of landslides). The model is calibrated with the output landslide area-frequency scaling law and the massif-averaged denudation rate, inferred from literature. We focus on the cumulative impact of landslides, over a single post-glacial period, on catchment slope distribution, hypsometry, exported sediment volume and erosion rate. Compared to a fluvial landscape, the inherited glacial topography shows a bimodal distribution of elevation for unstable slopes, near the crests and along the U-shaped valley walls. The time evolution of this distribution is characterized by a decrease in the number of unstable slopes as well as a lowering in maximum catchment elevations induced by landsliding. Despite the stochastic nature of landslides, our modeling results also show that landslide activity and induced erosion rates are greatest at the onset of the glacial retreat and then progressively decay during the interglacial period. In contrast, fluvial catchments show a more stable topography and fewer landslides resulting in lower erosion rates. This study quantitatively explores the non-linear interactions between landslides and catchment topographic evolution and documents the role of landslides in the erosion pulse during the Quaternary interglacial periods.

1 Introduction

The Quaternary period is characterized by oscillations from glacial to interglacial cycles overprinting a global climatic cooling trend over the Cenozoic era (Zachos et al., 2001). These successive climatic transitions have been suggested to be associated with abrupt and transient geomorphologic and topographic changes (Champagnac et al., 2014; Peizhen et al., 2001; Zhang et al., 2022). In high-latitude regions and mountain ranges, glaciers are usually considered the main geomorphic and erosion agents (Hallet et al., 1996; Herman et al., 2013, 2021; Herman and Champagnac, 2016; Métivier et al., 1999). The topographic changes resulting from glacial erosion are spatially variable over a single or multiple glacial-interglacial cycle (Seguinot and Delaney, 2021) of the Quaternary (Herman et al., 2011; Pedersen and Egholm, 2013; Sternai et al., 2013; Tomkin and Braun, 2002). Glaciated landscapes have in turn been widely studied to better understand past glacier dynamics and quantify glacial erosion rates and associated topographic changes at the Earth's surface (Ganti et al., 2016; Koppes et al., 2015; Pedersen and Egholm, 2013; Peizhen et al., 2001; Solomina et al., 2015; Sternai et al., 2013). Glacial and periglacial processes have strongly imprinted mountainous landforms, shaping U-shaped valleys, but also cirques, arêtes and hanging valleys, all characterized by marginal steep slopes and rugged topography (e.g. Anderson et al., 2006; Penck, 1905; Prasicek et al., 2015). In turn, glacial morphological features likely represent transient and mechanically unstable landforms under interglacial conditions (Herman and Braun, 2008; Prasicek et al., 2015), dominated by hillslope and fluvial processes. Understanding the interglacial evolution of formerly glaciated landscapes has remained challenging since it involves complex non-linear geomorphic processes and interrelated spatial/temporal scales. However, this understanding is a major need for assessing the ongoing response of mountainous environments to current climate warming (e.g. Zhang et al., 2022).

Interglacial periods are associated with overall warming climatic conditions, leading to cryosphere degradation (i.e. glacier retreat and permafrost recession), and in turn to a shift of the main geomorphic and erosion processes. Under interglacial conditions, paraglacial (Ballantyne, 2002) and periglacial (French, 2017) processes become more efficient and affect larger mountainous areas. Hillslope processes, including landsliding, rockfall and soil creep, affect formerly glaciated mountain slopes. Rivers transport remobilized and newly-produced sediments (Roussel et al., 2018) and can locally re-incise glacial valleys (e.g., Leith et al., 2018; Valla et al., 2010). Over the Quaternary, repetitive climatic oscillations between glacial and interglacial periods have caused frequent mismatches between dominant geomorphological processes and the organization or shape of the landscape on which they act. This has led to the hypothesis that these transient climatic/geomorphic conditions over the Quaternary could have led to an increase in erosion and sediment flux (Koppes et al., 2015; Koppes and Montgomery, 2009; Peizhen et al., 2001) and topographic relief (Champagnac et al., 2014), rather than the supposed greater efficiency of glacial erosion itself (Koppes and Montgomery, 2009).

In the following work, we focus on the transient phase from glacial to interglacial conditions, hereinafter referred to as the post-glacial period, i.e. when alpine glaciers retreated and left uncovered landscapes dominated by non-glacial geomorphic processes. In this context, steep parts of mountain hillslopes became more prone to mass wasting processes, favored by glacial debuttressing (Cossart et al., 2008) and permafrost retreat (e.g. Cathala et al., 2024; Lebrouc et al., 2013). The rapid climate change observed over the last decades has motivated research on the evolution of permafrost and its impact on high-elevation rockwall dynamics (Gallach et al., 2020; Magnin et al., 2017; Ravanel et al., 2017; Stoffel et al., 2024). In addition, gravitational instabilities, such as bedrock landslides or rockfalls, are widespread in mountainous landscapes and appear as one of the most efficient processes to shape them (Keefer, 1984). Hillslope activity transiently reshapes glacial morphological features leading to a postglacial increase in both the frequency and intensity (related to the volume) of mass wasting events (e.g. Korup, 2006; Zerathe et al., 2014). Landslides significantly contribute to catchment-scale erosion by mobilizing large bedrock volumes, which greatly impact sediment fluxes (Broeckx et al., 2020; Hovius et al., 1997; Zech et al., 2009). As a positive feedback loop, by decreasing the local base level, fluvial sediment export and local incision of formerly glaciated valleys can foster the hillslope response. The postglacial period is also associated with major changes in hillslope-channel connectivity (Brardinoni and Hassan, 2007; Cavalli et al., 2019; Müller et al., 2022) and in the drainage system (Comiti et al., 2019; Lane et al., 2017; Pitlick et al., 2021; Zhang et al., 2022). As such, this period appears complex due to rapid morphological changes and multiple geomorphic processes that all interact and drive major changes in both the hillslope domain and the drainage network. However, while previously-cited studies have already explored the geomorphological role of landslides during the last interglacial period, understanding which landscape areas are more affected during the postglacial times and how this landslide activity is distributed through both space and time remains mainly unanswered and not quantified. Therefore, quantifying the spatio-temporal impact of landslides on evolving postglacial landscapes is needed to better understand sediment production, transfer and potential storage along the source to sink pathway and assess the overall topographic evolution in mountainous environments.

While the landsliding impact on mountain topography appears clear after a single triggering event, such as a storm or an earthquake (Dahlquist et al., 2018; Meunier et al., 2008; Morriss et al., 2023; Roering, 2012), their role in long-term shaping of mountain ranges is not straightforward. To investigate the post-glacial period, landslide catalogues (Blondeau et al., 2021; Wood et al., 2015), bedload records (Lane et al., 2017), remote-sensing and geophysical methods have intrinsic limitations and integration times that are too short. Conversely, long-term mountain erosion estimates from geochronological and thermochronological methods (Herman et al., 2013) or large-scale sediment budgets (Kuhlemann et al., 2002) may have too long integration times to investigate interglacial periods. These approaches also cannot be generally used to disentangle the impacts of individual processes like landsliding from other forms of erosion. Terrestrial cosmogenic nuclides (TCN) have been commonly used to quantify catchment-wide erosion rates over 10²–10⁵ year timescales (Brown et al., 1995; Delunel et al., 2020; Mudd et al., 2016; Portenga and Bierman, 2011), covering glacial-interglacial cycles. Although this approach appears meaningful to address the postglacial period (∼ 10–20 kyr), TCN-derived erosion rates are averaged in both space (catchment) and time. In turn, this prevents exploring in detail the spatial distribution and temporal evolution of erosion during that period, as well as discriminating the different active geomorphological processes. Moreover, the cosmic ray attenuation depth (∼ 60 cm), which sets the integration time of TCN (von Blanckenburg, 2005), can be significantly smaller than the depth of large landslides observed in formerly glaciated catchments (Korup, 2006; Lavé et al., 2023; Niemi et al., 2005). Overall, this raises the question of the potential limitations of TCN-derived erosion rates in constraining the time evolution of post-glacial erosion in landscapes dominated by bedrock landsliding.

In this context, landscape evolution modelling (LEM) appears as a relevant approach to overcome the limited amount of data/observations and the intertwined spatial and temporal scales involved (Tucker and Hancock, 2010). Numerical modelling can combine complex surface processes, including tectonic uplift, hillslope and river dynamics integrating all the sediment transfer cascade and hillslope-channel connectivity, while allowing predictions of topographic evolution or sediment production rates cover large spatial and temporal scales. Different categories of models can be considered to study mass wasting processes (Campforts et al., 2022). Physically-based models produce realistic debris-flow (and river) propagation and deposition but may not be adapted for large-scale landscape evolution (Croissant et al., 2017; Davy et al., 2017; Dietrich et al., 1995; George and Iverson, 2014; Hergarten and Robl, 2015; Martin et al., 2023). Landscape evolution models (LEM) instead use reduced-complexity geomorphic laws to simulate the evolution of topography over possibly long timescales and large spatial scales (Carriere et al., 2020; Langston and Tucker, 2018; Liebl et al., 2021). Therefore, numerical modelling offers multiple ways to simulate hillslope processes, and their interactions, by highlighting diverse approaches, modeling complexity and spatio-temporal scales.

The aim of this study is to explore numerically, using a stochastic and reduced-complexity model, the role of landslides in the postglacial morphological dynamics of mountainous landscapes. We use the HyLands model (Campforts et al., 2020, 2022), which explicitly simulates bedrock landslides, to predict associated mass redistribution and the resulting catchment-averaged erosion rates and topographic evolution through multiple timescales. Thus, the HyLands model is a specific component used to generate landslides. Fluvial erosion, periglacial processes or diffusion processes are not modelled below. We discuss this point in detail in Sect. 5.1.1. We investigate the topographic impact of landslide activity on selected Alpine catchments, located in the Ecrins massif (France), showcasing a gradient of glacial imprint and deglaciation timing. An open question is the role of interglacial processes in erasing the inherited morphological signature of former glaciation, leading to an erosional “hot-moment”. More specifically, we aim to assess the timescales, rates and locations of topographic changes associated with the transient shift from glacial to interglacial periods, with a particular focus on the role of landsliding. Our main working hypothesis is that the different morphological signatures observed for Alpine catchments are evidencing both landslide activity and deglaciation timing. Alpine catchments do show a glacial topographic imprint, and here we test the capacity of landslides to (at least partly) reshape this glacial topographic inheritance over the postglacial period. The first objective of the study is to conduct a spatial analysis of simulated landslides to assess their magnitudes and locations within the investigated catchments. Then, a temporal analysis is performed to investigate the duration of the postglacial transient phase, in other words, how long it may require to achieve an interglacial-state topography (i.e., referring to the end of the transient phase), and erosion dynamics under landslide activity.

2 Study area

2.1 Selected catchments in the Ecrins massif

The Ecrins massif (south-east France, Fig. 1A) forms a high-elevation high-relief area of the southwestern Alps, and today still hosts glaciers in its upper catchments. The present-day topography was deeply impacted by glaciation (van der Beek and Bourbon, 2008), and several studies have focused on constraining the timing and extent of the Last Glacial Maximum (LGM, ca. 20 ka) and post-LGM glacier fluctuations (Delunel et al., 2010; Le Roy et al., 2017). In this context, we select three small (6–15 km² area) catchments to cover the entire Vénéon valley, from the river source, at the heart of the Ecrins massif, to the confluence with the Romanche river where tributary glaciers had a lower morphological impact (Fig. 1B). The Pilatte catchment, the highest and most glaciated catchment, peaks at ∼ 3600 m a.s.l., and has a minimum elevation of 2000 m. Modern glaciers represent ∼ 14 % of the total catchment area of approximately 15 km². With a downstream direction toward the north, its western and eastern parts are made of granitic and migmatic rocks (gneiss), respectively (source: French Geological Survey BRGM, https://infoterre.brgm.fr/, last access: 4 May 2025). The Etages catchment, partially-glaciated at present-day (∼ 12 %), displays similar characteristics with an area of ∼ 14 km² and an elevation range from 3564 to 1600 m a.s.l. at the confluence with the Vénéon river. The catchment is mainly underlain by granites with crestlines composed of gneiss in its south-eastern part (Barféty et al., 1984; Delunel et al., 2014). Both catchments show steep hillslopes (up to ∼ 2.2 m m⁻¹, i.e., 65°, Fig. 1C), located on the walls of the main U-shaped valley and along the highest rockwalls, considered as nunataks (Delunel et al., 2010; Marx et al., 2017), and a low-relief central valley bottom (Fig. 1D). The Etages catchment has been investigated by Delunel et al. (2014), with detailed geomorphological mapping and the use of ¹⁰Be concentrations in detrital material to trace the potential geomorphic sources for river sediments. Finally, the Pisse catchment is completely unglaciated today and is smaller than the two other catchments (∼ 6 km² total area). Its highest elevation at ∼ 3050 m occurs at its southern crest, while its lowest elevation of ∼ 1250 m is at the confluence with the adjacent Villard catchment. Its lithology is dominated by granites with some Jurassic limestones along its southwestern crest. Slopes are mostly gentle in the upper part of the catchment and get steeper downstream along the valley rockwalls. Despite different glacial imprints and elevation, the slope distributions for the studied catchments are relatively similar (Fig. 1C), with a modal slope around 35° (0.7 m m⁻¹) for all three catchments.

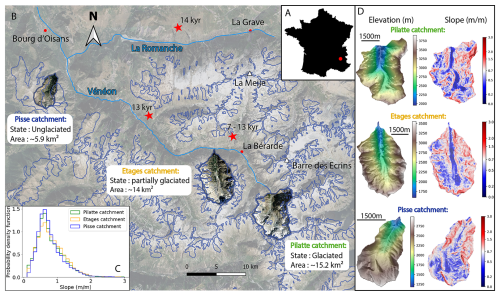
Figure 1 Geomorphological context of the study area. (A) Location of the Ecrins massif (red dot) in France. (B) Google satellite image of the Ecrins massif (background) with the three studied catchments and their characteristics: Pilatte (green label), Etages (yellow label) and Pisse (blue label). Blue thin line indicates the contour of the LGM ice extent (Delunel et al., 2010). Red stars report the estimated deglaciation timing (exposure of glacially-polished bedrocks and erratics; Delunel et al., 2010). (C) Probability density function of topographic slope for the three studied catchments (25 m resolution DEM from the French National Geographic Institute IGN). Similar distributions are observed, with a main slope mode around 0.7 m m⁻¹. (D) Modern elevation and slope maps for the three studied catchments. © Google Maps.

These catchments have experienced a gradual post-LGM deglaciation, following the progressive glacier retreat along the Vénéon valley from downstream (Pisse catchment) to upstream (Pilatte catchment). Following Delunel et al. (2010), the Pisse catchment likely started its deglaciation around 15 ka (based on deglaciation constraints upstream and downstream in the Romanche valley, e.g. Schwartz et al., 2017), while the Etages catchment may have been deglaciated between 13 and 7 ka (Fig. 1B). The glacier retreat in the Pilatte catchment has probably started slightly after the Etages catchment and can be considered at the end of the post-LGM deglaciation. As a consequence, the observed delay in glacier retreat between the three catchments (Fig. 1A) has likely been associated with a time-transgressive activation of periglacial processes like landslides, resulting in different topographic configurations today.

2.2 Catchment hillslope profiles

To visualize the hillslope morphologies in our studied catchments, we made topographic transects (Fig. 2) perpendicular to the trunk stream in each catchment. Classical glacial topographic features, including typical U-shape valleys (Fig. 3), are well documented, easily observable and have been suggested to result from the bimodal distribution of glacial erosion with elevation (Anderson et al., 2006; Bernard et al., 2025; Egholm et al., 2009; Herman et al., 2011; Steer et al., 2012). The observed bimodal hypsometry of glacial landscapes (Brocklehurst and Whipple, 2006) defines the boundaries between the valley overdeepening, driven by fast-moving ice with intense erosion by abrasion and quarrying, and areas with slower-moving ice exerting less erosive power (Coutterand, 2010; Leith et al., 2014). Alternatively, this bimodal hypsometry may be attributed to different patterns of cold-climate erosion around the ELA (Equilibrium Line Altitude) (Liebl et al., 2021). In both interpretations, the hillslope shoulder – a slope inflection between steep upper and steep lower hillslopes (Fig. 2 – conceptual figure), – is shaped during glacial periods (Louis, 1952; Valla, 2021). This topographic shouldering would result in a bimodal distribution of catchment elevations with steep slopes associated to both the glacier valley flanks (low elevations) and to the nunataks-crestlines area (i.e. periglacial regions at high elevations) (Coutterand, 2010; Liebl et al., 2021).

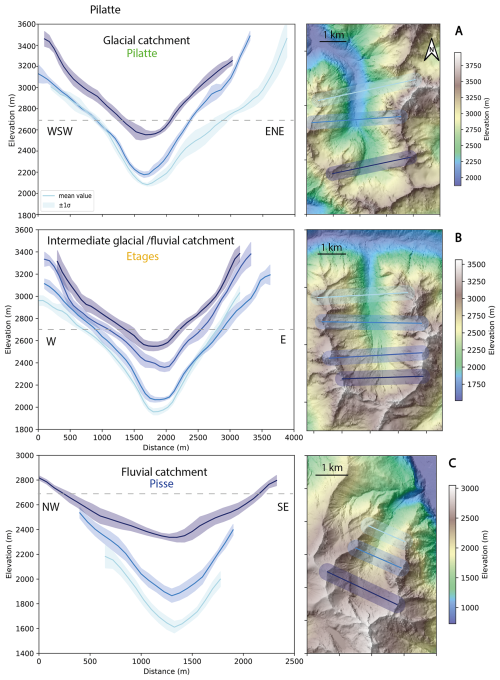
Figure 2 Swath topographic profiles for the three different catchments (Lehmann and Robert, 2024) (DEM, resolution: 50 cm, ESPG2154, from the French National Geographic Institute, Cusicanqui, 2024): (A) Glaciated catchment (Pilatte), (B) intermediate glacial-fluvial catchment (Etages), and (C) fluvial catchment (Pisse). Profiles are aligned based on their lowest area. The grey dashed line illustrates the 2700 m elevation, a threshold elevation around which the predicted landslides activity is lower (Figs. 6 and 7).

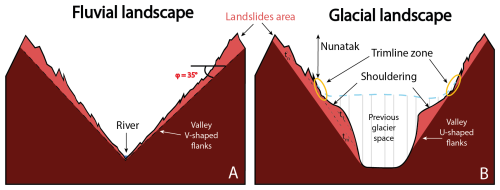
Figure 3 Conceptual sketches of theoretical fluvial (A) and glacial (B) landscapes. (A) Typical landscape dominated by fluvial erosion processes with V-shaped valley and homogeneous hillslopes slightly above the internal angle of friction (φ= 35° in this example). (B) Landscape dominated by glacial erosion processes. The main morphological characteristics such as U-shaped valley, periglacial nunatak zone, shouldering and the trimline zone (yellow circle) are shown (modified from Louis, 1952; Coutterand, 2010). The light-red color indicates potential landscape areas affected by landslide activity where different failure planes, associated to particular times, are illustrated (dashed black line and t_t, t_n, t_m).

Our two upper catchments (Pilatte and Etages catchments) show a clear U-shaped valley on each transect, even in the upstream part of the catchment. A slope inflection is also visible along most of the transects, which we interpret as evidence of shouldering (Fig. 3). For most of the transects, the increase in slope upslope of the shouldering corresponds to the glacial trimline (Penck, 1905). It corresponds to the highest zone of the glacier extent and usually the limit between prevailing glacier erosion processes and periglacial processes, whose locations match with the upper limits of the glacier cirque (Rootes and Clark, 2020) (Fig. 2). Conversely, the topographic transects for the unglaciated catchment (Pisse) tend to reveal a V-shaped valley, especially in the lower part of the catchment. The upper profile, however, is closer to those of the glacial and intermediate catchments, showing a clear inheritance from previous glaciations.

In the following, we will name the three studied catchments according to their glacial morphology imprint, i.e “glacial”, “intermediate glacial-fluvial” and “fluvial” for the Pilatte, Etages and Pisse catchments, respectively.

3 Modeling framework

Hylands is a reduced-complexity and stochastic landslide model (Campforts et al., 2020, 2022). It simulates both the erosion associated with deep-seated landslides and the induced sediment transport and deposition resulting from landslide runout. Hylands is part of the Landlab open-source framework (Barnhart et al., 2020; Hobley et al., 2017), which offers tools to combine multiple geomorphic laws on 2D regular grids. In the following, we use the 25 m resolution DEMs from the IGN (BD ALTI, French National Geographic Institute, https://www.ign.fr/, last access: 4 May 2025), as initial model topographies for the three studied catchments. The catchment boundaries were obtained from the geo-processing tools available at the “Eau France” service website: https://reseau.eaufrance.fr/geotraitements/viewer/bassin-versant (last access: 4 May 2025). We first here present the model and then our strategy for model calibration.

3.1 The HyLands model

3.1.1 Landslide triggering

In HyLands, the landslide source model combines a spatial probability P_s and a temporal probability P_t to compute a landslide failure probability $P_{\mathrm{failure}}=P_{\mathrm{s}}\cdot P_{\mathrm{t}}$. The spatial probability is computed following a modified Culmann criterion (Campforts et al., 2020; Culmann, 1875), which is a Mohr-Coulomb criterion applied to a finite slope analysis:

$$\begin{array}{}\text{(1)}& P_{\mathrm{s}}={\displaystyle \frac{H_s}{H_c}},\mathrm{with}{H}_c={\displaystyle \frac{\mathrm{4}C}{\mathit{\rho }g}}{\displaystyle \frac{\sin \mathit{\beta }\cos \mathit{\phi }}{\mathrm{1}-\cos (\mathit{\beta }-\mathit{\phi })}}\end{array}$$

where H_s (m) is the local hillslope height calculated between two adjacent cells of the grid and H_c is the maximum stable hillslope height (m), which depends on the cohesion C (kg m⁻¹ s⁻²), ρ the rock density set to 2700 kg m⁻³, g= 9.81 m s⁻² the gravitational acceleration, β the local topographic angle, and φ the angle of internal friction (Eq. 1). Both C and φare parameters that need to be calibrated in our modelling approach.

However, HyLands is not a deterministic model as it combines this spatial probability of failure to a temporal probability. Indeed, P_t controls the temporal occurrence of landslides and follows a Poisson law (Campforts et al., 2022):

$$\begin{array}{}\text{(2)}& P_{\mathrm{t}}=\mathrm{1}-e^{-\mathrm{d}t/t_{\mathrm{LS}}}\end{array}$$

where dt= 10 years is the simulation time step which remains constant during the model runs. t_LS (years) is the return time of landslides triggering events. In turn, if any slope change occurs, the probability of failure P_failure of a given cell is constant with time and is updated at very model iteration. The random nature of landslides is introduced using a grid of cells with a random number r between 0 and 1. Landslides will occur if r ≥P_failure at a particular cell (Campforts et al., 2020). Generating a different grid of r value, by setting the seed parameter differently, will necessarily induce a different pattern of landsliding.

3.1.2 Landslide erosion and deposition

When a landslide event is triggered, a failure plane initiates at the triggering point, generating an erosion scar. Following the Culmann criterion, the dip angle of this plan θ is the bisector of the local topography angle β, and the angle of internal friction of the material φ:

$$\begin{array}{}\text{(3)}& \mathit{\theta }={\displaystyle \frac{\mathit{\beta }+\mathit{\phi }}{\mathrm{2}}}\end{array}$$

The failure plane is propagated upstream of the critical node if the elevation of the neighboring cells exceeds the rupture surface.In this case, all the DEM cells above this surface are considered as unstable and mobilized by landsliding. Because our primary goal is to study landslide erosion without any potential feedback of deposited sediments, all sediments are instantaneously evacuated in this setup. It also means that in our set-up no topographic change can occur below the triggering points of simulated landslide sources.

3.2 Strategy for model calibration

Our objective is to use a calibrated and physically sound landscape evolution model, based on HyLands, to predict landslide activity during postglacial conditions in our study area. Note that in these simulations, we only consider the role of landslides in landscape evolution and erosion dynamics, without modeling fluvial erosion nor tectonic activity (e.g., uplift rate). We also assume that gravitationally triggered landslides as simulated in HyLands represent the combination of mass wasting events in alpine topography including rockfalls, debris flows, and shallow to deep-seated landslides, capturing the diverse range of slope failure processes. Our model calibration is performed on the Etages catchment following two steps:

1. Calibrating φ and C, which control the spatial probability of landslide occurrence, by comparing the modelled landslides area-frequency distribution (Sect. 3.3.2) and size-volume scaling relationship (Sect. 3.3.1), with those taken from natural landslide datasets elsewhere (Fig. 4; Delgado et al., 2022; Guzzetti et al., 2002).

2. Calibrating the landslide return time t_LS, which sets the temporal probability of landslide occurrence, by comparing modelled catchment-averaged erosion rates and observed erosion rates data derived from quartz ¹⁰Be concentrations in stream sediments (Sect. 3.3.2, Fig. 5), ranging between 0.27 and 1.1 mm yr⁻¹ in the Ecrins massif (Delunel et al., 2010). For the Vénéon valley and the studied catchments (i.e. Etages catchment), we can reduce this range to 0.7 to 1.1 mm yr⁻¹ for our model calibration (Fig. 5). Assuming that a rock sample records quartz ¹⁰Be accumulation over the time period corresponding to removal of the upper 60 cm of rock (Delunel et al., 2010; von Blanckenburg, 2005), these ¹⁰Be-derived erosion rates record apparent integration times of around 500 to 2500 years. We thus select a simulation time of 1500 years for the model calibration phase.

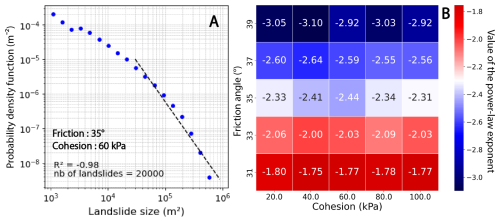
Figure 4 Calibration approach for the internal angle of friction and the cohesion in the HyLands model. Calibration outcomes result from multiple simulations, with similar input parameters, to get a larger dataset of landslides (see text for discussion). (A) Landslide size distribution, with a linear fit (dashed black line) on the power-law tail of the distribution. The cutoff value (i.e., minimum size where the linear fit starts) is set to 3 × 10⁴ m² . (B) Calibration matrix between the internal angle of friction (φ) and the cohesion (C). The angle of friction is calibrated based on the minimum difference between the power-law exponent of the simulated size distribution and the reference value (−2.3; van den Eeckhaut et al., 2007). Blue colors indicate output power-law exponents smaller than the reference value (−2.3, white colors) and red colors indicate predicted power-law exponents higher than the reference value.

Some combinations of parameters ($\mathit{\phi },C,t_{\mathrm{LS}}$) lead to too few landslides, preventing a statistical analysis of their resulting size distribution. To overcome this issue, we generate a large amount of landslide events and selected a similar number of landslides per simulation. To do this, we need to compile multiple simulations with similar parameters but different stochastic occurrence (different seeds) and reduce the return time (from t_LS= 1 × 10⁵ years to t_LS= 100 years). Because t_LS controls the occurrence of landslides without impacting their geometry, a small value of t_LS induces simulation outputs with large landslide datasets. This is particularly true given that the potential for landsliding remains significant throughout the simulation. The first approach is used for all the parameter calibration (Figs. 4A–B, 5), while the second approach was only used in the landslide size-frequency calibration (Fig. 4A) because the modified return time value can induce changes in landslide volumes and occurrences, and thus in output catchment-averaged erosion rates (Fig. 5).

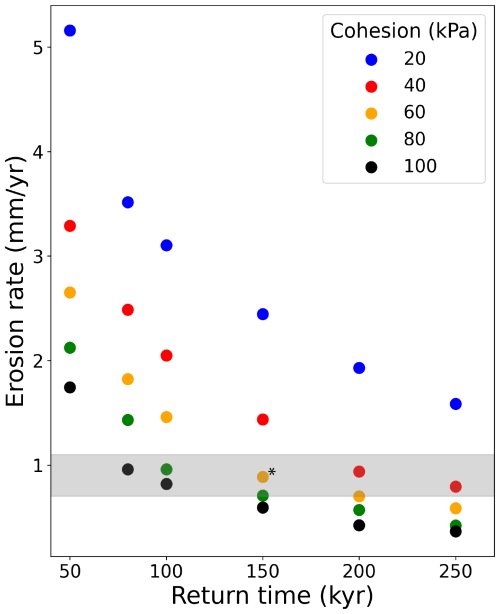
Figure 5 Calibration of the landslide return time and cohesion parameters based on the simulated catchment-averaged landslide erosion rate. Considering the calibrated angle of internal friction (35°, Fig. 4B), each dot represents a particular combination of landslide return time and cohesion (color code indicating the cohesion value). The selected combination is identified with a star (^*). The simulated erosion rate is an averaged catchment-scale erosion rate over a compilation of 20 different simulations (1500 years duration). The grey band illustrates the range of observed erosion rates from the literature (0.7–1.1 mm yr⁻¹; Delunel et al., 2010).

3.3 Model calibration

3.3.1 Calibration of the angle of internal friction: landslide area-frequency distribution

Because we lack detailed compilation of alpine mass-wasting events, HyLands will be calibrated against global compilations of landslide data. More specifically, we aim at constraining the cohesion and angle of internal friction parameters. Although not specific to our field site, this general calibration will allow us to assess the impact of gravity driven erosion in high alpine terrain and therefore proved sufficient for this study. For our calibration runs, we run HyLands from existing topography of the three catchments and set model parameters not involved in the calibration equal to those as reported in Table S1 in the Supplement.

Field inventories of landslides and rockfalls show a well-known shape for the frequency distribution of landslide area, highlighting several characteristics of a power-law relationship (Delgado et al., 2022; Guzzetti et al., 2002; Jeandet et al., 2019; Malamud et al., 2004; Stark and Hovius, 2001; Tanyaş et al., 2019; Tebbens, 2020): (1) the rollover value, matching the highest frequency of the landslide-area distribution, (2) the power-law scaling exponent, α, defined from the slope of the linear regression measured for large landslides events, and (3) the cutoff value, related to the divergence of the distribution from a power-law scaling. Except for a few parameter combinations (in the range of tested parameters of friction and cohesion), the simulated landslide size-frequency distributions we obtained did not display any clear rollover. This lack of rollover is probably due to the coarse resolution of the grid (25 m) which makes it impossible to visualize small landslides. Therefore, we do not use this criterion for our model calibration approach. The power-law scaling exponent is a key parameter as it describes the frequency of intermediate to large landslides, which convey most of the eroded volume. This exponent also varies significantly with the internal angle of friction (Fig. 4B). As no power-law exponent value exists for the French Alps landslide-rockfall inventories, we use as a reference the mean value α_mean= −2.3 suggested by Van Den Eeckhaut et al. (2007) from a global landslide compilation. Tanyaş et al. (2018, 2019) also carried out a landslide compilation and analysis of landslide size-frequency distributions, proposing a slightly larger power-law exponent (α_mean= −2.5). However, this inventory only considers earthquake-induced landslides. In addition, power-law exponents tend to be smaller for igneous or metamorphic rock (such as present in our study area) (Bennett et al., 2012), so we retain the value of −2.3 for our model calibration. In our calibration phase, we set the cutoff area at 3 × 10⁴ m² based on the shape of the linear regression fit and the good value of the Pearson correlation coefficient (Fig. 4A). Our cutoff value seems to be smaller but overall consistent with previously reported values (Tanyas et al., 2018, 2019).

The simulated landslide size-frequency distribution (Fig. 4A), in a log-log plot, illustrates the decrease in landslide number when increasing landslide size. From all simulated landslides (5 × 10⁴ in total; see Sect. 3.2), we randomly select 20 000 landslides to construct the landslide size-frequency distribution. This method ensures a homogeneous number of events between different combinations of input parameters (Fig. 4B). Therefore, we compare the simulated power-law scaling exponent α, resulting from different combinations of cohesion (C) and internal friction angle (φ), with the expected power-law exponent of −2.3. The power-law regression is computed using a log-log linear fit. The output matrix (Fig. 4B) shows a gradient for the power-law exponent α with increasing φ values. In our simulations, α varies strongly, between −1.7 and −3.1, when changing the internal angle of friction (31–39°, Fig. 4B). This range is consistent with global compilations of power-law exponents for landslide-area scaling (Tanyaş et al., 2018, 2019; Van Den Eeckhaut et al., 2007). We also observe little variability in α with cohesion (C). Therefore, we fix the internal angle of friction at φ= 35° which leads to simulated values of α close to −2.3. As the cohesion parameter seems to not influence the power-law exponent of the landslides size-frequency distribution, we calibrate this parameter using an alternative strategy (see Sect. 3.3.2).

As a verification of our model calibration, we also simulate the area-volume relationship for simulated landslide distributions (Fig. S1). The relevant cloud of landslides events (n= 426) shows a power-law scaling similar to those observed elsewhere with an intercept value of 0.84 and an exponent value γ= 1.49 (Fig. S1) (Larsen et al., 2010; Wood et al., 2015).

3.3.2 Calibration of landslide return time and cohesion: ¹⁰Be-derived erosion rate

To calibrate the cohesion and the landslide return time parameters, we compare simulated and ¹⁰Be-derived catchment-averaged erosion rates (Sect. 3.2, Fig. 5). Both model parameters impact nonlinearly the output erosion rate, and increasing t_LS or C leads to decrease the resulting erosion rates (Fig. 5). Several combinations of parameters predict a catchment-averaged erosion rated within the expected range (0.7–1.1 mm yr⁻¹; grey band). In the following, we use an intermediate parameter combination, C= 60 kPa and t_LS= 150 kyr, as the different possible model parameterizations (Fig. 5) lead to roughly similar spatial and temporal patterns in landslide activity.

We also ran simulations for two end-member parameter combinations: a minimum combination (C= 20 kPa and t_LS= 50 kyr) and a maximum combination (C= 100 kPa and t_LS= 250 kyr). Results show a strong variability in landslides frequency and associated erosion rates but a similar spatial landslide distribution (Fig. S2).

4 Results

4.1 Spatial distribution of landslide activity

Using the calibrated model, we investigate the impact of landslide activity on catchment topographic changes over 100 kyr time scales representing glacial-interglacial cycles). Over this timescale, the calibrated landscape evolution model generates different spatial patterns of landslide erosion across the three studied catchments (Fig. 6). In each catchment, landslide erosion is distributed heterogeneously, ranging from areas experiencing an intense landslide activity and significant topographic changes to overall unaffected areas. For the glacial catchment (Pilatte), significant topographic changes, up to 500 m, occur along its northeast ridges. Elsewhere, predicted landslides lead to smaller topographic changes of up to around 100 m (Fig. 6A). The intermediate glacial-fluvial catchment (Etages) shows erosion patches along its crests and summit walls. In some areas, cumulative erosion reaches 350 m, while smaller cumulative landslide erosion are observed on low-elevation hillslopes, just above the valley bottom (Fig. 6B). For the fluvial catchment (Pisse), landslide erosion is mainly focused on the downstream parts of the catchment where the valley narrows and slopes become steeper. Cumulative landslide erosion reaches up to 250 m, but the upper part of the catchment shows limited landslide activity (Fig. 6C). The final distributions of slope across the three catchments clearly highlight the locus of landslide activity. Indeed, landsliding results in homogenizing slopes slightly above the internal angle of friction (0.7, represented by white color in Fig. 6).

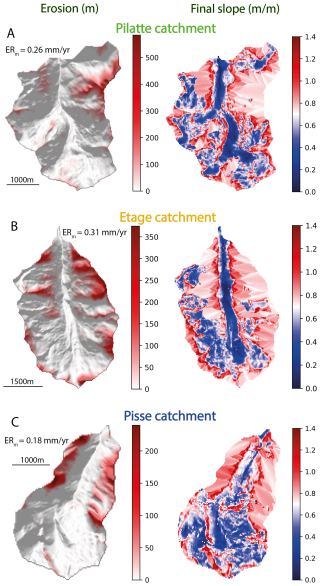
Figure 6 Simulation results of cumulative landslide erosion and final slope distribution for the studied different catchments (A – Pilatte, B – Etages, C – Pisse). Left panels display landslide erosion patterns with cumulative landslide erosion (red color) over 100-kyr simulation duration on the modern hillshade DEM. The catchment-averaged mean erosion rate is indicated (ER_m) Right panels show the final slope distributions where the landslide activity results in more homogenous slope patterns around the input internal angle of friction (0.7 m m⁻¹, white colors).

4.2 Spatial location of landsliding

For each catchment, we investigate the simulated evolution of both the hypsometry and slope distributions (Fig. 7A, D, E). As expected from the modern slope distribution (Fig. 1C), the initial catchment topographies (i.e., at 0 kyr) show a similar modal slope around 0.6 m m⁻¹. This modal slope is reached at different elevations for the different catchments: 2800, 2600 and 2600 m a.s.l. for the glacial, intermediate glacial-fluvial and fluvial catchment, respectively (Fig. 7A, D, G).

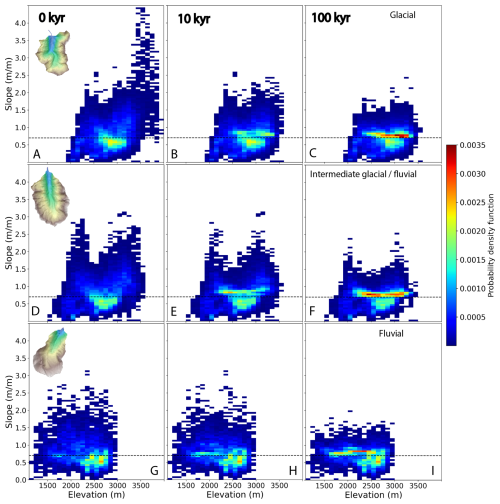
Figure 7 2D histograms of the catchment slope distributions (color scale) with elevation. The temporal evolution of catchment slopes and elevations during simulations is monitored at three different time steps: 0, 10, and 100 kyr (left, middle and right, respectively). Each row shows model results for a particular catchment: glacial (Pilatte, A–C), Intermediate glacial-fluvial (Etage, D–F), and Fluvial (Pisse, G–I). For all three catchments, steep slopes are erased and catchment slopes tend toward more homogeneous slopes around and just above the input internal angle of friction (0.7 m m⁻¹, i.e. 35°).

The initial model topographies of the glacial (Pilatte) and intermediate glacial-fluvial (Etages) catchments show a bimodal distribution of the elevations for steep slopes (Figs. 7A, D and 8) (Fig. S3).

The steepest slopes of the glacial (Pilatte) catchment range up to 4.5 m m⁻¹ (i.e between ∼ 63 and 77°) and are mostly restricted to the highest elevations (3000–4000 m) (Fig. 7A). A second peak of steep slopes, with lower magnitudes (up to 2.5 m m⁻¹ i.e ∼ 68°), is found around 2400 m. The intermediate glacial-fluvial (Etages) catchment also shows an initial topography with two similar “peaks” of steep slopes frequency (Fig. 8C). We observe maximum slopes around 3 m m⁻¹ (∼ 70°) between 2700 and the catchment crestline (∼ 3500 m), and in a narrower elevation range from around 2000 to 2400 m (Fig. 7D). In contrast, the fluvial (Pisse) catchment differs in having a relatively homogeneous distribution of slopes with elevation (Figs. 7G, S4). Throughout the simulations, catchment slopes exceeding the friction angle at 0.7 m m⁻¹ are affected by landslides, especially in the glacial catchment where significant changes can be noticed already after only 10 kyr simulation (Fig. 7B, E). Overall, after 100 kyr simulation, landslide activity has erased most of the steep slopes (almost three times less steep slopes, for high elevations, at the end of the simulation, Fig. 8C), i.e. above ∼ 1.5 m m⁻¹, reducing significantly in turn the bimodal distribution of elevation for the steepest slopes (Figs. 7C, F and 8C). The maximum catchment elevation has decreased for the glacial and intermediate glacial-fluvial catchments, while it remains approximately constant for the fluvial catchment after 100 kyr of simulation.

Figure 8 For the Etages catchment (intermediate glacial-fluvial), temporal evolution of (A) elevation distribution, (B) slope distribution, and (C–D) elevation distribution with slope threshold values (above or below 1 m m⁻¹). The colors illustrate the initial topography (red), an intermediate stage (20 kyr – light blue) and the final topography (100 kyr – dark blue).

During the simulations, we also observe a progressive increase in slope frequency slightly below 1 m m⁻¹ (i.e., 45°), concentrated around 2600–3200, 2400–3000 and 1900–2600 m for the glacial, intermediate glacial-fluvial and fluvial catchments, respectively (Figs. 7C, F, I and 8B). This new slope distribution evidences the shift from the initial steep slopes to final intermediate slopes that are closer to the input internal friction angle.

4.3 Temporal distribution of landslides

We now investigate the relationship between topographic changes and landslide activity (Fig. 9). Here, we identify each landslide by its time of occurrence and its triggering location, corresponding to its lowest elevation (Fig. 9). First, our results highlight the bimodal elevation distribution of the simulated landslides, roughly above 2800 m and below 2400 m, which appears persistent with time for the glacial and intermediate glacial-fluvial catchments (Fig. 9A, B). These two catchments also show an intense landslide activity for the first 20 kyr of simulation, with an apparent progressive decay with time. Large landslides occur throughout the 100 kyr of simulation time, illustrating the stochastic nature of landslide occurrence in HyLands. These model predictions are supported by the cumulative distribution of landslides volume through simulation time (Fig. 10A–C). For the glacial and intermediate glacial-fluvial catchments, more than half of the total landslide volume is predicted before 20 kyr. However, the cumulative number of landslides increases with time for these catchments. This discrepancy between the total landslide volume and the number of landslides illustrates the preferential occurrence of large landslides within the first 20 kyr. This interpretation is supported by the change in the probability density function of the landslide volumes after 20 kyr simulation time (Fig. S5). We do not observe this pattern for the fluvial catchment (Fig. S5C, F), although the largest landslides are still predicted during the first 20 kyr of simulation time.

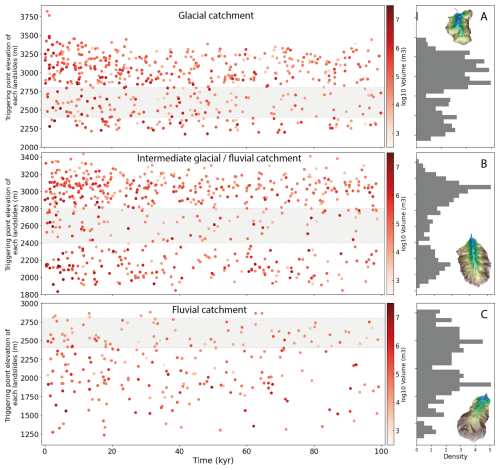
Figure 9 Triggering point elevation of each predicted landslide over the total simulation time (100 kyr) and their associated volume (red gradient colors). The landslide distributions with elevation (right panels for distributions) appear bimodal for the glacial and intermediate catchments (A–B) with two main elevation ranges around 2100 and 3000 m and no clear altitudinal distribution of predicted landslides for the fluvial catchment (C). The shaded band in between these two elevations highlights this altitudinal interval with fewer predicted landslides in the Etages catchment, and serves as a reference for the other two catchments.

Figure 10 Cumulative distribution of the predicted landslide volumes over the total simulation time (100 kyr) for the glacial (Pilatte – A), intermediate glacial/fluvial (Etages – B) and fluvial (Pisse – C) catchments. The orange lines are the total cumulative landslide volumes, while the blue lines display the predicted cumulative volumes for landslides located above (light blue) and below (dark blue) an elevation threshold of 2700 m. The yellow vertical dashed lines indicate the simulation time when 50 % of the total landslide volume is reached. Insets show the cumulative number of landslides generated during the simulation time for the two defined elevation classes.

Another interesting result is the inverse relationship between the predicted landslide volume and the number of landslides at different catchment elevations: at low elevations (< 2700 m), landslides are less frequent but large landslides are overrepresented; whereas at high elevations (> 2700 m), landslides are more frequent but large landslides are underrepresented. This assessment is particularly true for the glacial (Pilatte) and intermediate glacial-fluvial (Etage) catchments (Fig. 10A–B). For instance, the glacial catchment (Fig. 10A) displays twice as many landslide occurrences at high elevations (> 2700 m), with only a slightly larger eroded volume above than below 2700 m elevation.

Observations are significantly different for the fluvial catchment as the landslides are rather homogeneously distributed in the catchment (Fig. 9C). However, the high occurrences of landslides in the first 20 kyr are still noticeable (Fig. 10C) and large landslides tend to occur preferentially at low elevation (< 2200 m).

4.4 Temporal evolution of landslide erosion rate

The term `erosion rate' describes here only the predicted erosion induced by landslides and averaged over the catchment area. For each studied catchment, we compute the evolution of the catchment-averaged erosion rates using a 2 kyr time window, providing different statistics: mean, median, 25th and 75th percentiles of catchment-averaged erosion rates (Fig. 11). This temporal window emphasizes the general long-term trend of the predicted erosion rate by smoothing its high-frequency variations related to the stochasticity of landslide occurrence (Fig. S6). For all three catchments, the catchment-averaged erosion rates vary roughly between 10⁻⁵ and 10⁻¹ m yr⁻¹ when at least one landslide is triggered during the time window. The predicted mean erosion rate is always significantly higher than the median erosion rate (almost 10 times at the beginning of the simulation and around 100 times after 100 kyr of simulation time), but the same progressive decreasing trend is observed for both two statistical measures. In addition, the 25th percentile rapidly becomes null, highlighting that the catchment-averaged erosion rate is driven by large but infrequent landslides.

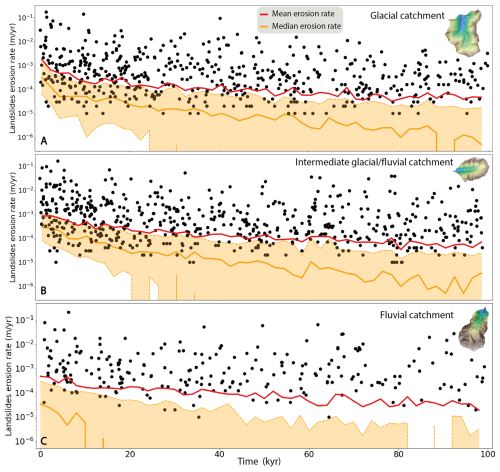
Figure 11 Temporal evolution of the catchment-averaged landslide erosion rate for the three studied catchments: (A) Glacial (Pilatte), (B) Intermediate glacial-fluvial (Etage), and (C) Fluvial (Pisse). Black dots illustrate the non-zero landslide erosion rates for each time step of one individual simulation, while red and orange lines depict respectively the mean and median (with 25th and 75th percentiles as dashed orange lines) erosion rates compiled from 20 individual simulations (with a smoothing temporal window of 2 kyr). For all catchments, the simulated landslide erosion rates decrease over time, especially during the first 20 kyr of simulation time, with different temporal trends depending on the catchment.

The glacial (Pilatte) catchment (Fig. 11A) shows a high mean erosion rate, above 1 mm yr⁻¹, with a rapidly decreasing trend during the first 10 kyr. Then, the mean erosion rate decreases more slowly until 60 kyr and becomes roughly constant at 0.1–0.2 mm yr⁻¹ over the last 40 kyr of simulation. A similar trend is observed for the intermediate glacial-fluvial catchment (Etages, Fig. 11B), but the initial erosion rate is ∼ 1 mm yr⁻¹ and lower than for the glacial (Pilatte) catchment. In contrast, the fluvial (Pisse) catchment (Fig. 11C) shows a progressive decrease in the mean erosion rate, from ∼ 0.6 to 0.06 mm yr⁻¹ after 60 kyr of simulation, with no observed peak in erosion rate at the beginning of the simulation. The median value for the fluvial catchment reaches rapidly zero within the first 20 kyr of simulation, illustrating the lower frequency of landslide occurrence compared to the glacial and intermediate glacial-fluvial catchments. Overall and for all studied catchments, predicted landslide erosion rates decrease by about an order of magnitude over 100 kyr, illustrating the progressive erasing of steep slopes associated to glacial morphological features.

5 Discussion

5.1 Modeling approach

Our landscape evolution model using HyLands has been designed to explore the impact of landslide activity in reshaping alpine landscapes during postglacial periods. Our numerical simulations succeed in reproducing a pulse of landslides activity during the postglacial period and its complex (non-homogeneous) impact on catchment hypsometry and slopes. However, this reduced-complexity model represents a simplified version of real hillslope dynamics, with limitations regarding its ability to predict in details all the richness of natural landforms, especially under the constraint of long simulation time (Tucker and Hancock, 2010). Therefore, we made several modeling choices (see Sect. 3.2 and 3.3) to minimize potential feedback loops and interaction between erosion processes, which may have impacted our results as discussed below.

5.1.1 Missing processes: rock uplift, fluvial erosion and sediment transport

As mentioned earlier, the model does not account for the impact of uplift, which can be considered as a limitation. Given the present-day rock uplift rate in the western European Alps, around 1 mm yr⁻¹ (Nocquet et al., 2016; Sternai et al., 2019), the total uplift over the simulation period (100 kyr) would be around 100 m. This theoretical uplift value is of the same order of magnitude than the average decrease in elevation caused by landslide erosion in the intermediate glacial-fluvial (Etages) and fluvial (Pisse) catchments (Figs. 6–7). In the glacial (Pilatte) catchment, the mean erosion is around 26 m, with maximum cumulated erosion of ∼ 500 m. Therefore, integrating rock uplift in the model, from either geodynamics, tectonic activity or glacial isostatic rebound (Sternai et al., 2019), could counterbalance the overall decrease in catchment elevation observed in our results. Indeed, post-glacial rebound can occur at km scale, promoting local rock uplift and potentially considered to be a significant factor in triggering landslides in some regions (Cossart, 2013). In addition, rock uplift has also been proposed as modulating the post-glacial geomorphic response and landscape transition from glacial to fluvial states (Prasicek et al., 2015), by allowing faster relief turnover times. In addition to uplift, tectonic activity could be associated with seismicity, another well-known triggering factor for landslides (Keefer, 1984; McColl, 2012). However, despite these limitations, we believe that our modeling approach stays appropriate to assess the hillslope stability over 100 kyr timescales, which is largely dependent on climatically-shaped alpine topography and bedrock mechanical strength. The impact of local earthquakes would mostly result in changing the timing of landslide activity, not the total volume of landslides.

The catchment-averaged erosion rate of 1 mm yr⁻¹, derived from published cosmogenic nuclide data (Delunel et al., 2010) and used for the return time calibration, is integrating a large fluvial network with multiple erosion processes (fluvial, hillslope, landslide) at the scale of the Ecrins massif. Considering effective sediment connectivity in the catchment (in our study area, main fluvial valleys are sediment bypass areas without significant incision but potential transient storage) and only landsliding to derive our catchment erosion rate, 1 mm yr⁻¹ is likely to be an end member minimum value for our simulations. Therefore, we ran a supplementary simulation with a lower cohesion value (20 kPa) while keeping the same return time (150 kyr), leading overall to a higher erosion rate (about 2–3 mm yr⁻¹, Fig. 5). The simulation results show a globally higher frequency of landslides, but with similar patterns in landslide occurrence, topographic changes and temporal trend in erosion rate (Fig.S7).

Finally, we did not include fluvial erosion and sediment export in our simulations. Ignoring sediment transport over either the postglacial period or a long timescale (100 kyr), which in reality should include multiple glacial-interglacial oscillations, is a strong model limitation for alpine erosion dynamics (Schlunegger and Hinderer, 2003). Indeed, sediment transfer dynamics over the Quaternary period are associated with glacial dynamics (Antoniazza and Lane, 2021), coupling between hillslopes and channels (Hovius et al., 2000), local fluvial incision (Leith et al., 2018; Valla et al., 2010) and potential transient sediment storage (Buechi et al., 2018). Rivers are also considered as the main agent of sediment transport during interglacial period (Koppes and Montgomery, 2009; Pitlick et al., 2021). Fluvial incision also leads to a lowering of the base level, which in turn creates more steep slopes at the hillslope toe. These changes combine to renew the landslide potential of these transient landforms. However, in this study we modeled a single interglacial period and provided a focus solely on hillslopes dynamics (i.e., no fluvial dynamics); both arguments result in a lower influence of the sediment dynamics for our results.

5.1.2 Model parameterization

Our modeling strategy and parameterization have inherent limitations, such as our initial input DEM (modern alpine topography) with a low resolution (25 m). Such resolution allows long simulation periods in a reasonable simulation time with the capability to still capture first-order erosion processes and topographic changes (Campforts et al., 2022). However, this relatively low resolution may hinder the presence of small-scale topographic roughness that could influence both landslide occurrence and magnitude. In addition, we ran our model simulations over 100 kyr, which is longer than any interglacial period during the Quaternary. This particularly long duration enables to constrain the timescale required for the decay of landslide activity, until reaching a state of hillslope stability at the catchment scale. The model duration of 100 kyr is not a realistic timescale for a post-glacial phase. However, it is an interesting and necessary duration which enables (1) to assess clear temporal trends of erosion rates, smoothing out landslide variability, and (2) to quantify the duration required to reshape the glacially-inherited topographic imprints and to reach stable catchment hillslopes.

Moreover, we consider the present-day topography of the studied catchments to start the post-glacial simulations and to perform our model calibration. Yet, these landscapes have likely been already subject to post-glacial hillslopes processes and landsliding since glacier retreat, limiting the number of hillslope instabilities in the modern topographies. In turn, this means that the simulated rates of erosion at the beginning of the simulations are likely minimum values for representing post-glacial conditions. However, extrapolating further is difficult since deglaciation is asynchronous both between and within the studied catchments: the U-shaped valley floors and walls, at rather lower elevations, are the first areas to have experienced landsliding, while higher-elevation areas such as ridges and cirques can be protected from instability for longer thanks to active permafrost and only recent glacier retreat.

Another strong assumption is to ignore sediment deposition on the resulting simulated topography. Landslides are among the most efficient processes for producing sediments (Keefer, 1984) in mountainous areas, which can then be available for transport from hillslopes to the drainage network. The sediment connectivity (Cavalli et al., 2019), especially for bedload sediment, from hillslopes to channels is a key indicator to quantify sediment yields and morphological changes along the source-to-sink profile (Comiti et al., 2019; Hooke, 2003; Lane et al., 2017; Micheletti et al., 2015). Thus, we explore the potential feedbacks of sediment deposition on landslide activity by testing the Hylands model with a complete storage of landslide-produced sediment in the catchment. In that case, coarse sediments are spread over the hillslopes, i.e. downstream of the landslide source, following a non-linear and non-local deposition law (Carretier et al., 2016). This deposition term depends on the transport distance which is driven by the critical slope, settled here equal to the tangent of the angle of internal friction (φ) (Campforts et al., 2022; Carretier et al., 2016). This new setup is the opposite of our main analysis (Ff = 1, Sect. 3.2), where we assumed a perfect sediment connectivity within the catchment, leading to instantaneous sediment export (Figs. S8–S9). However, the spatio-temporal landslide activity remains roughly similar to our previous simulations. Note that we have not computed the denudation rate without exported fine sediment because it would not be possible to compare it with the measured value.

Finally, our model parameterization assumes spatially uniform model parameters both within and between the three catchments. We used a single set of calibrated cohesion and internal angle of friction values (Figs. 3–4), without differentiation based on lithology, vegetation cover, elevation or glacial cover. This assumption may limit the model capacity in capturing the complex terrain roughness of modern alpine topographies, which may be a factor in increasing rock resistance to landsliding in natural environments. For example, in our catchment, the effect of the tree cover at low elevations is not included in the model. Thus, the expected reduction in landslide occurrence due to root reinforcement or changes in soil moisture (Muñoz et al., 2016) is not simulated. In addition, the role of high-elevation permafrost, its spatial variability and temporal evolution, on landslide activity (Magnin et al., 2017), is not captured by our simulations.

5.2 Spatio-temporal landslide activity over the Quaternary period

The long-term glacial inheritance on alpine landforms (e.g., Penck, 1905; Anderson et al., 2006; Sternai et al., 2013; Seguinot and Delaney, 2021) and the relative contribution of glacial and fluvial erosion to the Quaternary relief are still debated, highlighting especially the impact of fluvial and hillslopes processes during interglacial period of the Late-Pleistocene glaciations (Koppes and Montgomery, 2009; Leith et al., 2014, 2018; Montgomery and Korup, 2011).

In this context, our numerical results bring some insights into the role of these hillslope processes in the transition from glacial to fluvial morphologies.

5.2.1 Spatial landslide distribution and glacial imprint

The present-day catchment morphologies (Fig. 2) leave no doubt about the significant role of glacial processes in shaping the investigated landscapes in the Ecrins massif (Fig. 1). Our initial question about the role of landslide activity and their potential capacity to reshape this glacial topographic inheritance over the last post-glacial period can be discussed in light of the simulation outputs.

First, the spatial landslide activity pattern (Fig. 9) reveals that the parts of each catchment with the most obvious glacial morphologies are more subject to mass wasting processes. The steep slopes generated by glacial erosion, along the U-shaped valley walls and at high elevation (crestlines and nunataks), produce a bimodal distribution of landslides with elevation, while the shouldering (Fig. 3), i.e., the gentler slope interval at mid-slope, is much less affected by landslides. Therefore, our simulation results suggest that the transition from U-shaped to V-shaped valleys, as evidenced by the glacial (Pilatte) and fluvial (Pisse) catchments (Fig. 3), highlights the reshaping of the inherited glacial landscape through hillslope processes. However, the bimodal distribution of landslides with elevation is still noticeable after 100 kyr of simulation time (i.e., roughly ten times longer than the post-glacial period). Moreover, the number of modeled landslides and their spatial clustering is still significant for the glacial and intermediate glacial-fluvial catchments compared to the landslide pattern in the fluvial catchment (Pisse), which shows a more uniform distribution of landslides on hillslopes (Fig. 9). Thus, if the landslide activity and its spatial distribution can be considered as indicators of the hillslopes transition, our modeling results suggest that the glacial and intermediate glacial-fluvial catchments have not yet completed their post-glacial transition after 100 kyr simulation.

Second, the landslide volume distributions also illustrate a specific dynamic of mass wasting events in formerly glaciated catchments. For the upper catchments (glacial and intermediate glacial-fluvial), our modeling results suggest that modeled landslides are more frequent at higher elevations, near the crestlines, than at lower elevation near the valley bottoms (Fig. 10). As we are working with a real initial topography (present day), influenced by permafrost, this result is consistent with the recent deglaciation of the upper catchments. Indeed, nunataks and crestlines in this interior part of the massif may still benefit from the stabilizing role of permafrost and have not been impacted by landslides yet. Thus, the higher elevations of the catchment (i.e., above the trimline) still display steep and sharp slopes. Under a warming climate and the degradation of permafrost, these high-elevation and steep hillslopes will potentially be more and more prone to periglacial erosion processes (as is already the case for the intermediate glacial-fluvial catchment). In parallel, our simulations predict large landslides at the lower elevations (Figs. 9 and 10), corresponding to the U-shaped valley wall. These results are consistent with the effect of debuttressing where glacial unloading induces stress variations and steep, unprotected rock walls become targets for landslides (Hylands process), following glacial recession (e.g., Cossart et al., 2008). This is also supported by the temporal clustering of the large landslides in the first 20 kyr. Yet, the occurrence of large landslides, due to their stochastic nature, remains occasional afterwards, which is consistent with other studies (Ivy-Ochs et al., 2017; Schwartz et al., 2017; Zerathe et al., 2014).

Therefore, the persistence of landslide activity in the glacial and intermediate catchments, even after long simulation times, highlights that hillslope processes such as landslides, in response to glacial topographic inheritance, may not be the only factor explaining the fluvial morphology observed in our downstream catchment (Pisse).

5.2.2 Temporal landslide activity and transient topography

We show that the three catchments have a distinct modeled erosion dynamics explained by diachronous landslide activity following different glacial retreat times (Fig. 1). Following the previous spatial analysis (Sect. 5.2.1), the observed temporal decrease in landslide occurrence and in predicted erosion rates over the first ∼ 20 kyr (Fig. 11) reflects a decline in the proportion of unstable slopes during the immediate post-glacial period. The faster erosion modeled at the beginning of the simulation for the glacial and intermediate glacial-fluvial catchments (Fig. 11), compared to the fluvial catchment, highlights the role of landsliding during the transition from glacial to interglacial conditions. This initial and gradual pulse of erosion in the first 20 kyr of the simulation, which differs between the studied catchments, reflects the distinct topographic states with respect to landslide susceptibility. The glacial catchment (Pilatte) has not experienced intense periglacial processes, such as landslides, for as long, resulting in this high erosion rate following debutressing of unstable glacial hillslopes (Cossart et al., 2008). The slowing down of erosion rates in the two upper catchments (glacial and intermediate glacial-fluvial) is also illustrating this long-term transitional stage, in which hillslope processes may continue to control sediment production, but at a slower pace. With few landslides occurring at the end of our simulations, and associated to a low erosion rate, the fluvial (Pisse) catchment could be considered at the end of its transient phase and close to “post-glacial topographic steady-state” dominated by hillslope processes (i.e., no to few landslides).

The modelled pulse of erosion for the postglacial phase implies that the Late Pleistocene period, marked by the transition from glacial to hillslope processes, has reactivated alpine landforms by reshaping new steep and unstable hillslopes along the U-shaped valley walls or in the cirque areas. These particular morphologies (Fig. 2), resulting from glacial inheritance, sustain the potential for landslide erosion. However, our model results also show that simulated landsliding over 100 kyr (duration exceeding the typical interglacial period) is not sufficient for erasing steep glacial morphologies. Indeed, the simulated landslide activity – the bimodal landslide distribution (Fig. 9) – and the associated erosion rate are still significant at the end of our 100 kyr simulations, meaning that the hillslope system alone requires longer timescales than the typical Milankovitch cycle to reach a “interglacial-state” topography (i.e. where glacial imprint has been erased, no longer inducing hillslope instabilities). A longer simulation of 1 million years shows that the modeled erosion rate reaches a plateau in the first 100 kyr but then gradually decreases until 400 kyr (Fig. S9). This is the characteristic time required to obtain stable hillslopes in the absence of external forcing. Note that after a characteristic time, maybe more than 100 kyr, the final topography would result in a simple threshold slope model, close to the critical slope. However, compared to a simple slope threshold model, the stochastic aspect of our model enables to describe both individual landslide distribution and their timing during a post-glacial period.

First, results from this long term simulation can be compared to fluvial processes, which also have long timescales for reaching steady-state topographic conditions (Whipple, 2001). Since hillslope processes are also largely contributing to sediment production in alpine settings, the topographic response time to landsliding may play a role in the sediment transfer cascade which in turn would influence fluvial dynamics and erosion rates. Second, this relatively long activity of the hillslope system during the interglacial period – calibrated from cosmogenic-nuclide derived erosion rates (Sect. 3.3.2) – is also consistent with the absence of uplift and fluvial incision in our modeling approach. Including these model components in our simulations may decrease the duration of post-glacial landsliding activity for the studied catchments, with rock uplift promoting faster response of the hillslope-fluvial system as observed for natural settings (Prasicek et al., 2015).

Given the long persistence of landsliding from our simulations (> 100 kyr), the observed differences in landslide activity between the glacial/intermediate and fluvial catchments cannot be fully explained by the time lag in glacier retreat and the duration of the interglacial period (∼ 10 kyr, Fig. 1). We thus propose that the glacial imprint may have been less intense in the fluvial (Pisse) catchment than in the glacial and intermediate glacial-fluvial catchments (Pilatte and Etages), which could be explained by the more external position of the catchment in the massif and its overall lower elevations. This is consistent with the non-uniform impact of glacial processes on mountainous landforms (Herman et al., 2011; Sternai et al., 2013; van der Beek and Bourbon, 2008), resulting from different ice extent/thickness and erosion efficiency over glacial cycles (Pedersen and Egholm, 2013; Seguinot and Delaney, 2021).

5.3 Landsliding and topographic mountain evolution

5.3.1 The glacial/ interglacial transition: a hot moment for alpine erosion

Glacial erosion also does not appear to be spatially uniform throughout the glacial period (Seguinot and Delaney, 2021), and field studies have shown increased glacial erosion during the deglaciation period (Koppes and Montgomery, 2009). Therefore, key erosion moments of glacial dynamics occur at the end of the glacial period. Following this period, our model results suggest an additional pulse of rapid erosion, associated to landsliding within the first 10 kyr after deglaciation. Therefore, the glacial-interglacial transition seems to concentrate the most rapid rates of erosion and in turn, may contribute strongly to landscape changes and topographic relief evolution in alpine settings.

However, our simulations were carried out on the current topography, which is already the results of 2 million years of successive glacial-interglacial cycles. Thus, the hot-moment of erosion that we observe in the post-glacial period occurs in U-shaped valleys that are already well marked. As landslide potential is maintained by steep slopes, this shape of mature glacial valley may increase landslide activity compared with early Quaternary times. Overall, this reinforces the already-demonstrated key role of hillslopes processes in shaping long-term mountain topography (Burbank et al., 1996; Korup et al., 2007; Larsen and Montgomery, 2012).

5.3.2 Toward a “landslide buzzsaw”?

The final landslide patterns from our simulations show interesting similarity with the morphological changes associated with the glacial buzzsaw (Fig. 6). Previous studies have highlighted the impact of glacial erosion on mountain elevations and relief, referred as the “glacial buzzsaw” (Egholm et al., 2009; Herman et al., 2013, 2021; Mitchell and Montgomery, 2006; Thomson et al., 2010; Tomkin and Braun, 2002). This theoretical concept, based on the observed correlation between the position of the Equilibrium Line Altitude (ELA) and the mean and maximum height of mountains (Egholm et al., 2009), suggests that glaciers may have a strong control on mountain relief. In fact, by shaping cirques, glaciers create steep slopes at high elevations (Brozović et al., 1997), increasing erosion above the ELA. Although the “glacial buzzsaw” might be more complex in specific mountain ranges (Banerjee and Wani, 2018; Scherler, 2014), a concentration of surface area is usually observed around the ELA elevation (Egholm et al., 2009, 2017; Liebl et al., 2021; Pedersen et al., 2010; Prasicek et al., 2020; Steer et al., 2012).

For the three studied catchments, most of the landslide scars occur close to the catchment boundaries, i.e. along steep rock walls or along sharp ridge crests of the catchments and we observe a decrease in the maximum catchment elevation such as the glacial buzzsaw. However, we observe a concentration of hillslopes (around the angle of friction) over a larger elevation range (Fig. 7) around the shouldering than the glacial buzzsaw would be. Thus, by simulating the strong impact of landslides on slopes above the shouldering, we can question the role of hillslope erosion and similarly imagine a “landslides buzzsaw” during interglacial periods. Such a “landslide buzzsaw” would be more based on mechanisms presented in Mitchell and Montgomery (2006), with a perhaps more complex dependence on climate and lithology. However, by incorporating additional processes for glacial erosion, such as subglacial hydrology, the arguments underlying the glacial buzzsaw concept may also be debated regarding catchment topographic evolution (Herman et al., 2011) and become more complex. This concept of “landslide buzzsaw” may not be sustainable over long time periods since landslide activity will limit the occurrence of steep hillslopes. However, over Quaternary glacial cycles, successive glaciations and associated glacial/paraglacial erosion may sustain steep hillslopes at high elevations, further promoting the “landslide buzzsaw” during subsequent interglacial periods as proposed for instance for the European Alps (Delunel et al., 2020; Norton et al., 2010). This coupling between glacial and hillslope processes would be reinforced by the topographic impact of landsliding, affecting steep hillslopes at high elevations and producing lower slopes and lower-relief areas at or above the ELA (Fig. 6). This landscape conditioning would favor glacier development and erosion during the next glacial period, maintaining or enhancing the potential for glacial buzzsaw (Pedersen and Egholm, 2013).

6 Conclusions

The successive glacial-interglacial transitions during the Quaternary period have promoted landscape disequilibrium between the inherited topography and the dominant geomorphological processes. The HyLands model was used to study how post-glacial landslides shape alpine landscapes. We focused on landslide rates, locations, and the influence of interglacial processes on long-term landscape evolution.

We modeled the topographic evolution of three distinct catchments located in the Ecrins massif (French Alps, Fig.1), that we identified as glacial, intermediate glacial-fluvial and fluvial catchments based on their morphological characteristics (Fig. 2). For these three catchments, the highest and steepest slopes are the first topographic areas impacted by landslides (Fig. 6). Topographic changes are particularly pronounced in the glacial and intermediate catchments, where we observed a bimodal distribution of landslides corresponding to the bimodal distribution of steep slopes generated by glacial erosion. In this case, the high and steep slopes are most rapidly modified, inducing a decrease in slopes to values that are slightly greater than the internal angle of friction (Figs. 7, 8 and 9). This control of hillslope processes on the maximum mountain elevations and the topographic reshaping at particular elevations leads us to propose similarities between the `glacial buzzsaw' concept and postglacial landslide activity.

The results also highlight a high frequency of landslides during the first 20 kyr of our simulations (Figs. 9 and 10), which is associated with higher erosion rates. Landslide activity and magnitude, and the resulting erosion rates, at the beginning of each simulation follow the morphological gradient (from glacial to fluvial) observed in our three catchments (Fig. 11). Therefore, glacial topographic inheritance induces an intense period of post-glacial landslide activity, leading in turn possibly to regular `hot-moments` of landscape dynamics over the Quaternary.

Our study also concludes that hillslope processes, such as landslides, alone cannot drive the transient shift from glacial to fluvial morphology during interglacial periods. The magnitude of glacial erosion and the duration of glaciation may have been lower in downstream areas (i.e. in this study, within the fluvial catchment) may have led to a faster transition from glacial landscape to a fluvial one.

Finally, this study provides a basic model for understanding landslide dynamics and their impact on alpine landscape evolution. Additional components could be incorporated to enhance the model, such as fluvial processes, permafrost degradation or non-uniform rock properties to better capture the complex interactions occurring in mountain environments. In a future work, we intend to model the interactions between hillslope processes and glacial processes over multiple glacial-interglacial cycles to better estimate their relative contributions.