the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Identifying fracture-controlled resonance modes for structural health monitoring: insights from Hunter Canyon Arch (Utah, USA)
Guglielmo Grechi
Jeffrey R. Moore
Molly E. McCreary
Erin K. Jensen
Salvatore Martino
Progressive fracturing contributes to structural degradation of natural rock arches and other freestanding rock landforms. However, methods to detect structural changes arising from fracturing are limited, particularly at sites with difficult access and high cultural value, where non-invasive approaches are essential. This study aims to determine how fractures affect the dynamic properties of rock arches, focusing on resonance modes as indicators of structural health conditions. We hypothesize that damage resulting from fracture propagation may influence specific resonance modes that can be identified through ambient vibration modal analysis. We characterized the dynamic properties (i.e., resonance frequencies, damping ratios, and mode shapes) of Hunter Canyon Arch, Utah (USA), using spectral and cross-correlation analyses of data generated from an array of nodal geophones. Results revealed properties of nine resonance modes with frequencies between 1 and 12 Hz. Experimental data were then compared to numerical models with homogeneous and heterogeneous compositions, the latter implementing weak mechanical zones in areas of mapped fractures. All numerical solutions replicated the first two resonance modes of the arch, indicating these modes are insensitive to structural complexity derived from fractures. Meanwhile, heterogenous models with discrete fracture zones succeeded in matching the frequency and shape of one additional higher mode, indicating this mode is sensitive to the presence of fractures and thus most likely to respond to structural change from fracture propagation. An evolutionary crack damage model was then applied to simulate fracture propagation, confirming that only this higher mode is sensitive to structural damage resulting from fracture growth. While examination of fundamental modes is common practice in structural health monitoring studies, our results suggest that analysis of higher-order resonance modes can be more informative for characterizing fracture-driven structural damage.
- Article
(10692 KB) - Full-text XML
- BibTeX
- EndNote
Natural rock arches are rare and remarkable, culturally valued geologic landforms owing to their rarity, fragility, and beauty and to their significance to indigenous populations. Arches form and evolve over time in response to environmental and anthropogenic stresses whose weathering action can be aided by predisposing geological factors such as weak rock layers or rock mass fractures (Moore et al., 2020; Ostanin et al., 2017). Rock fractures nucleate and propagate in directions often reflecting principal stress orientations or following pre-existing discontinuities (Blair Jr., 1987; Bruthans et al., 2014; Cruikshank and Aydin, 1994; Řihošek et al., 2018). As fractures grow to critical lengths, material is shed through partial failures at the arch lintel and abutments, sometimes resulting in self-sculpture of ideal arch forms (i.e., the inverted catenary) but often contributing to reduced stability and ultimate collapse (Moore et al., 2020). Understanding how rock mass fractures impact the stability of rock arches and other natural landforms is crucial for developing effective monitoring strategies aimed at their preservation.
Ambient vibration modal analysis of geologic landforms can provide crucial data supporting site characterization, stability assessment, and vibration risk analysis (e.g., Bessette-Kirton et al., 2022; Finnegan et al., 2022; Kleinbrod et al., 2019; Mercerat et al., 2021). Dynamic structural properties, such as modal frequencies, damping ratios, and deformation patterns at resonance (i.e., mode shapes), are controlled by material properties and boundary conditions (Chopra, 2013; Doebling et al., 1996), meaning accurate in situ measurements provide data that can be used to create, calibrate, or refine structural models (Bottelin et al., 2017; Moore et al., 2018; Iannucci et al., 2020; Bessette-Kirton et al., 2022; Müller and Burjánek, 2023; Jensen and Moore, 2023). These dynamic properties can also be tracked over time for structural health monitoring (SHM) in order to detect and describe damage that may arise from natural and anthropogenic influences (Bottelin et al., 2013a, b; Burjánek et al., 2018; Colombero et al., 2021b; Geimer et al., 2022).
The small footprint and non-invasive nature of data generated using in situ ambient vibration approaches makes such methods particularly well suited for applications at culturally valued, fragile geological features (e.g., rock arches and towers) and protected heritage sites (e.g., historic structures), where non-destructive techniques are required (Ceravolo et al., 2016; Conati Barbaro et al., 2024; Dzubay et al., 2022; Finnegan et al., 2021; Häusler et al., 2021a; Pau and Vestroni, 2013). The dynamic properties of an arch evolve with fracture propagation: as fractures grow, the bulk material becomes softer (decreasing Young's modulus), and the landform may be increasingly separated from adjoining stable ground (increasing modal mass), resulting in resonance frequency decrease (Chopra, 2013; Clinton et al., 2006; Colombero et al., 2021b). In contrast, resonance frequencies may increase as material is shed during partial failure (decreasing modal mass). Such changes are anticipated to be detectable from ambient vibration modal analysis surveys, forming the basis for SHM techniques (Bottelin and Baillet, 2024; Çelebi, 2019; Doebling et al., 1996; Lévy et al., 2010). However, the nature of changes to mode shapes can be more challenging to predict and is likely to reflect complex, localized variations in structural properties created by fractures of varying length, aperture, and stiffness.
Previous studies have successfully used experimental ambient vibration modal analysis to calibrate numerical models, providing input on structural parameters such as material properties and boundary conditions (Bessette-Kirton et al., 2022; Grechi et al., 2024). However, past applications have mainly modeled rock masses as homogeneous, isotropic continuous media. This assumption can be appropriate at sandstone arches and tower sites with few fractures and uniform lithology (Finnegan et al., 2022; Geimer et al., 2020) but breaks down in cases of multiple lithologies or fractured rock masses, limiting the application of the approach. Moreover, in the hypothetical case of progressive landform failure, the influence of discrete internal and bounding fractures grows increasingly significant as rock mass fracturing progresses, meaning a transition from an isotropic continuum to a discontinuous rock mass may be anticipated as failure approaches (Taruselli et al., 2021). These cases of advanced failure with structurally relevant fractures are likely to be among the most critical for hazard analysis and mitigation (Zhang et al., 2020).
Here we present operational modal analysis and numerical eigenfrequency modeling for Hunter Canyon Arch, a unique natural arch located in southeastern Utah, which is deeply fractured at the interface of the lintel and cliff-side abutment. We hypothesized that these fractures influence the properties of certain resonance modes, and we evaluated results from operational and numerical modal analyses to test this hypothesis. Comparison between an isotropic continuous model and field data fails for higher-order modes (i.e., above mode 2), indicating that simple models do not replicate the observed fracture-controlled mechanical complexity of the arch. In contrast, numerical models implementing discrete weak mechanical regions in areas of mapped fractures matched key aspects of higher modes. Interestingly, all models were able to match the first two resonance modes, indicating that these are insensitive to structural complexity associated with fractures. Our results instead highlight how higher-order modes may be most sensitive to evolving fracture-controlled structural damage and that, once identified, these modes should be monitored over time to characterize structural changes caused by fracture propagation.
Hunter Canyon Arch (lat 38.5063, long −109.5928) is a large natural rock arch located 10 km southwest of Moab, Utah, composed of massive sandstone of the Jurassic Wingate Formation (Fig. 1a). The arch measures 35 m high and 4 m wide and spans 20 m at an azimuth of 30° N from the edge of a plateau. It is easily observed from the trail below, but access to the top requires a demanding overland hike. The lintel is deeply fractured where it abuts the adjoining cliff, with multiple intersecting discontinuities in this region (Fig. 1b, c) indicating potentially unstable conditions. The sharp and segmented geometry of the arch is inherited from the local geostructural setting and reflects comparably recent rockfall and partial collapse events sculpting the present-day form.

Figure 1(a) Aerial overview of Hunter Canyon Arch located near Moab, Utah (location inset). A pole density contour plot in equal angle projection showing the five fracture sets identified from our remote survey is shown in the lower-right inset. (b, c) Aerial views of Hunter Canyon Arch showing the main fracture traces (S0–S4) highlighted in different colors; camera locations for panels (b) and (c) are shown in panel (a). Dashed lines show fracture traces of S1 and S2 without exposed surfaces.
We performed a drone-based photogrammetry survey to construct a high-resolution point cloud of the study area from georeferenced images using the structure-from-motion software Agisoft Metashape (https://www.agisoft.com, last access: 16 January 2025). The resulting point cloud was processed and cleaned using CloudCompare (https://www.cloudcompare.org, last access: 16 January 2025) by applying a statistical outlier removal filter for general noise reduction. The output was then analyzed using the MATLAB toolbox Discontinuity Set Extractor 3.0 (Riquelme et al., 2014; Riquelme, 2015), which allows semi-automatic identification and classification of rock mass fractures through local statistical and cluster analyses. Five joint sets were recognized from this analysis (Fig. 1), including sub-horizontal bedding (S0) and four steeply dipping sets (dip direction/dip): S1 (187° N/82°), S2 (45° N/80°), S3 (124° N/83°), and S4 (082° N/85°). The geometry of the sub-vertical fractures creates a double-cusp shape in the area between the plateau and the arch (Fig. 1b), while two sub-vertical fractures and horizontal bedding partially isolate a rock volume on the cliff side of the abutment (S1 and S2; Fig. 1c). This fracture-bounded compartment is tilted toward the arch on the eastern side where its base is partially overhanging and the aperture of the back fracture (S2) is highest. Similarly, the fracture adjoining the lintel and abutment (S1) is characterized by greatest aperture on the eastern side (Fig. 1c).
3.1 Nodal array field experiment
We deployed nine Fairfield ZLand 5 Hz nodal geophones on 9 October 2022, recording three-component ambient vibration data during a 2 h survey period (Fig. 2a, b). We placed eight stations in an approximately linear array with 3 m spacing to cover the arch lintel and the most prominent part of the fractured abutment (stations H01–H07). An additional station (H08) was deployed on the arch abutment, but, due to the lack of suitable flat and debris-free bedrock, the geophone was positioned west of H07, interrupting the continuity of the linear array but still encompassing the fracture-bounded rock mass compartment closer to the arch. Station H09 was meanwhile positioned farther from the arch and abutment on the stable plateau to act as a local reference (Fig. 2a). All sensors were leveled, aligned to magnetic north (10° N magnetic declination), and adhered to bare bedrock surfaces using mounting putty to ensure good ground coupling. Continuous ambient vibrations were recorded at a sampling frequency of 250 Hz between 18:00 UTC (10:00 MST) and 20:00 UTC (12:00 MST). Winds were calm during the experiment, minimizing environmental disturbance and thus improving the signal-to-noise ratio of the vibration data. Other environmental factors, such as air temperature and relative humidity, varied little during the short duration of the experiment.

Figure 2(a) Aerial view of Hunter Canyon Arch showing array stations (colored circles) and the reference station (gray triangle), as well as the fracture traces at the arch lintel and abutment (dotted red lines). The lower-left inset shows an orthophoto of the array and fracture traces. (b) Nodal geophones deployed on the arch (H01 is not visible) and the near-fractured abutment. (c) Velocity power spectral densities for all components (i.e., transverse, radial, and vertical) and array stations. Decibel powers are relative to 1 m2 s−2 Hz−1. (d) Median and median absolute deviation values of the degree of polarization, β2 (circles), and the modal damping ratio, ζ (squares), for each of the nine identified resonance modes of Hunter Canyon Arch.
3.2 Spectral and array cross-correlation analyses
Ambient vibration data were analyzed for spectral content to identify resonance modes of Hunter Canyon Arch. The dataset was first examined to extract the longest undisturbed (e.g., due to wind, earthquakes, or anthropogenic noise) continuous time block for processing. This led us to reject the last 10 min of the recording. To process each array station and channel, we first removed the mean, linear trend, and applied instrument response correction via spectral division, finally band-passing data between 0.1 and 50 Hz. Horizontal channels were rotated to longitudinal (i.e., radial) and transverse (i.e., arch perpendicular) directions to align with the arch orientation (azimuth 30° N). Power spectral density (PSD) estimates of velocity were then computed following the approach of McNamara and Buland (2004). We used Welch's method (Welch, 1967) with stacked fast Fourier transforms of 60 s Hanning-tapered windows with 75 % overlap to reduce variance and smoothed over 0.1 Hz windows. We analyzed the resulting power spectra to manually identify spectral peaks that were hypothesized to represent resonance modes of the arch (Fig. 2c).
To further characterize the identified spectral peaks, we performed frequency-dependent polarization analysis (Koper and Hawley, 2010). Polarization attributes (i.e., azimuth, incidence angle, and degree of polarization) of each spectral peak were identified and extracted, focusing on the degree of polarization (β2) characterizing the extent to which particle motion is organized at the resonance frequencies. We additionally estimated the damping ratio (ζ) of identified resonance modes using the random decrement technique (RDT) (Ibrahim, 1977), which fits an exponentially decaying sinusoid to the band-passed waveform approximating the free response of the system at each resonance frequency (Geimer et al., 2022). To characterize modal deformation patterns (i.e., mode shapes) associated with the identified resonance frequencies, we performed cross-correlation analysis using eight of the deployed array stations, omitting the reference station (H09). Mode shapes are essential parameters in SHM studies as they represent specific deformation patterns at each resonance frequency, hence describing the relative displacement and phase relationships across different regions of the structure (Brincker and Ventura, 2015).
Cross-correlation modal analysis, also referred to as the natural excitation technique (NExT) (Farrar and James III, 1997), is a time-domain, output-only method used to estimate modal properties of vibrating structures by analyzing the cross-correlation functions between output response measurements under ambient excitation. We selected this analytical method over the frequency domain decomposition (FDD) and stochastic subspace identification (SSI) techniques (Brincker et al., 2001; Van Overschee and De Moor, 1996) on the basis of computational efficiency. The robustness of cross-correlation modal analysis, as compared to FDD and SSI, has previously been demonstrated in comparative studies (Bessette-Kirton et al., 2022; Häusler et al., 2021a), establishing it as a reliable approach for accurate modal property estimation of natural structures under ambient excitation. Array data were downsampled to 100 Hz and segmented into 5 min tapered windows, and spectral whitening was applied prior to the cross-correlation of each station pair (Bessette-Kirton et al., 2022; Lin et al., 2013). Maximum window amplitudes were used for time-domain normalization (Bensen et al., 2007) before stacking each station pair to obtain cross-correlograms for the transverse–transverse (TT), radial–radial (RR), and vertical–vertical (ZZ) components. All cross-correlograms were then filtered to 0.1 Hz bandwidth windows between 0.5 and 15 Hz, extracting the zero-time lag amplitude for each station pair while omitting autocorrelation values. The resulting curve for each station enables the visualization of mode shapes along the linear array, describing the amplitude and phase of relative modal displacements at each recording station (Fig. 3a). The curves were then normalized by the maximum root-mean-square (RMS) amplitude and averaged to obtain a mean mode shape curve with standard deviation. Finally, for each resonance frequency identified from spectral analysis, we finally extracted the average relative modal displacement for all components (i.e., TT, RR, and ZZ) at all stations to plot 3D modal vectors on the Hunter Canyon Arch surface model (Fig. 3b) (Grechi et al., 2024).
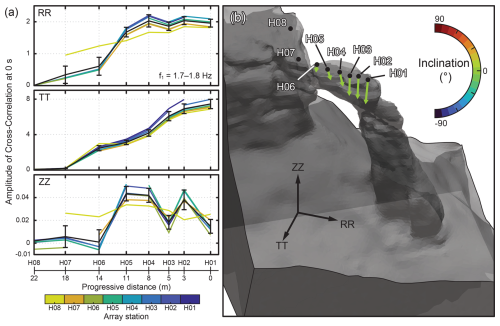
Figure 3(a) Array cross-correlation results for the radial (RR), transverse (TT), and vertical (ZZ) components for the first resonance mode of Hunter Canyon Arch (f1). Colored lines are the RMS-normalized amplitude at each station relative to other array stations. Bold black lines are the mean and standard deviation of the zero-lag cross-correlation amplitudes at every station. (b) 3D mode shape representation for f1. To improve the overall visualization of mode shapes, vectors are color-coded according to their inclination angle, where 0° indicates horizontal inclination.
3.3 Numerical modal analysis
We performed 3D finite-element eigenfrequency modal analysis (i.e., in the frequency domain and with no input excitation) to support the structural characterization of Hunter Canyon Arch. The aim was to replicate the dynamic behavior of the arch by matching field data (i.e., resonance frequencies and mode shapes), thus constraining structural and material properties of the fractured rock lintel and adjoining cliff (Geimer et al., 2020). To accurately recreate the arch geometry, we used the high-resolution 3D surface model from our photogrammetric survey. General model improvements were performed in Meshmixer (https://www.meshmixer.com, last access: 16 January 2025): smoothing surface irregularities, filling holes from limited image coverage, and transforming the surface mesh into a solid 3D object that we imported in the finite-element analysis software COMSOL Multiphysics (https://www.comsol.com, last access: 16 January 2025). Based on field surveying and results of spectral analysis, we cropped the final model to preserve the geophone array on the cliff-side abutment area where two major fractures exist (i.e., S1 and S2; Fig. 2a), removing distal areas not participating in modal deformation (e.g., reference station location H09) (Finnegan et al., 2022). Due to the lack of a detailed geological description of fracture geometry, persistence, and aperture and to the presence and locations of rock bridges at depth, we adopted different numerical representations to simulate the arch dynamics.
In a first modeling attempt, we simulated the arch and adjacent cliff as isotropic, continuous, and homogeneous. We assigned material properties representative of Wingate Sandstone derived from previous studies (Moore et al., 2018): density (ρ) and Poisson's ratio (ν) were set as 2200 kg m−3 and 0.25, respectively, while Young's modulus (E) was allowed to iteratively vary to match the first two measured resonance frequencies. All model outer boundaries were fixed at zero displacement to simulate the natural constraints of the surrounding rock mass. While continuum-modeling approaches have been successful in several past studies (Geimer et al., 2020), the assumption breaks down when structural complexities such as macroscopic fractures are involved (Burjánek et al., 2019; Moore et al., 2018). Subsequently, based on field observations of Hunter Canyon Arch, we implemented a heterogeneous numerical model through the simulation of the two fracture regions cutting the arch lintel and abutment (i.e., S1 and S2 in Figs. 1c and 2a). Starting from the continuous model, the two fracture regions were simulated as discrete domains of reduced isotropic elastic modulus (Er) (Burjánek et al., 2019; Grechi et al., 2024). We relied on our preliminary geologic model of the site, specifically on direct and remote surveys of fracture aperture and persistence, to generate these compliant mechanical zones. While S1 was modeled as a 1 m wide zone cutting entirely through the lintel, S2 was generated as a 2 m wide zone intersecting the rock mass for 8 m from the eastern side of the cliff and propagating to 8 m depth (Fig. 5a). Both reduced stiffness domains were implemented via model partitioning using block elements with the same orientation as the real fractures. For material properties, we assumed ρ and ν were invariant from the homogeneous case and followed the previously described iteration for calibrating Er of both fracture zones to best-match field data. Model calibration was obtained for Er values of 0.7 and 0.1 GPa for S1 and S2, respectively. To further explore structural complexity of the site and test different solutions for modeling fractures, we implemented two additional numerical models discretizing fractured regions with the same extent of the reduced stiffness domains. In the first, fractures were modeled as open zones, represented as open discontinuities with constant aperture and no material properties assigned. The best fit between numerical and field data was achieved for a constant fracture aperture value of 0.1 m. For the second case, we implemented two thin elastic layers with isotropic surface stiffness (KA) of 5 × 108 N m−3 to match measured resonance modes (Bottelin et al., 2017; Kulatilake et al., 2016). For all models, we extracted relative modal displacements in the transverse, radial, and vertical directions for the first four modeled resonance modes at points representative of array stations. Modeled mode shapes were then compared with experimental array cross-correlation results by analyzing the distribution of normalized vector magnitudes and angles (θ) between experimental and numerical vectors in 3D space. We calculated the angular difference between 3D experimental and numerical modal vectors as follows (Eq. 1):
where u and v are the vectors being compared, ∥u∥ and ∥v∥ are their magnitudes, and |uTv| is their dot product.
Spectral analysis revealed nine consistent peaks between 1.8 and 11.5 Hz across the nodal geophone array. The absence of these spectral peaks at the reference station indicates they can be interpreted as resonance modes of Hunter Canyon Arch (Fig. 2c). The first and most prominent peak occurs at 1.8 Hz (f1), with spectral amplitudes highest on the transverse component of arch stations (H01–H06) progressively decreasing toward the abutment (H07). The decrease in spectral power suggests the fundamental mode of the arch is out-of-plane bending. The second mode (f2= 4.2 Hz) shows similar features with spectral powers mostly concentrated on the transverse component of array stations and a marked decrease in spectral amplitude at station H07. Modal damping ratios were estimated at 0.6 % and 1.1 % for the first two modes, respectively, in agreement with results at other sandstone arch and tower sites in Utah (Häusler et al., 2021a; Moore et al., 2019). No evidence of these first two modes is found further on the cliff abutment at station H08, strengthening their interpretation as fundamental resonance modes of the arch. Multiple higher-order peaks are visible across the arch lintel and abutment stations (H01–H07) (i.e., 5.1, 5.3, 7.5, 8.5, 9.1, 10.1, 11.5 Hz). Two higher-order spectral peaks are visible at station H08 (i.e., f4= 5.3 and f5= 7.5 Hz). Damping ratios were also estimated for these higher-order modes, indicating an increasing trend with mode order (Fig. 2c). Only mode 3 exhibits an unexpectedly high damping ratio of 3.8 %, which is 2 to 3 times greater than adjacent modes (i.e., modes 2 and 4 have damping ratios of 1.1 % and 1.5 %, respectively). We computed the median β2 and median absolute deviation values at each resonance mode for all array stations. The analysis highlighted median β2 values in the range 0.7–1, indicating highly polarized motion indicative of organized modal deflection (Fig. 2c).
Results of cross-correlation analysis allowed us to describe mode shapes associated with resonance frequencies of the arch identified from spectral analysis (Fig. 4). The first two modes represent first- and second-order transverse bending and feature no involvement of the abutment station H08 (Fig. 4a and b). Higher-order modes are characterized by more complex modal deflection patterns, except for mode 6, which represents a first-order bending mode in the vertical direction (Fig. 4f). Mode shape complexity arises starting at modes 3 and 4, where modal vectors show greater variability between arch stations and involvement of the abutment and fracture zone, as can be observed by the higher amplitude of modal displacements at station H07 (Fig. 4c and d). Starting from these two modes and higher, strong similarity between stations H06 and H07 (i.e., the two stations at the transition from arch to abutment) can be observed both in modal vector orientation and magnitude. At mode 5, for example, a second-order horizontal bending mode with the node point at the middle of the arch, stations H07 and H08 show in-phase modal vectors characterized by comparable magnitude and orientation with stations located on the arch (Fig. 4e). Mode shapes for the last three identified resonance modes are characterized by a complex distribution of modal vectors, mostly concentrated in the radial and vertical directions but also involving the arch abutment.

Figure 4(a–i) 3D representation of the nine resonance modes of Hunter Canyon Arch via cross-correlation analysis. Arch models in panels (f) and (g) are rotated relative to other panels to improve the visualization of prevalent vertical in-plane deformation patterns. Modal vectors are normalized to the maximum array amplitude. To improve the overall visualization of mode shapes in a 2D view, vectors are colored according to their inclination angle, where 0° indicates horizontal inclination.
To improve our understanding of fracture control on arch dynamics, we compared results from continuous and heterogenous numerical models with field data. The heterogeneous model of Hunter Canyon Arch implemented using two reduced stiffness domains is shown in Figure 5a. For both numerical solutions we obtained several higher-order and complex resonance modes that showed poor correspondence with cross-correlation results. For this reason, we selected to analyze only those modes characterized by the highest relative modal mass (RMM) values (Fig. 5b). This direction-dependent parameter is frequently employed in engineering studies, as it measures the extent of mass participation at each resonance mode, allowing the assessment of the significance of specific eigenmodes in describing the dynamic behavior of a structure (Aenlle et al., 2021). For the continuous case, we were able to achieve a good match to the first two measured resonance modes in both frequency and mode shapes implementing an isotropic Young's modulus of 2.3 GPa, which is comparable to past results at sandstone arches and towers within the Wingate Formation (Geimer et al., 2020; Moore et al., 2019). However, modeled higher-order modes failed to reproduce field measurements in terms of frequency and mode shapes. The only exception is represented by the similarity between modeled mode 4 and measured mode 6 (i.e., first-order vertical bending mode). In this case, although the modeled mode order is not the same as field data and no evidence of third and fourth measured modes was found, the continuous model predicts a first-order vertical bending mode at 6.8 Hz (i.e., 20 % lower than the measured frequency). Therefore, due to the observed similarities in modal properties, we compared modeled mode 4 with measured mode 6 to further assess consistency in the vertical bending response predicted by numerical models. The same three eigenmodes of Hunter Canyon Arch are well resolved by the heterogeneous model implemented with fracture zones S1 and S2 (Fig. 5c). The presence of reduced stiffness domains simulating the compliant fractures within the model does not strongly affect either the frequency or the shape of the first two resonance modes of the arch. However, differences arise for the third modeled mode, where the inclusion of fractures yields a good match in frequency and mode shape to the third measured mode. The improved performance of the heterogeneous model in replicating the third resonance mode is also indicated by the distribution of normalized modal displacement vector amplitudes and angular differences between numerical and experimental vector orientations (Fig. 6). Among the analyzed modes, we found that mode 3 highlights the better match of all heterogenous models when implementing discrete weak layers in areas of mapped open fractures (i.e., reduced stiffness domains, open zones, and thin elastic layers), with average angular differences in the range 8–30°. Conversely, the continuous numerical model failed to resolve this resonance mode, as pointed out by differences in modal vector orientations up to 60° (Fig. 6).
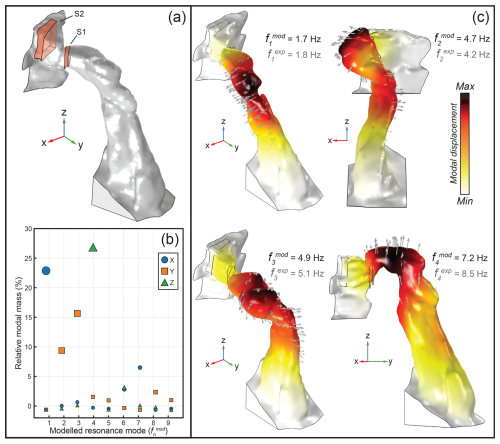
Figure 5(a) 3D finite-element model of Hunter Canyon Arch with details of S1 and S2 implemented as discrete volumes of reduced elastic modulus (red zones). (b) Relative modal masses in X, Y, and Z derived for all modeled resonance modes using the heterogeneous model. (c) Numerical modeling results (modes 1–4) for the reduced stiffness heterogeneous model. Modeled mode shapes and frequencies are shown for each mode (), while corresponding measured resonance frequencies are given in gray (). Model deformation, colormaps, and arrows show zero-phase displacement normalized relative to each mode. Modeled mode 4 ( 7.2 Hz) is compared to measured mode 6 ( = 8.5 Hz), as numerical analysis failed to replicate measured modes 4 and 5.
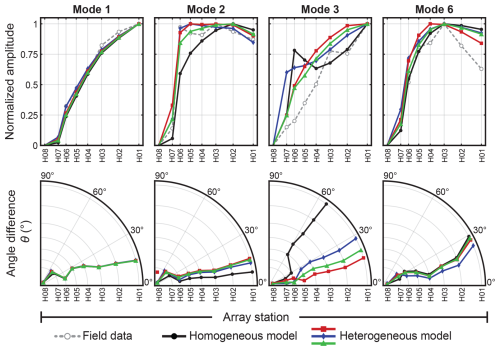
Figure 6Comparison between field data (e.g., Fig. 4) and numerical modeling representations of Hunter Canyon Arch. For each resonance mode, the normalized modal displacement amplitude (upper row) and angular difference (θ) between modeled and measured 3D modal vectors are shown for all array stations (lower row). Three different approaches were tested for simulating rock mass structural–mechanical heterogeneity: reduced stiffness domains (red squares), thin elastic layers (green triangles), and open fractures (blue diamonds).
To further investigate the contribution of fractures and the control they exert on the dynamic response of natural rock landforms, we created an evolutionary crack propagation model for Hunter Canyon Arch (Fig. 7). Starting from a hypothetical continuous isotropic stage (T0), for which no fractures were implemented, we simulated structural damage as a sequence of discrete stages with increasing crack depths (T1–T5) following a top-down propagation pattern to reach the actual site conditions (T6). This crack evolution pattern was implemented based on field observations. However, this assumption is likely also valid at sites characterized by similar geometrical, boundary, and fracture conditions where, for example, bounding or abutment fractures often exhibit similar propagation characteristics because of local tensile stress concentrations (Moore et al., 2020). For each modeled damage stage, we derived resonance frequencies and mode shapes to evaluate potential changes in the dynamic behavior of the arch due to increased crack propagation. Results show that mode 3 is characterized by a greater sensitivity to fracture propagation than the other modes. In fact, while modes 1, 2, and 4 undergo small shifts in their resonance frequency values (±2 %) with increasing crack depth, mode 3 features a decreasing trend up to −12 % at stage T6 (Fig. 7b). Meanwhile, the progressive deepening of S1 and S2 creates a marked shift in relative modal displacements of mode 3, with the shape at stage T6 closely matching our experimental results (Fig. 7c–f). On the other hand, other modeled resonance modes undergo smaller changes in deformation patterns, with numerical results that are comparable to field data for almost every damage stage, indicating their relative insensitivity to fracture depth.
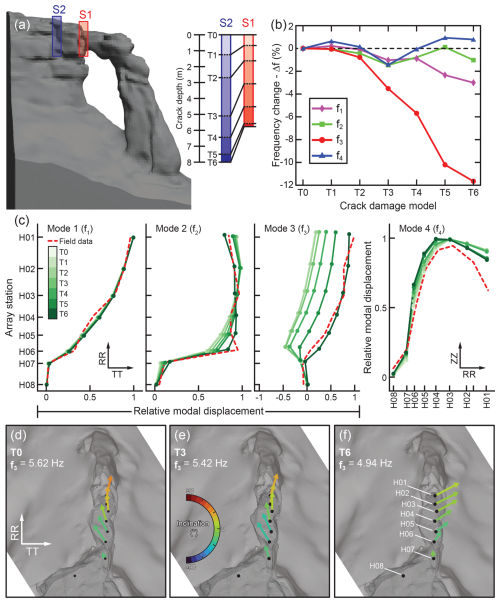
Figure 7Evolutionary crack damage model describing the effect of increasing crack depth on resonance modes of Hunter Canyon Arch. (a) 3D model of the arch with the locations of the two modeled fractures (S1 and S2). The inset sketch describes the seven modeled crack depth stages (T0–T6): T0 features no fractures (homogeneous case), while T6 reflects actual site conditions. (b) Modeled resonance frequency change for f1 to f4 as a function of increasing crack depth. (c) Progressive change in 2D resonance mode shape for the four modeled modes at different crack propagation stages. Experimental mode shapes are also provided (dashed red lines) to compare field and numerical modeling results. (d–e) 3D modeled mode shapes for at stages T0, T3, and T6; mode shapes are not shown for , , and , as they do not vary with crack propagation.
Ambient vibration array data generated at Hunter Canyon Arch enabled identification and characterization of nine resonance modes of the natural sandstone arch. This is the largest number of modes measured until now at a natural arch site (Geimer et al., 2020), demonstrating the value of array-based field data. We observed almost no involvement of the abutment stations H07 and H08 in modal deflection patterns of the first two resonance modes of the arch. However, starting at mode 3, we find greater correspondence between stations H06 (i.e., the last station on the arch) and H07, with modal vectors having comparable magnitudes and orientations. Hence, experimental data show how the modal deformation field related to higher-order resonance modes propagates to the cliffside across fracture S1 (i.e., the discontinuity dissecting the abutment), indicating these areas are elastically connected.
Similar evidence can be derived from the analysis of damping ratios. The first two resonance modes show low damping (≤ 1 %) in good agreement with results obtained at other sandstone arch sites (Geimer et al., 2020; Häusler et al., 2021a; Moore et al., 2019). These low damping values indicate that seismic energy is trapped within the structure and is unable to propagate to the surrounding rock mass due to the minimal contact area of the abutment and base surfaces compared to the overall modal mass of the arch (Häusler et al., 2021b). Starting from mode 3, higher-order resonance modes exhibit an increasing trend in damping ratios (Fig. 2c). This result is not unexpected, since complex deformation patterns, generally characterized by a greater number of node points, can aid in energy dissipation through relative motion and material-dependent internal friction mechanisms. However, mode 3 itself shows a marked increase in damping (up to 3.8 %), indicating some additional frequency-dependent seismic energy dissipation mechanism. We hypothesize this change could arise from the increasing participation of the abutment fracture area, and the corresponding fracture shear and normal compliance, in the modal deflection of the arch. In structural engineering, it is well documented that frictional interfaces, such as joints and connections, contribute to energy dissipation due to micro-slip and frictional losses under dynamic loading (Cimellaro, 2023; Lazan, 1968). This phenomenon, often referred to as interface or slip damping, is critical in dynamic analysis and structural design. In engineering geology, the role of fractures in modifying energy dissipation mechanisms is less extensively studied, and there is a higher degree of uncertainty due to the complex nature of rock fractures (i.e., geometry, properties, contact areas). Despite this, it is reasonable that frictional interactions at fracture interfaces and surface roughness can contribute to increased energy dissipation within rock masses (Bandis et al., 1983; Goodman, 1980; Habaraduwa Peellage et al., 2024).
The increase in energy dissipation at the fracture scale is also indirectly supported by our numerical modeling results. Although all models (i.e., continuous and heterogeneous) were able to resolve the first two (as well as the sixth) resonance modes of the arch, suggesting their mode shapes are independent of the contribution driven by discrete compliant zones, only the heterogeneous models could match the frequency and shape of mode 3. Changes in internal mechanical and boundary conditions (i.e., the introduction of fractures) did not affect mode shapes or frequencies for the first two resonance modes, demonstrating the insensitivity of these low-order modes to the modeled fractures. It is worth pointing out that the numerical representation of fractures is a complex approximation, as it involves many inherent simplifications and assumptions, especially in their geometrical discretization and mechanical characterization (Burjánek et al., 2019; Colombero et al., 2018). For this reason, after accurate reconstruction of the arch geometry, we adopted different numerical solutions for implementing fractures with the aim of testing the hypothesis of a fracture-controlled influence on the modal behavior of the arch. Our results suggest that, regardless of the adopted approach and parametrization (i.e., reduced stiffness domains, thin elastic layers, open fractures), the introduction of discrete compliant domains provides a better fit to experimental data than the continuous model for the third resonance mode of the arch. It is worth underlining that real fractures are characterized by more complex and heterogeneous structural–mechanical features than what was numerically recreated in this study, as they can include rock bridges, voids, and material infillings, while their aperture may vary strongly with depth (Colombero et al., 2017). Nonetheless, the results we obtained improved our engineering geological model of the site by providing evidence for the role of fractures in affecting the modal behavior of the arch.
Our evolutionary crack damage modeling indicated that the third resonance mode of the arch was particularly sensitive to simulated crack propagation at the arch abutment, undergoing substantial changes in frequency (−12 %) and mode shape (Fig. 7). Other modes exhibited less change (frequency shifts around ±2 %), and the first two modes especially were comparably insensitive to simulated crack propagation. These findings highlight the sensitivity of higher-order resonance modes to localized rock mass damage and additionally suggest that fundamental resonance modes might not always be the most informative proxies for detecting and monitoring the evolution of structural damage in natural rock landforms. Based on the results obtained at this site, we hypothesize that, when a finite number of discrete fractures actively constrain the mechanical and dynamic behavior of the landform, structural damage driven by the progressive growth of these fractures could be undetectable by fundamental resonance-mode monitoring. Instead, where well-developed dense fracture networks exist and the role played by individual fractures becomes less relevant, substantial changes in bulk properties may arise, causing variation in the structure's full dynamic response across many modes (Grechi et al., 2024).
The combination of our experimental and numerical modeling results indicates that higher-order resonance modes may be more sensitive to localized structural damage. This outcome is particularly relevant in relation to monitoring and conservation of damaged structures, as in structural health monitoring applications the first resonance modes are often considered the most informative to detect and track damage (Azzara et al., 2020; Clinton et al., 2006; Colombero et al., 2018, 2021a; Häusler et al., 2021b). However, since well-developed discontinuities serve as preferential pathways guiding damage and rock mass failure evolution, the consideration of fracture-sensitive, higher-order resonance modes could be valuable for identifying and monitoring progressive degradation of natural rock landforms at early stages. In particular, the evolution of fractures due to progressive failure could be assessed by discerning irreversible changes in modal properties of fracture-sensitive resonance modes (Alaei et al., 2023). It is worth noting that, although higher-order modes can provide valuable insights for the detection and monitoring of structural damage, their identification and characterization can pose challenges due to generally lower energy levels and more complex shapes compared to fundamental modes (Häusler et al., 2021a).
Our results also indicate the importance of array-based field data in providing a more robust analytical framework compared to single-station measurements for the investigation of sites characterized by complex structural and boundary conditions. Single-station ambient vibration data have been successfully used in the past in combination with 3D finite-element analysis to characterize the dynamic behavior of freestanding rock structures (Finnegan et al., 2022; Geimer et al., 2020; Moore et al., 2019; Starr et al., 2015). These in situ measurements have proved suitable for identifying and monitoring modal parameters, which can be used to calibrate numerical models by matching experimental and modeled results to derive rock-mass-scale material properties and describe modal strain fields (Bessette-Kirton et al., 2022; Moore et al., 2018). However, this approach can fail when dealing with complex settings where rock mass fractures can act as primary factors of structural heterogeneity (Grechi et al., 2024). Instead, the deployment of dense sensor arrays yields more comprehensive spatial coverage, which is crucial for identifying and characterizing resonance modes and relative modal shapes, particularly in discriminating higher-order modes or changes in modal shapes due to structural heterogeneities. Therefore, array data are valuable at sites with a high degree of structural complexity to provide an accurate description of modal behavior, including the influence of fractures, where initial array measurements can highlight fracture-controlled modes and repeated surveys can reveal structural changes associated with damage evolution.
This study investigated how fractures influence the dynamic behavior of a natural rock arch, with the hypothesis that specific resonance modes would be more affected by fractures and fracture propagation due to localized compliance effects. Ambient vibration array data from Hunter Canyon Arch, Utah, allowed us to characterize the properties of nine resonance modes, including modal frequencies, damping ratios, and mode shapes. Results of operational modal analysis supported our hypothesis, showing that fractures at the arch abutment affect the third resonance mode of the arch, as evidenced by significant changes in damping and mode shape. Numerical modeling further corroborated these findings, demonstrating that only models incorporating fractures could replicate the observed dynamic behavior of the arch and specifically mode 3 and that this mode was most sensitive to simulated fracture propagation exhibiting substantial changes in frequency and mode shape. Results of spectral and cross-correlation analyses showed no involvement of abutment or cliff sectors at the first two resonance modes. While the first two resonance modes exhibit low damping ratios, in agreement with results from other sandstone arch sites, we observed a strong increase in damping at mode 3 that we interpret as resulting from added energy dissipation mechanisms associated with fracture compliance. We tested various numerical modeling approximations of the site, including a homogenous model (i.e., without fractures) and heterogeneous models featuring different fracture configurations and an evolutionary crack propagation simulation. Results show that the first two modeled modes are insensitive to the simulated fractures. Heterogeneous models were able to better match field data for the third mode but could not match all, indicating remaining limitations of our models in capturing the complexities of spatially varying fracture geometry and compliance.
Despite the complexities in representing real fractures numerically, our results underscore the primary role of fractures in modifying the dynamic behavior of this natural arch at a specific resonance mode. In this sense, the significance of fracture-sensitive resonance modes in structural health monitoring is noteworthy because, while traditional approaches often prioritize the first or fundamental resonance modes, our study suggests that investigating higher-order modes may be crucial for identifying and monitoring the evolution of structural damage of natural rock landforms, especially where macroscopic compliant fractures are involved. These findings additionally emphasize the importance of generating in situ ambient vibration array data, particularly at sites with substantial structural complexity. The approach we present here, integrating array-based experimental modal analysis and numerical eigenfrequency modeling, not only enhanced our understanding of the dynamic behavior and structural conditions of the arch but also provided useful insights that can contribute broadly to refined structural health monitoring practices. The integration of experimental measurements and numerical modeling is essential for comprehensive assessment of the dynamic behavior of natural rock landforms, particularly those featuring complex fracture networks, paving the way for improved conservation strategies and risk management at natural heritage sites. Furthermore, calibrated numerical models (i.e., constrained by high-resolution structural characterization and site-specific geophysical investigations) are, in turn, crucial for scenario analyses where the role of preparatory processes and triggering actions can be weighed and used to guide preservation solutions.
The 3D photogrammetric model generated in this study is available for download at https://skfb.ly/oILIM (Moore and Grechi, 2025). Seismic data are available at https://doi.org/10.7914/SN/5P_2013 (Moore, 2013).
Conceptualization: GG, JRM, and SM. Data curation: GG, JRM, and EKJ. Formal analysis: GG. Funding acquisition: JRM. Investigation: GG, JRM, and MEM. Methodology: GG and JRM. Project administration: GG and JRM. Software: GG, JRM, and EKJ. Supervision: JRM. Validation: GG and JRM. Visualization: GG and JRM. Writing (original draft): GG and JRM. Writing (review and editing): GG, JRM, MEM, EKJ, and SM.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The authors thank Fan-Chi Lin and Elizabeth Berg for code used to conduct cross-correlation analyses and the University of Utah Center for High Performance Computing for computational resources. The authors are grateful to Adam Smith, Theresa Czech, and Madeleine Festin for their help with field activities.
This research has been supported by the National Science Foundation (grant no. CMMI-2150896).
This paper was edited by Wolfgang Schwanghart and reviewed by two anonymous referees.
Aenlle, M., Juul, M., and Brincker, R.: Corrigendum to “Modal Mass and Length of Mode Shapes in Structural Dynamics”, Shock Vib., 2021, 9821852, https://doi.org/10.1155/2021/9821852, 2021.
Alaei, A., Hejazi, M., Vintzileou, E., Miltiadou-Fezans, A., and Skłodowski, M.: Effect of damage and repair on the dynamic properties of Persian brick masonry arches, The European Physical Journal Plus, 138, 231, https://doi.org/10.1140/epjp/s13360-023-03781-0, 2023.
Azzara, R. M., Girardi, M., Iafolla, V., Padovani, C., and Pellegrini, D.: Long-Term Dynamic Monitoring of Medieval Masonry Towers, Frontiers in Built Environment, 6, 9, https://doi.org/10.3389/fbuil.2020.00009, 2020.
Bandis, S. C., Lumsden, A. C., and Barton, N. R.: Fundamentals of rock joint deformation, Int. J. Rock Mech. Min., 20, 249–268, https://doi.org/10.1016/0148-9062(83)90595-8, 1983.
Bensen, G. D., Ritzwoller, M. H., Barmin, M. P., Levshin, A. L., Lin, F., Moschetti, M. P., Shapiro, N. M., and Yang, Y.: Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements, Geophys. J. Int., 169, 1239–1260, https://doi.org/10.1111/j.1365-246X.2007.03374.x, 2007.
Bessette-Kirton, E. K., Moore, J. R., Geimer, P. R., Finnegan, R., Häusler, M., and Dzubay, A.: Structural Characterization of a Toppling Rock Slab From Array-Based Ambient Vibration Measurements and Numerical Modal Analysis, J. Geophys. Res.-Earth, 127, e2022JF006679, https://doi.org/10.1029/2022JF006679, 2022.
Blair Jr., R. W.: Development of natural sandstone arches in south-eastern Utah, International geomorphology 1986, Proc. 1st Conference, Manchester, UK, 15–21 September 1985, Vol. 2, 597–604, 1987.
Bottelin, P. and Baillet, L.: Original Insights Into Rock Slope Damage Processes Until Collapse From Passive Seismic Monitoring, Geophys. Res. Lett., 51, e2024GL109139, https://doi.org/10.1029/2024GL109139, 2024.
Bottelin, P., Lévy, C., Baillet, L., Jongmans, D., and Guéguen, P.: Modal and thermal analysis of les arches unstable rock column (vercors massif, french alps), Geophys. J. Int., 194, 849–858, https://doi.org/10.1093/gji/ggt046, 2013a.
Bottelin, P., Jongmans, D., Baillet, L., Lebourg, T., Hantz, D., Levy, C., Le Roux, O., Cadet, H., Lorier, L., Rouiller, J.-D., Turpin, J., and Darras, L.: Spectral Analysis of Prone-to-fall Rock Compartments using Ambient Vibrations, J. Environ. Eng. Geoph., 18, 205–217, https://doi.org/10.2113/JEEG18.4.205, 2013b.
Bottelin, P., Baillet, L., Larose, E., Jongmans, D., Hantz, D., Brenguier, O., Cadet, H., and Helmstetter, A.: Monitoring rock reinforcement works with ambient vibrations: La Bourne case study (Vercors, France), Eng. Geol., 226, 136–145, https://doi.org/10.1016/j.enggeo.2017.06.002, 2017.
Brincker, R. and Ventura, C.: Introduction to operational modal analysis, John Wiley and Sons, Inc, Chichester, West Sussex, 1, https://doi.org/10.1002/9781118535141, 2015.
Brincker, R., Zhang, L., and Andersen, P.: Modal identification of output-only systems using frequency domain decomposition, Smart Mater. Struct., 10, 441–445, https://doi.org/10.1088/0964-1726/10/3/303, 2001.
Bruthans, J., Soukup, J., Vaculikova, J., Filippi, M., Schweigstillova, J., Mayo, A. L., Masin, D., Kletetschka, G., and Rihosek, J.: Sandstone landforms shaped by negative feedback between stress and erosion, Nat. Geosci., 7, 597–601, https://doi.org/10.1038/ngeo2209, 2014.
Burjánek, J., Gischig, V., Moore, J. R., and Fäh, D.: Ambient vibration characterization and monitoring of a rock slope close to collapse, Geophys. J. Int., 212, 297–310, https://doi.org/10.1093/gji/ggx424, 2018.
Burjánek, J., Kleinbrod, U., and Fäh, D.: Modeling the Seismic Response of Unstable Rock Mass With Deep Compliant Fractures, J. Geophys. Res.-Sol. Ea., 124, 13039–13059, https://doi.org/10.1029/2019JB018607, 2019.
Çelebi, M.: S2HM of Buildings in USA, Seismic Structural Health Monitoring: From Theory to Successful Applications, Springer, Cham., 3–30, https://doi.org/10.1007/978-3-030-13976-6_1, 2019.
Ceravolo, R., Pistone, G., Fragonara, L. Z., Massetto, S., and Abbiati, G.: Vibration-Based Monitoring and Diagnosis of Cultural Heritage: A Methodological Discussion in Three Examples, Int. J. Archit. Herit., 10, 375–395, https://doi.org/10.1080/15583058.2013.850554, 2016.
Chopra, A. K.: Dynamics of structures: international edition, Pearson Education Limited, ISBN 0-273-77426-3, 2013.
Cimellaro, G. P. (Ed.): Seismic isolation, energy dissipation and active vibration control of structures, Vol. 2, Corrected publication, Springer, Cham, 492 pp., ISBN 978-3031211867, 2023.
Clinton, J. F., Bradford, S. C., Heaton, T. H., and Favela, J.: The observed wander of the natural frequencies in a structure, B. Seismol. Soc. Am., 96, 237–257, https://doi.org/10.1785/0120050052, 2006.
Colombero, C., Baillet, L., Comina, C., Jongmans, D., and Vinciguerra, S.: Characterization of the 3-D fracture setting of an unstable rock mass: From surface and seismic investigations to numerical modeling, J. Geophys. Res.-Sol. Ea., 122, 6346–6366, https://doi.org/10.1002/2017JB014111, 2017.
Colombero, C., Baillet, L., Comina, C., Jongmans, D., Larose, E., Valentin, J., and Vinciguerra, S.: Integration of ambient seismic noise monitoring, displacement and meteorological measurements to infer the temperature-controlled long-term evolution of a complex prone-to-fall cliff, Geophys. J. Int., 213, 1876–1897, https://doi.org/10.1093/gji/ggy090, 2018.
Colombero, C., Godio, A., and Jongmans, D.: Ambient Seismic Noise and Microseismicity Monitoring of a Prone-To-Fall Quartzite Tower (Ormea, NW Italy), Remote Sens., 13, 1664, https://doi.org/10.3390/rs13091664, 2021a.
Colombero, C., Jongmans, D., Fiolleau, S., Valentin, J., Baillet, L., and Bièvre, G.: Seismic Noise Parameters as Indicators of Reversible Modifications in Slope Stability: A Review, Springer Netherlands, 339–375 pp., https://doi.org/10.1007/s10712-021-09632-w, 2021b.
Conati Barbaro, C., Fiorucci, M., Grechi, G., Forti, L., Marmoni, G. M., and Martino, S.: Safeguarding archaeological excavations and preserving cultural heritage in cave environments through engineering geological and geophysical approaches, J. Archaeol. Sci. Reports, 60, 104868, https://doi.org/10.1016/j.jasrep.2024.104868, 2024.
Cruikshank, K. M. and Aydin, A.: Role of fracture localization in arch formation, Arches National Park, Utah, Geol. Soc. Am. Bull., 106, 879–891, https://doi.org/10.1130/0016-7606(1994)106<0879:ROFLIA>2.3.CO;2, 1994.
Doebling, S. W., Farrar, C. R., Prime, M. B., and Shevitz, D. W.: Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics: A literature review, Los Alamos National Laboratories, https://doi.org/10.2172/249299, 1996.
Dzubay, A., Moore, J. R., Finnegan, R., Jensen, E. K., Geimer, P. R., and Koper, K. D.: Rotational Components of Normal Modes Measured at a Natural Sandstone Tower (Kane Springs Canyon, Utah, U.S.A.), The Seismic Record, 2, 260–268, https://doi.org/10.1785/0320220035, 2022.
Farrar, C. R. and James III, G. H.: System identification from ambient vibration measurements on a bridge, J. Sound Vib., 205, 1–18, https://doi.org/10.1006/jsvi.1997.0977, 1997.
Finnegan, R., Moore, J. R., and Geimer, P. R.: Vibration of natural rock arches and towers excited by helicopter-sourced infrasound, Earth Surf. Dynam., 9, 1459–1479, https://doi.org/10.5194/esurf-9-1459-2021, 2021.
Finnegan, R., Moore, J. R., Geimer, P. R., Dzubay, A., Bessette-Kirton, E. K., Bodtker, J., and Vollinger, K.: Ambient Vibration Modal Analysis of Natural Rock Towers and Fins, Seismol. Res. Lett., 93, 1777–1786, https://doi.org/10.1785/0220210325, 2022.
Geimer, P. R., Finnegan, R., and Moore, J. R.: Sparse Ambient Resonance Measurements Reveal Dynamic Properties of Freestanding Rock Arches, Geophys. Res. Lett., 47, e2020GL087239, https://doi.org/10.1029/2020GL087239, 2020.
Geimer, P. R., Finnegan, R., and Moore, J. R.: Meteorological Controls on Reversible Resonance Changes in Natural Rock Arches, J. Geophys. Res.-Earth, 127, e2022JF006734, https://doi.org/10.1029/2022jf006734, 2022.
Goodman, R. E.: Introduction to rock mechanics, Wiley, New York, 478 pp., ISBN 0471041297, 1980.
Grechi, G., Moore, J. R., Jensen, E. K., McCreary, M. E., Czech, T. L., and Festin, M. M.: Modal Analysis of a Lava Tube Roof Complex: Tabernacle Hill, Utah, USA, Rock Mech. Rock Eng., 57, 1–10, https://doi.org/10.1007/s00603-024-03868-9, 2024.
Habaraduwa Peellage, W., Fatahi, B., and Rasekh, H.: Stiffness and damping characteristics of jointed rocks under cyclic triaxial loading subjected to prolonged cyclic loading, Int. J. Fatigue, 181, 108121, https://doi.org/10.1016/j.ijfatigue.2023.108121, 2024.
Häusler, M., Geimer, P. R., Finnegan, R., Fäh, D., and Moore, J. R.: An update on techniques to assess normal-mode behavior of rock arches by ambient vibrations, Earth Surf. Dynam., 9, 1441–1457, https://doi.org/10.5194/esurf-9-1441-2021, 2021a.
Häusler, M., Michel, C., Burjánek, J., and Fäh, D.: Monitoring the Preonzo Rock Slope Instability Using Resonance Mode Analysis, J. Geophys. Res.-Earth, 126, e2020JF005709, https://doi.org/10.1029/2020JF005709, 2021b.
Iannucci, R., Martino, S., Paciello, A., D'Amico, S., and Galea, P.: Investigation of cliff instability at Ghajn Hadid Tower (Selmun Promontory, Malta) by integrated passive seismic techniques, J. Seismol., 24, 897–916, https://doi.org/10.1007/s10950-019-09898-z, 2020.
Ibrahim, S. R.: Random Decrement Technique for Modal Identification of Structures, J. Spacecraft Rockets, 14, 696–700, https://doi.org/10.2514/3.57251, 1977.
Jensen, E. K. and Moore, J. R.: Coevolution of Rock Slope Instability Damage and Resonance Frequencies From Distinct‐Element Modeling, J. Geophys. Res.-Earth, 128, e2023JF007305, https://doi.org/10.1029/2023JF007305, 2023
Kleinbrod, U., Burjánek, J., and Fäh, D.: Ambient vibration classification of unstable rock slopes: A systematic approach, Eng. Geol., 249, 198–217, https://doi.org/10.1016/j.enggeo.2018.12.012, 2019.
Koper, K. D. and Hawley, V. L.: Frequency dependent polarization analysis of ambient seismic noise recorded at a broadband seismometer in the central United States, Earthquake Science, 23, 439–447, https://doi.org/10.1007/s11589-010-0743-5, 2010.
Kulatilake, P. H. S. W., Shreedharan, S., Sherizadeh, T., Shu, B., Xing, Y., and He, P.: Laboratory Estimation of Rock Joint Stiffness and Frictional Parameters, Geotechnical and Geological Engineering, 34, 1723–1735, https://doi.org/10.1007/s10706-016-9984-y, 2016.
Lazan, B. J.: Damping of materials and members in structural mechanics, Elsevier Science and Technology, Vol. XIII, 317 pp., ISBN 0080029345, 1968.
Lévy, C., Baillet, L., Jongmans, D., Mourot, P., and Hantz, D.: Dynamic response of the Chamousset rock column (Western Alps, France), J. Geophys. Res.-Earth, 115, F04043, https://doi.org/10.1029/2009JF001606, 2010.
Lin, F. C., Li, D., Clayton, R. W., and Hollis, D.: High-resolution 3D shallow crustal structure in Long Beach, California: Application of ambient noise tomography on a dense seismic array, Geophysics, 78, Q45–Q56, https://doi.org/10.1190/geo2012-0453.1, 2013.
McNamara, D. E. and Buland, R. P.: Ambiente noise levels in the continental United States, B. Seismol. Soc. Am., 94, 1517–1527, https://doi.org/10.1785/012003001, 2004.
Mercerat, E. D., Payeur, J. B., Bertrand, E., Malascrabes, M., Pernoud, M., and Chamberland, Y.: Deciphering the dynamics of a heterogeneous sea cliff using ambient vibrations: Case study of the Sutta-Rocca overhang (southern Corsica, France), Geophys. J. Int., 224, 813–824, https://doi.org/10.1093/gji/ggaa465, 2021.
Moore, J.: Structural health monitoring of rock arches and towers, International Federation of Digital Seismograph Networks [data set], https://doi.org/10.7914/SN/5P_2013, 2013.
Moore, J. R. and Grechi, G.: Hunter Arch, Sketchfab [code], https://skfb.ly/oILIM, last access: 16 January 2025.
Moore, J. R., Geimer, P. R., Finnegan, R., and Thorne, M. S.: Use of Seismic Resonance Measurements to Determine the Elastic Modulus of Freestanding Rock Masses, Rock Mech. Rock Eng., 51, 3937–3944, https://doi.org/10.1007/s00603-018-1554-6, 2018.
Moore, J. R., Geimer, P. R., Finnegan, R., and Michel, C.: Dynamic Analysis of a Large Freestanding Rock Tower (Castleton Tower, Utah), B. Seismol. Soc. Am., 109, 2125–2131, https://doi.org/10.1785/0120190118, 2019.
Moore, J. R., Geimer, P. R., Finnegan, R., and Bodtker, J.: Between a beam and catenary: Influence of geometry on gravitational stresses and stability of natural rock arches, Geomorphology, 364, 107244, https://doi.org/10.1016/j.geomorph.2020.107244, 2020.
Müller, J. and Burjánek, J.: In situ estimation of effective rock elastic moduli by seismic ambient vibrations, Int. J. Rock Mech. Min., 170, 105459, https://doi.org/10.1016/j.ijrmms.2023.105459, 2023.
Ostanin, I., Safonov, A., and Oseledets, I.: Natural Erosion of Sandstone as Shape Optimisation, Sci. Rep., 7, 17301, https://doi.org/10.1038/s41598-017-17777-1, 2017.
Pau, A. and Vestroni, F.: Vibration assessment and structural monitoring of the Basilica of Maxentius in Rome, Mech. Syst. Signal Pr., 41, 454–466, https://doi.org/10.1016/j.ymssp.2013.05.009, 2013.
Řihošek, J., Slavík, M., Bruthans, J., and Filippi, M.: Evolution of natural rock arches: A realistic small-scale experiment, Geology, 47, 71–74, https://doi.org/10.1130/G45421.1, 2018.
Riquelme, A.: Discontinuity Set Extractor, GitHub [code], https://github.com/adririquelme/DSE (last access: 16 January 2025), 2015.
Riquelme, A. J., Abellán, A., Tomás, R., and Jaboyedoff, M.: A new approach for semi-automatic rock mass joints recognition from 3D point clouds, Comput. Geosci., 68, 38–52, https://doi.org/10.1016/j.cageo.2014.03.014, 2014.
Starr, A. M., Moore, J. R., and Thorne, M. S.: Ambient resonance of Mesa Arch, Canyonlands National Park, Utah, Geophys. Res. Lett., 42, 6696–6702, https://doi.org/10.1002/2015GL064917, 2015.
Taruselli, M., Arosio, D., Longoni, L., Papini, M., and Zanzi, L.: Seismic noise monitoring of a small rock block collapse test, Geophys. J. Int., 224, 207–215, https://doi.org/10.1093/gji/ggaa447, 2021.
Van Overschee, P. and De Moor, B.: Subspace Identification for Linear Systems, Springer US, Boston, MA, https://doi.org/10.1007/978-1-4613-0465-4, 1996.
Welch, P.: The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms, IEEE T. Acoust. Speech, 15, 70–73, https://doi.org/10.1109/TAU.1967.1161901, 1967.
Zhang, W., Wang, J., Xu, P., Lou, J., Shan, B., Wang, F., Cao, C., Chen, X., and Que, J.: Stability evaluation and potential failure process of rock slopes characterized by non-persistent fractures, Nat. Hazards Earth Syst. Sci., 20, 2921–2935, https://doi.org/10.5194/nhess-20-2921-2020, 2020.




