the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Fluvial response to changes in the magnitude and frequency of sediment supply in a 1-D model
Marwan A. Hassan
In steep headwater reaches, episodic mass movements can deliver large volumes of sediment to fluvial channels. If these inputs of sediment occur with a high frequency and magnitude, the capacity of the stream to rework the supplied material can be exceeded for a significant amount of time. To study the equilibrium conditions in a channel following different episodic sediment supply regimes (defined by grain size distribution, frequency, and magnitude of events), we simulate sediment transport through an idealized reach with our numerical 1-D model “BESMo” (Bedload Scenario Model). The model performs well in replicating flume experiments of a similar scope (where sediment was fed constantly, in one, two, or four pulses) and allowed the exploration of alternative event sequences. We show that in these experiments, the order of events is not important in the long term, as the channel quickly recovers even from high magnitude events. In longer equilibrium simulations, we imposed different supply regimes on a channel, which after some time leads to an adjustment of slope, grain size, and sediment transport that is in equilibrium with the respective forcing conditions. We observe two modes of channel adjustment to episodic sediment supply. (1) High-frequency supply regimes lead to equilibrium slopes and armouring ratios that are like conditions in constant-feed simulations. In these cases, the period between pulses is shorter than a “fluvial evacuation time”, which we approximate as the time it takes to export a pulse of sediment under average transport conditions. (2) In low-frequency regimes the pulse period (i.e., recurrence interval) exceeds the “fluvial evacuation time”, leading to higher armouring ratios due to the longer exposure of the bed surface to flow. If the grain size distribution of the bed is fine and armouring weak, the model predicts a decrease in the average channel slope. The ratio between the “fluvial evacuation time” and the pulse period constitutes a threshold that can help to quantify how a system responds to episodic disturbances.
- Article
(7559 KB) - Full-text XML
-
Supplement
(11635 KB) - BibTeX
- EndNote
Mass movements in mountainous regions often deliver sediment directly to the stream network, resulting in coupled conditions that can trigger immediate channel responses during relatively large delivery events. Notably, delivery events can reset the local channel profile and govern construction and maintenance of channel bed architecture downstream of delivery points. The local response rate and trajectory following a delivery event is a function of the prevailing watershed flow regime, the magnitude of the delivery event, gradients in channel width (Ferrer-Boix et al., 2016), and in some instances the concentrated activity of aquatic species such as salmon (Hassan et al., 2008a). While lowland river systems have been the focus of a substantial body of research, less work has been carried out within steep mountain streams, particularly concerning mountain channel responses to changes in flow or sediment supply regimes.
In mountain streams, large, episodic inputs may temporarily dominate channel processes and morphology, significantly altering sediment transport and storage within the stream channel (Hassan et al., 2005, 2008b). Lisle et al. (1997) conducted flume experiments and numerical modelling that showed that sediment pulses are mainly reworked in situ, in contrast to a downstream translation in the form of a sediment wave. This finding is supported by Lisle et al. (2001), where little evidence of sediment waves was found in the field. Lisle and Church (2002) suggested that a stream channel responds to changes in the sediment supply by altering both storage and sediment transport rates. They describe that after a sediment pulse occurs, a first phase with low armouring rates allows for high transport rates in reworking the introduced material, corresponding to supply limited conditions. This is followed by a second phase in which armouring develops and transport rates decrease, corresponding to transport limited conditions. If the fluvial capacity is too low to evacuate the mass or grain size of material in the current hydrological regime, lag sediment can remain in the channel and dominate the local morphology for a long time (Benda et al., 2005; Brummer and Montgomery, 2006). Patterns of cyclic behaviour, associated with the rapid input of sediment from external sources, have been described in a number of field observations (Hassan et al., 2008b; Hoffman and Gabet, 2007; Madej, 1999, 2001; Madej and Ozaki, 1996; Miller and Benda, 2000; Roberts and Church, 1986) and some experimental studies (An et al., 2017a; Cui et al., 2003; Elgueta, 2014; Elgueta-Astaburuaga and Hassan, 2017; Ferrer-Boix and Hassan, 2014, 2015; Johnson et al., 2015; Sklar et al., 2009; Venditti et al., 2010; von Flotow, 2013). These studies observed fining of the bed surface, higher mobility and thus increased transport rates following such episodic sediment supply events. A reverse trend for coarsening and stabilizing of the bed was also noted as the supply was exhausted and a decrease in sediment transport rates followed (Church et al., 1998; Dietrich et al., 1989; Hassan and Church, 2000; Nelson et al., 2009). Cui and Parker (2005) support these findings using numerical modelling and further point out that abrasion can play an important role in the reworking of sediment pulses. Field observations (Benda, 1990; Pryor et al., 2011), and flume experiments (Luzi, 2014; Pryor et al., 2011) also document cycles of aggradation and degradation due to changes in the sediment supply. The observations discussed above suggest that changes in the sediment supply rate may lead to significant changes in bed elevation, bed surface texture, channel stability, and bed morphology. An analytical model developed by Blom et al. (2017) showed that the local channel geometry and surface grain size composition is mainly governed by long-term mean sediment supply rates and not by short-term changes in supply conditions. In contrast to cyclic sediment supply, cyclic hydrographs were found to mainly affect sediment transport rates and have a lesser impact on bed surface texture and channel morphology (Parker et al., 2007). Wong and Parker (2006) reported that cyclic hydrographs cause a part of the channel bed to undergo cyclic aggradation and degradation forming a hydrograph boundary layer. Cyclic sediment supply causes a similar effect which is termed the sedimentograph boundary layer (An et al., 2017b).
These findings imply that the morphological impact of the sediment pulse is most prevalent at the point of entrance, while the downstream portion mostly conveys the subsequently eroded material. The time needed for channel adjustments to occur after a large sediment input event depends on the amount and the texture of the delivered material. Brummer and Montgomery (2006) reported that 2 years after the supply event, the most mobile fractions (e.g., the fine fractions) were evacuated by a series of moderate floods while the largest grain sizes remained in the channel as lag deposits because flows were below their flow competence. Further, they showed that selective transport of sediment led to the development of an armour layer after only a few flow events. This armour layer protects the supplied material in the bed subsurface, increases bed stability, and causes lateral erosion and channel widening.
We expect the sediment transport rate in a channel to reach a long-term balance between erosional and depositional forces, even though there can be periodic changes in the short term. This state is defined as a “dynamic equilibrium” following Ahnert (1994). If the external forcing on the system changes, the channel will be in a transient state of adjustment towards a new dynamic equilibrium. Little attention has been directed to the question of what effect a change in the frequency of sediment supply events may have on the response of alluvial streams. Brunsden and Thornes (1979) proposed that if the frequency (i.e., recurrence interval) of disturbing events is shorter than the time necessary for a system to adjust to new boundary conditions (“relaxation time”), then transience will dominate the system and it may never achieve equilibrium (Brunsden, 1980). Wolman and Miller (1960) suggest that mountain channels experiencing direct inputs of sediment are good examples of such systems, where form is defined by extreme events rather than events of intermediate magnitude and frequency. The concept of this so-called “temporal sensitivity” was later elaborated on by Thomas (2001) and Brunsden (2001), although since their studies little attempt has been made in fluvial geomorphology to address this issue in practice. Bull (1991) applies the theory of Brunsden and Thornes (1979) to the impact of a hypothetical temporal succession of disturbance events on sediment storage, which can either increase or decrease the stream-bed elevation. The system processes the disturbance over the relaxation time, which together with a potential reaction time constitutes the total response time. If there is no further disturbance, the system status remains unchanged over a time of persistence. The concept from Bull (1991) is based on a system's trend towards a dynamic equilibrium between the forcing by, and the reworking of, disturbances. Howard (1982) concluded that if episodic inputs occur with a frequency that matches the inverse of the relaxation time, the output of the system will remain in a constant equilibrium with the average value of the forcing. Flume based insights about equilibrium conditions and timescales of adjustment to changes in sediment supply rates are discussed in some studies (Elgueta-Astaburuaga and Hassan, 2017; Pryor et al., 2011), but response times are only quantified in few cases (Podolak and Wilcock, 2013).
The paragraphs above illustrate how the frequency at which events occur may be fundamental in defining the response of a fluvial system to a change in boundary conditions. Therefore, it appears that event frequency should be a central aspect in investigations regarding the effect of episodic sediment supply on streams. Consequently, our understanding of involved processes remains incomplete. For example, it is uncertain whether the freshly delivered sediment that buries and is transferred over the bed surface is simply removed by the subsequent floods or whether there is some exchange between armoured and structured bed and the fine and mobile deposits. Furthermore, Hassan and Zimmermann (2012) asserted that it is important to study how quickly internal changes in grain size, channel morphology, and sediment storage occur when the stream shifts between cycles of aggradation and degradation.
Our main research objective is to describe the impact of episodic sediment supply on channel bed evolution in simulations using a 1-D morphodynamic numerical model for a bed of multiple grain sizes. We use the model to recreate conditions from experiments conducted at the Mountain Channel Hydraulic Experimental Laboratory, University of British Columbia, where a set of experiments were carried out to examine the impacts of episodic sediment supply on bed surface evolution and channel adjustment of a gravel bed stream (Elgueta, 2014; Elgueta-Astaburuaga, 2018; Elgueta-Astaburuaga and Hassan, 2017; von Flotow, 2013). Although these experiments provide detailed information on channel adjustment to changes in the sediment supply regime, they are limited in terms of the number of experiments and the range of scenarios that could be conducted. The performance of the model is tested against the experimental results obtained in the laboratory and then used to further explore controls and responses of the fluvial system to changes in flow and sediment supply regimes. The specific research questions addressed in this study are as follows:
-
Can the numerical model recreate the channel response that was observed in flume experiments of similar scope?
-
Does the sequencing of supply events play a role in the reaction of a gravel-bed stream, when several events of specified magnitudes occur in a different order?
-
How will different combinations of episodic sediment supply, obtained by varying their magnitude and frequency, impact channel evolution of a gravel-bed stream?
We applied the 1-D morphodynamic model BESMo (Bedload Scenario Model) to calculate capacity based sediment transport under different sediment supply regimes. We chose values for model parameters to match the flume experiments as closely as possible and used measurements of sediment transport rate, surface grain size distribution, and slope to calibrate the model. Matching our research questions, we then conducted two types of simulations:
-
In “event sequencing simulations”, we simulated different permutations of events to understand the role event succession plays in long-term channel response.
-
In “equilibrium simulations”, we used the same model setup and imposed different, but within each run regular, supply event frequencies. These simulations were run until we achieved a recurrent pattern in slope and grain size adjustment, allowing us to identify how the channel adjusts to the supply regime in the long term.
2.1 Model setup
The structure of the model is similar to other models designed to reproduce and interpret data from flume experiments (An et al., 2017a; Cui and Parker, 2005; Ferrer-Boix and Hassan, 2014; Wong and Parker, 2006). Figure 1 gives an overview of the implemented model components and their basic interaction. The model can be subdivided into a “hydraulic part” and a “sediment part”, both of which are subject to “external forcing” that varies in according to the modelling scenarios.
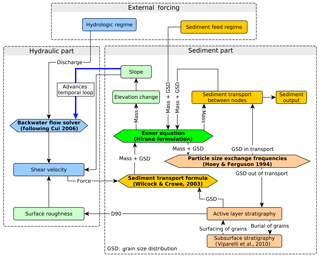
Figure 1Flowchart stating the main components of the model and the flow of information between them. The temporal loop is advanced as the new elevation affects the slope in the flow model. The components are coloured as follows: blue – flow related, dark yellow – sediment volume related, peach – particle size related, and green – geometry related.
We set up the modelling environment to run on a Compute Canada research cluster, which allows us to simulate many different input conditions in parallel and compare results quickly. We use a backwater flow model as suggested by Cui et al. (2006), implementing a threshold Froude number (Fr) to switch conditions between supercritical and subcritical flow:
The Froude number (Fr) is calculated as a function of discharge (Qw), gravity (g), channel width (wr) and water depth (h) (Eq. 1). The threshold Fr=0.9 simplifies the calculation of flow conditions, allowing us to spatially iterate through the nodes only once from downstream to upstream. In the case of subcritical flow, the water depth is solved locally as a function of downstream friction slope (Sf) and bed slope (S0) (Eq. 2a):
Water depth under supercritical flow conditions is calculated locally assuming steady uniform flow using the Manning–Strickler formulation (Eqs. 2b and 3), where αr is a coefficient of 8.1 (Parker, 1991) and roughness height (ks):
ks is calculated using the constants nk and Ds90, the surface grain size for which 90 % of the surface is finer:
In the case of steady and uniform flow the bed slope S0 is equal to the friction slope (Sf) with bed elevation (ηb) at downstream position x:
If the solution of the water depth with Eq. (2a) is numerically unstable on the current node distribution, the model subdivides the channel into more nodes and reiterates the subdivision until a stable backwater curve is found. This approach does not properly represent the location of hydraulic jumps (Cui et al., 2006), which should not be a problem as we average conditions over a node spacing of at least one channel width. Boundary shear stress (τb) is then calculated with the depth-slope product:
where ρ is the water density. τb is then converted to the shear velocity u*, which is used in the sediment routing component:
The volumetric unit bedload transport rate per size class qbi is calculated using the sediment transport function provided by Wilcock and Crowe (2003). The change in bed elevation ∂ηb for each node x per time step t follows from the Exner equation of mass conservation:
where λ is bed porosity. The volumetric bedload transport rate per unit width is given as qb and is calculated per grain size class i in the sediment mixture of n size classes:
The model incorporates subsurface stratigraphy using the active layer concept (Parker, 2008), which gives the Hirano equation:
where La is the active layer thickness, Fi is the surface frequency of the ith grain size class, fIi is the ith grain size class proportion exchanged between the surface and the subsurface, and qbi=pbiqb is the volumetric unit bedload transport rate of the ith grain size class where pbi represents the ith fraction of the bedload transport rate. The active layer thickness is calculated as La=naDs90, with the parameter na, representing the scale of bed fluctuations.
The grain size distribution of the sediment flux between the active layer and the substrate is either calculated from the subsurface texture when the bed degrades, or from a linear combination of surface and bedload grain size distributions when the bed aggrades (Hoey and Ferguson, 1994):
where fi is the fraction of the ith grain size class in the subsurface, and α is a constant. The vertical stratigraphy is stored in 10 cm high layers following Viparelli et al. (2010). By keeping track of grain size distributions within the surface and subsurface layers, the model can preserve the history of phases of erosion or aggradation. This allows emergent properties such as armouring layers to occur. To study the combined effect that the active layer thickness factor na and the active layer exchange ratio α have on the model results, we executed sensitivity runs shown in the Supplement to this paper (Supplement Figs. S1–S4).
The Exner equation (Eq. 8) in combination with the expression for the friction slope in Eq. (2) and the sediment transport function by Wilcock and Crowe (2003) form an non-linear advection–diffusion system that allows the calculation of bed elevation as a function of space and time (An et al., 2017a). An upwind scheme was used for the numerical discretization. The model needs an initial bed profile and an initial value of the surface grain size to be solvable. Sediment boundary conditions are given by the sediment feed rate and grain size distributions on the inlet, and a fixed bed elevation at the outlet of the simulated reach. The flow boundary condition is a water surface height of 0.1 m over normal flow at the outlet. The bedload transport function is used to calculate transport rates for each channel cross section. During the model run, changes of the sediment transport rate are dependent on changes in the sediment supply, channel slope, and surface grain size distribution.
2.2 Model calibration
We used data from flume experiments to calibrate the model. The objective of the flume experiments was to measure the adjustment of an alluvial steep channel to different frequencies of sediment supply. The experiments were carried out in a water recirculating flume which is 18 m long, 1 m wide, and 1 m deep in the Mountain Channel Hydraulic Experimental Laboratory at the University of British Columbia. Here we will provide a brief summary of the flume setup and experimental design, for more details see von Flotow (2013), Elgueta (2014), Ferrer-Boix and Hassan (2015), and Elgueta-Astaburuaga and Hassan (2017).
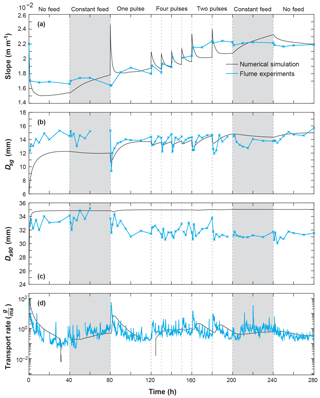
The experiment consisted of seven 40 h long runs with different sediment supply frequencies, while keeping the total sediment input the same at 300 kg per run. The experiments were run continuously, i.e., the bed surface at the end of run 1 was the starting condition for run 2 and so on. For all runs, flow was held constant so that the sediment feed regime could be studied with no changes in flow regime (Table 1). The difference between the runs was the spreading of the supply over a changing input frequency, which was either constant, in one pulse, in two pulses, or in four pulses. The bed was fixed in the first 1 m downstream section of the flume head box with stones equivalent to about Ds84 of the experimental bed material. In the remainder of the flume the bed initially consisted of 0.1 m of loose material with particle sizes ranging from 0.5 to 64 mm with a Ds50 of 5.64 mm, matching downscaled (by a factor of 3) conditions of a study reach in East Creek, British Columbia, Canada. The flume slope was set to 0.022 m m−1. Measurements include water depth, water surface slope, water velocity, bed surface slope, bed surface particle size distribution, bed elevation, sediment transport rate, and bedload texture. Measurements of the water surface elevation were conducted throughout the experiment using a mechanical point gauge with 0.001 m precision. Photos were used to manually sample bed surface grain size distributions and the bed elevation was recorded with a green laser scanner at a 2 mm resolution. The bed surface scans were used to measure the bed surface slope along the thalweg, i.e., the line of lowest elevation along the flume. Flow velocity measurements were conducted using an ADV profiler. The grain size and count of particles exiting the flume were recorded with a camera and a light table at the outlet of flume (Zimmermann et al., 2008). The transport rate measurements were done at 30 Hz and validated after the experiments by total exported weight.
Using the model described, we simulated a 12 m long and 1 m wide channel in 13 downstream nodes each spaced 1 m apart. The model was set to calculate sediment transport for all nodes in time steps of 10 s. All simulations used a constant water discharge of 0.065 m3 s−1 and a geometric mean grain size of 5.64 mm for both initial bed and sediment feed (full distribution shown in Fig. 2a). We chose to use a normally distributed approximation of the flume grain size with a width of σ=1.6 to be consistent with distributions used for the equilibrium simulations. This distribution and the original flume GSD are statistically the same. The initial channel slope was 0.022 m m−1, also matching the parameters from the flume experiments.
We calibrated the model by visually reducing the difference between measured and simulated values of bed slope (S), surface grain size parameters (Dsg, Ds90), and transport rate (qb). In the calibration runs more importance was given to recreating S, Dsg, and qb than to a good match in Ds90. We first increased the reference Shields stress () in the Wilcock and Crowe formula to roughly match simulated and measured qb. Afterwards, we varied the grain exchange ratio (α) (Eq. 11) and the coefficient of the active layer thickness (na). As we achieved a good visual match between simulation and flume measurements, we did not see the need to calibrate more parameters.
Table 1Overview of runs in the flume experiments. All runs were 40 h long. The texture of the initial bed mixture and the sediment feed were identical. Plots of resulting slope, Dsg, Ds90, and sediment transport are shown in Fig. 3. The symbols in column two signify the feed regime where 0 represents no feed, C represents constant feed, and 1, 2, and 4 represent the number of pulses in 40 h.

Initial slope 2.2 %; mixture Ds50 =5.64 mm; mixture Ds90 =11.2 mm, Qw=65 L s−1; duration of each run =40 h; total feed =300 kg per run. NA represents not available.
2.3 Event sequencing simulations
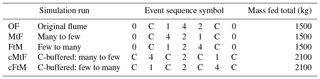
We explored the role that the sequencing of the pulse events could have on the flume study by simulating the “original flume” event sequence and comparing the result to alternative sequencing of events (see Table 2). The alternative event sequences are using the same pulse distributions (four pulses, two pulses, or one pulse over 40 h), but the pulse order is either from “few to many” (FtM) (i.e., one pulse, then two pulses, then four pulses) or from “many to few” (MtF) (i.e., four pulses, then two pulses, then one pulse) per 40 h phase. To allow the system more time to recover from pulse events, we simulated two more cases where each pulsed phase is buffered from the next one by a 40 h constant-feed phase. These runs are called “c-buffered: many to few” (cMtF) and “c-buffered: few to many” (cFtM).
Table 2Sequencing of events in runs that were simulated as permutations of the original flume experiment. Each of the seven periods was 40 h long and each run lasted 280 h in total. There was no sediment input during the no feed runs (0). Within all other period types, 300 kg of sediment was fed over 40 h, either constantly (C) or in pulses (one, two, or four events). Besides recreating the original flume sequence (OF), we simulated two runs where the pulsed events occur either in order from many pulses to few (MtF) or from few to many (FtM). To explore if the system could rebound from the impact of a certain pulse phase during a constant-feed phase, we created two additional runs where this was the case (cMtF and cFtM), which led to a 600 kg higher total sediment feed.
2.4 Equilibrium simulations
In our final set of experiments, we kept the frequency and magnitude of pulse events constant to achieve equilibrium slope and grain size conditions. The use of numerical modelling allows for the comparison of many simulations with differing grain size distributions, pulse frequencies, and pulse magnitudes. We expect a channel under episodic sediment supply to adjust synchronously to the frequency of external forcing events. The added sediment volume from a supply event will increase the channel slope at first. After the supply of sediment ends and material is removed from the channel, the slope will decrease, and the surface grain size will begin to reflect the sediment starved conditions. As the long-term sediment input equals the long-term sediment output, the channel will eventually achieve a condition where the capacity to erode material (through increased slope in conjunction with changes in the surface grain size) equals the depositional forcing (i.e., long-term sediment input) of the supply regime. In this state the adjustment of channel slope and grain size to each sediment input event will return to the same values after every pulse. All runs achieved this equilibrium condition within 20 000 simulation hours.
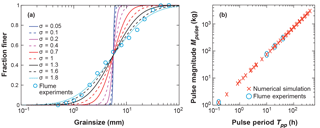
Figure 2(a) Variation of the grain size distribution between model runs (lines) and values from the flume experiments (circles). All distributions have a geometric mean grain size (Dsg) of 5.64 mm. The different σ values represent the width of the distribution, calculated for normal distributions in phi-scaled sediment sizes. The data for the flume experiments are roughly matched with σ=1.6. (b) Combinations of pulse magnitude and pulse period (or recurrence interval) used in the equilibrium model runs. As the total mass of supplied material is the same for all simulations, runs with high pulse frequencies (i.e., low pulse periods Tpp) are smaller in magnitude. Four of the combinations match the flume runs (circles).
To find the equilibrium slope resulting from different sediment supply regimes, we simulated different combinations of sediment supply frequency (Fpulse) and magnitude (Mpulse) for nine different grain size distributions (Fig. 2a). All distributions have the same mean grain size of 5.64 mm, but differ in the width of the distribution by the standard deviation (σ), which was chosen for a phi-scaled, normally distributed sample. While σ=0.05 represents a nearly uniform sediment mixture, σ=1.6 roughly matches the grain size distribution of the flume experiments. We used 11 grain size classes in the simulations and set the initial GSD to the feed GSD. Under the hydraulic conditions applied all grain sizes are initially mobile, which might change during the simulations due to the effect of armouring and changes in bed slope. Figure 2b shows the combinations of frequency and magnitude used in this study. Each model run delivered the same input mass over the simulation time (150 000 kg over 20 000 h). We then distributed this total mass over different pulse frequencies, with four of the combinations matching the flume experiments. Each pulse was 10 min in length. The lowest frequency was chosen to be one pulse every 400 h (pulse period time: Tpp=400 h), and the highest frequency was constant feed (one 10 min long pulse every 10 min). We selected a range of 40 pulse frequencies for which the whole number of cycles summed to 20 000 h. In total we executed 360 simulations, 9 different σ with 40 frequencies each.
3.1 Model calibration
Elgueta-Astaburuaga and Hassan (2017) describe the flume results we used for model calibration in detail. We will give a short summary of the findings here. An initial run without sediment feed over an unstructured bed showed a high sediment output while the bed armoured. This run was similar in output grain sizes and grain mobility to the run with one sediment pulse over a structured bed. This shows that active restructuring of the bed occurred in both of these runs. On the other end of the spectrum, the constant feed and four pulse runs were similar in their low sediment output and showed different grain mobility. This implies that the system reacts differently at a threshold frequency somewhere between two pulses per 40 h and four pulses per 40 h, which Elgueta-Astaburuaga and Hassan (2017) interpret as the relaxation time of the bed to a pulse event.
We used these experiments to test the ability of the numerical model to recreate the flume results in discharge, pulse frequency, pulse magnitude, slope, and grain sizes. In the experiment, mean grain size (Dsg) and slope (S) were measured over a central 2 m long section to avoid a bias of bed surface measurements due to inflow and outflow conditions. The measurement intervals varied between every 1 and every 20 h (depending on the pulse interval). The values for the numerical simulation are averaged over the whole reach and were recorded every 10 min during the simulation time. We achieved a best match in slope S, Dsg, Ds90, and the transport rate qb by increasing the reference Shields stress in the Wilcock and Crowe formula by a factor of 2. Wilcock (2001) suggests taking the same approach of increasing the threshold shear stress to match a sediment transport calculation to field data. Other researchers use this method to calibrate models to field and flume data (Chartrand et al., 2015).
Figure 3 shows the comparison between flume measurements and the calibrated model results with the grain exchange ratio α=0.45 (Eq. 11) and the active layer thickness factor na=2. The sensitivity of the model to changes in α and na is shown in Supplement Figs. S1–S4. Due to the long interval between measurements in the flume experiments, some short-term slope responses to individual sediment pulses might be hidden (e.g., after hours 80 and 180 in Fig. 3a). The model underpredicts both the slope and the mean surface grain size (Dsg) (see Fig. 3b) in the first 60 h, while the coarse grain size fractions (Ds90) and average transport rate are over predicted for the first 30 h (see Fig. 3c and d). This might be due to imperfect initial conditions or boundary effects in the flume experiments. For the rest of the simulation both slope and Dsg show good agreement with the flume results. D90 is overpredicted in the model, but this is seen as a minor issue because the simulated transport rates mainly depend on Dsg and the slope. The transport rate in the simulation lags behind the light table data, which might be due to our numerical implementation of diffusion. As the model matches the average transport rates well, we did not see the need to improve the temporal agreement.
3.2 Event sequencing simulations
After obtaining a good match between the model and the flume data, we simulated alternative event sequences as described in Table 2. Figure 4a shows the adjustment of slope in runs that preserved the same sediment feed volume and had the same duration as the flume experiments (OF, MtF, and FtM), but the frequency of events is ordered differently. At the end of the simulations, all runs approach the same slope value of 0.022 m m−1, which shows that the main factor determining the long-term slope is the total volume of sediment fed. The sequencing of events seems to play a role in the slope adjustment over the short term, here about 80 h after the events. On this short timescale, large pulses increase the slope quickly, while the smaller, more frequent pulses lead to a more gradual adjustment of slope. Figure 4b shows the runs where pulse phases were buffered by constant-feed phases (cMtF and cFtM), increasing the total sediment feed by 600 kg. This did not change the pattern of adjustment significantly compared to the earlier runs, as the constant-feed phases only prolonged the effect of the previous pulse phase.
The effect of event sequencing on the channel response in Dsg is shown in Fig. 4c for all runs in Table 2. The order of events only has a weak impact on patterns of adjustment in Dsg, as maximum grain size conditions are reached within 20–30 h. Afterwards no further adjustment occurs until the introduction of fine material with the next pulse lowers the surface grain size again. This means that armouring of the channel surface happens quickly in relation to the time between pulse events. The subsurface is made of the same grain size distribution as the sediment feed, so its mean size is 5.56 mm. Therefore, we can infer that an armouring ratio (Dsg∕Dsubg) of about 2.2 was reached within 20 h and then increased towards 2.7 over the following 260 h. A finer, less armoured surface at the time of each supply event is followed by a coarsening of the surface as the finer grain sizes are more mobile, and thus more easily evacuated in the time without feed between pulses.
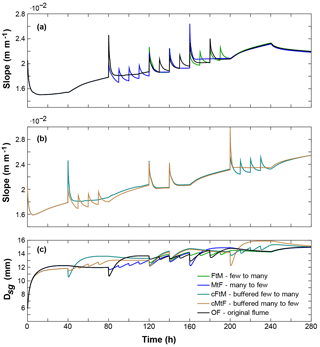
Figure 4Comparison of slope and mean surface grain size Dsg from runs with different event sequencing (see Table 2) (σ=1.6, factor of 2 increase of ). Event sequences are (a) rearranged pulse phases to the flume experiments and (b) a setup where the pulsed phases are buffered with constant-feed phases. Panel (c) shows Dsg for the runs in both (a) and (b).
3.3 Equilibrium simulations
Our second set of simulations explored the equilibrium conditions that are reached under different supply regimes. As we will explain in the discussion, the effect of the supply regime can be constrained to changes in slope (S) and the surface grain size distribution (GSDfluv), which in the following will be characterized by the armouring ratio between surface and subsurface mean grain size (Dsg∕Dsubg). After different times in the simulations, these parameters reach a time-independent periodic adjustment that is illustrated in Fig. 5 for the last 400 h of two simulations. Figure 6a shows box plots of the distribution of slope values during the last pulse of all 40 runs with σ=1.6. The presented normalized slopes (S∕Sconst) indicate how the slope for each pulse frequency compares to the constant-feed slope of runs with the same grain size distribution. Figure 6b shows the change in normalized mean slope (Smlp∕Sconst) with pulse frequency, which corresponds to the red lines in Fig. 6a and is our main indicator for the equilibrium state of the channel slope. Each line represents a different width σ of the GSD over 40 runs with increasing Tpp.
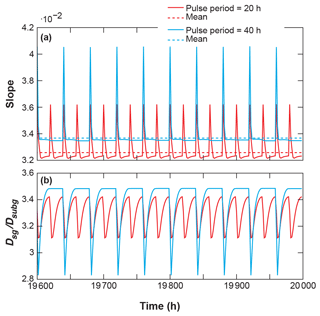
Figure 5(a) Slope and (b) armouring ratio for the last 400 h of 2 out of 40 experiments using σ=1.6. A run with a low event frequency is shown in blue, and a run with a high event frequency is shown in red. In these example runs the mean slope in equilibrium is higher for the run with longer pulse periods.
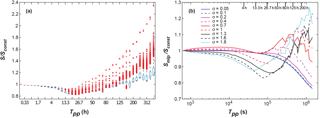
Figure 6(a) Distribution of the ratios of slope during the last pulse to the constant-feed slope for all 40 runs with σ=1.6. We normalized the values of the slope in the last pulse with the slope of the constant-feed run of the same grain size distribution width (σ), allowing for the comparison of the equilibrium slopes between runs with different σ. The red lines represent the normalized mean slopes (Smlp∕Sconst), which we chose as the main indicator for the equilibrium state of the channel slope. Note that data from longer pulse periods Tpp will contain more data points for the box plots, as there are more slope values recorded during the longer time between pulses (sampling every 10 min). The red crosses are outliers in the distribution of slope values, illustrating the extreme slope values during the time right after the pulse was introduced into the channel. (b) Mean slope ratios for all runs grouped by width of GSD (σ).
4.1 Extension of flume results with the numerical model
The numerical model shows good agreement with the temporal response of mean surface grain size and slope from the flume experiments. As the initial bed grain size distributions were well mixed, the good match in mean surface grain size also implies a good match in the armouring ratios. A series of runs with an alternative sequencing of events showed that, while the adjustment of mean surface grain size was not sensitive to the order of the pulsed phases, the evolution of slope differed considerably. In the cases where the first pulsed phase consisted of one large magnitude event (FtM and cFtM), the slope increased quickly and the following higher-frequency, lower magnitude pulse phases did not modify the system considerably. In contrast, cases where multiple smaller event phases occurred first (MtF and cMtF), the slope increased more gradually. All runs ended at about the same slope after the 280 h simulation time, which implies that while the low frequency, large magnitude events strongly alter the channel in the short term, the sequencing of events does not play an important role in the long run. The constant-feed-buffered runs (cFtM and cMtF) show similar behaviour to their unbuffered counterparts, as the constant-feed phases preserve the bed state of the previous pulse phase. The main driver of the slope adjustment is the total sediment feed, which is consistent with findings by Blom et al. (2017).
4.2 Development of timescales from the equilibrium simulations
The definition of a sediment supply regime can be based on different aspects of sediment input into a stream, either from outside or within the channel. For simplicity, we restrict the definition of a sediment supply regime to the input of material into the fluvial system from outside the active channel. Sediment supply from storage close to the channel can be viewed as external supply if it only occurs episodically (e.g., less than yearly) in large flooding events. This view allows us to describe the sediment supply regime by a combination of frequency, magnitude, and grain size distribution of sediment supply events over a multi-event time frame (as in Benda and Dunne, 1997a). The time frame must be long enough to contain enough sediment supply events to allow the stream bed to adjust to the external forcing by changing its internal configuration of sediment storage and bed structuring. Even though a natural channel might never reach an equilibrium to a certain sediment supply regime, it might produce regular patterns of transient adjustment to the supply events.
In our case, the forcing on the system is a combination of pulse frequency (Fpulse), pulse magnitude (Mpulse), pulse grain size distribution (GSDpulse), and water discharge (Qw). Due to the simple geometry and the lack of bedforms in a 1-D numerical model, the fluvial reaction to the forcing is restricted to the bedload transport rate (qb), channel slope (S), and channel grain size distribution (GSDfluv) (see Table 3). Pulse frequency and magnitude can be combined in the virtual pulse velocity (Upulse), with the magnitude normalized by reach width (wr) and length (lr):
A characteristic pulse period time (Tpp) for a sediment supply regime is the inverse of the pulse frequency:
We define a reach averaged fluvial export velocity in order to compare the sediment export of material to the pulsed sediment input. Considering a multi-event time frame Tsim(≫Tpp) for each simulation, we can assume that the fluvial system will adjust to the external forcing over time, leading to an adjustment of the reach averaged fluvial sediment transport to match the external forcing of the virtual pulse velocity:
Table 3List of forcing and reacting parameters, and timescales in our simulations with abbreviations and their dimension (T represents time and L represents length).

The time it takes to achieve an equilibrium state is highly dependent on the initial conditions of the simulations. Instead of using a process rate threshold to find an equilibrium time, we can infer a simulation-time independent relation between the supply regime (i.e., Tpp) and the state of the system in equilibrium (i.e., Ufluv, S, and GSDfluv). This way we only have to run simulations for long enough to verify equilibrium with the respective supply regime (in our case 20 000 h), and then observe properties of the channel at the very end of the simulation, even though equilibrium might have been achieved earlier.
When comparing the system state in equilibrium between many different supply regimes, while keeping the initial fluvial reworking capacity constant (mainly geometry and Qw), we can identify how the equilibrium conditions change under different supply regimes. Due to the fixed channel geometry in the 1-D model, only the bed slope (S) and the grain size distribution (GSDfluv) can adjust to the change in the supply regime.
To better compare the temporal adjustment to sediment pulses of different magnitudes and frequencies, we non-dimensionalized the pulse period Tpp with a fluvial evacuation time Tfe:
This timescale is a representation of how long it would take to remove a layer of sediment as long and as wide as the flume (lr and wr) with the thickness of the median feed grain size Dfg, under the average transport rate Ufluv, multiplied by an estimate of the ratio of feed grain size to armoured grain size (Dfg∕Dag)2, which can be interpreted as an inverse of the degree of potential bed armouring similar to Ds90∕Ds50 (Recking, 2012). We developed Eq. (15) visually by matching the inflection of lines in Fig. 7a to .
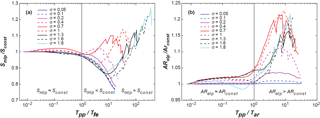
Figure 7(a) Mean slope ratios in non-dimensional timescale. : model runs with a high-frequency sediment supply show similar equilibrium slopes and armouring ratios as conditions of constant sediment feed (Smlp≈Sconst). : if the GSD is narrow (σ<0.4) or the pulse period is not much longer than the fluvial evacuation time, we observe lower equilibrium slopes than in constant-feed runs (Smlp<Sconst). Runs with either very low frequency of supply events or wide GSD (σ≥0.4) show equilibrium slopes that are higher than the respective constant-feed runs (Smlp>Sconst). (b) Relative armouring ratio in non-dimensional timescale. : low frequency of supply events leads to an increase in armouring ratio compared to constant-feed runs (ARelp>ARconst), especially for wide GSDs (σ≥0.4).
Figure 7a shows the same data as Fig. 6b, but in non-dimensionalized time Tpp∕Tfe. A ratio of can be interpreted as a condition in which the pulsed input of material occurs faster than the fluvial removal of a Dfg thick theoretical layer of material under average transport conditions modified by armouring. At a ratio of , the sediment is fed in time steps longer than the time that the fluvial system needs to remove said theoretical layer.
Figure 7b shows the normalized armouring ratio (ARelp∕ARconst), which was obtained by dividing the armouring ratio AR at the end of the last pulse for each simulation with the armouring ratio at the end of the corresponding constant-feed run. Similarly to the fluvial evacuation time that we used to non-dimensionalize the slope adjustment, we used an armouring time Tar to non-dimensionalize the grain size adjustment:
This timescale represents how long it would take to remove a layer of sediment as long and as wide as the flume (lr and wr) with the thickness of the supplied Df90, under the reach averaged transport rate , multiplied by an estimate of the ratio of the sediment supply Df90 to the Da90 of an armoured bed. We developed Eq. (16) visually by matching the inflection of lines in Fig. (7b) to .
4.3 Interpretation of the equilibrium simulations
The condition of constitutes a threshold in the slope adjustment to pulsed sediment supply. Pulse periods shorter than the fluvial evacuation time () lead to equilibrium slopes similar to the constant-feed equilibrium slopes (Smlp≈Sconst). In the case of narrow GSDs (σ<0.4), simulations with pulse periods longer than the fluvial evacuation time () show an up to 20 % lower slope than in the constant-feed equivalent run (Smlp<Sconst). In contrast, runs with either very low frequency of supply events or wide GSD (σ≥0.4) show equilibrium slopes that are up to 30 % higher than the respective constant-feed runs (Smlp > Sconst). Simulations with a wider range of material (σ>1) show a drop in Smlp∕Sconst right at , but then an increase in Smlp∕Sconst at longer pulse distances. We interpret conditions of lower Smlp to be less armoured, as they coincide with lower values of ARelp∕ARconst as shown in Fig. 7b. The simulations showing an intermittent decrease of Smlp seem to be in a state in which material can be efficiently exported from the system without having intense armouring limiting the slope adjustment. These large pulses increase the slope rapidly, leading to high shear velocities which causes high transport rates.
We interpret the cause for increasing slope and armouring ratios for long pulse periods in the following way. A longer time between pulses (Tpp>Tar) causes more intense armouring, which shows that the channel bed is starved of sediment between pulses, as finer grain fractions are removed from the surface. This leads to the development of an armouring layer, which restricts the incision into lower deposits, initially limiting the sediment output of the system (Ufluv<Upulse). This imbalance between input and output of material leads to an increased sediment storage over time, which due to the fixed geometry of the channel leads to an increase in slope. This can increase the shear velocity and in return leads to higher sediment output rates. This response loop between armouring and slope adjustment will continue until the sediment output matches the long-term sediment supply (Ufluv≈Upulse). Note that due to the restricted geometry of our model, slope and grain size are the main parameters in the channel that can change in response to the sediment supply regime. It is possible that other morphological adjustments (e.g., channel width) could compensate for the transport rate disequilibrium in a similar fashion.
The non-dimensionalized presentation of the simulation results shows two distinct modes of adjustment of the fluvial system to episodic sediment supply regimes: (1) “constant-feed-like” behaviour in runs where supply events are of high frequency and low magnitude. Under this kind of forcing the equilibrium slopes and armouring ratios are similar to equilibrium conditions of runs with constant sediment feed. (2) “Pulse-dominated” behaviour occurred in runs where sediment was fed in low frequency and high magnitude events.
An interesting finding is that when Tpp>Tfe, an increase in slope only occurs in simulations that have grain size distributions wide enough to allow armouring to occur. In these cases, we could use the timescale of Tar to determine if the armouring would be significant enough to prevent a decrease of the equilibrium slope. Even though armouring develops very quickly in both our simulations and the flume experiments, its long-term persistence in the time between sediment pulses is what governs the channel response. Hence, the grain size distribution in a series of supply events can be more important for the channel response in the long term than the frequencies and magnitudes of the individual events themselves.
It is notable that the channel response at Tpp=Tfe does not change abruptly, but the system response slowly tilts to either pulse-dominated on the one end, or constant-feed-like on the other end of the spectrum. While all constant-feed-like channels (for each σ) have very similar equilibrium properties, all pulse-dominated channels are different in both slope and armouring ratios.
4.4 Implications of the equilibrium simulations
Applying the threshold of between constant-feed-like and pulse-dominated supply regimes to the flume experiments is inconclusive. The unity of h lies between the constant-feed runs and the highest frequency runs (four pulses with Tpp=10 h), which means that we have no experimental constant-feed-like pulsed regime where Tpp<Tfe. Elgueta-Astaburuaga and Hassan (2017) found that the four-pulse phase caused a sediment transport response that was similar to the constant-feed runs, implying that Tfe would lie between 10 h and 20 h. The flume experiments were not executed long enough to reach equilibrium, which complicates the attribution of a specific channel response to a specific forcing. Besides recreating the 280 h flume experiment in the model, the 360 equilibrium simulations include four configurations that repeat the constant-feed and three pulse periods for 20 000 h. These four configurations only reached the equilibrium after about 12 000 h of simulated time, which is very long in comparison to the conditions of the flume experiments where each supply regime only lasted 40 h.
Table 4Application of the fluvial evacuation time to the rapids reach in East Creek. The system is assumed to be in equilibrium with a matching fluvial transport rate and long-term sediment supply rate. The time of active fluvial transport is estimated to be 100 h yr−1. We approximated the long-term fluvial transport rate Ufluv with three years of data from a sediment trap below the reach. We assumed that the subsurface grain size measurements reflect the average supply GSD and the surface grain size measurements represent the long-term average state of armouring in the reach. Besides the original “East Creek” data and the two “threshold” pulse frequency fits, we assumed four more scenarios with doubled armoured grain sizes or doubled fluvial transport rates to give a rough estimate of error bounds.
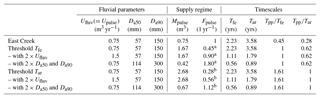
For all calculations: supply Df90 =90 mm, supply Df50 =32 mm, channel width =2.5 m, channel length = 72 m. Some frequencies calculated to match. a Tpp=Tfe and b Tpp=Tar
The numerical model was calibrated with only one set of flume experiments. As our study mainly focusses on comparing different simulation results from the same model, the applicability of our results to other flume studies or field cases is uncertain. However, we are confident that the numerical model is an adequate tool to gain insight on the effect of episodic sediment supply on fluvial channels in a general sense. For example if there was an inaccuracy in the calculation of the shear velocity, it would affect all model runs and thus be counterbalanced by relating the changed resulting slope to the constant-feed slope (Smlp∕Sconst), and the changed armouring ratio to the constant-feed armour ratio (ARelp∕ARconst).
We tested this by executing two additional batches of simulations with a 25 % decrease and a 25 % increase in the total mass fed respectively. If the experimental design would strongly affect the threshold between constant-feed-like and pulse-dominated conditions, we would expect these simulations to plot differently than the data in Fig. 7b. But as shown in Supplement Fig. S5 for the case of σ=1.6, the change in the slope ratio Smlp∕Sconst is relatively insensitive to the total feed volume. We also expect this to be the case when changing the grain size distributions to include large particles that are initially immobile with the applied discharge. In such simulations, the slope would increase to a point where these initially immobile grain sizes become mobile at a very high equilibrium slope. As we compare all results to the corresponding constant-feed equilibrium slope of the same grain size distribution, these conditions might collapse on the existing data as well. However, it is possible that the channel parameters would become extreme in a way that the empirically derived transport function by Wilcock and Crowe would no longer be realistically applicable.
As we developed the fluvial evacuation time Tfe and the armouring timescale Tar purely from observations in numerical simulations, their usefulness remains to be proven in the field. If such a threshold behaviour between episodic sediment supply event frequency and the fluvial adjustment of a channel exists, it should be possible to find signatures in channel morphology, sediment storage volume, or channel slope when comparing streams subject to different pulse periods and with different fluvial transport capacities. It is possible to use Eq. (15) with information about the long-term sediment supply volume, grain size supply, and average channel dimensions to calculate Tfe and thus infer the matching threshold pulse period where Tpp=Tfe. If the long-term sediment supply occurs in more frequent events than this threshold, the system can be assumed to experience constant-feed-like sediment supply. If the supply frequency is lower, we would expect to find a morphological signature of a pulse-dominated supply regime.
To provide an example application of the developed timescales, we applied Eqs. (15) and (16) to data from East Creek, which is a small creek in the Fraser watershed close to Vancouver in BC, Canada. The “rapids” channel section of this creek was used to design the flume experiments as a 1 to 6 Froude scaled model. Table 4 shows the resulting timescales in seven different scenarios that use the reported values for sediment supply, grain size distribution, and channel dimensions from Cienciala and Hassan (2013) and Papangelakis and Hassan (2016). In East Creek, we assume that of all the supplied sediment is contributed by annual events with a magnitude that matches the annual fluvial transport. As the calculated fluvial evacuation time Tfe is 2.23 years, this scenario implies that the system would behave in a constant-feed-like manner, which would only change if the supply events were more than 2.23 years apart on average (i.e., Tpp=2.23 years), as shown in the “threshold Tfe” calculation. Due to the high uncertainty in our assumption that the measured values represent equilibrium conditions, we calculated two more scenarios with double transport rates (2×Ufluv) and double armoured grain size (2×Da50 and Da90). The last three calculations in Table 4 show which pulse frequency is needed to match the armouring timescale (Tar). While we do not know if East Creek is in equilibrium with the sediment supply regime and the measurements used do not reflect long-term conditions, these calculations can still give a rough idea of whether a system is constant-feed-like in our classification of channel response to episodic supply regimes.
We characterized an episodic sediment supply regime in terms of event frequency, magnitude, and supplied grain size distribution. To test the effect that different episodic sediment supply regimes can have on the morphology of a mountain stream, we developed a numerical model to recreate and extend simulations from flume experiments. The model performs well in recreating the flume experiments in both slope and grain size distributions (GSD), which are the two variables that represent morphological adjustment in our model. Channel width is fixed and bedforms are assumed to be absent, even though bedforms did occur in the flume experiments.
To understand the extent to which event succession plays a role in the flume experiments, we simulated alternative pulse successions of large-to-small events (i.e., infrequent-to-frequent) and small-to-large events (i.e., frequent-to-infrequent), while keeping the total sediment volume feed the same. These simulations show that different pulse frequency sequences have no strong effect on the long-term slope and GSD of the bed surface. In the short term large pulse events can dominate the channel response causing an abrupt increase in slope, while the effect of subsequent smaller events is subdued as the channel is still adjusted to the large pulse. If smaller events dominate at first, the channel adjusts more gradually.
In our second set of simulations, we imposed different episodic sediment supply regimes with the same total sediment supply volume on the same initial channel geometries with constant discharge. While being kept constant within a run, the episodic supply regimes differed in event frequencies, magnitudes, and GSD. We simulated 40 different event frequencies for which the sum of event magnitudes matched an overall equal total sediment supply. All 40 pulse configurations were calculated for 9 GSD that differed in the width of the distribution σ around the same geometric mean grain size. The channels adjusted to the episodic sediment supply until they reached an equilibrium state in which each successive pulse led to the same slope and grain size adjustment. We compared this state between runs and found a distinctive regime change when the time between pulses (Tpp) became lower than a fluvial evacuation time (Tfe), which we developed as a measure of the time it takes to remove a Ds50 thick layer from the channel surface under average transport conditions, modified by a measure of potential armouring (see Eq. 15).
The condition of Tpp<Tfe causes a constant-feed-like sediment supply regime, as the model runs show similar slopes and surface grain size distributions as constant-feed runs of the same GSD. When Tpp>Tfe the sediment supply regime becomes pulse-dominated. Under these conditions, we observed a lower relative slope in cases where the GSD is narrow (σ < 0.4), as the long time between pulses in combination with a low armouring potential allows more erosion in the reach, ultimately lowering the equilibrium slope. If the GSD is wide enough to allow armouring (σ≥ 0.4), a stronger armouring layer can develop during the periods of selective transport of smaller grain sizes and bedload starvation. This limits the minimum slope and increases sediment storage (and thus slope) in the long term.
The application of the episodic supply regime classification to data from East Creek shows that the threshold to a pulse-dominated regime lies at the fluvial evacuation time of roughly 2.2 years. This creek probably receives sediment at a lower interval, which indicates a pulse-dominated regime. The armouring timescale lies around 3.5 years, indicating that if the long-term sediment supply was introduced over event frequencies between 2.2 and 3.5 years, it would be removed most efficiently and result in a lower slope.
Steeper channels than East Creek could show both a lower fluvial evacuation time (due to higher slope, smaller channel area) and a lower pulse frequency (more landslide dominated), which could make these channels more likely to be pulse-dominated. Further study of field cases is needed to strengthen the case for our classification of channel response types to episodic supply regimes. In natural rivers, there are further modes of adjustment that the system can undergo after receiving sediment pulses, for example changes in bed forms or the storage of excess material in sediment bodies along the channel. Still, the condition when a channel is receiving more material per pulse than what can be exported in the same time frame (i.e., the ratio of Tpp∕Tfe is above 1), should be observable in natural rivers as irregularities in channel long profiles due to increased sediment storage. In our model, we only supplied grain sizes that were transportable by the imposed flow conditions. In field streams it can be that the biggest clasts (e.g., boulders) are only transportable by extreme flow events, which would further increase the slope of reaches with high sediment supply.
The data and software code used in this study are available on request.
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-6-1041-2018-supplement.
TM and MAH developed the research questions and designed the setup of the flume experiments, while the data was collected by TM and others. The numerical model was developed by TM under supervision of MAH. TM conducted the simulations and the related data analysis. The paper was written by TM and MAH.
The authors declare that they have no conflict of interest.
Tobias Müller was supported by a Four Year Doctoral Fellowship from the
University of British Columbia and a travel grant from Stiftung für
Kanadastudien. The flume experiments were supported by NSERC and CFI grants
(to Marwan Hassan) and were conducted collaboratively by Maria Elgueta,
Claudia von Flotow, and the first author under the supervision of Marwan
Hassan. Computational resources were provided by WestGrid
(https://www.westgrid.ca, last acces: 6 November 2018) and Compute
Canada (https://www.computecanada.ca/, last acces: 6 November 2018).
Carles Ferrer-Boix provided support in the development of an early version of
the numerical model. We thank Eric Leinberger for improving the figures and
Conor McDowell for comments on an early draft of this work. We are grateful
for the comments and suggestions provided by three anonymous reviewers that
helped to clarify and improve this paper. Special thanks go to Gary Parker,
who provided critical comments and many suggestions that improved this paper,
and together with Chenge An provided suggestions regarding the revision of
the paper.
Edited by: Kimberly
Hill
Reviewed by: three anonymous referees
Ahnert, F.: Equilibrium, scale and inheritance in geomorphology, Geomorphology, 11, 125–140, https://doi.org/10.1016/0169-555x(94)90077-9, 1994. a
An, C., Cui, Y., Fu, X., and Parker, G.: Gravel-bed river evolution in earthquake-prone regions subject to cycled hydrographs and repeated sediment pulses, Earth Surf. Proc. Land., 42, 2426–2438, https://doi.org/10.1002/esp.4195, 2017a. a, b, c
An, C., Fu, X., Wang, G., and Parker, G.: Effect of grain sorting on gravel bed river evolution subject to cycled hydrographs: Bed load sheets and breakdown of the hydrograph boundary layer, J. Geophys. Res.-Earth, 122, 1513–1533, https://doi.org/10.1002/2016jf003994, 2017b. a
Benda, L.: The influence of debris flows on channels and valley floors in the Oregon Coast Range, USA, Earth Surf. Proc. Land., 15, 457–466, https://doi.org/10.1002/esp.3290150508, 1990. a
Benda, L. and Dunne, T.: Stochastic forcing of sediment supply to channel networks from landsliding and debris flow, Water Resour. Res., 33, 2849–2863, https://doi.org/10.1029/97WR02388, 1997a. a
Benda, L., Hassan, M. A., Church, M., and May, C. L.: Geomorphology of Steepland Headwaters: The Transition from Hillslopes to Channels, J. Am. Water Resour. As., 41, 835–851, https://doi.org/10.1111/j.1752-1688.2005.tb03773.x, 2005. a
Blom, A., Arkesteijn, L., Chavarrías, V., and Viparelli, E.: The equilibrium alluvial river under variable flow and its channel-forming discharge, J. Geophys. Res.-Earth, 122, 1924–1948, https://doi.org/10.1002/2017jf004213, 2017. a, b
Brummer, C. J. and Montgomery, D. R.: Influence of coarse lag formation on the mechanics of sediment pulse dispersion in a mountain stream, Squire Creek, North Cascades, Washington, United States, Water Resour. Res., 42, W07412, https://doi.org/10.1029/2005wr004776, 2006. a, b
Brunsden, D.: Applicable model of long term landform evolution, Z. Geomorphol. Supp., 36, 16–26, 1980. a
Brunsden, D.: A critical assessment of the sensitivity concept in geomorphology, Catena, 42, 99–123, https://doi.org/10.1016/s0341-8162(00)00134-x, 2001. a
Brunsden, D. and Thornes, J. B.: Landscape Sensitivity and Change, T. I. Brit. Geogr., 4, 463–484, https://doi.org/10.2307/622210, 1979. a, b
Bull, W. B.: Geomorphic responses to climatic change, Oxford University Press, https://doi.org/10.2307/215397, 1991. a
Chartrand, S. M., Hassan, M. A., and Radić, V.: Pool-riffle sedimentation and surface texture trends in a gravel bed stream, Water Resour. Res., 51, 8704–8728, https://doi.org/10.1002/2015wr017840, 2015. a
Church, M., Hassan, M. A., and Wolcott, J. F.: Stabilizing self-organized structures in gravel-bed stream channels: Field and experimental observations, Water Resour. Res., 34, 3169–3179, https://doi.org/10.1029/98wr00484, 1998. a
Cienciala, P. and Hassan, M. A.: Linking spatial patterns of bed surface texture, bed mobility, and channel hydraulics in a mountain stream to potential spawning substrate for small resident trout, Geomorphology, 197, 96–107, https://doi.org/10.1016/j.geomorph.2013.04.041, 2013. a
Cui, Y. and Parker, G.: Numerical Model of Sediment Pulses and Sediment-Supply Disturbances in Mountain Rivers, J. Hydraul. Eng., 131, 646–656, https://doi.org/10.1061/(asce)0733-9429(2005)131:8(646), 2005. a, b
Cui, Y., Parker, G., Lisle, T. E., Gott, J., Hansler-Ball, M. E., Pizzuto, J. E., Allmendinger, N. E., and Reed, J. M.: Sediment pulses in mountain rivers: 1. Experiments, Water Resour. Res., 39, 1239, https://doi.org/10.1029/2002wr001803, 2003. a
Cui, Y., Parker, G., Braudrick, C., Dietrich, W. E., and Cluer, B.: Dam removal express assessment models (DREAM). Part 1: model development and validation, J. Hydraul. Res., 44, 291–307, https://doi.org/10.1080/00221686.2006.9521683, 2006. a, b
Dietrich, W. E., Kirchner, J. W., Ikeda, H., and Iseya, F.: Sediment supply and the development of the coarse surface layer in gravel-bedded rivers, Nature, 340, 215–217, https://doi.org/10.1038/340215a0, 1989. a
Elgueta, M. A.: Channel adjustment of a gravel-bed stream under episodic sediment supply regimes, Master's thesis, University of British Columbia, https://doi.org/10.14288/1.0165847, 2014. a, b, c
Elgueta-Astaburuaga, M. A.: Effects of episodic sediment supply on channel adjustment of an experimental gravel bed, PhD thesis, University of British Columbia, https://doi.org/10.14288/1.0364558, 2018. a
Elgueta-Astaburuaga, M. A. and Hassan, M. A.: Experiment on temporal variation of bed load transport in response to changes in sediment supply in streams, Water Resour. Res., 53, 763–778, https://doi.org/10.1002/2016wr019460, 2017. a, b, c, d, e, f, g
Ferrer-Boix, C. and Hassan, M. A.: Influence of the sediment supply texture on morphological adjustments in gravel-bed rivers, Water Resour. Res., 50, 8868–8890, https://doi.org/10.1002/2013wr015117, 2014. a, b
Ferrer-Boix, C. and Hassan, M. A.: Channel adjustments to a succession of water pulses in gravel bed rivers, Water Resour. Res., 51, 8773–8790, https://doi.org/10.1002/2015wr017664, 2015. a, b
Ferrer-Boix, C., Chartrand, S. M., Hassan, M. A., Martín-Vide, J. P., and Parker, G.: On how spatial variations of channel width influence river profile curvature, Geophys. Res. Lett., 43, 6313–6323, https://doi.org/10.1002/2016gl069824, 2016. a
Hassan, M. A. and Church, M.: Experiments on surface structure and partial sediment transport on a gravel bed, Water Resour. Res., 36, 1885–1895, https://doi.org/10.1029/2000wr900055, 2000. a
Hassan, M. A. and Zimmermann, A. E.: Channel Response and Recovery to Changes in Sediment Supply, in: Gravel-Bed Rivers, John Wiley & Sons, Ltd, 464–473, https://doi.org/10.1002/9781119952497.ch33, 2012. a
Hassan, M. A., Church, M., Lisle, T. E., Brardinoni, F., Benda, L., and Grant, G. E.: Sediment Transport and Channel Morphology of Small, Forested Streams, J. Am. Water Resour. As., 41, 853–876, https://doi.org/10.1111/j.1752-1688.2005.tb03774.x, 2005. a
Hassan, M. A., Gottesfeld, A. S., Montgomery, D. R., Tunnicliffe, J. F., Clarke, G. K. C., Wynn, G., Jones-Cox, H., Poirier, R., MacIsaac, E., Herunter, H., and Macdonald, S. J.: Salmon-driven bed load transport and bed morphology in mountain streams, Geophys. Res. Lett., 35, L04405, https://doi.org/10.1029/2007gl032997, 2008a. a
Hassan, M. A., Smith, B. J., Hogan, D. L., Luzi, D. S., Zimmermann, A. E., and Eaton, B. C.: 18 Sediment storage and transport in coarse bed streams: scale considerations, in: Gravel-Bed Rivers VI: From Process Understanding to River Restoration, edited by Habersack, H. P. H. and Rinaldi, M., 473–496, Elsevier, https://doi.org/10.1016/s0928-2025(07)11137-8, 2008b. a, b
Hoey, T. B. and Ferguson, R.: Numerical simulation of downstream fining by selective transport in gravel bed rivers: Model development and illustration, Water Resour. Res., 30, 2251–2260, https://doi.org/10.1029/94wr00556, 1994. a
Hoffman, D. F. and Gabet, E. J.: Effects of sediment pulses on channel morphology in a gravel-bed river, Geol. Soc. Am. Bull., 119, 116–125, https://doi.org/10.1130/b25982.1, 2007. a
Howard, A. D.: Equilibrium and time scales in geomorphology: Application to sand-bed alluvial streams, Earth Surf. Proc. Land., 7, 303–325, https://doi.org/10.1002/esp.3290070403, 1982. a
Johnson, J. P. L., Aronovitz, A. C., and Kim, W.: Coarser and rougher: Effects of fine gravel pulses on experimental step-pool channel morphodynamics, Geophys. Res. Lett., 42, 8432–8440, https://doi.org/10.1002/2015gl066097, 2015. a
Lisle, T. E. and Church, M.: Sediment transport-storage relations for degrading, gravel bed channels, Water Resour. Res., 38, 1-1–1-14, https://doi.org/10.1029/2001wr001086, 2002. a
Lisle, T. E., Pizzuto, J. E., Ikeda, H., Iseya, F., and Kodama, Y.: Evolution of a sediment wave in an experimental channel, Water Resour. Res., 33, 1971–1981, https://doi.org/10.1029/97wr01180, 1997. a
Lisle, T. E., Cui, Y., Parker, G., Pizzuto, J. E., and Dodd, A. M.: The dominance of dispersion in the evolution of bed material waves in gravel-bed rivers, Earth Surf. Proc. Land., 26, 1409–1420, https://doi.org/10.1002/esp.300, 2001. a
Luzi, D. S.: Sediment transport and morphological response of a semi-alluvial channel: insights from a Froude scaled laboratory model, PhD thesis, University of British Columbia, https://doi.org/10.14288/1.0165910, 2014. a
Madej, M. A.: Temporal and spatial variability in thalweg profiles of a gravel-bed river, Earth Surf. Proc. Land., 24, 1153–1169, https://doi.org/10.1002/(SICI)1096-9837(199911)24:12<1153::AID-ESP41>3.0.CO;2-8, 1999. a
Madej, M. A.: Development of channel organization and roughness following sediment pulses in single-thread, gravel bed rivers, Water Resour. Res., 37, 2259–2272, https://doi.org/10.1029/2001wr000229, 2001. a
Madej, M. A. and Ozaki, V.: Channel response to sediment wave propagation and movement, Redwood Creek, California, USA, Earth Surf. Proc. Land., 21, 911–927, https://doi.org/10.1002/(sici)1096-9837(199610)21:10<911::aid-esp621>3.0.co;2-1, 1996. a
Miller, D. J. and Benda, L. E.: Effects of punctuated sediment supply on valley-floor landforms and sediment transport, Geol. Soc. Am. Bull., 112, 1814–1824, https://doi.org/10.1130/0016-7606(2000)112<1814:eopsso>2.0.co;2, 2000. a
Nelson, P. A., Venditti, J. G., Dietrich, W. E., Kirchner, J. W., Ikeda, H., Iseya, F., and Sklar, L. S.: Response of bed surface patchiness to reductions in sediment supply, J. Geophys. Res.-Earth, 114, F02005, https://doi.org/10.1029/2008jf001144, 2009. a
Papangelakis, E. and Hassan, M. A.: The role of channel morphology on the mobility and dispersion of bed sediment in a small gravel-bed stream, Earth Surf. Proc. Land., 41, 2191–2206, https://doi.org/10.1002/esp.3980, 2016. a
Parker, G.: Selective Sorting and Abrasion of River Gravel. I: Theory, J. Hydraul. Eng., 117, 131–147, https://doi.org/10.1061/(asce)0733-9429(1991)117:2(131), 1991. a
Parker, G.: Transport of Gravel and Sediment Mixtures, in: Sedimentation Engineering, American Society of Civil Engineers, vol. 110, 165–251, https://doi.org/10.1061/9780784408148.ch03, 2008. a
Parker, G., Hassan, M., and Wilcock, P.: 10 Adjustment of the bed surface size distribution of gravel-bed rivers in response to cycled hydrographs, in: Gravel-Bed Rivers VI: From Process Understanding to River Restoration, Elsevier, 241–285, https://doi.org/10.1016/s0928-2025(07)11127-5, 2007. a
Podolak, C. J. P. and Wilcock, P. R.: Experimental study of the response of a gravel streambed to increased sediment supply, Earth Surf. Proc. Land., 38, 1748–1764, https://doi.org/10.1002/esp.3468, 2013. a
Pryor, B. S., Lisle, T., Montoya, D. S., and Hilton, S.: Transport and storage of bed material in a gravel-bed channel during episodes of aggradation and degradation: a field and flume study, Earth Surf. Proc. Land., 36, 2028–2041, https://doi.org/10.1002/esp.2224, 2011. a, b, c
Recking, A.: Influence of sediment supply on mountain streams bedload transport, Geomorphology, 175-176, 139–150, https://doi.org/10.1016/j.geomorph.2012.07.005, 2012. a
Roberts, R. G. and Church, M.: The sediment budget in severely disturbed watersheds, Queen Charlotte Ranges, British Columbia, Can. J. Forest Res., 16, 1092–1106, https://doi.org/10.1139/x86-189, 1986. a
Sklar, L. S., Fadde, J., Venditti, J. G., Nelson, P., Wydzga, M. A., Cui, Y., and Dietrich, W. E.: Translation and dispersion of sediment pulses in flume experiments simulating gravel augmentation below dams, Water Resour. Res., 45, W08439. https://doi.org/10.1029/2008wr007346, 2009. a
Thomas, M. F.: Landscape sensitivity in time and space – an introduction, Catena, 42, 83–98, https://doi.org/10.1016/s0341-8162(00)00133-8, 2001. a
Venditti, J. G., Dietrich, W. E., Nelson, P. A., Wydzga, M. A., Fadde, J., and Sklar, L.: Effect of sediment pulse grain size on sediment transport rates and bed mobility in gravel bed rivers, J. Geophys. Res.-Earth, 115, F03039, https://doi.org/10.1029/2009jf001418, 2010. a
Viparelli, E., Sequeiros, O. E., Cantelli, A., Wilcock, P. R., and Parker, G.: River morphodynamics with creation/consumption of grain size stratigraphy 2: numerical model, J. Hydraul. Res., 48, 727–741, https://doi.org/10.1080/00221686.2010.526759, 2010. a
von Flotow, C.: Temporal adjustments of a streambed following an episodic sediment supply regime, Master's thesis, University of British Columbia, https://doi.org/10.14288/1.007421, 2013. a, b, c
Wilcock, P. R.: Toward a practical method for estimating sediment-transport rates in gravel-bed rivers, Earth Surf. Proc. Land., 26, 1395–1408, https://doi.org/10.1002/esp.301, 2001. a
Wilcock, P. R. and Crowe, J. C.: Surface-based Transport Model for Mixed-Size Sediment, J. Hydraul. Eng., 129, 120–128, https://doi.org/10.1061/(asce)0733-9429(2003)129:2(120), 2003. a, b
Wolman, M. G. and Miller, J. P.: Magnitude and Frequency of Forces in Geomorphic Processes, J. Geol., 68, 54–74, https://doi.org/10.1086/626637, 1960. a
Wong, M. and Parker, G.: One-dimensional modeling of bed evolution in a gravel bed river subject to a cycled flood hydrograph, J. Geophys. Res.-Earth, 111, F03018, https://doi.org/10.1029/2006jf000478, 2006. a, b
Zimmermann, A. E., Church, M., and Hassan, M. A.: Video-based gravel transport measurements with a flume mounted light table, Earth Surf. Proc. Land., 33, 2285–2296, 2008. a