the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Reconstructing lateral migration rates in meandering systems – a novel Bayesian approach combining optically stimulated luminescence (OSL) dating and historical maps
Jakob Wallinga
Identifying lateral migration rates of meandering rivers is relevant both for fluvial geomorphology and to support river management. Lateral migration rates for contemporary meandering systems are often reconstructed based on sequential remote-sensing images or historical maps; however, the time frame for which these sources are available is limited and hence likely to represent fluvial systems subjected to human influence. Here, we propose to use scroll bar sequences as an archive to look further back in time using optically stimulated luminescence (OSL) dating of sand-sized quartz grains. We develop a modelling procedure for the joint Bayesian analysis of (OSL) dating results and historical map data. The procedure is applied to two meanders from the Overijsselse Vecht, a medium-sized sand-bed river in the Netherlands. We obtained nine samples for OSL dating from scroll bars and combined OSL dating results with historical map data for the period 1720–1901 CE (Common Era). The procedure we propose here incorporates the strengths of both data types for reconstructing fluvial morphodynamics over longer time frames. Using an iterative modelling approach, we translate spatial uncertainty of historical maps into temporal uncertainty of channel position required for Bayesian deposition modelling. Our results indicate that meander formation in the Overijsselse Vecht system started around 1400 CE, and lateral migration rates were on average 2.6 and 0.9 m yr−1 for the two investigated bends, until river channelization around 1900 CE.
- Article
(4897 KB) - Full-text XML
-
Supplement
(1684 KB) - BibTeX
- EndNote
Rivers are one of the world's most important geomorphic agents and represent highly dynamic earth surface systems (Güneralp and Rhoads, 2011; Vandenberghe and Maddy, 2000). Meandering rivers represent the most common river type and can be found all over the world (Hooke, 2013). The mobility of their course has a significant effect on sediment transport and deposition, floodplain development, and landscape change (Kleinhans and Van den Berg, 2011). Related consequences for river management, hazards, and biodiversity pose a practical need to understand the timing and speed of lateral migration (Grabowski et al., 2014; Hooke, 2013; Lespez et al., 2015).
To determine whether changes in meander position and morphology have taken place, it is often necessary to consider relatively long timescales (Hooke, 2013). To establish recent lateral migration rates and reconstruct the planform of contemporary fluvial systems, sequential aerial photographs or topographical maps are often used (e.g. Pišút, 2002; Uribelarrea et al., 2003; Hooke and Yorke, 2010; Eekhout et al., 2013). Unfortunately, the lack of historical sources of this type limits long-term reconstructions of channel position, and reconstructions based on older maps may be strongly affected by spatial uncertainties and mapping inaccuracies. Moreover, as historical maps are often only available for cultivated areas, the fluvial systems displayed are likely to be affected by humans. Such influence can be either through river management (e.g. Hesselink et al., 2003; Frings et al., 2009) or through land-use changes which may change the hydrograph (e.g. Candel et al., 2018) as well as sediment input (e.g. De Moor et al., 2008; Hoffmann et al., 2009). Consequences may be great, as shown in a highly influential paper by Walter and Merritts (2008), who argued that the present-day meandering form of gravel-bedded mid-Atlantic streams in the USA is not a natural phenomenon but rather an artefact caused by mill ponds. Hence, to understand dynamics of fluvial systems and anthropogenic impacts on those systems, there is a need to extend the period of reconstruction to earlier periods, which requires reconstruction methods that do not rely solely on historical sources and/or remote sensing.
To resolve depositional ages and geomorphological process rates, the use of optically stimulated luminescence (OSL) dating to obtain absolute chronologies of fluvial deposits is becoming widespread (Lian and Roberts, 2006; Rittenour, 2008; Wallinga, 2002b). In addition, OSL is increasingly used to date young (<1000 years) sediments as part of late Holocene studies (Madsen and Murray, 2009). Yet, the application of OSL dating to reconstruct lateral migration rates has hardly been attempted (with a few notable exceptions; see, e.g., Rodnight et al., 2005; Rowland et al., 2005; Kemp and Rhodes, 2010). Such limited application of OSL dating for this purpose may well be related to challenges faced when applying luminescence dating to young fluvial sediments. Successful age determination requires the complete resetting of the OSL signal in at least part of the grains, a prerequisite that may not be met due to the limited light exposure during the subaqueous transport of grains in a turbid river.
Bayesian analysis of depositional sequences allows the construction of more precise and robust chronologies by combining ages obtained through a dating method with prior information on the order of events (Bronk Ramsey, 2008). Following pioneering work by Rhodes et al. (2003), Bayesian analysis is now increasingly applied to sequences of OSL ages, often in combination with ages obtained through other methods (e.g. 14C: Dreibrodt et al., 2010; U-series: Clark-Balzan et al., 2012; dendrochronology: Wallinga et al., 2012) or even multiple methods (e.g. Shanahan et al., 2013; Hobo et al., 2014; Guérin et al., 2017).
Several studies have combined OSL dating with evidence derived from historical maps and documentation as independent age control (e.g. Ballarini et al., 2003; Medialdea et al., 2014), age constraints (e.g. Nielsen et al., 2006; Madsen et al., 2007; Tamura et al., 2011; Kunz et al., 2014), or for historical contextualization of dating results (e.g. Clemmensen et al., 2007). However, the direct integration of OSL dates with legacy data provided by historical evidence into a single geochronology, i.e. where historical evidence is used to help determine the geochronology, is underexplored. An exception to this is the study by Hobo et al. (2014), who reconstructed the floodplain sedimentation of the Dutch river Waal using Bayesian age–depth models based on heavy-metal age estimates, OSL dates and age constraints derived from historical maps.
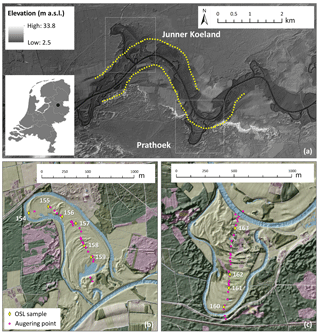
Figure 1Location of the study area (a), showing the two meander bends Junner Koeland (b) and Prathoek (c). Dotted line in panel (a) indicates the valley side; m a.s.l.: metres above sea level. White numbers along the coring transects in panels (b) and (c) indicate OSL sample locations by abbreviated sample code (all should be preceded by NCL-2415). Samples NCL-2415154–162 were collected in scroll bar deposits; sample NCL-2415163 was collected in a terrace remnant. Lithological cross sections and lithogenetic interpretation are provided in Candel et al. (2018). Digital elevation model (AHN2; horizontal resolution 5 m, vertical resolution 0.2 m): AHN (2018), Van Heerd et al. (2000). Topography (3200 pixels km−1): OpenTopo, Van Aalst (2017).
Here we combine OSL data and historical map evidence using Bayesian chronological modelling to reconstruct planform development and lateral migration rates of the Overijsselse Vecht, a medium-sized sand-bed river in the Netherlands. Our aim is to develop a modelling procedure using the Bayesian depositional sequences tool of OxCal (Bronk Ramsey, 2008) for the joint analysis of OSL dating results and historical map data that (1) allows quantitative analysis of historical maps in geochronological research and (2) supports the development of robust fluvial chronologies with quantified uncertainty that expand into larger time frames. With these methods we determine the age of scroll bar deposits along the Overijsselse Vecht and the average migration rate of two meanders that developed during the past 500 years. This information provides the geochronological basis for a palaeo-hydrological study on the Overijsselse Vecht (Candel et al., 2018).
The Overijsselse Vecht is a medium-sized river originating in Nordrhein-Westfalen in Germany and enters the Netherlands from the east near the town of Coevorden. This rain-fed river has a catchment size of 3785 km2 and a rather uniform valley gradient on Dutch territory of (Wolfert and Maas, 2007). The width of the abandoned channel (i.e. abandoned upon channelization) in the investigated meanders (see below) is ∼30 m, as derived from the present-day digital elevation model (DEM; Fig. 1). According to measurements in the period 1995–2015 of the discharge station in Mariënberg (just upstream of our study area), the average annual discharge and mean annual flood discharge amount to 22.8 and 160 m3 s−1 respectively. Average annual rainfall in the region amounts to 800–875 mm and average monthly temperatures vary between 4.5 and 5.0 ∘C in January and 22.5 and 23.0 ∘C in July (KNMI, 2017).
The Overijsselse Vecht was channelized in the late nineteenth and early twentieth century. The original river length of 90 km on Dutch territory was reduced to 60 km by cutting off 69 meanders (Wolfert and Maas, 2007). Weirs were installed to prevent vertical erosion of the river bed, and groynes and revetments were constructed to prevent lateral migration of the river channel (Wolfert et al., 1996; Wolfert and Maas, 2007). In recent decades, water managers have initiated several projects to restore the physical and ecological functioning of the river, which resulted in the need for increased understanding of river morphodynamics (e.g. Wolfert et al., 1996, 2009; Maas et al., 2007; Viveen et al., 2009) and ecological potential (e.g. Duursema, 2004).
The floodplain of the Overijsselse Vecht is flanked on both sides by extensive areas with coversand ridges and drift-sand dunes, overlying fluvio-periglacial deposits of Pleistocene age (Ter Wee, 1966, 1979; Kuijer and Rosing, 1994; geomorphological map of the Netherlands (1 : 50 000); for details, refer to Koomen and Maas, 2004). Its former valley is rather narrow (indicated by the yellow dotted lines in Fig. 1a) and many meanders appear to be laterally confined by relatively stable sides of the former valley. Relief in the area is limited; the floodplain and valley sides are located at ∼5.5 and ∼7 m a.s.l respectively. For this study we focused on two meander bends with large amplitudes that reach outside the former valley side, named Junner Koeland and Prathoek (Fig. 1).
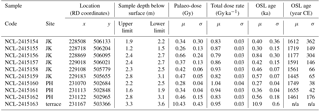
Table 1Overview of the six historical maps used in this study. All dates are indicated in CE (Common Era). Revision date indicates full or partial revision. The date used for analysis is based on the revision date or, if none is given, on the survey date. For the map sheet of the Hottinger atlas the survey covered 3 years; we therefore took the middle year to use in further analyses. GCPs: ground control points (as used for georeferencing); RMSE: root mean square error (expressed in metres) based on the residuals (or displacement vectors) of the GCPs after using a first-order polynomial transformation in the georectification procedure. JK: Junner Koeland; PH: Prathoek. Map sections are shown in Fig. 2. References list map source and publications on cartographers, survey techniques and depiction methods. References are detailed in the subscript.

1: Algemeen Rijks Archief. Genie-archief, situatiekaart 07. 2:
Wolfert et al. (1996). 3: Box (2007). 4: Versfelt (2003). 5: Versfelt and
Schroor (2005). 6: CC-BY Kadaster (2018a).
7: CC-BY Kadaster (2018b). 8: CC-BY
Kadaster (2018c). 9: Van der Linden (1973). 10: Van der Leest et al. (2005).
11: Stam (2006).
3.1 Lithological survey
For each meander bend a lithogenetic cross section was constructed based on multiple hand corings from meander base to apex (Fig. 1b, c), following a line perpendicular to the scroll bars, with cores obtained at high and low points in the scroll bar and swale topography. In a separate paper, Candel et al. (2018) provide details of these cross sections (including detailed facies descriptions and an explanation of the lithogenetic interpretation) and use the information to reconstruct palaeo-discharges. Here, we concentrate on those aspects that are directly relevant to the reconstruction of channel position throughout the lifetime of the meander. Most of the cores reached a depth of 4 to 6 m, penetrating the full point-bar deposits (extremely fine to coarse sand) including the channel lag (medium fine to coarse sand with gravel), which occurred at depths varying from 2.5 to 4 m below the surface. Some aeolian reworking occurred locally, as is evident from the DEM (Fig. 1). The lithological and geomorphological information was used to select the suitable depths to collect OSL samples (see below).
3.2 Analysis of historical maps
Maps show the position of the river channel at the time of the map survey; however, the use of this information for quantitative reconstruction of channel position over time is not straightforward. First of all, historical maps are likely less accurate than their modern counterparts. Hence there is an uncertainty in the exact position of the channel. In this section we outline how we quantify this spatial uncertainty. Next, to allow Bayesian analysis of the sequence, this spatial uncertainty must be translated into a temporal uncertainty. The necessity of this step and the approach we take are outlined in Sect. 3.4.
3.2.1 Georeferencing
Six historical maps (dating from 1720 to 1894/1901 CE (Common Era); Table 1, Fig. 2a–f) were selected for analysis. The selected maps vary in extent (e.g. focused on the Overijsselse Vecht or on the Netherlands as a whole), scale (varying from 1 : 14 400 to 1 : 50 000), and original purpose (military or topographical surveys); consequently, they vary in their display of the study area. We included these maps in our analysis based on the degree of topographical quality (i.e. sufficient detail for georeferencing) and a quality check to assess geodetic distortion (see Sect. 3.2.3). Younger maps (example for 1931 CE provided in Fig. 2g) did not provide relevant information as the meanders under investigation were cut-off during river channelization in the early twentieth century and were consequently no longer active. Older maps (>1720 CE) were also available for the area but had to be excluded from the analysis as georeferencing was impossible due to the limited topographical information on the maps. The historical context of the maps and information on the cartographers, survey techniques, and map depiction methods have been discussed in previous publications (see Table 1 for sources and references). For general background information on the use of historical sources and relevant concepts, see, e.g., Hooke and Kain (1982; particularly chap. 3 on accuracy and analysis), Petts et al. (1989), or Gurnell et al. (2003).
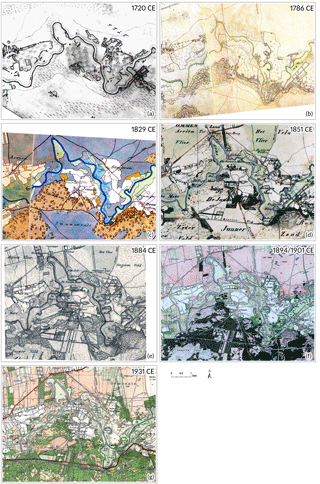
Figure 2(a–e) Sections of historical maps displaying the study area (for explanation refer to Table 1); (g) map showing the same area in 1931 CE (publication date). As section (f) consists of two map sheets two dates are listed (details in Table 1). Image references: (a) Algemeen Rijks Archief, Genie-archief, situatiekaart 07; (b) Versfelt (2003); (c) Versfelt and Schroor (2005); (d) CC-BY Kadaster (2018a); (e) CC-BY Kadaster (2018b); (f) CC-BY Kadaster (2018c); (g) CC-BY Kadaster (2018d).
The relevant map parts were used with the given digital image quality or scanned and saved at a resolution of 600 dpi. The maps were georeferenced using Esri's ArcMap (versions 10.3.1 and 10.5) based on static landscape features (e.g. churches, road crossings) that were displayed on both historical and reference maps. For the latter we used a digital elevation model (AHN2, 5 m horizontal resolution, 0.2 m vertical resolution) and a recent topographical map (OpenTopo) (AHN, 2018; Van Heerd et al., 2000; Van Aalst, 2017). Georeferencing maps of river landscapes can be challenging due to limited presence of stable landscape features in floodplains. As the valley of the Overijsselse Vecht is rather narrow (Fig. 1a), we were able to adequately georeference the map sections based on GCPs (ground control points) located close to, but not inside, the floodplain. We predominantly made use of clearly delineated features such as road crossings but occasionally included features with more irregular edges such as arable fields (ground control points are available in the Supplement). Maps were georectified using a first-order polynomial transformation (following, e.g., Downward et al., 1994; Leys and Werritty, 1999) and nearest-neighbour pixel resampling as this resulted in the sharpest display of the river channel (based on visual assessment). Subsequently all maps were displayed using the Dutch RDnew projection. The ground control points were exported from ArcMap as a *.txt file to use in the freely available software MapAnalyst (see below). Map quality was analysed using (1) a quantification of geospatial error or planimetric accuracy and (2) visualizations of geodetic distortions as generated by MapAnalyst. Both aspects are explained below.
3.2.2 Quantifying geospatial error
The root mean square error (RMSE) of the displacement vectors of the GCPs is often used as a quantification of geospatial error and was automatically calculated by ArcMap (Esri, 2018) according to
where and respectively represent the x and y component of the displacement vector that indicates the difference between the location of GCP i on the reference map and the location of the same point on the historical map after first-order polynomial transformation. The total number of GCPs is indicated by n. The RMSE was used to assess geospatial error or planimetric accuracy (for the range of spatial errors see RMSEs in Table 1), defined as “the extent to which distances and bearings between identifiable objects coincide with their true values” (Jenny and Hurni, 2011).
After georeferencing, the channel centre line was deduced from each map to reconstruct the channel position for each time slice. The RMSE was used to draw an error band around each centre line. The centre line and error band represent the positional mean and related standard deviation respectively. The channel centre lines and error bands were subsequently used in the chronological modelling (see Sect. 3.4). The final position of both investigated meanders was based on the abandoned channel as displayed by the DEM of the present-day situation. Historical evidence indicates that Prathoek was channelized between 1884 and 1901 CE (Fig. 2ef). Junner Koeland was channelized between 1894 (Fig. 2f) and 1906 CE, as indicated by the topographical map of the Netherlands 1 : 50 000 (map sheet Coevorden, surveyed between 1900 and 1906; not shown).
3.2.3 Visualization of geodetic distortion
Distortion grids were generated for each map section based on the GCPs using the software MapAnalyst (Jenny and Hurni, 2011; http://mapanalyst.org/, last access: 12 September 2017). A world file (*.txt) was created for the reference image and, together with the historical map image, loaded in MapAnalyst. In the *.txt file with GCPs that was generated with ArcMap, the first two columns show the map points indicated in pixel rows/columns, using the upper left corner as the origin. The third and fourth column show the points of the reference image, using the units of its coordinate system (in our case the Dutch RDnew projection with units in metres). Using a text editor, the points for the map and reference image were split into two separate files. In addition, each point pair was assigned an ID number in the first column to allow MapAnalyst to link the point pairs from the two files. For the map images MapAnalyst uses the lower left corner as origin instead of the upper left corner as is done in ArcMap; therefore, the pixel values in the y direction for the map points were converted prior to loading them in MapAnalyst. Map distortions were calculated using a 1 km raster and exported as *.png images.
3.3 OSL dating
OSL dating makes use of a low-intensity light signal emitted by mineral grains (e.g. quartz) upon optical stimulation. The intensity of the signal can be linked to the age of the sediment. The (latent) OSL signal builds up as the grains are exposed to natural ionizing radiation in the environment (from uranium, thorium, potassium, and cosmic rays; known as the environmental dose), which causes the accumulation of trapped charge in the crystal structure. When the grains are exposed to daylight during transport, the trapped charge is released and the OSL signal is reduced (bleached) to a low level, often close to zero. When the grains are deposited and buried, they are no longer exposed to light and the signal can build up again.
Through a comparison of the natural luminescence signal with that induced by laboratory irradiation, the environmental dose received by the grains since burial can be estimated (the palaeo-dose). Combined with information on the environmental dose rate experienced by the grains, the age can be calculated by age (ka) = palaeo-dose (Gy) ∕ dose rate (Gy ka−1) (see, e.g., Rhodes, 2011 for more information on OSL dating).
With dating of fluvial sediments, the assumption in luminescence dating that the OSL signal was completely zeroed prior to sediment burial is questionable (Murray et al., 1995) due to the limited exposure of grains to light when transported in turbid water (e.g. Wallinga, 2002a). This means that at the time of sediment burial, some trapped charge that was built up since the previous deposition may remain, which may consequently lead to a remnant OSL signal upon deposition and an overestimation of the age. Poorly bleached sediments mostly consist of a mixture of poorly bleached and well-bleached grains (Olley et al., 1998), which can be detected by broad and skewed equivalent dose distributions (e.g. Wallinga, 2002b). Heterogeneous bleaching in channel site samples may result in apparent doses ranging over several orders of magnitude and may limit the accuracy of dates (Murray et al., 1995; Olley et al., 1998), although methods have been developed to largely overcome these challenges (e.g. Galbraith et al., 1999; Cunningham and Wallinga, 2012).
3.3.1 OSL sampling
In total 10 samples were collected for OSL dating to determine the time of deposition and burial of the sediments. Six samples were collected in the Junner Koeland scroll bar deposits, three samples in the scroll bar deposits of Prathoek, and one sample in an early Holocene fluvial terrace remnant near Prathoek. To reduce the chances of sampling sediments that were reworked after initial scroll bar formation, we avoided sampling in swales. Samples were roughly evenly distributed over the scroll bar sequence (sample spacing ∼200 m; see Fig. 1b and c). The scroll bar samples were collected just above the channel lag deposit because (1) the channel lag can generally be recognized easily, thereby preventing accidentally sampling older deposits below the scroll bar deposit, (2) at this depth recent aeolian reworking of sediment can be excluded, and (3) the channel lag is located below the oxidation–reduction zone, supporting the assumption that the sediments have been water-saturated since deposition (and thus reducing uncertainty in calculating the environmental dose rate).
Samples for OSL dating were obtained through a modified Van der Staay suction corer (Wallinga and Van der Staay, 1999). First a hole was augered down to the desired depth, using an Edelman auger above the groundwater level and the suction corer below groundwater level. Then, the suction corer, with a loosely fitted PVC sample tube of 30 cm length at its end, was inserted in the hole and pushed down to the lower sample depth. After retrieving the suction corer, the sample tube was removed, and both ends were immediately covered with plastic caps and taped with light-impermeable black tape. Sampling locations were recorded with a GPS device with a horizontal precision of around 5 m.
3.3.2 OSL measurements
The samples were analysed in the laboratory of the Netherlands Centre for Luminescence dating in Wageningen, the Netherlands. Under amber safelight conditions, the sample tubes were opened and two subsamples were obtained from each core; material from the light-exposed outer ends of the tube was prepared for dose rate estimation (Sect. 3.3.3), while the material from the inside of the tube was suitable for palaeo-dose estimation. Luminescence measurements were performed on quartz grains of the fraction 212–250 µm. This fraction was obtained by a combination of sieving and subsequent treatment with HCl (to remove carbonates), H2O2 (to remove organic material), and HF (45 min at 40 %, to dissolve feldspars and etch the quartz grains). Samples were measured on a Risø TL/OSL DA-20 reader, using blue LEDs for stimulation and a 7.5 mm U340 filter for detection. The single-aliquot regenerative-dose protocol (SAR) (Murray and Roberts, 1998; Murray and Wintle, 2000, 2003) was used, with details as listed in Table 2. Net OSL signals were obtained using an early background subtraction approach (Cunningham and Wallinga, 2010). The preheat temperature was selected based on preheat plateau tests. With the applied procedure, a laboratory dose (i.e. exposure to a known amount of radiation) could accurately be recovered, as indicated by the average dose recovery ratio of 1.03±0.01. At least 22 aliquots, each consisting of ∼75 grains (2 mm mask size), were measured per sample (31 aliquots on average). The equivalent dose distributions were displayed in radial plots, constructed with the Luminescence package (Kreutzer et al., 2015) employed in R (version 3.2.4).
3.3.3 Dose rate
Light-exposed material from the outer ends of the sample tubes was prepared for dose rate estimation. Samples were dried and combusted, allowing the measurement of water and organic content, and then mixed with wax and moulded into pucks. These were measured on a high-resolution broad-range gamma-ray spectrometer, to determine radionuclide concentrations of K-40 and several radionuclides in the U and Th decay chains. From these, dose rates experienced by the quartz grains were calculated, taking into account attenuation due to water, organics, and grain size, and adding a contribution from cosmic rays (assuming instant burial to present depth). Methods are detailed in Wallinga and Bos (2010).
3.3.4 Palaeo-dose estimation
We analysed the equivalent dose distributions of all samples from scroll bar deposits using the unlogged version of the bootstrapped Minimum Age Model (bsMAM; Galbraith et al., 1999; Cunningham and Wallinga, 2012). This approach is specifically suited to our project as it takes into account the uncertainty of σb (see below) and allows the construction of likelihood distributions of the palaeo-dose, which can be used as priors for Bayesian analysis (Cunningham and Wallinga, 2012). The unlogged version of the MAM (Minimum Age Model) was used, as the logged version was not applicable to the youngest samples. Being aware of reservations with regard to using the unlogged model for older samples (Arnold et al., 2009), we checked that, for older samples, the results of logged and unlogged models were in agreement.
The (bootstrapped) MAM requires an estimate of overdispersion in the distribution that is not caused by heterogeneous bleaching (σb). Ideally, this estimate is based on the observed overdispersion for well-bleached samples from the same lithology, depositional environment, and age (e.g. Chamberlain et al., 2018). As none of the samples obtained from the Holocene scroll bars appeared to be well-bleached, we had to take another approach. This alternative is provided by the overdispersion obtained for the oldest and best-bleached sample (NCL-2415163; De distribution available in Fig. 6b), which was collected from an early Holocene terrace remnant. Although the depositional environment and age are different, the lithology of the material is nearly identical as the scroll bar deposits consist mostly of reworked fluvial deposits of Late Pleistocene/early Holocene age. The overdispersion of sample NCL-2415163 was 0.15±0.03, and this value was used as σb input for the bsMAM model. The bootstrapped MAM analysis of the equivalent dose distribution is combined with the sample dose rate to provide a likelihood distribution of estimated burial ages for each sample (see Cunningham and Wallinga, 2012). These age likelihood distributions are implemented as OSL priors in the Bayesian modelling (see Sect. 3.4). Sample NCL-2415163 did not suffer from poor bleaching and based on the normally distributed and relatively narrow equivalent dose distribution for this sample, the Central Age Model (CAM; Galbraith et al., 1999) was adopted for palaeo-dose estimation.
3.4 Bayesian reconstruction of river channel position
Bayesian statistical approaches were used to combine the numerical age data obtained from the historical maps and OSL dating, with auxiliary data on the stratigraphic order. This analysis was performed using the freely available OxCal software (version 3.4; main introduction to the programme described by Bronk Ramsey, 1995; see also Bronk Ramsey, 2009). Bayesian analyses of deposition sequences are normally based on age versus depth profiles (Bronk Ramsey, 2008). Here, we analyse age as a function of lateral migration distance, where the location of the oldest swale (meander base) is taken as the origin and distance is measured along the central axis of the scroll bar deposits. For each of the age constraints (OSL sample age or survey age of a historical map), we have both an age and a location along the central axis. In addition, we know that the meander grew from its base to the final position, providing an order for all information. In the Bayesian approach, all this information is combined to obtain a robust reconstruction of the channel position through time.
To jointly analyse the OSL priors and the historical map data, both were added as entries in a Bayesian deposition model using the P_Sequence (Fig. 3). This command fixes the chronology of the sampling points using the known order of events (based on the known meander expansion direction) and makes use of a Poisson distribution. With this depositional model, channel migration is assumed to be random (i.e. varying in rate but always positive) giving approximate proportionality to distance (factor z) (Bronk Ramsey, 2008). The P_Sequence model needs information on the size of the units (deposition events) within the sequence. Here, we chose to use the average dimension of a scroll bar as unit, i.e. the mean distance between two swales. Based on meander amplitude and the visual counting of scroll bars from the DEM, this distance was estimated to be 77 and 42 m for Junner Koeland and Prathoek respectively. This provides an event spacing (k0 value) of 0.013 events m−1 for Junner Koeland and 0.024 events m−1 for Prathoek. By applying the regular boundary function, the entire distributions were allowed to be used in the calculation.
Likelihood distributions of estimated burial age (see Sect. 3.3.4) were uploaded to the OxCal directory as priors (*.prior file), with the unit in years CE. For this OSL age data, the position is relatively well known (∼5 m), while there is considerable uncertainty in the time domain (age estimate).

Figure 3OxCal script as used for the fourth iteration for Junner Koeland. A similar script was used for Prathoek.
For the historical map data we assume the age is known exactly (survey date; see Table 1), while reconstructed locations are uncertain (up to 107 m; see RMSEs in Table 1). Incorporating this data into the Bayesian model requires uncertainty to be expressed in the time domain rather than spatial domain. Moreover, a slight correction is needed as the OSL data provide age information on the scroll bar formation (i.e. inner bank), while the channel centre line was reconstructed from the maps. Channel width varied significantly between the historical maps and may not represent the true low-water channel width of past times. The historical river channel was therefore deduced from each map as a low-water channel centre line. To make sure that the age of the map is assigned to the inner bank instead of the channel centre in the chronological analysis, we corrected the distance (z value) for each centre line using half the channel width. For this calculation, we assumed that channel width has been relatively stable throughout meander formation and is represented by the width of the abandoned channel (∼30 m) as derived from the DEM (Fig. 1).
Uncertainty in the spatial domain was calculated for each map based on σ (see Sect. 3.2.2) and assuming a normal distribution. To transpose this spatial uncertainty to an age uncertainty, the migration rate of the channel is required. This provides a problem, as the procedure aims at a reconstruction of channel position through time, which is needed to determine the migration rate. Nevertheless, a crude estimation of migration rate is possible based on the available data, and an iterative approach can be used to improve this estimation with the model output. For the first iteration error bands were converted to years using an estimated migration rate based on the bsMAM age of the OSL sample closest to the meander base and historically known maximum channelization date (1894 and 1906 CE for Prathoek and Junner Koeland respectively), when the channel reached its final position. For subsequent iterations, migration speed was calculated for each map individually by dividing the difference between the modelled mean ages for its error boundaries (in years) by the error width (in m). This migration rate was then used to convert RMSE (available in Table 1) to years. The converted RMSE (i.e. σ) was used together with the map age (i.e. the mean) as input for the next iteration. This process was repeated until the model outcome converged and remained stable. This required four iterations of the Bayesian model for both investigated meander bends.
Queries were built into the model to generate output for the requested distances, including the meander base (calculated by OxCal using extrapolation of the model; consequently, the uncertainty for this point will be larger) and the spatial boundaries of each error band to allow the calculation of a migration speed for each historical map as described above.
Upon convergence and stabilization of the model outcome, the deposition model of the final (i.e. fourth) iteration was used to interpolate ages throughout the scroll bar deposits. Using the graphical options in OxCal, interpolation results were plotted versus distance from the meander base as the origin toward the meander apex using linear interpolation in between the data points. Plots of the input data were created with the ggplot2 package (Wickham and Chang, 2016) employed in R (version 3.4.0).
We performed sensitivity tests to check model sensitivity to (1) the initial migration rate that was used to convert error bands to years, (2) the correction for channel width, and (3) a rigid versus variable k0 value. Test outcomes indicated that (1) either increasing or decreasing the initial migration rate by a factor of 2 yielded similar results after several iterations, (2) model outcome with and without using the channel correction differed only by a couple of years, and (3) a rigid or variable k0 value resulted in age differences of no more than 1 year. Based on these tests we concluded that model sensitivity to these factors is minor.
4.1 Historical maps
Figure 4 shows the distortion grid for the map of 1851 CE. As the grid appears virtually straight, geodetic distortions in the map section are minimal. Distortion grids for the other maps were similar (provided in the Supplement).
Table 3Results of the OSL dating. JK: Junner Koeland; PH: Prathoek; RD: Dutch coordinate system (Rijksdriehoekstelsel). Palaeo-doses and ages are based on the bootstrapped Minimum Age Model for all samples from scroll bar deposits (JK and PH) and the Central Age Model for the terrace sample; n/a: not applicable.
The channel centre lines that were deduced from the maps are shown in Fig. 5. On the map of 1894, Prathoek is already channelized (Fig. 2); therefore, this line is only drawn for Junner Koeland. Based on the current DEM and coring evidence, the georeferenced map dating from 1720 had to be rejected from the Bayesian modelling based on obviously erroneous representation of the river course. The 1720 map depicted the Junner Koeland meander where corings proved that river deposits were lacking, i.e. located too far west by up to 80 m. We tried to include the georeferenced map of 1786 in the Bayesian modelling, but this map resulted in poor model agreement (further discussed below). The correctness of this map was doubted because it displays the meander apex at Prathoek directed southwards instead of southwest like the other channel centre lines (Fig. 5). This would indicate that sedimentation towards the inner bend has taken place in order to move the apex westward, which seems unlikely. Based on this improbable meander planform and the statistical issue created by this map in the Bayesian modelling, we excluded it from further analyses.
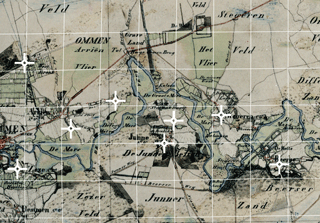
Figure 4Section of the georeferenced historical map of 1851 CE (details listed in Table 1), displaying ground control points (white crosses) and a distortion grid (in white; maze size of 1 km). The grid approaches a perfect grid, indicating that map distortion is minimal. Grid generated with MapAnalyst software by Jenny and Hurni (2011). Image reference historical map: CC-BY Kadaster (2018a).
4.2 OSL ages
The results of the OSL dating and bsMAM calculations are presented in Table 3. The spread in the equivalent doses of single aliquots for the scroll bar samples (example in Fig. 6a) shows that light exposure of the grains prior to deposition and burial was not sufficient to completely reset the quartz OSL signal of all grains. Strikingly, the equivalent dose distribution of many samples shows two distinct peaks: a younger population representing the age of recent transportation and deposition by the river and an older population with an age of about 11 ka, likely representing the depositional age of the grains prior to erosion and transport by the late Holocene Vecht river, as indicated by the OSL age obtained on a terrace remnant at Prathoek (circa 11 ka, Fig. 6b).
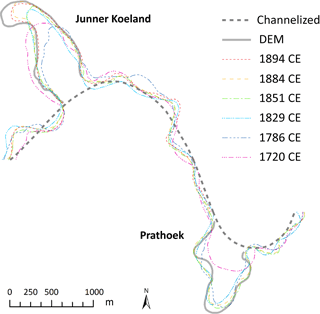
Figure 5Channel centre lines as derived from the historical maps listed in Table 1 and shown in Fig. 2. The DEM (digital elevation model) line represents the course of the meanders preserved upon abandonment at the time of channelization (between 1884 and 1901 CE for Prathoek and between 1894 and 1906 CE for Junner Koeland).
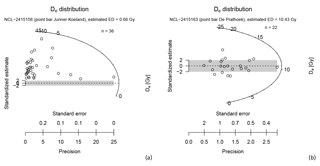
Figure 6Two radial plot examples showing (a) a scroll bar sample (NCL-2415156) from Junner Koeland and (b) the sample collected in a terrace remnant near Prathoek (NCL-2415163). The scroll bar sample in panel (a) is poorly bleached, showing a large population of grains with a De of about 10 Gy. Such equivalent doses are similar to those of the terrace sample in panel (b) (CAM: De10.43±0.43 Gy).
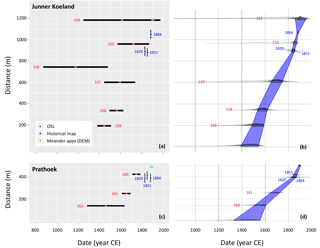
Figure 7Comparison of results before (a, c) and after (b, d) the Bayesian modelling for Junner Koeland (a, b) and Prathoek (c, d). Panels (a), (b) and (c), (d) have equal y axes, and panels (a), (c) and (b), (d) have equal x axes. The legend in panel (a) also applies to panel (c). In panels (a) and (c) the historical map data are indicated with error bars displaying RMSE of the georeferencing procedure (in m); the OSL results of the bootstrapped Minimum Age Model indicate the modelled mean and 1σ error bar (in years). In panels (b) and (d) the blue areas in the Bayesian models indicate the 68.2 % confidence interval. The data point indicating the meander base in panels (b) and (d) is calculated through extrapolation by the Bayesian model. The slope of the graphs in panels (b) and (d) indicates lateral migration rate. Red numbers indicate OSL samples (all should be preceded by NCL-2415). Blue numbers indicate the age of the historical maps (years CE) as used in the Bayesian analysis.
4.3 Reconstructed channel position and chronology
The Bayesian model was iteratively repeated until model results converged to similar output, which occurred after four iterations for both Junner Koeland and Prathoek; therefore, the deposition models that resulted from these iterations were used to interpolate ages throughout the scroll bar deposits. Table 4 lists both the un-modelled and modelled ages. The model agreement index (A value) should be above 60 % to indicate proper model functioning (Bronk Ramsey, 1995). The high A values in Table 4 show that the modelled ages fit the data well. The graphical output of the model as generated by OxCal is displayed on the right in Fig. 7b and d and demonstrates the improvement of the geochronology after the Bayesian modelling compared to the un-modelled data points shown on the left in Fig. 7a and c.
Table 4Results of the Bayesian model for (a) Junner Koeland, iteration 4, and (b) Prathoek, iteration 4.
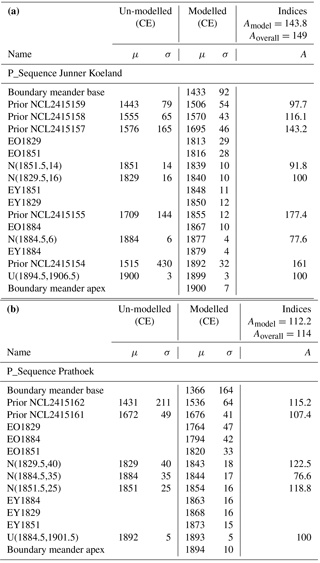
OSL sample NCL-2415156 suffered from very poor bleaching (Fig. 6a) and therefore had to be rejected from the Junner Koeland model; otherwise the model A value did not rise above 60 %. In addition, the historical map of 1894 had to excluded, as it resulted in poor agreement that could not be resolved by adjusting the model (e.g. k0 value). In the fourth (and final) iteration, the model had an A value of 143.8 % (Table 4a). For Prathoek, the poorly bleached sample NCL-2415160 resulted in poor agreement; after excluding this entry, the A value of the fourth iteration amounted to 112.2 %.
The Bayesian model also allows extrapolation of the results towards the meander base (Fig. 7). In our study area the positions of the two meander bases appear to be located close to the former valley side (Fig. 1); therefore, the modelled ages of the meander bases indicate the moment when the meanders sufficiently eroded the valley side to break free from lateral confinement. Model results indicate that this took place during the fourteenth century CE for Prathoek and about 65 years later during the fifteenth century for Junner Koeland. Subsequently, the meanders migrated outside the former river valley, reworking unconsolidated Pleistocene fluvial deposits and coversands, locally with Holocene drift sand on top. This occurred at an average rate of 2.6 and 0.9 m yr−1 for Junner Koeland and Prathoek respectively (calculated by dividing the distance from meander base to apex by the difference between their modelled mean ages). For both meanders, there seems to be an increase in lateral migration rate in the final stages prior to abandonment, roughly between 1825 and 1900 CE.
Our study demonstrates that the presented Bayesian chronological modelling approach combining OSL and historical map data improves the robustness of fluvial chronologies and can elongate them into longer time frames, compared to what could be achieved by using either data type separately (Fig. 7).
The use of historical maps to determine fluvial migration rates is often challenging due to limited options for georeferencing and uncertainty regarding planimetric accuracy. Historical maps can offer a diachronic perspective on the development of meander shape and channel position (Figs. 2, 5). For our case study this was, however, limited to recent history (after 1720 CE). When going further back in time, the availability of historical maps was limited and map quality was generally too coarse for a detailed reconstruction of meander migration. Doubts regarding the correctness of the maps dating from 1720 and 1786 resulted in excluding these maps from the Bayesian analysis in our study.
With a limited number of GCPs RMSE might underestimate the geospatial error (Esri, 2018; Hughes et al., 2006). When used as a rigid buffer around channel centre lines to determine whether channel changes larger than the assumed error buffer occurred (i.e. deviations that are so large that they cannot emerge from error) (e.g. Urban and Rhoads, 2003; Rhoades et al., 2009), this may result in not detecting small channel changes and could lead to false interpretations of channel stability. Other approaches have been proposed to account for this problem by analysing independent test points or using cross-validation techniques to develop spatially variable error buffers (Hughes et al., 2006; Lea and Legleiter, 2016). However, these methods were developed for aerial imagery where temporal uncertainty is absent and do not convert uncertainty in the spatial domain to uncertainty in the temporal domain. Additionally these methods generally require higher numbers of GCPs than could be registered for georeferencing the historical maps (e.g. 35 per image as used by Lea and Legleiter, 2016). In contrast, the Bayesian modelling methodology that we have presented permits a flexible interpretation of the RMSE buffer, which can easily be calculated even with lower numbers of GCPs, and the iterative procedure with the Bayesian model allows the conversion of the geospatial error into temporal uncertainty. This temporal uncertainty is included in the model as a probability density function, i.e. allowing all channel positions but each with a specific probability of occurrence.
In our analysis there are two potential sources of spatial uncertainty. The first is error in the GPS-measured location of OSL samples (∼5 m). The second is the distance between channel centre line (derived from the historical maps) and scroll bar deposit formed in the inner bend. As the historical maps are likely to display the low-water channel, we made use of the width of the low-water abandoned channel (as depicted on the DEM of the present situation) for deriving the location of scroll bar deposition from the channel centre lines (assuming a constant channel width of ∼30 m). There are indications that bankfull width varied over time (Candel et al., 2018), which would result in an additional spatial error in the location of scroll bar deposition. However, our sensitivity analyses indicate that minor changes in the location of model entries (i.e changing their z value by 15 m) has very limited effect on model outcome (i.e. only a couple of years), indicating model robustness against channel width changes and possible errors due to GPS accuracy of OSL sample locations.
The use of OSL to date young fluvial sediments is challenging, as limited light exposure during the subaqueous transport of grains in a turbid river may lead to an incomplete resetting of the OSL signal in at least part of the grains (Wallinga, 2002b). As demonstrated by Fig. 6 the sediments were indeed affected by poor bleaching, in some cases so extreme that the equivalent dose determined on most aliquots reflected the burial dose of the source material rather than the deposit of interest. The bootstrapped MAM approach yields very large uncertainties in such cases, and the Bayesian analysis indicates that these uncertainty estimates are reasonable. Only for two samples (NCL-2415156 and NCL-2415160, i.e. one from each meander) was the OSL age rejected by the Bayesian model. The Bayesian modelling significantly enhanced the interpretation of the OSL dating results and the robustness of the geochronology.
Through extrapolation, the Bayesian model could estimate the date of meander expansion beyond the former valley sides. From this pivotal moment in time, the meanders were no longer confined and large meanders formed. Our results indicate average lateral migration rates of 2.6 and 0.9 m yr−1 for Junner Koeland and Prathoek respectively. It seems likely that migration rates may have been much higher during brief periods, alternating with periods of relative standstill (Gurnell et al., 1994). However, our chronological data lack the precision and resolution to identify such fluctuations, possibly with the exception of a period with rapid migration in the period 1825–1900 CE.
The methods outlined in this paper provide the chronological constraints that are needed to relate meander expansion beyond the former valley side and changing river dynamics to climate and land-use changes. Such analysis is beyond the scope of this contribution and is reported separately by Candel et al. (2018).
Our study demonstrates that combining historical map data and OSL dates in the presented Bayesian modelling approach yields an integrated geochronology with a higher robustness than the sum of its parts. The analysis requires conversion of geospatial error from the historical maps into a temporal uncertainty, and we show that this is possible through an iterative approach. Our method incorporates the strengths of both data types (historical maps and OSL dating) for reconstructing fluvial morphodynamics and supports elongating fluvial sequences into larger time frames. Our study indicates that the meanders of the Overijsselse Vecht expanded beyond the former valley sides from about 1400 CE onwards and that the channels migrated at an average rate of up to 2.6 m year−1 during their lifetime (1400–1900 CE).
All data from this study are available under CC-BY 4.0 license at the 4TU.Centre for Research Data; see Quik and Wallinga (2018).
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-6-705-2018-supplement.
CQ performed the analyses of historical maps, while JW led OSL analyses. Subsequently CQ combined both data types in a Bayesian framework under JW's supervision. CQ wrote the draft manuscript, which was then improved and finalized by both authors.
The authors declare that they have no conflict of interest.
We would like to thank Ruud Jonker (Staatsbosbeheer Vechtdal) and Jan de Roos
(Camping de Roos) for the permission to do field work at Junner Koeland and
Prathoek; Jasper Candel and Wim Hoek for field assistance with OSL sample
collection; Alice Versendaal and Erna Voskuilen of the Netherlands Centre for
Luminescence dating for their work on the OSL samples; Gerard Heuvelink and
Sytze de Bruin for discussions on planimetric accuracy issues and statistics;
Roy van Beek, Erik van den Berg, and Gilbert Maas for assistance in
collecting historical maps; students Sjoukje de Lange, Jip Zinsmeister,
Pascal Born, and Karianne van der Werf of Utrecht University for their work
on the scroll bar coring transects; and Duco de Vries for his explanation on
the R Luminescence package. The constructive reviews of Ed Rhodes and
Janet Hooke formed a valuable contribution to the manuscript.
Edited by: Jean Braun
Reviewed by: Ed Rhodes
and Janet Hooke
AHN: De details van het Actueel Hoogtebestand Nederland (Details of the Digital Elevation Model of The Netherlands), available at: http://ahn.maps.arcgis.com/apps/Cascade/index.html?appid=75245be5e0384d47856d2b912fc1b7ed, last access: 22 February 2018.
Arnold, L. J., Roberts, R. G., Galbraith, R. F., and DeLong, S. B.: A revised burial dose estimation procedure for optical dating of young and modern-age sediments, Quat. Geochronol., 4, 306–325, https://doi.org/10.1016/j.quageo.2009.02.017, 2009.
Ballarini, M., Wallinga, J., Murray, A. S., Van Heteren, S., Oost, A. P., Bos, A. J. J., and Van Eijk, C. W. E.: Optical dating of young coastal dunes on a decadal time scale, Quaternary Sci. Rev., 22, 1011–1017, https://doi.org/10.1016/S0277-3791(03)00043-X, 2003.
Box, L.: Pieter de La Rive (1694–1771) “Directeur der Fortificatiën van Maastricht,” Caert Thresoor – Tijdschr. voor Geschied. van Cartogr., 3, 65–69, 2007.
Bronk Ramsey, C.: Radiocarbon calibration and analysis of stratigraphy: the OxCal program, Radiocarbon, 37, 425–430, https://doi.org/10.2458/rc.v37i2.1690, 1995.
Bronk Ramsey, C.: Deposition models for chronological records, Quaternary Sci. Rev., 27, 42–60, https://doi.org/10.1016/j.quascirev.2007.01.019, 2008.
Bronk Ramsey, C.: Bayesian analysis of radiocarbon dates, Radiocarbon, 51, 337–360, 2009.
Candel, J. H. J., Kleinhans, M. G., Makaske, B., Hoek, W. Z., Quik, C., and Wallinga, J.: Late Holocene channel pattern change from laterally stable to meandering caused by climate and land use changes, Earth Surf. Dynam. Discuss., https://doi.org/10.5194/esurf-2018-31, in review, 2018.
Chamberlain, E. L., Törnqvist, T. E., Shen, Z., Mauz, B., and Wallinga, J.: Anatomy of Mississippi Delta growth and its implications for coastal restoration, Sci. Adv., 4, eaar4740, https://doi.org/10.1126/sciadv.aar4740, 2018.
Clark-Balzan, L. A., Candy, I., Schwenninger, J. L., Bouzouggar, A., Blockley, S., Nathan, R., and Barton, R. N. E.: Coupled U-series and OSL dating of a Late Pleistocene cave sediment sequence, Morocco, North Africa: Significance for constructing Palaeolithic chronologies, Quat. Geochronol., 12, 53–64, https://doi.org/10.1016/j.quageo.2012.06.006, 2012.
Clemmensen, L. B., Bjørnsen, M., Murray, A., and Pedersen, K.: Formation of aeolian dunes on Anholt, Denmark since AD 1560: A record of deforestation and increased storminess, Sediment. Geol., 199, 171–187, https://doi.org/10.1016/j.sedgeo.2007.01.025, 2007.
Cunningham, A. C. and Wallinga, J.: Selection of integration time intervals for quartz OSL decay curves, Quat. Geochronol., 5, 657–666, https://doi.org/10.1016/j.quageo.2010.08.004, 2010.
Cunningham, A. C. and Wallinga, J.: Realizing the potential of fluvial archives using robust OSL chronologies, Quat. Geochronol., 12, 98–106, https://doi.org/10.1016/j.quageo.2012.05.007, 2012.
De Moor, J. J. W., Kasse, C., van Balen, R., Vandenberghe, J., and Wallinga, J.: Human and climate impact on catchment development during the Holocene – Geul River, the Netherlands, Geomorphology, 98, 316–339, https://doi.org/10.1016/j.geomorph.2006.12.033, 2008.
Downward, S. R., Gurnell, A. M., and Brookes, A.: A methodology for quantifying river channel planform change using GIS, IAHS Publ. Proc. Reports-Intern. Assoc. Hydrol. Sci., 224, 449–456, 1994.
Dreibrodt, S., Lubos, C., Terhorst, B., Damm, B., and Bork, H. R.: Historical soil erosion by water in Germany: Scales and archives, chronology, research perspectives, Quatern. Int., 222, 80–95, https://doi.org/10.1016/j.quaint.2009.06.014, 2010.
Duursema, G.: Leidraad voor ecologisch herstel van de Overijsselse Vecht, Waterschap Velt en Vecht, Coevorden, the Netherlands, 2004.
Eekhout, J. P. C., Hoitink, A. J. F., and Makaske, B.: Historical analysis indicates seepage control on initiation of meandering, Earth Surf. Proc. Land., 38, 888–897, https://doi.org/10.1002/esp.3376, 2013.
Esri: Fundamentals of georeferencing a raster dataset, available at http://desktop.arcgis.com/en/arcmap/10.3/manage-data/raster-and-images/fundamentals-for-georeferencing-a-raster-dataset.htm, last access: 25 January 2018.
Frings, R., Berbee, B., Erkens, G., Kleinhans, M., and Gouw, M.: Human-induced changes in bed shear stress and bed grain size in the River Waal (The Netherlands) during the past 900 years, Earth Surf. Proc. Land., 34, 503–514, https://doi.org/10.1002/esp.1746, 2009.
Galbraith, R. F., Roberts, R. G., Laslett, G. M., Yoshida, H., and Olley, J. M.: Optical dating of single and multiple grains of quartz from Jinmium rock shelter, Northern Australia: Part I, Experimental design and statistical models, Archaeometry, 41, 339–364, https://doi.org/10.1111/j.1475-4754.1999.tb00987.x, 1999.
Grabowski, R. C., Surian, N., and Gurnell, A. M.: Characterizing geomorphological change to support sustainable river restoration and management, Wiley Interdiscip. Rev. Water, 1, 483–512, https://doi.org/10.1002/wat2.1037, 2014.
Guérin, G., Antoine, P., Schmidt, E., Goval, E., Hérisson, D., Jamet, G., Reyss, J. L., Shao, Q., Philippe, A., Vibet, M. A., and Bahain, J. J.: Chronology of the Upper Pleistocene loess sequence of Havrincourt (France) and associated Palaeolithic occupations: A Bayesian approach from pedostratigraphy, OSL, radiocarbon, TL and ESR/U-series data, Quat. Geochronol., 42, 15–30, https://doi.org/10.1016/j.quageo.2017.07.001, 2017.
Güneralp, I. and Rhoads, B. L.: Influence of floodplain erosional heterogeneity on planform complexity of meandering rivers, Geophys. Res. Lett., 38, 1–6, https://doi.org/10.1029/2011GL048134, 2011.
Gurnell, A. M., Downward, S. R., and Jones, R.: Channel planform change on the river dee meanders, 1876–1992, Regul. River., 9, 187–204, https://doi.org/10.1002/rrr.3450090402, 1994.
Gurnell, A. M., Peiry, J. L., and Petts, G.: Using historical data in fluvial geomorphology, in: Tools in Fluvial Geomorphology, edited by: Kondolf, G. M. and Piégay, H., John Wiley & Sons, Ltd., Chichester, UK, 77–101, 2003.
Hesselink, A. W., Weerts, H. J. T., and Berendsen, H. J. A.: Alluvial architecture of the human-influenced river Rhine, The Netherlands, Sediment. Geol., 161, 229–248, https://doi.org/10.1016/S0037-0738(03)00116-7, 2003.
Hobo, N., Makaske, B., Wallinga, J., and Middelkoop, H.: Reconstruction of eroded and deposited sediment volumes of the embanked River Waal, the Netherlands, for the period AD 1631–present, Earth Surf. Proc. Land., 39(10), 1301–1318, https://doi.org/10.1002/esp.3525, 2014.
Hoffmann, T., Erkens, G., Gerlach, R., Klostermann, J., and Lang, A.: Trends and controls of Holocene floodplain sedimentation in the Rhine catchment, Catena, 77, 96–106, https://doi.org/10.1016/j.catena.2008.09.002, 2009.
Hooke, J. M.: River Meandering, in: Treatise on Geomorphology, edited by: Shroder, J. and Wohl, E., Academic Press (Elsevier Inc.), San Diego, CA, USA, 2013.
Hooke, J. M. and Kain, R. J. P.: Historical Change in the Physical Environment: A Guide to Sources and Techniques, edited by: Gregory, K. J., Butterworths, London, UK, 1982.
Hooke, J. M. and Yorke, L.: Rates, distributions and mechanisms of change in meander morphology over decadal timescales, River Dane, UK, Earth Surf. Proc. Land., 35, 1601–1614, https://doi.org/10.1002/esp.2079, 2010.
Hughes, M. L., McDowell, P. F., and Marcus, W. A.: Accuracy assessment of georectified aerial photographs: Implications for measuring lateral channel movement in a GIS, Geomorphology, 74, 1–16, https://doi.org/10.1016/j.geomorph.2005.07.001, 2006.
Jenny, B. and Hurni, L.: Studying cartographic heritage: Analysis and visualization of geometric distortions, Comput. Graph., 35, 402–411, https://doi.org/10.1016/j.cag.2011.01.005, 2011.
Kadaster: Topographische en Militaire Kaart van het Koninkrijk der Nederlanden, 1 : 50 000, map sheet 22 (publication date 1859), Digital file, Kadaster, Apeldoorn, the Netherlands, 2018a.
Kadaster: Topographical map of the Netherlands (Bonne), map sheet Coevorden (publication date 1897), Digital file, Kadaster, Apeldoorn, the Netherlands, 2018b.
Kadaster: Topographical map of the Netherlands (Bonne), map sheet 306 and 307 (publication date 1896 and 1904 respectively), Digital file, Kadaster, Apeldoorn, the Netherlands, 2018c.
Kadaster: Topographical map of the Netherlands, map sheet 306 and 307 (publication date 1931 and 1929 respectively), Digital file, Kadaster, Apeldoorn, the Netherlands, 2018d.
Kemp, J. and Rhodes, E. J.: Episodic fluvial activity of inland rivers in southeastern Australia: Palaeochannel systems and terraces of the Lachlan River, Quaternary Sci. Rev., 29, 732–752, https://doi.org/10.1016/j.quascirev.2009.12.001, 2010.
Kleinhans, M. G. and Van den Berg, J. H.: River channel and bar patterns explained and predicted by an empirical and a physics-based method, Earth Surf. Proc. Land., 36, 721–738, https://doi.org/10.1002/esp.2090, 2011.
KNMI: Klimaatatlas: langjarige gemiddelden 1981–2010 (Climate atlas: longterm averages 1981–2010), available at: http://www.klimaatatlas.nl/, last access: 7 September 2017.
Koomen, A. J. M. and Maas, G. J.: Geomorfologische Kaart Nederland (GKN) – Achtergronddocument bij het landsdekkende digitale bestand (Alterra-rapport 1039) (The Geomorphological map of the Netherlands in digital format), Alterra, Wageningen, the Netherlands, 2004.
Kreutzer, S., Dietze, M., Burow, C., Fuchs, M. C., Schmidt, C., Fischer, M., Smedley, R. K., and Fuchs, M.: R Package “Luminescence” – Comprehensive Luminescence Dating Data Analysis, version 0.5.1, 217 pp., available at: http://CRAN.R-project.org/package=Luminescence (last access: 16 March 2016), 2015.
Kuijer, P. C. and Rosing, H.: Bodemkaart van Nederland: schaal 1 : 50.000, Toelichting bij het kaartblad 21 Oost Zwolle, Staring Centrum, Wageningen, the Netherlands, 1994.
Kunz, A., Pflanz, D., Weniger, T., Urban, B., Krüger, F., and Chen, Y. G.: Optically stimulated luminescence dating of young fluvial deposits of the middle Elbe river flood plains using different age models, Geochronometria, 41, 36–56, https://doi.org/10.2478/s13386-013-0140-7, 2014.
Lea, D. M. and Legleiter, C. J.: Refining measurements of lateral channel movement from image time series by quantifying spatial variations in registration error, Geomorphology, 258, 11–20, https://doi.org/10.1016/j.geomorph.2016.01.009, 2016.
Lespez, L., Viel, V., Rollet, A. J., and Delahaye, D.: The anthropogenic nature of present-day low energy rivers in western France and implications for current restoration projects, Geomorphology, 251, 64–76, https://doi.org/10.1016/j.geomorph.2015.05.015, 2015.
Leys, K. F. and Werritty, A.: River channel planform change: Software for historical analysis, Geomorphology, 29, 107–120, https://doi.org/10.1016/S0169-555X(99)00009-4, 1999.
Lian, O. B. and Roberts, R. G.: Dating the Quaternary: progress in luminescence dating of sediments, Quaternary Sci. Rev., 25, 2449–2468, https://doi.org/10.1016/j.quascirev.2005.11.013, 2006.
Maas, G., Corporaal, A., Kranendonk, R., and Wolfert, H.: Ruimte voor kleine rivieren: Overijsselse Vecht op koers?, Alterra, Wageningen, the Netherlands, 2007.
Madsen, A. T. and Murray, A. S.: Optically stimulated luminescence dating of young sediments: A review, Geomorphology, 109, 3–16, https://doi.org/10.1016/j.geomorph.2008.08.020, 2009.
Madsen, A. T., Murray, A. S., and Andersen, T. J.: Optical Dating of Dune Ridges on Rømø, a Barrier Island in the Wadden Sea, Denmark, J. Coast. Res., 235, 1259–1269, https://doi.org/10.2112/05-0471.1, 2007.
Medialdea, A., Thomsen, K. J., Murray, A. S., and Benito, G.: Reliability of equivalent-dose determination and age-models in the OSL dating of historical and modern palaeoflood sediments, Quat. Geochronol., 22, 11–24, https://doi.org/10.1016/j.quageo.2014.01.004, 2014.
Murray, A. S. and Roberts, R. G.: Measurement of the equivalent dose in quartz using a regenerative-dose single-aliquot protocol, Radiat. Meas., 29, 503–515, https://doi.org/10.1016/S1350-4487(98)00044-4, 1998.
Murray, A. S. and Wintle, A. G.: Luminescence dating of quartz using an improved single-aliquot regenerative-dose protocol, Radiat. Meas., 32, 57–73, https://doi.org/10.1016/S1350-4487(99)00253-X, 2000.
Murray, A. S. and Wintle, A. G.: The single aliquot regenerative dose protocol: Potential for improvements in reliability, Radiat. Meas., 37, 377–381, https://doi.org/10.1016/S1350-4487(03)00053-2, 2003.
Murray, A. S., Olley, J. M., and Caitcheon, G. G.: Measurement of equivalent doses in quartz from contemporary water-lain sediments using optically stimulated luminescence, Quaternary Sci. Rev., 14, 365–371, https://doi.org/10.1016/0277-3791(95)00030-5, 1995.
Nielsen, A., Murray, A. S., Pejrup, M., and Elberling, B.: Optically stimulated luminescence dating of a Holocene beach ridge plain in Northern Jutland, Denmark, Quat. Geochronol., 1, 305–312, https://doi.org/10.1016/j.quageo.2006.03.001, 2006.
Olley, J., Caitcheon, G., and Murray, A.: The distribution of apparent dose as determined by optically stimulated luminescence in small aliquots of fluvial quartz: Implications for dating young sediments, Quat. Geochronol., 17, 1033–1040, https://doi.org/10.1016/S0277-3791(97)00090-5, 1998.
Petts, G. E., Möller, H., and Roux, A. L.: Historical Change of Large Alluvial Rivers, edited by: Petts, G. E., Möller, H., and Roux, A. L., John Wiley & Sons, Ltd., Chichester, UK, 1989.
Pišút, P.: Channel evolution of the pre-channelized Danube River in Bratislava, Slovakia (1712–1886), Earth Surf. Proc. Land., 27, 369–390, https://doi.org/10.1002/esp.333, 2002.
Quik, C. and Wallinga, J.: Data from: Reconstructing lateral migration rates in meandering systems; a novel Bayesian approach combining OSL dating and historical maps, https://doi.org/10.4121/uuid:1ca25393-aa99-48dc-b382-0506322bc449, 2018.
Rhoades, E. L., O'Neal, M. A., and Pizzuto, J. E.: Quantifying bank erosion on the South River from 1937 to 2005, and its importance in assessing Hg contamination, Appl. Geogr., 29, 125–134, https://doi.org/10.1016/j.apgeog.2008.08.005, 2009.
Rhodes, E. J.: Optically Stimulated Luminescence Dating of Sediments over the Past 200,000 Years, Annu. Rev. Earth Pl. Sc., 39, 461–488, https://doi.org/10.1146/annurev-earth-040610-133425, 2011.
Rhodes, E. J., Bronk Ramsey, C., Outram, Z., Batt, C., Willis, L., Dockrill, S., and Bond, J.: Bayesian methods applied to the interpretation of multiple OSL dates: High precision sediment ages from Old Scatness Broch excavations, Shetland Isles, Quaternary Sci. Rev., 22, 1231–1244, https://doi.org/10.1016/S0277-3791(03)00046-5, 2003.
Rittenour, T. M.: Luminescence dating of fluvial deposits: applications to geomorphic, palaeoseismic and archaeological research, Boreas, 37, 613–635, https://doi.org/10.1111/j.1502-3885.2008.00056.x, 2008.
Rodnight, H., Duller, G. A. T., Tooth, S., and Wintle, A. G.: Optical dating of a scroll-bar sequence on the Klip River, South Africa, to derive the lateral migration rate of a meander bend, Holocene, 15, 802–811, https://doi.org/10.1191/0959683605hl854ra, 2005.
Rowland, J. C., Lepper, K., Dietrich, W. E., Wilson, C. J., and Sheldon, R.: Tie channel sedimentation rates, oxbow formation age and channel migration rate from optically stimulated luminescence (OSL) analysis of floodplain deposits, Earth Surf. Proc. Land., 30, 1161–1179, https://doi.org/10.1002/esp.1268, 2005.
Shanahan, T. M., Peck, J. A., McKay, N., Heil, C. W., King, J., Forman, S. L., Hoffmann, D. L., Richards, D. A., Overpeck, J. T., and Scholz, C.: Age models for long lacustrine sediment records using multiple dating approaches – An example from Lake Bosumtwi, Ghana, Quat. Geochronol., 15, 47–60, https://doi.org/10.1016/j.quageo.2012.12.001, 2013.
Stam, H. (Ed.): Grote Historische Topografische Provincie Atlassen, Uitgeverij Nieuwland, Tilburg, the Netherlands, 2006.
Tamura, T., Bateman, M. D., Kodama, Y., Saitoh, Y., Watanabe, K., Yamaguchi, N., and Matsumoto, D.: Building of shore-oblique transverse dune ridges revealed by ground-penetrating radar and optical dating over the last 500 years on Tottori coast, Japan Sea, Geomorphology, 132, 153–166, https://doi.org/10.1016/j.geomorph.2011.05.005, 2011.
Ter Wee, M. W.: Geologische kaart van Nederland 1 : 50.000, Toelichtingen bij het kaartblad 16 Steenwijk Oost, Geologische Stichting, Afdeling Geologische Dienst, Haarlem, the Netherlands, 1966.
Ter Wee, M. W.: Toelichting bij de geologische kaart van Nederland 1 : 50.000 – Blad Emmen West en Emmen Oost (17∘ W en 17∘ O), Rijks Geologische Dienst, Haarlem, the Netherlands, 1979.
Urban, M. A. and Rhoads, B. L.: Catastrophic Human-Induced Change in Stream-Channel Planform and Geometry in an Agricultural Watershed, Illinois, USA, Ann. Assoc. Am. Geogr., 93, 783–796, 2003.
Uribelarrea, D., Pérez-González, A., and Benito, G.: Channel changes in the Jarama and Tagus rivers (central Spain) over the past 500 years, Quaternary Sci. Rev., 22, 2209–2221, https://doi.org/10.1016/S0277-3791(03)00153-7, 2003.
Van Aalst, J. W.: OpenTopo, available at: http://www.opentopo.nl, last access: 28 November 2017.
Vandenberghe, J. and Maddy, D.: The significance of fluvial archives in geomorphology, Geomorphology, 33, 127–130, https://doi.org/10.1016/S0169-555X(99)00119-1, 2000.
Van der Leest, A., Stam, H., and Wonink, H.: Grote Historische Topografische Atlas Overijssel, ±1905, schaal 1 : 25.000, edited by: Schilders, E., Uitgeverij Nieuwland, Tilburg, the Netherlands, 2005.
Van der Linden, J. A.: Topographische en Militaire Kaart van het Koninkrijk der Nederlanden, Fibula-van Dishoeck, Unieboek B. V., Bussum, the Netherlands, 1973.
Van Heerd, R. M., Kuijlaars, E. A. C., Teeuw, M. P., and Van 't Zand, R. J.: Productspecificatie Actueel Hoogtebestand Nederland, Rapportnummer MDTGM 2000.13, Rijkswaterstaat Meetkundige Dienst, Delft, the Netherlands, 2000.
Versfelt, H.: De Hottinger-atlas van Noord-en Oost-Nederland 1773–1794, Heveskes, Groningen, the Netherlands, 2003.
Versfelt, H. and Schroor, M.: De atlas van Huguenin – Militair-topografische kaarten van Noord-Nederland, 1819–1829, Heveskes, Groningen, the Netherlands, 2005.
Viveen, W., Maas, G. J., and Schoorl, J. M.: Sedimenthuishouding in het stroomgebied van de Nederlands-Duitse Vecht: Potenties voor herstel van natuurlijke rivierdynamiek, Alterra, Wageningen, the Netherlands, 2009.
Wallinga, J.: On the detection of OSL age overestimation using single-aliquot techniques, Geochronometria, 21, 17–26, 2002a.
Wallinga, J.: Optically stimulated luminescence dating of fluvial deposits: a review, Boreas, 31, 303–322, https://doi.org/10.1080/030094802320942536, 2002b.
Wallinga, J. and Bos, I. J.: Optical dating of fluvio-deltaic clastic lake-fill sediments – A feasibility study in the Holocene Rhine delta (western Netherlands), Quat. Geochronol., 5, 602–610, https://doi.org/10.1016/j.quageo.2009.11.001, 2010.
Wallinga, J. and Van der Staay, J.: Sampling in waterlogged sands with a simple hand-operated corer, Anc. TL, 17, 59–61, 1999.
Wallinga, J., Den Ouden, J., Cunningham, A., Copini, P., Versendaal, A., Sass-Klaassen, U., Bos, G., Beerens, A., and Riksen, M.: Bootstrap-Bayesian OSL approach for poorly-bleached sediment sequences tested with dendrochronological age constraints, Conf. Pap. European Geosciences Union General Assembly, 20–27 April 2012, Vienna, Austria, Vol. 14, 2012.
Walter, R. C. and Merritts, D. J.: Natural Streams and the Legacy of Water-Powered Mills, Science, 319, 299–304, https://doi.org/10.1126/science.1151716, 2008.
Wickham, H. and Chang, W.: R Package “ggplot2”, version 2.2.1, available at: https://cran.r-project.org/web/packages/ggplot2/index.html (last access: 18 July 2017), 2016.
Wolfert, H., Corporaal, A., Maas, G., Maas, K., Makaske, B., and Termes, P.: Toekomst van de Vecht als een halfnatuurlijke laaglandrivier: Bouwstenen bij de grensoverschrijdende Vechtvisie 2009, Alterra, Wageningen, the Netherlands, 2009.
Wolfert, H. P. and Maas, G. J.: Downstream changes of meandering styles in the lower reaches of the River Vecht, the Netherlands, Geol. en Mijnbouw/Netherlands J. Geosci., 86, 257–271, 2007.
Wolfert, H. P., Maas, G. J., and Dirkx, G. H. P.: Het meandergedrag van de Overijsselse Vecht: Historische morfodynamiek en kansrijkdom voor natuurontwikkeling, DLO-Staring Centrum, Wageningen, the Netherlands, 1996.






