the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Experimental evidence for bifurcation angles control on abandoned channel fill geometry
Léo Szewczyk
Jean-Louis Grimaud
Isabelle Cojan
The nature of abandoned channels' sedimentary fills has a significant influence on the development and evolution of floodplains and ultimately on fluvial reservoir geometry. A control of bifurcation geometry (i.e., bifurcation angle) on channel abandonment dynamics and resulting channel fills, such as sand plugs, has been intuited many times but never quantified. In this study, we present a series of experiments focusing on bedload transport designed to test the conditions for channel abandonment by modifying the bifurcation angle between channels, the flow incidence angles and the differential channel bottom slopes. We find that disconnection is possible in the case of asymmetrical bifurcations with high diversion angle (≥30∘) and quantify for the first time an inverse relationship between diversion angle and sand plug length and volume. The resulting sand plug formation is initiated in the flow separation zone at the external bank of the mouth of the diverted channel. Sedimentation in this zone induces a feedback loop leading to sand plug growth, discharge decrease and eventually to channel disconnection. Finally, the formation processes and final complex architecture of sand plugs are described, allowing for a better understanding of their geometry. Although our setup lacks some of the complexity of natural rivers, our results seem to apply at larger scales. Taken into account, these new data will improve fluvial (reservoir) models by incorporating more realistic topography and grain size description in abandoned channels.
- Article
(4668 KB) - Full-text XML
-
Supplement
(403 KB) - BibTeX
- EndNote
Abandoned channels are ubiquitous features of the alluvial plain, which have a huge impact on the fluvial system evolution and properties. First, abandoned channels form local topographic lows that trap sediments (Aalto et al., 2008; Lauer and Parker, 2008; Dieras et al., 2013) and host wetlands (Novitsky et al., 1996; Ward et al., 1999). Second, the fine-grain fraction of their filling may influence active channels migration, as clays are more resistant to erosion than sandy sediments (Howard, 1992; Smith et al., 1998; Berendsen and Stouthamer, 2000; Schwendel et al., 2015). Last, abandoned channels are filled with sediments of varied permeability, which may impact flow path in active alluvial plains (Flipo et al., 2014) and ultimately in the resulting geological reservoir (Miall, 1996; Willis and Tang, 2010; Colombera et al., 2017; Cabello et al., 2018). Indeed, recent studies have shown that sedimentary fills are complex bodies and may contain coarser sediments than initially assumed (Hooke, 1995; Toonen et al., 2012; Dieras et al., 2013). When integrated to reservoir flow simulations, these coarse deposits may drastically change the connectivity of otherwise isolated sand bodies (e.g., point bars; Donselaar and Overeem, 2008).
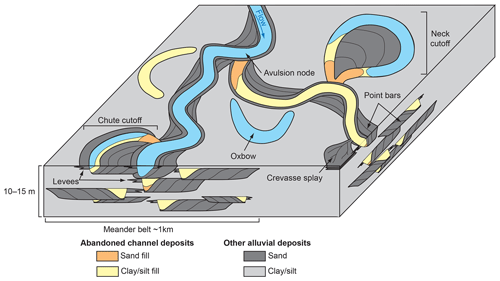
Figure 13-D sketch showing the occurrences of deposits associated with abandoned channels in an alluvial plain.
Currently, abandoned channels are studied on the field (Hooke, 1995; Constantine et al., 2010; Dieras et al., 2013) but less so in numerical models and experiments. Different styles of abandonment are observed in fluvial systems (i.e., cutoffs, avulsions), implying the formation of sedimentary fills of various grain sizes and geometries (Allen, 1965; Toonen et al., 2012; Fig. 1). A common thread to existing models is that abandonment is the consequence of the formation of a wedge-shaped sand plug in one of two channels shortly after a bifurcation (Fig. 1). Disconnected channels are then mostly filled by fine-grained overbank flood sediment (Bridge et al., 1986; Plint, 1995; Bridge, 2003). The coarse deposits are introduced beforehand as bedload, i.e., as long as there is a connection with the active channel. The dynamics at the bifurcation during the disconnection phase have therefore a key control on the sediment architecture of later abandoned channels (Bertoldi, 2012; Bolla Pittaluga et al., 2015; Constantine et al., 2010; Kleinhans et al., 2013).
Based on field studies, the geometry of the bifurcation, particularly the upstream bifurcation angle, is thought to control the duration of (dis)connection and therefore sand plug accretion and geometry (Fisk, 1947; Shields et al., 1984; Shields and Abt, 1989), but most authors agree that bifurcations remain overlooked in alluvial plains (Constantine et al., 2010; Kleinhans et al., 2013).
Existing numerical and experimental studies focus on the parameters controlling discharge and sediment partitioning at bifurcation (Bulle, 1926; de Heer and Mosselman, 2004; Kleinhans et al., 2008, 2013; Salter et al., 2018, 2019) and bifurcation (in)stability (Bertoldi and Tubino, 2007; Bolla Pittaluga et al., 2003, 2015; Iwantoro et al., 2019). To our knowledge, no study currently exists that focuses specifically on quantifying the condition(s) for abandoning channels at a bifurcation and on the resulting sediment architecture.
In this work, we study experimentally and quantify for the first time the influence of bifurcation geometry, specifically the diversion angle, on fluvial channel abandonment. We focus on (1) abandonment potential and the associated processes and (2) the extent and geometry of the sedimentary bodies formed by bedload deposition in abandoned channels, i.e., sand plugs and sandbars.
2.1 Experimental design
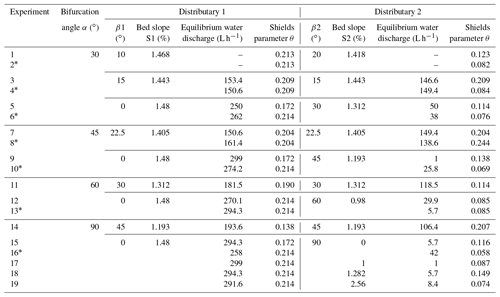
Experiments were carried out in the Geomorphic Lab of the Centre de Géosciences of MINES ParisTech, Fontainebleau. A modular flume with fixed walls was built. It was composed of three branches: one inlet and two distributary channels connected through a bifurcation area (Fig. 2). Each channel had a width W of 4 cm and a length of about 75 cm. The global slope of the experiment was 1.48 % while the slopes in distributaries 1 and 2, respectively, S1 and S2, varied with the configuration (Table 1). The bifurcation area was modular to allow different angles between the inlet and the distributary channels. Three angles were considered (Table 1, Fig. 2). The bifurcation angle α was the angle between the two distributaries. The incidence angles β1 and β2 were the angles between the inlet channel and the stream-left and -right distributaries, respectively (Fig. 2). When β1=0, β2=α and corresponded to a diversion angle, as usually defined.
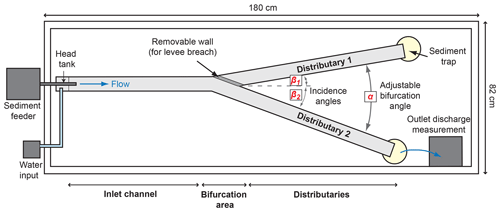
Figure 2Overhead view of the experimental setup together with the different angles considered and the levee breach setup.
The experiments started in an empty flume and typically lasted 90 to 100 min. Input water and sediment discharges were constantly fed at rates of 300 and 0.6 L h−1, respectively. Both fluxes were calibrated beforehand to allow formation of sedimentary structures without filling the flume too quickly, allowing observations to be made. The water was delivered through a head tank to reduce turbulence in the incoming flow. The water was dyed in blue using food colorant in order to enhance contrast in pictures. The sediment was a well-sorted, rounded to sub-angular, fine (d50=209 µm) Fontainebleau sand. Sediment traps allowed quantifying the volume of sediment that bypassed the distributaries.
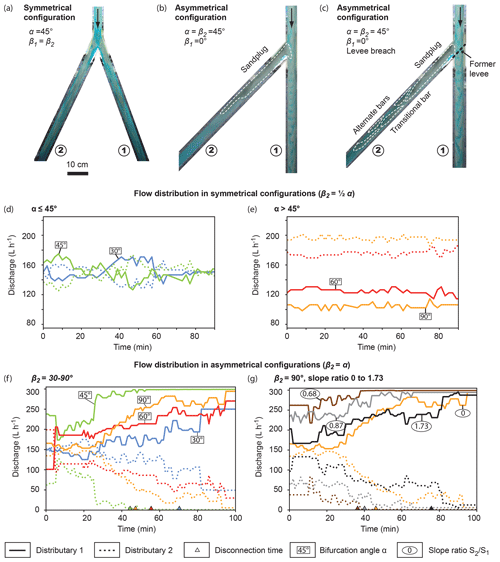
Figure 3Evolution of the experiments. (a–c) Overhead pictures of the setup for symmetrical (a) and asymmetrical configurations without (b) and with levee breach (c). (d–f) Evolution of water discharge measurement at the output of the distributary channels for symmetrical (d–e) and asymmetrical (f–g) configurations. (g) Asymmetrical 90∘ configurations with varying slope ratios S2∕S1.
A total of 16 experiments were designed to explore the influence of bifurcation angle α values ranging from 30 to 90∘ and β1 and associated β2 values ranging from 0 to 90∘ (Exps. 1 to 16) (Table 1). A first set of four symmetrical (, Exps. 3, 7, 11 and 14) (Fig. 3a) and five asymmetrical (β1≠β2, Exps. 1, 5, 9, 12 and 15) (Fig. 3b) configurations was built. A second set of seven experiments (Exps. 2, 4, 6, 8, 10, 13 and 16) replicated the configurations of the first set (except for Exps. 11 and 14) with the addition of a removable wall placed at the entrance of distributary 1 parallel to the orientation of distributary 2 (Figs. 2 and 3c) (Table S1 in the Supplement). The wall was removed after the system had reached equilibrium (identical input and output sediment discharges) to simulate a levee breach (Fig. 3c). In all asymmetrical configurations (except for Exps. 1 and 2), distributary 1 was straight (β1=0) so that β2 was a diversion angle (Table 1).
A final set of three experiments (Exps. 17, 18 and 19) was designed to determine if the observed effects of a given diversion angle could be counterbalanced by a slope variation in the deviated distributary. The experiments had the same planar geometry as Exp. 15 (∘, slope ratio ), but the slope at the bottom of distributary 2 was modified so that three additional different slope ratios S2∕S1 could be tested (i.e., respectively, 0.68, 0.87 and 1.73 in Exps. 17, 18 and 19).
2.2 Data acquisition
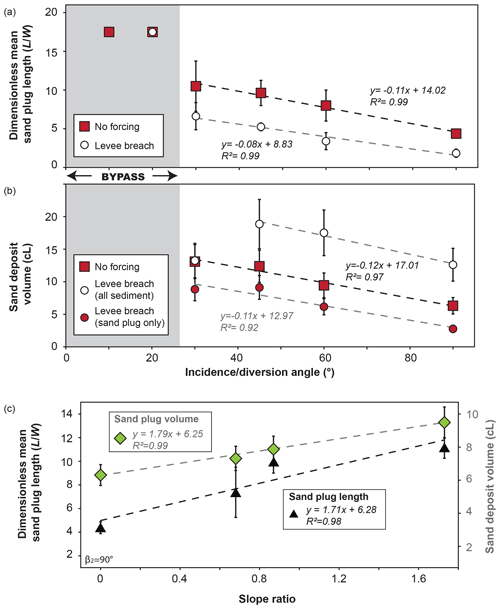
Free surface elevation was periodically measured in all channels. Water discharge was measured out of the two distributaries using a system similar to that of Salter et al. (2019). Water was flowing out of the channel into a cylinder with a hole at the bottom small enough to allow variation of the level in the cylinder. The weight evolution was measured within the cylinder using a digital scale and converted into discharge using a calibration curve. Figure 3d, e, f and g show the resulting water discharge partitioning for experiments without removable wall. Pictures of the flume were taken every minute by an overhead camera to observe sand bodies' formation and measure their length. The sand body's total length, i.e., including both subaerial and submarine parts, was measured from pictures. Sand plug construction was reported by increments of 15 min for asymmetrical configurations without levee breach (Fig. 4). Sand plug length was measured at the last location where it extended over the whole channel width and at its downstream limit. In the following, the mean of these two measurements is used to speak of sand plug length (Fig. 4). The final digital elevation models (DEMs) of the deposits were computed from 3-D photogrammetric surveys taken by two cameras mounted on a mobile rail using the Agisoft PhotoScan Professional v1.4 software (Fig. 5). The DEMs (precision of 0.4 to 0.5 mm) were used to produce mean longitudinal elevation profiles and to measure the longitudinal slope of sediment deposited in disconnected channel 2 (Fig. 6). Finally, sand plug volume calculated from DEMs and sand plug length L – divided by channel width W – were compared to bifurcation angles and slope ratios (Fig. 7).
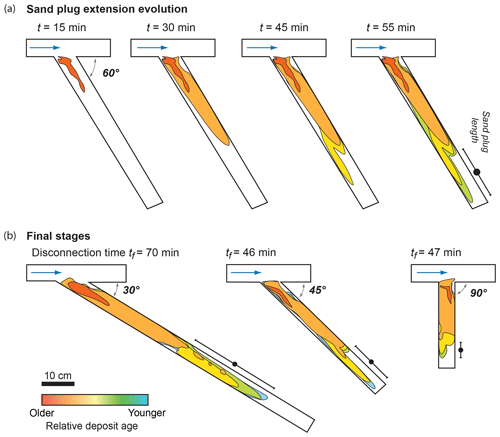
Figure 4Planar growth of sand plug from overhead pictures. (a) Consecutive growth phases of the sand plug for β2=30∘. (b) Final states of the sand plug for different β2 angles. Contours are drawn every 15 min. The mean sand plug length is represented with a black circle, together with uncertainties.
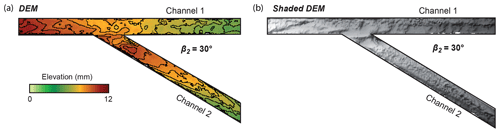
Figure 5Final topography of Experiment 5 showing the active (1) and disconnected (2) channels. (a) Elevation DEM. (b) Shaded relief of the same DEM. Contour lines represent 1.5 mm elevation.
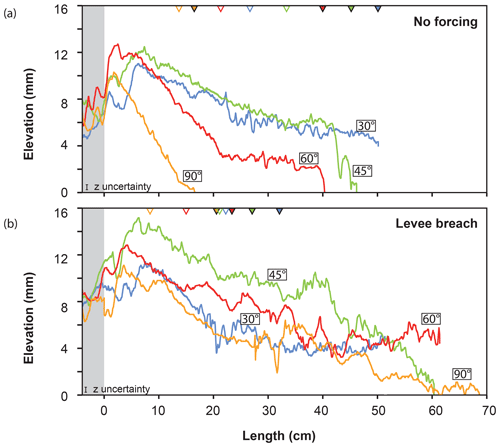
Figure 6Mean longitudinal elevation profiles of the sand plugs for increasing β2 angles without (a) and with levee breach (b). Profiles were corrected for bottom slope to facilitate comparisons. The grey area corresponds to the active channel. Empty triangles correspond to the furthest location where the sand plug occupies the entire channel width, while full triangles indicate the subaqueous extremity of the sand plug.
2.3 Sediment transport law
A sediment transport law was calibrated to compare the experimental results with theory using the methods of Seizilles et al. (2013) and Delorme et al. (2017). A series of runs were carried out with constant water and sediment feed rates in a 3 cm wide flume. The experiment was repeated with different sediment discharges Qs, and the equilibrium slope was measured each time after 10–15 h to estimate the associated Shields parameter θ (Fig. 8a). A critical Shields parameter θc – where a threshold of motion (i.e., > 0 g s−1 m−1) was attained (Fig. 8a) – was estimated using
The critical Shields parameter was then used to estimate channel slope at threshold (see Métivier et al., 2017 and references therein):
where is the dimensionless discharge, ρ and ρs the densities of water and sediment, μ the friction angle, Cf the turbulent friction coefficient, and a transcendental integral. In our setup, ρ=1000 kg m−3, ρs=2650 kg m−3, and μ≈0.7. Cf varied between 0.02 and 0.1 as an uncertainty estimate (Fig. 8b).
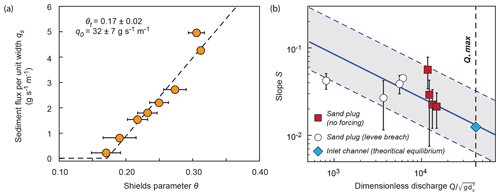
Figure 8(a) Transport law. Volumetric flux per unit width, as a function of Shield parameter θ. The dashed line corresponds to Eq. (1) fitted to the data. (b) Regime relationship between dimensionless discharge Q∗ and slope measured in the experiments. The solid blue line corresponds to the threshold theory (Eq. 2, θt=0.17 and Cf=0.06). The shaded area and dashed lines indicate uncertainty based on varying friction coefficient Cf value.
In experiments where a disconnection was observed, Q values were measured 2 min before disconnection to compare sand plug slope with Q∗ according to the threshold theory (Fig. 8b). Finally, a run was performed for about 10 h in a 4 cm wide flume with a 1.48 % bottom slope to mimic the inlet channel conditions. The resulting bed slope was compared to the theory (Fig. 8b).
Each experiment began with a short (15–20 min) phase of progradation of the sediment down to the bifurcation point. The sediment started forming a sandbar downstream of the sediment feeder and then split into alternate bars that migrated through the inlet channel. Once the sediment reached the bifurcation, it was partitioned into the distributaries, except when a removable wall was present. After an adjustment period, water discharge was considered at equilibrium when it remained constant – or slightly varied around a constant value – in each channel (Fig. 3). The associated water partitioning could be equal (i.e., identical in both branches) or unequal (i.e., different discharges in both branches). Sediment bypassing each distributary channel at equilibrium was roughly proportional to discharge partitioning. A distributary channel was considered disconnected when no bedload movement was observed. Usually, such disconnection occurred before water discharge equilibrium was attained (Fig. 3f and g).
3.1 Bifurcation geometries allowing channel disconnection
In the case of symmetrical bifurcations (Fig. 3a, d and e), no disconnection occurred. For low bifurcation angle (α ≤ 45∘, Exps. 3 and 7), a stage of soft avulsions (as defined by Salter et al., 2018) was observed initially (Fig. 3d). In this case, equilibrium with equal water partitioning was attained after both distributaries had been filled with sediment.
For high bifurcation angles (α≥60∘, Exps. 11 and 14), unequal water discharge partitioning lasted from the beginning of the experiment (Fig. 3e), and no soft avulsion stage was observed. The degree of such discharge asymmetry increased with bifurcation angle (Fig. 3e). Discharge partitioning in replicates of experimental runs 11 and 14 showed that the favored distributary channel was randomly chosen due to the interaction between the flow, the upstream alternate bars and the wedge of the bifurcation point. This indicated that the unequal water partitioning was not due to a tilt in the experimental setup.
All asymmetrical configurations reached equilibrium with unequal water discharge partitioning (Fig. 3f and g). In Exps. 1 and 2 (β1=10∘, β2=20∘), no disconnection was observed. In the other asymmetrical experiments (i.e., Exps. 3, 4, 9, 10, 12, 13 and 15 to 19), disconnection was always attained and a sand plug formed (Fig. 3b and c). Water discharge partitioning was unequal between the two distributaries. A sand plug started to form in distributary channel 2 and as a response the straight distributary (β1=0) captured an increasingly important portion of the flow (Fig. 3f). Discharge asymmetry observed at equilibrium was globally proportional to β2. In Exp. 9 (β2=45∘), disconnection was reached very quickly (50 min) due to the development of an additional sandbar on top of the sand plug that steered the flow towards the first distributary (Fig. 3f). This was the only occurrence of such a phenomenon out of the 19 experiments. In all experiments, fluctuations of water discharge were observed. Visual inspections showed that these fluctuations were linked to the migration of alternate bars in the inlet channel (Bertoldi and Tubino, 2007). A bar located stream right immediately before the bifurcation provided sediment to the distributary 2 and temporarily decreased its water discharge, favoring deposition and construction of the sand plug. A bar located stream left immediately before the bifurcation temporarily decreased sediment supply and increased water discharge to distributary 2, favoring sediment entrainment.
Levee breach experiments reached final equilibrium 5 to 10 min after distributary 1 was opened. Their final equilibrium state was very similar to that of the experiments made without levee breach in the same configuration (Fig. 3b and c). In asymmetrical experiments with levee breach (Exps. 6, 10, 13 and 16), sediment remained in transit through distributary 2 before the opening of distributary 1. This allowed the deposition of alternate bars (Fig. 3c) in distributary 2. In the asymmetrical experiments without levee breach (i.e., Exps. 5, 9, 12, 15, 17, 18 and 19), all sediment that entered distributary 2 was deposited to form a sand plug (Figs. 3b and 5b).
Figure 3g shows discharge partitioning under varying slope ratios S2∕S1 (0, 0.68, 0.87 and 1.73) for the same bifurcation angles (β1=0, ∘). In each case, the same final steady state (Qw1≈290 L h−1, Qw2≈10 L h−1) was reached and distributary channel 2 disconnected (Fig. 3g). A sand plug thus formed, albeit at a different speed. Overall, the time required to reach disconnection increased with slope ratio (Fig. 3g). Experiment 15 () did not strictly follow the trend and showed the slowest sand plug building rate of the four experiments.
3.2 Sand plug formation dynamics and architecture
During sand plug formation, discharge gradually decreased in distributary channel 2, until a constant value was attained (Fig. 3f) and no more sediment motion was observed. Sand plug growth processes and final architecture were very similar in all these experiments, regardless of the incidence angle (Fig. 4).
The formation of the sand plug initiated on the external side of the diverted channel, immediately after the bifurcation (Fig. 4). Visual inspection showed that in this area flow velocity was the lowest, allowing the deposition of sand that initiated the first fixed sandbar. This first bar anchored to the external bank of the channel and quickly grew downstream and towards channel centerline (Fig. 4a). It then widened and lengthened until its growth stopped. Other bars then formed from the sides of previously formed sandbar(s) and stretched downstream, resulting in a composite sand plug (Figs. 4a and 8). When sand was deposited over the entire width of the channel, a thalweg formed across the sand plug. It allowed sediment transfer downstream until it was buried by a sandbar that disconnected the whole channel. Overall, a slight decrease of sand plug growth speed with diversion angle is observed.
In the case of levee breach experiments (Exps. 6, 10, 13 and 16), alternate bars formed in distributary 2 before the opening of distributary 1 (Fig. 3c). After the levee breach, the discharge abruptly decreased in distributary 2, initiating the rapid (2–5 min) formation of the sand plug. In the meantime, a transient knickpoint formed along the inlet channel to allow for bed slope adjustment. Parts of the existing alternate bars at the bifurcation were thus reworked (Fig. 8). A small plug, mostly consisting of the reworked deposits, formed rapidly at the entrance of distributary channel 2.
Sand plug long slope increased with the diversion angle (from 2.5 % to 7.8 %; Table 1). This was the most visible in the no-forcing scenarios, as there was no interference from previously deposited alternate bars (Fig. 6a). Bars after the plug itself showed the shallower slopes (Fig. 6b). In the case of a levee breach, the sand plug slope was slightly steeper when the diversion angle was lower than or equal to 45∘ (Table S1). Figure 8b shows that sand plug slopes are overall consistent with the threshold theory when compared to the dimensionless discharge, with deviations towards lower or steeper slopes than the theory depending on the forcing scenario. The upstream end of the sand plug was about 4 to 8 mm more elevated than the active channel bed (Figs. 5a and 6a) and was slightly elevated compared to the water elevation in the active channel, similarly to a levee in natural systems. In the case of a levee breach, the inherited geometry caused by the alternate bars is preserved, resulting in a sand plug with a roughly equal maximum elevation but a higher overall elevation (Fig. 6b).
3.3 Controls on sand plug length and volume
Relationships between incidence angle β2 and sand plug length and volume, as well as between differential bottom slope and sand plug length and volume were found in asymmetrical configurations (Fig. 7). Above a 30∘ threshold value of β2 required to form a sand plug, sand plug length linearly decreased with β2 (Fig. 7a). In the case of a levee breach, sand plugs were shorter for a given β2 value (Fig. 7a). In fact, the regression lines calculated in the cases without and with levee breach returned coefficient values of about −0.11 and −0.08, respectively. This induces a slow convergence of sand plug lengths towards higher angles and shows that the sand plugs formed by a levee breach are slightly less affected by the β2 value.
Without levee breach, the sand plug was the only bedload deposit in the disconnected distributary (Exps. 5, 9, 12 and 15) (Figs. 3b and 5b). Its volume steadily decreased with β2, following a roughly linear relationship (Fig. 7b). With a levee breach (Exps. 6, 10, 13 and 16), the total volume of sediment also decreased linearly with β2, but was globally higher. Indeed, in the levee breach experiments the sand plug accounts for only part of the sand volume deposited in the distributary, the rest being accounted for by the alternate bars formed during the channel active phase. When only the volume of the sand plug itself is taken into account, sand plug volume was thus lower than in the no-forcing cases (Fig. 7b). Figure 7c indicates that the length and volume of the sand plug was also slightly affected by the slope ratio. The sand plug became more elongated and thinner as the slope increased in distributary 2 and consequently sand plug slope overall decreased with an increase of the slope ratio, from 0.68–0.87 (Exps. 15 and 17) to 1.73 (Exp. 19).
4.1 Bifurcation angle control on abandonment
In this study, channel disconnection was possible for highly asymmetrical bifurcation (i.e., α=β2 and β2≥30∘) (Exps. 5, 6, 9, 10, 12, 13 and 15 to 18). In symmetrical configurations, no disconnection was observed although an effect on discharge partitioning occurred. Such discharge imbalance can be attributed to the bifurcation angle value alone, since the slopes of both distributaries are equal. Experiments 1 and 2 demonstrated that even in asymmetrical cases, no disconnection is possible if the diversion angle is too low (∘) or the bifurcation not asymmetrical enough. Hence, bifurcation geometry indeed controls the disconnection of channel as proposed by Fisk (1947), Shields et al. (1984) and Shields and Abt (1989). Moreover, our results suggest that disconnection is more sensitive to incidence angle value than bifurcation angle value alone. In essence, the value of the flow deviation from its original trajectory has more impact than the value of flow divergence between the distributaries. The fact that disconnection was observed despite slope advantage in the diverted distributary channel (Figs. 3g and 7c) (Table 1) is another strong argument in favor of planar geometry control on bifurcation (dis)equilibrium.
In symmetrical experiments, water discharge shifted from a soft avulsion regime with roughly equal partitioning (e.g., Salter et al., 2018) to an unequal partitioning as bifurcation angle α increased (Fig. 3d and e). Considering the trend in Fig. 3d and e, we may hypothesize that abandonment would have occurred at some point if the bifurcation angle α had been increased further. In a comparable set of experiments, Bertoldi and Tubino (2007) and Salter et al. (2019) showed that disconnection may also be possible for low-angle symmetrical configurations (respectively, 30∘ and 16∘). Their work focused on delta networks, where bifurcations can be considered stable with two active distributaries of a width inferior to that of the upstream channel. In their experiments, Bertoldi et al. (2007) and Salter et al. (2019), respectively, had a ratio of 0.66 and 0.7. In that case, the downstream migration of an alternate bar at equilibrium with the upstream channel into a narrower distributary may easily lead to sand plug formation. In our fluvial-channel-focused experiments, where an avulsion generally led to channel abandonment in favor of the other, the ratio between the width of each distributary and the width of the upstream channel was 1 (Fig. 2). The distributaries could accommodate the alternate bars' migrations, preventing disconnection. Furthermore, Bertoldi et al. (2007) and Salter et al. (2019) demonstrated that discharge asymmetry is largely a function of flow aspect ratio upstream of the bifurcation. In our experiment, upstream water depth was usually 4 mm; thus, aspect ratio was about 10, which is propitious to equal flow partitioning in symmetrical bifurcation geometry (Salter et al., 2018).
4.2 Bifurcation angle control on sand plug extent
Numerous field studies intuited a relationship between the incidence angle and the length of the sand plug, stating that a low incidence angle produced a longer sand plug (Fisk, 1947; Allen, 1965; Gagliano and Howard, 1984; Shields et al., 1984; Shields and Abt, 1989; Dieras et al., 2013). This was explained by the fact that bedload is easily diverted into the channel at low angles and on a longer distance before deposition. With increasing bifurcation angles, a smaller fraction of the bedload enters the channel, resulting in shorter and smaller sand plugs. Our experiments show that bedload partitioning is proportional to discharge partitioning and that final discharge partitioning is controlled by the diversion angle (Fig. 3). As a result, sand plug volumes and lengths linearly decrease with diversion angle (Figs. 7a–b). Sand plug volumes and lengths are also modulated by the slope of the abandoned channel (Fig. 7c). Sudden events such as levee breaching create shorter and less voluminous sand plugs, as less bedload material is mobilized to build the sand plug due to the faster disconnection (Fig. 7a and b).
The fast disconnection and limited sand plug length and volume observed in the case of a levee breach (Fig. 7a and b) can also be explained by the rapid entrenchment of the flow in channel 1. The newly opened channel 1 has a slope advantage as no aggradation occurred during the first phase of the experiment. As the result of incision and knickpoint retreat, a threshold that prevents part of the bedload to enter distributary 2 is created (Slingerland and Smith, 2004) and the flow is preferentially funneled in the distributary channel 1. It is worth noting that the effect of levee breaching on sand plug length and volume decreases slightly when the incidence angle increases (Fig. 7a and b), with a slight convergence towards higher angles. The slight difference in regression line values between the no-forcing and levee breach scenarios also hints that although the sand plug extent and volume are controlled by the diversion angle, different triggers might initiate sand plug formation depending on the scenario.
As bedload partitioning varies with discharge partitioning in our setup, a smaller fraction of bedload enters the deviated distributary and this fraction diminishes in time with discharge, until disconnection. In a flume with comparable geometry, Bulle (1926) measured the bedload partitioning in distributaries and found that around 90 % of the bedload was steered in the deviated distributary for angles ranging from 30 to 150∘. However, this was at the cost of maintaining the discharge equal in both distributaries, by adjusting water slope using sluice gate elevation at the end of each distributary (Bulle, 1926; Lindner, 1953). The resulting water slope ratios were likely far above the ones we used, since we did not observed equal discharge partitioning (i.e., Fig. 3g). Hence, a comparison of sediment partitioning between Bulle (1926) and the present work does not seem relevant.
4.3 Mechanism for channel abandonment
Beyond the influence of the bifurcation angle, other mechanisms have been invoked to explain channel disconnection: the Shields number of the system upstream of the bifurcation and its effects on the aspect ratio (Wang et al., 1995; Bertoldi et al., 2009; Bolla Pittaluga et al., 2015) and bars' presence (Bertoldi and Tubino, 2007; Bertoldi, 2012), as well as the sinuosity upstream of the bifurcation and the slopes in each distributaries (Kleinhans et al., 2013; Van Dijk et al., 2014). Based on the results of this study, one may argue that it is the difference of channel bed slope associated with the bifurcation geometry – and not the bifurcation geometry itself – that leads to abandonment. The experiments presented in Fig. 3g show that this is not the case in the experiments with asymmetrical bifurcations, as a high diversion angle is a sufficient condition for hydraulic disconnection. Having a reasonable slope advantage to the diverted channel does not reverse the final outcome; it only affects the time needed to disconnect the channel and the extent of the deposits.
Another proposed mechanism is that low discharge in one channel induces sedimentation, which would in turn further reduce the discharge in the channel by plugging it or by changing the bed slope, creating a feedback loop leading to disconnection (Zolezzi et al., 2006; Bertoldi, 2012). Based on this study, this is discounted as abandonment would have been observed when discharge partitioning was unequal from the beginning in symmetrical configurations with incidence angles above the 30∘ threshold (Fig. 3e). The sand plug does create a feedback loop that helps disconnection, but the timing of the discharge decrease in distributary 2 during the asymmetrical experiments shows that it is not the discharge imbalance that initiates the sand plug formation. It is rather the formation of the sand plug that induces the change in discharge partitioning (Fig. 3f), leading to disconnection.
Eddies were observed on the external bank of the channel, immediately downstream of the bifurcation, in which water was slowed and sediment deposited. Bulle (1926) observed that these eddies were produced by flow separation at the bifurcation. These eddies were also found in numerical modeling by de Heer and Mosselman (2004) and van der Mark and Mosselman (2012), and observed by Constantine et al. (2010) on the Sacramento River and were named the “flow separation zone”. The latter authors observed that the width of the flow separation zone increases with the incidence angle value. In our experiments, the wider flow separation zone in the diverted channel led to the formation of the first stage of the sand plug against the external bank of the diverted channel just downstream of the bifurcation (Fig. 4). This in turn led to a further reduction of the flow diverted in the channel, favoring deposition and growth of the sand plug, until the channel got disconnected. At low values of β, this flow separation zone was too narrow to initiate the feedback loop. When β reached 30∘, it became wide enough to create a larger and higher sandbar and start the feedback loop.
4.4 Comparison with field cases and upscaling
Although our model represents a very simplified setup, it has been purpose built to study the influence of bifurcation geometry on disconnection and on bedload deposits partitioning and geometry in abandoned channels. As such, it complements previous studies focusing on equilibrium configurations relative to water and sediment flows (Bolla Pittaluga et al., 2003, 2015; Bertoldi and Tubino, 2007; Edmonds and Slingerland, 2008; Bertoldi et al., 2009; Salter et al., 2018, 2019). River channel section and slope are thought to adjust to water discharge (see Métivier et al., 2017 and references therein). For instance, Lacey's law states that river width scales with the square root of water discharge (Lacey, 1930). Both the equilibrium slope of the inlet channel and the slopes of disconnected channels observed in the experiment are consistent with the threshold theory and remain within the uncertainty range (Fig. 8b). However, in the case of a levee breach, equilibrium slopes are gentler than the theoretical equilibrium slope, and in the case of no-forcing scenarios, slopes are steeper. These deviations would confirm that abandonment trigger was dominated by channel entrenchment in the former case and by plug construction in the latter. As our experimental observations are compatible with Lacey's law and the threshold theory, even in such constrained settings (i.e., fixed wall), they are likely to apply in nature.
An intermediate scale between our flume experiment and natural systems is the irrigation system channels, which also have fixed width. Intake plugging is an issue that many water management engineers face, and the question of optimal diversion angle value has been intensively studied. Novak et al. (1990) and Munir (2011) state, for instance, that a 30 to 45∘ diversion angle is desirable to limit silting up of the channel, whereas a 90∘ angle is “the least desirable one”. This statement is consistent with the present study where channels with high diversion angles are easily plugged and disconnected. Neary et al. (1999) observed sedimentation patterns similar to this study (i.e., a sandbar anchored on the external bank of the deviated channel immediately downstream of the bifurcation) in a 90∘ lateral intake adjoining the Ohio River, both in the actual intake and numerical simulations. Hence, the first-order observations made in this study seem to apply at larger scales such as larger waterways.
In natural cases, avulsion and disconnection are usually accompanied by the enlargement of the new dominant channel path (Kleinhans et al., 2008) and eventually change of bifurcation angle with time (Bertoldi, 2012). Both impact sand plug construction. In our experiments, channel walls were fixed and the dominant flow immediately occupied a channel equal in width to the inlet channel. As a result, disconnection rates were likely faster than when the channel could erode its bank to adjust its shape, similarly to natural systems. Such delay would probably favor the building of larger sand plugs in abandoned channels. To our knowledge, no relationship between diversion angle and sand plug length has been quantified on the field yet. Constantine et al. (2010) found no significant correlation between the incidence angle and the emerged length of the sand plug based on aerial photographs. However, they did find a negative correlation between incidence angle and gravel fill depth below water measured at the apex of abandoned meanders. Such measurements are more comparable to our results (i.e., taking into account the submerged part of the sand plug) and seem to be adequate when investigating on the field for a relationship between incidence angle and bedload deposits. The fact that the subaerial plugs length in abandoned channels is not related to bifurcation angles may be due to fine-grain deposition over the sand plug after disconnection. More field investigations would be required to test this hypothesis.
4.5 Sand plug architecture integration to reservoir modeling
The sand plug formation processes observed experimentally in this study are the same independently of the bifurcation geometry and occurrence or absence of levee breach (Figs. 4 and 9). Sand plugs are not simply sediment wedges deposited at the mouth of the disconnected channels (Fisk, 1947; Allen, 1965) but complex bedload features formed by bars amalgamation (Fig. 9). Sand plugs have a major slope break separating the thicker upstream part that actually plugs the channel and the downstream part and lateral width variation on the downstream part (Fig. 9). Inherited topography affects the sand plug final architecture (Fig. 6b). For instance, alternate sandbars may be found isolated in the channel. During disconnection, the sand plug may rework some of the previously deposited bars to form transitional bars (Figs. 3c and 9). Together, they form a consistent coarse-grain plug that extends inside the paleo-river path.
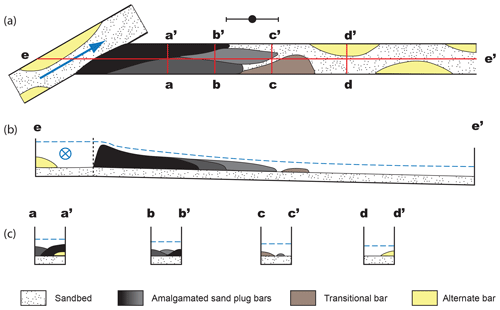
Figure 9Conceptual architecture of sand plug derived from experimental observations: overhead view (a), longitudinal profile (b) and transverse sections (c).
In natural cases, the successive episodes of construction would imply the presence of grain-size variations in the internal structure of the sand plug. These heterogeneities would include permeability baffles formed at the interface between sandbars during low energy phases and possible erosional surfaces formed during phases of high energy, increasing permeability. In these cases, the internal structure of a sand plug could be comparable to that of a complex point bar (Deschamps et al., 2012; Cabello et al., 2018) and thus form a good reservoir in itself.
Finally, the presence of bedload deposits in disconnected channels demonstrates how the abandoned channel fills could be connectivity bridges rather than permeability barriers, especially in the upstream part of abandoned channels (Larue and Hovadik, 2006; Donselaar and Overeem, 2008). This could have a significant impact on fluvial river models. Indeed, common models for meandering channels migration (e.g., Parker et al., 2011) usually assume that abandoned channels are 100 % filled by mud plug, with consequences on the erodibility of alluvial plains and thus channel migration (Howard, 1996). Using a dependence of sand plug length and volume on diversion angles will influence the overall connectivity in reservoir modeling (i) at the scale of channel fills and potentially (ii) at the scale of channel belts. For instance, sand plug lengths vary between 5 and 12 W in the present study (Fig. 7a). The latter is in the range of the wavelength for typical meandering rivers (Williams, 1986) and would allow a connection between about three to four point bars. This suggested length of bedload deposits is consistent with the presence of bedload deposits mapped in low sinuosity avulsion channels by Stouthamer (2001) and Toonen et al. (2012) three to five meander bends downstream of the bifurcation point. Exploring the ranges of sand plug lengths is therefore a promising research area for reservoir characterization in the future. For instance, the construction and amalgamation of plug bars may be different in curved channel than in the straight channels used in this study.
Based on the series of experiment designed to force channel abandonment under constant water and sediment discharge, we find the following:
-
Above a diversion angle threshold of 22.5∘, discharge partitioning becomes unequal. Disconnection occurs when the diversion angle is greater than or equal to 30∘.
-
Sand plug length and volume linearly decrease with the diversion angle.
-
The incidence angle controls the width of the flow separation zone in the diverted channel. When the incidence angle is high enough, sand plug formation begins in this zone and its presence creates a feedback loop leading to further deposition until disconnection occurs.
-
The sand plug is a complex structure formed by amalgamated and interconnected sandbars of various lengths, widths, elevation and slope, which may increase the connectivity of fluvial reservoirs, in particular between otherwise isolated point bar deposits.
Movies of the experiments and topography data (point clouds) of the final state of the experiments are available in the OSF data repository (https://doi.org/10.17605/OSF.IO/MTR69; Szewczyk, 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-8-275-2020-supplement.
LS and JLG built the flume and designed the experiments with input from IC. LS carried out all experiments. All authors contributed to writing the manuscript.
The authors declare that they have no conflict of interest.
We are indebted to Aurélien Baudin, Cyril Leipp, Yasmina Habaoui, David Marquez and Loic Marlot for their help during the building of the flume. We thank Joël Billiotte, Cyril Castanet, François Métivier, Gerard Salter and Damien Huyghe for fruitful discussions on this work, as well as Richard Hale and John Shaw for their positive reviews. We also thank Lisanne van Rijn for her careful review of our English. This work is part of the first author's PhD thesis and the FLUMY program for channelized reservoirs.
This research has been supported by the Institut du Carnot M.I.N.E.S. (grant no. 2017-1700557).
This paper was edited by Paola Passalacqua and reviewed by Richard Hale and John Shaw.
Aalto, R., Lauer, J. W., and Dietrich, W. E.: Spatial and temporal dynamics of sediment accumulation and exchange along Strickland River floodplains (Papua New Guinea) over decadal-to-centennial timescales, J. Geophys. Res., 113, 1–22, 2008.
Allen, J. R. L.: A review of the origin and characteristics of recent alluvial sediments, Sedimentology, 5, 89–191, 1965.
Berendsen, H. J. and Stouthamer, E.: Late Weichselian and Holocene palaeogeography of the Rhine–Meuse delta, The Netherlands, Palaeogeogr. Palaeocl., 161, 311–335, 2000.
Bertoldi, W.: Life of a bifurcation in a gravel-bed braided river, Earth Surf. Proc. Land., 37, 1327–1336, 2012.
Bertoldi, W. and Tubino, M.: River bifurcations: Experimental observations on equilibrium configurations: River bifurcations, Water Resour. Res., 43, 1–10, 2007.
Bertoldi, W., Zanoni, L., Miori, S., Repetto, R., and Tubino, M.: Interaction between migrating bars and bifurcations in gravel bed rivers, Water Resour. Res., 45, 1–12, 2009.
Bolla Pittaluga, M., Repetto, R., and Tubino, M.: Channel bifurcation in braided rivers: Equilibrium configurations and stability, Water Resour. Res., 39, 1–13, 2003.
Bolla Pittaluga, M., Coco, G., and Kleinhans, M. G.: A unified framework for stability of channel bifurcations in gravel and sand fluvial systems: Gravel bed and sand bed river bifurcations, Geophys. Res. Lett., 42, 7521–7536, 2015.
Bridge, J. S.: Rivers and floodplains: forms, processes, and sedimentary record, Blackwell Pub, Oxford, UK, Malden, MA, USA, 491 pp. 2003.
Bridge, J. S., Smith, N. D., Trent, F., Gabel, S. L., and Bernstein, P.: Sedimentology and morphology of a low-sinuosity river: Calamus River, Nebraska Sand Hills, Sedimentology, 33, 851–870, 1986.
Bulle, H.: Untersuchungen über die Geschiebeableitungbei der Spaltung von Wasserläufen, VDI Verlag, Berlin, Germany, 42 pp., 1926 (in German).
Cabello, P., Domínguez, D., Murillo-López, M. H., López-Blanco, M., García-Sellés, D., Cuevas, J. L., Marzo, M., and Arbués, P.: From conventional outcrop datasets and digital outcrop models to flow simulation in the Pont de Montanyana point-bar deposits (Ypresian, Southern Pyrenees), Mar. Petrol. Geol., 94, 19–42, 2018.
Colombera, L., Mountney, N. P., Russell, C. E., Shiers, M. N., and McCaffrey, W. D.: Geometry and compartmentalization of fluvial meander-belt reservoirs at the bar-form scale: Quantitative insight from outcrop, modern and subsurface analogues, Mar. Petrol. Geol., 82, 35–55, 2017.
Constantine, J. A., Dunne, T., Piégay, H., and Mathias Kondolf, G.: Controls on the alluviation of oxbow lakes by bed-material load along the Sacramento River, California, Sedimentology, 57, 389–407, 2010.
de Heer, A. and Mosselman, E.: Flow structure and bedload distribution at alluvial diversions, Delft University of Technology & WL, Delft, the Netherlands, 1–6, 2004.
Delorme, P., Voller, V., Paola, C., Devauchelle, O., Lajeunesse, É., Barrier, L., and Métivier, F.: Self-similar growth of a bimodal laboratory fan, Earth Surf. Dynam., 5, 239–252, https://doi.org/10.5194/esurf-5-239-2017, 2017.
Deschamps, R., Guy, N., Preux, C., and Lerat, O.: Analysis of Heavy Oil Recovery by Thermal EOR in a Meander Belt: From Geological to Reservoir Modeling, Oil Gas Sci. Technol., 67, 999–1018, 2012.
Dieras, P. L., Constantine, J. A., Hales, T. C., Piégay, H., and Riquier, J.: The role of oxbow lakes in the off-channel storage of bed material along the Ain River, France, Geomorphology, 188, 110–119, 2013.
Donselaar, M. E. and Overeem, I.: Connectivity of fluvial point-bar deposits: An example from the Miocene Huesca fluvial fan, Ebro Basin, Spain, AAPG Bull., 92, 1109–1129, 2008.
Edmonds, D. A. and Slingerland, R. L.: Stability of delta distributary networks and their bifurcations: Stability of deltaic bifurcations, Water Resour. Res., 44, 1–13, 2008.
Fisk, H. N.: Fine Grained Alluvial Deposits and their Effects on Mississippi River Activity, Mississippi River Commission, Vicksburg, Mississippi, USA, 82 pp., 1947.
Flipo, N., Mouhri, A., Labarthe, B., Biancamaria, S., Rivière, A., and Weill, P.: Continental hydrosystem modelling: the concept of nested stream–aquifer interfaces, Hydrol. Earth Syst. Sci., 18, 3121–3149, https://doi.org/10.5194/hess-18-3121-2014, 2014.
Gagliano, S. M. and Howard, P. C.: The neck cutoff oxbow lake cycle along the lower Mississippi, River Meandering, Proceedings of the Conference Rivers '83, 24–26 October 1983, New York, USA, American Society of Civil Engineers, 147–158, 1984.
Hooke, J. M.: River channel adjustment to meander cutoffs on the River Bollin and River Dane, northwest England, Geomorphology, 14, 235–253, 1995.
Howard, A. D.: Modeling Channel Migration and Floodplain Sedimentation in Meandering Streams. Lowland Floodplain Rivers: Geomorphological Perspectives, edited by: Carling, P. and Petts, G. E., John Wiley, Hoboken, USA, 41–41, 1992.
Howard, A. D.: Modeling channel evolution and floodplain morphology, in Floodplain Processes, edited by: Anderson, M. G., Walling, D. E., and Bates, P. D., John Wiley & Sons, Hoboken, USA, 15–62, 1996.
Iwantoro, A. P., van der Vegt, M., and Kleinhans, M. G.: Morphological evolution of bifurcations in tide-influenced deltas, Earth Surf. Dynam. Discuss., https://doi.org/10.5194/esurf-2019-63, in review, 2019.
Kleinhans, M. G., Jagers, H R. A., Mosselman, E., and Sloff, C. J.: Bifurcation dynamics and avulsion duration in meandering rivers by one-dimensional and three-dimensional models, Water Resour. Res., 44, 1–31, 2008.
Kleinhans, M. G., Ferguson, R. I., Lane, S. N., and Hardy, R. J.: Splitting rivers at their seams: bifurcations and avulsion: Bifurcations and avulsion, Earth Surf. Proc. Land., 38, 47–61, 2013.
Lacey, G.: Stable channels in alluvium, Minutes of the Proceedings of the Institution of Civil Engineers, 229, 259–292, 1930.
Larue, D. K. and Hovadik, J.: Connectivity of channelized reservoirs: a modelling approach, Petrol. Geosci., 12, 291–308, 2006.
Lauer, J. W. and Parker, G.: Net local removal of floodplain sediment by river meander migration, Geomorphology, 96, 123–149, 2008.
Lindner, C. P.: Diversions from alluvial streams, T. Am. Soc. Civ. Eng., 118, 245–288, 1953.
Métivier, F., Lajeunesse, E., and Devauchelle, O.: Laboratory rivers: Lacey's law, threshold theory, and channel stability, Earth Surf. Dynam., 5, 187–198, https://doi.org/10.5194/esurf-5-187-2017, 2017.
Miall, A. D.: The Geology of Fluvial Deposits, Springer Berlin Heidelberg, Berlin, Heidelberg, Germany, 582 pp., 1996.
Munir, S.: Role of Sediment Transport in Operation and Maintenance of Supply and Demand Based Irrigation Canals: Application to Machai Maira Branch Canals: UNESCO-IHE PhD Thesis, Delft, the Netherlands, 2011.
Neary, V. S., Sotiropoulos, F., and Odgaard, A. J.: Three-Dimensional Numerical Model of Lateral-Intake Inflows, J. Hydraul. Eng. 125, 126–140, https://doi.org/10.1061/(ASCE)0733-9429(1999)125:2(126), 1999.
Novak, P., Moffat, A., Nalluri, C., and Narayanan, R.: Hydraulic Structures, Pitman, London, UK, 546 pp., 1990.
Novitzky, R .P., Smith, R. D., and Fretwell, J. D.: Wetland functions, values, and assessment, US Geological Survey Water Supply Paper 2425, Washington D.C., USA, 79–86, 1996.
Parker, G., Shimizu, Y., Wilkerson, G. V., Eke, E. C., Abad, J. D., Lauer, J. W., Paola, C., Dietrich, W. E., and Voller, V. R.: A new framework for modeling the migration of meandering rivers, Earth. Surf. Proc. Land., 36, 70–86, 2011.
Plint, A. G.: Sedimentary facies analysis: a tribute to the research and teaching of Harold G. Reading. Special publication of the International Association of Sedimentologists. Blackwell Science, Oxford, UK, Cambridge, Mass, USA, 400 pp., 1995.
Salter, G., Paola, C., and Voller, V. R.: Control of Delta Avulsion by Downstream Sediment Sinks, J. Geophys. Res.-Earth, 123, 142–166, 2018.
Salter, G., Voller, V. R., and Paola, C.: How does the downstream boundary affect avulsion dynamics in a laboratory bifurcation?, Earth Surf. Dynam., 7, 911–927, https://doi.org/10.5194/esurf-7-911-2019, 2019.
Schwendel, A. C., Nicholas, A. P., Aalto, R. E., Sambrook Smith, G. H., and Buckley, S.: Interaction between meander dynamics and floodplain heterogeneity in a large tropical sand-bed river: the Rio Beni, Bolivian Amazon, Earth Surf. Proc. Land., 40, 2026–2040, 2015.
Seizilles, G., Lajeunesse, E., Devauchelle, O., and Bak, M.: Cross-stream diffusion in bedload transport, Phys. Fluids, 26, 1–13, 2013.
Shields, F. D. and Abt, S. R.: Sediment deposition in cutoff meander bends and implications for effective management, Regul. River, 4, 381–396, 1989.
Shields, F. D., Nunnally, N. R., and Asce, A. M.: Environmental aspects of clearing and snagging, J. Environ. Eng., 110, 152–165, 1984.
Slingerland, R. and Smith, N. D.: River avulsions and their deposits, Annu. Rev. Earth Pl. Sc., 32, 257–285, 2004.
Smith, N. D., Slingerland, R. L., Pérez-Arlucea, M., and Morozova, G. S.: The 1870s avulsion of the Saskatchewan River, Can. J. Earth Sci., 35, 453–466, 1998.
Stouthamer, E.: Sedimentary products of avulsions in the Holocene Rhine–Meuse Delta, The Netherlands, Sediment. Geol., 145, 73–92, 2001.
Szewczyk, L.: Relevant data for the Esurf paper “Experimental evidence for bifurcation angles control on abandoned channel fill geometry”, OSF data repository, https://doi.org/10.17605/OSF.IO/MTR69, 2020.
Toonen, W. H. J., Kleinhans, M. G., and Cohen, K. M.: Sedimentary architecture of abandoned channel fills, Earth Surf. Proc. Land., 37, 459–472, 2012.
van der Mark, C. F. and Mosselman, E.: Effects of helical flow in one-dimensional modeling of sediment distribution at river bifurcations, Earth Surf. Proc. Land., 38, 502–511, 2012.
van Dijk, W. M., Schuurman, F., van de Lageweg, W. I., and Kleinhans, M. G.: Bifurcation instability and chute cutoff development in meandering gravel-bed rivers, Geomorphology, 213, 277–291, 2014.
Wang, Z. B., De Vries, M., Fokkink, R. J., and Langerak, A.: Stability of river bifurcations in 1D morphodynamic models, J. Hydraul. Res., 33, 739–750, 1995.
Ward, J. V., Tockner, K., and Schiemer, F.: Biodiversity of floodplain river ecosystems: ecotones and connectivity, Regul. River., 15, 125-139, 1999.
Williams, G. P.: River meanders and channel size, J. Hydrol., 88, 147–164, 1986.
Willis, B. J. and Tang, H.: Three-Dimensional Connectivity of Point-Bar Deposits, J. Sediment. Res., 80, 440–454, 2010.
Zolezzi, G., Bertoldi, W., and Tubino, M.: Morphological Analysis and Prediction of River Bifurcations, in: Braided Rivers, edited by: Sambrook Smith, G. H., Best, J. L., Bristow, C. S., and Petts, G. E., Blackwell Publishing Ltd., Oxford, UK, 233–256, 2006.