Emerging crescentic patterns in modelled double sandbar systems under normally incident waves

Double sandbar systems often characterize the surf zone of wave-dominated beaches and display a variety of poorly explained spatial configurations. Here, we explore the morphodynamic stability of double-barred beaches using a model based on linear stability analysis. Surf zone hydrodynamics are described by coupling depth and wave-averaged conservation of mass and momentum with the wave energy and phase equations, including roller dynamics. A simplified sediment transport formulation relates flow to seabed changes. Under normal wave incidence, an alongshore uniform coast with a cross-shore profile characterized by the presence of two sandbars can be unstable, thereby resulting in the development of crescentic and/or rip channel patterns. Our study demonstrates that sandbar coupling can be either in phase (highs and lows of both sandbars are at the same alongshore position) or out of phase (highs and lows of one sandbar correspond to lows and highs of the other sandbar). In line with observations, results of simulations show a large variability in the possible emerging bottom patterns. Our analysis indicates that modes of which the amplitude of the inner sandbar perturbation is larger than that of the outer sandbar are dominant for large height–depth differences between the two sandbar crests and small offshore wave heights. Patterns related to the outer sandbar dominate for small values of the difference in sandbar depth. For intermediate differences between the two sandbar depths, patterns on both longshore bars appear to be fully coupled (similar growth rates and strongly correlated pattern shapes). For relatively large waves and large depth over the outer sandbar, patterns can also develop close to the shoreline and/or inner surf zone together with patterns in the inner or outer sandbar.

1 Introduction

Multiple sandbar systems have been observed in a variety of settings worldwide. We specifically focus on the dynamics of double sandbar systems in the surf zone, where the sandbars almost constantly affect (and are affected by) wave transformation and onshore–offshore exchanges of sediment. Alongshore changes in double sandbar configurations sometimes result in rhythmic patterns, usually called crescentic bars or rip channels (Fig. 1).

Figure 1 Multiple sandbars along the Libyan coast (Image from Google, DigitalGlobe 2012).

The development of alongshore patterns in multiple sandbar settings has been studied through observations (e.g. Castelle et al., 2007, 2015) and numerical studies (e.g. Klein and Schuttelaars, 2006; Price and Ruessink, 2013, and references herein), and has also been considered in the wider framework of a conceptual model of sequential beach changes by Short and Aagaard (1993). Both this conceptual model and field data (e.g. Castelle et al., 2007) indicate that the inner and outer sandbars are likely to be characterized by different spatial and temporal scales. In a double-barred system, like the one considered in this study, the inner sandbar usually displays crescentic features with an alongshore spacing (distance between consecutive sandbar horns) smaller than the one characterizing the outer sandbar. Moreover, in the case of accretionary conditions, Short and Aagaard (1993) assume that the inner sandbar responds faster than the outer one. The Short and Aagaard (1993) model also indicates that beach configurations can involve coupling between the sandbars and/or coupling between the inner sandbar and the shoreline, where transverse sandbars can be present as well (Ribas et al., 2015).

We use the term “coupling” here to indicate the development of crescentic inner–outer sandbar configurations that are either in phase or out of phase. Ruessink et al. (2007) used wavelet analysis to show that inner sandbar alongshore patterns become coupled to the pattern of the outer sandbar. Coupling was concurrent with the onshore migration of the outer sandbar whose alongshore shape was characterized by the presence of crescents so that, when the two sandbars became close, the inner bar developed an alongshore variability in response to the onshore propagating outer bar. Using a 9.3-year dataset of video images collected at low tide on the Gold Coast (Australia), Price and Ruessink (2011, 2013) showed that coupling between the outer and inner sandbar occurred for 40 % of the available observations. Out of the coupled sandbar patterns, the in-phase coupling occurred 85 % of the time. Finally, changes in wave height or angle of wave approach can determine both the alongshore shape of each of the sandbars and control the possible coupling configuration (see also Thiebot et al., 2012). Castelle et al. (2015) describe a variety of coupling patterns occurring along the French coast and used satellite and video imagery to show the occurrence of in-phase or out-of-phase coupled configurations. It should be pointed out that while remote sensing provides increasing evidence of coupling between sandbars, bathymetric surveys providing details about the 3D morphology of the system remain scarce and sparse. More observations are available to describe the coupling between shoreline and sandbar patterns (e.g. Coco et al., 2005; Ruessink et al., 2007; Price et al., 2014).

The conditions leading to transitions from alongshore uniform to variable have been ascribed to wave height (or wave power) and/or to parameters combining hydrodynamic and sedimentological characteristics (e.g. sediment fall velocity or Iribarren number). More specifically, the development of alongshore variability or the straightening of crescentic sandbars (Garnier et al., 2013) have been ascribed to low-energy and high-energy events, respectively. Recent observations and model results (Price and Ruessink, 2013; Garnier et al., 2013) show instead that changes in sandbar morphology (from alongshore uniform to variable and vice versa) do not follow a straightforward cause–effect relationship and that changes in the double sandbar system can be driven by a variety of interconnected factors (from wave angle to preceding bathymetry). Video imagery provides high resolution in time and large spatial coverage but is not necessarily capable of providing detailed measurements of the 3D morphology of the sandbars (an exception is provided by Price et al., 2013), and the sensitivity to preceding conditions requires more attention.

With respect to the formation mechanism, crescentic sandbars have attracted the attention of nearshore scientists for decades. Initially, their appearance has been ascribed to the presence of a template in the hydrodynamic forcing, namely edge waves. Edge waves would provide regular alongshore amplitude variations in the hydrodynamics that could be reflected onto the sandbar configuration (Bowen and Inman, 1971; Huntley, 1980; Holman and Bowen, 1982; Aagaard, 1991). A different approach focusing on feedback between hydrodynamics, sediment transport and morphological change indicates that the pattern could emerge as a result of self-organizing processes (see Coco and Murray, 2007, and references therein). This approach is based on the possibility that nonlinear coupling between hydrodynamics and sediment transport can control and actually promote the evolution of seabed perturbations eventually resulting in a spatially regular (and self-organized) pattern. In terms of field observations and modelling, most of the studies addressing the emergence of crescentic patterns have primarily focused on planar (e.g. Falqués et al., 2000; Caballeria et al., 2002) and single-barred (e.g. Caballeria et al., 2002; Damgaard et al., 2002; Reniers et al., 2004) beaches. Many studies followed and analysed various aspects of crescentic sandbar formation, from the influence of settings typical of embayed beaches (e.g. Castelle and Coco, 2012) to the influence of time-varying forcing (Castelle and Ruessink, 2011) and offshore bathymetric perturbations (Castelle et al., 2012).

In this contribution we aim to systematically address the role of initial bathymetry on the coupling between sandbars, an area that so far has received only limited attention (see also Price et al., 2014). Specifically, we wish to investigate if sandbar coupling can freely emerge, or if it is always the response of one sandbar to the development of a pattern in the other sandbar. We use linear stability analysis so that we can better focus on initial growth of the features and on the interactions that cause the emergence of the sandbar patterns. Adoption of a partly analytical approach also ensures the possibility of performing an exploration of the parameter space in a minimal amount of time, especially compared to nonlinear simulations. Other modelling studies of morphological evolution of double-barred beaches also used linear stability analysis to analyse the depth-averaged and wave-averaged equations coupled to sediment transport and morphological evolution. Calvete et al. (2007) used linear stability analysis to show that the initial cross-shore beach profile can be as important as wave height in determining the growth rate and alongshore spacing of crescentic bars. The work of Klein and Schuttelaars (2006), for example, showed that the magnitude of the longshore current and wave height are directly related to the preferred spacing and the growth rate, respectively. Modelling of oblique incident waves on double sandbar systems (Klein and Schuttelaars, 2006; Price et al., 2013) show that the coupling between the two sandbars occurs through the development of a meandering alongshore current. In agreement with field observations, simulations (Smit et al., 2008) have also shown that the outer sandbar develops into a crescentic system characterized by a larger spacing than that of the inner sandbar and attributes such differences to the larger water depth of the outer sandbar crest. Relaxing the assumption of depth-averaged motions and accounting for the circulation currents associated with undertow still results in the development of a coupled double sandbar system (Dronen and Deigaard, 2007). These studies, although reproducing the emergence of alongshore variability in double sandbar systems, do not address the possible coupling between the two sandbars.

More recently, for the case of normally incident waves, Castelle et al. (2010a, b) used a nonlinear model to investigate feedbacks between the inner and the outer sandbar. The work is of particular relevance because it proposes a novel framework to analyse the coupling that moves beyond the traditional “template” versus “self-organization” debate (Coco and Murray, 2007). The computations of Castelle et al. (2010a, b), and also others like Price et al. (2013), start from an initial bathymetry characterized by a double-bar system, with a crescentic bar superimposed to the outer bar. The use of this type of initial configuration favours the growth of crescentic shapes in the inner bar, with the same wavelength as the one in the outer bar, which originally might have developed through self-organization. These authors named this phenomenon “morphological coupling”. In terms of physical processes, the contributions by Castelle et al. (2010a, b) address the role of breaking-induced (dominant for large spacing of the crescents or strong breaking conditions) versus friction-induced circulation (dominant for small spacing of the crescents). This balance induces the emergence of patterns that in broad terms are in phase when wave focusing by refraction is dominant and out of phase when breaking-induced circulation is the primary flow driver.

Overall, it appears that only a limited number of studies have extensively explored the sandbar response to offshore wave characteristics but, aside from the initial study by Brivois et al. (2012) that analysed the stability of two different beach profiles at Truc Vert beach (France), have not attempted to systematically study the role of initial bathymetry on the evolution of the double sandbar systems. Here, we use a model based on linear stability analysis, namely MORFO62 (Ribas et al., 2012), to study the combined role of hydrodynamic conditions forced by normally incident waves and initial alongshore uniform cross-shore sandbar profile on the evolution of double sandbar systems. The different emerging patterns are then characterized. Special attention is devoted to distinguishing when the emerging patterns evolve autonomously (an individual sandbar) or when they are truly the result of morphological coupling (both sandbars interacting with each other).

2 Numerical model

The model describing the surf zone hydrodynamics is based on the depth-averaged and time-averaged momentum and continuity equations coupled to the wave energy and phase equations. The momentum balance and water mass conservation equations read

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle \frac{\partial v_i}{\partial t}}& +v_j{\displaystyle \frac{\partial v_i}{\partial x_j}}=-g{\displaystyle \frac{\partial z_{\mathrm{s}}}{\partial x_i}}-{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }D}}{\displaystyle \frac{\partial }{\partial x_j}}\left(S_{ij}^{\mathrm{W}}+S_{ij}^{\mathrm{R}}-S_{ij}^{\mathrm{t}}\right)\\ & -{\displaystyle \frac{{\mathit{\tau }}_{\mathrm{b}i}}{\mathit{\rho }D}}\\ {\displaystyle \frac{\partial D}{\partial t}}& +{\displaystyle \frac{\partial }{\partial x_j}}\left(D{v}_j\right)=\mathrm{0},i,j=\mathrm{1},\mathrm{2}.\end{array}\end{array}$$

In this notation, the Einstein convention is adopted; i.e. if an index appears twice in a term we assume a summation over that index. Here, x_i indicates the horizontal spatial coordinates (x₁∕x and x₂∕y are the cross-shore and alongshore directions, respectively), t is time, the vector $\mathit{v}(x_{\mathrm{1}},x_{\mathrm{2}},t)$ is the wave-averaged and depth-averaged mass flux current, $z_{\mathrm{s}}(x_{\mathrm{1}},x_{\mathrm{2}},t)$ represents the mean sea level and $D=z_{\mathrm{s}}-z_{\mathrm{b}}$ is the total mean depth, by which $z_{\mathrm{b}}(x_{\mathrm{1}},x_{\mathrm{2}},t)$ is the mean sea bottom bed level. Furthermore, $S_{ij}^{\mathrm{W}}$ and $S_{ij}^{\mathrm{R}}$ are the radiation stresses due to waves and rollers, while $S_{ij}^{\mathrm{t}}$ represents the turbulent Reynolds stresses, τ_bi indicates the bed shear stress, g is gravity and ρ is the water density.

The wave energy balance equation reads

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& {\displaystyle \frac{\partial E}{\partial t}}+{\displaystyle \frac{\partial }{\partial x_j}}\left(\left(v_j+c_{\mathrm{g}j}\right)E\right)+S_{jk}^{\mathrm{W}}{\displaystyle \frac{\partial v_k}{\partial x_j}}=-{\mathcal{D}}^{\mathrm{W}},\\ & j,k=\mathrm{1},\mathrm{2},\end{array}\end{array}$$

where $E=\frac{\mathrm{1}}{\mathrm{8}}\mathit{\rho }g{H}_{\mathrm{rms}}^{\mathrm{2}}$ is the wave energy density, with H_rms being the wave height, c_gj are the components of the group velocity and 𝒟^W represents the wave energy dissipation rate due to wave breaking. The roller energy balance equation reads

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& {\displaystyle \frac{\partial }{\partial x_j}}\left(\mathrm{2}\left(v_j+c_j\right)R\right)+{\mathcal{S}}_{jk}^{\mathrm{R}}{\displaystyle \frac{\partial v_k}{\partial x_j}}=-{\mathcal{D}}^{\mathrm{R}}+{\mathcal{D}}^{\mathrm{W}},\\ & j,k=\mathrm{1},\mathrm{2}.\end{array}\end{array}$$

R is the energy density of the rollers, c_j are the components of the phase velocity and 𝒟^R represents the wave energy dissipation rate due to the rollers. The wavenumber $\mathit{K}(x_{\mathrm{1}},x_{\mathrm{2}},t)$ ($\mathit{K}=(K_{\mathrm{1}},K_{\mathrm{2}})$) of the waves obeys the equation

$$\begin{array}{}\text{(4)}& \mathit{\sigma }+v_j{K}_j=\mathit{\omega }{\mathit{\sigma }}^{\mathrm{2}}=g\left|\mathit{K}\right|\tanh \left(\right|\mathit{K}\left|D\right),\end{array}$$

where σ and ω are the intrinsic and the absolute wave frequencies, respectively. The wave energy dissipation rate is parameterized using the formulation by Church and Thornton (1993):

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\mathcal{D}}^{\mathrm{W}}& ={\displaystyle \frac{\mathrm{3}{B}^{\mathrm{3}}\mathit{\rho }g\mathit{\sigma }{H}_{\mathrm{rms}}^{\mathrm{3}}}{\mathrm{32}\sqrt{\mathit{\pi }}D}}\left(\mathrm{1}-{\left(\mathrm{1}+{\left({\displaystyle \frac{H_{\mathrm{rms}}}{{\mathit{\gamma }}_{\mathrm{b}}D}}\right)}^{\mathrm{2}}\right)}^{-\mathrm{2.5}}\right)\\ & \left(\mathrm{1}+\tanh \left(\mathrm{8}\left({\displaystyle \frac{H_{\mathrm{rms}}}{{\mathit{\gamma }}_{\mathrm{b}}D}}-\mathrm{1}\right)\right)\right),\end{array}\end{array}$$

in which B (B³=2.2) is a parameter describing the type of breaking, and γ_b (=0.42) is the expected saturation value of H_rms∕D. The roller energy dissipation rate is modelled following Ruessink et al. (2001):

$$\begin{array}{}\text{(6)}& {\mathcal{D}}^{\mathrm{R}}={\displaystyle \frac{\mathrm{2}gR\sin \left({\mathit{\beta }}_{\mathrm{rol}}\right)}{c}},\end{array}$$

where β_rol (≤0.1) is the angle of the wave–roller interface. Wave radiation stresses, stresses due to roller propagation and turbulent Reynolds stresses (Svendsen, 2006) are expressed as

$$\begin{array}{}\text{(7)}& \begin{array}{rl}& {\mathcal{S}}_{ij}^{\mathrm{W}}=E\left({\displaystyle \frac{c_{\mathrm{g}}}{c}}{\displaystyle \frac{K_i{K}_j}{K^{\mathrm{2}}}}+\left({\displaystyle \frac{c_{\mathrm{g}}}{c}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\right){\mathit{\delta }}_{ij}\right)\\ & {\mathcal{S}}_{ij}^{\mathrm{R}}=\mathrm{2}R{\displaystyle \frac{K_i{K}_j}{K^{\mathrm{2}}}}\\ & S_{ij}^{\mathrm{t}}=\mathit{\rho }{\mathit{\nu }}_{\mathrm{t}}D\left({\displaystyle \frac{\partial v_i}{\partial x_j}}+{\displaystyle \frac{\partial v_j}{\partial x_i}}\right),i,j=\mathrm{1},\mathrm{2},\end{array}\end{array}$$

where δ_ij is the Kronecker delta symbol and the turbulent kinetic diffusivity is

$$\begin{array}{}\text{(8)}& {\mathit{\nu }}_{\mathrm{t}}=M{\left({\displaystyle \frac{{\mathcal{D}}^{\mathrm{W}}}{\mathit{\rho }}}\right)}^{\frac{\mathrm{1}}{\mathrm{3}}}{H}_{\mathrm{rms}},\end{array}$$

with M (M=1.0) being a parameter that characterizes the turbulence. With respect to shear stresses, we use a linear friction law τ_bi=ρμv_i ($i=\mathrm{1},\mathrm{2}$) with $\mathit{\mu }=\left(\frac{\mathrm{2}}{\mathit{\pi }}\right)c_{\mathrm{D}}{u}_{\mathrm{rms}}$. We model the drag coefficient as

$$\begin{array}{}\text{(9)}& c_{\mathrm{D}}={\left({\displaystyle \frac{\mathrm{0.40}}{\ln \left(D/z_{\mathrm{0}}\right)-\mathrm{1}}}\right)}^{\mathrm{2}},\end{array}$$

where z₀ (z₀=1.0 cm) is the bed roughness and u_rms is the wave orbital velocity at the edge of the wave-induced boundary layer:

$$\begin{array}{}\text{(10)}& u_{\mathrm{rms}}={\displaystyle \frac{H_{\mathrm{rms}}}{\mathrm{2}}}{\displaystyle \frac{g}{c}}{\displaystyle \frac{\cosh \left(\left|K\right|z_{\mathrm{0}}\right)}{\cosh \left(\left|K\right|D\right)}}.\end{array}$$

To simulate the morphological evolution, the hydrodynamic field must be coupled to a sediment transport formulation and to the conservation of sediment mass. Bed evolution is described as

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{\partial z_{\mathrm{b}}}{\partial t}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{1}-p}}{\displaystyle \frac{\partial q_j}{\partial x_j}}=\mathrm{0},j=\mathrm{1},\mathrm{2},\end{array}$$

where z_b represents the mean sea level, p (=0.4) is the porosity of the seabed and q_j are the components of the volumetric sediment transport, whose parameterization is given by the Soulsby–van Rijn formula (see Soulsby, 1997), expressed in the form

$$\begin{array}{}\text{(12)}& q_i=A_{\mathrm{s}}{\left(u_{\mathrm{stir}}\right)}^{\mathrm{2.4}}\left(v_i-\mathit{\gamma }{u}_{\mathrm{stir}}{\displaystyle \frac{\partial h}{\partial x_i}}\right),i=\mathrm{1},\mathrm{2},\end{array}$$

where A_s depends on the sediment properties and γ is a bed slope coefficient. The term A_s(u_stir)^2.4 is the depth-integrated sediment concentration (C_di). Following Ribas et al. (2012), u_stir is a stirring velocity that takes into account the depth-averaged currents, the wave orbital velocity and the roller-induced turbulence velocity. The last term in the equation takes into account the tendency of the sand to move downslope towards an equilibrium profile, where $h(x_{\mathrm{1}},x_{\mathrm{2}},t)$ stands for the perturbation of the sea bottom with respect to an alongshore uniform background (equilibrium) bathymetry.

The system of equations, when alongshore uniformity is assumed, allows for a state of morphodynamic equilibrium (steady state) for the hydrodynamic forcing conditions. By following a standard linear stability analysis (e.g. Dodd et al., 2003; Calvete et al., 2005), the system of equations is linearized with respect to alongshore periodic perturbations of the form $\mathrm{\Phi }(x_{\mathrm{1}},x_{\mathrm{2}},t)=\mathit{\text{Re}}\left\{\mathit{\varphi }\left(x_{\mathrm{1}}\right)e^{\mathit{\sigma }t+ik{x}_{\mathrm{2}}}\right\}$, where Re stands for the real part of a complex variable. For each alongshore wavenumber k, an eigenvalue problem is solved and a number of modes ϕ_i with eigenvalues σ_i are found. For a given set of forcing conditions (wave height and period; normal incidence is assumed throughout this study) and a cross-shore profile, the output of the analysis consists of the cross-shore pattern ϕ, the alongshore wavelength of the pattern $\mathit{\lambda }=\mathrm{2}\mathit{\pi }/k$, the growth rate Re(σ), and the characteristic growing time or e-folding time, $\mathit{\tau }=\mathrm{1}/\mathit{\text{Re}}\left(\mathit{\sigma }\right)$. Boundary conditions and more details about the model are given in Ribas et al. (2012) and in Calvete et al. (2005).

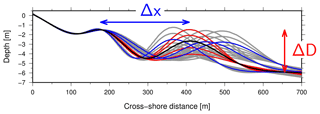
The model has been applied to a series of different bathymetries to study the effect of the distance, Δx, and difference in water depth, ΔD, between the two sandbars. Figure 2 shows the series of cross-shore profiles that will be considered in this study. We have tried to isolate individual effects and, for example, profiles in red will specifically address the sensitivity to the difference in water depth between the two sandbars (notice that ΔD is varied by changing the depth over the outer sandbar). Similarly, profiles in blue will directly assess the role of the distance between sandbar crests.

Figure 2 Geometry of cross-shore beach profiles used in this study. Different colours are used to highlight that some of the profiles were specifically designed to analyse the effect of variations in the distance or in the relative depth between sandbar crests.

3 Results

We initially present an example of the model analysis for a specific bathymetry (alongshore uniformity of the initial cross-shore profile is considered) and offshore wave conditions. For this case, we use a significant wave height H_rms=1.5 m and a wave period T=10 s with normally incident waves. The first step of a linear stability analysis is evaluating the equilibrium state, which represents the morphodynamic equilibrium previously discussed, of the equations presented in the previous section considering a fixed seabed. We assume that the bathymetry of the equilibrium state results from a morphodynamic evolution that occurs over a long temporal scale compared with the growth of the emerging morphological pattern.

Figure 3 shows the bottom cross-shore profile that is characterized by the presence of two sandbars with crests at about 200 and 480 m in the cross-shore direction, with the distance between the sandbar crests Δx=280 m and a difference of about ΔD=2.5 m between the bar depths. The other panels show other characteristics of the hydrodynamic and sediment transport (for example, notice the effect of the sandbar on wave transformation). The basic state, different for different cross-shore beach profiles, is then perturbed and possible emerging modes are analysed in terms of their growth rate. Figure 4 shows the growth rates for the example being analysed. Three different modes are present, with the fastest growing one, mode 1, characterized by an alongshore spacing close to 420 m (the wavenumber is about 0.015 m⁻¹). The second and third modes are characterized by slower growth rates and an alongshore spacing close to 170 and 500 m, respectively.

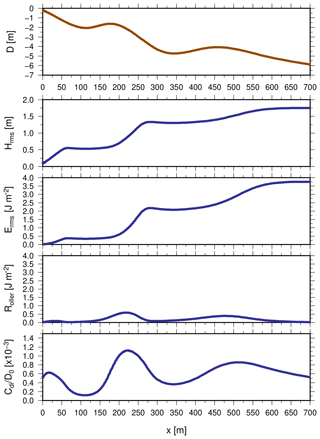
Figure 3 Basic state variables for a typical cross-shore beach profile (shoreline is at x=0). From top to bottom: (a) water depth, (b) wave height, (c) wave energy, (d) roller energy and (e) depth-averaged sediment concentration.

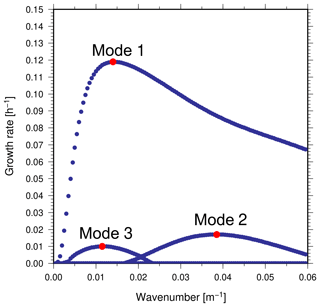
Figure 4 Growth rates as a function of the wavenumber for H_rms=1.5 m and T=10 s. The bathymetry considered in this case is the same as presented in Fig. 3.

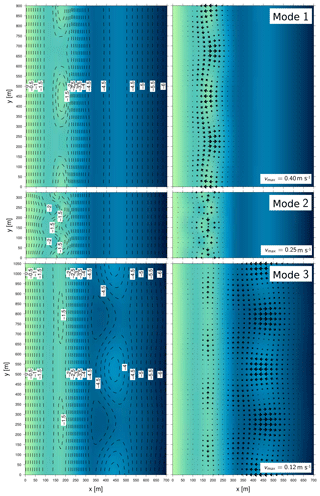
Figure 5 Fastest growing modes for the peaks in the growth rates shown in Fig. 4. The water depth (left) and depth-averaged currents (right) of each of the three modes are shown for bottom perturbations of 0.5 m of amplitude. The maximum velocities are indicated for each mode.

The water depth and circulation patterns associated with the fastest growing value of each of the three modes are shown in Fig. 5. The patterns display some evident differences with respect to which of the two sandbars develops a crescentic shape. The mode 1 represents the classic emerging crescentic sandbar, and only the inner sandbar becomes crescentic. Circulation over the inner sandbar consists of onshore flow over the shoals and offshore flow in the lower and/or channel areas consistent with the traditional mechanism of crescentic sandbar or rip channel formation (Falqués et al., 2000; Calvete et al., 2005). The pattern of mode 2 is the result of morphodynamic feedbacks mainly acting in the zone between the inner sandbar and the shoreline. Circulation and morphology also develop close to the shoreline in the form of transverse bars aligned to the lower and/or channel areas of the inner sandbar crescents. Finally, mode 3 shows an instability of the outer sandbar with small in-phase signatures on the inner sandbar. The growth rate of the different modes can be understood following Ribas et al. (2015). The pattern related to the fastest growing mode, mode 1, arises in the areas of more intense dissipation of wave energy (both in wave and roller energy, Fig. 2) and where the gradients in depth-averaged sediment concentration are large (Fig. 2). Similarly, mode 2 is associated with an instability extending close to the shoreline, where the gradient in depth-averaged concentration leads to the development of transverse sandbars associated with an offshore flow (Ribas et al., 2015). Mode 3 is characterized by less intense circulation and depth-averaged concentration that extends to the inner sandbar.

Applying linear stability analysis to the beach profiles shown in Fig. 2 results in a variety of beach responses, each identified by a specific mode. The patterns that are predicted to emerge vary largely, and we have attempted to group them using a criterion based on the difference in the maximum amplitude of the perturbations over the inner and outer sandbars. If the amplitude of the perturbation of one of the sandbars is over 80 % larger than the amplitude of the other sandbar, we consider that only the sandbar with the largest perturbation amplitude will develop into a crescentic sandbar. If the amplitude of either the inner or outer sandbars is between 40 % and 80 % larger, that sandbar will dominate the coupling. If the difference in the maximum amplitude perturbation is below 40 %, the two sandbars are considered to be fully coupled. Also, just as shown in Fig. 5 for mode 2, several emerging configurations also involve changes close to the shoreline. If the amplitude of the perturbation close to the shoreline is at least 20 % of the largest amplitude, we consider that a pattern emerges close to the shoreline. It turns out that such shoreline patterns never dominate the dynamics in the present simulations, but they always appear coupled to a perturbation in the inner or outer sandbar. In Fig. 6 we show the different patterns obtained and use the letters I and O to indicate patterns that are associated only with the inner or outer sandbar, respectively. The symbols + and – are used to indicate possible in-phase or out-of-phase coupling so that, overall, a pattern indicated with the symbols O+ refers to a configuration where the dominant effect of the instability is over the outer sandbar (letter O), while the inner sandbar shows some limited in-phase coupling (symbol +). When the coupling between sandbars is obvious, we denote the patterns with the letters IO and add the symbol + or –, depending on whether the sandbars show in-phase or out-of-phase coupling. The possible effect on shoreline and/or inner surf zone morphology that is observed in some modes is indicated by the subscript s.

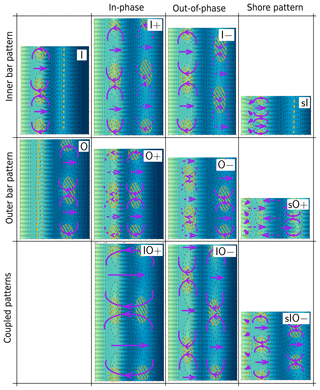
Figure 6 Morphological patterns obtained in this study. The letters I and O indicate a dominance of the inner and outer sandbars, respectively. Patterns indicated with the code IO represent modes where both sandbars are simultaneously unstable. The symbols + and – are used to indicate possible in-phase or out-of-phase coupling. Modes affecting shoreline and/or inner surf zone morphology have been indicated by the subscript s.

Figure 7 Morphological patterns for three unstable modes as a function of ΔD and Δx. Each code represents a different pattern (detailed in Fig. 6). The top (a–c), centre (d–f) and bottom (g–i) panels represent results obtained for a wave height equal to 1.0, 1.5 and 2.0 m.

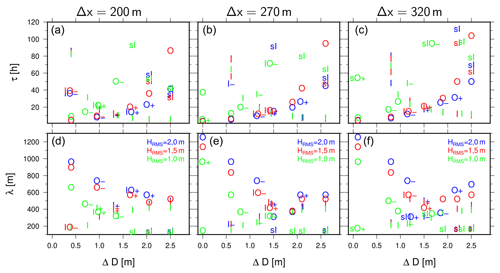
Figure 8 Growth time (a–c) and rip channel spacing (d–f) as a function of ΔD. The left (a, d), centre (b, e) and right (c, f) panels represent results obtained for Δx=200, 270 and 320 m, respectively. Blue, red and green symbols refer to wave height equal to 1.0, 1.5 and 2.0 m.

We have run simulations over the bathymetries presented in Fig. 2 using three different values of wave height (equal to 1.0, 1.5 and 2.0 m) and keeping the wave period fixed (equal to 10 s). Results are presented in Figs. 7 and 8. Figure 7 shows the emerging modes as a function of wave height, sandbar distance (Δx) and sandbar depth difference (ΔD). Figure 8 shows the corresponding growth rates and spacings. Three unstable modes are usually present, but when wave height is smallest (H_rms=1.0 m), only two modes are unstable. The first mode, the fastest growing one, displays a similar pattern for the three values of the wave height considered. When the difference between the sandbar crests, ΔD, is large, the fastest growing mode is of type I, which implies that the inner sandbar develops into a crescentic shape. Because of the large difference in water depth between sandbar crests, the outer sandbar is essentially inactive, while when ΔD is small most of the wave breaking is concentrated on the outer sandbar, which develops crescents (type O). For intermediate differences in the water depth between the sandbar crests, a transition from type I to O can be observed. In most cases, the transition occurs through the development of an I+ pattern (the amplitude of the pattern is larger at the inner sandbar, and the outer sandbar reflects limited in-phase coupling). As ΔD decreases, an instability of type O– is more likely to develop (the amplitude of the pattern is larger at the outer sandbar, and the inner sandbar reflects limited out-of-phase coupling). For H_rms=1.5 m, the transition also results in the development of fully coupled patterns, namely type IO. While the patterns show an evident dependence on ΔD, the role of Δx on the emergent patterns is limited (Fig. 7). The pattern of the second mode, characterized by lower growth rates, can be characterized as follows. Given a specific combination of ΔD and Δx, if the mode 1 instability is of type I, then for the mode 2 the instability is type O. No mode 1 configuration affects shoreline morphology, while modes associated with changes at the shoreline appear more frequently as mode 2 and 3, especially if ΔD is large.

In order to understand the differences between the IO modes and the modes I or O, additional experiments have been carried out. For example, simulations for which modes I+ or I– were originally found were repeated, but without sediment transport in the outer bar. As a result, modes with similar growth rates and spacing were found, but with no extension to the outer sandbar. The same results were found in the equivalent experiments for O+ and O–. For conditions leading to modes IO, cancelling the sediment transport over any of the two sandbars resulted in pattern emergence focused over a single bar (the one where sediment transport was not cancelled), but now with large differences in the growth rate and spacing compared to the IO mode. IO should then be considered as a mode that develops as a result of the simultaneous interaction between the two sandbars.

Given that the sensitivity of the characteristics of the growing sandbars to Δx is limited, we fixed its value (equal to 200, 270 and 320 m) and specifically looked at the growth rates and spacings (Fig. 8). Results can be interpreted by looking at the dependencies of the individual types of patterns. For example, independent of the value of wave height, patterns of type I consistently show a marked decrease in the growth time, with increasing ΔD (see top panels in Fig. 8). The decrease in growth time is accompanied by a moderate increase in the spacing of the rip channels (the spacing of mode I never exceeds 400 m). The same is observed for all distances between the sandbar crests considered in this study. Mode O shows almost the opposite because the growth time increases with ΔD, while the spacing of the rip channels diminishes (for Δx=320 m a slight increase in spacing is observed for very large ΔD). The largest rip channel spacing observed for mode O is in excess of 1200 m, which is about twice the largest spacing observed for mode I. Finally, the modes that have a shoreline signature are all characterized by large values of ΔD, large growth times and short spacing (about 200 m).

4 Discussion

We focused on the morphodynamics of double sandbar systems and investigated under which conditions the systems are unstable to perturbations that ultimately result in the development of surf zone patterns like rip channels and/or crescentic sandbars. We used linear stability analysis to discover the morphological configurations that can arise as a result of the feedbacks between hydrodynamics, sediment transport and morphological change. We primarily focused on the sensitivity to the initial seabed cross-shore profile, by varying the distance between sandbar crests or varying the difference between the water depth over the two sandbar crests. We generally observe large variability in the response of the system to changes in bathymetric details. This is not entirely unexpected, since the amount of wave breaking induced by the 3D morphology of the outer sandbar is critical to determine if the two sandbars are coupled or if the pattern emerges in correspondence of only one of the two sandbars. This is in agreement with the findings by Castelle et al. (2010a) showing that the type of horizontal flow circulation over the outer sandbar (driven either by refraction or by wave breaking) is ultimately responsible for the possible coupling between sandbars. For this reason, while the distance between the sandbar crests is unimportant in determining which pattern emerges (Fig. 7), the difference in water depth is a critical parameter to determine the shape and characteristics of the fastest growing mode. In our model, a large difference in the water depths over the two sandbar crests (e.g. ΔD=2.5 m) implies that limited wave set-up and breaking occur over the outer sandbar, which is essentially inactive. In this case, the fastest growing mode is always related to the inner sandbar, which becomes unstable (Fig. 9) following the physical mechanisms described by Calvete et al. (2005). When the difference between the sandbar water depths is small (e.g. ΔD=0.5 m), strong wave breaking occurs over the outer sandbar and the fastest growing mode is related to the outer sandbar (Fig. 9). Coupling between the two sandbars occurs for intermediate differences in the water depth of the sandbar crests, while the presence of emerging configurations that involve the shoreline only occurs for the largest water depth difference (Fig. 9). This behaviour is also evident when looking in detail at the spacing of the emerging rip channel pattern and at the growth time of the mode (Fig. 10). As synthesized in Figs. 9 and 10, results bear little dependency on Δx and the overall behaviour of the system is governed by ΔD and H_rms. When ΔD is small, the presence and characteristics of an emerging mode depend on the value of H_rms. As shown in Fig. 10, for small ΔD the outer sandbar spacing depends on H_rms, but tends to be large, while for large ΔD the dependency of the spacing to H_rms is smaller. Inner sandbar modes dominate instead for large ΔD and small H_rms.

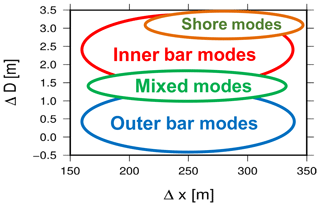
Figure 9 Sketch of the most likely fastest growing modes as a function of the geometry of the cross-shore profile. ΔD represents the difference between the water depth over the two sandbar crests while Δx is the distance between the two sandbar crests.

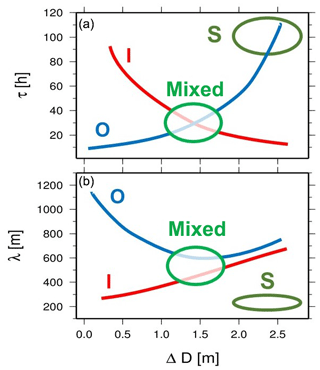
Figure 10 Sketch that summarizes our findings in terms of (a) growth time and (b) crescentic sandbar spacings. The colours refer to the modes in Fig. 9.

Regarding the morphological coupling discussed by other authors (Castelle et al., 2010a; Price et al., 2014), our results derived from linear stability analysis can distinguish between modes that develop in one of the bars only and modes that induce the emergence of a pattern over the other sandbar. At the same time, we obtain modes that develop simultaneously over the two sandbars. In the first case, we interpret that there is a primary mode affecting one of the sandbars, with the other sandbar evolution being passively slaved to its morphodynamics. In the second case, the pattern developing over the two bars is related to the same mode and, therefore, the emerging pattern shows full sandbar coupling. This full morphodynamic coupling occurs for intermediate differences of sandbar depth. For small differences of depth, pattern emergence over the outer bar dominate, whilst for larger differences of bars' depths the main pattern is located at the inner bar (although the wavelength of the crescentic bars on the inner and on the outer bar appear to be very similar). For cross-shore profiles that allow for large waves to reach the shoreline, the model predicts the formation and coupling of shoreline patterns, even though the model does not include swash dynamics, and we considered a fixed shoreline. The transition from forced to fully coupled occurs smoothly in the parameter space that has been examined. Since our analysis of the model dynamics is linear, the concept of coupling is limited to the initial morphological formation and, since linear stability analysis focuses on the fastest growing wavelength, coupling at half of the outer bar wavelength cannot occur. Also, we do not simulate the nonlinear interactions between competing wavelengths, which might lead to coupling over longer timescales (days to weeks) or the final equilibrium configuration. Both important aspects can be studied using analysis that includes nonlinear mode interactions and that are suited to studying the long-term evolution and possibly the equilibrium of these systems.

Despite our attempts to provide a detailed description of hydrodynamics and morphodynamics, the model remains simplified and does not include a number of physical processes that in the context of surf zone morphodynamics can be relevant. As for the case of many surf zone morphodynamic studies, hydrodynamic forcing is simplified, and the effects of directional and frequency spread in the wave field as well as tidal variations are neglected. One could expect that the primary effect related to these processes was a decrease in the growth time of the features without necessarily affecting the type of morphodynamic patterns that grow. We also neglected the role of wave angle (we only considered normally approaching waves) that has been shown to be relevant for the coupling of sandbar systems (Price and Ruessink, 2011; Price et al., 2013). On the other hand, we include a detailed modelling of the effect of wave-induced rollers that has been shown to be important for the development of surf zone features (Ribas et al., 2011; Calvete et al., 2012), but whose effect on double sandbar systems had not been considered before. Finally, the study does not address some of the possible effects on sediment transport associated with undertow and wave asymmetry and, particularly for varying cross-shore beach profiles, it could quantitatively affect the results. Despite these shortcomings, the model reproduces morphodynamic patterns, which are consistent with the presence of coupled sandbar patterns. Although the objective of this contribution is limited to a numerical analysis of the possible emerging patterns arising in double sandbar configurations, model results are in qualitative agreement with observations of the Truc Vert (France) double sandbar system (Castelle et al., 2015), where transverse bars are coupled to inner bars during moderate conditions, and inner–outer bar coupling is observed for more energetic conditions (we stress that parameter settings are not necessarily representative of Truc Vert). Lack of detailed and systematic measurements of bathymetric evolution of coupled sandbar systems remains the biggest obstacle to model testing in this area of research. We envisage that future development in the extraction of bathymetry from video images will be hugely beneficial to this area of research (Van Dongeren et al., 2008).

Our findings have clear implications for the understanding of observed coupled sandbar patterns. Coupled sandbar systems are usually considered as the result of one sandbar affecting another. Our results indicate that coupling can also emerge as a result of a single mode. The apparent differential growth of each sandbar might lead one to think that one sandbar is forcing the coupling over the other sandbar. Our results indicate that a coupled pattern, with perturbations over each sandbar of different amplitude, can also arise without invoking one sandbar as a forcing mechanism. In addition, our results indicate that a variety of modes can grow for similar conditions. Although we do not deal with the nonlinear behaviour of the patterns, one can envisage that growth and interaction between multiple modes can become a source of spatial variability in the observed pattern.

5 Conclusions

In order to gain insight into the physical processes that govern the development of coupled sandbar patterns, we have analysed the linear stability of a system of equations describing the morphodynamics of a double sandbar system. Our results indicate the development of a variety of morphological configurations, where inner and outer sandbars show in-phase and out-of-phase coupling or no coupling. Our study points at the combined influence of offshore wave characteristics and the initial cross-shore bed profile in determining the alongshore wavelength and growth rate of the fastest growing mode and/or pattern. Overall, inner bar modes are dominant for large differences between the two water depths of the sandbars and small offshore wave heights, while patterns related to the outer sandbar dominate for small values of the difference in sandbar depths. For intermediate differences between the two sandbars depths, patterns on both longshore bars appear to be fully coupled. Relatively large waves and large depth over the outer sandbar can induce secondary patterns close to the shoreline and/or inner surf zone. Although initial qualitative comparisons appear to support our modelling, continued model development, particularly in trying to address the effects of cross-shore wave-induced sediment transport, remains critical to improve the understanding and predictability of these natural systems.