Short communication: Field data reveal that the transport probability of clasts in Peruvian and Swiss streams mainly depends on the sorting of the grains

We present field observations from coarse-grained streams in the Swiss Alps and the Peruvian Andes to explore the controls on the probability of material entrainment. We calculate shear stress that is expected for a mean annual water discharge and compare these estimates with grain-specific critical shear stresses that we use as thresholds. We find that the probability of material transport largely depends on the sorting of the bed material, expressed by the D₉₆∕D₅₀ ratio, and the reach gradient but not on mean annual discharge. The results of regression analyses additionally suggest that among these variables, the sorting exerts the largest control on the transport probability of grains. Furthermore, because the sorting is significantly correlated neither to reach gradient nor to water discharge, we propose that the granulometric composition of the material represents an independent, yet important control on the motion of clasts in coarse-grained streams.

1 Introduction

It has been proposed that the transport of coarse-grained material in mountainous streams occurs when flow strength – or bed shear stress – exceeds a grain-size-specific critical shear stress (Miller et al., 1977; Tucker and Slingerland, 1997; Church, 2006). This has been documented based on flume experiments (e.g., Meyer-Peter and Müller, 1948; Dietrich et al., 1989; Carling et al., 1992; Ferguson, 2012; Powell et al., 2016) and field observations (e.g., Paola and Mohring, 1996; Lenzi et al., 2006; Mueller et al., 2005; Lamb et al., 2008), and related concepts have been employed in theoretical models (Paola et al., 1992; Tucker and Slingerland, 1997). Whereas flow strength is mainly a function of discharge, energy gradient and channel width (e.g., Slingerland et al., 1993; Hancock and Anderson, 2002; Pfeiffer and Finnegan, 2018; Wickert and Schildgen, 2019), the threshold shear stress itself has been considered to depend on grain-specific variables, such as grain size and the arrangement of clasts including hiding and protrusion effects (Carling, 1983; Parker, 1990; van den Berg and Schlunegger, 2012; Pfeiffer and Finnegan, 2018), but not on the shape of individual grains (Carling, 1983) – or at least this variable plays a minor role only (Komar and Li, 1986). In addition, the threshold shear stress has also been related to the reach gradient (Lamb et al., 2008; Turowski et al., 2011; Pfeiffer and Finnegan, 2018). Here, we provide field data from coarse-grained single-thread streams in the Swiss Alps and braided rivers in the Peruvian Andes to illustrate that amongst the various variables, the sorting of the grains exerts the largest control on the transport probability. The field sites are located close to water gauging stations so that we have good constraints on the streams' discharge in our analyses. We determined the grain size distribution of gravel bars at these locations and calculated, within a probabilistic framework using Monte Carlo simulations, the likelihood of sediment transport for a mean annual water discharge Q_mean and for discharge percentiles. We explored whether the related flows are strong enough to shift the D₈₄ grain size, which is considered to build the sedimentary framework of gravel bars as recent flume experiments have shown (MacKenzie and Eaton, 2017; MacKenzie et al., 2018). We thus considered the mobilization of the D₈₄ grain size as a priori condition – and thus as a threshold – for a change in the sedimentary arrangement of the target gravels bars.

The braided character of streams in Peru, however, complicates the calculation of sediment transport probabilities mainly because water flows frequently in multiple active channels, and channel widths vary over short distances. For these streams, we selected reaches (ca. 100 m long) where several active braided channels merge to a single one, before branching again. We are aware that this could eventually bias the results towards a greater material mobility, mainly because flows in single-thread segments are likely to have a greater shear stress than in braided reaches where the same water runoff is shared by multiple channels.

2 Methods and datasets

2.1 Entrainment of bedload material

Sediment mobilization is considered to occur when bed shear stress τ exceeds a grain-size-specific threshold τ_c (e.g., Paola et al., 1992) as follows:

$$\begin{array}{}\text{(1)}& \mathit{\tau }\mathit{>}{\mathit{\tau }}_{\mathrm{c}}.\end{array}$$

Threshold shear stress τ_c for the dislocation of grains with size D_x (see Sect. 2.3.1 for further specifications) can be obtained using Shields (1936) criteria ϕ for the entrainment of sediment particles:

$$\begin{array}{}\text{(2)}& {\mathit{\tau }}_{\mathrm{c}}=\mathit{\varphi }\left({\mathit{\rho }}_{\mathrm{s}}-\mathit{\rho }\right)g{D}_x,\end{array}$$

where g denotes the gravitational acceleration, and ρ_s (2700 kg m^−s) and ρ denote the sediment and water densities, respectively.

Bed shear stress τ is computed through (e.g., Slingerland et al., 1993; Tucker and Slingerland, 1997)

$$\begin{array}{}\text{(3)}& \mathit{\tau }=\mathit{\rho }gRS.\end{array}$$

Here, S denotes the energy gradient, and R is the hydraulic radius, which is approximated through water depth d where channel widths W>20 d (Tucker and Slingerland, 1997), which is the case here. The combination of expressions for (i) the continuity of mass including flow velocity V, channel width W, and water discharge Q,

$$\begin{array}{}\text{(4)}& Q=VWd;\end{array}$$

(ii) the relationship between flow velocity and channel bed roughness n (Manning, 1891),

$$\begin{array}{}\text{(5)}& V={\displaystyle \frac{\mathrm{1}}{n}}{d}^{\mathrm{2}/\mathrm{3}}{S}^{\mathrm{1}/\mathrm{2}};\end{array}$$

and (iii) an equation for Manning's roughness number n (Jarrett, 1984),

$$\begin{array}{}\text{(6)}& n=\mathrm{0.32}{S}^{\mathrm{0.38}}{d}^{-\mathrm{1}/\mathrm{6}},\end{array}$$

yields a relationship where bed shear stress τ depends on reach gradient, water discharge and channel width (Litty et al., 2017).

$$\begin{array}{}\text{(7)}& \mathit{\tau }=\mathrm{0.54}\mathit{\rho }g{\left({\displaystyle \frac{Q}{W}}\right)}^{\mathrm{0.55}}{S}^{\mathrm{0.935}}\end{array}$$

This equation is similar to the expression by Hancock and Anderson (2002), Norton et al. (2016), and Wickert and Schildgen (2019) with minor differences regarding the exponent on the channel gradient S and on the ratio Q∕W. These are mainly based on the different ways of how bed roughness is considered. Note that this equation does not consider a roughness length scale (both vertical and horizontal) because we have no constraints on this variable.

We explored whether Eq. (5) could be solved using the Darcy–Weisbach friction factor f instead of Manning's n. According to Ferguson (2007), the friction factor f varies considerably between shallow- and deep-water flows and depends on grain size D_x relative to water depth d and, thus, on the relative roughness. Ferguson (2007) developed a solution referred to as the variable power equation (VPE), which accounts for the dependency of f on the relative importance of roughness-layer versus skin friction effects and thus on the D_x∕d ratios (see also Bunte et al., 2013). Calculations where the VPE was employed indeed revealed that roughness-layer effects have an impact on flow regimes where $D_{\mathrm{84}}/d>\mathrm{0.2}$ (Schlunegger and Garefalakis, 2018), which is likely to be the case in our streams. However, similar to Litty et al. (2016), we are faced with the problem that we have not sufficient constraints to analytically solve Eq. (5) with the VPE. We therefore selected Mannings's n instead, which allowed us to solve this equation analytically.

2.2 Monte Carlo simulations

Predictions of sediment transport probability are calculated using Monte Carlo simulations performed within a MATLAB computing environment. We conducted 10 000 simulations, and the results are reported as the probability (in percent) of τ>τ_c (Eq. 1). All variables that are considered for the calculations of both shear and critical shear stress (Eqs. 7 and 2, respectively) are randomly selected within their possible ranges of variation (Table 1). Except for the Shields variable ϕ that we consider to follow a uniform distribution between 0.03 and 0.06 (see Sect. 2.3.1 for justification), we infer that all other variables follow normal distributions, defined by their means and corresponding standard deviations.

To ensure that no negative values introduce a bias to these iterations, only strictly positive values for channel widths and gradients are considered. In the case of water discharge, both null and positive values are kept for further calculations. Values excluded from the calculations, i.e., returning negative water discharge or null or negative channel width–slope gradient, yield “NaN” in the resulting vector. For each of the 10 000 iterations, τ and τ_c are compared, which yields either “1” (τ>τ_c) or “0” (τ≤τ_c). The sediment transport probability is then calculated as the sum of ones divided by the number of draws, from which the number of “NaN” values was subtracted before. Note that <2500 “NaN” were obtained for Rio Chico (PRC-ME17), which we mainly explain by the ca. 150 % relative standard deviation of the mean annual water discharge estimated for that river.

2.3 Parameters, datasets, uncertainties and sensitivity analyses

2.3.1 Shields variable ϕ and threshold grain size

Assignments of values to ϕ vary and diverge between flume experiments (e.g., Carling et al., 1992; Ferguson, 2012; Powell et al., 2016) and field observations (Mueller et al., 2005; Lamb et al., 2008). Here, we considered that at the incipient motion of D₈₄, the Shields variable ϕ is equally distributed between 0.03 and 0.06 (Dade and Friend, 1998) during the 10 000 iterations. We also explored a slope-dependency of ϕ (Lamb et al., 2008; Bunte et al., 2013; Pfeiffer et al., 2017; Pfeiffer and Finnegan, 2018), where

$$\begin{array}{}\text{(8)}& \mathit{\varphi }=\mathrm{0.15}{S}^{\mathrm{0.25}}.\end{array}$$

However, applying this slope-dependent characterization of ϕ did not change our overall finding that the transport probability is dependent on the sorting of the material (Fig. S1 in the Supplement). In the same context, Turowski et al. (2011) reported a larger variation in the threshold conditions for the mobilization of clasts than those employed here. However, their streams have energy gradients between 0.06 and 0.1, with the consequence that some of the material is entrained during torrential floods. The related conditions thus differ from those of the much flatter streams (reach gradients <0.02), which we explored in this paper. Finally, we did not explicitly include a grain-size specific hiding (e.g., Eq. A8 in Pfeiffer and Finnegan, 2018) or a protrusion function (e.g., Carling, 1983; Sear, 1996; van der Berg and Schlunegger, 2012) in our analysis, but we suggest that the selected range between 0.03 and 0.06 considers most of the complexities and scatters of ϕ values that are related to the hiding of small clasts and the protrusion of large constituents (Buffington et al., 1992; Buffington and Montgomery, 1997; Kirchner et al., 1990; Johnston et al., 1998). In summary, we infer that the selection of uniformly distributed ϕ values between 0.03 and 0.06 does account for the large variability of ϕ values that are commonly encountered in experiments and field surveys where energy gradients range between 0.001 and 0.02, which is the case here.

We consider that the most important critical shear stress is that required to move D₈₄, rather than any other grain size percentile. We acknowledge that other authors preferentially selected the D₅₀ grain size as a threshold to quantify the minimum flow strengths τ_c to entrain the bed material (e.g., Paola and Mohrig, 1996; Pfeiffer and Finnegan, 2018; Chen et al., 2018). The selection of D₅₀ results in a lower threshold and a greater transport probability than the employment of D₈₄. However, among the various grain sizes, D₈₄ has been considered to best characterize the sedimentary framework of a gravel bar (Howard, 1980; Hey and Thorne, 1986; Grant et al., 1990), and more recent experiments have also shown that D₈₄ better characterizes the channel form stability than D₅₀ (MacKenzie et al., 2018). Accordingly, flows that dislocate the D₈₄ grain size are considered strong enough to alter the gravel bar architecture. We therefore followed the recommendation by MacKenzie et al. (2018) and selected the D₈₄ grain size to quantify the threshold conditions in Eq. (2).

2.3.2 Grain size data

We collected grain size data from streams where water discharge has been monitored during the past decades. These are the Kander, Lütschine, Rhein, Sarine, Simme, Sitter and Thur rivers in the Swiss Alps (Fig. 1a). The target gravel bars are situated close to a water gauging station. At these sites, five to six digital photographs were taken with a Canon EOS PR. The photos covered the entire lengths of these bars. A meter stick was placed on the ground and photographed together with the grains. Grain sizes were then measured with the Wolman (1954) method using the free software package ImageJ 1.52n (https://imagej.nih.gov, last access: 7 August 2019). Following Wolman (1954), we used intersecting points of a grid to randomly select the grains to measure. A digital grid of 20 cm×20 cm was calibrated with the meter stick on each photo. The size of the grid was selected so that the spacing between intersecting points was larger than the b axis of most of the largest clasts (Tables 1 and S2 in the Supplement). The grid was then placed on the photograph with its origin at the lower-left corner of the photo. The intermediate or b axis of approximately 250–300 grains (ca. 50 grains per photo; Table S2) underneath a grid point was measured for each gravel bar. In this context, we inferred that the shortest (c axis) was vertically oriented and that the photos displayed the a and b axes only. In cases where more than half of the grain appeared to be buried, the neighboring grain was measured instead. In the few cases where the same grain lay beneath several grid points, then the grain was only measured once. Only grains larger than a few millimeters (> 4–5 mm, depending on the quality and resolution of the photos) could be measured. While the limitation to precisely measure the finest-grained particles potentially biases the determination of D₅₀, it will not influence the measurements of the D₈₄ and D₉₆ grain sizes, as the comparison between sieving and measuring of grains with the Wolman (1954) method has disclosed (Watkins et al., 2020). In addition, as will be shown below, the consideration of the D₉₆∕D₈₄ instead of the D₉₆∕D₅₀ ratios yields a similar positive relationship to the mobility of grains. We complemented the grain size datasets with published information on the D₅₀,D₈₄ and D₉₆ grain size (Litty and Schlunegger, 2017; Litty et al., 2017) for further streams in Switzerland (six additional rivers) and Peru (21 sites) (Fig. 1a and b; Table 1). For a few streams in Switzerland, Hauser (2018) presented D₈₄ grain size data from the same gravel bars as Litty and Schlunegger (2017), but the photo was taken 1 year later and possibly from a different site. For these five locations, we took the arithmetic mean of both surveys (Table 1, data marked with c). All authors used the same approach upon collecting grain size data, which justifies the combination of the new with the published datasets.

Table 1 Channel morphometry (width and gradient), grain size and water discharge measured at the research sites. The table also shows the results of the various calculations (critical shear stress τ_c, shear stress τ of a flow with a mean annual runoff Q_mean and probability of sediment transport occurrence related to this flow).

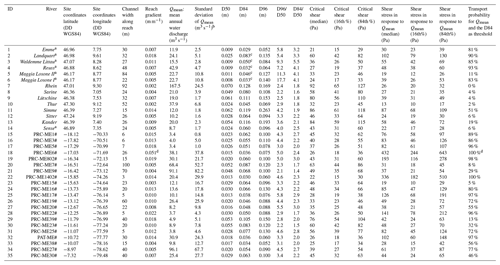
Italic: Swiss rivers; roman text: Peruvian rivers. Water discharge data from the Swiss rivers are taken from the Swiss Federal Office for the Environment (FOEN: https://www.hydrodaten.admin.ch/, last access: 10 September 2019). Reported values represent discharges monitored over the period 1990–2011, except for the Rhein (1977–1990). Water discharge and drainage basin size data from the Peruvian rivers are taken from Reber et al. (2017) and Litty et al. (2017). #The grain size data from the Peruvian streams are taken from Litty et al. (2017). ^a The grain size data, channel width and gradient data from the Emme, Landquart, Reuss, Maggia and Sense rivers are taken from Litty and Schlunegger (2017). ^b While standard deviation on annual water flow represents interannual variance for Switzerland, it represents intra- annual variance in Peru. ^c Mean values of measurement results by Hauser (2017) and Litty and Schlunegger (2017). ^d The results are possibly biased by an error in the slope, which appears too steep; the consideration of a flatter slope (0.013) still yields 99 %.

Figure 1 (A) Map showing the sites where grain size data have been measured in the Swiss Alps. The research sites are close to water gauging stations; (B) map showing locations for which grain size and water discharge data are available in Peru (Litty et al., 2017).

We finally assigned an uncertainty of 20 % to the D₈₄ threshold grain size, which considers the variability in D₈₄ within a gravel bar as the analysis of the intra-bar variation in D₈₄ for selected gravel bars in Switzerland shows (Table S2). The assignment of a 20 % uncertainty to the D₈₄ threshold grain size also considers a possible bias that could be related to the grain size measuring technique (e.g., sieving in the field versus grain size measurements using the Wolman method; Watkins et al., 2020). However, it is likely to underestimate the temporal variability in the grain size data. Indeed, a repeated measurement on some gravel bars in Switzerland has revealed that up to 2-fold differences in grain size could be possible (Hauser, 2018).

2.3.3 Water discharge data

The Federal Office for the Environment (FOEN) of Switzerland has measured the runoff values of Swiss streams over several decades. We employed the mean annual discharge values over 20 years for these streams (Table S3) and calculated 1 standard deviation thereof (see Table 1). For the Peruvian streams, we used the mean annual water discharge values Q_mean reported by Litty et al. (2017) and Reber et al. (2017). These authors obtained the mean annual water discharge (Table 1) through a combination of hydrological data reported by the Sistema Nacional de Información de Recursos Hídricos and the TRMM-V6.3B43.2 precipitation database (Huffman et al., 2007). They also considered the intra-annual runoff variability as 1 standard deviation from Q_mean to account for the strong seasonality in runoff for the Peruvian streams, which we employed in this paper. For the Peruvian streams, the assigned uncertainties to Q_mean are therefore significantly larger than for the Swiss rivers (Table 1). A reassessment of the interannual variability in water discharge for those streams in Peru where the gauging sites are close to the grain size sampling location (distance of a few kilometers) yields a 1 standard deviation of ca. 50 %, which is still much larger than for the Swiss rivers (Table S3). We therefore run sensitivity tests where we considered scenarios with different relative values for 1σ standard deviations of Q_mean.

We additionally ran sensitivity tests to explore how the mobility probability changes if discharge quantiles instead of Q_mean are considered (Table S4). We ran a series of Monte Carlo simulations for various discharge quantiles and then calculated the resulting probability of sediment mobilization for each of these quantiles. We then multiplied the occurrence probability of each discharge quantiles (listed by the Swiss authorities and calculated for the Peruvian streams based on 4 to 98 years equivalent daily records) with the corresponding transport probability and summed the values. This integration provides an alternative estimate of transport probability (Table S4).

2.3.4 Channel width data

For the Swiss streams, channel widths and gradients (Table 1) were measured on orthophotos and lidar DEMs with a 2 m resolution provided by Swisstopo. From this database, gradients were measured over a reach of ca. 250 to 500 m. All selected Swiss rivers are single-thread streams following the classification scheme of Eaton et al. (2010), and flows are constrained by artificial banks where channel widths are constant over several kilometers. For these streams, we therefore measured the cross-sectional widths between the channel banks, similar to Litty and Schlunegger (2017).

We complemented this information with channel width (wetted perimeter) and energy gradient data for 21 Peruvian streams that were collected by Litty et al. (2017) in the field and on orthophotos taken between March and June. This period also corresponds to the season when the digital photos for the grain size analyses were made (May 2015). We acknowledge that widths of active channels in Peru vary greatly on an annual basis because of the strong seasonality of discharge (see above and large intra-annual variability in discharge in Table 1). We therefore considered scenarios where channel widths are twice as large as those reported in Table 1.

The uncertainties on reach gradient and channel width largely depend on the resolution of the digital elevation models underlying the orthophotos (2 m lidar DEM for Switzerland and 30 m ASTER DEM for Peru). It is not possible to precisely determine the uncertainties on the gradient values. Nevertheless, we anticipate that these will be smaller for the Swiss rivers than for the Peruvian streams mainly because of the higher resolution of the DEM. We ran sensitivity models where we explored how the probability of material transport changes in the Swiss rivers for various uncertainties on channel widths, energy gradients and mean annual discharge values.

3 Results

3.1 Grain size data, critical and bed shear stress, and transport probability

The grain sizes range from 8 to 70 mm for D₅₀, 29 to 128 mm for D₈₄ and 52 to 263 mm for D₉₆. The smallest and largest D₅₀ values were determined for the Maggia and Rhein rivers in the Swiss Alps, respectively (Table 1). The grain sizes in the Swiss rivers also reveal the largest spread where the ratio between the D₉₆ and D₅₀ grain size ranges between 2.2 (Sarine) and 17.7 (Maggia Losone I), while the corresponding ratios in the Peruvian streams are between 2.1 (PRC-ME9) and 5.8 (PRC-ME17). In the Swiss Alps, the critical shear stress values τ_c (median) for entraining the D₈₄ grain size range from ca. 20 Pa (Emme river) to ca. 90 Pa (Rhein and Simme rivers). In the Peruvian Andes, the largest critical shear values are <80 Pa (PRC-ME39). The shear stress values related to the mean annual water discharge Q_mean range from ca. 15 to 100 Pa in the Alps and from 20 to >400 Pa in the Andes. Considering the strength of a mean annual flow and the D₈₄ grain size as threshold, the probability of sediment transport occurrence in the Peruvian Andes and in the Swiss Alps comprises the full range between 0 % and 100 %.

Rivers that are not affected by recurrent high-magnitude events (e.g., debris flows) and where the grain size distribution is not perturbed by lateral material supply are expected to display a self-similar grain size distribution (Whittaker et al., 2011; D'Arcy et al., 2017; Harries et al., 2018), characterized by a linear relationship between the D₈₄∕D₅₀ and D₉₆∕D₅₀ ratios. In case of the Maggia river, the largest grains are oversized if D₅₀ and the grain size distribution of the other streams are considered as reference (Fig. 2a). This could reflect a response to the supply of coarse-grained material by a tributary stream where the confluence is <1 km upstream of the Maggia sites. Alternatively – and possibly more likely – it reflects the response to the high-magnitude floods in this stream (Brönnimann et al., 2018) that could explain why the largest grains tend to be oversized. In particular, while the ratio between the last and first quantiles of discharge is <150 in the Swiss streams on the northern side of the Alps, the ratio is 860 in the Maggia river. Such ratios are not rare in Peru. However, the Peruvian streams appear to have adapted to such a large discharge variability through their network of braided channels that are not confined by artificial banks along most of the streams. In either case, because the grains in the Maggia river have a different size composition than the other streams (Fig. 2a), we excluded the Maggia data from further analyses. From this dataset, we then explored whether D₈₄ depends on the sorting of the grains (D₉₆∕D₅₀ ratio), but a possible negative correlation between these variables is very weak (R²=0.2) with a p-value of 0.011 (Fig. 2b).

Figure 2 (a) Relationship between ratio of the D₉₆∕D₅₀ and D₈₄∕D₅₀, implying that the D₉₆grain sizes of the Maggia gravel bars are too large if the D₅₀ is taken as reference and if the other gravel bars are considered. (b) Relationships between D₈₄ and sorting, expressed by the D₉₆∕D₅₀ ratio. The Maggia data are not considered in this figure. However, the negative correlation between these variables is weak. Blue diamonds correspond to the Swiss rivers, while grey circles are Peruvian ones.

3.2 Correlations between channel metrics, water discharge, material sorting and transport probability

The probability of sediment transport occurrence correlates positively with the reach gradient (R²=0.46, p-value =0.016 for Swiss rivers; R²=0.34, p-value =0.0056 for streams in Peru; Fig. 3a). For the Peruvian rivers, the probability of occurrence also scales negatively with channel width (R²=0.37, p-value =0.0033; Fig. 3b) and critical shear stress τ_c (R²=0.48, p-value =0.00047; Fig. 3d), which itself depends on the threshold grain size D₈₄. No significant correlations are found between the transport probability and mean annual water discharge for the Swiss and Peruvian rivers (Fig. 3c).

Figure 3 Relationships between transport probability and (a) reach gradient, (b) channel width, (c) mean annual discharge and (d) critical shear stress that depend on the D₈₄. Blue diamonds correspond to the Swiss rivers, while grey circles are Peruvian ones.

Notably, the probability of material transport correlates positively and linearly with the D₉₆∕D₅₀ ratio (Fig. 4a). The observed relationship appears stronger for the Swiss rivers (R²=0.76), than for the Peruvian streams (R²=0.36), and both correlations are significant with p-values of 0.00022 and 0.0041, respectively. These correlations suggest that poorer-sorted bed material, here expressed by a high D₉₆∕D₅₀ ratio, has a greater transport probability than better-sorted sediments. If the normalized residuals are plotted against the sorting, then they do not show any specific and significant patterns and, therefore, appear independent of the sorting (Fig. 4b). This suggests that the inferred linear relationships between the transport probability and the D₉₆∕D₅₀ ratio are statistically robust. Although Fig. 4a implies that the regression for the Swiss rivers (slope: 0.16±0.06; intercept: $-\mathrm{0.34}\pm \mathrm{0.31}$) differs from that of the Peruvian streams (slope: 0.18±0.11; intercept: $-\mathrm{0.02}\pm \mathrm{0.46}$), the regression parameters do not significantly differ when considering them within their 95 % confidence intervals. In addition, sites with larger values of D₉₆∕D₅₀ tend to be associated with smaller values of D₈₄ (albeit with a weak correlation), but as noted earlier the influence of D₈₄ on the critical shear stress is not sufficient to explain the observed relationship between mobility and D₉₆∕D₅₀ in the Swiss streams.

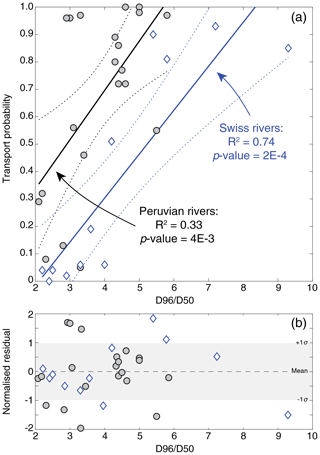
Figure 4 (a) Relationships between the probability of sediment transport occurrence and the D₉₆∕D₅₀ ratio, which we use as proxy for the sorting of the gravel bar, in the Swiss and Peruvian rivers. (b) Normalized residuals that are plotted against the sorting. The normalized residuals do not show any specific and significant patterns. Blue diamonds correspond to the Swiss rivers, while grey circles are Peruvian ones.

Because the sorting itself could potentially depend on channel metrics and water discharge, we explored possible correlations between these variables. We find that the D₉₆∕D₅₀ ratio negatively correlates with channel widths for Peruvian streams (R²=0.20, p-value =0.040) but not with any of the other variables in both mountain ranges (e.g., reach gradient, mean annual discharge and discharge variability; see Fig. S5). In the same sense, the positive relationship between the D₉₆∕D₅₀ ratio and the reach gradient in the Swiss rivers (R²=0.23) is statistically not significant (p-value =0.12). As mentioned above, the D₉₆∕D₅₀ ratio negatively correlates with D₈₄, but the correlation is weak and explains 20 % of the observations only (Fig. 2b).

3.3 Discharge quantiles, uncertainties on reach slopes and channel widths

The use of discharge quantiles yields sediment transport probabilities that are positively and linearly correlated with the transport probability estimated with Q_mean (Fig. S4). In addition, the correlations are very similar between the Swiss (slope: 0.74±0.02; intercept: 0.05±0.01) and Peruvian streams (slope: 0.73±0.19; intercept: 0.03±0.14). The mean annual discharge estimates Q_mean are likely biased by infrequent but large-magnitude floods, which could explain the 25 % larger transport probabilities if Q_mean is used as reference discharge.

The assignments of different uncertainties on reach gradients, channel widths and discharge have no major influence on the inferred relationships between transport probability and sorting (Tables S6 and S7). For the Peruvian streams, however, assignments of 2-fold-larger values to channel widths will decrease the transport probability for a given sorting by ca. 10 %–15 %, consistent with Figs. 3b and S5 that illustrate negative correlations between channel width, D₉₆∕D₅₀ ratio and transport probability. The inferred linear relationship between both variables, however, will remain (Table S7).

4 Discussion

4.1 Controls of channel metrics on the transport probability

Our analysis documents a slope dependency of sediment transport probability for the Swiss and Peruvian streams. Such a relationship has been documented before for mountainous rivers in the USA (Torizzo and Pitlick, 2004; Pfeiffer and Finnegan, 2018) and for other sites including the Alps (Van den Berg and Schlunegger, 2012). Pfeiffer and Finnegan (2018) reported transport probabilities, at conditions of an annual flow, that range between 8% and nearly 100 % for the west coast in the USA, 1 % and 12 % for the Rocky Mountains, and <10 % for the Appalachian Mountains. These estimates are generally lower than the probabilities reported here. This most likely reflects the effect of the low channel gradients of the US streams that are ca. 3 times flatter than the rivers analyzed here (Table 1). These differences thus emphasize the controls of the reach gradient on the entrainment probability of coarse-grained bed material.

The regression analysis also documents that channel widths and critical shear stress have an influence on the transport probability of clasts. This is particularly the case for the braided streams in Peru where wider channels and greater critical shear stresses tend to lower the transport probability (Fig. 3b, d). Since braided streams dynamically adjust their channel widths to changes in the caliber and the rates of the supplied material (Church, 2006), a dependency of transport probability on channel width and grain-size specific threshold (including D₈₄) was expected. The absence of corresponding relationships in the Swiss streams is probably due to the managed geometry of these streams where artificial banks constrain the channel widths over tens of kilometers.

4.2 Controls of material sorting on the transport probability

Interestingly, our regression analysis of the variables disclosed a positive correlation between the D₉₆∕D₅₀ ratio of the bed material and the transport probability. This relationship maintains if transport probabilities are calculated based on discharge quantiles (Table S4) and if larger channel width and discharge variability particularly for Peruvian streams are considered (Table S7). Such a dependency will also remain if critical shear stress is calculated using a different grain size percentile. This is because grain size D_x linearly propagates into the Eq. (2) and thus into the probability of τ>τ_c. Therefore, although the resulting probabilities will adjust according to the threshold grain size, the relationships between the D₉₆∕D₅₀ ratio and the mobilization probability will not change. Furthermore, because of the linear relationship between the D₈₄/D₅₀ and D₉₆∕D₅₀ ratios (Fig. 2), the same dependency of transport probability on the sorting will also emerge if the D₉₆∕D₈₄ ratios are used. This suggests that the sorting of the bed material has a measurable impact on the mobility of gravel bars and thus on the frequency of sediment mobilization irrespective of the selection of a threshold grain size. In addition, there appears to be a feedback where a poorer sorting (large D₉₆∕D₅₀ ratio) tends to be associated with a lower D₈₄ (Fig. 2), which additionally increases the sediment transport probability. We note that while the data are relatively scarce and scattered (i.e., the same transport probability for a ca. 2-fold difference in the D₉₆∕D₅₀ ratio), the relationships observed between the probability of transport occurrence and the degree of material sorting are significant with p-values ≪0.05. Finally, for a given D₉₆∕D₅₀ ratio, the probability of material transport tends to be greater in the Peruvian than in the Swiss rivers (Fig. 4a). We tentatively explain the apparent small divergence in the transport probability between both settings (i.e., regression parameters overlap within their 95 % confidence interval) by the differences in the flow patterns (braided versus single-thread artificial channels).

4.3 Controls on the sorting of the bed material

None of the possible variables such as channel reach gradient, mean water discharge and discharge variability are significantly correlated with the bed material sorting (Fig. S5). Exceptions are the Peruvian streams where wider channels tend to be associated with a better sorting (i.e., lower D₉₆∕D₅₀ ratio). We lack further quantitative information to properly interpret these patterns, but it appears that material sorting represents an additional yet independent variable that influences the probability of transport, at least for the sites we have investigated in this paper. Because the sorting of the bed material in the analyzed streams appears not to strongly depend on the hydrological conditions at the reach scale, it could possibly reflect an inherited supply signal from further upstream (Pfeiffer et al., 2017). Indeed, detailed grain size analyses along fluvial gorges in the Swiss Alps have shown that the hillslope-derived supply of large volumes of sediment perturbs the granulometric composition of the bed material (van den Berg and Schlunegger, 2012; Bekaddour et al., 2013). Using the results of flume and numerical experiments, Jerolmack and Paola (2010) suggested that these source signals are likely to be shredded during sediment transport as a consequence of what they considered as ubiquitous thresholds in sediment transport systems. However, based on a detailed analysis of downstream fining trends in alluvial fan deposits, Whittaker et al. (2011), D'Arcy et al. (2017) and Brooke et al. (2018) proposed that primary source signals of grain size compositions are likely to propagate farther downstream in a self-similar way. Accordingly, the original grain-size sorting of the supplied material could be maintained although a general fining of the sediments along the sedimentary routing system would be observed. This idea could offer an explanation of why the D₉₆∕D₅₀ ratios are to a large extent independent from other variables. It also points to the importance of sediment supply not only for controlling the bankfull hydraulic geometry of channels (Pfeiffer et al., 2017) but also for the sorting of the material. Finally, a supply control could possibly explain why sorting appears to vary with D₈₄, albeit with a poor correlation, where a better sorting tends to be associated with larger D₈₄.

4.4 Relative importance of sorting versus gradient on the transport probability

Because gradient and sorting are independent variables and since the transport probability depends linearly on both variables, the transport probability can be described as a linear but weighted combination of gradient and sorting. We therefore assess whether the transport probability (Tp) in both the Swiss (i=1) and the Peruvian (i=2) rivers can be predicted using a multiple linear regression: $T{p}_i={\mathit{\alpha }}_i{S}_{\mathrm{n}}+{\mathit{\beta }}_i{G}_{\mathrm{n}}+{\mathit{\delta }}_i$, where S_n and G_n are the sorting and gradient normalized to their respective maximum, and α, β, and δ are the regression parameters. We decided to normalize both the sorting and gradient to their maximum values so that both variables vary on a similar [0–1] range, and the inferred linear coefficients α, β and δ can be directly compared between the Swiss and the Peruvian rivers. The model outputs show that when sorting and gradient are combined, then the predictions of the transport probability in both the Swiss (R²=0.85, $p=\mathrm{2.24}\times {\mathrm{10}}^{-\mathrm{4}}$) and the Peruvian (R²=0.61, $p=\mathrm{1.9}\times {\mathrm{10}}^{-\mathrm{4}}$) rivers are significantly improved compared to simple linear regressions. The results also reveal that the relative importance of sorting on the transport probability is greater (α is 1.22±0.26 for the Swiss streams and 1.46±0.41 for the Peruvian streams) than the relative controls of reach gradient (β is 0.62±0.27 for the Swiss streams and 0.67±0.20 for the Peruvian rivers). The comparison of the estimated factors thus suggests that the relative importance of sorting on the transport probability could be twice as large as the controls of gradient, although our estimation is associated with large uncertainties (2.0±1.0 in Switzerland; 2.2±0.9 in Peru). Interestingly, we also note that the apparent greater probability of transport in the Peruvian rivers, as we infer based on all simple linear regressions reported in Figs. 3 and 4, remains with our multiple linear regression analysis (δ is $-\mathrm{0.42}\pm \mathrm{0.12}$ for the Swiss streams and $-\mathrm{0.28}\pm \mathrm{0.19}$ for the Peruvian streams; Fig. 5). Again, this suggests that an additional component (intrinsic geomorphic setting such as, e.g., braided vs. single thread) may contribute to the observed higher probability of sediment transport in the Peruvian rivers than in the Swiss ones. The search for an answer to this questions, however, is beyond the scope of this paper and would require additional research.

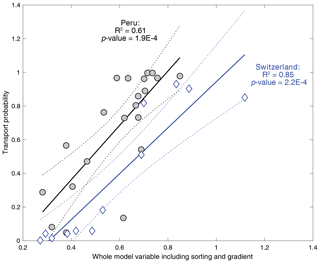
Figure 5 Transport probability for the Swiss and Peruvian rivers plotted as a function of the combined response to gradient and sorting. Blue diamonds correspond to the Swiss rivers, while grey circles are Peruvian ones. Both best multiple linear regression fits (solid line) and their 95 % confidence intervals (dashed curves) are presented. Note that the variables on the axis are adjusted as a result of projecting the multiple linear regression models onto a bivariate plot.

5 Conclusions

We confirm the results of previous research that the transport probability of coarse-grained material in mountainous streams largely depends on the reach gradient. We also find a positive correlation between the D₉₆∕D₅₀ ratio of the bed material and the transport probability where a poorer sorting of the material results in a larger probability of material entrainment. Despite the large scatter in the dataset, this relationship is statistically significant with p-values ≪0.05, which suggests that the sorting of coarse-grained bed sediments has a measurable impact on the mobility of the bedload material. Regression analyses additionally reveal that sorting exerts a greater control on the transport probability than reach gradient. Furthermore, the lack of a significant correlation between reach gradient and sorting implies that both variables are largely independent from each other, at least for the investigated rivers in Switzerland and Peru. We therefore propose that the sorting of the bed material represents an additional, yet important variable that influences the mobility of material on gravel bars. Finally, we identify two main open questions that we cannot resolve with our dataset. First, Fig. 5 illustrates that 15 % of the transport probability observations in Switzerland and 40 % of the data in Peru cannot be fully explained by a combination of sorting and reach gradient, and interpretations thereof most likely require the consideration of the anthropogenic management of the streams (braided and free flow in Peru versus engineered single-thread channels in Switzerland). Second, we have not identified a significant correlation between the sorting and the other variables such as reach gradient, water discharge and discharge variability. This led us to propose that material supply need to be included in the discussion as well. Furthermore, the critical shear stress, through its dependency on D₈₄, is also a function of the sorting (albeit with a weak correlation; Fig. 2b). This could invoke a possible feedback where a poorer sorting tends to be associated with lower D₈₄ and thus with a lower critical shear stress, which further promotes the mobility of grains. We do not have the required data to fully address these latter two questions and suggest that it could serve as a topic in future research.