the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Climate changes and the formation of fluvial terraces in central Amazonia inferred from landscape evolution modeling
Ariel Henrique do Prado
Renato Paes de Almeida
Cristiano Padalino Galeazzi
Victor Sacek
Fritz Schlunegger
Climate changes have been considered an essential factor controlling the shaping of the recent alluvial landscapes in central Amazonia, with implications for explaining the biogeographic patterns in the region. This landscape is characterized by wide floodplains and various terrace levels at different elevations. A set of older terraces with ages between 50 and >200 ka occupy the higher portions of central Amazonia, whereas multiple terraces next to floodplains occur at lower elevations and display ages of a few thousand years. These lower terraces, referred to as middle–lower terraces, reveal what can be perceived as a stochastic pattern both in space and time. Despite the widespread occurrence of these geomorphic features, no process-oriented analysis has been conducted to explain their formation. Here, we develop a landscape evolution model referred to as SPASE (Sedimentary Processes and Alluvial Systems Evolution) to explicitly account for fluvial erosion and deposition in combination with lateral channel migration to explore the controls on terrace development. The model results show that the higher terraces were deposited under the condition of a higher base level for the basins upstream of the confluence between the Solimões and Negro rivers. The subsequent decrease in the base level initiated a phase of gradual incision, thereby resulting in the current fluvial configuration. The model also predicts that high-frequency climate changes resulted in the construction of middle–lower terraces at various elevations which, however, are all situated at lower elevation than the higher terrace levels. Our model shows that dry-to-wet shifts in climate, in relation to the modern situation, yield a landscape architecture where middle–lower terrace levels are better preserved than wet-to-dry changes in climate, again if the current situation is considered as reference. Finally, our results show that fast and widespread landscape changes possibly occurred in response to high-frequency climate changes in central Amazonia, at least since the Late Pleistocene, with great implications for the distribution and connectivity of different biotic environments in the region. Because of this short timescale of response to external perturbations, we suggest that the streams in central Amazonia possibly also respond in rapid and sensitive ways to human perturbations.
- Article
(11683 KB) - Full-text XML
-
Supplement
(8752 KB) - BibTeX
- EndNote
The lowlands of the central Amazonia host one of the largest systems of alluvial deposits on Earth, composed of extensive Quaternary fluvial terraces with wide incised valleys where modern rivers flow (Fig. 1) (Rossetti et al., 2005; Pupim et al., 2019; Sioli, 1984). These deposits are of great relevance for the reconstruction of both the evolution of the physical landscape and the patterns of biotic diversity in the region (Ribas et al., 2012; Ribas and Aleixo, 2019; Pupim et al., 2019; Bicudo et al., 2019). The areas that currently display terraces were part of a large depositional system in which rivers in this region had high deposition and avulsion rates in an aggradational pattern (Hoorn et al., 2010; Pupim et al., 2019; Wilkinson et al., 2010). During this stage, flooded environments covered much larger areas, because they were not restricted to incised valleys as is currently the case. During the Late Pleistocene, most likely because of an adjustment of the river's long profile to a lowering of the base level or a change in discharge, the main rivers started to incise to reach their modern position. This phase of incision was associated with a widening of the valleys, which was accomplished through channel migration and lateral bank erosion (Merritts et al., 1994). This long-term period of fluvial erosion was accompanied, at a shorter timescale, by multiple cycles of incision and aggradation, which resulted in the formation of both cut terraces and cut-and-fill sequences with various depositional ages and elevations (Pupim et al., 2019). Sea-level changes have been proposed as the controlling mechanisms for the formation of these cycles (Irion and Kalliola, 2010); however, the depositional ages show that the cycles of aggradation and incision occurred at a different frequency or phase than the cycles of sea-level changes during the Pleistocene (Pupim et al., 2019). In fact, there is ample evidence for the occurrence of Cretaceous bedrock exposed at the bottom of the Amazon River next to the confluence with the Negro River (Ianniruberto et al., 2018; Gualtieri et al., 2020), implying no net aggradation since the last glacial maximum. Therefore, the Holocene sea-level rise cannot be used to explain the occurrence of incised floodplains upstream of the confluence with the Negro River. Climate-driven discharge variations is another mechanism that has been used to explain the multiple phases of aggradation and erosion because such controls have the potential to impose changes on the course of the main and tributary rivers through changes in the sediment supply and the rivers' capacity to evacuate the supplied material (e.g., Tucker and Slingerland, 1997). There is indeed ample evidence that rainfall rates have varied in central Amazonia during the last 200 kyr (Cheng et al., 2013; Mertes and Dunne, 2007; Fritz et al., 2004). In addition, the pattern of terrace ages suggests that the related cyclicity of sediment accumulation and erosion has been quite similar to that of rainfall variations (Pupim et al., 2019). As yet, no quantitative model has been employed to test the hypothesis of a climate-driven control on the formation of the various terraces in central Amazonia.

Figure 1Topography of central Amazonia with key geographical designations such as cities, rivers and geological and geomorphic features including terrace levels (lowlands), floodplains (wetlands) and drainage network. The red square illustrates the location of the city of Manaus. Dotted red rectangle represents the region that is reproduced in the model and that represents the model grid. This illustration is based on a digital elevation model from the Shuttle Radar Topography Mission (SRTM).
Here, we develop a landscape evolution model (LEM), which is tailored to reproduce alluvial processes at a 104-year temporal scale and for a spatial extent of several 106 km2, which is comparable in size as the Sacek (2014) model. This new model also introduces a simplified approach to reproduce lateral erosion and the formation of cut terraces. We start with a model that is calibrated with current field-based data from central Amazonia including the relationships between water and sediment discharge, and the modern topography along the Solimões River in an area between the confluence with the Iça and Negro rivers (Fig. 1). Using this calibrated model, we consider the landscape response to different conditions of water discharge, sediment flux and base-level changes. We focus on these parameters because of their high-frequency variability, which is compatible with the dynamics of the terrace formation in central Amazonia (Cheng et al., 2013; Mertes and Dunne, 2007; Fritz et al., 2004; Pupim et al., 2019). We then compare the model results with the modern topography. The ultimate scope is to quantitatively explore possible controls on the formation of terrace levels in central Amazonia, which has occurred at a frequency of approximately 104 years.
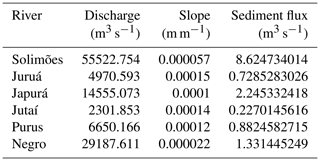
The study area (Fig. 1) is situated in central Amazonia to the west of the city of Manaus, which is near the confluence between the Negro and the Solimões rivers. The study region, which is approximately 300 000 km2 large, additionally hosts four major tributary streams of the Solimões River, which are from the west to the east: the Jutaí River, the Juruá River, the Japurá River and the Purus River. While the Solimões and the Japurá rivers are sourced from the Andean orogen, the Negro River is sourced from the Guiana Shield, and the other streams have their headwaters in the Fitzcarrald Arch (Filizola and Guyot, 2009; Regard et al., 2009). At Manaus downstream of the confluence with the Negro River, the mean water discharge of the Amazon River is approximately 130 000 m3 s−1 and the mean annual flux of suspended sediment amounts to approximately 500×106 t yr−1 (Ianniruberto et al., 2018; Filizola and Guyot, 2011). In the tributary rivers, mean water discharge values vary from approximately 2000 m3 s−1 for the Jutaí River to approximately 30 000 m3 s−1 for the Negro River. Except for the Jutaí and Japurá rivers, gauging records of suspended sediment loads also exist for the other major streams in the study area. The values range from 25×106 t yr−1 for the Juruá River to approximately 100×106 t yr−1 for the Purus River (Filizola and Guyot, 2009).
The morphology of the study region is characterized by the occurrence of multiple terrace levels and floodplains. Conventionally, these are referred to as wetlands for the floodplains and lowlands for the higher-elevated terraces (see Fig. 1 and Räsänen et al., 1990). Estimates of the elevation differences between the highest terrace level (e.g., green colored lowland surfaces in Fig. 1) and the floodplain (blue colored wetlands) range from approximately 10 to >30 m over a distance of hundreds of meters. This estimate is based on a Shuttle Radar Topography Mission (SRTM) digital elevation model, which, however, has not been corrected for the tree coverage. Note that this could possibly add a bias in the modeling, which we address in the discussion section. In addition, several low-altitude terrace levels, referred to as middle–lower terraces, have been mapped in the study area inside the wetlands in Fig. 1 (Pupim et al., 2019). Estimates of the heights of the middle–lower terraces are associated with large uncertainties, but because they are at a lower elevation than the higher terraces their heights are less than 10 m relative to the floodplain at flood stage. The floodplain widths vary between approximately 15 km (Jutaí River) and 60 km (Solimões River). In addition, multiple local streams originate in the terrace levels and display a dendritic drainage pattern (Fig. 1).
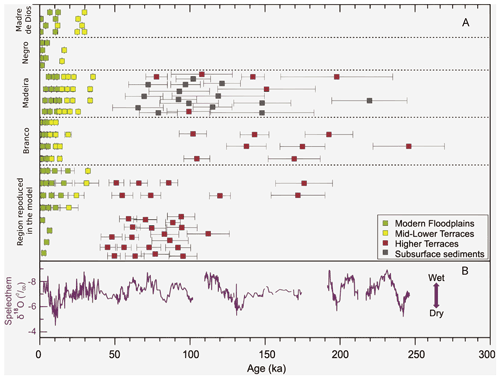
Figure 2Chronology of sediment deposition representing the formation of terraces in Amazonian lowlands compared with Quaternary climate records from Pupim et al. (2019). (a) OSL and 14C ages from late Quaternary deposits and (b) speleothem 18O records.
Ages for some of these terrace levels have been established with optically luminescence dating techniques and measurements of 14C concentrations in organic matter. As shown by Pupim et al. (2019), these analyses yielded ages between 50 and >200 ka for the highest terrace levels and ages of <50 ka for the lower terrace levels adjacent to the floodplains. These results are summarized in Fig. 2 with optically stimulated luminescence (OSL) ages of the studied sedimentary profiles across fluvial terraces in central Amazonia and published 14C and OSL ages from late Quaternary deposits from other Amazonian sites in Fig. 2a. The ages are presented in groups (rows) related to river systems to highlight the regional variability of the sedimentary processes. Sample location, sedimentary and dating details, and references can be found in Pupim et al. (2019). The main domains are modern floodplains (green squares); middle–lower terraces (yellow squares); higher terraces (red squares). Subsurface sediments (gray squares) are remnants of older deposits at the base of a younger terrace. In Fig. 2b, there are speleothem 18O records from Cueva del Diamante cave (purple line) indicating precipitation changes in western Amazonia (Cheng et al., 2013). The reported ages, the elevations and the spatial occurrences of the middle–lower terraces do not show a distinct pattern nor a clustering or a trend in any direction (Pupim et al., 2019). Although these ages reveal a large scatter and the sampling is still very sparse, we suggest that they record two distinct phases of landscape evolution. The first one is recorded by the highest terrace levels, which formed when the streams in the study area accumulated material over a larger area as revealed by the data of Pupim et al. (2019) in Fig. 2. This accumulation of fluvial deposits is superseded by a phase of erosional recycling. This second period started sometime during the Late Pleistocene and was associated with a shift towards a period with short-term (104-year) variations of climate (Cheng et al., 2013; Fritz et al., 2004; Mertes and Dunne, 2007). It has been proposed that this shift in paleoclimate eventually resulted in the formation of cut-and-fill terrace sequences and cut terraces in central Amazonia (see Fig. 4 in Pupim et al., 2019).
Following the scope of this paper, we developed a landscape evolution model which allows us to simulate fluvial processes of erosion, transport and deposition of sediments in alluvial landscapes (e.g., Tucker and Slingerland, 1997; Braun, 2006; Sacek, 2014). This model, which is referred to as SPASE (Sedimentary Processes and Alluvial Systems Evolution) is implemented in Python. The source code is openly accessible and can be downloaded from the GitHub repository (https://github.com/Ariel-H-Prado/SPASE_Model.git, last access: 26 May 2022). In the context of the Late Pleistocene to Holocene terrace systems in central Amazonia, the search for the controls on the depositional and erosional cycles requires a conceptual model that considers short-term (104-year) variations of base level and climate changes (Cheng et al., 2013; Fritz et al., 2004; Mertes and Dunne, 2007), leading to the formation of cut-and-fill terrace sequences and cut terraces in central Amazonia. This model also needs to be able to simulate the erosion of the valley margins in response to the lateral migration of channels. In fact, such a process has been considered as essential to understand the formation and the widening of the in-valley floodplains in central Amazonia (Merritts et al., 1994).
3.1 Model setup and governing equations
To simulate fluvial erosion and mass transport, previously developed LEMs, such as CAESAR, SIBERIA and others (Beaumont et al., 1992; Braun, 2006; Hancock et al., 2010; Sacek, 2011, 2014), considered both fluvial processes, such as the long-distance advection of material by rivers and slope processes including local mass transport by hillslope diffusion for slopes flatter than a threshold and advection for steep slopes (Tucker and Slingerland, 1997; Braun, 2006; Sacek, 2014). Since the Amazon alluvial system has very gentle slopes and because the area bordering the floodplains and terraces is occupied by a dense vegetation cover, we do not consider that hillslope processes largely contribute to the redistribution of sediment in the channel network inside the model grid. In fact, all material in the model domain is considered to result from either accumulation and/or erosion by fluvial and channelized processes only. However, the sediment supply from outside of the model grid could indeed be produced by hillslope processes in a steeper landscape, e.g., the Andes, which is considered as a boundary condition (see Sect. 3.3).
Upon modeling fluvial dynamics, we proceed following Beaumont et al. (1992) and employ a stream power law where, for a given channel, the carrying capacity of sediment, Qeqb, which is equivalent to the maximum volume of sediment per unit time [L3 T−1] a stream can carry, is given by the equation
Here, Qr is the water discharge in the channel [L3 T−1] and S is the slope [L L−1]. Note that in order to maintain the consistency of the equation, we set the dimension of the constant Kf to [T L. This constant Kf is the dimensional transport coefficient that adjusts the carrying capacity (Qeqb). The constants m and n determine whether the discharge and slope have a linear () or a power (m≠1 and n≠1) relationship with Qeqb. Here, we follow the experimental results and field observations of Whipple and Tucker (2002) and set m≥1 and fixed n=1. We then estimate the values for the parameters Kf and m (Table 1) through an ordinary least-squares fitting on Eq. (1). This is accomplished using modern water and suspended sediment discharge data for multiple Amazonian rivers obtained from Filizola and Guyot (2009) and using slope values that we obtained from the SRTM digital elevation model. In this context, we infer that the sediment discharge in the current Amazonia rivers is at capacity. A table with the used modern values is presented in the Supplement (Table S3).
Similar to Braun (2006), the entrainment, deposition and transport of sediment in a channel (in suspension or as bedload) is computed by Eq. (2), where the erosion/deposition rate is considered proportional to the difference between the carrying capacity (Qeqb) and sediment discharge, Qsed [L3 T−1]:
Here, W denotes the channel width [L] and Lf is the erosion/deposition length scale [L], which is a material property. From Eq. (2), it follows that if Qsed<Qeqb, sediment entrainment will occur. In this case, Lf takes the length-scale property of the river bed load, La. Alternatively, the model will simulate the occurrence of deposition if Qsed>Qeqb. In this case, Lf takes the length-scale property of the suspended load in the river, Ls, where Ls<La.
To simulate lateral erosion we infer that there is no bedrock confinement for the channels and that the eroded material is homogeneous in composition and strength. Therefore, the volume of sediment B [L3] that a channel can laterally erode at a particular site is computed through
where hterrace is the height of the terrace adjacent to the channel [L], hchannel is the height of the channel surface [L], and hdepth is the depth of the channel [L]. Ale is the rate at which an area is laterally eroded per unit time [L2 T−1]. This rate is defined as
Here, α1 and α2 are the lateral erosion coefficients, which depend on the erosional resistance of the lateral margins of the channels. These coefficients are defined through an iterative process where different values are assigned to the α1 and α2 parameters and where the impact on the model floodplains are then analyzed. We finally accepted those values for the α1 and α2 parameters where the simulated floodplain widths of the Solimões and Juruá rivers correspond to the current situation and where the lateral migration of the model streams will not result in an obvious increase of the floodplains' widths. As another constraint, we inferred that this development towards the modern nearly stable condition had to occur within less than 20 kyr, mainly because this corresponds to the timescales recorded by the terrace levels. An example of the model behavior with a different value for α1 is shown in the Supplement (Figs. S9 and S10).
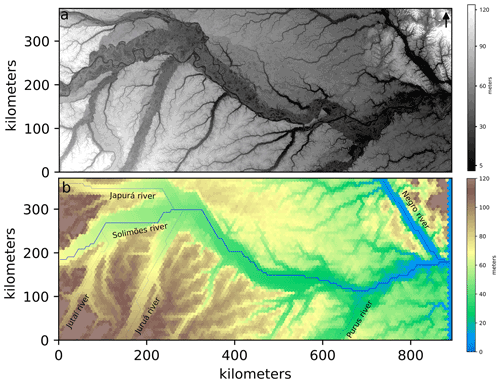
Figure 3(a) Shuttle Radar Topography Mission (SRTM) digital elevation model of central Amazonia, with a resolution of 90 m at the Equator. (b) Initial topography and configuration of the numerical simulations. The blue lines represent the channels and the thickness of the line is proportional to the discharge of the corresponding stream.
Because one model cell can potentially contain both a part of a channel belt floodplain and a portion of a bordering terrace, it is necessary to record two elevation values upon modeling lateral erosion (Eqs. 3 and 4). One elevation variable, referred to as hchannel in Eq. (3), represents the elevation of the active channel and the floodplain, and the other elevation parameter hterrace in Eq. (3) considers the elevation of a possibly older and higher terrace within the same cell. All maps in this paper illustrate the elevation of terraces (hterrace) inside each cell. Additionally, the coefficient hdepth in Eq. (3) plays an important role upon modeling the lateral migration of the channels since it simulates the recycling of sediments that is associated with this process. In this context, accumulation of sediment (where Qsed>Qeqb) might raise the channel floor within a particular model cell. This can initiate a lateral shift of the active channel to a neighboring cell if its elevation is lower than the cell hosting the active channel. For a detailed description of the numerical solutions for the equations, their implementation in the model and the way of how the drainage network and the lakes are calculated, the reader is referred to the Supplement (Sect. S1).
3.2 Setup of the initial scenario
We use the modern topography as the initial condition. This surface was reconstructed over a regular mesh with 129×62 points, where each point corresponds to a center of a regular hexagonal cell. This input topography was obtained from the Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) for the area of interest (Fig. 3a). The DEM was smoothed and adjusted for the grid of the model through the QGIS openly accessible software. As mentioned before and addressed in the discussion, a limitation in the use of the SRTM is that the tree canopy heights are included in the elevation model.
The initial landscape displays six main rivers entering the grid. These are the Solimões, Japurá, Juruá, Jutaí, Purus and Negro rivers (Figs. 1 and 3b). For these streams, water flux values were obtained by the HydroRivers model for the locations where they enter the study area (Lehner and Grill, 2013). Also for these locations, the sediment discharge of these streams was then estimated by applying Eq. (1), thereby using the calibrated parameters of Kf and m and the slopes S that we measured along the corresponding reach (Table 2). Modern average rainfall rate in the region is 3000 mm yr−1 (Espinoza et al., 2009), and the runoff coefficient (effective proportion of rainfall) is set to 50 % (Guimberteau et al., 2013). For simplification, all erosional and transport processes occur over the same material, here considered as sand. The bedrock at Manaus is considered as a rigid material that cannot be eroded. Therefore, the elevation at Manaus is defined as the minimum base level in the model, locked at 0 m in the model (Fig. 3).
Table 2Current discharge, slope and sediment flux of the rivers outside of the grid. The sediment flux was calculated using the Eq. (1) and the parameters in Table 1.
In order to make the initial topography more stable upon modeling, the numerical model was run using the smoothed DEM as initial topography with the model parameters of Tables 1 and 2 during 10 kyr inside the model. The output topography for this scenario (Fig. 3b) was then used as initial topography for all the climatic and base-level tests in this work.
3.3 Boundary conditions for the modeled scenarios
For the model scenarios where different climate conditions are taken into account, it is necessary to consider the variation of the rainfall rate outside of the model grid, which induces a change of the water discharge of the six main rivers entering the model grid and consequently impacts the sediment flux. We used the following relationship in order to estimate the sediment flux, Qsed. For the rivers entering the grid, sediment discharge Qsed for a given water discharge Qr is computed through
The value for γ is obtained through a regression of Eq. (5) using data from Filizola and Guyot (2009) about water discharge and sediment flux of the main rivers in the Amazonian lowlands as constraints. This regression yields a value of approximately 0.5 for the exponent γ on Eq. (5) (see also Fig. S7). The parameter α varies for each river and is defined as
in which and are the current sediment and water flux of the rivers listed in Table 2 (Fig. S8 shows this relation for the six main rivers). We note that this relationship between sediment and water flux, scaled through γ based on modern observations, is considered as a constant value during all model runs. Accordingly, we infer that sediment discharge in the major Amazonian rivers occurs at near capacity conditions, which we consider as a valid assumption.
Additionally, all cells on the right edge of the grid are considered as sink cells. They also control the elevation of the base level of the grid. For the generation of the initial topography, the sink cells are kept at a fixed position. This corresponds to the elevation of the bedrock at Manaus, which we set to 0 m (see above).
The controls of climatic variations on the formation of terraces are explored in the framework of two scenarios, the results of which are detailed in the following sections. In scenario 1 (Fig. 4), a dryer period is simulated by a 30 % decrease of the current water input during the first 10 kyr, which is then followed, until 20 ka, by an instantaneous increase in the water supply up to the same level as the current water input. Scenario 2 is similar but considers first a 30 % increase of the water input during the first 10 kyr (Fig. 5), thereby simulating a wetter period, which is superseded by a 10 kyr long model run during which the water supply is instantaneously reduced to the current level. The 30 % increase or decrease in rainfall on central Amazonia during the Holocene is based on estimates proposed by van Breukelen et al. (2008) and Cheng et al. (2013). In both scenarios, after shifting to a drier or wetter period, the model returns to the modern climate setting to evaluate what would be preserved in the landscape from such climatic shifts. In these models, a change in precipitation rates will affect the water input into the model, which is the sum of the water flux where the stream enters the grid and the runoff that is generated through rain on the grid itself. Both scenarios start with the same initial topography (Fig. 3b), and the grid base level is locked at a bedrock elevation of 0 m, thereby considering the occurrence of a bedrock in the Amazon trunk stream at the downstream end of our model. The consequence of such a fixed base level is that sediment does not get eroded or deposited after the confluence of the Solimões and Negro rivers although that the high water supply of the Negro River lowers the sediment to water discharge ratio, which, in turn, would actually promote a phase of erosion. Following these model runs, we also explore a third scenario where we allow the base level first to increase and then to decrease to the modern situation.
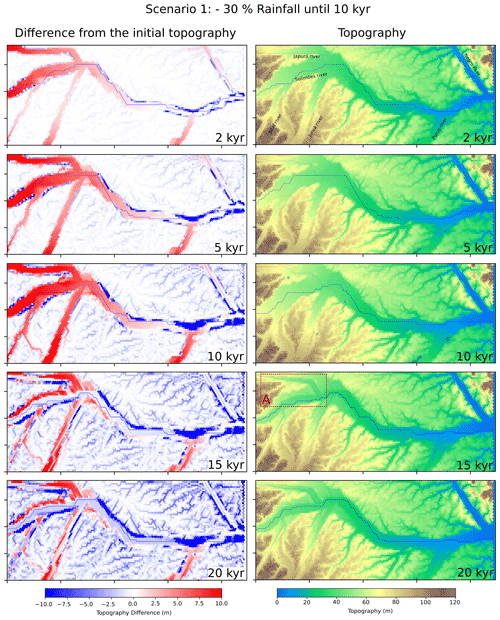
Figure 4Results of the landscape evolution of scenario 1. The left figures show the difference of the model topography in relation to the initial topography, with colors saturated in red for values in elevation differences higher than 10 m and in blue for values below −10 m. The right column shows the model topography itself. The occasional blue stains on the map represent lakes (local minima). Location A indicates new terrace levels being formed around the Japurá River.
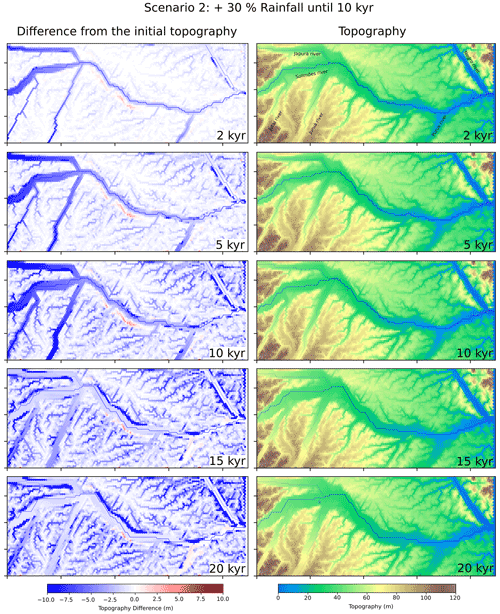
Figure 5Results of the landscape evolution of scenario 2. The left figures show the difference of the model topography in relation to the initial topography, with colors saturated in red for values in elevation differences higher than 10 m and in blue for values below −10 m. The right column shows the topography itself. The occasional blue stains on the map represent lakes (local minima).
4.1 Scenario 1: shift to drier and then wetter conditions
The model results of scenario 1, which commences with a dry period, show that sediment starts to accumulate in the upstream part, and the wave of accumulation progresses from upstream to downstream. As a consequence, the average slope of the Solimões River and its main tributaries increases in pace with the accumulation of sediment. This change towards steeper channel gradients occurs during the first 5 kyr, after which a nearly steady-state situation is established with constant topographic gradients. At this stage, a total of approximately 13 m of sediment has accumulated along the Solimões River upstream of the Juruá River confluence (Fig. 4, at 2, 5 and 10 ka). Also during the first 10 kyr with drier conditions, the course of the Solimões trunk river is deflected to the north at the confluence with the Purus River. The Purus River flows from the south and experiences, similar to the other main tributaries in the model, a phase of sediment accumulation in the upstream part. In the confluence area, this northward-directed shift of the Solimões River initiates a wave of erosion along the northern banks of this stream (Fig. 4). The model simulates the occurrence of lateral bank erosion also along those river segments where sediment accumulation occurs (Fig. 4). This is mainly caused by the meandering of the channel's course to the lateral floodplain boundaries, which then initiates a phase of lateral erosion as long as higher terrace levels form cut banks. These results document that the SPASE model reproduces one of the first order features of a meandering stream such as cut banks despite the simple model architecture.
During the subsequent 10 kyr long period of scenario 1, the modeled increase in water input causes a wave of erosional recycling of the previously deposited sediments. An example can be seen in Fig. 4 where new terrace levels are formed, e.g., around the Japurá River (see location A in figure). This phase of downcutting is associated with a phase of valley widening mainly along the main rivers, thus forming cut terraces (Fig. 4, at 15 and 20 ka). At the end of the model run, just a fraction of the previously deposited sedimentary material is preserved (red cells on Fig. 4 at 20 ka). The model results predict that such terrace fragments mainly occur in the upstream part of the Solimões River and next to the Japurá, Juruá, Jutaí and Purus rivers.
4.2 Scenario 2: shift to wetter and then drier conditions
In the second model run, which corresponds to a scenario where water supply is increased during the first 10 kyr and then decreased to modern conditions, the landscape response is different. In particular, the increase in water runoff initiates a wave of erosion from upstream to downstream, which is also associated with a widening of the floodplain through lateral bank erosion. Erosion and valley lowering results in a decrease of the energy gradient and in the formation of new floodplains at a lower elevation (Fig. 5, at 2, 5 and 10 ka) of approximately 10 m. During the last 10 kyr when the model water input is the same as the modern one, the model rivers adapt an aggradational pattern, but the rivers' thalwegs do not reach the same initial elevations. At the end, no new terrace levels are formed (Fig. 5, at 15 and 20 ka). Finally, during the evolution of this model scenario, the main rivers do not show any preferential direction of lateral bank erosion. Similar to the previous model run, the topography response to each climate change occurs mainly in the first 5 kyr, after which nearly steady-state conditions are reached. Note that in comparison to scenario 1 (Fig. 4), the changes in the landscape are much fewer (Fig. 5).
4.3 Scenario three: topography response due to base-level variations
To simulate the consequences of a hypothetical base-level variation on the topography of central Amazonia, we consider a scenario where the base level gradually increases until 35 m during the first 10 kyr, which is followed by a rapid base-level drop to the elevation of the bedrock at 0 m (Fig. 6). The water input is equal to the current water input during the entire scenario.
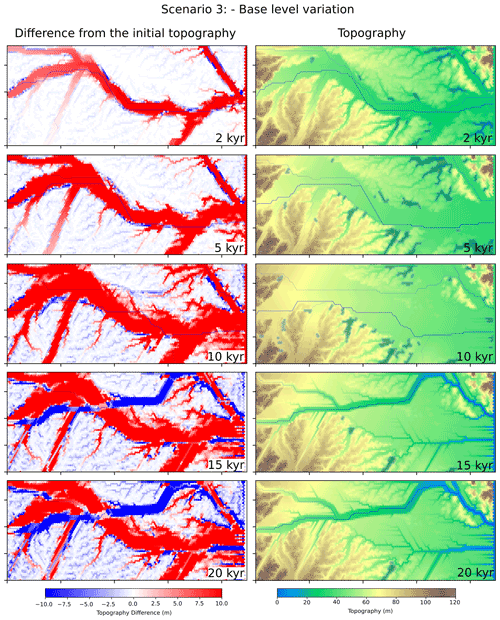
Figure 6Model results showing the landscape evolution of scenario 3. The model water input is constant and equal to the current water input. The left panels show the difference of the model topography in relation to the initial topography, with colors saturated in red for values in elevation differences higher than 10 m and in blue for values below −10 m. The right column shows the topography itself. The occasional blue stains on the map represent lakes (local minima).
During the first 10 kyr, the main rivers turn to an aggradational pattern and thus adjust their long-stream profile to the increasing base level, even accumulating new sedimentary material above older terraces near the interfluve area of the Solimões and Negro rivers (red cells on Fig. 6 at 2, 5 and 10 ka). The smaller tributaries, with a lower sediment discharge, are not able to accumulate sediment in response to the base-level rise at the same pace as the main rivers, thus forming shallow lakes within their own valleys (inundated cells on Fig. 6 at 2, 5 and 10 ka). During the second period of the model run the main rivers initiate a phase of erosion, which occurs in response to the drop in the base level. This downwearing is associated with a period of valley widening. In addition, the model predicts that streams can adapt to a new course. This is exemplified by a northward shift of the Solimões River that takes the course of the Negro River towards the end of the model grid (Fig. 6 at 15 and 20 ka). Such shifts in the course of the major streams is due to the random position of the avulsive rivers during the aggradational stage and the preservation of their last configuration during the incision stage.
The numerical model (SPASE) presented in this work simulates the evolution of alluvial landscapes. It is capable of reproducing the formation of floodplains and terraces at conditions similar to central Amazonia. The tested scenarios allow us to quantitatively explore the responses of the central Amazonia topography to climatic and base-level changes.
5.1 Model behavior
On the floodplains, the occurrence of erosion or sediment accumulation in the modeled scenarios are inherently related to the difference between the sediment transport capacity, which depends on water discharge and slope (Eq. 1 in Sect. 3), and the sediment discharge (Eq. 2 in Sect. 3). Accordingly, as we start our calculations with the conditions where sediment discharge in the model streams is at capacity, then any changes in either water or sediment discharge will initiate a phase of channel steepening or flattening in order to re-establish the at-capacity conditions. Accordingly, by applying Eq. (5), we infer that the rivers in our model are at capacity upstream the model grid during the model runs. Since most of these rivers have their sediment sources either in the high Andes or in the elevated plateaus with a generally thick regolith cover (an exception is the Negro River), we anticipate that sufficient sediment is available to be eroded by overland flow erosion so that sediment flux of the major streams is at capacity. Accordingly, if we maintain sediment discharge at a constant value and only change water supply, then an increase or a decrease in water discharge will respond in a flatter or steeper channel gradient, respectively, in order to reach a condition where sediment discharge equals the sediment transport capacity. In addition, because data on modern sediment and water discharge in the Amazonian streams (Filizola and Guyot, 2009) suggest that sediment discharge relates to water discharge with an exponential factor of γ∼0.5 (Eq. 5 in Sect. 3), Fig. S7), then changes in the sediment transport capacity are less than shifts in water discharge. Therefore, provided that sediment discharge in the current Amazonian rivers is at capacity, as has been inferred upon setting up the initial conditions (Fig. 3), then a 30 % drop in water supply will decrease the sediment transport capacity by approximately 16 %. In this case and according to Eq. (1), the channel and thus the entire floodplain will steepen, depending on the combined effect of the deposition rate of sediment (Eq. 2) and the width of the floodplain. Sediment accumulation will then proceed from upstream to downstream because the modeled change in the water budget is considered as downstream directed forcing. In the same sense, a 30 % increase in water discharge will increase the sediment supply by the same amount, i.e., 16 %. Because an increase in water runoff shifts the model streams to a condition where sediment flux is at under capacity, the model rivers will start to entrain sediment, thereby flattening the valley floor, as revealed by the model results (Fig. 5). Because in either scenario, erosion will continue on the higher elevated terraces adjacent to the trunk streams, the sediment contribution in the tributary streams will first be high and then decrease with time. As a consequence, the elevation of the main valley floor will not be the same as the initial situation after several model cycles (Fig. 5). The model response to changes in water discharge and precipitation thus ultimately reflects the effect of the sediment rating curve, which yields a non-linear relationship (γ=0.5) between water and sediment discharge.
The model shows that terrace levels form not only where the sediment transport capacity outpaces the sediment discharge but also where the meanders' cut banks approach the lateral margin of a floodplain. A terrace level might thus even form during a period when sediment accumulation occurs, particularly where the model streams start to erode the lateral banks of a floodplain (Fig. 4). The combination of cut bank erosion and sediment accumulation and/or erosion on the floodplains result in a pattern where the terrace levels appear as randomly distributed within the Amazonian landscape and at various elevations. As outlined in the following section, the model results thus offer an explanation for why published ages and elevation of terrace levels record a pattern which is rather difficult to correlate with specific changes in external forcings.
We also conduct model runs where we change the initial precipitation conditions (see Figs. S11 to S19). The model predicts that the erosion of the elevated plateaus adjacent to the trunk rivers becomes larger as we increase the precipitation rates (1000 to 3000 mm as initial condition). However, the patterns at which the low-elevated terraces form will not change. Therefore, a change of the initial precipitation rates will not alter the main conclusions.
5.2 Spatial distribution of middle–lower terrace levels
The model outputs predict what appears to be a random distribution of middle–lower terrace levels, particularly if the dry-to-wet climate change scenario is considered. This pattern is caused by lateral shifts of the main rivers during both the aggradation and incision phases. These lateral shifts occur where the sediment flux exceeds the sediment transport capacity, which forces the streams to accumulate a fraction of the transported sediment. The models show that such conditions occur randomly along most of the main streams. Exceptions are observed at the confluence of streams where the tributary stream is in an aggradational state. Such aggradation locally increases the elevation in the tributary floodplain relative to that of the trunk stream, with the consequence that it reduces the possibility and thus the probability of the trunk stream to laterally shift towards the tributary river. In this sense, the trunk river is pushed towards the opposite floodplain margin where erosion can form a cut terrace.
The model results also show that climatic variations that occur at the scale of thousands of years in central Amazonia (Cheng et al., 2013; Fritz et al., 2004; Mertes and Dunne, 2007) can have a large influence on the cycles of sediment aggradation and incision. The main differences in the topographic responses between the two climatic conditions are mainly observed within the floodplains, because the channels steepen during dryer periods in response to sediment accumulation, and they flatten during wetter periods as sediment is entrained in the floodplains. Both scenarios result in the formation of terrace levels at different locations and elevations. Whereas the drier-to-wetter climate change scenario results in the formation of new middle–lower terrace levels that have quite a large preservation potential and that could eventually be mapped over a larger area, the wetter-to-drier climate change scenario returns model results where new terrace levels are poorly preserved. Following these model results, we thus propose that the middle–lower terrace systems in central Amazonia mainly reflect the response to climate cycles from drier to wetter in comparison to modern conditions. These results could offer a solution of why published terrace ages neither show at distinct clustering of ages nor a particular spatial pattern. We explain this by the short response times in combination with the high frequency of climate change and the rather stochastic pattern at which channels migrate laterally.
It is important to note that the initial topography that we used for our model was based on the SRTM digital elevation model (DEM) where the elevation of trees was maintained upon calculating the DEM. This introduces a bias in the sense that the difference in elevations between the terraces and the floodplains are larger in the DEM than they actually should be. This implies that the spatial extents where sediment accumulations during the drier periods could be even larger than our model suggests. This implies that our modeling results can be considered as conservative scenarios of landscape change.
5.3 Response of low-gradient landscapes to climate changes and contrasts to mountainous areas
The model results show that climatic variations that occur at the scale of thousands of years in central Amazonia (Cheng et al., 2013; Fritz et al., 2004; Mertes and Dunne, 2007) can have a large influence on the cycles of sediment aggradation and incision, and that the middle–lower terrace systems in central Amazonia mainly reflect the response to climate cycles from drier to wetter in comparison to modern conditions. This is different from the cyclicity recorded by terrace systems, e.g., in the Andean mountain belt valleys where terrace levels have been related to wetter-to-drier climate cycles, also relative to the modern climate (e.g., Steffen et al., 2009; Veit et al., 2016). The main difference between these environments is that in mountain belts, hillslopes have been considered as an additional landscape component where sediment can be stored during dry periods, whereas the material gets mobilized and supplied to the drainage network during wet climates, resulting in a temporary accumulation of material in the valley floor. During dry conditions, the hillslopes are considered as stable, which allows the trunk streams to recycle the previously deposited sediment in the valley floor, thereby forming a terrace level. Such a mechanism at work in mountainous areas has also been reproduced with numerical models (e.g., Tucker and Slingerland, 1997; Norton et al., 2016). This is, however, different from our case where the buffering effect of hillslopes is missing, since the central Amazonian landscape is mostly flat and far from the Andean mountain belt. Therefore, we mainly see the channel's responses to climate change, which thus have an aggradation–incision cyclicity and which thus contrasts to that in mountain valleys.
5.4 Controls of base-level changes on the formation of the highest terrace levels
The scenario where we model the landscape response to an increase and then a decrease in the local base level (Fig. 6) provides an explanation why the topography of central Amazonia has preserved terrace levels at a high elevation (Fig. 5 at 10 ka). Such a scenario has the potential to form wide floodplains at higher elevations. As the base level drops, the rivers start to recycle previously deposited material. In addition, the rivers can take new courses. The model results thus predict that major changes in the channel network can preferentially be initiated following a phase of major sediment accumulation, possibly controlled by a higher base level at the downstream end of the model. Published ages of the higher terraces suggest that these geomorphic features are also made up of multiple terrace sequences with a stochastic pattern of ages and elevations, which is a feature that is similar to the middle–lower terrace levels but at a higher elevation (Fig. 2). Accordingly, using the model results of scenarios 1 and 2, we suggest that the formation of the higher terrace levels, possibly conditioned by a higher local base level, was superimposed by high-frequency climate changes. Accordingly, it is very likely that at such a stage of a higher base level, climate cycles would also cause the formation of cut-and-fill terrace sequences with a similar stochastic distribution of ages as those of the middle–lower terraces. This suggests that we can expect a superposition of low-level, high-frequency terraces on terrace deposits occurring at high levels, yielding a complex pattern in the landscape architecture.
According to the scenarios described herein, the current configuration of the terraces and floodplains in central Amazonia could be explained by aggradational and incisional processes controlled by high-frequency climatic variations and local base-level changes, which however occurred at a lower frequency. In particular, the higher terraces were deposited in a condition of a higher base level for the basins upstream of the confluence between the Solimões and Negro rivers. The subsequent decrease in the base level initiated a phase of gradual incision, thereby resulting in the current fluvial architecture. The high-frequency climate changes then yielded in the construction of middle–low terraces at various elevations, which however, are all situated at a lower elevation than the higher terrace levels. Our model shows that dry-to-wet shifts in climate, in relation to the modern situation, returns a landscape architecture where middle–lower terrace levels are better preserved than wet-to-dry changes in climate, again if the current situation is considered as reference.
Our results also show that fast and widespread landscape changes possibly occurred in response to high-frequency climate changes in central Amazonia, at least since the Late Pleistocene, with great implications for the distribution and the connectivity of different biotic environments in the region. Because of this short timescale of response to external perturbations, we suggest that the central Amazonian streams in the study area, and also at a broader scale, possibly respond in a rapid and sensitive way to human perturbations. This could be, for instance, the ongoing deforestation with implications for sediment flux and hydrology, and particularly the planned construction of multiple hydropower dams (Latrubesse et al., 2017; Best, 2019) with major implications on water discharge and local base levels as we have modeled in our contribution.
The open-source landscape evolution model SPASE is freely available at https://doi.org/10.5281/zenodo.6583431 (do Prado, 2022).
SRTM data were provided by http://srtm.csi.cgiar.org (NASA, 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-10-457-2022-supplement.
RPdA designed the study together with AHdP. AHdP developed the model with support by VS and RPdA. CPG prepared the geological framework and synthesized data on water discharge, channel widths and sediment flux. AHdP analyzed the model results together with RPdA, CPG, VS and FS. AHdP wrote the manuscript with support from FS and RPdA. All authors approved the current version.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author wishes to thank Beatriz Cardoso Silveira for comments made on earlier versions of this paper.
This research has been supported by the São Paulo Research Foundation (FAPESP, grant nos. 2016/03091-5, 2018/23899-2, 2017/06874-3 and 2018/02197-0), the National Research Foundation of Korea (NRF, grant no. 2019R1A6A1A10073437), the University of Bern, Innovative Training Network S2S (grant no. 860383), CNPq (grant nos. 305218/2009-3 and 426654/2018-8), the Royal Society – Newton Advanced Fellowship (NAF/R2/192188) and CAPES-PPGG (demanda social).
This paper was edited by Greg Hancock and reviewed by two anonymous referees.
Beaumont, C., Fullsack, P., and Hamilton, J.: Erosional control of active compressional orogens, in: Thrust Tectonics: London, edited by: McClay, K. R., Springer-Science + Business Media B. V., 1–18, https://doi.org/10.1007/978-94-011-3066-0, 1992.
Best, J.: Anthropogenic stresses on the world's big rivers, Nat. Geosci., 12, 7–21, https://doi.org/10.1038/s41561-018-0262-x, 2019.
Bicudo, T. C., Sacek, V., Almeida, R. P., Bates, J. M., and Ribas, C. C.: Andean Tectonics and Mantle Dynamics as a Pervasive Influence on Amazonian Ecosystem, Sci. Rep., 9, 16879, https://doi.org/10.1038/s41598-019-53465-y, 2019.
Braun, J.: Recent advances and current problems in modelling surface processes and their interaction with crustal deformation, Geol. Soc. Lond. Spec. Publ., 253, 307–325, https://doi.org/10.1144/GSL.SP.2006.253.01.16, 2006.
Cheng, H., Sinha, A., Cruz, F. W., Wang, X. F., Edwards, R. L., d'Horta, F. M., Ribas, C. C.,Vuille, M., Stott, L. D., and Auler, A. S.: Climate change patterns in Amazonia and biodiversity, Nat. Commun., 4, 1411, https://doi.org/10.1038/ncomms2415, 2013.
do Prado, A. H.: Ariel-H-Prado/SPASE_Model: SPASE – 26.05.2022 (SPASE), Zenodo [code], https://doi.org/10.5281/zenodo.6583431, 2022.
Espinoza, J. C., Ronchail, J., Guyot, J. L., Cochonneau, G., Naziano, F., Lavado, W., de Oliveira, E., Pombosa, R., and Vauchel, P.: Spatio-temporal rain-fall variability in the Amazon basin countries (Brazil, Peru, Bolivia, Colombia, and Ecuador), Int. J. Climatol., 29, 1574–1594, https://doi.org/10.1002/joc.1791, 2009.
Filizola, N. and Guyot, J. L.: Suspended sediment yields in the Amazon basin: an assessment using the Brazilian national data set, Hydrol. Process., 23, 3207–3215, https://doi.org/10.1002/hyp.7394, 2009.
Filizola, N. and Guyot, J. L.: Fluxo de sedimentos em suspensão nos rios da Amazônia, Rev. Bras. Geosci., 41, 566–576, https://doi.org/10.25249/0375-7536.2011414566576, 2011.
Fritz, S. C., Baker, P. A., Lowenstein, T. K., Seltzer, G. O., Rigsby, C. A., Dwyer, G., Tapia, P. M., Arnold, K. K., Ku, T., and Luo, S.: Hydrologic variation during the last 170,000 years in the Southern Hemisphere tropics of South America, Quatern. Res., 61, 95–104, https://doi.org/10.1016/j.yqres.2003.08.007, 2004.
Gualtieri, C., Martone, I., Filizola Junior, N. P., and Ianniruberto, M.: Bedform Morphology in the Area of the Confluence of the Negro and Solimões-Amazon Rivers, Brazil, Water, 12, 1630, https://doi.org/10.3390/w12061630, 2020.
Guimberteau, M., Ronchail, J., Espinoza, J. C., Lengaigne, M., Sultan, B., Polcher, J., Drapeau, G., Guyot, J. L., Ducharne, A., and Cialis, P.: Future changes in precipitation and impacts on extreme streamflow over Amazonian sub-basins, Environ. Res. Lett., 8, 1–13, https://doi.org/10.1088/1748-9326/8/1/014035, 2013.
Hancock, G. R., Lowry, J. B. C., Coulthard, T. J., Evans, K. G., and Moliere, D. R.: A catchment scale evaluation of the SIBERIA and CAESAR landscape evolution models, Earth Surf. Proc. Land., 35, 863–875, https://doi.org/10.1002/esp.1863, 2010.
Hoorn, C. , Wesselingh, F. P., Ter Steege, H., Bermudez, M. A., Mora, A. , Sevink, J., Sanmartín, I., Sanchez-meseguerA., Anderson, C. L., Figueiredo, J. P., Jaramillo, C., Riff, D., Negri, F. R., Hooghiemstra, H., Lundberg, J., Stadler, T., Särkinen, T., and Antonelli, A.: Amazonia Through Time: Andean uplift, climate change, landscape evolution, and biodiversity, Science, 330, 927–931, https://doi.org/10.1126/science.1194585, 2010.
Ianniruberto, M., Trevethan, M., Pinheiro, A., Andrade, J. F., Dantas, E., Filizola, N., Santos, A., and Gualtieri, C.: A field study of the confluence between Negro and Solimões Rivers. Part 2: bed morphology and stratigraphy, Compt. Rendus Geosci., 350, 43–54, https://doi.org/10.1016/j.crte.2017.10.005, 2018.
Irion, G. and Kalliola, R.: Long-term landscape development processes in Amazonia, in: Amazonia: Landscape and Species Evolution: A Look into the Past, edited by: Hoorn, C. and Wesselingh, F., Oxford, Wiley-Blackwell, 185–197, https://doi.org/10.1002/9781444306408.ch22, 2010.
Latrubesse, E., Arima, E., Dunne, T., Park, E., Baker, V. R., d'Horta, F. M., Wight, C., Wittmann, F., Zuanon, J., Baker, P. A., Ribas, C. C., Norgaard, R. B., Filizola, N., Ansar, A., Flyvbjerg, B., and Stevaux J. C.: Damming the rivers of the Amazon basin, Nature, 546, 363–369, https://doi.org/10.1038/nature22333, 2017.
Lehner, B. and Grill, G.: Global river hydrography and network routing: baseline data and new approaches to study the world's large river systems, Hydrol. Process., 27, 2171–2186, 2013.
Merritts, D. J., Vincent, K. R., and Wohl, E. E.: Long river profiles, tectonism, and eustasy: a guide to interpreting fluvial terraces, J. Geophys. Res., 99, 14031–14050, https://doi.org/10.1029/94JB00857, 1994.
Mertes, L. A. K. and Dunne, T.: Effects of tectonism, climatic change, and sea-level change on the form and behaviour of the modern Amazon River and its floodplain, in: Large Rivers: Geomorphology and Management, edited by: Gupta, A., Wiley, Chichester, 115–144, ISBN 978-0-470-84987-3, 2007.
NASA – National Aeronautics and Space Administration: Shuttle Radar Topographic Mission (SRTM), http://srtm.csi.cgiar.org, last access: November 2018.
Norton, K. P., Schlunegger, F., and Litty, C.: On the potential for regolith control of fluvial terrace formation in semi-arid escarpments, Earth Surf. Dynam., 4, 147–157, https://doi.org/10.5194/esurf-4-147-2016, 2016.
Pupim, F. N., Sawakuchi, A. O., Almeida, R. P., Ribas, C. C., Kern, A. K., Hartmann, G. A., Chiessi, C. M., Tamura, L. N., Mineli, T. D., Savian, J. F., Grohmann, C. H., Bertassoli Jr., D. J., Stern, A. G., Cruz, F. W., and Cracraft, J.: Chronology of terra firme formation in Amazonian lowlands reveals a dynamic Quaternary landscape, Quaternary Sci. Rev., 210, 154–163, https://doi.org/10.1016/j.quascirev.2019.03.008, 2019.
Räsänen, M. E., Salo, J. S., Jungnert, H., and Pittman, L. R.: Evolution of the western Amazon lowland relief: impact of Andean foreland dynamics, Terra Nova, 2, 320–332, https://doi.org/10.1111/j.1365-3121.1990.tb00084.x, 1990.
Regard, V., Lagnous, R., Espurt, N., Darrozez, J., Baby, P., Roddaz, M., Calderón, Y., and Hermoza, W.: Geomorphic evidence for recent uplift of the Fitzcarrald Arch (Peru):a response to the Nazca Ridge subduction, Geomorphology, 107, 107–117, https://doi.org/10.1016/j.geomorph.2008.12.003, 2009.
Ribas, C. C. and Aleixo, A.: Diversity and evolution of Amazonian birds: implications for conservation and biogeography, Anais da Academia Brasileira de Ciências, 91, 1–9, https://doi.org/10.1590/0001-3765201920190218, 2019.
Ribas, C. C., Aleixo, A., Nogueira, A. C. R., Miyaki, C. Y., and Cracraft, J.: A paleobiogeographic model for biotic diversification within Amazonia over the past three million years, P. Roy. Soc. B, 279, 681–689, https://doi.org/10.1098/rspb.2011.1120, 2012.
Rossetti, D. F., Toledo, P. M., and Góes, A. M.: New geological framework for Western Amazonia (Brazil) and implications for biogeography and evolution, Quatern. Res., 63, 78–89, https://doi.org/10.1016/j.yqres.2004.10.001, 2005.
Sacek, V.: Modelagem numérica conjunta de processos sedimentares e tectônicos em bacias sedimentares, PhD thesis, Universidade de São Paulo, São Paulo, https://doi.org/10.11606/T.14.2011.tde-21062013-151844, 2011.
Sacek, V.: Drainage reversal of the amazon river due to the coupling of surface and lithospheric processes, Earth Planet. Sc. Lett., 401, 301–312, https://doi.org/10.1016/j.epsl.2014.06.022, 2014.
Sioli, H.: The Amazon and its main afluents: hydrography, morphology of the river courses, and river types, in: The Amazon, edited by: Sioli, H., Springer, Dordrecht, 127–165, https://doi.org/10.1007/978-94-009-6542-3_5, 1984.
Steffen, D., Schlunegger, F., and Preusser, F.: Drainage basin response to climate change in the Pisco valley, Peru, Geology, 37, 491–494, https://doi.org/10.1130/G25475A.1, 2009.
Tucker, G. E. and Slingerland, R.: Drainage basin responses to climate change, Water Resour. Res., 33, 2031–2047, https://doi.org/10.1029/97WR00409, 1997.
van Breukelen, M. R., Vonhof, H. B., Hellstrom, J. C., Wester, W. C. G., and Kroon, D.: Fossil dripwater in stalagmites reveals Holocene temperature and rainfall variation in Amazonia, Earth Planet. Sc. Lett., 275, 54–60, https://doi.org/10.1016/j.epsl.2008.07.060, 2008.
Veit, H., May, J.-H., Madella, A., Delunel, R., Schlunegger, F., Szidat, S., and Capriles, J. M.: Palaeo-geoecological significance of Pleistocene trees in the Lluta Valley, Atacama Desert, J. Quatern. Sci., 31, 203–213, https://doi.org/10.1002/jqs.2857, 2016.
Whipple, K. and Tucker, G.: Implications of sediment-flux-dependent river incision models for landscape evolution, J. Geophys. Res., 107, 1–20, https://doi.org/10.1029/2000JB000044, 2002.
Wilkinson, M. J., Marshall, L. G., Lundberg, J. G., and Kreslavsky, M. H.: Megafan environments in northern South America and their impact on Amazon Neogene aquatic ecosystems, in: Amazonia, Landscape and Species Evolution: A Look into the Past, edited by: Hoorn, C. and Wesselingh, F. P., Blackewell, 162–184, ISBN 978-1-4051-8113-6, 2010.





