Geospatial modelling of large-wood supply to rivers: a state-of-the-art model comparison in Swiss mountain river catchments

Different models have been used in science and practice to identify instream large-wood (LW) sources and to estimate LW supply to rivers. This contribution reviews the existing models proposed in the last 35 years and compares two of the most recent geographic information system (GIS)-based models by applying them to 40 catchments in Switzerland. Both models, which we call here the empirical GIS approach (EGA) and fuzzy-logic GIS approach (FGA), consider landslides, debris flows, bank erosion, and mobilization of instream wood as recruitment processes and compute volumetric estimates of LW supply based on three different scenarios of process frequency and magnitude. Despite being developed following similar concepts and fed with similar input data, the results from the two models differ markedly. In general, estimated supply wood volumes were larger in each of the scenarios when computed with the FGA and lower with the EGA models. Landslides were the dominant process identified by the EGA, whereas bank erosion was the predominant process according to the FGA model. These differences are discussed, and results are compared to available observations coming from a unique database. Regardless of the limitations of these models, they are useful tools for hazard assessment, the design of infrastructure, and other management strategies.

1 Introduction

The influence of wood in watercourses is manifold. On the one hand, there are various ecological benefits of large wood (LW), as it provides habitats and a food source for many organic organisms, thus promoting rich biodiversity (Harmon et al., 1986; Steel et al., 2003; Wondzell and Bisson, 2003). LW also affects stream hydraulics by altering the channel morphology and sediment control (Montgomery and Piégay, 2003; Wohl and Scott, 2016). On the other hand, large quantities of LW may be mobilized during infrequent, high-magnitude floods and may induce potential hazards for human settlements and infrastructure (Lucía et al., 2015b, 2018; Rickli et al., 2018; Ruiz-Villanueva et al., 2013; Steeb et al., 2017b). Consequently, river managers are challenged to maintain a good ecological status of rivers while minimizing potential hazards.

From a flood protection perspective, the main problem regarding LW in streams is wood accumulation at bridges and weirs, which reduces or even clogs the entire river cross-section and leads to backwater rise and consequent inundation (Comiti et al., 2016; Lassettre and Kondolf, 2012; Piégay et al., 1999; Rickenmann et al., 2016). The associated damage potential of LW may depend, among other variables, on the volume of transported LW (Mazzorana et al., 2018). Large-wood transport is governed by the flow conditions, river morphology (Ruiz-Villanueva et al., 2020), the size and shape of individual wood pieces (i.e. large logs or rootwads are more prone to clogging; Bezzola et al., 2002), the mode in which wood is being transported (i.e. if logs are transported congested or not; Braudrick et al., 1997; Ruiz-Villanueva et al., 2019), and the availability or supply of wood. Wood supply occurs by numerous geomorphic processes including bank erosion, channel migration, mass wasting (e.g. landslides, debris flows), and natural tree mortality and fall (Benda and Sias, 2003). These processes can be highly variable, on both temporal and spatial scales (Gasser et al., 2019).

Despite numerous existing approaches and efforts (see following section), the quantitative estimation of LW supply volume and the definition of contributing source areas based on different recruitment processes remain very challenging. The estimation of exported wood involves many uncertainties that are difficult to quantify because LW transport happens at the end of a long process cascade, usually starting with precipitation as a trigger, followed by a flood formation and the occurrence of recruitment processes as wood suppliers as well as the increased discharge as a transport medium. In addition, any type of model developed to estimate and quantify wood supply should be validated with field observations, data that are very scarce (Comiti et al., 2016; Nakamura et al., 2017; Wohl et al., 2019; Gurnell and Bertoldi, 2020).

This work reviews the state of the art in wood supply modelling and presents a comparison of two recent geographic information system (GIS)-based approaches that were developed in the context of an applied research project funded by the Swiss Federal Office for the Environment. First, the literature review provides an updated compilation of published approaches to model recruitment processes to quantify LW supply, classifying the approaches by model type and summarizing their main characteristics, such as processes considered and their temporal and spatial scales. We then focus on two GIS-based models that were developed based on a similar general concept, used similar input data, and were applied to the same study sites. The models were validated with a unique observation dataset of supplied wood during single events in a large number of catchments in Switzerland (Steeb, 2018; Steeb et al., 2019a). Despite their similarities, the models differ in some respects and result in somewhat different outcomes. These differences are used to stress the limitations and strengths of the two models, to compare them with other recent approaches included in the literature review, and to discuss uncertainties and challenges related to the modelling of LW supply. In addition, we also consider implications for flood hazard assessment and river management.

Table 1 Comparison of published wood supply models. Highlighted in italics: models used for comparison in this work, the empirical GIS approach (EGA) and fuzzy-logic GIS approach (FGA).

2 Large-wood-supply models: a review

Over the last decades, different approaches have been developed to quantify LW supply at both reach and catchment scales. Gregory et al. (2003) provided a summary of the first attempts to simulate wood supply, i.e. mostly mathematical models developed from conceptual descriptions of selected wood recruitment processes. Later, Gasser et al. (2019) reviewed recent approaches and evaluated whether the stabilizing effect of vegetation on total LW supply was considered or not. In this work, we compile and expand these previous overviews to provide an updated review of published approaches to model recruitment processes and to quantify LW supply (Table 1; numbering therein used for reference in this section). We classify the approaches by model category (i.e. empirical, deterministic, stochastic, or GIS-based) and summarize their main characteristics (i.e. processes considered, spatial and temporal scales, inputs and outputs, and whether they were validated with field observations or not). The evolution of these models illustrates and contributes to the scientific understanding of the complex processes involved in wood supply to rivers. Some of the earliest approaches (e.g. 1, 21, and 22) were designed to simulate long-term delivery of wood to river reaches from adjacent riparian forest by tree mortality, windthrow, or bank erosion. Subsequent models attempted to describe these input processes over larger portions of river networks (3, 4, 6, 23, and 24) but maintained a long-term perspective. Few studies included other processes, such as channel avulsion 4 and 22. These earlier models were developed in the US, most of them in the Pacific Northwest and a few in the south-east (4) or the Rocky Mountains (23). Later, researchers started to apply and develop models elsewhere, e.g. in New Zealand (24).

Martin and Benda (2001) and Benda and Sias (2003) (16) were pioneers in considering mass movements (i.e. landslides and debris flows) as wood recruitment processes, and they established the first conceptual framework for LW budgeting. This approach was further applied in US mountain rivers (8 and 20) before it was adapted to shorter timescales for mountain rivers in Italy and Switzerland (14 and 29). Focusing on shorter time windows and on episodic disturbances (e.g. floods) aggregated at the catchment scale, researchers proposed empirical equations based on field observations of exported wood and catchment characteristics (28 and 29). As most of the data used to derive such empirical formulas originated from steep headwater streams and mountain rivers in Switzerland, Austria, and Japan, application to larger catchments is associated with considerable uncertainty.

The rapid proliferation of remote sensing and the advances in computing sciences and GIS applications (Bishop and Giardino, 2022) resulted in the development of another group of models (i.e. geospatial models). These GIS-based models allow a spatially explicit assessment of different LW recruitment processes, the identification of source areas, and the estimation of LW volumes, expanding the analysis to larger areas, covering multiple (sub-)catchments. Rimböck (2001) (5) developed a GIS-based model to identify potential recruitment areas of LW in mountain streams, resulting from bank erosion, landslides, and windthrow. In this approach, he used wood volume reduction factors to distinguish between the potential LW volume (i.e. maximum volume that could potentially be supplied) and the estimated wood volume exported or supplied during exceptional floods. Mazzorana et al. (2009) (10) developed a procedure to determine the relative propensity of mountain streams in Bolzano Province (Italy) to supply wood due to floods, debris flows in tributaries, bank erosion, and shallow landslides, based on empirical indicators. Kasprak et al. (2012) (18) used light detection and ranging (lidar) data to estimate tree height and recruitable tree abundance throughout a watershed in coastal Maine in the US and to determine the likelihood for the stream to recruit channel-spanning trees at the reach scale and assess whether mass wasting or channel migration was a dominant supply mechanism. Ruiz-Villanueva et al. (2014c) (12) estimated potential LW volumes recruited from landslides, bank erosion, and fluvial transport during floods in the Central Mountain Range in Spain. The authors applied a GIS model including multi-criteria and multi-objective assessments using fuzzy-logic principles together with reduction factors for predefined scenarios. The method included the analysis of the hillslope-channel network connectivity and the resistance of the vegetation to be eroded. This approach was recently adapted and applied to mountain catchments in Switzerland, considering debris flows as supply processes as well (13), and it has been further used in the present study. Also applied in Swiss mountain catchments, Steeb et al. (2017a, 2019b) (11) proposed a GIS approach to model source areas of LW and to estimate potential supply and exported wood volumes based on reduction factors derived from an extensive empirical database of flood events with LW occurrence (Steeb, 2018; Steeb et al., 2019a, 2022). In Switzerland and other countries around the Alps, some private engineering companies and consultants, specialized in natural hazards, developed their own GIS-based models to estimate the potential LW supply from different recruitment processes (e.g. von Glutz, 2011; Hunziker, 2017).

However, one important aspect of the above-mentioned GIS-based models (10, 5, 12, and 11) is that they do not attempt to simulate the actual recruitment processes (e.g. landslides, debris flows, bank erosion), but they used available information on areas susceptible to recruitment processes (e.g. from hazard maps, although these are usually derived from previous modelling studies) or expert-based buffers. An intermediate approach was proposed by Rigon et al. (2012) (19), who applied a geostatistical bivariate analysis (weight of evidence method; Bonham-Carter et al., 1990) to identify unstable areas based on weighting factors. Lucía et al. (2015a) (14) estimated potential LW recruitment in a mountain basin in Italy modelling shallow landslides with a hillslope stability model (Montgomery and Dietrich, 1994) coupled to a connectivity index (Cavalli et al., 2013). The approach was further developed by Franceschi et al. (2019) (15), who used detailed forest information based on a single tree extraction from lidar data and combined it with a 1D hydraulic model to evaluate channel widening and LW downstream propagation. Cislaghi et al. (2018) (27) proposed one of the first physically based stochastic models to simulate shallow landslides combined with the forest stand characteristics to estimate LW recruitment from hillslopes. Similarly, Gasser et al. (2018, 2020) (26) proposed two frameworks to model shallow landslides and geotechnical and hydraulic bank erosion applying two physically based stochastic models together with a tree detection algorithm (Dorren, 2017) to estimate LW supply. Zischg et al. (2018) (9) presented a LW recruitment model coupled to a 2D hydrodynamic model to estimate LW recruitment from bank erosion in the flood influence zone of the river. In this approach, wood volumes were also estimated based on a single tree detection algorithm applied to a normalized digital surface model.

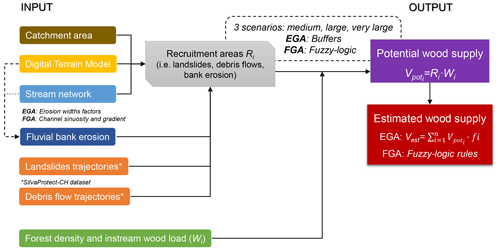
Figure 1 Conceptual model of the empirical GIS approach (EGA) and the fuzzy-logic GIS approach (FGA). V_pot: potential wood supply [m³]; V_est: estimated supplied wood [m³]; i: recruitment process [–]; R: recruitment area [ha]; W: forest density or instream wood load [m³ ha⁻¹]; f: volume reduction factor [–]. Three different scenarios were defined (see Sect. 3.5): medium scenario (medium to high frequency and intermediate magnitude), large scenario (relatively low frequency and medium to high magnitude), and very large scenario (very low frequency and very high magnitude).

3 Geospatial modelling of large-wood supply in Swiss mountain catchments

3.1 General concept

In this contribution, two LW models were compared: the empirical GIS approach (EGA) by Steeb et al. (2017a, 2019b) and the fuzzy-logic GIS approach (FGA) by Ruiz-Villanueva and Stoffel (2018), which is a variation of the model presented by Ruiz-Villanueva et al. (2014c). Both the EGA and FGA are based on a similar general concept (Fig. 1) and fed with similar input data and defined equivalent scenarios (see following subsections) to make comparison possible. Both models were developed in the context of WoodFlow, a Swiss research programme aimed at creating knowledge and methods to analyse instream wood dynamics, with particular attention to watercourses in the Alpine region (FOEN, 2019).

The general concepts and main steps of the GIS-based approaches were to (i) identify the recruitment areas on the hillslopes and along the stream network that may contribute woody material to streams, such as areas affected by landslides, debris flows, and bank erosion; (ii) create three different scenarios based on the process frequency and magnitude; and (iii) provide estimates of potential LW supply V_pot (i.e. worst-case scenarios) and supplied wood volumes for each scenario V_est. The methods aim at estimating supply wood volumes at the catchment scale and do not include the analysis of wood transfer (i.e. transport and deposition) through the stream network.

Potential large-wood supply V_pot was calculated by the intersection of the modelled recruitment areas with forest cover. During a flood, however, only a part of the LW potential is actually recruited and exported out of the catchment. Therefore, empirically derived volume reduction factors (EGA) or fuzzy-logic principles (FGA) were applied to best-estimate actual supplied LW volumes V_est. Modelling results were validated by comparison with available empirical data documented after flood events in Switzerland (Steeb et al., 2021, 2022). This dataset documents recruited and transported quantities of large wood together with the associated catchment and flood-specific parameters, including the associated recruitment processes (Table S1 in the Supplement).

3.2 Input data

3.2.1 Catchment areas and stream network

The topographical catchment areas (feature polygons), which define the spatial extent of the investigation, were available from the geodataset “topographical catchments of Swiss waterbodies” (FOEN, 2015). The stream network of Switzerland at a scale of 1:25 000 (swissTLM3D, © 2016 swisstopo, DV033594) was pre-processed by adding information on channel width as derived from a Swiss-wide ecomorphological dataset (Ökomorphologie Stufe F © FOEN; Zeh Weissmann et al., 2009). Based on this dataset, the channel width was known for 42 % (25 800 km) of the total Swiss streams' length. For the remaining 58 %, we extrapolated channel width based on stream order (Strahler, 1957) and altitude classes (Table S2).

The stream network and channel widths were used to define intersections and connectivity between the hillslope processes and the streams, to estimate the bank-erosion-prone areas (Sects. 3.3 and 3.4), and to assign values of instream dead wood volumes (Sect. 3.2.3).

3.2.2 SilvaProtect-CH and the identification of landslide and debris flow trajectories

For the modelling of the two recruitment process categories landslide and debris flow, both GIS models used the SilvaProtect-CH dataset from Losey and Wehrli (2013). As part of the SilvaProtect-CH project, several natural hazard processes were modelled over the entire Swiss territory using partly physically based models. As a result, process trajectories that describe the topographic flow path and runout distances (from starting to deposition zone) of the investigated natural hazard processes were readily available (details are provided in the Supplement). These trajectories were processed further to identify potential recruitment areas of LW supply (Sects. 3.3. and 3.4).

Figure 2 Example of the wood stock raster map in the Grosse Melchaa catchment near Stöckalp (canton of Obwalden). Background: digital terrain model (hillshade), © swisstopo.

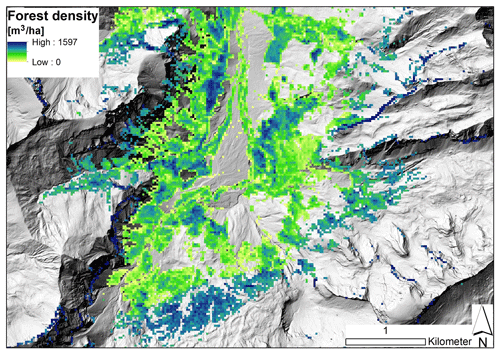
3.2.3 Forest density and instream wood load

The density of living trees in Swiss forests [m³ ha⁻¹] was derived from a Swiss nationwide raster map with an original resolution of 25 m × 25 m (rescaled to 1 m × 1 m; Fig. 2). The raster map is based on a growing stock model developed by Ginzler et al. (2019) that quantifies forest density in relation to tree height (based on airborne stereo imagery), canopy cover, topographic position index, mean summer temperature, and elevation. The EGA and FGA models further consider an estimate of deadwood on the forest floor [m³ ha⁻¹] (i.e. equal to 5 % of living tree density) based on empirical data of the Swiss National Forest Inventory (NFI; WSL, 2016).

Additionally, instream wood loads were included in the calculations, accounting for potential LW volumes from accumulated deadwood in the channel. Detailed information on wood loads across the stream network was not available, so based on a literature review by Rickli and Bucher (2006) and Ruiz-Villanueva et al. (2016), volumes of instream wood were assigned to the different streams grouped by channel width (EGA) or by stream order (FGA) classes (see following sections).

3.3 The empirical GIS approach (EGA)

Debris flow and landslide trajectories from SilvaProtect-CH were constrained by intersection with the stream network and forest cover. Only landslide trajectories with starting points within a 50 m distance from the stream network were considered. This limitation was supported by the landslide database of Rickli et al. (2016), where 44 % of all documented landslides showed a runout distance of less than 50 m (around 80 % are within a distance of 100 m). For each scenario (Sect. 3.5), different buffer widths w_b were applied on both sides of the relevant debris flow and landslide trajectories (i.e. medium scenario: w_b = 5 m; large scenario: w_b = 10 m; very large scenario: w_b = 15 m). The buffer widths were chosen in ranges according to a Swiss landslide database (Rickli et al., 2016). Potential recruitment areas were finally extracted as the overlap of the buffered trajectories with the forest layer.

The extent of bank erosion in the EGA was assumed to be proportional to the given channel width. Scenario-specific erosion width factors e_w (i.e. a multiple of the channel width) were empirically derived from observations after the well-documented August 2005 flood in Switzerland, for which a large dataset was analysed and made available (Bachmann Walker, 2012; Hunzinger and Durrer, 2008). Scenario-specific erosion width factors were e_w = 1.5 for the medium scenario, e_w = 3 for the large scenario, and e_w = 4.5 for the very large scenario. The resulting buffer widths were added to the original channel width. Potential recruitment areas due to bank erosion were finally extracted as the overlap of the buffered stream network with the forest layer.

The estimation of previously stored wood load within the river network (i.e. instream deadwood) was based on empirical values of wood storage per stream hectare. Rickli et al. (2018) documented instream wood storage for 10 reaches in Swiss torrents. This database was complemented with 39 additional values from various other European rivers, based on a literature review by Ruiz-Villanueva et al. (2016), in order to have reliable derivations. Finally, we assigned wood load values into three channel width classes (i.e. < 5 m = 94 m³ ha⁻¹, 5–10 m = 67 m³ ha⁻¹, > 10 m = 42 m³ ha⁻¹).

Table 2 Overview of volume reduction factors f, classified by scenario and recruitment process.

Potential source areas from different recruitment processes may partly overlap. For this reason, a priority sequence was determined so that such overlapping areas were not counted more than once. This was defined according to the following principle: the closer to the channel a recruitment process occurs, the higher the priority (instream wood > debris flow > bank erosion > landslide). For example, overlapping areas of debris flows and bank erosion were assigned to the process area debris flow.

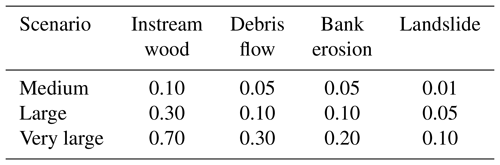
Potential recruitment areas were finally used to calculate the potential LW supply V_pot by multiplying the process areas with the respective forest density (for debris flows, landslides, and bank erosion) or wood load (for instream deadwood). From the resulting potential LW supply, the actual LW supply V_est was estimated. To do so, volume reduction factors f were used, which assumed different values depending on the recruitment process and scenario of process magnitude (Table 2). The volume reduction factors were empirically determined with three different approaches (Steeb et al., 2019b): (1) comparison with literature data, including values from other studies and models that proposed reduction factors; (2) comparison of potential vs. observed recruitment areas; and (3) comparison of estimated vs. observed wood volumes in well-documented catchments during the 2005 flood (see the five blue catchments in Fig. 3).

Figure 3 Location of the 40 test catchments (orange; with many nested sub-catchments). The five catchments in blue (Chiene, Chirel, Grosse Melchaa, Landquart, Kleine Emme) were used to calibrate the volume reduction factors from the EGA approach so that the estimated supplied wood was of the same order of magnitude as the observed values from past flood events. Background: digital terrain model (hillshade), © swisstopo.

Values of observed LW supply volumes and recruitment areas together with the associated catchment- and flood-specific parameters were taken from a complementary empirical dataset that was also part of the WoodFlow research programme. In total, the LW database consisted of 210 data entries. Most entries (171) refer to events in Switzerland. Also included are flood events from Japan, Italy, Germany, and France (Steeb et al., 2019a).

The EGA model was originally developed with ArcGIS 10.1 (© ESRI) and updated with ArcGIS 10.8 (© ESRI). The toolbox is freely available for download (Steeb et al., 2023).

3.4 The fuzzy-logic GIS approach (FGA)

The areas prone to landslides and debris flows were defined based on the linear trajectories provided by the SilvaProtect-CH database. To transform these lines into areas (i.e. pixels, as the FGA is entirely raster-based), the density of the lines was used to classify the terrain into three intensity scenarios (Sect. 3.5). High trajectory density was assumed to represent areas that are more prone to landslides or debris flows, more likely of a higher frequency and therefore lower magnitude. Low trajectory density was assumed to represent areas that are less prone to mass movements, more likely affected by higher-magnitude and thus lower-frequency events. The thresholds to classify the three areas were based on four natural breaks (Fig. S1a in the Supplement). In the case of mass movements, the delivery of wood to the stream network depends not only on the area of the landslide, but also on its connectivity to the channel (Ruiz-Villanueva et al., 2014c). Once the trajectories were converted to density pixels, the connectivity between these pixels and the stream network was established for landslide-prone pixels, as a function of both the distance to the channel and the terrain slope. In addition, a buffer area of influence was also established around these areas to include toppled trees that may be recruited indirectly by the action of landslides. Trees located in a landslide-prone pixel or in the toppling influence area (defined as a buffer equal to 2 times the mean tree height; here 100 m) may reach the channel if they were close enough (Euclidean distance to channel network < 50 m) or further away (Euclidean distance up to 100 m) but on a steep slope (> 40 %). In the case of debris flows, all pixels were assumed to be connected to the stream network.

Areas prone to bank erosion were computed based on channel sinuosity and gradient (as proxies for channel lateral migration and transport capacity; Ruiz-Villanueva et al., 2014c), the channel width, and a defined width ratio. The width ratio was used to estimate the potential resulting channel width after bank erosion during floods. It was calculated analysing a European database (Ruiz-Villanueva et al., 2023), including several rivers and flood events in Switzerland and six other countries, and three scenarios were defined for different channel width classes (nine classes ranging from < 3 to > 50 m). The stream network provided by the ecomorphology database (Sect. 3.2.1) was grouped by the channel width classes considered, and the width ratio was assigned to estimate the resulting potential erodible width for each stream segment (Fig. S1). The width ratio (ranging between 1 and 4) generally increases with scenario intensity and decreasing channel width. The resulting buffers were transformed to pixels, and the final pixels prone to bank erosion were assigned based on channel sinuosity and gradient. Stream segments characterized by high sinuosity and high gradient were assumed to be more prone to bank erosion.

The described variables (i.e. landslide-prone areas, connectivity, debris-flow-prone areas, bank-erosion-prone areas, sinuosity, and gradient) were transformed to fuzzy sets using the Fuzzy Membership tool initially developed in ArcGIS 10.1 and updated to ArcGIS 10.7 (© ESRI) with a linear membership function. The resulting converted fuzzy variables were combined (e.g. landslide-prone pixels and connectivity, sinuosity, and gradient) with the Fuzzy Overlay tool (© ESRI). As a result, all pixels were transformed to fuzzy values ranging from 0 to 1; they were then used to compute the volume of wood by multiplying the fuzzy pixel value by the forest density pixel value (Sect. 3.2.3). In the case of overlapping pixels, priority was given to areas prone to debris flows, then bank erosion and finally landslides (as in the EGA approach). The final calculation also considered the accumulated wood load within the river network, but applying a slightly different approach than for the EGA. This was estimated by assigning wood load values based on the literature (Ruiz-Villanueva et al., 2016) to the different river segments grouped by stream order classes following the approach of Wohl (2017) (i.e. stream order < 3: 60 m³ ha⁻¹; order between 3 and 6: 120 m³ ha⁻¹; order > 6: 50 m³ ha⁻¹) and multiplied by fuzzy layers. The toolbox is freely available for download (Ruiz-Villanueva and Steeb, 2023).

3.5 Model scenario definition

Three different scenarios were designed to estimate supplied wood volumes based on a qualitative assessment of the frequency and intensity of the wood recruitment processes involved. These scenarios are called medium scenario (medium to high frequency and intermediate magnitude), large scenario (relatively low frequency and medium to high magnitude), and very large scenario (very low frequency and very high magnitude).

Most of the documented floods with LW occurrence that were used to validate the GIS models had a precipitation and/or peak runoff return period of 50–150 years, which was assigned to the large-volume scenario. The other two scenarios refer to approximate return periods and were determined using ad hoc volume reduction factors (EGA) or the fuzzy-logic rules (FGA) because they could not be quantified more precisely due to a lack of data.

In addition to the estimated supplied wood volumes for each scenario, a potential wood volume was also computed. The potential volume was assumed to be the maximum wood volume supplied at the catchment scale, computed without any reduction by a coefficient (EGA) or by the fuzzy-logic values (FGA).

3.6 Test catchments

In the 40 catchments analysed in this work (Fig. 3), considerable amounts of LW were recruited and transported during past floods, and the resulting LW volumes were well documented (mainly from the August 2005 flood; Rickli et al., 2018, and Steeb et al., 2017b). Table S1 in the Supplement provides an overview of the 40 test catchments and their characteristics.

3.7 Model result analysis

Model results were first compared to observed wood volumes during floods and then analysed in terms of (modelled) wood volumes per scenario, potential wood volume, wood volume supplied by different recruitment or supply processes (i.e. landslides, debris flows, and bank erosion), and the estimated instream wood volume.

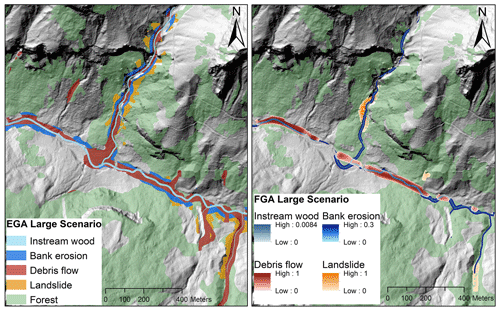
Figure 4 Large-scenario comparison of model outputs from the EGA (left) and FGA (right) at the Spiggebach torrent within the Chiene river catchment (canton of Bern). Potential recruitment areas are shown for landslides (orange), debris flows (red), and bank erosion (dark blue). The stream network (light blue) also includes instream wood loads. Background: digital terrain model (hillshade), © swisstopo.

Statistical analyses were realized with the software RStudio Version 2021.9.0.351 (R Studio Team, 2021). Differences between the two models and between them and the available observations were analysed in terms of mean values, standard deviation (SD), and root mean square error (RMSE) and tested by the nonparametric Wilcox (Mann–Whitney) or Kruskal–Wallis tests for two or more groups, respectively (Stats package; R Core Team, 2019). Differences in the distributions of observed versus estimated wood supply volumes (large scenario) were tested using the Kolmogorov–Smirnov test. Significance was set to a p value < 0.05. The dependence of wood volume on catchment controlling variables was verified by means of scatterplots, regression analysis, and correlation (ggally package; Schloerke et al., 2021).

4 Results

4.1 Comparison between model outputs and model approaches (EGA/FGA)

The two GIS approaches provide geospatial outputs – the EGA in the form of feature class polygons and the FGA in pixel-based raster files – that can be visualized on a map, as shown in Fig. 4. Potential recruitment areas for debris flow, landslide, and bank erosion are generally larger for the EGA; i.e. the defined EGA buffer widths provide more supply-prone areas than the respective combination of FGA fuzzy layers within the same perimeter.

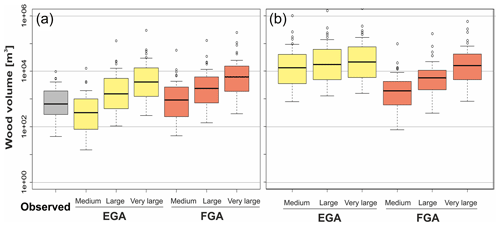
Figure 5 Boxplots of wood supply (a) and potential (b) volume (m³) estimated by the two models EGA and FGA and the three scenarios (i.e. medium, large, very large). “Observed” refers to the reported LW volumes after flood events (n=40; shown in grey colour), in most cases equivalent to the large scenario.

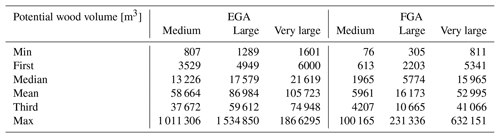
Table 3 Statistical values of observed and estimated LW supply volumes for the three scenarios (i.e. medium, large, and very large) and the two models (i.e. EGA and FGA) for all studied catchments. “Observed” refers to the reported LW volumes after flood events, in most cases equivalent to the large scenario.

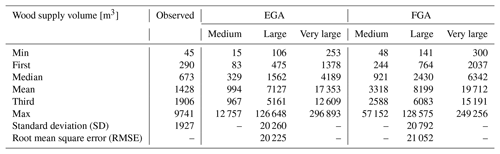
The estimated supply and potential wood volumes for the three scenarios and the two models are shown in Fig. 5 together with the available observations. The comparison between modelled and observed wood volumes is presented in Sect. 4.3; the focus here is on differences between the two models. In general terms, Fig. 5a highlights that the estimated supply wood volumes for each scenario were larger when computed by the FGA and lower by the EGA. For example, for the medium scenario, the averaged wood volumes were 994 and 3318 m³ for the EGA and FGA, respectively. The differences were slightly reduced for the other two scenarios, for which volumes equal to 7127, 17 353, 8199, and 19 712 m³ were obtained (for the large and very large scenarios and the EGA and FGA, respectively; Table 3).

The variation in estimated wood supply is similarly high for both models, as shown by the statistical values in Table 3. Except for the maximum value of the very large scenario, the FGA generally has slightly larger percentile values. The standard deviation for the large scenario is 20 260 for the EGA and 20 792 m³ for the FGA. The estimated wood supply volumes of the EGA and FGA correlate well, with only narrow scattering (Fig. S6a), and the residuals increase similarly with increasing catchment size (Fig. S6b).

Table 4 Potential LW supply volumes for the three scenarios (i.e. medium, large, and very large) and the two models (i.e. EGA and FGA) for all studied catchments.

Significantly higher values were computed for the large and very large scenarios compared to the medium scenarios, with a similar pattern shown by the two models. Larger differences were observed when comparing the estimated potential volumes (Fig. 5b and Table 4). In this case the EGA resulted in much higher values than the FGA (especially for medium and large scenarios), which is a result of much larger potential recruitment areas (Fig. 4). Accordingly, the percentile values of EGA potential LW supply volumes show more variability. Figure S3 shows that for the EGA, the estimated LW supply volume corresponds to 8 % of the potential wood supply volume on average. In the case of the FGA, this ratio varies much more, with an average of 47 %.

4.2 Contribution from different supply processes

The main difference between the two models was the estimated contribution from each supply process to the obtained wood volume. Landslides were the dominant process in the case of the EGA, with a contribution of up to more than 60 % of the computed wood volume (for the large scenario), whereas bank erosion was the predominant process in the FGA model for all scenarios (Fig. 6). Debris flows played an intermediate role in supplying wood according to the two models; however, the importance of this process varied depending on the scenario. For the medium scenario, the EGA model showed a similar percentage of average wood supplied by landslides and debris flows. The FGA, contrastingly, computed most of the average wood volume supplied by bank erosion and only a low percentage of wood supplied by landslides and debris flows. Only for the very large scenario is the importance of landslides, in terms of percentage of supplied wood, equal to or even greater than the volume estimated from bank erosion with the FGA.

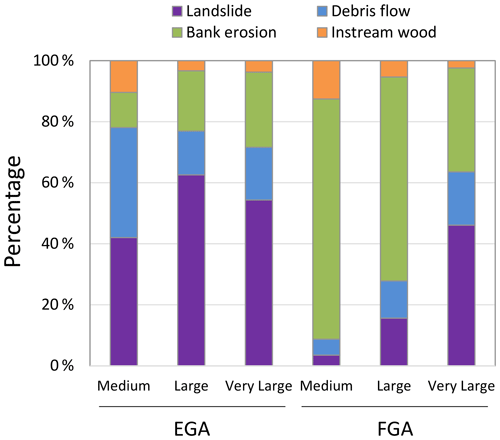
Figure 6 Large-wood volumes supplied by each process, model, and scenario, averaged for all 40 study sites.

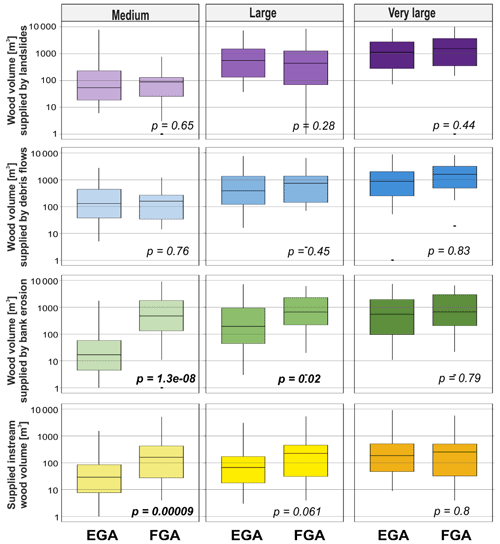
Figure 7 Wood volume supply estimated for landslides, debris flows, and bank erosion and estimated supplied instream wood by the two models and the three scenarios. The p value is from the Wilcoxon test (significant values shown in bold).

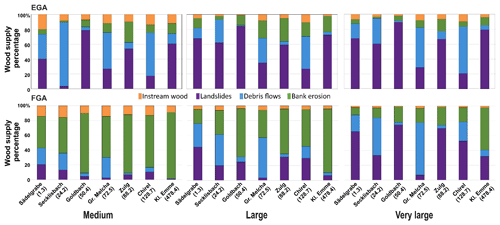
Figure 8 Percentage of wood volume supplied by each process, model, and scenario for selected studied sites; the names and catchment area (km²) are provided in the abscissa.

The difference between the contribution of each process to the estimated volumes is clearly shown in Figs. 7 and 8 (with the FGA resulting in generally higher volumes than the EGA). The graph illustrates that statistically significant differences were found between the computed supply wood volumes by the two models and by bank erosion processes. The median wood supply values (see black lines within boxplots of Fig. 7) are about a factor of 1000 and 10 larger for the FGA than for the EGA and for the medium and large scenarios, respectively. This explains the relative dominance of bank erosion for the FGA (see also Fig. 8) for the medium and large scenario. The wood volumes supplied by the other processes were not significantly different between the two models. Only the estimated instream wood volume for the medium scenario showed a significant difference between the EGA and the FGA, with larger volumes computed by the latter.

However, the contribution of each process to the computed wood volume varied according not only to the model but also to the site. Figure 8 shows a selected sub-dataset of catchments with different drainage areas, revealing the large variability in the dominant wood supply process and the dominance of different processes over the others in the two models. In general, the FGA approach shows a larger contribution from landslides and debris flows in smaller catchments, while landslides are the major contributor to wood supply regardless of the catchment size for the EGA. Bank erosion is a minor contributor to the estimated supply in the EGA for most sites and irrespective of the scenario used. However, bank erosion is the most relevant process for the FGA, which is clearly illustrated by the Kleine Emme river catchment, the largest of the study sites of the dataset, for which the FGA estimates the largest contribution by this process. The EGA model, on the other hand, estimated a larger contribution from landslides for this site.

The proportion of instream wood loads remains constant, independent of catchment size (2 %–13 % of total wood supply). The contributions of debris flows and landslides are highly variable depending on topography and can be dominant for small (e.g. Secklisbach) or large catchments (e.g. Grosse Melchaa or Chirel).

Figure 9 (a) Modelled LW V_est (large scenario) versus observed wood volume V_obs during past events. The black line shows the line of equality (1:1 line). (b) Ratio of $V_{\text{est}}/V_{\mathrm{obs}}$ versus catchment area.

4.3 Estimated and observed wood volumes

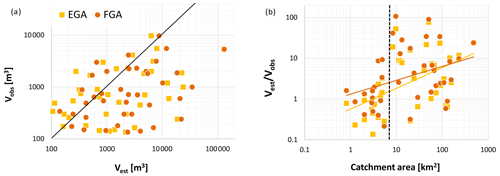
The comparison between observed LW volumes V_obs and estimated (modelled) LW volumes V_est is shown in Fig. 9a. There is a relatively large scattering when comparing observed and estimated wood loads. Both under- and overestimation of V_obs are observed for both models, with a larger tendency for overestimation. Overestimation remains generally within 2 orders of magnitude (typically higher values for the FGA), and underestimation remains within 1 order of magnitude (typically lower values for the EGA).

Figure 9b further shows the ratio of $V_{\text{est}}/V_{\text{obs}}$ vs. catchment area. Both under- and overestimation of V_obs are present over > 2 orders of magnitude for all catchment areas. However, in general, overestimation increases with increasing catchment size for both models. There is a shift around a catchment area of 7 km², above which overestimation is significantly larger (with a factor of > 10). In catchments with areas less than 7 km², estimated wood supply is generally underestimated (see dashed line in Fig. 9b).

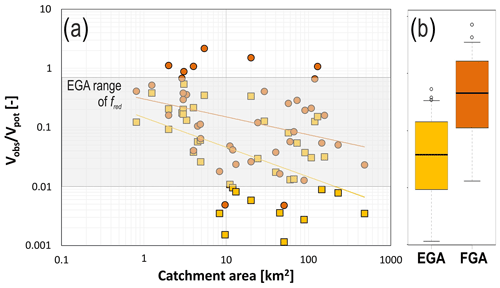
Figure 10 Ratio of observed wood volumes and potential wood volumes computed by the two models for all sites and their catchment areas. The grey rectangle shows the reduction factor range used for EGA computations.

This tendency of overestimation with increasing catchment size can also be explained by comparing the ratio of observed and potential wood volume $V_{\text{obs}}/V_{\text{pot}}$ versus catchment area (Fig. 10a). With increasing catchment size, there is a trend of decreasing ratio values of $V_{\text{obs}}/V_{\text{pot}}$. This means in larger catchments, the volume reduction factors (FGA) and the fuzzy rules (FGA) are often not small enough to reduce the wood potential accordingly, creating overestimation of wood volumes (V_est > V_obs).

Since potential wood volumes are much higher for the EGA (Table 4 and Fig. 5b), the ratio of $V_{\text{obs}}/V_{\text{pot}}$ is also much smaller in the case of the EGA (almost 1 order of magnitude difference, as shown in Fig. 10b). For the FGA few examples (i.e. six orange dots in Fig. 10a) exist for which the potential wood volume is even smaller than the observed wood volume ($V_{\text{obs}}/V_{\text{pot}}$ > 1).

A statistically different distribution could only be observed for the FGA compared to the observed values. The comparison between the values obtained by the EGA and those observed and between the values obtained by the EGA and those obtained by the FGA showed no significantly different distributions (Table S3). This outcome is also illustrated in the histograms of Fig. S7.

5 Discussion

5.1 Major differences between the two models and remaining challenges

Both the EGA and FGA are based on a similar general concept, were fed with similar input data (e.g. stream network, forest density, areas affected by landslides and debris flows), and run with defined equivalent scenarios which made the comparison possible. However, there are also some methodological differences that resulted in different model outputs. Here we describe them, while in the following section we discuss our results, comparing them to current knowledge and other existing methodologies.

The most relevant difference between the EGA and FGA is the approach to defining the areas affected by bank erosion and thus the contribution of this recruitment process and the estimated wood supply volumes. The EGA uses buffers around the stream network computed for each scenario with one specific width factor, independent of the original channel width. The resulting buffer widths were added on both sides of the original channel width (Sect. 3.3). The FGA also assigned scenario-specific buffers, computed with width ratios that vary according to nine channel width classes (Fig. S1). Half of the resulting buffer widths were added on both sides of the original channel width. As a result, potential bank erosion recruitment areas are generally larger for the EGA than for the FGA. However, the reduction factors used for the EGA assumed that between 5 % and 20 % of the potential wood volume within these areas contributes to the estimated wood supply, which resulted in a much lower estimated wood volume. In the case of the FGA, the entire forested area identified as prone to bank erosion along the river network contributes to wood supply, and the volume is reduced based on fuzzy-logic pixel values (computed based on sinuosity and channel slope and going up to 30 % of the potential), which resulted in a much larger volume. This difference is particularly relevant for the medium scenario, for which the bank erosion widths identified by both models are quite similar, but the resulting wood volumes significantly differ (e.g. average wood volume equal to 114 and 2613 m³ for the EGA and FGA, respectively, for all sites). Moreover, the erodibility of the channel banks was not considered in the models. Anthropic elements such as bank protection, check dams, and bridges or the presence of bedrock may limit bank erosion and widening, and thus wood supply. This information was not available at the required resolution and spatial scale for the catchments analysed and could therefore not be included. This also results in an overestimation of the computed wood volumes due to bank erosion, which may be more relevant in the FGA than in the EGA (for which the volume reduction coefficient could be more easily adjusted).

As shown in Sect. 4.2, landslides are the dominant recruitment process in the case of the EGA, whereas bank erosion is the predominant process in the FGA model. In both models, for landslides and debris flows, the input data were the trajectories from the SilvaProtect-CH database, but the EGA applies an expert-based buffer for each scenario to those trajectories, while the FGA groups them in three classes according to their density. In addition, the fuzzy connectivity applied in the FGA further reduces the areas identified as prone to mass movements (only for landslides). This hillslope-channel network connectivity is another methodological difference between the two models. In the EGA, as a proxy for connectivity, only landslide trajectories within 50 m distance from the stream network were considered. The FGA considers connectivity as a function of both the distance to the channel and the terrain slope (as used by Ruiz-Villanueva et al., 2014c). It is noteworthy that both models use Euclidean distance, but no geomorphometric measures (e.g. steepest downslope direction), as often used to assess sediment connectivity (e.g. Cavalli et al., 2013).

The EGA generally produces much larger potential recruitment areas for landslides and computes larger wood supplied by landslides than the FGA, for all three scenarios. For the FGA, landslides are a minor supplier of wood for the medium and large scenarios, while their contribution in the very large-volume scenarios significantly increases.

Existing observations show that mass-wasting processes, such as debris flows and landslides, often are the most relevant recruitment processes in smaller headwater catchments (e.g. Rigon et al., 2012; Hassan et al., 2016; Seo et al., 2010). In contrast, (lateral) bank erosion is often prevalent farther downstream in larger mountain or lowland rivers, resulting in large volumes of LW supply by this fluvial recruitment process. This was observed after the large flood in 2005 in Switzerland (Steeb et al., 2017b), the large flood in the Magra river catchment in Italy in 2011 (Lucía et al., 2015b; Comiti et al., 2016), and along the Emme river catchment in 2014 (Ruiz-Villanueva et al., 2018). In smaller streams, bank erosion and channel widening can also be significant, especially in natural reaches (no stream regulation works), as seen after severe flash floods in Braunsbach, Germany, in 2016 (Lucía et al., 2018). In most of these cases, only a small proportion (< 30 %) of the total recruited wood was supplied by mass-wasting processes, and the majority of the supply was due to bank erosion and channel widening along the river network.

Such catchment-size-specific trends of dominant recruitment processes are not clearly prevalent in the model results of the EGA and FGA. Generally, the variability in the recruitment processes and thus in the wood supply is very large, in both empirical data and in modelling results, highlighting the importance of other catchment- and event-specific characteristics. The relationship of estimated LW supply with catchment characteristics is shown in Fig. S2. The highest correlation is seen for forested stream length, which can be interpreted as a proxy for potential supply volume for bank erosion. High correlations also exist for Melton ratio and relief ratio, both surrogates for watershed slope, a factor that is directly related to stream power and debris flow and landslide propensity. In general, V_obs from the EGA shows slightly higher correlations (R²) with catchment characteristics than the FGA. More research is needed to better understand wood recruitment processes and to improve predictive models on a physical basis. This will help to determine where and how likely mass wasting (landslides) or bank erosion could occur.

The results in Sect. 4.3 indicate that there is both under- and overestimation of wood supply volumes. As shown in Fig. S4, potential LW supply V_pot generally increases with catchment size. During a convective storm event, often only a part of the catchment is affected, and therefore geomorphologically active, so that LW supply may easily be overestimated (V_est > V_obs). In smaller catchments and torrents, sporadic recruitment processes such as landslides or debris flows can dominate and deliver large amounts of wood at once so that wood supply may be underestimated by our models (V_est < V_obs).

Another important aspect regarding the overestimation of the calculated wood volumes by the FGA and EGA is the assumption that the estimated volumes are supplied and exported to the outlet of the catchment, which may not be the case if the wood is being deposited along the way. The models do not consider the transfer of the wood along the river network (as, for example, in the approaches of Franceschi et al., 2019, or Zischg et al., 2018).

A less relevant difference between the models, and in terms of the total contribution to the wood volume estimations, is the approach used to assign previously deposited instream wood loads. The EGA assigns instream wood load values into three channel width classes (Sect. 3.3), whereas the FGA assigns wood load values into three stream order classes (Sect. 3.4). The main divergence comes from the assumption that the smaller channels contain the largest instream wood load for the EGA (following observations in 10 small mountain streams in Switzerland from Rickli et al., 2018), while the FGA assumes that larger loads are present in medium-order channels (as proposed by Wohl, 2017). Despite the different approaches, both models used empirical data from Ruiz-Villanueva et al. (2016) to assign volumes, and the resulting wood load volumes were only significantly different in the case of the medium scenario (Fig. 7).

These differences in the methodologies result in differences in the outcomes, in terms of the potential and estimated wood supply. The EGA generally produced larger potential recruitment areas. The volume reduction factors applied in the EGA are, however, on average much smaller than the respective fuzzy-logic values created in the FGA (Fig. S3). As a result, estimated wood supply is generally larger for the FGA, as shown in Sect. 4.1. For our test catchments, the application of simple empirical volume reduction factors as part of the EGA model has proven to be similarly accurate in estimating LW volumes, in comparison with a spatially explicit approach such as the FGA model. Still, both the expert-based buffer widths and the reduction factors were defined for the test catchments and validated for similar catchments located in the Alps and pre-Alps, and so they should be carefully tested if applied to other rivers with different characteristics. The fuzzy-logic approach indirectly includes this uncertainty or imprecise information (i.e. buffer widths and volume reduction factors) and allows it to be computed without prior existing observations or knowledge. In both cases, the two models may over- or underestimate the wood volumes but allow reliable computation of wood supply volumes at the catchment scale and for three scenarios.

5.2 Qualitative comparison of the EGA and FGA with other similar approaches

As described in the introduction, only a few approaches have been proposed to compute wood supply at the catchment scale considering different recruitment processes (e.g. landslides, debris flows, bank erosion). Most of the model frameworks described in Sect. 2, particularly those based on GIS and geoprocessing (e.g. Mazzorana et al., 2009), do not attempt to simulate the actual recruitment processes but use existing information on areas susceptible to certain processes (like the EGA and FGA) from hazard maps or other sources or apply expert-based buffers (like the EGA). Most existing models simulate only one recruitment process explicitly, i.e. landslides or bank erosion (Lucía et al., 2015a; Cislaghi et al., 2018; Zischg et al., 2018; Gasser et al.; 2018, 2020), and a few consider mass movements and fluvial processes (e.g. Franceschi et al., 2019). Yet, a model that simulates coupled processes to compute wood supply is still lacking. In existing approaches, physically based models are combined with empirical approaches to identify recruitment areas from one single process and compute wood supply at the catchment scale. Still, these models require additional input data, such as precipitation, discharge, soil characteristics, etc., which is usually not available or is challenging to obtain at the desired resolution. In addition, they are much more expensive in terms of computational time, which limits their application to larger areas. Therefore, there is a gap between the current state-of-the-art of geomorphic process modelling and wood recruitment and supply estimation.

Moreover, the majority of existing models used to predict wood supply are deterministic in that they do not consider the natural process variability and parameter uncertainties. Only the fuzzy-logic approach (Ruiz-Villanueva et al., 2014c; Ruiz-Villanueva and Stoffel, 2018) indirectly considers uncertainty, but it does not represent a description of the physical supply processes. A few stochastic models have been proposed (e.g. Bragg, 2000; Eaton et al., 2012; Gregory et al., 2003) to simulate wood recruitment, but they were designed to work at the scale of the river reach only. At the catchment scale, a probabilistic multi-dimensional approach has recently been proposed (Cislaghi et al., 2018) to study wood sources from hillslopes, modelling areas susceptible to landslides, but it neglects other processes such as bank erosion. The latter process has been considered in one of the most recent studies on LW (Gasser et al., 2020).

On the other hand, empirical estimation formulas (e.g. Steeb, 2018; Rickenmann, 1997; Uchiogi et al., 1996) are easier and faster to apply to estimate LW supply. However, they provide only an estimate for the whole catchment under investigation, without any spatial differentiation. The EGA and FGA, on the other hand, support a comprehensive spatial overview and direct attention to areas in which a more precise assessment of the instream wood situation is necessary, e.g. through field surveys or expert assessments. Figure S5 shows that the EGA and FGA modelling results approximately correspond to the 50 %–90 % relation between V_obs and catchment area, as described with the empirical formula of Steeb (2018).

5.3 Uncertainty in the observed and modelled LW volumes

The two GIS approaches presented here yielded similar orders of magnitude of LW supply for a given catchment and for the three designed scenarios. Still, several uncertainties associated with the estimation of LW supply remain, and they are not just related to the obtained results and the applied methodologies, but also to the available observations (coming from surveys after flood events) used for calibration and validation.

The observed wood volumes V_obs were compiled mostly from technical reports of post-event analyses, and these values might in some cases be only rough estimates, with a considerable uncertainty. LW volumes were estimated based on LW deposits and piles in the field, for which the volume and the corresponding wood content (or pore volume, respectively) must be estimated. The assessment of the wood volume of such accumulations might be challenging, and uncertainty might be high (Spreitzer et al., 2020; Thevenet et al., 1998). Some of the observed wood volumes V_obs were also determined based on forest loss areas, for which a pre-event forest density value W must be assumed. In the analysis made with the GIS models, the forest density raster map of Ginzler et al. (2019) was used, which may differ from values used during the post-event surveys. Furthermore, the time gap between a LW-transporting flood event and the survey year from which the forest density map is derived needs to be accounted for. Depending on this relationship, wood volumes may be underestimated (i.e. survey year after flood event) or overestimated (i.e. survey year before flood event). This circumstance could also explain why, in some cases of the FGA calculations, the potential wood volume is even smaller than the observed wood volume ($V_{\text{obs}}/V_{\text{pot}}$ > 1; see Fig. 10a). This discrepancy appeared mostly in one large catchment (i.e. Chirel) and its subcatchments (i.e. Fildrich, Goldbach, Rütigrabe) and could be related to the forest density data used to compute the wood supply volumes, which were computed with the forest after the large flood in 2005.

The observations we used remain a unique and extensive dataset (Steeb et al., 2019a), which allowed us to parametrize the models more accurately. The EGA uses empirical volume reduction factors that were derived from this dataset for the conversion of V_pot to V_est. In the case of debris flows, for example, the volume reduction factors f also rely on an event analysis of the August 2005 flood in Switzerland by Rickenmann et al. (2008), who showed that, on average, 11 %–19 % of all torrents in the main investigated mountain river catchments were associated with debris flow activity. This percentage range was used to define the reduction factors as shown in Table 2. This highlights the importance of in-depth post-flood event analyses, as these provide valuable empirical datasets that can be used to validate and further develop models to estimate supplied LW volumes. The application of models should not replace fieldwork surveys, but they should be used in a complementary manner.

Another source of uncertainty is given by the SilvaProtect-CH trajectories. Since their input data, in particular geology, provide a large-scale representation of natural conditions (see text in the Supplement), the SilvaProtect-CH trajectories are best suitable for use in a catchment-scale range. Furthermore, SilvaProtect-CH trajectories generally result in a pessimistic picture under unfavourable conditions (e.g. no consideration of the stabilizing influence of vegetation cover). As a consequence, only a small part of the trajectories is expected to be active during rainfall and consequent floods. In addition, the actual runout zones of mass-wasting processes may often be shorter than the modelled trajectories.

One important limitation of the EGA and FGA models presented in this study is that the available input forest cover does not provide any further information about the forest typology, structure, and species composition. Despite the role that differences in forest may play in stabilizing the soil and slopes and in influencing bank erosion and hillslope stability (Gasser et al., 2019), the two methods do not explicitly consider this effect. Moreover, the type, structure, and stage of forest stand control the extent to which trees can be uprooted and recruited and supplied to rivers (Mazzorana et al., 2009; Ruiz-Villanueva et al., 2014c). This aspect was described as the vegetation resistance defined by Ruiz-Villanueva et al. (2014c) based on the tree species and forest stage, the structural classification of forested areas made by Blaschke et al. (2004), and the availability indicator used by Mazzorana et al. (2009). Unlike in the approach used by Franceschi et al. (2019) or Gasser et al. (2018), who detected individual trees from high-resolution lidar data, in our case there was no information available with the spatial resolution required to take account of the dimensions, proportion of different species, the stage (e.g. remnant or reforested), or the age of the forest stand. Neglecting the different response of different forest types may result in an overestimation of supplied volumes.

As discussed above, modelling and quantification of wood supply volumes is characterized by many uncertainties. After all, the two models presented in this study allow quantification of the magnitude of the expected LW supply; thus further expert judgement and knowledge of local (geomorphic) characteristics are required to adequately interpret the results. The ratio between predicted and observed LW volumes varies by about 1–2 orders of magnitude. For comparison it is noted that a similar or even larger range of uncertainty can be expected for the estimation of bedload volumes transported during floods (e.g. Rickenmann and Koschni, 2010).

5.4 Implications for hazard assessment and river management

From a practical perspective, geospatial LW modelling results can be used for hazard assessment, infrastructure design, and the definition of management strategies. From a scientific perspective, further applications are possible. For example, estimated wood volumes can be applied as input for a wood transport model, such as Iber-Wood (Ruiz-Villanueva et al., 2014a, b, 2015) or other approaches (e.g. Mazzorana et al., 2011), to define realistic boundary conditions. Furthermore, if no observation data are available for reference, estimated wood volumes from the EGA and FGA can be used to quantify blocking probabilities due to LW at bridge piers or at other critical cross-sections (Schalko, 2019; Schalko et al., 2018; Schmocker and Weitbrecht, 2013).

As described in Sect. 4.2, the average proportion of instream deadwood (instream wood load) from the total potential LW supply in the 40 test catchments ranged between 2 %–13 % (Fig. 6). This range is confirmed by other studies and event analyses (Dixon, 2013; Rickli et al., 2018; Waldner et al., 2009). It can be concluded that instream deadwood generally accounted for only a small proportion of the total LW transported during past floods in Switzerland. Rather, it is freshly recruited wood that made up the majority of the transported wood volumes. Deadwood alone, both on the forest floor and in the channel itself, may therefore only lead to a limited increase in risk from a natural-hazard-management perspective. As a consequence, the artificial removal of deadwood from the stream and its surroundings is not always necessary, keeping in mind the ecological benefits of instream wood.

The EGA and FGA are area-wide products that can be applied in any Swiss catchment. They use a standardized procedure and nationwide homogeneous data, which facilitates a comparison between catchments (FOEN, 2019). The methodology is flexible and can be adapted to other regions outside Switzerland if recruitment processes (especially with regard to SilvaProtect-CH trajectories) were modelled with more generic approaches.

Both models have already been used by practitioners for some engineering applications. One limitation that has been identified by some practitioners is the use of licensed software, as both the EGA and FGA have been developed in ESRI software and require some advanced licenses that may not always be available to private companies. Future developments may consider the migration to open-source software.

Furthermore, there is still a need to analyse and model the propagation of LW through the river network, for example by applying hydraulic modelling (e.g. Ruiz-Villanueva et al., 2014a, b) or the recently proposed network approaches such as those applied to sediment transfer (Finch and Ruiz-Villanueva, 2022).

The two models presented here correspond to a hazard index mapping in terms of processing depth and degree of detail for a hazard assessment. The geospatial modelling results indicate areas of potential LW recruitment, however without precise information on the intensities occurring or the transfer and propagation through the river network. In contrast, the estimated LW supply for the large scenario is based on the data of events with a return period of approximately 50 to 150 years. The approach presented here is a useful tool to give a comprehensive overview and direct attention to areas where a more precise assessment of the LW situation is probably useful, for example in connection with an estimation of sediment loads in torrents.

6 Conclusions

Two GIS-based models are presented in this contribution to identify large-wood (LW) sources and to estimate LW supply to rivers. Both models, called the empirical GIS approach (EGA) and fuzzy-logic GIS approach (FGA), consider landslides, debris flows, bank erosion, and mobilization of instream wood as recruitment processes. The results are volumetric estimates of LW supply based on three different scenarios of process frequency and magnitude. Results of model applications to 40 Swiss catchments were used to compare both the two models with each other and the performance in relation to observed (empirical) LW volumes. Further, a literature review of existing LW supply models proposed in the last 35 years was conducted and set into context, and remaining challenges were identified.

The EGA shows significantly higher values for potential LW supply. However, after reducing the potential volume with different methods, estimated LW supply volumes are of the same order of magnitude for both models, with the FGA showing generally somewhat larger values. In the case of the EGA, landslides are the dominant recruitment process, whereas bank erosion is dominant for the FGA. Both models show under- and overestimation of observed wood volumes V_obs, with more tendency for overestimation. Overestimation stays generally within 2 orders of magnitude (typically larger values for the FGA), and underestimation stays within 1 order of magnitude (typically smaller values for the EGA).

The modelling and quantification of wood supply volumes are characterized by many uncertainties. After all, the two models presented in this study allow quantification of the magnitude of the expected LW supply; thus further expert judgement and knowledge of local (geomorphic) characteristics are required to adequately interpret such results. LW supply modelling can be further improved by integrating more physically based and/or probabilistic inputs for the spatial identification of recruitment processes. Likewise, the parametrization and validation of LW supply models remain complex. Post-flood event analysis provides valuable empirical datasets that can be used to validate results and further develop LW supply models that can be useful for hazard assessment, infrastructure design, and the definition of management strategies.