Initial shape reconstruction of a volcanic island as a tool for quantifying long-term coastal erosion: the case of Corvo Island (Azores)

Long-term coastal erosion is not yet well studied given that it is difficult to quantify. The quantification of long-term coastal erosion requires reconstruction of the coast's initial geometry and the determination of where and when the erosion started. Volcanic islands fulfill these two conditions: their initial shape is roughly conical and the age of the lavas that generated this geometry is easily measured. We have developed a method to reconstruct the initial shape of simple volcanic edifices from aerial and submarine topographic data. The reconstructed initial shape and associated uncertainties allow us to spatially quantify the coastal erosion since the building of the island. This method is applied to Corvo Island in the Azores archipelago. We calculated that, due to coastal erosion, the island has lost a volume of 6.5 ± 2.7 km³ and roughly 80 % of its surface area since it first came into being. Taking the large uncertainty in the age of the topmost lava flows (0.43 ± 0.34 Myr) into account, we have estimated that Corvo Island has lost an average of 5000 to 100 000 m³ yr⁻¹ of its volume due to coastal erosion. Lastly, we show a strong correlation between long-term coastal erosion and the spatial distribution of the waves. Specifically, we highlight a stronger control on erosion by smaller and more frequent waves than by storm waves. The next step will be to apply this method to other volcanic islands in order to (i) streamline and improve the method and (ii) verify the correlations observed in the present study.

1 Introduction

One of the major material fluxes on the Earth's surface is the flux of material from the continents to the ocean. This flux results mainly from the weathering and erosion of continental surfaces by precipitation, glaciers, and winds and the transport of this eroded material by rivers, glaciers, and winds to the ocean, where it can be deposited. The study of this flux is of primary importance because it is directly linked to the rate of renewal of continental surfaces and to a significant part of the supply of particles and dissolved elements to the ocean (Martin and Whitfield, 1983; Milliman and Meade, 1983; Tréguer et al., 1995; Syvitski et al., 2003; Viers et al., 2009; Milliman and Farnsworth, 2013). This flux conditions geochemical cycles on a global scale and over long timescales (> 10 kyr) (e.g., Kronberg, 1985; Raymo et al., 1988; Schlünz and Schneider, 2000). Part of this material flux to the ocean is generally neglected: the input of material from coastal erosion. This flux is difficult to quantify on a global scale and has been estimated to be approximately 1 % of the material input by rivers (Huggett, 2008).

Recent studies have revisited the quantification of this flux and have shown that the sediment input to the ocean from coastal erosion can be significant and even locally exceed the sediment input from rivers (Rachold et al., 2000; Landemaine, 2016; Regard et al., 2022). It is therefore possible that the material flux from the continent to the ocean produced by coastal erosion has been far from negligible on a global scale and over long timescales.

It is therefore necessary to quantify coastal erosion over large timescales and space scales in order to integrate this parameter into geochemical, geodynamic, and paleoenvironmental models.

Coastal erosion has been studied almost exclusively on a short-term timescale of less than 1 century and under a temperate climate (Prémaillon et al., 2018; Young and Carilli, 2019) by a comparison of the cliff top position over time (e.g., Moses and Robinson, 2011; Dewez et al., 2013; Rosser et al., 2013; Letortu et al., 2015; Costa et al., 2019; Prémaillon et al., 2021). Over the long term, i.e., over thousands to millions of years, it is more complicated to quantify coastal erosion because geomorphic markers may have been eroded and are poorly dated (Bird, 2011). In order to fill this gap in knowledge, cosmogenic nuclides have been applied along cross-shore profiles in order to quantify the mean rate of cliff retreat (e.g., Regard et al., 2012; Hurst et al., 2016; Raimbault et al., 2018). These approaches are promising but give a local millennial mean retreat rate, require the presence of a large and accessible shore platform, and demand a long analytical process. A complementary approach consists of evaluating the topography difference from the reconstructed topography in different epochs. This measure of erosion rate requires the quantification of the eroded volume and the time over which the erosion occurred. The ideal configuration consists of a monogenic massif whose age and initial geometry are known. This ideal configuration is rare (Bird, 2011) but can be, however, found on volcanic islands (e.g., Quartau et al., 2010; Huppert et al., 2020).

The coastlines of oceanic volcanic islands have the advantage of having been established at a well-defined time, during the emergence of a volcano (Ramalho et al., 2013), with a young, non-eroded, regular shape (Karátson et al., 2010). In addition, its end is relatively predictable, with the disappearance of the island under subsidence or erosion (Ramalho et al., 2013). It is also plausible to reconstruct the paleo-topography of volcanoes (Karátson et al., 2010; Lahitte et al., 2012; Favalli et al., 2014; Karátson et al., 2016).

Volcanic islands are widespread across the world. An automatic quantification of the eroded volume by coastal erosion would make it possible to study the influence of factors such as climate or geodynamics on this erosion and hence to determine their relative importance with regards to long-term coastal erosion. In the present work, we propose an approach to reconstruct the initial aerial and submarine volcano island topography and to calculate the eroded volume by coastal erosion.

2 Background and hypotheses

In this study, “initial” shape refers to the theoretical surface of the volcanic island at the time of its maximum subaerial extent. In terms of timing in the history of the island, this maximum extension corresponds to the transition from the growth phase to the degradation phase of the edifice. During the growth phase, volcanic progradation, with the formation of lava deltas, extends the shoreline (Ramalho et al., 2013) and dominates the erosive processes, whereas during the degradation phase, erosive processes become predominant (Ferrer-Valero and Hernández-Calvento, 2020). We consider that this transition marks the point in time when the coastal erosion began. It is hard to know whether this transition is gradual or abrupt, and dating this moment is difficult. This moment likely follows the setting of the flows constituting the top of the sea cliffs, and thus the age of these flows indicates the age of the initial shape. Therefore, we disregard the young flows that mostly fill the existing valleys, creating deltas, which in turn are rapidly eroded (see Discussion). The initial silhouette is marked by a break in slope at sea level, at the transition between the aerial and submarine areas (e.g., Ramalho et al., 2013), which we will later refer to as IE.

Numerous authors (e.g., Urgeles et al., 1999; Mitchell et al., 2003; Hildenbrand et al., 2008; Germa et al., 2010, 2015; Lahitte et al., 2012; Salvany et al., 2012; Lavigne et al., 2013; Torrecillas et al., 2013; Ricci et al., 2015a, b; Karátson et al., 2016) have proposed various methods for reconstructing the initial onshore shape of volcanic islands. These methods are based on the analysis of the onshore topography and spatial distribution of geological units on a volcanic island. These methods consist of determining which geological units and which part of the current topography of a volcanic island are representative of its maximum extent and initial shape. Then, using topographic data, the initial edifice topography can be reconstructed either by kriging interpolation (e.g., Hildenbrand et al., 2008; Germa et al., 2010) or by using a synthetic solid of revolution for the 3D geometry if the island is radially symmetric (e.g., Karátson et al., 2016).

The aim of these methods is to quantify the total aerial erosion of each studied volcano in order to establish the geomorphological evolution of these volcanoes. When applied to volcanic islands, these methods reconstruct the edifice down to the intersection with the sea level and can be used to estimate the maximum island extension. However, volcanic island edifices are not limited to their aerial part. As a result, the methods that reconstruct the volcano morphology ignore the submarine geomorphology. Yet, the submarine realm of volcanoes offers other constraints to better reconstruct the initial edifice geometry and to quantify coastal erosion (Quartau et al., 2010, 2014, 2015; Quartau and Mitchell, 2013).

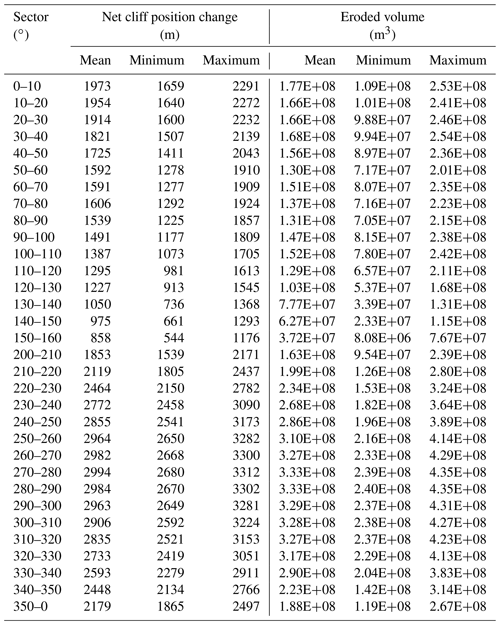
In many settings, coastal erosion results in the formation of an erosional shelf below sea level and a coastal cliff above sea level (Trenhaile and Bryne, 1986; Sunamura, 1992; Anderson and Anderson, 2010; Quartau et al., 2010, 2018; Ramalho et al., 2013). The junction between the shelf and the cliff corresponds to the base of the coastal cliff; this will be referred to as the shoreline angle (SLA) (Fig. 1). The vertical position of the SLA does not depart from the current mean sea level by more than a few meters (Wright, 1970; Trenhaile, 1972; Anderson and Anderson, 2010). As they approach the coast, the waves conserve their energy until they break. From this point on, the energy of the swell is dissipated: one aspect of this dissipation is erosion of the bedrock to about 10 m below sea level (Dietz and Menard, 1951; Trenhaile, 2000, 2001; Sunamura, 2021). The erosional feature formed during the present-day sea level by wave action therefore has a theoretical depth ranging from around 0 m at the coast to about 10 m at the edge, and it is called a shore platform. The variations in sea level can cause the formation of a series of platforms which can be called a shelf (Fig. 1). In this case, each platform is called a marine terrace. At the coast, the waves weaken the cliff base through a variety of phenomena, leading to a stochastic gravitational collapse over time. The mechanics of the cliff collapse process are beyond the scope of this study. We assume that cliff collapse occurs frequently at the millennial timescale. Thus, the succession of gravitational collapses results in cliff retreat, which may be related to wave energy (e.g., Trenhaile, 2001; Anderson and Anderson, 2010; Ramalho et al., 2013; Huppert et al., 2020; Zhao et al., 2020; Young et al., 2021).

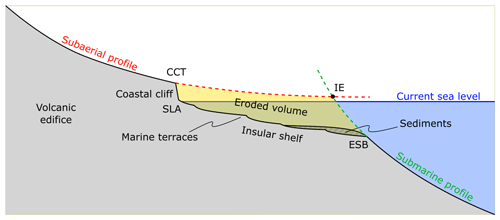
Figure 1 Schematic representation of a radial topographic profile of a volcanic island. The initial aerial and submarine profiles are demarcated with dashed lines. CCT: coastal cliff top. SLA: shoreline angle. ESB: erosional shelf break. IE: initial extension. Note the presence of marine terraces, corresponding to different low eustatic levels, and sediments on the insular shelf.

In the case of volcanic islands, the erosional shelf that generally surrounds the aerial part of the volcanic edifice is called an insular shelf (e.g., Quartau et al., 2010; Ramalho et al., 2013). The inner bound of this shelf is the base of the coastal cliff and its outer bound is the shelf break. This latter is characterized by a rapid increase in the slope from a few degrees on the shelf to a greater slope seaward; the threshold is sometimes fixed to 15^∘ (Quartau et al., 2010). The depth of the shelf break theoretically corresponds to the limit of wave action during the lowest relative sea level the island has experienced (Quartau et al., 2010; Ramalho et al., 2013). If the island is older than the Last Glacial Maximum (LGM) and its vertical displacement is negligible, the depth of the shelf break is theoretically around 130 m, i.e., LGM level (around 120 m) plus wave action limit (around 10 m) (Shepard, 1973; Yokoyama et al., 2000; Trenhaile, 2001; Quartau et al., 2010). If the shelf edge has been covered by sediments or by volcanic progradation, the apparent depth of the shelf break is reduced; in this case, the shelf break is called a depositional shelf break (DSB) (Quartau et al., 2010). By contrast, if it has not been covered by any material, it is called an erosional shelf break (ESB) (Quartau et al., 2010). Data suggest that sediment deposits do not progress much further than the ESB, which marks a significant change in the slope (Quartau et al., 2010).

In summary, the range of coastal erosion is spatially limited by the ESB on its ocean side and by the cliff up to its top (coastal cliff top or CCT) on its land side (Fig. 1). It is possible to consider that the aerial part of the volcanic edifice above the CCT is only subject to fluvial erosion, whereas the submarine part of the edifice below the ESB (Fig. 1) is not subject to erosive processes except for gravitational collapses at the shelf edge, which may form an embayment (Ramalho et al., 2013; Chang et al., 2021) and headwall retreat of canyons that develop on the submarine slopes (Krastel et al., 2001; Casalbore et al., 2017; Quartau et al., 2018).

For edifices with a radial symmetry, the topography can be subdivided into one aerial and one submarine radial profile (Mitchell et al., 2002). Following the models of Peterson and Moore (1987), DePaolo and Stolper (1996), and Ramalho et al. (2013), we can estimate the volcano aspect before coastal erosion via two extended radial profiles. The first one is aerial; it runs from the volcano center to the CCT. The second profile is submarine, below the ESB (Fig. 1). These two profiles intersect at a point called the initial extension (IE), which corresponds to the theoretical original boundary between the aerial and submarine parts of the edifice.

Theoretically, the IE must be located near the sea level at the time of volcanic island building. Thus, the IE could also serve as a proxy for estimating the net relative sea level change experienced by the island since its formation. This vertical motion estimation is relative to the sea level, and consequently, it is highly dependent on the eustatic sea level at the time of volcanic activity. The sea level at this time can be estimated through sea level curves (Shackleton, 2000; Waelbroeck et al., 2002; Bintanja and van de Wal, 2008; Rohling et al., 2009; Spratt and Lisiecki, 2016) but nevertheless requires that the volcano age is precisely known, which is quite challenging.

Coastal erosion is traditionally measured by a value of total horizontal retreat (in m); it can be derived as a rate per unit of time (m yr⁻¹). However, over the long term, coastal erosion will not affect the same area of the coast depending on the relative sea level (Huppert et al., 2020). For example, during a sea level highstand, i.e., during an interglacial period, coastal erosion occurs mostly horizontally via coastal cliff retreat, whereas during sea level fall or lowstand, i.e., during a glacial period, coastal erosion mainly affects the erosional shelf, in such a way that its surface appears to move downward (Ramalho et al., 2013, Fig. 8). As a result, when the eustatic level is intermediate, the already carved shelf is newly eroded, possibly forming marine terraces, without retreat of the coastal cliff (Fig. 1). Therefore, the total retreat of the coastal cliff, i.e., the shelf width, cannot be a proxy for the total amount of coastal erosion (e.g., Huppert et al., 2020), and consequently, we cannot use the horizontal measurement to accurately quantify the long-term coastal erosion rate. Nevertheless, the net cliff position change can be an indicator of the minimum coastal retreat and of the radial distance above the cliffs lost by erosion. However, using the topographic reconstruction of the initial shape of volcanic islands, we can calculate a total eroded volume by coastal erosion (Fig. 1). We will therefore use the eroded volume as a metric to quantify long-term coastal erosion on volcanic islands: one advantage of this is that it lumps together various types of erosion due to various processes (e.g., sea cliff erosion, vertical erosion of the seabed in the surf zone, or landslides/gravity failures).

3 Method

3.1 Workflow and preliminary comment

This method aims to quantify the volume of material removed by coastal erosion on volcanic islands. The method steps are as follows (Fig. 1):

• We assume a radial symmetry of the island or part of it and determine its center.

• We reconstruct the pre-erosion aerial topography of the island along a global aerial radial profile, including all topographic data on the aerial part of the island.

• We reconstruct the submarine topography of the island along a global submarine radial profile, including all bathymetric data around the island.

• The intersection between the aerial and submarine profiles allows us to calculate an eroded volume and its uncertainty according to the uncertainties in reconstructed aerial and submarine topographies.

Compared to the measurement of the shelf width (e.g., Quartau et al., 2010), this method is used not only to calculate an eroded volume and its uncertainty but also to provide evidence that portions of the shelf have possibly been lost due to gravity collapses. Indeed, if the reconstructed IE is further from the center of the island than the ESB, this may indicate that the edge of the platform has collapsed, causing a retreat and elevation of the apparent position of the ESB.

Because it is based on topographic reconstruction, this method relies on a long-term integrative view of coastal erosion and does not aim to represent the complex geomorphological evolution of coastal cliffs and insular shelves related to the interplay between the processes involved (Ramalho et al., 2013). In order to provide a standard workflow that can be easily applied to a large number of study sites (with easy adaptations according to specific available topographical and geological data), the method is based on simple and intentionally reductionist working hypotheses and at the same time on a careful estimation of the uncertainty in eroded volumes that would be less constrained by considering only the aerial topography alone. Some of the hypotheses can be adapted according to the available data. For example, the hypothesis of complete radial symmetry of the volcanic edifice adopted to treat the following illustrative case study is not mandatory for our approach. For other islands, radial symmetry can be assumed for only a portion of the island. This flexibility should allow us to compare coastal erosion values between the different sites where the method is applied.

We illustrate this method using the simple case of Corvo Island.

3.2 Choice of island

The method proposed here is based on the hypothesis of a simple geometry of volcanic edifices. This method is therefore preferentially applied to volcanic islands composed of a single central edifice that is roughly conical in shape with a dominant radial symmetry, similar to many stratovolcanoes (Karátson et al., 2010). Alternatively, it can be applied to a portion of an island that meets these criteria. Suitable islands for this method might be mainly young volcanic islands with a simple and known volcanic history. Another selection criterion is the availability of high-resolution aerial and submarine topographic data. These two data sets are necessary to reconstruct the initial aerial and submarine profiles of the island and to determine the maximum extension of the island. For the aerial part, a 30 m resolution global elevation database (e.g., SRTM1, ASTER, ALOS) is sufficient to capture the geometry of volcanic islands with a diameter larger than 1 km. By contrast, global bathymetric databases, such as GEBCO, only offer a 500 m horizontal spacing of the grid nodes, which is insufficient to account for the submarine geometry of the edifice and to clearly identify an insular shelf. High-resolution bathymetric data around the island are therefore necessary to clearly identify the boundary between the insular shelf and the non-eroded submarine slopes of the volcanic edifice.

3.3 CCT and ESB mapping

It is quite simple to identify the coastal cliff top (CCT): it is generally a marked break in slope on the edges of the island. It can be mapped on satellite imagery as well as on topographic data except, for example, when this break in slope is smoothed by strong aerial erosion. The CCT corresponds to the inflection point where the slope starts to increase oceanward.

The ESB corresponds to a gentler break in slope than the cliff top; it instead corresponds to a smooth transition, tens to hundreds of meters wide, from a slope of a few degrees on the insular shelf to a slope of a few tens of degrees on the submarine slopes of the volcanic edifice. Sedimentation on the platform may cover the ESB such that only seismic imagery can be used to identify the ESB (Quartau et al., 2010, 2012). However, given the scarcity of such data, the ESB is determined from the shelf morphology. Using seismic and topographic data, Quartau et al. (2010) determined that, on the Azores, the ESB corresponds to an absolute maximum slope threshold of the insular shelf edge of 15^∘. Therefore, we decided to follow Quartau et al. (2010) and extract the slope map from the bathymetry raster to locate the ESB on the edge of the insular shelf where the slope becomes greater than 15^∘ seaward. Since this transition is usually abrupt, the ESB's position is unequivocal.

The mapping of the CCT and ESB results in two concentric polygons (Fig. 2). The area in between these polygons is identified as being the area where coastal erosion takes place. The area outside this area is considered to have been little altered by erosion, and therefore it is still very close to the initial shape of the volcanic edifice: its aerial part, with the exception of the caldera, corresponds to the initial aerial volcano shape; its submarine, outside, part represents the initial submarine shape.

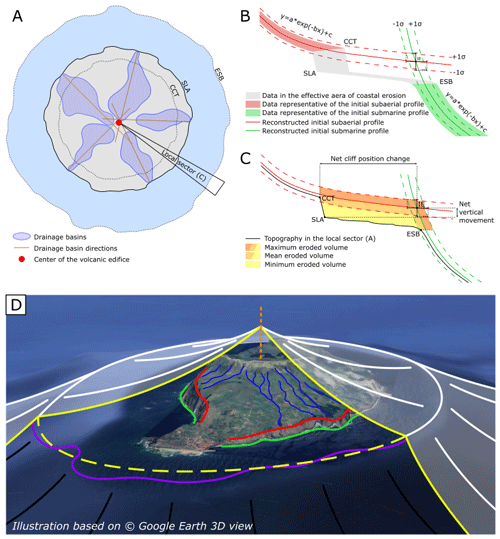
Figure 2 Topographic reconstruction method. (a) Mapping of the CCT and ESB markers and the determination of the center of the edifice. Overhead view. (b) Calculation of the radial aerial and submarine topographic profiles representative of the initial shape. (c) Quantification of the net cliff position change, eroded volume and vertical movement. (d) Illustration of the topographic reconstruction applied to Corvo Island (based on © Google Earth 3D view), as an example to better visualize the eroded volume below the reconstructed shape (yellow) and between the CCT (red) and the ESB (purple).

3.4 Determination of the center of the volcanic edifice

In the following, it is necessary to determine the horizontal position of the center of symmetry of the volcanic edifice. This point does not necessarily correspond to the center of the central crater. One solution is to calculate the barycenter of the concentric elevation contours, but this method is only applicable for very regular edifices that have experienced very little erosion (Karátson et al., 2010). Instead, we have chosen here a second method developed by Favalli et al. (2014) to determine the center of Mount Somma (Italy), a highly eroded edifice of which only the northwestern part of the slopes remains. This method determines the position of the center of the edifice as the center point of the radial drainage network (Fig. 2). The contours of the watershed are determined based on topographic data. The highest point of the watershed and its outlet are then extracted: the watershed direction is defined as the line connecting the two points. The directions of the different watersheds intersect in the summit area of the island. The center of the volcanic edifice is then defined as the barycenter of all intersection points of all watershed directions.

3.5 Radial distance–elevation profiles

Once the center of the edifice is determined, the distance of each point in the aerial and submarine topographic data to the center is calculated. This is used to represent the elevation of each data point as a function of its distance to the center and to collapse all these points into a radial profile. It also allows us to calculate two best-fit regression curves: one for the aerial points inside the CCT and one for the submarine part outside the ESB (Fig. 2). Following the work of Karátson et al. (2010, 2016) and Favalli et al. (2014), we fit the aerial topographic data with a decreasing exponential because it is best suited for the type of volcano we are interested in, i.e., initially radially symmetric stratovolcanoes (Favalli et al., 2014; Karátson et al., 2016). The exponential profile was originally noted by Gee et al. (2001) but without a theoretical explanation. Here we assume that, similarly to the aerial profile, the submarine topographic profiles follow an exponential function.

The general form of the regression using the exponential function is

$$\begin{array}{}\text{(1)}& y=a{e}^{-bx}+c,\end{array}$$

where y is the elevation, x is the distance to the center of the edifice, and a, b, and c are the parameters of the equation. The uncertainty is propagated by calculating the bounds of this regression at ±1σ, with $y+\mathrm{1}\mathit{\sigma }=y+\mathrm{\Delta }y$ and $y-\mathrm{1}\mathit{\sigma }=y-\mathrm{\Delta }y$. Δy is calculated by taking the total derivative of y according to a, b, and c, leading to the following equation:

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }y=e^{-bx}\mathrm{\Delta }a+x{e}^{-bx}\mathrm{\Delta }b+\mathrm{\Delta }c,\end{array}$$

where Δa, Δb, and Δc are the respective residual standard errors in the parameters a, b, and c. The intersection of both the aerial and submarine exponential radial profiles estimates the position of the geomorphic marker IE. The intersections of the ±1σ bounds result in the estimation of both vertical and horizontal uncertainties in the position of the IE (error envelope in Fig. 2).

3.6 Quantification of the eroded volume, net cliff position change, and vertical movement

The calculated radial profiles can be converted into a synthetic initial shape by creating a surface of revolution, i.e., rotating the profile around the radial axis of symmetry that is the center of the edifice (Lahitte et al., 2012; Favalli et al., 2014; Karátson et al., 2016). The total eroded volume of the island can be calculated by the difference between the calculated initial topography and the current topography, for the whole island or by angular segments around the island. The eroded volume related to the coastal erosion corresponds to the part of this calculated volume contained in between the horizontal position of the CCT and the depth of ESB (Fig. 2), considering the spatial variations in the CCT and the ESB around the island and provided that the island has not experienced sea levels occupying elevations above the CCT or below the ESB. The uncertainty in the altitude of the profile (Δy) is typically on the order of 10 to 100 m. This uncertainty takes into account the imperfection of radial symmetry; a deviation from radial symmetry results in a greater vertical dispersion of points in the radial profile. Radial symmetry can be considered sufficient if the uncertainty domain of the IE position remains above the insular shelf, i.e., constrained between the horizontal position of the CCT and the depth of the ESB. We will see that these assumptions are confirmed in the case of Corvo Island (Sect. 5.2).

The volume below the calculated −1σ profile is the minimum eroded volume, the volume below the calculated mean profile is the mean eroded volume, and the volume below the calculated +1σ profile is the maximum eroded volume (yellow to salmon colors in Fig. 2). Therefore, it is possible to quantify a total eroded volume related to the coastal erosion. It is also possible to further spatially quantify the degree to which the calculated eroded volumes depend on the position at the edge of the island (with respect to the center of the island, denoted “sector” in the following). Moreover, we can also measure the different net cliff position changes around the island, by measuring the horizontal distance between the IE and the CCT. Lastly, the difference between the calculated IE elevation and the current sea level could be used to estimate the total subsidence or uplift (relative to the past sea level at the time of the initial shoreline formation) that the island has experienced, with the uncertainty in the vertical error bar of the IE. Figures 3, 4, and 5 illustrate the topographic reconstruction and quantification processes for the real case of Corvo Island.

4 Corvo Island setting and available data

4.1 Corvo Island

The Azores are a volcanic archipelago located in the middle of the North Atlantic Ocean at the junction between the American, Eurasian, and Nubian plates. The archipelago consists of nine main islands; two of them, Corvo and Flores, are on the American plate, and the others are on the wide border between the Eurasian and Nubian plates. These islands are quite young (2 Ma to the present, except Santa Maria Island which is 6 Myr old; see Feraud et al., 1980), modest in size (several kilometers to tens of kilometers wide), and of modest elevation (several hundred meters), with the exception of Pico Island, the elevation of which exceeds 2 km. The archipelago is characterized by a temperate oceanic climate. However, in this region, autumn and winter are marked by frequent storms, characterized by a strong wave regime from the west and northwest (Rusu and Guedes Soares, 2012). The Azores are frequently impacted by these storms, especially as the temperate climate prevents the development of protective coral reefs (Quartau et al., 2012). The tidal range in the archipelago is less than 2 m (Ávila et al., 2005).

Because of their modest elevations, the Azores do not generate considerable orographic rainfall and therefore the relics of their initial aerial volcanic morphology are still relatively well preserved (Ramalho et al., 2013). This makes it possible to reconstruct their geological and morphological history (Quartau et al., 2014). In addition, the oceanic climate and frequent storms expose the archipelago to strong coastal erosion, resulting in the formation of large coastal cliffs. These characteristics make the Azores a prime location for the study of coastal erosion and the evolution of coastal morphology on volcanic islands (Quartau et al., 2010, 2012, 2014, 2018; Ramalho et al., 2017; Melo et al., 2018; Ng et al., 2019).

Corvo is the smallest of the main islands and the northernmost island of the archipelago (Fig. 3). This small island measures approximately 5 km on its north–south axis and 3 km on its east–west axis. It is dominated by a volcanic edifice, the Central Volcano, which reaches 720 m in elevation and whose caldera measures approximately 2 km in diameter. The last stage of this edifice, which gives its general shape to the island, was formed 0.43 ± 0.34 Myr ago and is composed of alkaline basalts (K–Ar dating; Dias, 2001; França et al., 2006). Another smaller and younger edifice, forming parasitic cones, has developed on the southern slope of the island, overlying the older volcanic morphology of the central volcano. Its last eruption occurred 80–100 kyr ago (Dias, 2001; França et al., 2002, 2006). The island's coastline is almost exclusively made up of very high coastal cliffs, ranging from 150–200 m high in the east to more than 600 m in the west, except in the south, where the coast consists of a lava delta from the youngest edifice. This coast has been anthropized via the installation of coastal infrastructures and an airfield (França et al., 2002; Pacheco et al., 2013).

Figure 3 (a) Location of Corvo Island. (b) Corvo Island seen from the southeast (© Google Earth 3D view). C: topographic shaded relief map of the volcanic edifice of Corvo (ASTER and EMODnet data). White line: study area. Black line: ESB. Green line: coastline, SLA. Red line: CCT. Yellow line: edges of the central volcano caldera. Blue lines: drainage network on the slopes of the central volcano. Gray dot: center of the volcanic edifice.

The insular shelf surrounding Corvo Island has a quasi-circular shape approximately 8 km in diameter, roughly centered on the central volcano crater (Fig. 3). The absence of large concavities on the rim of this shelf suggests that the island has not experienced any major collapse since its formation, unlike neighboring islands such as Faial Island or Pico Island (Costa et al., 2015; Marques et al., 2021) and numerous volcanic edifices (Holcomb and Searle, 1991). The general aerial shape of the central volcano as well as the shape of the insular shelf therefore suggest that Corvo Island is made up of a single, radially symmetric central volcanic edifice (apart from the parasitic southern cones) with a radius of approximately 4 km (Melo et al., 2018). The presence of high coastal cliffs confirms the major role of coastal erosion in the morphological evolution of Corvo. This makes Corvo Island an ideal case for testing our approach.

In order to satisfy the working hypothesis of one single, radially symmetric volcanic edifice, our study excludes the southern sector of the island, between the directions 160 and 200^∘ N with respect to the center of the edifice (Fig. 3), containing the younger parasitic cones. Our analysis extends up to a distance of 10 km from the center of the edifice, which corresponds approximately to the geographic boundary of the submarine edifice.

4.2 Data

The method has been designed to be broadly applicable, and therefore we preferred the use of global topographic data. We decided to use ASTER topographic data, which have a horizontal resolution of 1 arcsec or approximately 30 m.

The global GEBCO data are too coarse in resolution to identify the contours of the insular shelf. As a result, we used the EMODnet database. This database covers the entire European territory, of which the Azores are part, and offers aerial and submarine topographic data around Corvo with a horizontal resolution of 150 to 200 m per pixel, which is sufficient for our analysis.

These different data sets are initially delivered in longitude/latitude in the WGS84 datum. To rectify the deformations induced by this coordinate system, we have re-projected the data onto UTM (zone 25N, WGS 72 datum; Fig. 3).

5 Results

5.1 Location of the CCT, ESB, and the center of the volcanic edifice

The center of the island (39.7056^∘ N, 31.1111^∘ W), determined from the analysis of the drainage network within the CCT polygon, does not correspond precisely to the center of the central volcano caldera, it is located slightly further to the south (Fig. 3).

The coastal cliff top (CCT) has a complex shape, with a marked protrusion to the southeast. This shape does not appear to be centered on the defined center of the edifice; its centroid is noticeably to the southeast of it. The CCT is located between 800 and 3000 m from the center of the edifice (from west to southeast, respectively) (Fig. 3).

The shape of the erosional shelf break (ESB) looks more like a circle with a slight north–south elongation. It has a radius of approximately 4000 m, and it is almost centered on the center of the edifice (Fig. 3). The mean depth of the ESB in our study area is 107.25 m below current sea level.

5.2 Topographic reconstruction

Figure 4 shows the radial elevation profiles of the ASTER and EMODnet data points. The radial profiles are demarcated by two point clouds with relatively low dispersion, reflecting a strong radial symmetry of the edifice. However, we notice a prominence above the point cloud roughly 1500 m north from the center of the edifice. This topographic anomaly corresponds to the northern edge of the main crater and does not seem to have been noted in previous geomorphological studies on Corvo. The parameters of the regression and associated uncertainties (Eqs. 1 and 2) are reported in Table 1. Vertical uncertainties (Δy) are of the order of ±70 m for the aerial fit and ±50 m for the submarine fit. The two curves intersect at a point (IE) located 3795 ± 318 m from the center of the island and 23 ± 104 m above the current sea level. As discussed previously, the IE indicates the maximum (initial) extension of the island. The IE is shown in purple in Fig. 5. It is obvious that the IE is slightly internal to the ESB contour.

Table 1 Parameters and their residual standard error used in Eqs. (1) and (2) to calculate the initial radial topographic profiles of Corvo (Fig. 4).

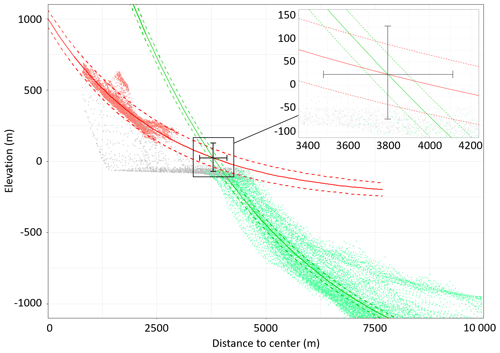
Figure 4 Elevation of the topographic data versus the distance to the center of the edifice and the initial aerial (red) and submarine (green) radial exponential profiles reconstructed with their uncertainty domain. Red dots: elevation grid points in the initial aerial domain; the red dots, found at higher elevations than all the others for the most part, belong to the northern sector. Green dots: elevation grid points in the initial submarine domain. Gray dots: data in the coastal erosion area.

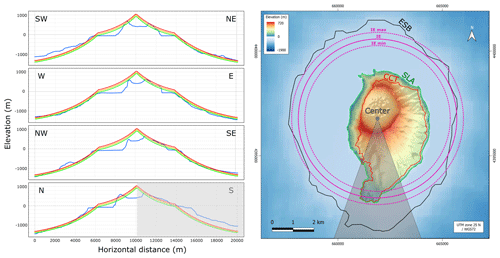
Figure 5 Left: comparison between the present-day radial topographic profiles of the Corvo volcanic edifice (blue lines) and the mean (yellow lines), minimum (green lines), and maximum (orange lines) reconstructed topographic profiles from different directions. Right: similar topographic map to the one provided in Fig. 3 (ASTER and EMODnet data) showing the initial extension of the island (solid purple line) with the uncertainty values (dashed purple lines). The gray area shows the southern sector where the volcanic progradation is located and which has been subsequently discarded for the analysis.

5.3 Eroded volume and surface area lost.

We divided our study area into 10^∘ sectors. For each sector, we calculated the radial horizontal distance between the mean position of the CCT and the position of the IE (“Net cliff position change”) and the eroded volume as the difference between the reconstructed initial topography and the current topography (Table 2). The eroded volumes are presented as a rose diagram in Fig. 6.

Table 2 Net cliff position change and eroded volume calculated by 10^∘ sectors around Corvo Island.

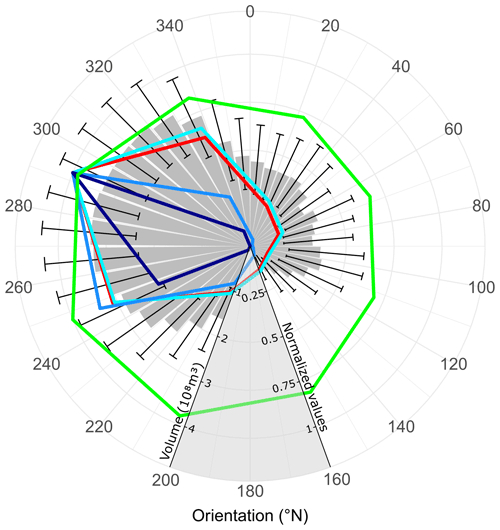
Figure 6 Total eroded volume (gray columns) with respect to direction. The wave data from Rusu and Guedes Soares (2012) are shown in color and in values normalized by their maximum (see Tables 2 and 3 for the detailed actual values). Red: spatial distribution for the waves. Light blue: spatial distribution for the waves with H_s < 5 m. Blue: spatial distribution for the waves with 5 m < H_s < 10 m. Dark blue: spatial distribution for the waves with H_s > 10 m. Green: mean H_s of the waves.

The eroded volume was calculated inside the area between the current horizontal position of the CCT and the current mean depth of the ESB (see the Method section). The calculated volume is only counted when the reconstructed initial topography is above the current topography. Over the study area, i.e., the southern sector of the island is excluded, the total eroded volume by the sea is evaluated as roughly 6.5 ± 2.7 km³. The corresponding surface area eroded by the sea is approximately 37.2 ± 3.6 km² (area between the CCT and ESB). Compared to the current Corvo Island surface area above the cliffs without the southern sector spanning 9.1 km², we infer that the island has lost roughly 80 % of its surface area following coastal erosion and relative sea level change. The sectorization of this eroded volume provides insight into the erosion distribution (Table 2, Fig. 6).

6 Discussion

6.1 Method robustness, limitations, and uncertainties

The use of offshore bathymetry to infer coastal erosion is not new, but it has been limited to a relatively shallow depth (< 120 m) (Quartau et al., 2010; Huppert et al., 2020; Zhao et al., 2020). Mitchell et al. (2003) used the deep submarine topography of the Canary Islands to quantify erosion on the submarine flanks, but they did not try to fit the topographic profiles with a geometrical model. Our approach here takes advantage of all the available offshore topographic data to better constrain the paleo-topographic profiles including the deep part of the island flanks. In particular, we show that the submarine profiles of Corvo Island are consistent with an exponential model, which, to our knowledge, is a novelty of our contribution.

Theoretically, the calculated aerial exponential profile is close to but probably below the original surface of the island. Hillslope and fluvial erosion may have lowered the surface of the island during its history. Germa et al. (2010, 2015), Lahitte et al. (2012), Ricci et al. (2015a, b), and others have solved this problem by only considering the hillcrest points in the calculation of the regression curve, which are a priori the least eroded points of the surface. Favalli et al. (2014) increased the weight of the highest points during the regression. Meanwhile, Karátson et al. (2016) selected the most representative surface points using morphometric indices and focusing on the planèzes to perform the regression. Because the aerial part of Corvo is poorly incised by subaerial erosion, selecting only the highest points leads to very few points and a poor regression. As a result, we decided to keep all the points to perform the regression. Obviously, the selected points to which the fit is applied can be adapted in other examples according to the degree of incision or available geological data concerning preserved surfaces (Lahitte et al., 2012; Germa et al., 2015). Such adaptations do not affect the core of our method.

In our reconstructions, we ignore the sediment that may cover the platform (Ricchi et al., 2020). In order to evaluate the error induced by this bias, we explore the (very uncertain) possibility that all the eroded material was deposited on the slopes of the edifice beyond the shelf break. The error is calculated by considering that the sediments have a prism shape from the shelf break to the abyssal plain (depth or zb of ∼ 2000 m for Corvo). The section of this deposit is A₂= (zb ⋅ Δx)$/\mathrm{2}$, where Δx is the width of the shelf corresponding to these sediments. This section must be similar to section A₁ corresponding to the island coastal erosion. Let us consider that it has a triangular shape; therefore A₁= h_c ⋅ (xIE − Δx − xSLA)$/\mathrm{2}$, where h_c is the cliff height and xIE and xSLA are the distance of IE and SLA to the center of the edifice. Assuming A₁=A₂, we find for Corvo that the width of the platform is overestimated by 20 %, a value that is certainly overestimated by the fact that we do not take the circular shape of the island into account. As observed for the volumetric bias, this value results in an error of less than 13 %. The error value increases with the height of the cliffs and decreases with the depth of the abyssal plain. This bias is therefore minor, which is consistent with the relatively low average sediment thicknesses (3 to 15 m) imaged by Ricchi et al. (2020).

Our method requires that the initial shape of the volcanic edifice, or part of it, has radial symmetry associated with a given center. This hypothesis can be easily tested, for example by dividing the island into different sectors and by comparing the predicted center (by applying our method) of each sector with the others. In the case of the symmetry not holding for the whole island, in case of multiple volcanic edifices, or if the island is not circular, our approach can be still applied independently for some selected sectors. Note that the uncertainty in eroded volume associated with a deviation from a perfect radial symmetry is taken into account by the uncertainty computed between the topography and the exponential model defined from the calculated center of the island.

The method is based on a late surfacing of the edifice. We consider that the flows that caused this surfacing occurred during a relatively short period of time. The good quality of the fits that we present supports this view. This does not preclude later lava flows which may have created deltas as flows enter the sea. If there are some left, most of them must have been eroded. The bias introduced is therefore an underestimation of the eroded volume. We expect that the volumes of deltas eroded in this way are relatively small compared to our estimates of the total eroded volume: if this were not the case, there would be alterations to the circular or elliptical shape of the building. These alterations are detectable as shown in the southern part of Corvo Island; we do not detect them on the other sides. This shows that the lavas younger than the surface of the edifice only introduce a minor bias in our estimates of the total eroded volume.

The uncertainties (including systematic errors in the profiles due to the slight erosion of the aerial part) in the eroded volumes range from ±28 % to $-\mathrm{78}\mathit{\%}/+\mathrm{106}$ %, depending on the sector. Thus, the best sectors have an uncertainty of close to 25 %. This error is comparable with the errors associated with annual to decadal measurements (e.g., Moses and Robinson, 2011; Earlie et al., 2013; Young, 2018). The uncertainty in the total eroded volume is ±42 % (slightly better than the published values; see Averes et al., 2021; Regard et al., 2022). These uncertainties depend on the number of points used to calculate the fit. Therefore, our method is deemed to be more robust for higher-resolution data and for larger islands.

6.2 Interpretations from topographic reconstruction

As per the suggestions of Melo et al. (2018), we obtain an initial aerial edifice with a radius of nearly 4 km and a height close to 1 km (without considering the formation of the caldera). Considering a total eroded volume of 6.5 ± 2.7 km³ over a time period of 0.43 ± 0.34 Myr, we can estimate that coastal erosion has caused an average net loss of approximately 5000 to 100 000 m³ of rock per year. This material flux from Corvo Island to the ocean has probably varied a lot during the eustatic level variations, and it remains difficult to quantify the part of this flux reaching the deep ocean.

In addition to being able to quantify the total eroded volume by coastal erosion, the reconstruction of the initial shape of Corvo Island allows us to obtain the elevation of the junction relative to the current sea level between the aerial and submarine profiles, which is assumed to be the initial extension (IE) of the island. The IE is 23 ± 104 m above current sea level. The uncertainty in this value is too large and too close to the current sea level to interpret it as a marker of the vertical dynamic of the island.

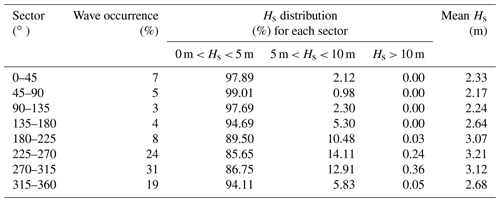
Table 3 Model outputs for wave data from Rusu and Guedes Soares (2012) used for this study. H_s: significant wave height (m).

It is worth noting that the topographic anomaly observed in Fig. 4 corresponds to the northern sector. There, the aerial elevation is higher than elsewhere on the island with respect to the radial symmetry, meanwhile the insular shelf is also wider. This indicates a vertical and horizontal protrusion. Together with the protrusion caused by the younger volcanic edifice in the southern sector of the island, these protrusions give the total edifice a slight elongation along the north–south axis. As with the southern protrusion of volcanic origin, it is conceivable that the northern one is also due to volcanic processes. This volcanism would be older than the central volcano because it would be almost totally erased by the sea, leaving a wider insular shelf in this sector. However, geological studies by Dias (2001) and França et al. (2002, 2006) do not seem to support this. Another solution to explain this elongation is a tectonic origin. The deformation of the edifice along its north–south axis during its evolution would be due to the dynamics of the Mid-Atlantic Ridge (Pueyo Anchuela et al., 2006). This slight elongation is not considered in our working hypotheses; if true, it would imply that the cliff retreat and eroded volume values in the northern sector are underestimated.

6.3 Comparison with available wave data

In order to perform an early analysis of the factors controlling the long-term coastal erosion, wave data from model outputs from Rusu and Guedes Soares (2012) (calculated from the KNMI/ERA-40 Wave Atlas, Sterl and Caires, 2005) were compared with the directional eroded volume data in Fig. 6. These wave data are calculated from a global wave model (Table 3) and provide information, per 45^∘ quadrant, about the directional distribution of the waves, the distribution and average of the significant wave height (H_s). To observe the effect of significant wave height, we present wave data subdivided into three classes: H_s < 5 m, 5 m < H_s < 10 m, and H_s > 10 m (Table 3 and Fig. 6).

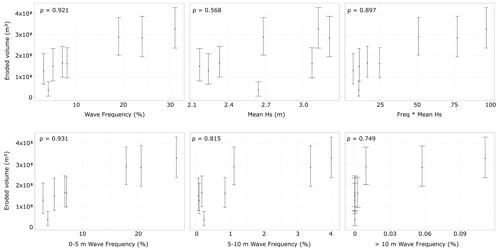
Figure 7 Quantification of the correlations (ρ) between the eroded volume and the mean significant wave height (H_s) and frequency. Each point is a direction sector measuring 45^∘.

There appears to be a clear spatial correlation between the spatial distribution of the waves and the eroded volumes. There is also a slight correlation between the mean significant wave height and eroded volume, but this appears to be less marked. These correlations are analyzed by plotting the values of our results against the values given by Rusu and Guedes Soares (2012) and by calculating their correlation coefficients (ρ) (Fig. 7). It appears from the correlations (Fig. 7) as well as the visual inspection (Fig. 6) that the eroded volume is much better correlated with the distribution of the waves rather than with the mean wave height. In particular, the frequency of small waves (H_s < 5 m) is better correlated with eroded volume than that of large waves (5 m < H_s < 10 m) and even more than those of very large waves (H_s > 10 m). Thus, if we assume that modern wave data are representative of the long period of erosion of Corvo Island and contrary to the assertion by Anderson and Anderson (2010) and Ramalho et al. (2013) that mainly storm waves control coastal erosion, our results indicate a stronger control by smaller and more frequent waves, in accordance with the conclusions of Huppert et al. (2020).

Lastly, it appears that the maximum wave activity, which is located between 240 and 340^∘ N, is opposite the locus of the minimum eroded volume, which is located between 120 and 160^∘ N (Fig. 6). This minimum coastal erosion could be due to the protection that the island, and particularly the lava delta in the southern sector, offers against the dominant swell via a shading effect.

In view of the correlation between waves and coastal erosion, despite the uncertainties in the absolute values of the eroded volumes, the method seems capable of accurately capturing the spatial variations in this erosion around the island. These results open up promising perspectives that must be confirmed by new data on Corvo Island and the application of this method to other volcanic islands.

7 Conclusions

We have developed a method to reconstruct the initial shape of simple volcanic islands from aerial and submarine topographic data. It allows us to spatially quantify the total eroded volume by coastal erosion integrated over the age of the maximum island extension. We show that the submarine topography below the platform is consistent with an exponential model, though different from the aerial topography of the island.

Applying this method to the Corvo Island in the Azores archipelago, we calculated that, at its maximum extension, the radius of the island was approximately 3.8 km for a peak elevation of roughly 1 km. Comparing this reconstructed shape with the current shape, we estimated that the island had lost a volume of approximately 6.5 ± 2.7 km³ and an area of roughly 37.2 ± 3.6 km² along its coast, due to coastal erosion and sea level change; this corresponds to more than three-quarters of its initial surface. We estimated that Corvo Island has lost, on average, between 5000 and 100 000 m³ of material per year since its maximal extension due to coastal erosion. Lastly, the comparison of the eroded volume values with the available wave data shows a strong spatial correlation between wave frequency and coastal erosion. Furthermore, contrary to the assertion of previous researchers, moderate but frequent waves appear to have a greater control on coastal erosion than storm waves.

Similar studies on other volcanic islands could streamline and improve our method, provide new results for different lithologies and ages, and provide additional evidence for the influence of wave climate on long-term coastal erosion.