Short Communication: Numerically simulated time to steady state is not a reliable measure of landscape response time

Quantifying the timescales over which landscapes evolve is critical for understanding past and future environmental change. Computational landscape evolution models are one tool among many that have been used in this pursuit. We compare numerically modeled times to reach steady state for a landscape adjusting to an increase in rock uplift rate. We use three different numerical modeling libraries and explore the impact of time step, grid type, numerical method for solving the erosion equation, and metric for quantifying the time to steady state. We find that modeled time to steady state is impacted by all of these variables. Time to steady state varies inconsistently with time step length, both within a single model and among different models. In some cases, drainage rearrangement extends the time to reach steady state, but this is not consistent in all models or grid types. The two sets of experiments operating on Voronoi grids have the most consistent times to steady state when comparing across time step and metrics. On a raster grid, if we force the drainage network to remain stable, time to steady state varies much less with computational time step. In all cases we find that many measures of modeled time to steady state are longer than that predicted by an analytical equation for bedrock river response time. Our results show that the predicted time to steady state from a numerical model is, in many cases, more reflective of drainage rearrangement and numerical artifacts than the time for an uplift wave to propagate through a fixed drainage network.

1 Introduction

The concepts of steady-state landscapes and characteristic timescales for landscapes to transition from one steady state to another, i.e., response times, have been widely used as a framework for interpreting landforms and landscape evolution (e.g., Whipple, 2001; Whipple and Meade, 2004; Hilley et al., 2004; Stolar et al., 2006; Whipple and Meade, 2006; Roe et al., 2008; Forzoni et al., 2014; Goren, 2016; Armitage et al., 2018), as well as what signals may be preserved in the sedimentary record (e.g., Allen and Densmore, 2000; Castelltort and Van Den Driessche, 2003; Simpson and Castelltort, 2012; Romans et al., 2016; Li et al., 2018; Straub et al., 2020; Tofelde et al., 2021). If landscapes evolve to a predictable steady form that is a function of environmental drivers, presumably we could invert landscape form to infer these environmental drivers (e.g., Snyder et al., 2000; Densmore, 2004; Kirby and Whipple, 2012; Whittaker, 2012; Hurst et al., 2019; Adams et al., 2020). Further, steady-state morphology is a well-established way to compare modeled landscapes (e.g., Tucker and Bras, 1998; Tucker and Whipple, 2002; Gasparini et al., 2004; Anders et al., 2008; Roering, 2008; Han et al., 2015; Shobe et al., 2018; Campforts et al., 2022).

While steady state can be used to imply a variety of different conditions, here we specifically consider topographic steady state (e.g., Willett and Brandon, 2002). To determine whether a landscape has reached topographic steady state, we need to know how to measure it (either in the field or in a simulation). There are many options for how to measure topographic steady state in a computational model, and accordingly, an initial question is which steady-state metric in a numerical model is most reliable. If we measure steady state using erosion rates or sediment fluxes, over what timescales should these fluxes be measured? Further, can we expect variability in sediment flux under steady conditions? If steady state is measured using landscape metrics, such as total relief, which metrics are used? Similarly, how much variability in these metrics is acceptable while still maintaining a steady state?

Once a criterion for steady state is established, a computational model can be used to measure the time it takes for a landscape to reach steady state following a perturbation. Given an understanding of steady-state timescales, many different inferences may be drawn with implications for the interpretation of specific landscapes on Earth or other planets. If a particular configuration of initial and boundary conditions results in landscapes that reach steady state relatively quickly (in comparison with variations in environmental forcings), then we can expect similarly configured real landscapes to reach steady state. However, if landscapes take so long to adjust that environmental changes happen more frequently, we might expect to rarely observe steady-state landscapes. Similarly, if we can establish that response times of simulated landscapes to perturbations behave systematically and predictably as a function of the environmental drivers, then simulated response times could theoretically be used to establish characteristic timescales for processes (e.g., Whipple et al., 2017; Lyons et al., 2020). Further, if timescales of landscape evolution and/or natural forcings are known in study landscapes, models could be used to test competing landscape evolution scenarios, interpret processes controlling landscape evolution, and establish the impact of competing timescales on landscape form (e.g., Densmore et al., 2007; Attal et al., 2008; Godard et al., 2013; Whittaker and Boulton, 2012; Mackey et al., 2014; Brocard et al., 2016). Establishing the reliability of the time to steady state derived from landscape evolution models is thus important for interpreting outcomes from these models and connecting inferences drawn from them with datasets collected on Earth.

To our knowledge, no study has comprehensively evaluated whether topographic steady state extracted from a 2D landscape evolution model (LEM) is a reliable measure of landscape response time. To fill this gap, we quantify steady state with different landscape evolution models that use different numerical methods and grid types. In all of our model scenarios we evaluate four different metrics for quantifying steady state. We show that flow-routing methodology has a large control on time to steady state in our modeling experiments but that the impact of flow routing on drainage reorganization also varies with grid type. Similarly, the computational time step and method for quantifying steady state also impact the time to steady state. In other words, we find the time to steady state from numerical models to be inconsistent and, in some cases, of minimal use when interpreting real landscapes, especially when considering the outcome of a single or very small set of landscape simulations.

2 Motivation

Determining when a landscape evolution model has reached steady state seems like a simple task, yet landscape evolution modelers are not consistent in their practice. To identify some of the different criteria used to determine when steady state is reached, we surveyed 30 different publications that apply the concept of steady state using a numerical model (Howard, 1994; Fernandes and Dietrich, 1997; Tucker and Bras, 1998; Roering et al., 2001; Stark and Stark, 2001; Istanbulluoglu and Bras, 2005; Gasparini et al., 2007; Stolar et al., 2007; Anders et al., 2008; Attal et al., 2008; Davy and Lague, 2009; Armitage et al., 2011; Perron and Fagherazzi, 2012; Refice et al., 2012; Braun and Willett, 2013; Goren et al., 2014; Han et al., 2015; Croissant and Braun, 2014; Carretier et al., 2016; Shelef and Hilley, 2016; Zhang et al., 2016; Campforts et al., 2017; Kwang and Parker, 2017; Shobe et al., 2017; Whipple et al., 2017; Li et al., 2018; Theodoratos et al., 2018; O'Hara et al., 2019; Salles, 2019; Steer, 2021). These publications span 3 decades. The list has 30 unique first authors, although some first authors are later authors in other papers on the list. We recognize that this is not an exhaustive list, but we think these 30 papers generally illustrate what we have informally observed throughout our modeling careers.

It is not our intention to criticize any papers. Accordingly, we do not describe practices of a single study. We were as generous as we could be with our interpretation of what criteria were used to determine steady state. For example, if the criteria were not described in the text but could be implied from a plot, we interpreted that study as having criteria.

A total of 20 of these 30 papers stated that steady state is reached when rock uplift and erosion rates are equal, or equivalently the sediment flux rate is equal to the product of the average upstream rock uplift rate and the drainage area. In other words, steady state is reached when the change in elevation is zero. Of these 20 papers, three papers state that they used a defined threshold other than zero. Four of the 30 papers assumed steady state is reached when the mean elevation is unchanging, and none of these provided a threshold to determine when unchanging elevation is reached. Two of the papers used unchanging sediment flux through time to indicate steady state, and they did not state a threshold. Four of the papers did not state the criteria used to determine that steady state is reached. None of these papers provided enough information to recreate the criteria. For example, papers that do not use averaged criteria do not state where measurements are made: does every point on the landscape have an erosion rate that matches the rock uplift rate? Or is the average erosion rate equal to the average rock uplift rate?

Based on these observations, we are motivated to test whether or not the metric and the threshold matter when calculating the time to steady state.

3 Modeling environments

The three modeling environments used in this paper were chosen because the authors have experience using them. The choice of these models says nothing about the value of these modeling environments or the value and variety of other modeling environments. We do not assume that these models represent the behavior of all modeling environments. That said, these three modeling environments allow us to explore the sensitivity of the time to steady state to multiple grid types and numerical methods.

3.1 TTLEM

TTLEM is part of the TopoToolbox MATLAB library. Many readers may be familiar with the DEM (digital elevation model) analysis tools that are contained within TopoToolbox (e.g., Schwanghart and Scherler, 2014). TTLEM is an LEM that is distributed with these tools and uses the TopoToolbox library for many of the core functions within the LEM, e.g., flow routing (Campforts et al., 2017) (available at https://github.com/wschwanghart/topotoolbox; last access: 7 December 2022).

TTLEM contains three numerical algorithms for solving the stream power equation on a raster grid. In this study we use TTLEM computer models that implement the Fastscape implicit numerical algorithm, an explicit finite-difference algorithm, and the total variation diminishing finite-volume method (TVD_FVM). The Fastscape numerical algorithm was designed to be more stable than most finite-difference methods (Braun and Willett, 2013). TVD_FVM is designed to be highly accurate and limit numerical diffusion (Campforts and Govers, 2015).

3.2 Landlab

Landlab is Python library for modeling surface processes on regular and irregular grids (Hobley et al., 2017; Barnhart et al., 2020a). In this study we implement computer models that use raster, hexagonal, and Voronoi grids. (Landlab also supports radial grids but these are not tested in this study.) Landlab is open-source and available through GitHub (https://github.com/landlab/landlab; last access: 14 October 2022). This study used Landlab version 2.4.2.dev0. Landlab is in active development and is currently maintained through CSDMS (Tucker et al., 2022). The stream power process component used in all Landlab computer models in this study implements a version of the Fastscape implicit finite-difference numerical algorithm (Braun and Willett, 2013).

3.3 CHILD

The CHILD modeling environment was developed in the late 1990s (e.g., Tucker et al., 1999, 2001a, b). It operates on a triangular irregular network, forming a Voronoi diagram, here referred to as a Voronoi grid for consistency with the other grid types. CHILD uses an explicit finite-difference solution of the stream power process equation.

CHILD is a C$++$ code that is open-source and available through GitHub (https://github.com/childmodel/child; last access: 8 September 2022). Although CHILD is no longer actively in development, it was widely used in the past 20 years and continues to be used at the time of writing. Because of its familiarity to the authors, its application on a Voronoi grid, and its advanced stage of development, we used it in this study.

3.4 LEMs and comparison rational

Using the three modeling environments described above, we created seven different LEMs which we use to calculate the time to steady state. These different LEMs are described in Table 1. These three modeling environments allow us to compare how the grid type and the numerical method for solving the stream power equation impact the time to steady state.

Table 1 Table of different LEMs used in this study. We use the LEM abbreviated names in column 1 to refer to the different model scenarios. The first letter in the abbreviated name stands for the modeling environment: T for TTLEM, L for Landlab, and C for CHILD. The second letter stands for the grid type: R for raster, H for hexagonal, and V for Voronoi. The third letter stands for the numerical method used to solve the stream power equation: I for implicit, E for explicit, and T for TVD_FVM.

4 Stream power equation

All of the model environments we consider use the stream power equation to represent the evolution of fluvial profiles. We only consider fluvial erosion in our LEMs. Erosion is sustained throughout all simulations by uniform, steady rock uplift. The equation controlling the change in topographic elevation at each node is

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}t}}=U-K{A}^m{S}^n,\end{array}$$

where z is node elevation, t is time, dt is the computational time step, U is the rock uplift rate, K is the erodibility parameter, A is the drainage area at a node, S is the topographic slope (negative of the spatial derivative in elevation assuming directionality is in the downslope direction) at a node, and m and n are positive exponents. Note that the second set of terms on the right-hand side of Eq. (1) constitutes the widely used stream power equation (SPE) that describes detachment limited fluvial incision,

$$\begin{array}{}\text{(2)}& E=K{A}^m{S}^n,\end{array}$$

where E is fluvial incision. Derivations, dynamics, and limitations of the SPE have been described in detail in numerous publications and we refer interested readers to such sources (e.g., Howard, 1994; Whipple and Tucker, 1999; Lague, 2014).

5 Experimental set-up

Each of our numerical experiments quantified the time it takes for a low-rock-uplift-rate, steady-state landscape to fully adjust to an increase in rock uplift rate using a specific LEM scenario (Table 1), initial condition, and a range of computational time step lengths. We did not formally quantify the initial low-uplift landscapes to be at steady state. Instead we generated initial conditions with simulations that ran for 100 million years. As will be apparent from our results, this is more than enough time for our landscapes to reach steady state regardless of the chosen metric or threshold for identifying steady state. In some cases we stopped the initial runs before 100 million years because the landscape became perfectly static. This experimental design, in which an initially steady landscape is perturbed by changing the uplift rate, is similar to previous modeling studies (e.g., Rosenbloom and Anderson, 1994; Whipple and Tucker, 1999, 2002; Gasparini et al., 2007; Attal et al., 2011), which is why we chose it.

As described below, we kept as much constant among the simulations with different LEMs as possible. However, we did not do anything to change the models from “off the shelf”. In other words, we used the modeling environments without changing any of the internal code that implements the numerical algorithms. Where appropriate, we did change parameters within the different modeling environments to try to ensure that their behavior was as comparable as possible. For example, all the raster models use D8 flow routing (Tarboton, 1997), and this was an option that we chose when using the LRI model to make it more similar to the TRI model. In contrast, there are multiple ways to calculate a topographic gradient at a grid cell in a computational model. The algorithm used to make this calculation is not chosen by the user for these models, and accordingly we can not ensure that each model calculates the topographic gradient in the same way.

The simulations that created the initial steady-state landscape were started from a surface with elevation values randomly chosen between 0.0 and 1.0 m. The random-elevation initial surface was used because it creates more realistic looking drainage networks. The raster grids had 200 by 200 nodes, and the spacing between nodes in the x and y direction was 100 m. All the simulations using a raster grid in different models used the same exact initial topographic surface (LRI, TRI, TRT, and TRE). The numerical experiments that use a Voronoi grid are created from a Delaunay triangulation of staggered rows of nodes spaced 100 m apart in the x direction. The initial condition was a similar noisy surface as used with the raster grids, and the same exact initial surface was used in the CVE and LVI simulations. Regardless of the type of grid, all the grids were ≈20 km by ≈20 km with ≈100 m resolution.

The boundary conditions used in all simulations were the same. All of the nodes on the perimeter of grid were open boundaries where water can exit, but not enter, the grid. The elevation of the perimeter boundary nodes was fixed at 0 m and did not change during the simulations. In other words, the perimeter nodes were not uplifted but the rest of the grid was uplifted. U and K were spatially uniform and set at 10⁻⁴ m yr⁻¹ and $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{6}}$ yr⁻¹, respectively, in all the initial simulations. m and n were also spatially uniform and set at 0.5 and 1, respectively.

We explored how the time step value, dt in Eq. (1), impacts the time to steady state. Each model should be stable and produce the correct analytical solution when the time step satisfies the Courant–Friedrichs–Lewy condition:

$$\begin{array}{}\text{(3)}& C_{\max }>v{\displaystyle \frac{\mathrm{d}t}{\mathrm{d}x}},\end{array}$$

where C_max is the Courant number of ≈1.0 in stable conditions, v is the speed at which an erosional wave will move through the network, and dx is the spacing between nodes. When using the stream power process equation with n=1, v is approximated as

$$\begin{array}{}\text{(4)}& v\approx K{A}^m.\end{array}$$

To calculate the maximum time step for a stable Courant condition (dt, Eq. 3), we needed to know the largest drainage area in the modeled network to estimate the fastest wave speed (Eq. 4). We estimated the size of the largest drainage to be one-fourth of the total area of the grid, or ∼49 km². This value was intended as an overestimation, ensuring that we calculated a stable time step with Eqs. (3) and (4). For the values chosen for K and m, C_max=1, and our estimated value for the maximum drainage area, we calculated a stable dt of 2857 years. We then chose dt=2500 years as the base-case model time step because it should result in stable simulations. We explored how the time to steady state changed by changing dt. We ran four simulations with each model, reducing dt to 250 years and increasing dt to 25 000 and 100 000 years, or approximately 10 and 40 times greater than the stable condition, respectively.

The decision to use time steps longer than the estimated stable time step is motivated by the results shown by Braun and Willett (2013). They state that their numerical algorithm, which is the implicit numerical method used in TRI and all Landlab models, is accurate even when the time step is more than 100 times the stable condition. The stability of the algorithm is also discussed in Braun and Deal (2023). However, simulations from models employing either the explicit finite-difference or TVD_FVM algorithms did not produce accurate or even sensible results, with time steps longer than the predicated stable value. Hence results with all times steps are only shown from models using the implicit solution.

We use the steady initial conditions (elevation unchanging everywhere through time) produced from each model simulation and time step combination as the initial condition for the corresponding transient simulations. We increase the rock uplift rate uniformly across the grid by a factor of 5 to $U=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{4}}$ m yr⁻¹. As the landscape evolves in response to the new higher uplift rate, we track the steady-state metrics to quantify differences in the time to steady state.

In all of our initial simulations we re-calculated flow directionality at every time step. However, after running the simulations we observed that in some cases the drainage network was rearranged, and we wanted to explore how this affects the time to steady state. Thus, we performed two more numerical experiments using TTLEM with the three different numerical methods (TRI, TRE, TRT). First we re-ran all of the TTLEM numerical models but did not reroute flow at every time step during the transient simulations. In other words, we forced the network to remain static during the adjustment to a higher uplift rate. This is an available option within the TTLEM modeling environment that is controlled in the input file. Second, we generated new steady-state initial conditions and used them for another set of uplift increase experiments. For these simulations, we started with a different initial white noise grid to create the low-uplift steady-state topography. Because the initial white noise determines the network details, these landscapes have a different network despite being run with the same model, parameters, and boundary conditions.

6 Time to steady state

Here we describe the metrics we use to empirically quantify the time to steady state. We also describe the analytical equation previously presented by Whipple and Tucker (1999) and Whipple (2001) that we use to predict the time for a rock uplift signal to propagate through a detachment-limited river network. In the section “Time to steady-state results”, we will compare the empirically derived steady-state times with the analytically predicted values.

6.1 Numerically modeled

Theoretically steady state is reached when Eq. 1 is equal to zero, or when the rock uplift rate U and fluvial incision rate E are equal at every node. Although steady state is often used and referred to in numerical modeling studies, the criteria for reaching steady state, or determining when E=U everywhere on the grid, are not always explicitly described. Here we test four metrics for determining when steady state is reached. We refer to these collectively as the steady-state metrics.

The temporal change in maximum elevation, $\mathrm{\Delta }{z}_{\max }^t$, was calculated as

$$\begin{array}{}\text{(5)}& \mathrm{\Delta }{z}_{\max }^t=|\max \left(z_i^t\right)-\max \left(z_i^{t-\mathrm{100}\mathrm{000}}\right)|,\end{array}$$

where $\max \left(z_i^t\right)$ is the maximum grid elevation within the domain at time t, i is the node index, and $\max \left(z_i^{t-\mathrm{100}\mathrm{000}}\right)$ is the maximum grid elevation within the domain at time t−100 000.

The temporal change in mean elevation, $\mathrm{\Delta }{z}_{\mathrm{mean}}^t$, was calculated as

$$\begin{array}{}\text{(6)}& \mathrm{\Delta }{z}_{\mathrm{mean}}^t=|\mathrm{mean}\left(z_i^t\right)-\mathrm{mean}\left(z_i^{t-\mathrm{100}\mathrm{000}}\right)|,\end{array}$$

where $\mathrm{mean}\left(z_i^t\right)$ is the mean grid elevation within the domain at time t, and $\mathrm{mean}\left(z_i^{t-\mathrm{100}\mathrm{000}}\right)$ is the mean grid elevation within the domain at time t−100 000.

The maximum temporal change in elevation, $\mathrm{\Delta }{z}_{\max \left(\mathrm{loc}\right)}^t$, was calculated as

$$\begin{array}{}\text{(7)}& \mathrm{\Delta }{z}_{\max \left(\mathrm{loc}\right)}^t=\max \left(|z_i^t-z_i^{t-\mathrm{100}\mathrm{000}}|\right).\end{array}$$

The difference between Eqs. (5) and (7) is that the former finds the difference between the maximum elevation of the entire domain at two different times, whereas the latter finds the difference in elevation at every node in the landscape between two different time steps and uses the maximum of those differences. The units on all of the elevation change metrics are meters.

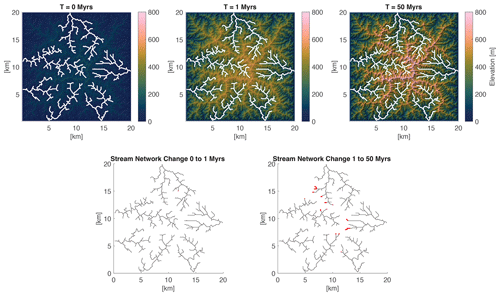
Figure 1 The top row shows the topography at three different times from the TRI experiment with dt=100 ka. The bottom row shows the networks after 1 Myr (left) and 50 Myr (right), with network locations that have changed colored in bold red. Note that there is only one location of change between time 0 and 1 Myr.

Finally, the temporal change in sediment flux, ΔQs^t, was calculated as

$$\begin{array}{}\text{(8)}& \mathrm{\Delta }Q{s}^t=\sum Q{s}_i^t-\sum Q{s}_i^{t-\mathrm{100}\mathrm{000}},\end{array}$$

where $\sum Q{s}_i^t$ is the summation of the erosion rate at every node on the landscape at time t, and $\sum Q{s}_i^{t-\mathrm{100}\mathrm{000}}$ is the summation of the erosion rate at every node on the landscape at time t−100 000. Here sediment flux refers to the flux of all material eroded from the bed. The models do not track the flux of sediment load explicitly when using the SPE, which is why we use the local erosion rate as a proxy for sediment flux. In all of the grids the cell size is nearly uniform; hence, the summation of erosion rate is a good proxy for the sediment flux. The units of ΔQs are meters per year.

In all cases the steady-state metrics are calculated over a temporal difference of 100 000 years, which was set by the longest time step of the simulations being compared. This was done to ensure equivalent comparisons between the simulations as some degree of difference in the time to steady state would be expected if we calculated these metrics over different time intervals between simulations. The first time that the topographic metrics were calculated is at 100 000 years into the simulation. With the sediment flux metric, the first calculation is done at 200 000 years because there is no sediment flux at time zero in the simulation.

As a landscape evolves towards steady state, all of the steady-state metrics should approach zero. When exactly a new steady state is reached could be defined as when the metric value passes below a predetermined threshold. The strictest definition would be when a metric reaches zero. We note that differences in the accuracy of calculations in different modeling environments could lead to some of the metrics never reaching zero. Also, the time at which a particular metric appears to reach zero will depend on the floating point precision of the programming environment in which the metric is calculated. One could also use the rate of change in the value of a steady-state metric as a criterion for reaching steady state.

We do not state what method should be used to determine when steady state is reached. We present the results using different threshold values. We also present the time series of the different metrics so the reader can decide whether a change in the rate of change of a metric over time is a reasonable method for determining steady state.

6.2 Analytical equation

Following Whipple and Tucker (1999), Whipple (2001) showed that the predicted response time to an increase in rock uplift in a river network evolving according to Eq. (1) and with n=1 is

$$\begin{array}{}\text{(9)}& T_{\mathrm{A}}={\displaystyle \frac{\mathit{\beta }}{K}},\end{array}$$

where

$$\begin{array}{}\text{(10)}& \mathit{\beta }=k_a^{-\frac{m}{n}}{\left(\mathrm{1}-{\displaystyle \frac{hm}{n}}\right)}^{-\mathrm{1}}\left(L^{\mathrm{1}-\frac{hm}{n}}-x_c^{\mathrm{1}-\frac{hm}{n}}\right).\end{array}$$

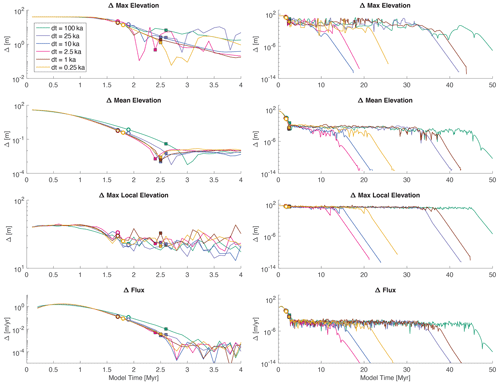
Figure 2 Time series of four different steady-state metrics, each in a different row, from the TRI experiments. The two columns show the same data, but the left column is zoomed in on only the first 4 million years of the time series. The different colors represent the different time step values; the circles are the analytical response time calculated using the average channel length in Eq. (9), and the squares are the analytical response time calculated using the longest channel length in Eq. (9).

In Eq. (9), T_A is the analytical time to steady state, K is the erodibility in Eq. (2), and L is the length of the longest channel in the network. In Eq. (10), x_c is hillslope length, and m and n are the exponents in Eq. (2). Equation (10) also requires empirical parameters k_a and h from the equation developed by Hack (1957):

$$\begin{array}{}\text{(11)}& A=k_a{\left(x_{\mathrm{d}}\right)}^h,\end{array}$$

where x_d is distance from the divide and A is drainage area. Note that Eq. (10) only holds when $\frac{hm}{n}\ne \mathrm{1}$, which is the case in all of our experiments.

We use data from the largest watershed in the modeled landscapes to calculate k_a and h. In simulations in which there is drainage rearrangement, and hence slight changes in these parameters while the simulation approaches a steady state, we use values calculated from the network at the end of the simulation time, which was 50 million years for the majority of our simulations. As none of our simulations formally included hillslopes, i.e., we do not consider diffusion and the diffusion constant was set to 0 in our simulations, we set x_c in Eq. (10) to 0.

We note that Eq. (9) is the time for the signal from an increase in rock uplift to move through a river network. It does not include the response time of hillslopes. However, our numerical simulations do not include hillslopes, so this equation should approximate the time to steady state in our experiments.

7 Time to steady-state results

Example maps of an evolving topography are shown in the top row of Fig. 1. As expected, the total relief of the landscape, or the difference between maximum and minimum elevation, grows in response to the increase in rock uplift rate. As the landscape evolves, the drainage network remains almost fixed, with only a few small changes in the channel headwaters (bottom row of Fig. 1).

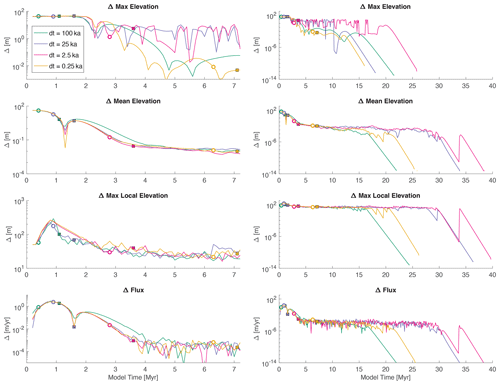
Figure 3 Time series of four different steady-state metrics from the LRI experiments. Refer to the caption in Fig. 2 for details.

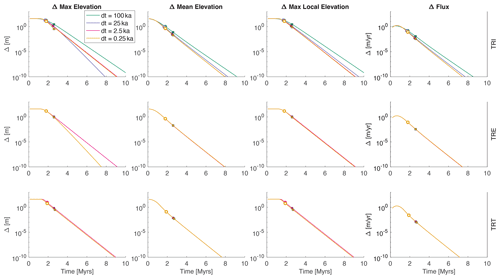
The time series of the different metric values for the TRI experiments with different time steps are shown in Fig. 2. For a given metric, the time series for the different time step values (different colored lines) have similar patterns. For example, the zoomed-in view (left column) of the change in maximum elevation (top row) remains constant initially, as the value is controlled by the change in rock uplift rate until the erosional wave has propagated upstream. Once the erosional wave reaches the uppermost parts of the network, the value begins to generally decline, but not monotonically. When looking at the zoomed-out view (right column), the change in maximum elevation appears to bounce around in a contained range of values, until taking a sharp decline with time. If a perfect steady state was reached, this metric (and all the metrics) would go to zero within the computational accuracy of the model. The time at which the sharp decline occurs varies by ≈40 Myr for the change in maximum elevation metric, and the time of the sharp decline does not change systematically with the time step value.

The time series of the different metric values for the LRI experiments with different time steps are shown in Fig. 3. Although the patterns for a given metric are similar to those observed in Fig. 2, there are some differences. For example, in the TRI experiments (Fig. 2), the time to reach steady state predicted using the longest channel in each landscape (squares) seems to roughly match an inflection (here meaning change in slope) in the time series of the change in mean elevation metric. When comparing with the change in mean elevation metric in the LRI experiments (Fig. 3), the general patterns of the time series are similar. However, the predicted time to steady state using the longest channel in the LRI experiments does not consistently match the inflection in the time series of the change in mean elevation metric.

Time series of all our metrics in all of our numerical experiments with continual flow routing are illustrated in Fig. 4. Each column of Fig. 4 shows the time series of one of the four steady-state metrics. We recognize that these plots are difficult to see at this zoomed-out scale. However, it is possible to see that the results in Figs. 2 and 3 illustrate behavior that is similar to all of the models.

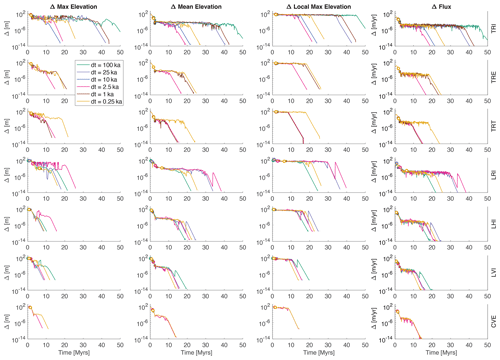
Figure 4 Time series of four different steady-state metrics, in columns. Each row has results from a different LEM (Table 1). The x axis is time in millions of years in all the plots. Note that the extent of the x and y axes is the same in all the panels. Circles and squares are used to show the different analytical times to steady state (see the caption of Fig. 2); however, they are difficult to see at this scale.

One way to determine the time to steady state would be to set a threshold value that a metric must decline below to reach steady state. We calculated the time to steady state using the different metrics with a range of threshold values for the TRI numerical simulations (Fig. 5). When the threshold value is relatively large, the metric values often increase and decrease around the value. In those cases, we used the first time that the metric crossed below the threshold value, as that would likely be the method in a numerical model. (In other words, a model may run until the metric threshold value is reached.) However, it is worth noting that given the variability that persists in the metric values for extended periods (Fig. 4) and depending on the choice of threshold, the apparent time to steady state can vary significantly if you instead consider the last time that a given metric value is above the threshold value.

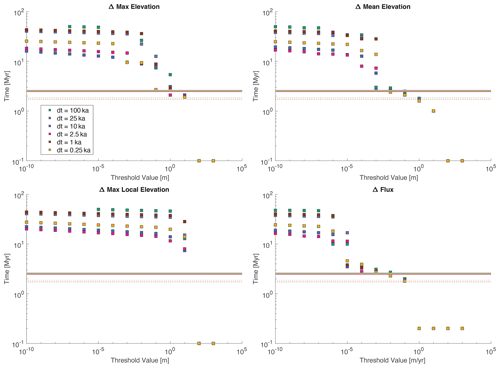
Figure 5 Plots of time to steady state (y axes) resulting from different metric threshold values (x axes) from the TRI numerical experiments. The dashed horizontal lines illustrate the analytical time to steady state using the average channel length. The solid horizontal lines illustrate the analytical time to steady state using the longest channel length.

The changes in maximum elevation, mean elevation, and sediment flux all have threshold values that provide times to steady state that generally agree with the analytical response time, regardless of the time step. The threshold value should be relatively large (considering the range we used) but not too large. When using the maximum change in local elevation, none of the illustrated threshold values are a good match to the analytical prediction. Of course we could have found a threshold value of maximum change in local elevation that predicted times to steady state that roughly match the analytical solution, but that is not the point of our study. Further, it would be impossible to know what threshold matches the analytical prediction before doing the modeling experiments.

Before doing the computational experiments, we hypothesized that the empirical steady state would vary monotonically with time step, in part because this is implied by the results of Braun and Willett (2013), e.g., their Fig. 4, exploring the dynamics of the implicit solution to the stream power equation. However, our experiments illustrate a lack of relationship between empirical steady state and time step. This is illustrated in Fig. 5. For any given threshold value, the smallest estimated time to steady state (y axis) is not necessarily produced using the smallest time step, and the longest time to steady state is not necessarily produced using the longest time step.

We wanted to rule out the possibility that this lack of relationship was because of an initial landscape and network configuration that, just by chance, led to odd results. Thus, we re-ran all of the TTLEM simulations on different steady-state landscapes that were produced using the same process as the first set of simulations, just with a different initial random surface. In these alternative TTLEM simulations, there is again no relationship between time to steady state and time step. (Results are not shown, except for dt=2.5 ka in Figs. 2 and 5. One of the dt=2.5 ka results in those figures is from the alternative initial condition.)

When comparing the evolving topographies, we observed that the CVE simulations have no drainage rearrangement, despite rerouting flow at every time step. The LVI simulations have some drainage rearrangement but very little. In contrast, in some of the TTLEM simulations, we observed small changes in the network across the landscape (Fig. 1). Thus, we hypothesized that drainage rearrangement was playing a part in the variation in times to steady state.

To test this hypothesis, we re-ran the initial set of TTLEM simulations, but this time we did not reroute the flow after every time step during the transient simulations (Fig. 6). What we found is that there is much less variation among the time series with different time steps when comparing with the initial set of simulations with continual calculation of flow routing. The time series of all the steady-state metrics in the simulations without drainage rearrangement are different from the TTLEM simulations with drainage rearrangement. With a fixed network, all of the metrics remain nearly steady in the initial response, and then they monotonically decline.

Figure 6 This figure is similar to Fig. 4 except we show TTLEM results without rerouting the flow after every time step. In other words, there was no drainage rearrangement in these simulations. The extent of the x and y axes in all of the time series is the same.

8 Implications and conclusions

At a minimum, the results of our experiments highlight that when simulating landscape evolution scenarios and considering topographic steady state – and especially time to steady state – it is critical to report both the metric being used and the threshold value for that metric to assess steady state. Based on Fig. 5, the changes in mean elevation and sediment flux appear to have a range of threshold values that give results that reasonably correspond to the response time predicted from the analytical solution. However, these threshold values are not necessarily the same threshold values that should be used with other modeling environments for the same metric.

Comparing our experiments where flow routing is recomputed at every time step (Fig. 4) with those where the drainage network is fixed (Fig. 6) suggests that small perturbations in drainage network structure over time (e.g., single pixel-to-pixel changes in divide location or along the course of individual drainages, Fig. 1) likely cause the longer time to steady state compared to the analytical predictions. Recent work highlighting that divide migration and drainage network instability may be more the norm (e.g., Willett et al., 2014; Whipple et al., 2017; Beeson et al., 2017; Forte and Whipple, 2018; Val et al., 2022) complicates the assumption of a static drainage network implied by calculations of the analytical response time. In fact, the analytical response time predicts only the time for an erosional signal to propagate through a fixed network (Whipple, 2001). Any adjustment in river network topology is not considered in the calculation, nor is hillslope adjustment time. Although predictions from Eq. (9) have been used synonymously with time to steady state, they are not the same. The analytical response time might be better captured in a 2D numerical model as the time that the last channel reach on the landscape starts responding to an erosional wave.

Any drainage network rearrangement in the modeling results presented above comes solely from the flow-routing algorithm and numerical artifacts. Our modeling scenarios did not consider any processes or driving conditions that might physically lead to drainage rearrangement, such as landslides (e.g., Campforts et al., 2022) or lateral channel migration (e.g., Kwang et al., 2021). The majority of prior results arguing for pervasive drainage network reorganization consider scenarios with spatial gradients in either K or U, which our simple experiments do not include. It is possible that the time to steady state from 2D simulations driven by spatial gradients in environmental drivers and which generally induce greater amounts of network reorganization, like those considered for divide migration by Whipple et al. (2017) and Lyons et al. (2020), may be less sensitive to the initial conditions and small perturbations in the network than our simulations here. However, testing this is beyond the scope of this short communication.

In summary, if we are primarily concerned with the legitimacy of using results of landscape simulations to establish the timescale of processes or the evolution of specific landscapes, it is not immediately apparent that time to steady state estimated from 2D numerical simulations is any more or less grounded in reality than the analytical solution. However, the variability of modeled time to steady state based on a metric and threshold illustrates the importance of stating all model conditions and how they were determined. Based on our experiments, we provide a set of recommendations for considering steady state and response times from 2D simulations. First and foremost, it is critical to remain mindful of the importance of the initial conditions (e.g., the random noise grid or estimates of paleotopography) in dictating landscape evolution (e.g., Willgoose et al., 1991; Perron and Fagherazzi, 2012; Ferrier et al., 2013; Han et al., 2014; Ward and Galewsky, 2014; Kwang and Parker, 2019) and to treat properties related to response times as more stochastic. Thus, one potentially useful approach is to consider the analytical response time to be a minimum response time, as was suggested by Whipple (2001). Ranges of more reasonable response times, incorporating some stochastic degree of minor drainage reorganization, can be estimated from multiple 2D simulations with different initial topographic conditions (i.e., random noise) for a given fixed set of other environmental factors. However, one should be mindful of whether drainage rearrangement is a numerical artifact or driven by processes and environmental variability that might lead to network rearrangement. Also, our results highlight that the choice of grid is meaningful in terms of reliability of modeled time to steady state, with either Voronoi or hex grids more likely to produce estimates that do not vary as much as a function of dt. Thus, these grid types may be more suitable where reliability of response times is important or where simulations run with different dt might be compared.

Generalized modeling studies that use synthetic landscapes, as we do here, are extremely valuable tools in the geomorphic community. Our study says nothing about using 2D numerical models for interpreting landscape forms, either during the transient response or at quasi-steady state, or as a function of nondimensional time within a simulation. The absolute most conservative reaction to our results would be to ignore response times as derived from 2D landscape evolution models. However, we advocate for a more nuanced approach. We suggest that care be taken to ensure the measurement fits the question. The time it takes for a knickpoint to propagate through a network is not necessarily the time it takes for a numerical model to reach a pure steady state, and these two things should not be conflated.

We stress that none of our results are based on observed natural watersheds or landforms that have data informing local rates and processes. For example, numerical models can be used to interpret dominant processes since a perturbation, as long as we have calibrated parameters and use the observed network pattern (e.g., Barnhart et al., 2020b, c). Our results illustrate that the details of a river network matter, and thus results from one river network do not necessarily apply to another river network. Further, numerical artifacts should not be interpreted as representing natural behavior. Finally, how something is measured matters, and clarifying how measurements are made in landscape evolution modeling studies should be general best practice.