The influence of a vegetated bar on channel-bend flow dynamics

Point bars influence hydraulics, morphodynamics, and channel geometry in alluvial rivers. Woody riparian vegetation often establishes on point bars and may cause changes in channel-bend hydraulics as a function of vegetation density, morphology, and flow conditions. We used a two-dimensional hydraulic model that accounts for vegetation drag to predict how channel-bend hydraulics are affected by vegetation recruitment on a point bar in a gravel-bed river (Bitterroot River, Montana, United States). The calibrated model shows steep changes in flow hydraulics with vegetation compared to bare-bar conditions for flows greater than bankfull up to a 10-year flow (Q₁₀), with limited additional changes thereafter. Vegetation morphology effects on hydraulics were more pronounced for sparse vegetation compared to dense vegetation. The main effects were (1) reduced flow velocities upstream of the bar, (2) flow steered away from the vegetation patch with up to a 30 % increase in thalweg velocity, and (3) a shift of the high-velocity core of flow toward the cut bank, creating a large cross-stream gradient in streamwise velocity. These modeled results are consistent with a feedback in channels whereby vegetation on point bars steers flow towards the opposite bank, potentially increasing bank erosion at the mid- and downstream ends of the bend while simultaneously increasing rates of bar accretion.

1 Introduction

Channel-bend morphodynamics along meandering rivers influence channel morphology, river migration rates, channel–floodplain connectivity, and aquatic habitat. River point bars, fundamental to channel-bend morphology (Blondeaux and Seminara, 1985; Ikeda et al., 1981), steer flow and induce convective accelerations (Dietrich and Smith, 1983) that influence boundary shear stress (Dietrich and Whiting, 1989) and sediment transport fields (Dietrich and Smith, 1983; Legleiter et al., 2011; Nelson and Smith, 1989). Channel migration rates are furthermore controlled by the collective processes of bar accretion and bank erosion. Bars along the inner bends of river meanders, although typically broadly described as point bars, also comprise chute bars, tail bars, and scroll bars that reflect distinct formative conditions (e.g., obstructions and/or stream power variations) and produce distinct morphodynamic feedbacks (Kleinhans and van den Berg, 2011).

Channel dynamics are tightly coupled with the recruitment and succession of riparian vegetation on river bars (Amlin and Rood, 2002; Eke et al., 2014; Karrenberg et al., 2002; Nicholas et al., 2013; Rood et al., 1998). Plants change local hydraulics (Nepf, 2012; Rominger et al., 2010) and sediment transport conditions (Curran and Hession, 2013; Manners et al., 2015; Yager and Schmeeckle, 2013), resulting in strong feedbacks between the recruitment and growth of woody riparian vegetation and bar building (Bendix and Hupp, 2000; Dean and Schmidt, 2011) that can influence the morphology of rivers at multiple scales (Bywater-Reyes et al., 2017; Osterkamp et al., 2012). Pioneer vegetation can occur on all bar types but is most likely to survive on nonmigrating bars, such as forced alternating point bars (Wintenberger et al., 2015). Plant traits including height, frontal area, and stem flexibility vary with elevation above the baseflow channel, influencing both the susceptibility of plants to uprooting during floods and their impact on morphodynamics (Bywater-Reyes et al., 2015, 2017; Diehl et al., 2017a; Kui et al., 2014). Vegetation effects on hydraulics, bank erosion, and channel pattern also depend on the uniformity of vegetation distribution on bars, which can vary depending on wind versus water-based dispersal mechanisms (Van Dijk et al., 2013), and on whether plants occur individually or in patches (Manners et al., 2015).

Experimental work in flumes has shown that vegetation is vital to sustaining meandering in coarse-bedded rivers (Braudrick et al., 2009). Vegetation's effect on stabilizing banks, steering flow, and impacting morphodynamics furthermore depends on seed density and stand age. Uniform vegetation on bars has been shown, experimentally, to decrease bank erosion rates, stabilize banks, and increase sinuosity of meander bends (Van Dijk et al., 2013). Gran and Paola (2001) showed that vegetation, by increasing bank strength, generates secondary currents associated with oblique bank impingement that may be more important than helical flows generated by channel curvature. Other experiments have generally suggested vegetated bars decrease velocities over the bar and push flow toward the outer bank. For example, tests in a constructed, meandering laboratory stream with two reed species planted on a sandy point bar showed that vegetation reduced velocities over the vegetated bar, increased them in the thalweg, strengthened secondary circulation, and directed secondary flow toward the outer bank (Rominger et al., 2010). Another study in the same experimental facility, but using woody seedlings planted on the point bar, also found reduced velocities in the vegetated area of the bar, with the greatest reductions at the upstream end, and the effect varying with vegetation architecture and density (Lightbody et al., 2012). In a flume study where meandering effects were simulated in a straight channel by placing dowels representing vegetation patches in alternating locations along the edges of the flume, vegetation reduced velocity within and at the edges of the vegetation patch and increased velocities near the opposite bank (Bennett et al., 2002). Experiments in a high-curvature meandering flume, in contrast, showed that vegetation inhibited high shear-stress values from reaching the outer bank (Termini, 2016), inconsistent with studies simulating moderate sinuosity channels.

Vegetation's effect on river morphodynamics has also been simulated with computational models. Reduced-complexity models that approximate the physics of flow have successfully reproduced many of the features observed in channels influenced by vegetation, such as the development of a single-thread channel (e.g., Murray and Paola, 2003). Two-dimensional models that use shallow-water equations and, in some cases, sediment transport relations, provide an alternative that may be less dependent on initial conditions and more capable of representing the physics of vegetation–flow interactions (Boothroyd et al., 2016, 2017; Marjoribanks et al., 2017; Nelson et al., 2016; Nicholas et al., 2013; Pasternack, 2011; Tonina and Jorde, 2013). Investigations of channel-bend dynamics influenced by vegetation using two-dimensional models often represent vegetation by increasing bed roughness (see Green, 2005, and Camporeale et al., 2013, for comprehensive reviews). Nicholas et al. (2013) simulated bar and island evolution in large anabranching rivers using a morphodynamic model of sediment transport, bank erosion, and floodplain development on a multi-century timescale, where vegetation was modeled using a Chezy roughness coefficient. Asahi et al. (2013) and Eke et al. (2014) modeled river bend erosional and depositional processes that included a bank-stability model and deposition dictated by an assumed vegetation encroachment rule. Bertoldi and Siviglia (2014) used a morphodynamic model coupled with a vegetation biomass model, which accounted for species variations in nutrient and water needs to simulate the co-evolution of vegetation and bars in gravel-bed rivers. Vegetation was modeled as increased bed roughness via the Strickler–Manning relation that varied linearly with biomass. Their model showed two scenarios: one where flooding completely removed vegetation, and one where vegetation survived floods, resulting in vegetated bars. These two alternative stable states (bare versus vegetated bars) have been found experimentally as well (Wang et al., 2016).

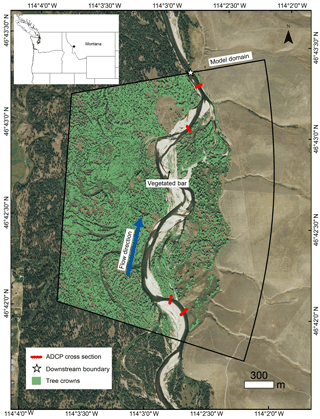
Figure 1 Bitterroot River, Montana, showing model domain, location of acoustic Doppler current profiler (ADCP) velocity measurement cross sections, downstream boundary, tree crowns mapped from airborne lidar, and the location of the vegetated bar. Inset map shows location in the northwestern US.

Although the aforementioned models produce many of the features of river morphodynamic evolution, when vegetation drag is dominant over bed friction, using conventional resistance equations (e.g., Manning's) to model vegetation's effect on the flow introduces error. Increasing the roughness within vegetated zones increases the modeled shear stress and therefore artificially inflates the sediment transport capacity at the local scale (e.g., vegetation patch or bar), although reach-scale results may be appropriate (Baptist et al., 2005; James et al., 2004). Vegetation drag can also be treated in computational models by representing plants explicitly as cylinders (e.g., Baptist et al., 2007; Vargas-Luna et al., 2015), comparable to the approach of many flume studies, or by accounting for drag from foliage, stems, and streamlined vegetation, but such an approach is currently not widely adopted because of limited ability to specify all parameters (e.g., Boothroyd et al., 2015, 2017; Jalonen et al., 2013; Västilä and Järvelä, 2014). Vargas-Luna et al. (2015) showed, through coupling of numerical modeling and experimental work, that representing vegetation as cylinders is most appropriate for dense vegetation. Iwasaki et al. (2015) used a two-dimensional model that accounted for vegetation drag (as cylinders) to explain morphological change of the Otofuke River, Japan, caused by a large flood event in 2011 that produced substantial channel widening and vegetation-influenced bar building. They found that vegetation allowed bar-induced meandering to maintain moderate sinuosity, whereas in the absence of vegetation, river planform would switch from single thread to braided. Marjoribanks et al. (2017) modeled the effects of vegetation mass blockage and drag, specifying vegetation as cylinders, for a small (∼ 5 m wide by 16 m long), straight river reach, and found velocity reduced broadly throughout the channel.

As the above review suggests, there have been considerable advances in laboratory and computational modeling of vegetation effects on hydraulics that complement understanding of bar and bend morphodynamics and reciprocal interactions between riparian vegetation and river processes (Corenblit et al., 2007; Gurnell, 2014; Osterkamp and Hupp, 2010; Schnauder and Moggridge, 2009). Challenges persist, however, in representing field-scale complexities in a modeling framework that allows for testing field-scale interactions between plants, flow, and channel morphology on vegetated point bars. Here, we tackle key elements of this problem by investigating how the distribution of woody vegetation on a point bar influences bend hydraulics and flow steering across a range of flood magnitudes using a two-dimensional modeling approach informed by high-resolution topography and vegetation morphology data that spatially define vegetation drag. We model a range of vegetation densities and plant morphologies representing different stages of pioneer woody vegetation growth on a point bar. We vary discharge in the model to represent the stage-dependent effects of vegetation on hydraulics, as well as different flood stages that may be important for the recruitment of plants and the erosion or deposition of sediment within the channel bend. We predict that the presence of woody vegetation affects bar and meander dynamics by steering flow, thereby influencing the morphodynamic evolution of vegetated channels. Our objectives are to (1) determine which vegetation morphology and flow conditions result in the greatest changes to channel-bend hydraulics, and (2) infer how these changes in hydraulics would impact channel-bend morphodynamics and evolution. The insights derived from our analysis are relevant for understanding ecogeomorphic feedbacks in meandering rivers and how such feedbacks are mediated by plant traits and flow conditions, and for riparian plant species management along river corridors.

2 Methods

2.1 Study area

To meet our objectives, we model a point bar-bend sequence on the Bitterroot River, southwest Montana, United States (Fig. 1). Our field site has a pool-riffle morphology and a wandering pattern, with channel bends, point bars, and woody vegetation on bars and floodplains. The study reach is located on a private reserve (MPG Ranch) with minimal disturbance to the channel and floodplain, and flow and sediment supply are relatively unaltered by flow regulation, because the only significant dam in the contributing watershed is ∼ 120 km upstream of the study reach, on a tributary. Annual mean discharge is 68 m³ s⁻¹, bankfull Shields number is 0.03, median grain size is 23 mm, and drainage area is ∼ 6200 km². Woody bar vegetation is composed of sand bar willow (Salix exigua) and cottonwood (Populustrichocarpa) seedlings, saplings, and young trees (Fig. 2a, c). Ponderosa pine (Pinus ponderosa), gray alder (Alnus incana), and black cottonwood (Populus trichocarpa) comprise mature floodplain forest species.

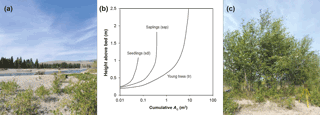
Figure 2 Modeled vegetated bar (a) on the Bitterroot River, showing sparse Populus seedlings and saplings. Average cumulative A_c (projected vertical frontal area) of Populus varies with height above the bed, and the age and size of the individual (b); the greatest cumulative A_c is reached for young trees (c). The average A_c profile for seedlings (sdl), saplings (sap), and young trees (tr) was used to assign an A_c value based on flow depth for each run. Photo credit: Sarah Doelger.

2.2 Flow model

To characterize the influence of a vegetated bar on channel-bend hydraulics, we used an edited version of FaSTMECH, a hydrostatic, quasi-steady flow model contained within iRIC (Nelson et al., 2016; http://i-ric.org/en/index.html). FaSTMECH solves the depth- and Reynolds-averaged momentum equations in the streamwise and stream-normal directions, in a channel-fitted curvilinear coordinate system, using a finite-difference solution (Nelson et al., 2003, 2016). By convention, values of u and v are positive downstream and toward the left bank, respectively. Bed stress closure is achieved through a drag coefficient (C_d) scheme. Details of the modeling process, beyond those provided in the text here, can be found in the Supplement.

We created the flow model domain in FaSTMECH by characterizing the topography and flow boundary conditions (discharge and water surface elevation at the downstream boundary) of a study reach on the Bitterroot River, Montana (Fig. 1). We surveyed channel topography with a combination of airborne lidar, echosounder and real-time kinematic (RTK) GPS surveys (see the Supplement). The resulting curvilinear orthogonal grid we created had an average cell size of 2.5 by 2.5 m for calibration runs (described below), and 5 by 5 m for the remaining runs. We linked transducer stage measurements at the downstream end of the study reach to discharge derived from USGS gaging station no. 2344000, Bitterroot River near Darby, Montana, corrected by contributing area for our field site. Water surface elevations at the downstream boundary for modeled discharges were extracted from the stage–discharge relationship. Discharge was measured at the field site and compared to the adjusted USGS 12344000 value and found to agree within 10 % (Table 1).

Table 1 Calibration flows, showing the channel drag (C_d) and lateral eddy viscosity (LEV), and the root mean square error (RMSE), water surface elevation (WSE), and depth-averaged velocity ($\stackrel{\mathrm{‾}}{U}$).

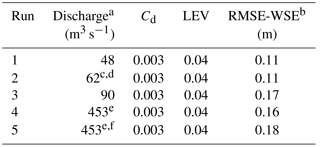
^a Corrected by contributing area from USGS 12344000. ^b More details on WSE are available in the Supplement. ^c Law-of-the-wall derived $\stackrel{\mathrm{‾}}{U}$ had RMSE of 0.24 m s⁻¹, mean measured $\stackrel{\mathrm{‾}}{U}$ 1.21 m s⁻¹, and mean modeled $\stackrel{\mathrm{‾}}{U}$ 1.05 m s⁻¹ (15 % error); see the Supplement for more details. ^d Discharge measured at site was within 10 % of contributing-area-corrected discharge. ^e Q₂ flow. ^f Vegetation model turned on.

FaSTMECH uses relaxation coefficients to control changes in a parameter between iterations (Nelson, 2013). Relaxation coefficients were set to 0.5, 0.3, and 0.1 for ERelax, URelax, and ARelax, respectively, through trial and error. Convergence was found after 5000 iterations (mean error discharge < 2 %), considered indicative of adequate model performance for FaSTMECH (Nelson, 2013). We calibrated channel characteristics (bed roughness specified as C_d and lateral eddy viscosity, LEV) and considered them fixed after calibration (Table 1). We used a constant C_d, an approach that has been shown elsewhere to perform comparably to variable roughness in FaSTMECH (e.g., Segura and Pitlick, 2015). We set C_d to minimize the root mean square error (RMSE) of modeled water surface elevation (WSE) versus WSE measured in the field from 2011 to 2015, over a range of calibration flows (see the Supplement). In this calibration process, we manually varied C_d values from 0.01 to 0.001, resulting in a C_d of 0.003 and lowest RMSEs for WSE from 0.11 to 0.16 m for the lowest and highest calibration flows, respectively (Table 1). Similarly, we manually varied LEV from 0.01 to 0.001 during model calibration, resulting in a LEV value of 0.04, which minimized RMSE of depth-averaged velocity ($\stackrel{\mathrm{‾}}{U}=$ 0.24 m s⁻¹; Table 1) between modeled values and those measured at four cross sections (Fig. 1) (see the Supplement for details). The RMSE ranges obtained through calibration are consistent with values reported in other studies that have used FaSTMECH (e.g., Legleiter et al., 2011; Mueller and Pitlick, 2014; Segura and Pitlick, 2015), providing confidence in model performance.

To address the stage-dependent nature of the impact of a vegetated bar in altering bend hydraulics, we modeled flows with magnitudes corresponding to flows with return periods of 2 (Q₂; 453 m³ s⁻¹), 10 (Q₁₀; 650 m³ s⁻¹), 20 (Q₂₀; 715 m³ s⁻¹), and 100 (Q₁₀₀; 800 m³ s⁻¹) years. We converted Cartesian coordinate velocity (U_x, U_y) to streamwise and stream-normal values (Fig. 3; the Supplement).

Figure 3 Region around the vegetated bar, showing cross-section (XS) locations and the conventions of the curvilinear grid to which model output was converted.

2.3 Modeling vegetation's impact on channel-bend hydraulics

We edited FaSTMECH to account for vegetation form drag (F_D) using the following drag equation for rigid vegetation:

$$\begin{array}{}\text{(1)}& F_{\text{D}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }{C}_{\text{d,v}}{A}_{\text{c}}n{U}_c^{\mathrm{2}},\end{array}$$

where C_d,v is vegetation drag coefficient, A_c is projected vertical frontal area of vegetation (Nepf, 1999; Vargas-Luna et al., 2015, 2016), n is the stem density (number of stems m⁻²), and U_c is the approach velocity. Drag (F_D) is calculated per bed area (distributed over vegetation polygons). For U_c, we used node velocity (after Jalonen et al., 2013). The vegetation drag coefficient (C_d,v) was assigned a value of 1, a first-order approximation also used by others (Boothroyd et al., 2016; Nepf et al., 2013; Vargas-Luna et al., 2016). We modeled vegetation as cylinders by assuming the cylindrical stem frontal area is equal to A_c, specifying vegetation parameters by polygon with an associated n and height (m; allows for partitioning of A_c by flow depth). The model assumes a logarithmic velocity profile, although we recognize this is an oversimplification of how factors such as vegetation submergence alter velocity profiles (e.g., Manners et al., 2015).

We focused our analyses on a point bar (Fig. 1) that supports woody riparian vegetation (Populus seedlings, saplings, and young trees) most likely recruited mainly by flood dispersal. In our model simulations, we varied vegetation density (number of stems m⁻²) and A_c (m² plant⁻¹) on the vegetated bar for each of the four flows, and we compared model output to a no-vegetation (no veg) scenario. We considered two vegetation density cases: sparse (sps) and dense (dns). Our sparse case was based on the average density (0.02 stems m⁻²) obtained from the airborne lidar (see the Supplement for more details). Our dense case (20 stems m⁻²) was based on the average from random vegetation density plots measured on the bar, which ranged from < 1 to 227 stems m⁻² and is consistent with other dense field-measured values (Boyd et al., 2015; van Oorschot et al., 2016; Wilcox and Shafroth, 2013). For A_c, we used ground-based lidar to capture vegetation structure (Antonarakis et al., 2010; Bywater-Reyes et al., 2017; Manners et al., 2013; Straatsma et al., 2008). We scanned Populus patches representing different stages of pioneer woody vegetation growth: seedlings (sdl), saplings (sap), and young trees (tr). From these scans (postprocessed in the same manner described in Bywater-Reyes et al., 2017), we established an A_c–height relationship (Fig. 2b), from which depth-dependent A_c was extracted for each model run by assigning A_c based on the average bar flow depth from the corresponding no-vegetation scenario.

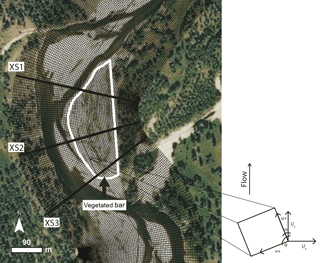
To test whether overbank (floodplain) vegetation (i.e., beyond the vegetated bar) contributes to flow steering in the main channel and influences the hydraulics of the cut bank – bar region of interest (Fig. 3), we included runs with and without floodplain vegetation for each of the four flows and seven bar vegetation scenarios, resulting in 56 model runs. We represented floodplain vegetation as was observed from airborne lidar (see the Supplement for details). These analyses showed that the hydraulics of the cut bank – bar region of interest (Fig. 3) were insensitive to whether or not floodplain vegetation (i.e., beyond the vegetated bar) was present across the range of modeled flow conditions. Therefore, the descriptions of hydraulics we present in the results section are based only on scenarios varying bar vegetation conditions.

We considered hydraulic (u, v) solutions for three cross sections at locations across the bar and cut bank of the channel bend, representing the upstream, midstream, and downstream portions of the bar (Fig. 3). We additionally considered the hydraulics and potential for bed mobility spatially, using the Shields number, τ^*, as an indicator of bed mobility:

$$\begin{array}{}\text{(2)}& {\mathit{\tau }}^{*}={\displaystyle \frac{\mathit{\tau }}{\left({\mathit{\rho }}_{\text{s}}-\mathit{\rho }\right)gD}},\end{array}$$

where τ is boundary shear stress, ρ_s is sediment density, g is acceleration due to gravity, and D is grain diameter. We used the median grain diameter from pebble counts collected on the study bar and along cross sections (Fig. 1). We compared the solutions for vegetation runs for each flow to no-vegetation scenarios to evaluate which configurations had the greatest influence on hydraulics.

3 Results

The effects of point bar vegetation on modeled hydraulics across our study reach are presented here in several ways. First, we compare vegetation results, for different density and growth stages, to the no-vegetation case; and second, we compare results spatially at different cross sections across the bar at different discharges. For the no-vegetation case, velocity and shear stress were generally highest in the thalweg and lower over the bar (Fig. 4). Downstream velocity (u) was generally greater than stream-normal velocity (v). The greatest v magnitudes were for the downstream cross section (XS1; Fig. 5c, d). With increasing flow magnitude, both u (Fig. 5b) and v (Fig. 5d) decreased within the thalweg region but stayed relatively constant over the bar. A similar trend was seen at the mid-bar cross section (XS2) with u decreasing within the thalweg region as flow magnitude increased but remaining relatively constant over the bar (Fig. 6). In contrast, u increased within the thalweg region and over the bar with increasing flow (Fig. 7a, b) at the upstream cross section (XS3), whereas v stayed relatively constant (Fig. 7c, d).

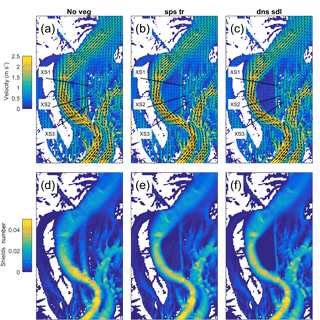
Figure 4 Plan view comparison of channel-bend hydraulics (velocity, a–c; Shields number, d–f) for the Q₁₀ no-vegetation (a, d), sparse young trees (b, e), and dense seedlings (c, f) runs. Velocity and Shields number are reduced on the bar with increasing size or density of plants, and flow paths within the thalweg and adjacent to the vegetation patch become more concentrated.

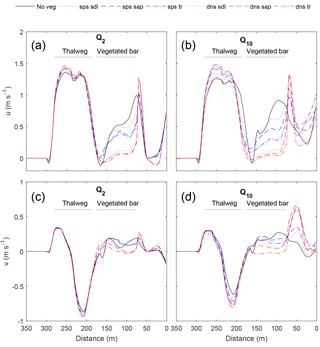
Figure 5 Effect of the vegetated bar on the streamwise (u; a, b) and stream-normal (v; c, d) velocities at the downstream cross section (XS1) for the Q₂ (a, c) and Q₁₀ (b, d) flows, with distance from the river right-end point (Fig. 4). With increasing discharge, plant size (seedling to young trees) and density, u is increased and v decreased within the thalweg. Both u and v (positive downstream and toward left bank, respectively) are decreased over the bar, and for the sparse young trees and all dense scenarios increased at the edge of the patch.

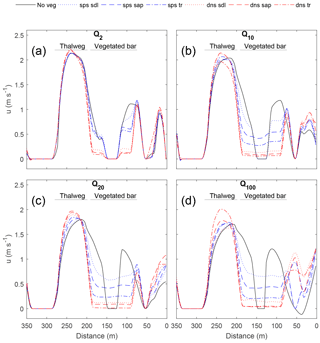
Figure 6 Effect of the vegetated bar on the streamwise (u) velocity at the midstream cross section (XS2) for the Q₂ (a), Q₁₀ (b), Q₂₀ (c), and Q₁₀₀ (d) flows, with distance from the river right-end point (Fig. 4). In the thalweg, u increases and the maximum shifts toward the left bank. On the bar, velocity is decreased in the patch and increased at the right edge of the patch.

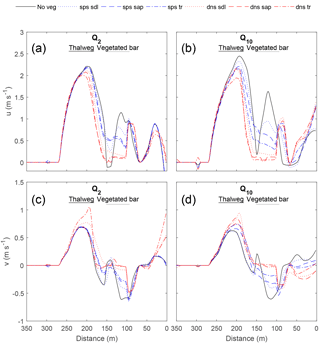
Figure 7 Effect of the vegetated bar on the streamwise (u; a, b) and stream-normal (v; c, d) velocities at the upstream cross section (XS1) for the Q₂ (a, c) and Q₁₀ (b, d) flows, with distance from the river right-end point (Fig. 4). In the thalweg and at the head of the bar, u is decreased with increasing seedling size and density. For Q≥Q₁₀, v became more negative adjacent to the vegetation patch.

The manner in which different vegetation densities and growth stages influenced hydraulics varied spatially around the bend. In general, adding vegetation increased velocity within the thalweg and at the edge of the vegetation patch compared to the no-vegetation case, creating concentrated flow paths adjacent to the patch while reducing velocity and shear stress at the head of the bar and within the vegetation patch. The effect of the vegetated bar on channel-bend hydraulics became more pronounced with discharges increasing from Q₂ to Q₁₀. Furthermore, sparse vegetation behaved similarly to the no-vegetation scenario for low flows but had an increasing effect on hydraulics at Q₁₀. Vegetation effects increased steeply from Q₂ to Q₁₀ with modest changes thereafter. In general, hydraulics were more sensitive to plant morphology differences (A_c) for sparse conditions compared to dense conditions (Figs. 5–7).

At the downstream end of the bar (XS1; Fig. 5), vegetation increased the magnitude of downstream (u) and stream-normal (v more negative) velocity within the thalweg region, and reduced velocities over the bar. For flows ≥ Q₁₀, the high-velocity core became more concentrated and shifted away from the bar. Results for the Q₂₀ and Q₁₀₀ flows were similar to that of the Q₁₀ (Fig. S2). This thalweg effect became more pronounced with increasing plant density and plant size, except in the case of dense young trees, which behaved more similarly to the bare bar scenario for the Q₁₀ flow. Amplification of thalweg velocities at XS1 was greatest for the dense sapling scenario, with 17 and 12 % increases in u and v, respectively, for Q₁₀, and increases in velocity magnitude for flows > Q₁₀. On the vegetated bar, u and v decreased within the vegetated patch, with u values reduced up to 56 % for the sparse young tree scenario and up to 95 % for the dense scenarios – these magnitudes are well above uncertainty in velocities. With increasing plant size and density, the values of u and v at the right edge of the vegetation patch were greater than or nearly equal to that in the thalweg, with a particularly large increase for dense scenarios. Thus, flow velocities were decreased within the patch, increased adjacent to the patch, and were deflected toward the left bank.

At the midstream position (XS2), downstream velocities (u) in the thalweg region were greater than at XS1. The impact of the vegetation patch on u for XS2 was pronounced, with u increased up to 30 % within the thalweg and the maximum value of u shifted toward the left bank with increasing plant size, density, and discharge (Fig. 6). Like XS1, the thalweg effect reached a maximum for dense saplings at Q₁₀. As flow increased (Q₂₀ and Q₁₀₀), dense trees had the greatest effect on increasing thalweg u. On the bar, the effect on u for XS2 was similar to XS1. Values of u decreased with increasing size and density of plants, and u increased at the right outer edge of the vegetation patch. Over the bar, u was reduced up to 99 % for the dense scenarios compared to the no-vegetation scenario and increased at the edge of the patch up to 3300 %. At XS2, v values were small compared to XS1 and XS3, and were relatively insensitive to the presence of the vegetation patch (Fig. S3).

At the upstream end of the bar (XS3; Fig. 7), an opposite trend in changes in u within the thalweg was observed. With increasing seedling size and density, u decreased within the thalweg and at the head of the bar, with a maximum reduction in u of 29 % for dense scenarios. Results for the Q₂₀ and Q₁₀₀ flows were similar to that of the Q₁₀ (Fig. S4). For Q≥Q₁₀, v was more positive to the left (70 %) of the vegetation patch and within the thalweg, and more negative to the right of the vegetation patch. Within the vegetation patch, u and v were reduced (96 and 100 %, respectively). Thus, flow was steered away from the vegetation patch.

4 Discussion

4.1 Impact of vegetation on channel-bend hydraulics

Our results illustrate that vegetation enhances flow steering on bars, complementing previous work on bend dynamics in the absence of vegetation. Dietrich and Smith (1983) showed that bars steer flow in a manner that forces the high-velocity core toward the concave bank. They additionally found that flow over the heads of bars resulted in stream-normal components of velocity (v) and boundary shear stress (τ_n) directed toward the concave bank. Laboratory studies by Blanckaert (2010), representing sharp meander bends, illustrated that curvature-induced secondary flow associated with topographic steering concentrates most discharge over the deepest, outer parts of a bend and influences bed topography via vertical, downwelling velocities that contribute to pool scour and inward, near-bed velocities that help maintain steep, transverse bed slopes. In our simulations, the presence of dense vegetation increased downstream velocity (u) within the thalweg up to 30 % and shifted the high-velocity core toward the cut bank, at the mid- and downstream sections of the channel bend investigated. Vegetation effects on stream-normal velocity (v) also illustrated flow steering toward the concave bank. Vegetation increased the magnitude of v at both the up- and downstream ends of the channel bend, by increasing stream-normal flow toward the cut bank at the head of the bar and around the toe of the bar, where positive v values within the thalweg region at the upstream cross section show outward flow steering. By extension, stream-normal shear stress, is directed toward the concave bank. At the head of the bar, flow was additionally slowed within the channel (u decreased) and steered away from the vegetation patch, increasing flow within a side channel adjacent to the bar head and creating concentrated flow paths adjacent to the patch.

This modeling effort also contributes to evaluation of the stage dependence of flow steering by bars. Whiting (1997) hypothesized that convective accelerations arising from flow steering would be most important at low flows, whereas Legleiter et al. (2011) showed that steering from bars continued to be important with increasing discharge. Our results suggest that flow steering will continue to be important over a range of flows for vegetated bars; i.e., vegetation effects on flow did not decrease with increasing discharge, consistent with Abu-Aly et al. (2014). We found that vegetation began to have a detectable impact on channel-bend hydraulics for flows greater than Q₂, when plants were inundated, and that vegetation-induced alteration of hydraulics was initially steep from Q₂ to Q₁₀, with modest changes thereafter.

In general, we found the impact of the vegetated bar on channel-bend hydraulics to vary with both plant density and morphology, and our modeling illustrated nuances in these relationships. Plant morphology differences affected hydraulics preferentially for sparse cases, whereas dense cases were similar. Dense young trees did not always result in the maximum alteration to channel-bend hydraulics – particularly for u during the Q₁₀ flow. At the downstream end of the bar, the high-velocity core became more concentrated and shifted away from the bar with increasing plant density and plant size, except in the case of dense young trees. Dense young trees behaved more similarly to the bare bar scenario for Q₁₀. This indicates there may be thresholds whereby increasing density and size of vegetation no longer results in an additional hydraulic effect in some cases. Together, these results suggest altered bend hydraulics caused by bar vegetation may be most pronounced for vegetation-inundating flows up to Q₁₀ under sparse-vegetation conditions. We may expect vegetation–morphodynamic interactions to be strongest as recruited sparse woody riparian vegetation matures under moderate flow conditions (> Q₂ to Q₁₀), or conversely, if a bare bar establishes dense vegetation. This is consistent with the biogeomorphic phase concept (Corenblit et al., 2007, 2015a, b), whereby established vegetation has strong feedbacks with geomorphic processes but with the additional constraint of enhanced interactions under a specific range of flow magnitudes.

We acknowledge that some of our findings may be influenced by limitations of our modeling approach, which reflect persistent challenges in characterizing the complexities of vegetation architecture and flow in a modeling framework. Simplifications including representing plants as rigid cylinders (after Vargas-Luna et al., 2016) with a constant drag coefficient of 1 are consistent with other studies but likely overestimate vegetation drag at higher discharges, when the canopy is inundated and plants are more streamlined, reducing A_c and C_d,v (James et al., 2004). Future research directions include (1) refining how vegetation drag is represented, especially for sparse vegetation; (2) quantifying changes in drag that result from streamlining and reconfiguration during inundation; (3) including variations in drag coefficient for vegetation to represent depth dependence and complexities of vegetation architecture; and (4) evaluating effects of non-logarithmic vertical velocity structures (Aberle and Järvelä, 2013; Boothroyd et al., 2017; Nepf, 2012; Västilä et al., 2013; Västilä and Järvelä, 2014; Whittaker et al., 2013).

4.2 Implications for channel morphology and evolution

The reduction of velocity and shear stress within the thalweg at the bar head caused by the presence of the vegetated bar would be expected to decrease sediment transport in this region. Van Dijk et al. (2013), in an experimental channel, found bar vegetation to increase fine-sediment deposition upstream of the vegetation patch, analogous to the bar head of our work. This may contribute to bar-head maintenance, such that the head of the bar is not eroded. Maintenance of the bar head would be countered by the potential for chute cutoff (van Dijk et al., 2014) or channel switching that may result because of concentrated flow paths. Along the inside (river right) edge of the vegetated bar, a lower-elevation, chute-channel-like region is present, in which flow was concentrated and velocities increased as vegetation size and density increased. Seedling establishment was not successful in the lower-elevation region during the study period, possibly because higher shear stresses in this region limited fine-sediment deposition conducive to recruitment and/or exceeded uprooting thresholds (Bywater-Reyes et al., 2015). The concentrated flow paths adjacent to the vegetation patch, on the inside of the bar, may be characteristic of conditions on vegetated bars along channel bends more generally, where both ridge and swale topography and chute bars may be present (Kleinhans and van den Berg, 2011), and where chute cutoffs and vegetation roughness and cohesion interact to influence morphodynamics (e.g., Braudrick et al., 2009). Seedlings often recruit along floodlines (Schnauder and Moggridge, 2009), forming rows of trees. Low-velocity areas within the rows induce fine-sediment deposition, steering flow away from the rows, and increasing velocity and shear stress adjacent to the rows such that sediment is transported in these regions. This process has been invoked to explain how vegetation creates vegetated islands (Gurnell et al., 2001), alternating patterns of vegetated ridges and adjacent channels (Tooth and Nanson, 2000), and the evolution of anabranching channels (Tooth et al., 2008). Van Dijk et al. (2013) found flood-dispersed vegetation recruited on bars resulted in island braiding, whereas vegetation distributed uniformly across the floodplain maintained a single-thread meandering channel with increased sinuosity and decreased bend wavelength. Our analysis, more comparable to the flood-dispersed case, shows the potential for development of vegetated islands but also for obstruction of chute cutoff through bar-head maintenance; chute cutoff may be more likely in the absence of vegetation (Constantine et al., 2010).

The production of a low-velocity region over the vegetated bar could increase fine-sediment deposition, consistent with flume and field observations. Elevated sediment deposition within patches of woody seedlings, with variations depending on plant characteristics, has been documented in meandering (Kui et al., 2014) and straight (Diehl et al., 2017b) flumes. Gorrick and Rodríguez (2012), working in a flume in which vegetation patches were simulated with dowels, documented elevated fine-sediment deposition within the patches. Zones of fine-sediment deposition on bars associated with roughness from vegetation or instream wood can in turn create sites for plant germination and seedling growth (e.g., Gurnell and Petts, 2006). If reduced velocities result in increased deposition of sediment on the bar, bar accretion would induce additional topographic steering. This feedback would be expected to accelerate channel migration rates.

The increase in velocity and shift of the high velocity core toward the cut bank combined with low velocities within the vegetation patch would create a large velocity gradient across the channel. A larger velocity gradient within the thalweg compared to over the bar would be expected to alter the dynamics of bank erosion. Parker et al. (2011) proposed that as a simple rule, bank erosion rate, $\dot{n}$, is proportional to an erosion coefficient, k, and half the streamwise velocity difference between the two banks, Δu:

$$\begin{array}{}\text{(3)}& \dot{n}=k\mathrm{\Delta }u.\end{array}$$

The parameter, k, represents the material cohesion and vegetation root properties that control bank erosion and varies between 10⁻⁸ and 10⁻⁷ (dimensionless). For an assumed k, vegetation-induced velocity gradients across the channel are expected to alter bank erosion rates.

Vegetation “pushing” flow toward the outer bank is analogous to “bar push” (Allmendinger et al., 2005; Parker et al., 2011), whereby a rapidly accreting point bar may cause erosion at the outer bank (Eke et al., 2014; van de Lageweg et al., 2014). This increase in bank erosion would be countered by deposition of fine sediment on the bar resulting from the vegetation-induced reduction in velocity in this region, that may in turn induce additional “push” through bar building (e.g., Eke et al., 2014). Coarse bank roughness counters this effect, pushing the high-velocity core back toward the center of the channel (Gorrick and Rodríguez, 2012; Thorne and Furbish, 1995). The balance between erosion of the bank and deposition on the bar would thus dictate whether net erosion or net deposition within the active channel occurs, inducing changes in channel width (Eke et al., 2014), and altering channel morphology.

5 Conclusion

The presence of a vegetated bar in a gravel-bed river altered both streamwise and stream-normal components of velocity vectors for overbank flows, with an increasing effect with discharge and both plant density and size. Vegetation steered flow away from the vegetated bar, creating concentrated flow paths in surrounding low-elevation side channels and a low-velocity region over the vegetated patch. Flow was slowed at the apex of the bar and increased within the thalweg around the bend. These changes in hydraulics could increase fine-sediment deposition on the bar, potentially creating hospitable sites for vegetation recruitment, and increasing bank erosion that is dependent on stream-normal velocity gradients. This pattern would tend to reduce stream-normal sediment transport at the bar head but increase it around the remainder of the bend.

Following the pattern of hydraulics, we would expect vegetation to change the morphodynamic evolution of channels with vegetation pushing flow in a manner typically attributed to bars, and increasing bank erosion rates. Bank retreat may induce bar building, which could be accelerated by fine-sediment deposition within the vegetation patch. This feedback would induce additional topographic steering from the presence of the bar. With a numerical model, we have characterized mechanisms by which channels with vegetated bars may evolve different morphologies and migration rates compared to those without, thereby contributing to our understanding of ecogeomorphic feedbacks in river–floodplain systems (Gurnell, 2014) and of how life influences landscapes (Dietrich and Perron, 2006).

Appendix A: List of terms

Ac	vegetation frontal area (m2)
Cd	channel drag coefficient
Cd,v	vegetation drag coefficient
D	median grain size (m)
FD	vegetation drag (N m−2)
g	acceleration due to gravity (m s−2)
k	bank erosion coefficient
u	streamwise component of velocity (m s−1)
$\stackrel{\mathrm{‾}}{U}$	depth-averaged velocity (m s−1)
Ux	x component of velocity in Cartesian coordinate system (m s−1)
Uy	y component of boundary velocity in Cartesian coordinate system (m s−1)
Uc	approach velocity (m s−1)
v	stream-normal component of velocity (m s−1)
ρ	density of water (kg m−3)
ρs	density of sediment (kg m−3)
τ	boundary shear stress (N m−2)
τ*	Shields number
n	stem density (number of stems m−2)
$\dot{n}$	bank erosion rate

Information about the Supplement

Supporting experimental procedures and additional result figures can be found in the Supplement.