the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Entrainment and suspension of sand and gravel
Jan de Leeuw
Michael P. Lamb
Gary Parker
Andrew J. Moodie
Daniel Haught
Jeremy G. Venditti
Jeffrey A. Nittrouer
The entrainment and suspension of sand and gravel are important for the evolution of rivers, deltas, coastal areas, and submarine fans. The prediction of a vertical profile of suspended sediment concentration typically consists of assessing (1) the concentration near the bed using an entrainment relation and (2) the upward vertical distribution of sediment in the water column. Considerable uncertainty exists in regard to both of these steps, especially the near-bed concentration. Most entrainment relations have been tested against limited grain-size-specific data, and no relations have been evaluated for gravel suspension, which can be important in bedrock and mountain rivers. To address these issues, we compiled a database with suspended sediment data from natural rivers and flume experiments, taking advantage of the increasing availability of high-resolution grain size measurements. We evaluated 12 dimensionless parameters that may determine entrainment and suspension relations and applied multivariate regression analysis. A best-fit two-parameter equation (r2=0.79) shows that near-bed entrainment, evaluated at 10 % of the flow depth, decreases with the ratio of settling velocity to skin-friction shear velocity (), as in previous relations, and increases with Froude number (Fr), possibly due to its role in determining bedload-layer concentrations. We used the Rouse equation to predict concentration upward from the reference level and evaluated the coefficient βi, which accounts for differences in the turbulent diffusivity of sediment from the parabolic eddy viscosity model used in the Rouse derivation. The best-fit relation for βi (r2=0.40) indicates greater relative sediment diffusivities for rivers with greater flow resistance, possibly due to bedform-induced turbulence, and larger ; the latter dependence is nonlinear and therefore different from standard Rouse theory. In addition, we used empirical relations for gravel saltation to show that our relation for near-bed concentration also provides good predictions for coarse-grained sediment. The new relations extend the calibrated parameter space over a wider range in sediment sizes and flow conditions compared to previous work and result in 95 % of concentration data throughout the water column predicted within a factor of 9.
- Article
(6388 KB) - Full-text XML
-
Supplement
(505 KB) - BibTeX
- EndNote
The suspension of sediment by water plays a critical role in the dynamics of rivers, river deltas, shallow marine environments, and submarine canyons and fans. For example, suspended sediment dominates the load of lowland rivers and builds land in subsiding river deltas and coastal landscapes (Ma et al., 2017; Syvitski et al., 2005; Wright and Parker, 2004a). The transport of sediment on the continental shelf is dominated by the suspension of mud and sand due to wave and current bottom traction (Cacchione et al., 1999; Nittrouer et al., 1986). Suspended sediment provides the negative buoyancy of turbidity currents that move sand and gravel to the deep sea. The suspension of gravel is important in large floods, such as outburst floods (Burr et al., 2009; Larsen and Lamb, 2016), and in steep mountain canyons (Hartshorn et al., 2002), where it can contribute to bedrock erosion (Lamb et al., 2008a). Suspended sediment transport is also important in landscape engineering, such as river restoration (Allison and Meselhe, 2010), fish habitat (Mutsert et al., 2017), and the capacity of dams and reservoirs (Walling, 2006). The balance between entrainment and deposition from suspension determines patterns of deposition and erosion in these environments and therefore controls landform morphology and stratigraphic evolution (Garcia and Parker, 1991; Paola and Voller, 2005). To predict suspended sediment flux across these environments, we need robust theory for the entrainment of sediment from the bed and the vertical distribution of suspended sediment in the water column.
We focus here on understanding the suspended sediment load of cohesionless grains that are entrained from the bed (i.e., suspended bed material) rather than wash load. Most models for sediment suspension are based on the application of Rouse theory (Rouse, 1937; Vanoni, 1946),
where C (L3 L−3) is the volumetric sediment concentration at elevation (z; L) above the bed, Ca (dimensionless) is the reference near-bed concentration at z=a (unit: L), and H (L) is the flow depth. P denotes the dimensionless Rouse number,
in which ws (L T−1) is the particle settling velocity, κ is the dimensionless von Karman constant of 0.41, u∗ (L T−1) is the bed shear velocity, and β is a dimensionless factor that accounts for differences between the turbulent diffusivity of sediment and the parabolic eddy viscosity model used to derive the Rouse equation (e.g., Graf and Cellino, 2002). Although more sophisticated models exist, some of which abandon the Rouse theory entirely in favor of a more rigorous turbulence model (Mellor and Yamada, 1982), the Rouse equation remains a useful and tractable approach for modeling and field application (Graf and Cellino, 2002; van Rijn, 1984; Wright and Parker, 2004b). The Rouse equation was derived assuming an equilibrium suspension whereby the upwards volumetric flux of sediment per unit area due to turbulence (Fz; L T−1) is balanced by a downwards gravitational settling flux (Cws) (Fig. 1) (Rouse, 1937). It predicts the shape of the concentration–depth profile, with a greater gradient in concentration for larger P (Fig. 1). By mass balance, the difference between entrainment, Fza, and settling, Caws, fluxes per unit area near the bed (at z=a) controls the bed deposition rate, dzb∕dt (L T−1) (Parker, 1978), i.e.,
where λ (dimensionless) is the bed porosity, and is a dimensionless sediment entrainment rate or entrainment parameter (Garcia and Parker, 1991). At steady state, Eq. (3) reduces to Ca=Es; thus, the near-bed entrainment rate, Es, is necessary to predict both the vertical distribution of suspended sediment at steady state (i.e., Ca in Eq. 1) and the rate of erosion and deposition for disequilibrium suspensions (Eq. 3).
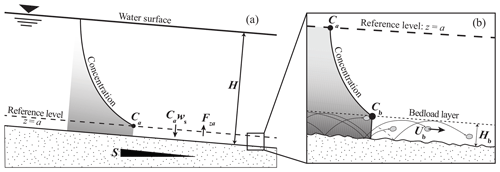
Figure 1(a) Conceptual diagram of suspended sediment concentration–depth profile of a river of depth H and bed slope S, showing the volumetric sediment concentration, Ca, settling flux per unit bed area, Caws, and entrainment flux per unit bed area, Fza, at the reference level of z=a, in which z=0 is bed elevation. (b) Near-bed zone below the reference level showing the bedload layer with concentration Cb, bedload velocity Ub, and bedload-layer height Hb.
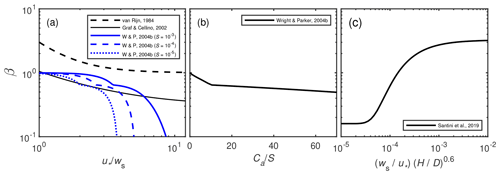
Figure 2Existing relations for the factor β (Eq. 2) as a function of (a) shear velocity normalized by setting velocity (van Rijn, 1984; Graf and Celino, 2002; Wright and Parker, 2004b), (b) near-bed concentration normalized by slope Ca∕S (Wright and Parker, 2004b), and (c) as proposed by Santini et al. (2019). In panel (a), the Wright and Parker relation (denoted W & P) used Ca calculated from the entrainment relation of Wright and Parker (2004b).
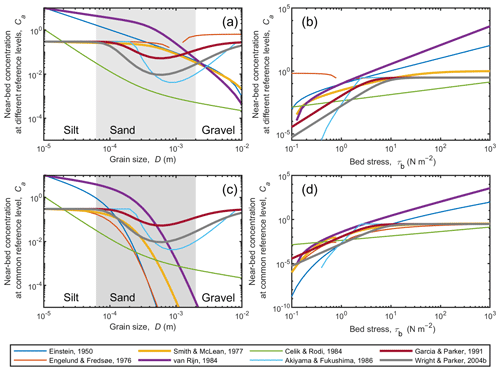
Figure 3Existing relations for near-bed suspended sediment concentration under equilibrium conditions (i.e., Es=Ca) at the reference level, z=a, specified by each study as a function of (a) grain size and (b) bed stress. In panels (c) and (d) the predicted concentrations are interpolated to a common reference level, a=0.05H, using the Rouse equation with β=1 to better compare models.
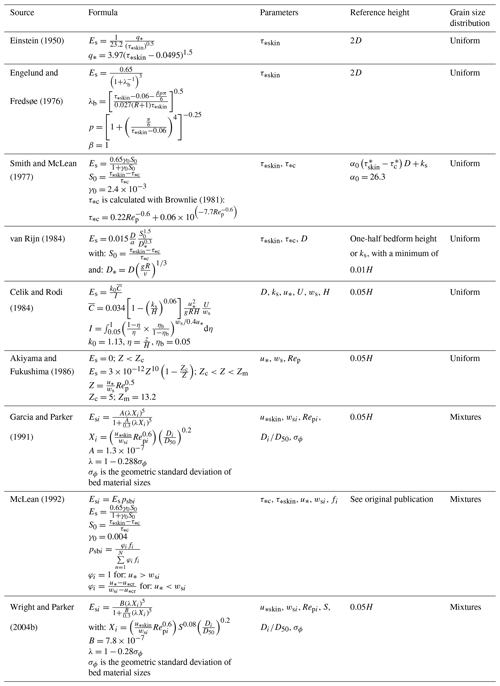
The application of Eqs. (1)–(3) requires the specification of β, Es and a, and the approach in previous work has been to identify important dimensionless variables and fit data from flume experiments and natural rivers to these variables (e.g., Smith and McLean, 1977; van Rijn, 1984; Garcia and Parker, 1991). Owing to differences in datasets analyzed and the dimensionless variables explored, there is considerable deviation in the form of previous models and their predictions (Figs. 2 and 3, Tables 1 and 2). For example, Einstein (1950), Engelund and Fredsøe (1976), van Rijn (1984), and Smith and McLean (1977) used a relation for a that depends primarily on grain diameter (D; L) and secondarily on or Shields number, (where τb (ML−1T−2) is bed stress, ρs (M L−3) is sediment density, and ρw (M L−3) is fluid density). Their rationale was based on the idea that there is a well-mixed near-bed zone of bedload transport and that suspended sediment is entrained from this zone (Fig. 1b). Thus, they developed relations for a that scale with the height of bedload saltation. In contrast, Garcia and Parker (1991) and Wright and Parker (2004b) argued for a simpler approach and used a reference height that is a small fraction of the flow depth, and they proposed a=0.05H as a useful reference height, with no dependence on D.
In practice the factor β is often neglected (i.e., β=1) under the assumption that the parabolic eddy viscosity assumption used to derive Eq. (1) represents the turbulent transport of fine suspended sediment well. β<1 in Eq. (2) has been attributed to damping of turbulence due to sediment-induced stratification, which alters the eddy viscosity (Einstein, 1955; Graf and Cellino, 2002; Wright and Parker, 2004a), and to flocculation, which increases the settling velocity of fine-grained sediment (e.g., Bouchez et al., 2011; Droppo and Ongley, 1994). Some formulas (van Rijn, 1984; Santini et al., 2019) and datasets (Graf and Cellino, 2002; Lupker et al., 2011) indicate β>1, which implies enhanced mixing of sediment relative to momentum (Table 1; Fig. 2). Graf and Cellino (2002) showed that turbulence generated by bedform roughness results in better sediment mixing and thus in a higher β. Field and flume data (Chien, 1954; Coleman, 1970; van Rijn, 1984) indicate that β is greater than unity for the coarse grain size fraction of the suspended material (Greimann and Holly, 2001). Nielsen and Teakle (2004) argued that the Fickian diffusion model in the derivation of the Rouse equation is not valid for steep concentration gradients, resulting in β>1. Most previous relations show a trend of decreasing β with increasing (van Rijn, 1984; Graf and Cellino, 2002; Wright and Parker, 2004b) (Fig. 2a), which could be due to turbulence damping associated with high concentration suspensions. Wright and Parker (2004b) showed that β is also a function of reference concentration divided by slope (Ca∕S) (Fig. 2b), which they attributed to sediment stratification. Santini et al. (2019) found that β is a function of and the ratio between flow depth and bed grain size (H∕D) (Fig. 2c).
Compared to β, even larger uncertainty exists in the dimensionless entrainment rate, Es. In previous work, Es was assessed by measuring the near-bed concentration for equilibrium suspensions, since Es=Ca under those conditions (i.e., in Eq. 3). Previous work found that Ca was a function of bed stress and grain size (Fig. 3; Table 2) (Einstein, 1950; Engelund and Fredsoe, 1976; Smith and McLean, 1977; van Rijn, 1984; Cedik and Rodi, 1984; Akiyama and Fukushima, 1986; Garcia and Parker, 1991; Wright and Parker, 2004b). While holding bed stress constant, most relations predict smaller Ca with increasing grain size across the sand regime, as expected, but some surprisingly show increasing Ca for coarse sands and gravel (Akiyama and Fukushima, 1986; Garcia and Parker, 1991; Wright and Parker, 2004b) (Fig. 3a, c). Due to the greater weight and settling velocity of larger particles, this behavior is unrealistic and likely occurs because these coarse particles are outside the data range used to fit the relations. Despite the importance of gravel suspension in steep mountain rivers and megafloods, data do not exist to evaluate the models in the gravel regime. All relations show increasing Ca with bed stress, as expected, but there are orders of magnitude differences in the predictions for Ca (Fig. 3b). Part of this deviation is due to differences in the reference level (z=a) (Fig. 3b), but even when using a common reference level (a=0.05H; Fig. 3d), significant variability still exists. Some of the variance is also due to extrapolating the models beyond the range in which they were calibrated; for example, van Rijn (1984) predicts concentrations greater than 100 % at high shear stresses.
We revisited the problem of sediment entrainment and the suspension of cohesionless bed sediment by compiling a large database of sediment-size-specific data for bed–sediment mixtures, testing existing relations against the database, and proposing improved relations for Es and P. Several existing formulas for Es are applicable only to uniform-sized bed sediment (Akiyama and Fukushima, 1986; Celik and Rodi, 1984; Einstein, 1950; Engelund and Fredsøe, 1976; van Rijn, 1984; Smith and Mclean, 1977) (Table 2). However, given the strong control of grain size on near-bed concentrations, accurate formulas likely need to make grain-size-specific predictions for sediment mixtures (Garcia and Parker, 1991; McLean, 1992; Wright and Parker, 2004b). Our database takes advantage of high-resolution grain size measurements using laser diffraction (Lupker et al., 2011; Gitto et al., 2017; Haught et al., 2017; Santini et al., 2019), which allows a single concentration profile to be separated into many grain-size-specific concentration profiles. Our dataset also contains a wide range grain sizes, extending into the silt regime (median bed sizes range from 44 to 517 µm), and expands on the number of field measurements compared to previous efforts. We are unaware of studies on Ca for gravel, but data do exist for saltation heights, velocities, and bedload fluxes for gravel, and calibrated relations for these variables also exist (Chatanantavet et al., 2013; Sklar and Dietrich, 2004). To attempt to better constrain suspension of very coarse sand and gravel, we used existing semiempirical saltation theory for gravel to check for consistency between sand suspension data and what might be expected for near-bed gravel concentrations.
2.1 Suspended sediment profiles
Based on previous theory, we searched for available datasets from rivers and flume experiments that had suspended sediment profiles (C(z)), depth-averaged flow velocity (U), flow depth (H), channel bed slope (S), bed material grain size (D), and the grain size distribution of the bed material and suspended sediment samples (Tables 3 and S1 in the Supplement). Some of the experimental studies used a narrow grain size distribution, and, like previous work, we assumed that the sediment distribution from these studies was uniform. Many of the older datasets were used in empirical regressions from previous relations (e.g., Garcia and Parker, 1991; van Rijn, 1984; Wright and Parker, 2004b). In addition, we used a river dataset from the Yellow River (Moodie, 2019), which provides a fine-grained end-member. In total, our database contains 180 concentration profiles from eight rivers and 62 profiles from six different experimental studies. We analyzed only the grain fractions coarser than 62.5 µm (i.e., sand). The mud fraction was present in the bed only in small amounts, and following previous work, mud was assumed to require a different approach, potentially due to supply limitation (Garcia, 2008), cohesion, or flocculation. Grain size distributions in older studies were determined from sieve analysis of bed material and suspended sediment samples. The more recent studies used laser diffraction techniques, which have the advantage that a larger number of grain size classes can be distinguished. We calculated the grain-size-specific suspended sediment concentration (Ci) using
where fi (dimensionless) is the mass fraction of grains of the ith size and Ctot is the total suspended sediment concentration for all sizes. In addition, we computed the D50 (median grain size) and D84 of the bed material using linear interpolation between the logarithm of D and the cumulative size distribution.

Figure 4(a) Example of suspended sediment data linearized in Rouse coordinates with a fitted Rouse profile (Eq. 1), in which z is the elevation above the bed, H is the flow depth, and extrapolation to the reference level at z=a gives the reference concentration, Ca. (b) Effect of the choice of reference level elevation on the r2 of the best-fit entrainment relation, Esi, to the data.
Concentration profiles in the database typically contain three to eight measurements in the vertical dimension. The Rouse profile was fitted to the profile data for each grain size class in log-transformed space using linear least squares to find Pi (Fig. 4a). Confidence bounds (68 %; 1σ) for the fitted coefficients were obtained using the inverse R factor from QR decomposition of the Jacobian. Data were excluded from further steps in the analysis if the ratio between the upper and lower bound of the confidence interval was greater than 10, as these data do not follow a Rouse relation for unknown reasons (e.g., measurement error) and would appear as sparse outliers. We also eliminated points with Pi<0.01, as these profiles are nearly vertical, which poorly constrains settling velocity to be very near zero. Of the data analyzed, 201 points (15 %) were excluded based on these criteria. Some studies (Bennett et al., 1998; Muste et al., 2005) have shown that P (or β) can vary over the flow depth, but this effect cannot be incorporated into our approach; instead we found one value of Pi that best fit the concentration profile for each grain size class.
We used the Rouse equation (Eq. 1) for each grain size class to extrapolate or interpolate the concentration to a reference level at 10 % of the flow depth; i.e., we set a=0.1H and ). Extrapolation to very near the bed can be difficult due to large concentration gradients and poorly constrained near-bed processes such as interactions with bedforms. However, a reference level that is too far away from the bed may poorly capture the exchange of sediment with the bed. Previous researchers used reference levels that were either at some fraction of the flow depth (Akiyama and Fukushima, 1986; Celik and Rodi, 1984; Garcia and Parker, 1991; Wright and Parker, 2004b) or that were related to the bed roughness height (Einstein, 1950; Engelund and Fredsøe, 1976; Garcia and Parker, 1991; Smith and Mclean, 1977) (Table 2). We explored the collapse of the entrainment data for both types of reference levels. For each reference level, we fit our preferred and best-fitting two-parameter entrainment relation (as described in the Results section) to the data with as the first parameter and the Froude number as the second parameter. We found that a reference level at a fraction of the flow depth gave a better collapse of the entrainment data than a reference level related to the saltation layer height. Furthermore, we also tested different flow depth fractions and found that the fit improved, in a least-squared sense, as the reference level moved to a larger fraction of the flow depth (Fig. 4b). However, there is little change in r2 once the reference level is higher than ∼10 % of the flow depth. Therefore, we used a reference level at 10 % of the flow depth for all results shown below.
For sediment mixtures, the grain-size-specific near-bed concentration is partially controlled by the fraction of each grain size class in the surface bed material. To account for this effect, Garcia and Parker (1991) introduced an entrainment rate (Esi) for each grain size class that is linearly weighted by the fraction of that material in the bed:
where Cai is the near-bed concentration of that grain size class and Fbi is the mass fraction of bed material that falls in that grain size class. For uniform sediment, the entrainment rate (Esi) is equivalent to the near-bed concentration (Cai).
2.2 Independent parameters and profile fitting
Here we review the independent parameters that we evaluated for dependencies with a dimensionless entrainment rate, Esi, and for βi in the Rouse number. The primary group of parameters describes the ratio between bed stress and grain size or grain settling velocity. These parameters include the ratio between shear velocity and settling velocity (), whereby we evaluated the total shear velocity as
assuming steady, uniform unidirectional flow. Others have proposed that entrainment depends on the skin-friction portion of the total shear stress, u∗skin, rather that the total shear stress. To estimate u∗skin , we used the Manning–Strickler relation,
where ks=3D84 is the grain roughness on the bed, Hsk is the depth due to skin friction, and (e.g., Wright and Parker, 2004b). To calculate the particle settling velocity, we followed Ferguson and Church (2004) for each grain size class,
in which is the submerged specific density of sediment, ν (L2 T−1) is the kinematic viscosity of the fluid, C1=18 and C2=1 are constants set for natural sediment, and Di is the grain diameter within the size class of interest. Another parameter that relates to the ratio between bed stress and gravity acting on the grains is the Shields number,
and we again assumed steady, uniform flow to find τb=ρgHS. Similar to the shear velocity, it is also possible to calculate a Shields number for the skin-friction component of the total shear stress,
where by definition. Shields numbers can be rewritten in terms of through the use of a particle drag coefficient,
which we also evaluated (i.e., ).
The next group of parameters describes dimensionless particle sizes, including the particle Reynolds number,
Likewise, this parameter can also be calculated with the skin-friction component of the shear velocity,
A particle Reynolds number can be defined without shear velocity as
For sediment mixtures, the relative particle size might play a role due to hiding and exposure effects (Garcia and Parker, 1991; Wright and Parker, 2004b); this effect can be captured with . Sediment-induced density stratification can decrease entrainment by damping near-bed turbulence, and this effect is thought to be most important in deep, low-gradient rivers (Wright and Parker, 2004b). Wright and Parker (2004b) proposed that the ratio of near-bed concentration to bed slope is a good predictor for stratification, , for which they used Ca at 5 % of the flow depth. Large, low-gradient rivers also have small Froude numbers and low bed slopes, so we evaluated the Froude number and slope as additional parameters. The Froude number was calculated as
The entrainment rate could also be affected by turbulence or changes to the boundary layer from bed roughness or bedforms, which tend to correlate with a flow resistance friction coefficient (e.g., Engelund and Hansen, 1967),
We also evaluated H∕D50 as a proxy for flow resistance due to grain roughness.
In order to find relations that explain the variation in our best-fit Esi and Pi values from the vertical concentration profiles, we regressed the Esi and Pi values against the 12 variables described above (Eqs. 6–16). In some applications, like reconstructing flow conditions from sedimentary strata, it is useful to have an entrainment relation that depends on u∗skin, while for forward modeling a relation based on u∗ is preferred. The two shear velocities are highly correlated; therefore, we explored two versions of the fit relations using either u∗ or u∗skin, but not both at the same time. Because the Rouse parameter, Pi, by definition depends inversely on (or ) (Eq. 2), we found the best-fit relations for Pi rather than βi to avoid spurious correlation. We then solved for the equivalent relation for βi using the definition of Pi (Eq. 2). We started the analysis by testing all models with one explanatory variable and ranked the models according to the coefficient of determination from linear least-squares regression (r2) evaluated in log–log space. Next, a second parameter was used in addition to the first best-fitting parameter, and the resulting two-parameter models were ranked according to r2. The procedure was repeated with additional parameters until the increase in r2 was smaller than 0.04. For the fitting of multiparameter models, we varied the exponents on each parameter in the model simultaneously to find the combination of exponents that yielded the best fit. This approach gave a higher r2 compared to the stepwise approach used in previous work (e.g., Garcia and Parker, 1991) of first fitting the dominant variable and then fitting the secondary variables to the residuals. In addition, we tested fitting with the York method (Table S2), which gives less weight to data with large errors (York, 1968), but found only minor differences, so all results presented use the simpler linear least-squares method. All parameters were used to evaluate relations for Esi and βi except for Di∕D50, which we used only for Esi since it is relevant for particle–particle interactions at the bed surface. In the results we report two versions of the best-fitting one-, two-, and three-parameter models: one version that is based on the total bed shear stress and one version that is based on the skin-friction component of the bed shear stress. Model fits using all possible combinations of the input parameters are given in Table S2.
2.3 Comparison to theory for gravel
Although gravel suspension is important in bedrock and steep mountain rivers, as well as during megafloods, we are not aware of datasets of near-bed concentration in the gravel range. Following previous work (McLean, 1992; Lamb et al., 2008a), our approach was to derive the near-bed concentration in the bedload layer and then use Rouse theory to predict that concentration at 0.1H to compare with the sand dataset (e.g., Fig. 1b). The near-bed volumetric concentration within the bedload layer can be calculated by continuity as
where qb (L2 T−1) is the volumetric bedload flux per unit width, Hb (L) is the bedload-layer thickness, and Ub (L T−1) is the bedload velocity. Most relations for bedload flux take the form
where m and n are empirical constants, which we set to m=5.7 and n=1.5 (Fernandez Luque and van Beek, 1976), and τ∗c is the critical Shields number at initial motion, which we set according to Lamb et al. (2008b):
The bedload-layer height and velocity were determined from Chatanantavet et al. (2013). They compiled a large dataset of gravel saltation observations and found a good fit with the following relations:
Equations (17)–(21) were combined with a flow resistance relation (Eq. 7, assuming no form drag) and Cd=0.7 for gravel (Lamb et al., 2017) to calculate Cb in the bedload layer using a numerical iterative scheme. Manipulating the equations revealed that Cb is a function of only τ∗ and Fr. To calculate Ca for gravel, we extrapolated the concentration profile (Fig. 1b) from the top of the saltation layer to 0.1H using the Rouse equation (Eq. 1). To obtain the Rouse number, we used our best-fit one-parameter model that uses total shear velocity (u∗) (see Table 4). We then used a wide range of input parameters ( and ) relevant to the suspension of gravel in mountain rivers and large floods to predict a range of expected values of Ca for gravel. Although Eqs. (20) and (21) have not been tested for high Shields numbers in the suspension regime, they have reasonable limiting values (Ub=0.6U, Hb=H) and provide a starting place to compare sand entrainment and gravel saltation theories.
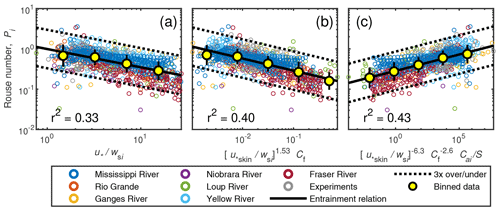
Figure 5Best-fit models for the Rouse number for grain-size-specific data with one parameter (a), two parameters (b), and three parameters (c); equations are in bold in Table 4. The plotting is done such that the exponent on the last parameter is unity; e.g., Eq. 23 in panel (b) was rewritten as to allow for comparison to plots of Garcia and Parker (1991) and Wright and Parker (2004b). Yellow filled symbols are the geometric mean, and the error bars indicate the geometric standard deviation within each arbitrarily spaced bin.
3.1 Rouse number, Pi
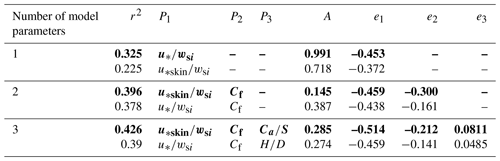
Equation (1) was fit to the concentration profile data wherein Pi was treated as a fitting parameter. Then Pi was regressed against the hypothesized controlling variables (Eqs. 11–16). Figure 5 and Table 4 show the results for Pi including our best-fitting one-, two-, and three-parameter models. The variable with the most explanatory power is (; r2=0.33). The best-fit two-parameter model that includes Cf is better than the predictions of the one-parameter model (r2=0.40). Going from a two-parameter model to a three-parameter model brings a smaller improvement (r2=0.43). Therefore, we recommend the two-parameter model for combined accuracy and simplicity:
although there are a number of models using different variables that yield similar r2 values (Table S2), and some combinations might be preferred over others depending on the application. Equation (22) indicates that sediment is better mixed in the water column with larger and with a larger bed roughness coefficient, Cf. Equation (22) performs well compared to previous relations, as is shown by a box plot of measured-to-predicted ratios (Fig. 6). For the best-fit two-parameter model, the measured-to-predicted ratio falls between 0.74 and 1.29 for 50 % of the data. Using a Rouse number with a constant β=0.94 also provides a reasonably good fit and an improvement over several more involved relations (Fig. 6).
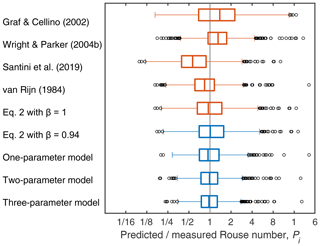
Figure 6Box plot of predicted versus measured Rouse number, Pi, for our models and previous models. The best-fit one-, two-, and three-parameter models correspond to the equations in bold in Table 4.
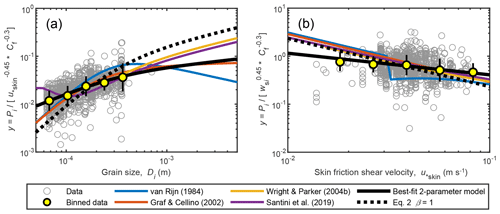
Figure 7The Rouse number, Pi, has been normalized to isolate the effect of (a) grain size and (b) skin-friction shear velocity to check for spurious correlation. Yellow filled symbols are the geometric mean, and the error bars indicate the geometric standard deviation within each bin. The best-fit two-parameter model is Eq. (22).
Equation (22) can be rewritten for βi using Eq. (2), and by assuming that u∗ in Eq. (2) is actually u∗skin, as
Because some of the dimensional quantities appear in multiple dimensional variables and because the dimensional variables are not necessarily independent from each other, we tested for spurious correlations by rearranging the two-parameter relation for βi to isolate the dimensional dependencies on grain size and skin-friction shear velocity (Fig. 7). The data and our model show a decrease in suspended sediment mixing in the water column with larger grain sizes, as expected (Fig. 7a). Previous relations show the same trend, but the relations of van Rijn (1984) and Graf and Cellino (2002) have stronger dependencies in the sand regime. Suspended sediments are better mixed with increasing skin-friction shear velocity (Fig. 7b). The data suggest that Pi varies proportionally to , whereas standard Rouse theory (Eq. 2) indicates that Pi is proportional to .
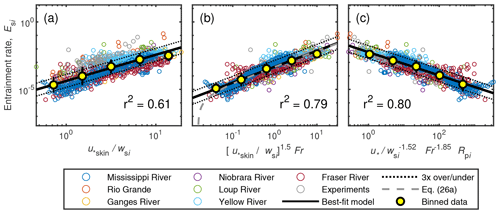
Figure 8Best-fit models for the dimensionless entrainment rate, Esi, for grain-size-specific data with one parameter (a), two parameters (b), and three parameters (c); equations are in bold in Table 5. The plotting is done such that the exponent on the last parameter is unity to allow for comparison to plots of Garcia and Parker (1991) and Wright and Parker (2004b). Yellow filled symbols are the geometric mean, and the error bars indicate the geometric standard deviation within each bin.
3.2 Dimensionless entrainment rate, Esi
Results for the best-fit dimensionless entrainment rate are shown in Fig. 8 and Table 5, and all possible variable combinations are given in Table S1. The following one-parameter relation gives the best fit with the data for Esi (r2=0.61) (Fig. 8a):
The Froude number was the most significant second parameter:
which has a significantly better fit (r2=0.79) than the best-fitting one-parameter relation (Fig. 8b). The addition of a third variable to the model gives little further improvement of the fit (Fig. 8c; r2=0.80), and many of the variables used as a third parameter give a similar level of improvement (Table S1). Using Eq. (25), 80 % of the entrainment data are predicted within a factor of 3 (Figs. 8b, 9). Along with our proposed new relation (Eq. 25), we also compared the dataset against the previous relations (Fig. 9). The box plots in Fig. 9 highlight that some relations systematically underpredict (Wright and Parker, 2004b) or overpredict the entrainment rate (Garcia and Parker, 1991). In addition, previous relations have a larger spread in measured-to-predicted ratios than Eq. (25). To check for spurious correlation in the dimensionless variables, we rearranged our two-parameter entrainment relation (Eq. 25) to isolate the dependencies of entrainment rate on grain size (Fig. 10a) and skin-friction shear velocity (Fig. 10b). Our relation indicates that entrainment depends on grain size to the −3.1 power in the sand range, whereas previous relations suggest a much weaker dependence. Compared to previous work, our relation also suggests a relatively weak dependence on skin-friction shear velocity ().
Table 5One-, two-, and three-parameter models for the entrainment parameter of the form . The two best-fitting versions of each model are shown, one with u∗ and one with u∗skin, and the bold value is the best fitting of the two (highest r2). See Table S2 for all model fits.
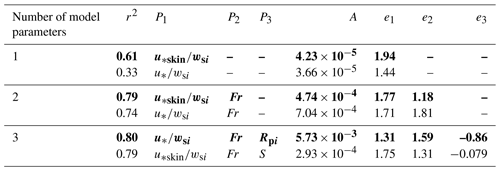
Figure 9Box plot of predicted versus measured entrainment parameters, Esi, for our models and previous models. The best-fit one-, two-, and three-parameter models correspond to the equations in bold in Table 5.
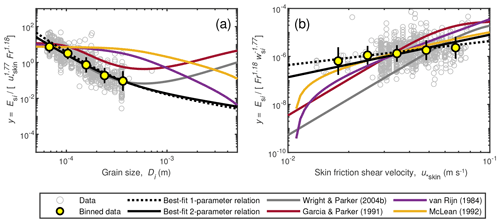
Figure 10Entrainment parameter, Esi, normalized to isolate the effect of (a) grain size and (b) skin-friction shear velocity to check for spurious correlation. Yellow filled symbols are the geometric mean, and the error bars indicate the geometric standard deviation within each bin. The best-fit models are Eqs. (24) and (25).
Similar to Garcia and Parker (1991) and Wright and Parker (2004b), we modified Eq. (25) such that the predicted entrainment rate is limited at 0.3, as total suspended sediment concentrations greater than 30 % by volume are not physically reasonable for dilute, turbulent flows. In addition, a threshold (0.015), best fit by eye, was added to the entrainment relation because the concentration data fall below the trend of the regression relation at the lower flow strengths (Fig. 8b), suggesting a threshold of significant sediment entrainment at the reference level. The resulting equation has the following form (Fig. 8b):
The equivalent formula for the best-fit two-parameter model without a form drag correction (Table 5) is
3.3 Predicting sediment concentration
In Sect. 3.1 and 3.2 we found the best-fit models for the dimensionless entrainment rate (Esi) and Rouse number (Pi). However, ultimately, we want to predict the sediment concentration throughout the water column, and the best-fit models for (Esi) and (Pi) do not necessarily combine to yield the best-fit model for sediment concentration owing to nonlinearity in Esi, Pi, and the Rouse equation (Eq. 1). Here we used different combinations of our preferred one-, two-, and three-parameter models for entrainment (Esi) and the Rouse number (Pi) to predict the grain-size-specific concentrations at each data point in the water column for all our entries in the database and assessed model performance (Table 6). The concentration predictions improve as more parameters are added to the entrainment model, whereas a Rouse model with more than one parameter makes the predictions worse (Table 6). Our preferred model for concentration throughout the water depth uses the two-parameter model to predict the entrainment rate and the one-parameter model for the Rouse number (Fig. 11). Such a model gives significantly better predictions than the most basic formulation that uses one-parameter models for entrainment and the Rouse number (r2 of 0.87 versus 0.65; Table 6). The goodness of fit is also fairly constant over the height of the flow; the upper 1∕3 of the flow has a slightly lower r2 (0.80) than the predictions from the lowest 1∕3 of the flow (r2=0.89) (Fig. 11); 95 % of the data are predicted within a factor of 9.
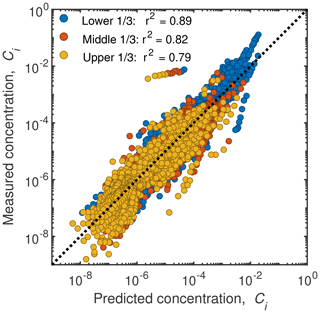
Figure 11Measured versus predicted grain-size-specific concentration for each sample in the water column. Colors indicate the relative elevation in the water column of each sample. The predictions are from the two-parameter model to predict the entrainment rate and the one-parameter model for the Rouse number .
3.4 Extension to gravel
The suspended sediment data that we used to calibrate the entrainment relation cover material in the sand range. To evaluate how our entrainment relation performs for coarser suspended sediment, we used the empirical saltation equations for gravel to infer bedload-layer concentrations, Cb, and interpolated these to the reference level (0.1H) to infer Ca for gravel (Sect. 2.3). Importantly, the gravel concentrations at the reference height can be predicted from the saltation model (Sect. 2.3) using only the independent parameters of Fr and τ∗, similar to our best-fitting two-parameter entrainment model. To compare to gravel, we assumed a uniform sediment size and used the version of our best-fit two-parameter model that does not include a form drag correction (Eq. 26b). This was done because gravel saltation studies were typically performed over a planar bed, whereas form drag likely played a significant role in the sand datasets owing to dunes. The marked parameter space in Fig. 12 shows the expected range of Cb and Ca for a wide range of model input parameters for gravel: and . Predicted concentrations in the gravel bedload layer are up to several orders of magnitude higher than the predictions from our entrainment relation at 10 % of the flow depth (Fig. 12). However, due to the rapid decrease in sediment concentration away from the bed predicted by the Rouse profile, the concentration inferred at 0.1H for gravel overlaps the empirical relation for sand, implying that Eq. (27) might also be a good predictor of gravel entrainment.
Table 6Coefficient of determination (r2) of grain-size-specific sediment concentration at each sample elevation in the water column for different combinations of models for the entrainment, Esi, and Rouse, Pi, parameters. The favored model combination is highlighted in bold font.
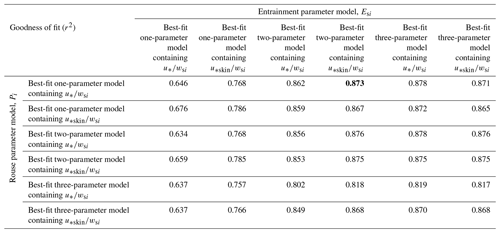
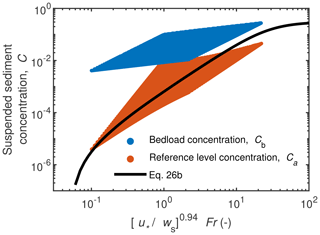
Figure 12Best-fit two-parameter model for sediment entrainment without form drag, Eq. (26b), presented here for uniform gravel. The plotting is done such that the exponent on the last parameter is unity to allow for comparison to plots of Garcia and Parker (1991) and Wright and Parker (2004b). The colored regions are prediction envelopes for synthetic gravel data using the bedload-layer equations to estimate the bedload volumetric concentration, Cb, and the Rouse profile to interpolate higher in the water column to the reference level at z=0.1H (Ca). The synthetic data envelope represents a wide range of parameter space: and .
4.1 Physical rationale for model dependencies
The explanatory variables in the models for Pi and βi are and Cf. The dependency on these parameters could reflect processes that result in the turbulent diffusivity for suspended sediment being different from the parabolic relation used in the derivation of the Rouse profile (e.g., Bennett et al., 1998). Compared to standard Rouse theory, in which the Rouse parameter is inversely dependent on (or ), our results indicate a significant nonlinearity. Our one-parameter model indicates that concentration profiles are better mixed than standard theory for small and are more stratified for larger , with a transition point at about , corresponding to βi=1. Sediment-induced stratification is often cited (Winterwerp, 2006; Wright and Parker, 2004b, a) as a factor that decreases the mixing of sediment (i.e., β<1). This effect is particularly important when the absolute concentration is high and may help explain why our best-fit model is more stratified (i.e., β<1) than standard Rouse theory for large . An alternative hypothesis by Nielsen and Teakle (2004) is that for steep concentration gradients, the size of the turbulent eddies is large relative to the mean height of sediment in the flow. Under these circumstances, large eddies might more effectively mix sediment that is concentrated close to the bed. This process may explain the better mixed concentration profiles we observed (i.e., βi>1) compared to standard theory at small when near-bed concentration gradients are large.
Our relation implies that βi correlates positively with the flow friction coefficient Cf. This dependency could be from bedforms; bedforms increase Cf due to form drag (Engelund and Hansen, 1967), and they may also increase the vertical mixing of sediment by deflecting transport paths up the stoss side of dunes and mixing suspended sediment in the turbulent wake in the lee of dunes. Similarly, Santini et al. (2019) found that β correlated positively with H∕D (Fig. 2c), which is another measure for bed roughness in flows without bedforms. In agreement, Graf and Cellino (2002) reviewed a number of experimental studies and found that β<1 for experiments without bedforms and β>1 for experiments with bedforms. Flow resistance (Cf) can also be smaller in flows with sediment-induced stratification, which correlates with smaller βi (e.g., Wright and Parker, 2004a).
Our new empirical relation for sediment entrainment suggests that only (or ) and Fr are needed to predict entrainment rate, similar to the forward model we developed for the suspension of gravel (Sect. 2.3). The ratio describes the fluid forces relative to gravitational settling; similar parameters have appeared in all previous relations that we reviewed (Table 2). The reason for the increase in entrainment with the Froude number is less clear. A small Froude number implies a deep and low-gradient flow, and Froude numbers are typically smaller in natural rivers compared to flume experiments. Wright and Parker (2004b) introduced an entrainment relation with a bed slope dependency and argued that entrainment in large low-sloping rivers is reduced due to stratification effects. Sediment-induced stratification causing the damping of turbulence might be the cause of the Fr dependency in our relation. Regardless, we found a better fit with the data using Fr than using or S (Table S2), the parameters suggested by Wright and Parker (2004b). The Froude number might also influence the size and shape of bedforms (Vanoni, 1974), which can affect boundary layer dynamics and near-bed turbulence, as well as surface waves. The Froude number is the ratio between inertial to gravitational forces or, more formally, the ratio of a unidirectional flow velocity to the celerity of a shallow water wave (i.e., ). However, we do not think these are the reasons why the dependence of Esi on Fr emerges in our analysis; rather, our forward model (Sect. 2.3) suggests that it emerges as a controlling parameter because of the role of U and H in determining bedload-layer concentrations, which is discussed in more detail in Sect. 4.3.
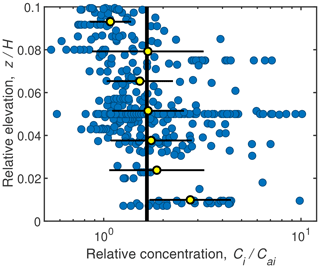
Figure 13Grain-size-specific concentration, Ci, from the lowest 10 % of the flow (i.e., below the reference level z=0.1H) relative to the concentration at the reference level, Cai, as a function of depth above the bed, z, relative to the flow depth, H. Yellow filled symbols are the geometric mean; the error bars indicate the geometric standard deviation within each elevation bin, and the black line is the geometric mean of all data representing Ci=1.66Cai.
Many of the dimensionless parameters we evaluated correlate with each other in rivers. While or was consistently the dominant variable, several of the possible secondary variables had similar explanatory power as the ones given in our preferred models. For sediment entrainment, some of the more highly ranked variables are Ca∕S and τ∗skin in one-parameter models and H∕D50, S and Di∕D50 in two-parameter models; for the Rouse number they include Rp,skin and τ∗ for one-parameter models and Rep and Ca∕S in two-parameter models (Table S2). In addition, there is some systematic deviation between datasets for different rivers (Fig. 8), and different parameters and exponents might better minimize residuals at specific locations. While our model has been fit to a large dataset, it has not been validated with independent data. More data are clearly needed on grain-size-specific concentration profiles for equilibrium suspensions under a wide range of , Fr, and particle sizes, including coarse sand and gravel.
4.2 Predicting sediment concentration below the reference level
Combining the predictions for the grain-size-specific reference concentration and Rouse parameter allows for the calculation of the grain-size-specific sediment concentration throughout the water column (Fig. 11). Our relation shows that the grain-size-specific sediment concentration at any given elevation can be predicted to relatively high accuracy (r2=0.87) using the preferred combination of a two-parameter entrainment relation and the one-parameter Rouse number relation (Sect. 3.3). However, it is unclear how to evaluate the sediment concentration below the reference level, which could constitute a significant portion of the sediment load. Bedload fluxes are notoriously difficult to estimate; further, it is unclear if the region below the reference level is entirely bedload or if it is bedload and suspended load (e.g., Fig. 1b). Ashley et al. (2020) showed how bedload sediment fluxes can be estimated from discharge-averaged suspended sand concentrations, but their method does not predict the concentration profile. One approach might be to assume that the sediment concentration is uniform below the reference level at Ci=Cai, as might be the case in a well-mixed bedload layer (e.g., McLean, 1992) (Fig. 1b). However, this assumption is inconsistent with our analysis of the saltation equations, which shows that bedload layers should have greater concentrations and be less than 10 % of the flow depth (Fig. 12), especially for sand in deep flows. A second approach is to use the Rouse profile to extrapolate towards the bed or towards the top of the bedload layer; however, this approach is also problematic because the Rouse profile predicts infinitely large concentrations at the bed. Some of our datasets had concentration measurements below the reference level (Fig. 13). The data are scattered, but the binned data points suggest a nearly constant concentration with elevation below the reference level. For lack of a better method, we propose using the geometric mean of these data as Ci=1.66Cai to approximate the concentration–depth profile below the reference level (Fig. 13).
4.3 Extension to gravel and bedload-layer theory
The transport of sand and gravel is often modeled using different empirical formulas, which hinders the modeling of systems of mixed gravel–sand transport (Wilcock and Crowe, 2003) and gravel–sand transitions (Paola et al., 1992; Lamb and Venditti, 2016). Gravel can also be in suspension in bedrock and steep mountain rivers, as well as during large floods (Hartshorn et al., 2002; Larsen and Lamb, 2016), and it would be useful to have an entrainment relation to model sediment transport and bedrock erosion in these settings (Lamb et al., 2008a; Scheingross et al., 2014). Unfortunately, sand and gravel are often treated separately, which limits our ability to develop a unified sediment transport theory. Our entrainment relation for sand matches expectations from gravel saltation models (Fig. 12), suggesting that the entrainment relation may be used for sand, gravel, or mixtures of the two. However, we currently lack data on gravel suspension profiles, and developing methods to acquire such data should be the focus of future efforts. It is also unclear how entrainment is complicated by bimodal mixtures (Wilcock and Crowe, 2003) and complex flow hydraulics in steep rivers with large roughness that can significantly affect lift forces and near-bed turbulence (Lamb et al., 2017).
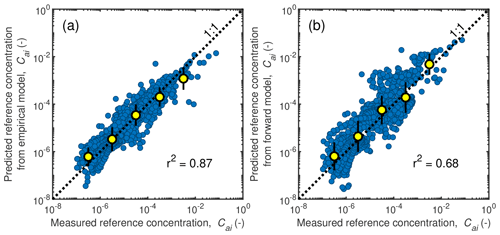
Figure 14Measured versus predicted grain-size-specific near-bed concentration, Cai, at the reference level z=0.1H for (a) our two-parameter empirical relation (Eq. 25) and (b) for the forward modeling approach using the bedload-layer equations (Sect. 4.3). Data (blue markers) are from the entire database of suspended sand described in Sect. 2.1 (Table S1) at z=0.1H. Yellow symbols are the geometric mean, and the error bars indicate the geometric standard deviation within each bin.
The good fit between the modeled gravel concentrations and the measured sand data for near-bed sediment concentration suggests that the bedload-layer equations (Sect. 2.3) might also be used to generate a forward model for near-bed sediment concentration that works for sand and gravel systems, similarly to previous efforts (e.g., McLean, 1992). To evaluate this possibility, we used the saltation equations (Eqs. 17–21) to calculate sediment concentrations within the bedload layer for conditions corresponding to our dataset entries for sand-bedded rivers. To extend Eq. (18) to grain size mixtures, we let D=Di and and used a hiding function (Parker et al., 1982) so that
where τ∗c50 is the critical Shields number for the median-sized bed sediment. Equation (28) accounts for the hiding of smaller grains between larger grains, which renders the smaller grains less mobile, and the exposure of larger grains into the flow, which renders them more mobile. For γ=1, all grains in a bed mixture move at the same bed stress, while for γ=0, the critical stress for motion is proportional to grain weight. Gravel-bedded rivers typically have γ=0.9 (Parker, 1990). For sand, we evaluated the critical Shields number following Brownlie (1981),
rather than Eq. (19), which is intended for gravel only. We then calculated the concentrations at 10 % of the flow depth using the Rouse equation (Eq. 1) with the best-fit one-parameter model for the Rouse number. Although the saltation equations in Sect. 2.3 were calibrated for gravel, similar relations have also been used for sand (e.g., Lamb et al., 2008a).
Surprisingly, the near-bed sand concentrations for the entries in our database (Sect. 2.1) are relatively accurately predicted by the bedload forward model without any parameter fitting (Fig. 14b). In fact, the predictions by the bedload-layer forward model are only slightly worse than the predictions by our preferred two-parameter entrainment model (Fig. 14a) that was fit to the data (r2 of 0.68 vs. 0.87). Importantly, the forward model yields the same controlling parameters as the empirical model, namely the Shields number, the Froude number, and the bed grain size distribution. The forward model suggests that the dependence of Esi on (or ) is predominantly because larger correlates with larger τ∗ and larger bedload-layer concentrations (Eqs. 17 and 18), as well as more efficient mixing of the bedload-layer sediment up to the reference height (Eq. 1). Less intuitive is the dependence of Esi on the Froude number. In the forward model, this dependence is because larger Fr for the same τ∗ correlates with larger Di∕H (which can be shown by manipulating Eq. 7). In turn, larger Di∕H with constant τ∗ correlates with greater bedload fluxes ( in Eq. 18), smaller bedload-layer heights (due to smaller H in Eq. 21), and slower bedload-layer velocities (due to smaller U in Eq. 20), all of which increase the sediment concentration in the bedload layer (Eq. 17). Thus, the forward model indicates that the Fr dependency on Esi emerges because bedload-layer dynamics depend on U and H, and explanations for this dependency that rely on stratification, bedforms, or surface waves are not necessary. The bedload-layer model, while slightly more complicated to implement, may provide a more robust solution when working outside the parameter space used to derive the empirical model, since it has a more physical basis. For example, the forward model can explicitly account for gravity and other physical properties of the sediment and fluid. In addition, the bedload-layer model allows for a more mechanistic link between the bedload and suspended load and avoids uncertainty in how to evaluate the sediment concentration below the reference level. The model might likely be improved by accounting for bedform-induced form drag, especially for sand-bedded rivers. That said, more accurate predictions are still achieved with the empirical entrainment relation.
We proposed new empirical models for the entrainment of bed material into suspension and for the shape of the concentration profile governed by the Rouse parameter. The models were obtained by regression against suspended sediment data from eight different rivers and six experimental studies. The data cover a wide range of bed material grain sizes (44–517 µm) and flow depths (0.06–32 m) and include grain-size-specific data with up to 60 size classes. Our analysis of these data suggests that the near-bed sediment concentration increases with the ratio between shear velocity or settling velocity ( or ) and the Froude number – both parameters also emerge as the key controlling variables in a forward model based on bedload-layer concentrations. A parameter such as , which represents the ratio of fluid force to particle settling, was also present in previous relations. The Froude number dependence is less clear; it could be due to stronger sediment-induced stratification in large low-Fr rivers, but our forward model indicates that it emerges because flow velocity and flow depth impact bedload-layer concentrations. Our preferred Rouse parameter model for the shape of the concentration profile suggests that the sediment concentration is better mixed in the water column with larger and a larger bed friction coefficient, Cf. The Rouse number is not inversely proportional to , unlike standard Rouse theory, indicating that sediment is more stratified than expected with and better mixed than expected with , possibly due to the competing effects of sediment-induced stratification when absolute concentrations are large (corresponding to large ) and enhanced turbulent mixing when concentration gradients are steep (corresponding to small ). The dependence of the Rouse number on the bed friction coefficient might result from increased turbulence close to the bed in rivers with large bed roughness or bedforms. We also demonstrated that near-bed concentrations can be accurately predicted with saltation equations that have been tested previously for gravel, suggesting a unified framework to model sand and gravel transport in rivers.
All data used in the analysis are provided in Table S1 of the Supplement. Model results for all possible variable combinations are given in Table S2.
Table S1 contains all the suspended sediment data that were used to find the empirical relations. Table S2 contains all entrainment and Rouse number models ranked according to goodness of fit as indicated by r2. The supplement related to this article is available online at: https://doi.org/10.5194/esurf-8-485-2020-supplement.
MPL and GP conceived the study. JdL compiled data and led data analysis with input from MPL. MPL and JdL wrote the initial paper. AJM, DH, JGV, and JAN supplied suspended sediment data and contributed to the final paper.
The authors declare that they have no conflict of interest.
We thank everyone involved in the suspended sediment data collection in the Yellow River (Brandee Carlson, Hongbo Ma) and the Fraser River (Nicola Rammell, Kate Donkers, Jacqui Brown, Michael Wong, Michelle Linde, and Alex Gitto). We thank the reviewers and editor Eric Lajeunesse for their helpful comments.
This research has been supported by the US National Science Foundation (grant no. EAR 1427262), the Caltech Discovery Fund, and the NSF Graduate Research Fellowship (grant no. EAR 1842494).
This paper was edited by Eric Lajeunesse and reviewed by two anonymous referees.
Akiyama, J. and Fukushima, Y.: Entrainment of noncohesive sediment into suspension, 3rd International Symposium on River Sedimentation, edited by: Want, S. Y., Shen, H. W., and Ding, L. Z., University of Minnesota, Minneapolis, Minnesota, USA, 803–813, 1986.
Allison, M. A. and Meselhe, E. A.: The use of large water and sediment diversions in the lower Mississippi River (Louisiana) for coastal restoration, J. Hydrol., 387, 346–360, https://doi.org/10.1016/j.jhydrol.2010.04.001, 2010.
Ashley, T. C., McElroy, B., Buscombe, D., Grams, P. E., and Kaplinski, M.: Estimating bedload from suspended load and water discharge in sand bed rivers, Water Resour. Res., 56, e2019WR025883, https://doi.org/10.1029/2019WR025883, 2020.
Barton, J. R. and Lin, P. N.: A study of the sediment transpot in alluvial streams, Colorado A&M College, Fort Colins, USA, CO, Report 55JRB2, 1955.
Bennett, S. J., Bridge, J. S., and Best, J. L.: Fluid and sediment dynamics of upper stage plane beds, J. Geophys. Res., 103, 1239–1274, 1998.
Bouchez, J., Lupker, M., Maurice, L., Perez, M., and Gaillardet, J.: Prediction of depth-integrated fluxes of suspended sediment in the Amazon River?: particle aggregation as a complicating factor, Hydrol. Process., 794, 778–794, https://doi.org/10.1002/hyp.7868, 2011.
Brooks, N. H.: Laboratory studies of the mechanics of motion of streams flowing over a movable-bed of fine sand, Dissertaion (PhD), California Institute of Technology, Pasadena, CA, https://doi.org/10.7907/JB2P-1H91, 1954.
Brownlie, W. R.: Prediction of Flow Depth and Sediment Discharge in Open Channels, W. M. Keck Laboratory of Hydraulics and Water Resources Report, 43A. California Institute of Technology, Pasadena, CA, USA, https://doi.org/10.7907/Z9KP803R, 1981.
Burr, D. M., Carling, P. A., and Baker, V. R.: Megaflooding on Earth and Mars, Cambridge University Press, Cambridge, UK, 2009.
Cacchione, D. A., Wiberg, P. L., Lynch, J., Irish, J., and Traykovski, P.: Estimates of suspended-sediment flux and bedform activity on the inner portion of the Eel continental shelf, Mar. Geol., 154, 83–97, 1999.
Celik, I. and Rodi, W.: A deposition-entrainment model for suspended sediment transport, Universität Karlsruhe, Karlsruhe, Germany, 1984.
Cellino, M.: Experimental study of suspension flow in open channels, Dissertation, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland, 1–234, 1998.
Chatanantavet, P., Whipple, K. X., Adams, M. A., and Lamb, M. P.: Experimental study on coarse grain saltation dynamics in bedrock channels, J. Geophys. Res.-Earth, 118, 1161–1176, https://doi.org/10.1002/jgrf.20053, 2013.
Chien, N.: The present status of research on sediment transport, T. Am. Soc. Civ. Eng., 121, 833–868, 1954.
Colby, B. R. and Hembree, C. H.: Computations of total sediment discharge, Niobrara River near Cody, Nebraska, U.S. Geological Survey Water Supply Paper 1357, Washington, D.C., USA, 1–187, 1955.
Coleman, N. L.: Flume studies on the sediment transport coefficient, Water Resour. Res., 6, 801–809, https://doi.org/10.1029/WR006i003p00801, 1970.
Coleman, N. L.: Velocity profiles with suspended sediment, J. Hydraul. Res., 19, 211–229, https://doi.org/10.1080/00221688109499516, 1981.
Droppo, I. G. and Ongley, E. D.: Flocculation of suspended sediment in rivers of southeastern Canada, Water Res., 28, 1799–1809, https://doi.org/10.1016/0043-1354(94)90253-4, 1994.
Einstein, H. A.: The Bed-Load Function for Sediment Transportation in Open Channel Flows, Technical Report, Soil Conservation Service, U.S Department of Agriculture, Washington, D.C., USA, 1026, 1–31, 1950.
Einstein, H. A.: Effect of heavy sediment concentration near the bed on velocity and sediment distribution, MRD Sediment Series, University of California, Berkeley, California, USA, 1955.
Engelund, F. and Fredsøe, J.: A Sediment Transport Model for Straight Alluvial Channels, Nord. Hydrol., 7, 293–306, 1976.
Engelund, F. and Hansen, E.: A Monograph on Sediment Transport in Alluvial Atreams, Danish Tech. Press, Copenhagen, Denmark, 1967.
Ferguson, R. I. and Church, M.: A simple universal equation for grain settling velocity, J. Sediment. Res., 74, 933–937, https://doi.org/10.1306/051204740933, 2004.
Fernandez Luque, R. and van Beek, R.: Erosion And Transport Of Bed-Load Sediment, J. Hydraul. Res., 14, 127–144, https://doi.org/10.1080/00221687609499677, 1976.
Garcia, M.: Sedimentation engineering: processes, measurements, modeling, and practice, Americal Socieny of Civil Engineers, Manual 110, Reston, Virginia, USA, https://doi.org/10.1061/9780784408148, 2008.
Garcia, M. and Parker, G.: Entrainment of Bed Sediment into Suspension, J. Hydraul. Eng., 117, 414–435, https://doi.org/10.1061/(ASCE)0733-9429(1991)117:4(414), 1991.
Gitto, A. B., Venditti, J. G., Kostaschuk, R., and Church, M.: Representative point-integrated suspended sediment sampling in rivers, Water Resour. Res., 53, 2956–2971, https://doi.org/10.1002/2016WR019187, 2017.
Graf, W. H. and Cellino, M.: Suspension flows in open channels; experimental study, J. Hydraul. Res., 40, 435–447, https://doi.org/10.1080/00221680209499886, 2002.
Greimann, B. P. and Holly Jr., F. M.: Two-phase flow analysis of concentration profiles, J. Hydraul. Eng., 127, 753–762, 2001.
Hartshorn, K., Hovius, N., Dade, W. B., and Slingerland, R. L.: Climate-driven bedrock incision in an active mountain belt, Science, 297, 2036–2038, https://doi.org/10.1126/science.1075078, 2002.
Haught, D., Venditti, J. G., and Wright, S. A.: Calculation of in situ acoustic sediment attenuation using off-the-shelf horizontal ADCPs in low concentration settings, Water Resour. Res., 53, 5017–5037, https://doi.org/10.1002/2016WR019695, 2017.
Hubbell, D. W. and Matejka, D. Q.: Investigations of sediment transportation, Middle Loup River at Dunning, Nebraska: with application of data from turbulence flume, U.S. Geological Survey Water Supply Paper 1476, Washington, D.C., USA, 1–123, 1959.
Jordan, P. R.: Fluvial sediment of the Mississippi River at St. Louis, Missouri, U.S. Geological Survey Water Supply Paper 1802, Washington, D.C., USA, 1–89, 1965.
Lamb, M. P. and Venditti, J. G.: The grain size gap and abrupt gravel-sand transitions in rivers due to suspension fallout, Geophys. Res. Lett., 43, 3777–3785, https://doi.org/10.1002/2016GL068713, 2016.
Lamb, M. P., Dietrich, W. E., and Sklar, L. S.: A model for fluvial bedrock incision by impacting suspended and bed load sediment, J. Geophys. Res.-Earth, 113, 1–18, https://doi.org/10.1029/2007JF000915, 2008a.
Lamb, M. P., Dietrich, W. E., and Venditti, J. G.: Is the critical shields stress for incipient sediment motion dependent on channel-bed slope?, J. Geophys. Res.-Earth, 113, 1–20, https://doi.org/10.1029/2007JF000831, 2008b.
Lamb, M. P., Brun, F., and Fuller, B. M.: Direct measurements of lift and drag on shallowly submerged cobbles in steep streams: Implications for flow resistance and sediment transport, Water Resour. Res., 53, 7607–7629, https://doi.org/10.1002/2017WR020883, 2017.
Larsen, I. J. and Lamb, M. P.: Progressive incision of the Channeled Scablands by outburst floods, Nature, 538, 229–232, https://doi.org/10.1038/nature19817, 2016.
Lupker, M., France-Lanord, C., Lavé, J., Bouchez, J., Galy, V., Métivier, F., Gaillardet, J., Lartiges, B., and Mugnier, J. L.: A Rouse-based method to integrate the chemical composition of river sediments: Application to the Ganga basin, J. Geophys. Res.-Earth, 116, 1–24, https://doi.org/10.1029/2010JF001947, 2011.
Lyn, D. A.: Turbulence and turbulent transport in sediment-laden open-channel flows, W. M. Keck Laboratory, California Institute of Technology, Report KH-R-49, Pasadena, CA, USA, https://doi.org/10.7907/Z9J964BP, 1986.
Ma, H., Nittrouer, J. A., Naito, K., Fu, X., Zhang, Y., Moodie, A. J., Wang, Y., Wu, B., and Parker, G.: The exceptional sediment load of fine-grained dispersal systems?: Example of the Yellow River, China, Sci. Adv., 3, 1–8, 2017.
McLean, S. R.: Depth-integrated suspended-load calculations, J. Hydraul. Eng., 117, 1440–1458, 1992.
Mellor, G. L. and Yamada, T.: Development of a turbulence closure model for geophysical fluid problems, Rev. Geophys., 20, 851–875, 1982.
Moodie, A. J.: Yellow River Kenli Lijin Station Survey, Zenodo, https://doi.org/10.5281/zenodo.3457639, 2019.
Muste, M., Yu, K., Fujita, I., and Ettema, R.: Two-phase versus mixed-flow perspective on suspended sediment transport in turbulent channel flows, Water Resour. Res., 41, W10402, https://doi.org/10.1029/2004WR003595, 2005.
Mutsert, K. De, Lewis, K., Milroy, S., Buszowski, J., and Steenbeek, J.: Using ecosystem modeling to evaluate trade-offs in coastal management?: Effects of large-scale river diversions on fish and fisheries, Ecol. Model., 360, 14–26, https://doi.org/10.1016/j.ecolmodel.2017.06.029, 2017.
Nielsen, P. and Teakle, I. A.: Turbulent diffusion of momentum and suspended particles?: A finite-mixing-length theory, Phys. Fluids, 16, 2342–2348, https://doi.org/10.1063/1.1738413, 2004.
Nittrouer, C. A., Curtin, T. B., and DeMaster, D. J.: Concentration and flux of suspended sediment on the Amazon continental shelf, Cont. Shelf Res., 6, 151–174, 1986.
Nittrouer, J. A., Mohrig, D., and Allison, M.: Punctuated sand transport in the lowermost Mississippi River, J. Geophys. Res., 116, F04025, https://doi.org/10.1029/2011JF002026, 2011.
Nordin, C. F. and Dempster, G. R.: Vertical distribution of velocity and suspended sediment Middle Rio Grande New Mexico, U.S. Geol. Surv. Prof. Pap. 462-B., B1–B20, https://doi.org/10.3133/pp462B, 1963.
Paola, C. and Voller, V. R.: A generalized Exner equation for sediment mass balance, J. Geophys. Res., 110, 1–8, https://doi.org/10.1029/2004JF000274, 2005.
Paola, C., Parker, G., Seal, R., Sinha, S. K., Southard, J. B., and Wilcock, P. R.: Downstream fining by selective deposition in a laboratory flume, Science, 258, 1757–1760, https://doi.org/10.1126/science.258.5089.1757, 1992.
Parker, G.: Self-formed straight rivers with equilibrium banks and mobile bed. Part 1. The sand-silt river, J. Fluid Mech., 89, 109–125, 1978.
Parker, G.: Surface-based bedload transport relation for gravel rivers, J. Hydraul. Res., 28, 417–436, https://doi.org/10.1080/00221689009499058, 1990.
Parker, G., Klingeman, P. C., and McLean, D. G.: Bedload and size distribution in paved gravel-bed streams, J. Hydr. Eng. Div.-ASCE, 108, 544–571, 1982.
Rose, C. P. and Thorne, P. D.: Measurements of suspended sediment transport parameters in a tidal estuary, Cont. Shelf Res., 21, 1551–1575, https://doi.org/10.1016/S0278-4343(00)00087-X, 2001.
Rouse, H.: Modern Conceptions of the Mechanics of Fluid Turbulence, T. Am. Soc. Civ. Eng., 102, 463–505, 1937.
Santini, W., Camenen, B., Le Coz, J., Vauchel, P., Guyot, J.-L., Lavado, W., Carranza, J., Paredes, M. A., Pérez Arévalo, J. J., Arévalo, N., Espinoza Villar, R., Julien, F., and Martinez, J.-M.: An index concentration method for suspended load monitoring in large rivers of the Amazonian foreland, Earth Surf. Dynam., 7, 515–536, https://doi.org/10.5194/esurf-7-515-2019, 2019.
Scheingross, J. S., Brun, F., Lo, D. Y., Omerdin, K., and Lamb, M. P.: Experimental evidence for fluvial bedrock incision by suspended and bedload sediment, Geology, 42, 523–526, https://doi.org/10.1130/G35432.1, 2014.
Sklar, L. S. and Dietrich, W. E.: A mechanistic model for river incision into bedrock by saltating bed load, Water Resour. Res., 40, 1–22, https://doi.org/10.1029/2003WR002496, 2004.
Smith, J. D. and Mclean, S. R.: Spatially Averaged Flow Over a Wavy Surface, J. Geophys. Res., 82, 1735–1746, 1977.
Sumer, B. M., Kozakiewicz, A. B., Fredsøe, J., and Deigaard, R.: Velocity and concentration profiles in sheet-flow layer of movable bed, J. Hydraul. Eng., 122, 549–558, 1996.
Syvitski, J. P. M., Vo, C. J., Kettner, A. J., and Green, P.: Impact of humans on the flux of terrestrial sediment to the global coastal ocean, Science, 308, 376–381, 2005.
Vanoni, V. A.: Transportation of Suspended Sediment by Water, T. Am. Soc. Civ. Eng., 111, 67–102, 1946.
Vanoni, V. A.: Factors determining bed forms of alluvial streams, J. Hydr. Eng. Div.-ASCE, 100, 363–377, 1974.
van Rijn, L.: Sediment transport, part 2: Suspended load transport, J. Hydraul. Eng., 110, 1613–1641, 1984.
Walling, D. E.: Human impact on land – ocean sediment transfer by the world's rivers, Geomorphology, 79, 192–216, https://doi.org/10.1016/j.geomorph.2006.06.019, 2006.
Wilcock, P. R. and Crowe, J. C.: Surface-based Transport Model for Mixed-Size Sediment, J. Hydraul. Eng., 129, 120–128, https://doi.org/10.1061/(ASCE)0733-9429(2003)129:2(120), 2003.
Winterwerp, J. C.: Stratification effects by fine suspended sediment at low, medium, and very high concentrations, J. Geophys. Res.-Oceans, 111, 1–11, https://doi.org/10.1029/2005JC003019, 2006.
Wright, S. and Parker, G.: Density Stratification Effects in Sand-Bed Rivers, J. Hydraul. Eng., 130, 783–795, https://doi.org/10.1061/(ASCE)0733-9429(2004)130:8(783), 2004a.
Wright, S. and Parker, G.: Flow Resistance and Suspended Load in Sand-Bed Rivers: Simplified Stratification Model, J. Hydraul. Eng., 130, 796–805, https://doi.org/10.1061/(ASCE)0733-9429(2004)130:8(796), 2004b.
York, D.: Least squares fitting of a straight line with correlated errors, Earth Planet. Sc. Lett., 5, 320–324, 1968.