The destiny of orogen-parallel streams in the Eastern Alps: the Salzach–Enns drainage system

The evolution of the drainage system in the Eastern Alps is inherently linked to different tectonic stages of the alpine orogeny. Crustal-scale faults imposed eastward-directed orogen-parallel flow on major rivers, whereas late orogenic surface uplift increased topographic gradients between the foreland and range and hence the vulnerability of such rivers to be captured. This leads to a situation in which major orogen-parallel alpine rivers such as the Salzach River and the Enns River are characterized by elongated east–west-oriented catchments south of the proposed capture points, whereby almost the entire drainage area is located west of the capture point. To determine the current stability of drainage divides and to predict the potential direction of divide migration, we analysed their geometry at catchment, headwater and hillslope scale covering timescales from millions of years to the millennial scale. We employ χ mapping for different base levels, generalized swath profiles across drainage divides and Gilbert metrics – a set of local topographic metrics quantifying the asymmetry of drainage divides at hillslope scale. Our results show that most drainage divides are asymmetric, with steeper channels west and flatter channels east of a common drainage divide. Interpreting these results, we propose that drainage divides migrate from west towards east so that the Inn catchment grows at the expense of the Salzach catchment and the Salzach catchment consumes the westernmost tributaries of the Mur and Enns catchments. Gilbert metrics across the Salzach–Enns and Salzach–Mur divides are consistent with inferred divide mobility. We attribute the absence of divide asymmetry at the Inn–Salzach divide to glacial landforms such as cirques and U-shaped valleys, which suggest that Pleistocene climate modulations are able to locally obscure the large-scale signal of drainage network reorganization. We suggest that the eastward-directed divide migration progressively leads to symmetric catchment geometries, whereby tributaries west and east of the capture point eventually contribute equally to the drainage area. To test this assumption, we have reconstructed the proposed drainage network geometries for different time slices. χ mapping of these reconstructed drainage networks indicates a progressive stability of the network topology in the Eastern Alps towards the present-day situation.

1 Introduction

The drainage system of a collisional orogen is inherently linked to its tectonic and climatic evolution (Beaumont et al., 1992; Willett, 1999; Montgomery et al., 2001; Willett et al., 2001; Garcia-Castellanos et al., 2003; Cederbom et al., 2004; Bishop, 2007; Miller et al., 2007; Roe et al., 2008; Champagnac et al., 2012; Herman et al., 2013; Robl et al., 2017a). In a zone of plate convergence, crustal shortening is a primary control on the horizontal and vertical metrics of the mountain range (Houseman and England, 1986; Royden et al., 1997; Robl and Stüwe, 2005a; Robl et al., 2008b, 2017a; Bartosch et al., 2017). Progressive shortening leads to thickening of light, buoyant crust, which results in surface uplift and the formation of high alpine topography (e.g. Molnar and Lyon-Caen, 1988). The horizontal geometry of the mountain range reflects compression in and stretching perpendicular to the direction of plate convergence. In such a stress field, blocks of the brittle upper crust are advected along major strike-slip fault zones. This process is commonly referred to as lateral extrusion (e.g. Tapponnier et al., 1982; Ratschbacher et al., 1989, 1991; Robl and Stüwe, 2005a, b; Robl et al., 2008b).

As a consequence of the horizontal and vertical motion of the crust, drainage systems are also advected (Clark et al., 2004; Miller and Slingerland, 2006; Stüwe et al., 2008; Castelltort et al., 2012; Kirby and Whipple, 2012; Miller et al., 2012; Fox et al., 2014; Goren et al., 2015; Yang et al., 2016; Guerit et al., 2018; Eizenhöfer et al., 2019). However, rivers are not just passive markers of crustal deformation; they also adjust their channel slopes to the contributing drainage area, uplift rate and bedrock properties until longitudinal channel profiles are graded and long-term erosion rates are in balance with uplift rates (Kooi and Beaumont, 1996; Whipple, 2001; Willett et al., 2001; Goren et al., 2014; Robl et al., 2017b). However, tectonic and climatic conditions are not steady over an orogenic cycle. The signal of temporal variations is routed via mobile knickpoints in channels through the entire drainage system (Wobus et al., 2006; Kirby and Whipple, 2012; Perron and Royden, 2013; Royden and Perron, 2013; Robl et al., 2017b). Evidence for a previous tectonic phase is erased from their shapes once all knickpoints have left the drainage system at the drainage divides. The velocity of knickpoint migration depends strongly on different factors such as lithology, upstream drainage area, the amplitude of base-level drop and sediment supply (Crosby and Whipple, 2006; Loget and Van Den Driessche, 2009); it ranges between 0.001 and 0.1 m yr⁻¹ (e.g. van Heijst and Postma, 2001).

Across-divide gradients in erosion rate (strictly speaking, the rate of change in surface elevation) result in lateral divide shifts and eventually in river captures. The difference in erosion rate is usually reflected in an asymmetric topography on which the drainage divide migrates from the steep towards the less steep side (e.g. Gilbert, 1877; Robl et al., 2017a, b; Whipple et al., 2017; Forte and Whipple, 2018). The reorganization of the drainage system due to divide migration (continuous) and river piracy events (discrete) lasts at least 1 order of magnitude longer than the upstream migration of knickpoints in channels (e.g. Goren, 2016; Robl et al., 2017b). Furthermore, changes in the contributing drainage area as a consequence of mobile divides introduce a positive feedback, whereby the adaption of channel profiles to changing catchment size amplifies across-divide differences in the erosion rate (Willett et al., 2014). As a consequence, information on long-term major tectonic phases associated with a large-scale reorganization of the drainage pattern persists in the drainage network topology and can be revealed by analysing the geometric properties of the drainage system and its divides, although evidence from channel profiles has already vanished (Willett et al., 2014; Goren et al., 2015; Yang et al., 2015; Hergarten et al., 2016; Beeson et al., 2017; Robl et al., 2017a, b; Winterberg and Willett, 2019). However, the relation between drainage divide migration and topographic asymmetry is not unique. While migrating drainage divides are usually asymmetric, there are specific tectonic, lithological or climatic scenarios in which asymmetric drainage divides can be stable.

In this study, we aim to decipher the morphological state of drainage divides in the Eastern Alps to (a) distinguish between mobile and immobile drainage divides and (b) constrain the potential direction of divide migration by applying a set of morphometric tools that consider divide disequilibrium at catchment, headwater and hillslope scale. Furthermore, we discuss our results in light of proposed changes in the drainage pattern since the onset of topography formation (Oligocene) in the Eastern Alps (Frisch et al., 1998; Handy et al., 2015) and explore how these changes may have affected the stability of the divides compared to the present-day situation.

1.1 The drainage system of the Eastern Alps

The drainage system of the Eastern Alps is characterized by two principal drainage divides (Robl et al., 2008a, 2017a) (Fig. 1). One major divide follows the main ridge of the Eastern Alps including the highest peaks and separates the Inn, Salzach and Enns catchments to the north from the Drau and Mur catchments to the south. The Danube (and eventually the Black Sea) represents the common base level of all those rivers, but their confluence is located in the Pannonian Basin hundreds of kilometres away from the Eastern Alps. A second major drainage divide separates Alpine rivers that flow into the Adriatic Sea (e.g. Adige River) from the Mur–Drau drainage system. The configuration of the drainage systems was controlled by extrusion tectonics. Major tectonic lineaments (mainly strike-slip-dominated faults, i.e. Inn Valley Fault, Salzach–Ennstal–Mariazell–Puchberg (SEMP) Fault, Mur–Mürz Fault, Periadriatic Lineament (PL), and Möll Valley Fault) confine a corridor of lateral extrusion, where crustal blocks were actively squeezed out to the east towards the Pannonian Basin (e.g. Ratschbacher et al., 1989, 1991). Almost all major streams of the Eastern Alps follow these major tectonic lineaments for several tens of kilometres (Robl et al., 2008a, 2017a; Bartosch et al., 2017). Hence, they flow parallel to the strike of the mountain range, instead of leaving the orogen towards north and south, following the general topographic gradient (Fig. 1).

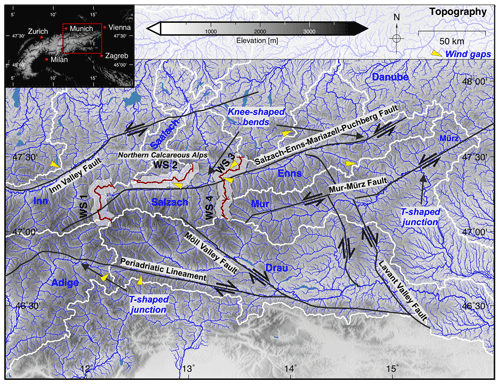
Figure 1 Topographic map of the study area and the drainage pattern of the Eastern Alps. The inset shows the position of the study area within the European Alps. Blue lines indicate the drainage pattern, and the line width is proportional to the log ₁₀ of the contributing drainage area. Drainage divides are shown by thick white lines. Major faults are indicated by solid black lines, and the direction of motion is shown by arrows. The red line and the grey contours indicate the course of the swath profiles shown in Fig. 3. Yellow triangles illustrate the occurrence of prominent wind gaps.

The courses of the Salzach and Enns rivers in the north and the Mur and Mürz rivers in the south are characterized by knee-shaped bends and T-shaped river junctions, whereby rivers abruptly leave their tectonically preconditioned valleys and drain towards the forelands in the north and south, respectively (Robl et al., 2008a, 2017a). Such sudden river course changes in concert with the observation of wind gaps at the Salzach–Enns valleys and the Salzach–Saalach drainage divide (Fig. 1), as well as the provenance of sediments along the Enns valley (Dunkl et al., 2005; Neubauer, 2016), are consistent with the proposed reorganization of the Salzach and Enns drainage systems (Kuhlemann et al., 2001; Dunkl et al., 2005; Robl et al., 2008a).

Major valleys south of the alpine main ridge also show a strong tectonic control (Robl et al., 2017a). The eastern tributaries of the Adige River and the western tributaries of the Drau River roughly follow the Periadriatic Lineament (Fig. 1). The occurrence of a prominent wind gap between the Adige and Drau rivers, as well as T-shaped river junctions at the tributaries of the Adige River, is discussed in terms of river piracy events and an ongoing reorganization of the drainage system (Robl et al., 2017a).

1.2 Co-evolution of topography and drainage system of the Eastern Alps

Morphological observations (e.g. Robl et al., 2008a) and provenance analyses (e.g. Kuhlemann et al., 2001, 2002; Kuhlemann, 2007; Neubauer, 2016) give evidence for several large-scale modifications of the Eastern Alpine drainage system. The evolution of the drainage system is inherently linked to the late Oligocene–early Miocene indentation (Handy et al., 2015) of the Adriatic into the European plate. At the onset of indentation, the landscape of the Eastern Alps was characterized by a hilly topography (Frisch et al., 2001), which was drained by a series of northward-flowing rivers (Frisch et al., 1998; Kuhlemann et al., 2006; Kuhlemann, 2007).

During early to middle Miocene times, lateral extrusion tectonics, confined by a set of crustal-scale strike-slip and associated normal faults, started and rocks at the Tauern Window were exhumed rapidly. These processes initiated a large-scale reorganization of the drainage system, whereby faults imposed an eastward-directed orogen-parallel flow on major rivers (Frisch et al., 1998). This tectonic stage set the paleo-courses of the Enns, Mur and Drau rivers (Dunkl et al., 2005; Kuhlemann et al., 2006; Kuhlemann, 2007). Evidence for a changing drainage pattern was recorded by the sedimentary pile deposited in the northern Molasse basin (Kuhlemann et al., 2006) and in inner alpine basins (Dunkl et al., 2005). The sedimentary record consists of characteristic rocks of surrounding Austroalpine units. During the middle and late Miocene, rocks from Penninic and Subpenninic units of the rising Tauern Window, which were previously overlain by Austroalpine units, appear in the sediments of the northern foreland basin (Frisch et al., 1998).

Provenance analyses of sediments reveal the reversal of flow directions and potential stream capture events during the late Miocene (Kuhlemann, 2007). Frisch et al. (1998) and Dunkl et al. (2005) suggested that the initially northeast-directed Mur River changed its course to the current southeast-directed drainage path during the middle Miocene (Fig. 1). The detection of wind gaps (Fig. 1; Robl et al., 2008a) and the analysis of the sedimentary composition of intra-orogenic basins (Neubauer, 2016) suggest similar changes in the Salzach and Enns drainage systems. The abrupt increase in stream power, a few kilometres upstream but mostly downstream of the knee-shaped river bend (Fig. 1), and a knickpoint analysis of tributaries may indicate a stream capture event during the Pleistocene forcing a base-level lowering of the Salzach River (Robl et al., 2008a).

However, the drainage development since the early Pliocene is poorly constrained. In particular, the impact of the Pleistocene glaciations, resulting in flat valley floors of the trunk streams and hanging valleys with large knickpoints at tributaries (Robl et al., 2008a; Norton et al., 2010; Valla et al., 2010), altered the geometry of rivers and obscured the tectonic record of preceding tectonic events (Robl et al., 2017a).

2 Methodology

All topographic analyses are based on the EU-DEM (data funded under GMES, Global Monitoring for Environment and Security preparatory action 2009 on Reference Data Access by the European Commission) digital elevation model with a spatial resolution of approximately 25 m.

2.1 χ mapping

In order to detect potentially mobile drainage divides due to across-divide differences in erosion rate, we follow the approach of Willett et al. (2014) by employing the so-called χ transform (Perron and Royden, 2013; Royden and Perron, 2013). This approach is based on the detachment-limited model for bedrock channel incision (Howard, 1980, 1994; Hergarten, 2002), according to which the erosion rate is

$$\begin{array}{}\text{(1)}& E=K{A}^m{\left({\displaystyle \frac{\partial H}{\partial x}}\right)}^n.\end{array}$$

Here, H and x are elevation and the longitudinal coordinate along the river profile, increasing in the upstream direction. K represents the erosional efficiency. The contribution of the channel slope $\frac{\partial H}{\partial x}$ and drainage area A to river incision is represented by the exponents m and n. The change in surface elevation at a given uplift rate U is then given by

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\partial H}{\partial t}}=U-E.\end{array}$$

The increase in contributing drainage area (and hence discharge) with downstream distance leads to the curvature of the channel profile, which obscures the record of spatial or temporal changes in uplift rate in the geometry of the river channel. The χ transform eliminates the curvature of the river profile by transforming the longitudinal coordinate x to a new coordinate χ (Perron and Royden, 2013; Royden and Perron, 2013). The contributing drainage area can be eliminated if the transformation satisfies the condition

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\mathrm{d}x}{\mathrm{d}\mathit{\chi }}}={\left({\displaystyle \frac{A}{A_{\mathrm{0}}}}\right)}^{\mathit{\theta }},\end{array}$$

where $\mathit{\theta }=m/n$ is the concavity index. This is achieved by

$$\begin{array}{}\text{(4)}& \mathit{\chi }=\int {\left({\displaystyle \frac{A}{A_{\mathrm{0}}}}\right)}^{-\mathit{\theta }}\mathrm{d}x,\end{array}$$

where the integration starts from an arbitrary given reference point x₀, while A₀ is also an arbitrary reference catchment size, which only affects the absolute scale of the χ values (A₀=1 km² in this study).

Then the erosion rate is

$$\begin{array}{}\text{(5)}& E=K{\left({\displaystyle \frac{\partial H}{\partial \mathit{\chi }}}\right)}^n.\end{array}$$

Under spatially and temporally uniform tectonic and climatic conditions, χ-transformed steady-state river profiles are thus straight lines. We calculated χ values for all channels with a contributing drainage area A≥1 km² and θ=0.5. As χ is computed in the upstream direction from a given base level, the restriction to A≥1 km² does not affect the χ map itself but only removes the uppermost river segments. Such a restriction is necessary as χ increases rapidly when approaching a drainage divide and the resulting high χ values would shadow across-divide contrasts in χ. The value of 1 km² is a trade-off between data density and the deviation of the real erosion rate from the rate predicted by the stream power law. Hergarten et al. (2016) found a moderate deviation in slope of about 20 % at A=1 km² for Taiwan. As this deviation applies to both sides of the considered drainage divides, it has a minor effect on the conclusions drawn from χ mapping.

Major rivers of the Eastern Alps exit the mountain range to the foreland at an elevation of about 400 m. We therefore chose this elevation as the common base level (H(x₀)=400 m). In order to limit the influence of spatial heterogeneity in tectonics and climate on χ at drainage divides, we also computed χ for a series of higher base levels (600, 800 and 1000 m).

The analysis of across-divide differences in χ exploits the fact that channels originating at a common drainage divide (i.e. similar channel head elevation) and sharing the same base-level elevation are steep if χ is small (Willett et al., 2014). Hence, across-divide differences in χ indicate differently steep rivers on both sides of the divide, averaged from the base level to the channel head. Generalizing the ideas of Gilbert (1877) and applying the stream power relation, steeper channels result in higher erosion rates, and hence drainage divides should migrate towards the high χ catchments.

2.2 Generalized swath profiles

We employ generalized swath profiles (Hergarten et al., 2014) to explore differences in headwater relief across drainage divides. The drainage divide represents the curved baseline of the swath profile. The signed minimum distance (Euclidian distance) of every data point of the digital elevation model to the baseline is computed, and coordinate pairs (profile coordinate, distance) are binned. Topographic maxima and minima representing the summit domain and the drainage system, respectively, as well as the mean elevation and standard deviation indicating the degree of landscape dissection are represented as a function of signed distance from the drainage divide. The half-width of the swath profiles is 5 km.

2.3 Gilbert metrics

To investigate the symmetry of drainage divides and potential anomalies at the hillslope scale, we determine the so-called Gilbert metrics, originally proposed by Gilbert (1877) and formalized by Whipple et al. (2017). Across-divide differences in channel head elevation, hillslope gradient and local relief (represented by Gilbert metrics) were computed with Divide Tools (Forte and Whipple, 2018), a collection of morphometric functions based upon TopoToolbox (Schwanghart and Scherler, 2014).

Channel heads at the transition from the hillslope to the fluvial domain are defined by a contributing drainage area threshold of 1 km². Hence, channel head elevation is the elevation at this point. The local relief is the maximum elevation (H_max) within a circular window minus the elevation of the channel head. We chose the default window size with a radius of 0.5 km (Forte and Whipple, 2018), which encloses the nearby ridge lines but does not reach far beyond. The slope gradient is the average topographic gradient between the channel head and the highest point within the analysed window. These metrics are averaged (arithmetic averaging) at each side of the watershed. Δ values (e.g. Δ_Elevation) represent the difference in the averaged metrics of the two sides of the drainage divide. Eventually, Δ values are normalized to a range from −1 to 1 so that every deviation from 0 evidences an asymmetric drainage divide. Following the nomenclature of Forte and Whipple (2018), we refer to these metrics as Gilbert metrics.

3 Results

By applying a set of standard morphometric analyses, we discovered several distinctly asymmetric drainage divides. We found divide asymmetry considering information from entire catchments, headwaters and even hillslopes.

3.1 χ mapping: across-divide differences at catchment scale

We find distinct χ anomalies at the divides of the Salzach catchment and the Inn and Adige (WS 1) catchments in the west, the Saalach (WS 2) catchment in the north, and the Enns (WS 3) and Mur (WS 4) catchments in the east (Figs. 1 and 2a–d). Across-divide differences in χ between the Salzach catchment and the Drau catchment in the south are small. As a clear trend, all streams at the western side of roughly north–south-trending drainage divides feature significantly lower χ values than adjacent streams east of the divides. We observe this trend at WS 1, where tributaries of the eastern Salzach River show significantly higher χ values than tributaries of the western Inn River. Similar anomalies in χ occur at WS 3 and WS 4, where the tributaries of the Enns and Mur rivers feature higher χ values than tributaries of the Salzach River. At WS 2, separating the Salzach from the Saalach catchment, higher χ values are observed north of the divide within the Saalach catchment.

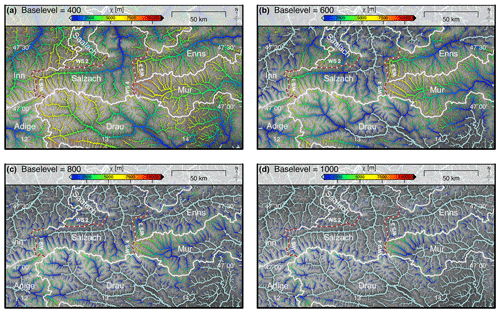
Figure 2 Drainage pattern of the Eastern Alps calculated for increasing base levels and colour-coded for χ. All streams with a contributing drainage area larger than 1 km² are shown. The line width of the channels is proportional to log ₁₀ (drainage area). White lines and annotations represent the major drainage divides. (a) Base level set to 400 m of elevation. (b) Base level set to 600 m of elevation. (c) Base level set to 800 m of elevation. (d) Base level set to 1000 m of elevation.

Patterns of across-divide gradients in χ are insensitive to stepwise increases in the base level from 400 m (Fig. 2a) to 600 m (Fig. 2b) and 800 m (Fig. 2c), and they are tantamount to a shift of the starting point of the χ computation towards the headwaters. However, starting the χ integration at the headwaters of the investigated catchments by setting a base level of 1000 m (Fig. 2d), several across-divide χ gradients disappear or are even reverted, as observed at WS 1. There, and in contrast to lower base levels, tributaries of the Inn River feature higher χ values than tributaries of the Salzach River. The rivers on both sides of WS 2 and WS 3 show similar χ values. However, the distinct χ anomaly observed at WS 4 remains. All tributaries of the Mur show higher χ values than tributaries across the divides to the Drau, Salzach and Enns catchments. Beyond that, the analysis shows that χ gradients across the Mur and Enns drainage divides increase with increasing base levels.

For a base level of 400 m, absolute values of χ, extracted at the channel heads on both sides of the investigated drainage divide, reflect the described across-divide χ gradients quantitatively (Fig. 3). At the westernmost drainage divide of the Salzach catchment, the distribution of χ ranges between 3190 and 6740 m in the Inn–Adige catchment and between 5810 and 8890 m in the Salzach catchment. Mean values of χ are 4887 m at the Inn–Adige side and 7525 m at the Salzach side of the drainage divide. The χ gradient indicates that the average steepness of the channels is higher at the Inn–Adige side than at the Salzach side of the divide. At the eastern drainage divides of the Salzach catchment, the Salzach–Enns and the Salzach–Mur divide, the χ distribution of the Salzach ranges between 2670 and 6530 m, while channel heads at the Enns and Mur catchment feature χ values between 4410 and 9100 m. Mean values of χ are 4267 and 5443 m at the Salzach catchment, and they are 6360 and 8093 m at the Enns and Mur catchments. The χ gradients indicate higher average channel steepness at the Salzach side of the divides. Across-divide gradients at the northern Salzach–Saalach divide are distinctly smaller than those at the western and eastern Salzach watersheds. The χ distribution ranges between 3670 and 6220 m at the Salzach side and between 3390 and 8130 m at the Saalach side. Mean χ is slightly shifted towards higher values at the Saalach (5834 m) relative to the Salzach side (4829 m). This, however, is caused by the long tail of the skewed-right χ distribution of the Saalach catchment.

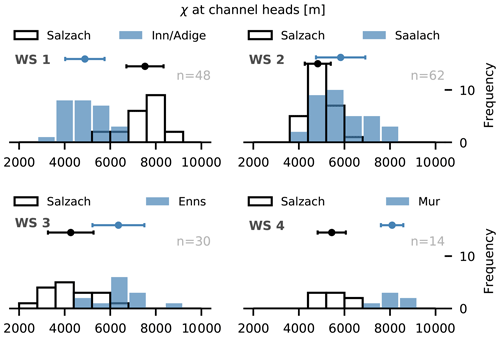
Figure 3 The χ values measured at channel heads of the investigated catchments. Histograms with a black outline represent the Salzach drainage basin. Histograms with a blue filling represent the adjacent Inn–Adige (WS 1), Saalach (WS 2), Enns (WS 3) and Mur (WS 4) drainage basins with n as the total number of data points. Data are divided into 10 equally spaced bins. Error bars indicate the standard deviation, and filled circles are the mean values of the dataset.

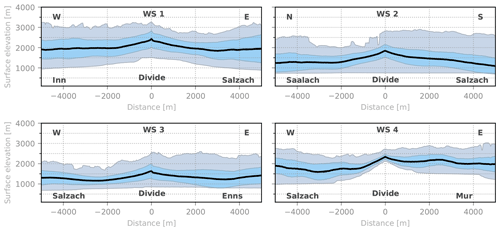
Figure 4 Generalized swath profiles (Hergarten et al., 2014) across the profile lines (drainage divides) shown in Fig. 1. The profiles have a half-width of 5 km to each side of the profile line (drainage divide). The black line indicates the mean elevation. The blue contours represent the standard deviation, and the grey contours represent the extreme values within the swath segments.

3.2 Swath profiles: across-divide differences at headwater scale

The four curved swath profiles perpendicular to the watershed segments WS 1–WS 4 indicate a series of distinct across-divide differences in the headwater relief (Figs. 1 and 4). At first glance, WS 1 appears to be roughly symmetric with a steady decrease in mean (H_mean) and minimum elevation (H_min) with increasing distance from the divide. Up to a distance of 2 km, the drop in H_mean is larger at the Inn side of the divide. At a distance of 5 km, H_min is slightly lower at the Salzach side in comparison to the Inn side. At this distance, the swath corridor has already reached the trunk valley of the Salzach drainage system but reaches only a small tributary of the Inn River at the other side of the divide. Overall, the relief (H_max−H_min) is larger at the Inn than at the Salzach side of the divide. The Saalach–Salzach drainage divide (Fig. 4, WS 2) shows a strong asymmetry in H_mean and relief but no spatial trend in H_min. The latter is bound up with the fact that the drainage divide exhibits a wind gap, which connects the valley floors of the Salzach and Saalach rivers without a significant drop in valley floor elevation (Fig. 1). In contrast, the eastern divides of the Salzach catchment show a strong asymmetry (Fig. 4, WS 3 and 4). The drop in H_min and H_mean with increasing distance from the divides is distinctly more pronounced at the Salzach side than at the Enns and Mur sides of the drainage divide. In consequence, high gradients in H_min and H_mean form towards the west, and gentle gradients arise towards the east.

3.3 Gilbert metrics: across-divide differences at hillslope scale

The Gilbert metrics suggested by Forte and Whipple (2018) comprise three measures characterizing the local differences at drainage divides (i.e. channel head elevation, mean upstream relief, mean upstream gradient). Overall, a strong divide asymmetry at hillslope scale is only observed at the Salzach–Mur drainage divide (Fig. 5).

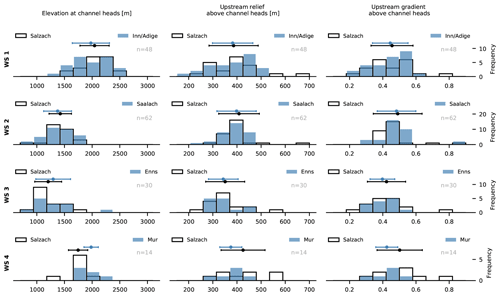
Figure 5 Gilbert metric histograms (Forte and Whipple, 2018) for the investigated watersheds of the study area. Histograms with a blue filling represent the adjacent Inn–Adige (WS 1), Saalach (WS 2), Enns (WS 3) and Mur (WS 4) drainage basins with n as the total number of data points. Data are divided into 10 equally spaced bins. Error bars indicate the standard deviation, and filled circles are the mean values of the dataset.

At the westernmost drainage divide of the Salzach catchment, elevations at channel heads (Fig. 5, WS 1) lie in the range between 1100 and 2600 m. At the Salzach basin, channel head elevations show a unimodal distribution with a mean value of 2044 m, while the distribution at the Inn–Adige basin is bimodal and has a mean value of 1977 m. Overall differences are small but indicate a slight shift towards lower channel head elevations at the Inn–Adige side of the drainage divide. The upstream relief ranges between 200 and 660 m, and it is uniformly distributed within the Salzach but skewed-left distributed in the Adige catchment. Mean values of upstream relief are similar in the Salzach and Inn–Adige catchment with 386 and 382 m, respectively. Analogous to the upstream relief, the upstream gradient is uniformly and skewed-left distributed in the Salzach and Inn–Adige catchments, respectively. Values for the upstream gradient are in the range of 0.2 and 0.8, with mean values of 0.45 for the Salzach and 0.44 for the Inn–Adige catchments. Beside outliers, the upstream relief and upstream gradient appear slightly larger in the Inn–Adige catchment than in the Salzach catchment.

At the Salzach–Saalach drainage divide, differences in all Gilbert metrics are small. Elevation at channel heads (Fig. 5, WS 2) ranges between 740 and 1750 m with mean values of 1424 and 1370 m at the Salzach and Saalach side of the divide. The upstream relief and the upstream gradient range between 250 and 760 m and between 0.35 and 1.1 in the Salzach and Saalach catchment, respectively.

While the eastern drainage divide, separating the Salzach from the Enns and the Mur catchments, features consistently large anomalies in χ, Gilbert metrics representing the hillslope scale indicate a largely symmetric Salzach–Enns and a distinctly asymmetric Salzach–Mur drainage divide. The channel head elevation of the Salzach–Enns divide (Fig. 5, WS 3) ranges between 840 and 2200 m, with mean values of 1206 and 1296 m at the Salzach and Enns side of the divide. The lower channel head elevation is also reflected by a slightly higher mean upstream relief and mean upstream gradient in the Salzach in comparison to the Enns catchment. Mean values are 351 m and 0.42 for the Salzach and 343 m and 0.4 for the Enns catchment.

The divide between the Salzach and Mur catchments is characterized by the largest across-divide differences in all Gilbert metrics (Fig. 5, WS 4). The elevation at the channel head lies between 1350 and 2220 m. On average, the channel head elevation is distinctly lower in the Salzach catchment (1747 m) than in the Mur catchment (1982 m). Lower channel head elevations result in a larger mean upstream relief and higher upstream gradient for the Salzach (425 m, 0.5) in comparison to the Mur catchment (375 m, 0.42).

4 Discussion

Gilbert (1877) already recognized that cross-divide differences in erosion rate result in mobile watersheds, whereby catchments featuring higher erosion rates grow at the expense of adjacent catchments with lower erosion rates. In the simplest case with overall uniform conditions, the erosion rate increases with channel steepness in the drainage and topographic gradient in the hillslope domain. Hence, divide asymmetry suggests drainage divide migration from the steep towards the less steep side (Gilbert, 1877; Willett et al., 2014; Robl et al., 2017b; Forte and Whipple, 2018). Asymmetry at drainage divides may occur at catchment, headwater and hillslope scale but may not necessarily be observed at all these scales. For example, a change in drainage area due to a river capture event may cause a χ anomaly at the drainage divide, which predicts drainage divide mobility. However, if the signal – expressed by an upstream-migrating knickpoint or knick zone – has not yet reached the divide, the divide may still be symmetric at the hillslope scale, indicating divide stability at that time. Glacially controlled base-level lowering (e.g. Hallet et al., 1996; Whipple et al., 1999; MacGregor et al., 2000; Brocklehurst and Whipple, 2002; Montgomery, 2002; Anderson et al., 2006; Haeuselmann et al., 2007; Züst et al., 2014) with an increase in local relief at the north-facing side of divides may cause a strong asymmetry at hillslope scale but will not result in an anomaly in χ maps as long as the drainage network topology remains unchanged.

4.1 Challenges and limitations interpreting drainage divide asymmetries

A direct determination of present-day divide migration rates is challenging as migration rates are in the range of millimetres per year (Goren et al., 2014) and major river capture events are rarely observed (Brocard et al., 2012; Yanites et al., 2013). In concert with sediment provenance (Frisch et al., 1998; Kuhlemann, 2007) and erosion rates based on cosmogenic nuclides (e.g. Dixon et al., 2016), topographic metrics serve as a proxy for drainage divide mobility.

Due to the superposition of climatic, tectonic and lithological signals in tectonically active, glacially modified mountain ranges, the interpretation of topographic metrics in terms of stable versus mobile drainage divides is not unique and paved with some pitfalls. For example, the topography of the Eastern Alps reflects different tectonic phases with a spatiotemporally diverse vertical and horizontal crustal velocity field controlling uplift rates and horizontal advection (i.e. lateral extrusion) (Ratschbacher et al., 1989, 1991; Robl et al., 2008b; Bartosch et al., 2017), changing climatic conditions governing peculiarity and even rates of erosional surface processes (e.g. Herman et al., 2013; Dixon et al., 2016), and substrate properties limiting the steepness of landforms as an expression of the long-term tectono-metamorphic evolution of the mountain range (Schmidt and Montgomery, 1995; Kühni and Pfiffner, 2001; Schmid et al., 2004; Robl et al., 2015). In particular, the strong glacial imprint altered topographic metrics and affected exhumation and erosion rates (e.g. Dixon et al., 2016; Fox et al., 2016), whereby the turnover time from glacial to fluvial landscape characteristics is controlled by lithology (Robl et al., 2015) and uplift rate (Prasicek et al., 2015). Then gradients in the erosion rate reflect rather a transient landscape state due to glacial–interglacial periods than across-divide differences resulting from the reorganization of the drainage system.

While a transient state caused by changing climatic or tectonic conditions is often considered the most likely reason for divide asymmetry, spatial heterogeneity in tectonics and climate may in principle reproduce the same topographic characteristics, but even in a steady state (e.g. Whipple et al., 2017). In the fluvial regime, contrasts in uplift rate, lithology and precipitation play similar roles. The crucial question in this context is whether there is a sharp topographic contrast at the drainage divide or a gradual variation. In a steady state with only vertical tectonic movement, the local steepness of the topography is related to the properties at the respective point. Thus, sharp across-divide contrasts in topography require discontinuous variations in precipitation or lithology or the existence of active faults close to the drainage divide, i.e. a sharp contrast in uplift rate. However, drainage divides do not move towards such discontinuities in general (Robl et al., 2017b), so sharp across-divide contrasts in topography due to tectonics or lithology should be rare. This is, however, not necessarily true if horizontal advection is involved. Then a divide that is stable in an absolute frame is mobile in the moving system and thus asymmetric with a sharp contrast. The conditions for the development of such stable divides were investigated by Eizenhöfer et al. (2019) by computing the crustal velocity governed by over-thrusting at a flat–ramp–flat geometry and modelling the response of the drainage system. Beyond this, contrasts in precipitation may cause sharp asymmetries at drainage divides because the pattern of precipitation is influenced by the topography, although the control of precipitation on the geometry of river channels is still debated (e.g. Burbank et al., 2003; Dadson et al., 2003; Molnar, 2003; Reiners et al., 2003; Wobus et al., 2003; Hodges et al., 2004).

Concerning the question of whether the across-divide asymmetry of the topography is pronounced or rather subtle, the analysis of stream profiles has only limited benefits as the stream power law does not capture the hillslopes. This limitation also affects all analyses based on the χ transform. The vertical distance between the channel head and base level divided by χ is the average steepness of the channel, but it provides no explicit information on the steepness of the dividing ridge itself. Consequently, a low increase in χ at the lower channel reach may result in a steep channel on average and small χ values even at the channel heads. Even if a stable divide can be excluded by other arguments, this implies that χ anomalies at drainage divides may indicate potential divide mobility in the future, rather than currently mobile divides (Forte and Whipple, 2018). Without doubt, many factors and processes may lead to an amplification or emergence of across-divide gradients in χ and complicate the interpretation of χ in terms of divide stability (Whipple et al., 2017; Forte and Whipple, 2018). As a strategy to counteract some of these pitfalls, a series of χ maps with progressively raised base levels narrows down the impact of spatial heterogeneity in tectonics and climate from the catchment to headwater scale. This allows for statements on the position of the disturbance within the drainage system and potential divide mobility in the far and in the near future.

In this context, the question may arise of whether χ mapping, i.e. the consideration of χ alone without regard to differences in elevation, is as good as computing an average channel steepness from the differences in elevation and in χ values. According to Eq. (5), the slope of a χ-transformed river profile is a proxy for the erosion rate at a given erodibility. The χ values at the end of the rivers would be inversely proportional to this slope if they were at the same elevation everywhere. This means that both approaches are equivalent if the steepness of the hillslopes is the same at both sides of the drainage divides. Otherwise, the interpretation of χ maps is not entirely free from an influence of the hillslopes, even if the lower limit of catchment size is large enough to ensure the applicability of the stream power law. If the hillslopes at one side are steeper, the channel heads (defined here by a minimum drainage area of 1 km²) are at a lower elevation, so the consideration of χ alone overestimates the mean steepness of the channel. This means that χ mapping implicitly captures the steepness of the hillslopes to some degree if applied across drainage divides. With regard to the relevance of the hillslope regions for the migration of the drainage divides, this might even be seen as an advantage of χ mapping over mean channel steepness.

The Gilbert metrics, a set of local topographic measures, characterize hillslopes at both sides of the investigated divide (Forte and Whipple, 2018) and hence the (a)symmetry of the divide itself. In contrast to χ mapping, there are no far-field effects, and significant asymmetry of the dividing ridge should correspond in principle to across-divide gradients in the erosion rate and divide mobility. However, in active, glacially modified mountain ranges, several factors and processes make the interpretation of these metrics challenging. Landslide-controlled threshold hillslopes emerge, on which incision rates in the drainage system are high (Montgomery et al., 2001). Then the relationship between the topographic gradient and hillslope erosion rate breaks down, and dividing ridges become symmetric although they feature across-divide gradients in erosion rate and migrate. For the European Alps, an average limiting slope stability angle of 25^∘ is reported (Schmidt and Montgomery, 1995; Kühni and Pfiffner, 2001), so most of the divides in the study area are prone to landsliding. However, in particular within the formerly glaciated realm of the Alps, many of the non-soil mantled hillslopes are distinctly steeper and still feature glacial landscape characteristics (Robl et al., 2015). There, local metrics such as relief, gradient or channel head elevation rather indicate the impact of the last glaciations on topography than long-term trends in drainage network reorganization. Glacial overprint does not primarily affect the first-order drainage networks, but it has a strong impact on local relief (e.g. Brocklehurst and Whipple, 2002; van der Beek and Bourbon, 2008; Norton et al., 2010; Salcher et al., 2014). Aspect-controlled differences in relief formation due to glacial erosion (e.g. north- versus south-facing mountain flanks) result in local, reversible compensating motions of the divides (Robl et al., 2017a) that may counteract the regional trend during the turnover time from glacial to fluvial landscapes. Hence, such local disturbances cover large-scale and long-lasting changes in the drainage network topology. Generalized swath profiles and χ maps with a base level at the headwaters may bridge the gap between the catchment and hillslope scale and assist in detecting local peculiarities as described above.

Summarizing, the major advantage of Gilbert metrics lies in the analysis of short-wavelength high-amplitude signals, e.g. the development of escarpments (e.g. Tucker and Slingerland, 1994). In contrast, the reorganization of drainage patterns forced by tectonic processes represents a large length scale – a low-amplitude signal taking place in millions of years (Robl et al., 2015) – which can be targeted by the calculation of χ maps. Headwater processes and the position of the erosional signal can be addressed by varying the base level for the χ transformation and the extraction of generalized swath profiles. We hereinafter discuss the behaviour of the drainage divides in consideration of the described pitfalls.

4.2 Mobility of drainage divides in the Eastern Alps

The observed asymmetry of drainage divides in the study region, with steep western and less steep eastern sides, may in principle result from spatial heterogeneity at the drainage divides with sharp contrasts in uplift rate, substrate properties or precipitation. Furthermore, over-thrusting along ramps may result in asymmetric but still stable drainage divides. Hence, divide asymmetry does not necessarily indicate divide mobility. However, there is no evidence that the drainage divides analysed here follow such lithological or tectonic structures. Sharp contrasts in precipitation require (i) a sequence of decrease, recovery and decrease in precipitation rate in the east–west direction as well as (ii) an inversion of the north–south contrast along a drainage divide (WS 1), both at rather small scales. Furthermore, the observed west–east asymmetry of divides is not consistent with the thrusting direction of major alpine units, which occurred roughly from south to north. In consequence, it appears unrealistic that the observed pattern is entirely controlled by climate, lithology or active faults, although some influence of climate (and also tectonics or lithology) cannot be excluded. Summarizing, the known long-term reorganization of the drainage network (Frisch et al., 1998, 2001) accompanied by changes in contributing drainage area appears to be the most likely interpretation of the observed topographic pattern and is enhanced by progressively increasing the base level for χ computation. Shifting the observational scale from presumable tectonically and climatically heterogeneous catchments to their more homogenous headwaters shows no qualitative changes in the χ pattern. The χ anomalies across the divides – as already described by Robl et al. (2017a) and Winterberg and Willett (2019) – remain up to a base level of 800 m (Figs. 2 and 3). Our results therefore suggest that the drainage divides of the investigated catchments are mobile and follow a general trend. At north–south-running drainage divides, tributaries feature lower χ values west of the dividing ridge and are hence steeper on average than tributaries draining towards east (Fig. 2). However, this trend in χ breaks down at some divides for a base level of 1000 m, characterizing headwaters only.

Gilbert metrics characterizing divides at the hillslope scale are consistent with the χ pattern at the Salzach–Enns and Salzach–Mur drainage divides and indicate that these divides are currently mobile. However, and in contrast to the χ pattern (up to a base level of 800 m), they indicate divide stability at the Inn–Salzach drainage divide (Figs. 2 and 3). In particular at the latter divide, glacial landforms such as cirques and U-shaped valleys are abundant and we interpret the missing hillslope-scale asymmetry of this divide as a result of glacial erosion, which temporally stops divide migration (Robl et al., 2017b). However, Robl et al. (2017a) showed that the impact of variable glacial erosion across divides is small and reversible. We suggest that the topographic signal of cold climate processes, primarily acting during the Pleistocene, locally obscures the large-scale signal of drainage network reorganizations in many parts of the Eastern Alps and in general limits the applicability of Gilbert metrics in glacially shaped mountain ranges.

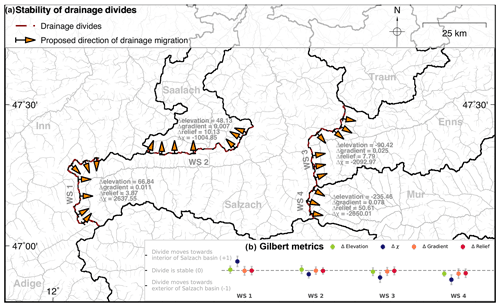
Figure 6 Proposed direction of drainage migration of the main drainage divides in the study area. (a) The major drainage basins are annotated. Orange arrows indicate the proposed migration direction of divides based on χ. Gilbert metrics for each investigated catchment are shown. Positive Δelevation and Δχ values as well as negative Δrelief and Δgradient indicate migration towards the Salzach drainage basin. (b) Normalized Δ plot of Gilbert metrics. Negative values of Δrelief and Δgradient are standardized to positive values such that all positive values indicate a migration towards the Salzach basin. The error bar and filled circles indicate 1 standard deviation and mean values, respectively.

We suggest that the proposed drainage divide migration from west to east is inherently linked to the plan view geometry of the Salzach and Enns catchments south of the Northern Calcareous Alps (Figs. 1, 2 and 6). In this domain, the main stem of the Salzach and Enns still follows the SEMP, which is one the major tectonic lineaments of the Eastern Alps (Wang and Neubauer, 1998). It has been proposed that during the mid-Miocene, the Salzach and Enns formed a common catchment with an eastward-directed flow path (e.g. Neubauer, 2016) but were separated by major river piracy events due to headward-eroding south–north-draining rivers (Kuhlemann et al., 2001; Dunkl et al., 2005; Robl et al., 2008a). As a consequence, the major portion of the Salzach and Enns drainage areas is located west of their capture points and by reversing the flow direction only to a minor amount east of the capture points. This is consistent with the current asymmetry of the catchments, with a large western and a small eastern sub-catchment, and explains the observed across-divide gradients in χ. Long eastward-directed channel segments in concert with distinctly elongated catchments result in a slow decrease in catchment size in the upstream direction. Hence, χ accumulates to large χ values at the western drainage divides and low χ values at the eastern drainage divides. Integrating from a common base level up to the same channel head elevation, large and small χ values on different sides of a common divide (Inn–Salzach, Salzach–Enns and Salzach–Mur divides) are the expression of a low and high average channel steepness of long west–east-draining and short east–west-draining channel segments, respectively. This, however, implies that observed χ anomalies at the investigated drainage divides are the consequence of the early to mid-Miocene lateral extrusion tectonics (Ratschbacher et al., 1989, 1991), whereby the activity of crustal-scale faults imposed a nonideal flow direction on major rivers (Robl et al., 2008b, 2017a). The indicated drainage network reorganization from orogen-parallel to orogen-perpendicular flow is a long-lasting process. While river piracy events cause a sudden large-scale modification of the drainage network, drainage divide migration and flow direction reversal is a slow continuous process at rates of a few millimetres per year (Goren et al., 2014), which explains the longevity of morphological disequilibrium after changes in the tectonic forcing.

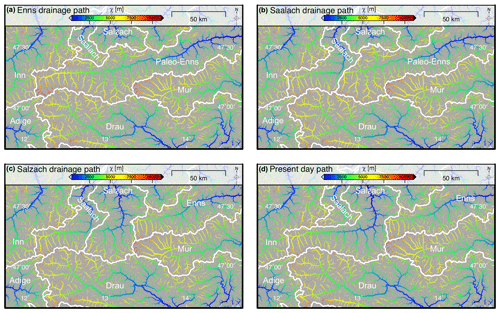
Figure 7 The χ-coloured drainage pattern of reconstructed paleo-drainage geometries of the Eastern Alps. All streams with a contributing drainage area larger than 1 km² are shown, and the line width of the channels is proportional to log₁₀(drainage area). The base level for χ computation is set to 400 m. White lines and annotations represent the major drainage divides. (a) Enns drainage path–drainage scenario assuming an elongated Enns catchment representing the mid-Miocene situation as suggested by Frisch et al. (1998). (b) Saalach drainage path–drainage scenario assuming that the Saalach captured the westernmost part of the Paleo-Enns catchment. (c) Salzach drainage path–drainage scenario assuming that both the Saalach and Salzach took over parts of the Paleo-Enns catchment as suggested by Robl et al. (2008a). (d) Present-day drainage pattern for comparison.

4.3 Stability of divides for different evolutionary states

Based on provenance analyses and geomorphological studies, it has been proposed that different tectonic phases have triggered a repeated reorganization of the drainage system since the onset of topography formation in the Eastern Alps (Frisch et al., 2000; Kuhlemann et al., 2001; Dunkl et al., 2005; Kuhlemann, 2007; Keil and Neubauer, 2009; Neubauer, 2016). As the position of past drainage divides is not well constrained, we test if and how different catchment geometries, roughly mimicking the catchment geometry suggested for different phases of the drainage evolution, affect the stability of drainage divides (Fig. 7). We focus on the plan view geometry of catchments only and do not consider potential topographic (e.g. uplift of the Northern Calcareous Alps) or base-level (e.g. inversion of the northern foreland basin, the Molasse basin) changes. In order to create the proposed drainage patterns for different time slices, we dammed valleys and forced rivers to drain across prominent wind gaps (see Fig. 1 for wind gaps), which changes the large-scale system of rivers but leaves the small-scale network topology unaffected. As the χ computation considers the network topology only and does not require further topographic information, it is less important to reconstruct the evolution of the topography of the Eastern Alps in detail.

For the period of lateral extrusion during the early to mid-Miocene, it was suggested that the Salzach and Enns formed a common drainage system (Paleo-Enns) with an orogen-parallel flow path following the SEMP Fault from west to east (Fig. 7a) (Frisch et al., 1998). Compared to the present-day drainage pattern (Fig. 7d), the elongated catchment, with its long main stem and numerous short tributaries contributing drainage area from south and north, causes very high χ values at the eastern domain of the drainage system. In particular, the Inn–Paleo-Enns drainage divide is characterized by high across-divide gradients in χ, but even the southern drainage divide between the Paleo-Enns and Drau indicates a strong χ anomaly. This suggests that the early to mid-Miocene situation, with elongated catchments featuring hundreds of kilometres of orogen-parallel flow, were prone to river piracy events and the migration of drainage divides.

The timing of the following drainage network reorganization is not well known. However, streams originating south of the SEMP Fault and draining towards the northern foreland basin eroded headwards and captured the eastward-draining Paleo-Enns (Salzach–Enns) drainage system (Frisch et al., 1998). Currently, two rivers, the Salzach and the Enns, follow the SEMP for more than 100 km each but abruptly change their course in a knee-shaped bend towards north (Fig. 1). These sudden changes in flow direction most likely indicate capture points. In addition, a suspicious wind gap separating the Saalach from the Salzach valley with a vertical drop of only a few metres (Fig. 1) may indicate that the Paleo-Enns was once captured by the Saalach River but redirected again, potentially during the Pleistocene glaciations (Robl et al., 2008a) (Fig. 7b and c).

Although not yet constrained by provenance studies, a potential capture of the Paleo-Enns drainage system by the Saalach River would stabilize the westernmost drainage divide (Inn–Saalach divide). This is indicated by a decrease in the across-divide χ gradient similar to the present situation (Fig. 7d). However, in this scenario, the western drainage divide of the Enns catchment shows a distinct across-divide χ gradient with high χ values at the Paleo-Enns and low χ values at the Saalach side of the divide, which would result in a progressive flow direction reversal of the upper Enns River.

It is still debated at which time the orogen-parallel Paleo-Enns River was captured by the south–north-draining Salzach River (Fig. 7c). A Pleistocene, glacially induced activation of the northward-directed drainage outflow blocking the passage at the Saalach–Salzach wind gap is discussed (Robl et al., 2008a). A similar event recently happened in Yukon, Canada, due to climate warming and glacial retreat (Headley, 2017; Shugar et al., 2017). Assuming a Pleistocene capture event due to waxing or waning of glaciers, the origin of the Salzach (similar to the nearby Lammer River) must have inevitably been located south of the Northern Calcareous Alps (NCA). Beyond others, one argument for such a scenario is the small amount of flow reversal of the former Enns River east of the capture point. However, the concurrent drainage through the Saalach and Salzach valley would lead to the disappearance of the χ gradient across the Saalach and Salzach watershed (Fig. 7c). The watershed separating the Salzach from the Enns basin complies with the present-day location of the watershed (Fig. 7c and d) and the χ distribution shows a similar χ anomaly, indicating an eastward drainage divide migration as proposed for the present-day situation.

5 Conclusion

The tectonic evolution of the Eastern Alps caused a repeated reorganization of the drainage network since the onset of topography formation in the late Oligocene to early Miocene. We applied various morphometric methods to constrain the potential mobility of drainage divides on the catchment, headwater and hillslope scale. Based on our analysis, we came to the following conclusions.

The vast majority of drainage divides in the investigated domain are asymmetric at the catchment, headwater and even hillslope scale, which evidences drainage divide mobility, whereby the steeper side of the divide migrates towards the less steep side of the divide.

The western side of the considered drainage divides is in general steeper than the eastern side, so the general direction of divide migration is west towards east. This implies that the Inn catchment grows at the expense of the Salzach catchment, and the Salzach catchment consumes tributaries of the Enns and Mur catchments.

At some divides, metrics characterizing hillslopes (Gilbert metrics) are not consistent with those characterizing larger scales. We found that glacial imprint locally obscures large-scale signals of drainage network reorganization. Hence, the applicability of the classical Gilbert metrics in glacially modified mountain ranges such as the Eastern Alps is limited.

The general drainage migration trend from west towards east is probably caused by the geometry of catchments, which dates back to the period of lateral extrusion in the early to mid-Miocene. The activity of major faults north and south of the central axis of the Eastern Alps imposed orogen-parallel flow directions on major rivers. Subsequent capture events restored orogen-perpendicular flow, but relics of the lateral extrusion period remained: elongated catchments west of the capture point, with an approximately 100 km long east-draining main stem and short tributaries draining south–north and north–south.

Analysing catchment geometries that roughly mimic the drainage pattern from the early to mid-Miocene towards the present situation shows that anomalies in χ at the divides decreased, indicating that divide stability increased over time. Currently, across-divide anomalies in average channel steepness (and hence erosion rate) occur mostly at north–south-running watersheds (i.e. Inn–Salzach, Salzach–Enns, Salzach–Mur), where tributaries with short and long flow lengths from channel heads to the base level meet at the divides. However, as continuous divide migration is slow and major capture events at these divides are not expected, we suggest that the observed disequilibrium is long-lasting.

The timing of river piracy events and rates of drainage divide migration are still not well constrained. There is a great need for additional provenance studies of river sediments, as well as dating river terraces and cave sediments.