the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Short communication: Analytical models for 2D landscape evolution
Philippe Steer
Numerical modelling offers a unique approach to understand how tectonics, climate and surface processes govern landscape dynamics. However, the efficiency and accuracy of current landscape evolution models remain a certain limitation. Here, I develop a new modelling strategy that relies on the use of 1D analytical solutions to the linear stream power equation to compute the dynamics of landscapes in 2D. This strategy uses the 1D ordering, by a directed acyclic graph, of model nodes based on their location along the water flow path to propagate topographic changes in 2D. This analytical model can be used to compute in a single time step, with an iterative procedure, the steady-state topography of landscapes subjected to river, colluvial and hillslope erosion. This model can also be adapted to compute the dynamic evolution of landscapes under either heterogeneous or time-variable uplift rate. This new model leads to slope–area relationships exactly consistent with predictions and to the exact preservation of knickpoint shape throughout their migration. Moreover, the absence of numerical diffusion or of an upper bound for the time step offers significant advantages compared to numerical models. The main drawback of this novel approach is that it does not guarantee the time continuity of the topography through successive time steps, despite practically having little impact on model behaviour.
- Article
(6608 KB) - Full-text XML
- BibTeX
- EndNote
While the elevated but incised landscapes of mountain belts testify to the cumulated actions of tectonics, erosion and climate, unravelling how these processes act and interact to shape the Earth's surface remains one of the most challenging issues in Earth sciences (e.g. Molnar and England, 1990; Willett, 1999; Whipple, 2009; Steer et al., 2014; Croissant et al., 2019). Numerical models have been pivotal to understanding how topography and erosion respond to spatial and temporal changes in climate and tectonics (e.g. Howard et al., 1994; Whipple and Tucker, 1999; Tucker and Whipple, 2002; Carretier and Lucazeau, 2005; Thieulot et al., 2014; Croissant et al., 2017). At the mountain scale, numerical models generally account for geomorphological processes using effective and reduced-complexity erosion laws such as the stream power incision model (SPIM) for rivers (e.g. Howard et al., 1994) and diffusion for hillslopes (e.g. Roering et al., 1999). In particular, the SPIM is popular in landscape evolution models (LEMs) as its physical expression resolves to a non-linear kinematic wave equation, which offers simple finite-difference or finite-volume solutions in 1 and 2D (e.g. Pelletier, 2008; Braun and Willett, 2013; Campforts and Govers, 2015; Campforts et al., 2017). Despite these benefits, these numerical solutions have several drawbacks: (1) their stability or consistency requires the use of a small time step that must respect the Courant condition, i.e. that an erosional wave cannot travel over a distance greater than one or a few node spacings during one time step, and (2) they are prone to numerical diffusion and therefore only offer approximate solutions. Numerical schemes in 2D have recently been developed to reduce the time-step dependency on grid spacing (Braun and Willett, 2013) or numerical diffusion (Campforts and Govers, 2015). In 1D, evolution of river profiles can be derived using analytical solutions determined by the method of the characteristics (Luke, 1972, 1974, 1976; Weissel and Seidl, 1998; Whipple and Tucker, 1999; Lavé, 2005; Pritchard et al., 2009; Royden and Taylor Perron, 2013). These solutions have been successfully used in formal inversion of river profiles (Goren et al., 2014a; Fox et al., 2014; Goren, 2016), but they have been largely ignored in forward landscape evolution models, despite their inherent exact accuracy. This likely results from the apparent absence of an analytical solution in 2D.
In this study, I extend the applicability of these 1D analytical solutions to 2D problems by developing a new type of landscape evolution model based on analytical solutions. I first demonstrate how this model, that I refer to as Salève, can be used to compute – in a single time step – a steady-state topography in 2D. I then develop a dynamic version of Salève to solve for transient landscape changes under heterogeneous or time-variable uplift. Last, I demonstrate the ability of Salève to accurately model the propagation of knickpoints in LEMs and to account for river, colluvial and hillslope erosion.
Most LEMs require the computation of river water discharge as the main driver of river erosion and sediment transport. While flow algorithms based on physical considerations offer more accurate solutions (e.g. Davy et al., 2017), water routing in 2D LEMs is generally achieved using simple flow algorithms, like the steepest slope (O'Callaghan and Mark, 1984) or the multi-flow direction (Quinn et al., 1991; Freeman, 1991). The Fastscape algorithm, and other graph-based approaches, offers a very efficient means to order nodes along the steepest water flow path and to compute river discharge and drainage area (Braun and Willett, 2013; Schwanghart and Scherler, 2014). A single receiver and potentially several donors are attributed to each node of the topographic grid to recursively build a node stack (or graph) from the outlet node to the crest nodes of each catchment. Each node is therefore associated with its outlet node through a single flow path. These flow paths represent 2D trajectories in the (x, y) space that can be converted to pseudo-1D trajectories (i.e. to directed acyclic graphs) using the node ordering of the stack. For instance, local river slope along the water flow can be computed by simply differentiating elevation over the distance along the river length l between successive nodes. The 2D LEMs solving for river erosion using a single flow algorithm and local river slope or water discharge are therefore fundamentally solving a 1D problem, based on a 2D description of the flow. To be more accurate, they actually solve for a series of 1D problems, with one 1D problem for each catchment connected to an outlet.
In 1D, a classical detachment-limited approach to describe the rate of change in river elevation change z with time t is the SPIM (Howard and Kerby, 1983; Howard, 1994; Whipple and Tucker, 1999; Lague, 2014):
where U is the uplift rate, K′ the erodibility, Qw=rA the water discharge with A the drainage area, r the mean daily runoff, and m and n are two exponents. This equation can be cast in a more commonly used form, as a function of drainage area, by defining an effective erodibility :
This equation corresponds to a non-linear kinematic wave equation with a celerity representing the speed at which information propagates along the river (e.g. Rosenbloom and Anderson, 1994; Weissel and Seidl, 1998; Whipple and Tucker, 1999; Royden and Taylor Perron, 2013). Following Royden and Taylor Perron (2013), this migrating information can be referred to as slope patches. Integrating the inverse of this celerity along the river path, from the river outlet at l=0 to a point of coordinate l along the river, defines the river response time:
Using this response time and assuming a constant but potentially heterogeneous uplift rate U(l) or a uniform but potentially variable uplift rate U(t), river profile elevation can be derived analytically assuming A is known (see derivation in Royden and Taylor Perron, 2013). As I intend to implement a solution in a LEM, the solution needs to remain practical. In particular, it is noticeable that the response time and celerity become independent of local river slope when n=1, which is a classical choice in forward or inverse landscape evolution models (e.g. Goren et al., 2014a; Fox et al., 2014). Under this condition and assuming a constant and homogeneous uplift rate U, the steady-state river profile elevation is
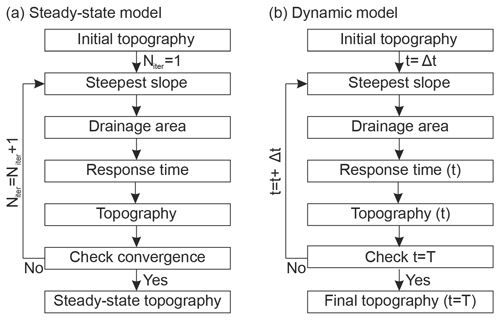
and with zbase the base-level elevation. Note that this solution is asynchronous as steady state is achieved for an increasing response time in the upstream direction. Importantly, as the flow network is not known a priori, this integral solution still requires one to numerically compute a flow network and drainage area over a discretized grid. In the following, I adapt this formalism to develop two modelling approaches which either computes the steady-state topography of a landscape or solves for its dynamic evolution (Fig. 1).
This solution (Eq. 4) can be extended to spatially variable uplift rate U(l) by simply using the response time of the receiver node τR(l) and its elevation zR(l):
Obviously, this operation needs to be performed iteratively and in the correct node order, from the outlet node towards the upstream direction using the node stack or graph (Braun and Willett, 2013; Schwanghart and Scherler, 2014). Ignoring hillslope processes, I use this solution to attempt computing the steady-state topography with Salève in a single iteration (Fig. 2). The initial topography consists of a flat surface with a random noise discretized by a regular grid. I use m=0.5, corresponding to the classical unit stream power, U=10 mm yr−1, yr−1, m d−1 and a square model domain of extent L=10 km with a resolution of 50 m, corresponding to npt=40.401 points. Flow over the topography is computed using the single-flow algorithm provided by TopoToolbox (Schwanghart and Scherler, 2014), which efficiently exploits the directed acyclic graph structure of the flow network (Phillips et al., 2015).
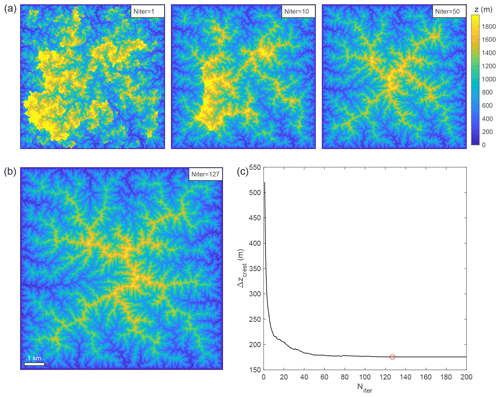
Figure 2Modelled steady-state topographies obtained after (a) 1 (left panel), 10 (middle panel) and 50 (right panel) iterations. (b) The steady-state topography is obtained after 127 iterations. (c) Convergence of the iterative algorithm inferred from the degree of crest disequilibrium Δzcrest, computed as the average of the absolute difference of elevation between crest nodes of juxtaposing catchments. Red dot indicates model shown in panel (b). Note that in panel (a), the colour map is bounded by the maximum elevation of the steady-state topography shown in panel (b).
The obtained solution looks very roughly like a classical steady-state topography, and yet it is not strictly at steady state (Fig. 2). Indeed, during this first iteration, the scheme used (Fig. 1a) imposes the constraint that rivers develop over the flow network defined by the initial topography and, in turn, does not ensure that the nodes located on the same crest of two juxtaposing catchments share the same response time or the same elevation. This leads to an excessive elevation as some rivers have planar length greater than predicted. This is the main limit of this 1D algorithm that cannot ensure the optimality of the 2D organization of the river network at steady state after only one iteration (Fig. 2).
However, repeating this operation by computing the topography and then updating the flow network (i.e. by computing the steepest slope, node order, and drainage area or discharge) after each iteration leads to a steady-state topography after a few tens of iterations Niter (Fig. 2). To assess the convergence of this iterative procedure, I define the degree of crest disequilibrium Δzcrest as being the average of the absolute difference of elevation between crest nodes of juxtaposing catchments. I find that Δzcrest follows a rapid decay with Niter until reaching a slower decay phase when Niter≥40. Δzcrest never reaches 0 m, even after 100 iterations, as differences of elevation can remain along the two sides of the crests, as in other LEMs, due to the non-continuity of the spatial discretization for grid-based models (Fig. 2c). However, the model reaches a stable solution at Niter=127. Note that running the same model but with a different initial topography leads to a variability of this required number of iterations due to the initial configuration of the flow network.
Changing U, K and L while keeping npt constant does not lead to a significant change in the number of iterations required to reach steady state (Fig. 3). This shows that the convergence of this algorithm is independent of the model parametrization. However, increasing the number of points npt leads to an increase in the number of iterations required to reach steady state, which scales with , or in other words with the number of nodes in one of the horizontal dimensions (Fig. 3). This scaling emerges due to the more numerous numbers of local (i.e. among direct neighbours) permutations of the crest location required to reach a stable fluvial organization when increasing npt.
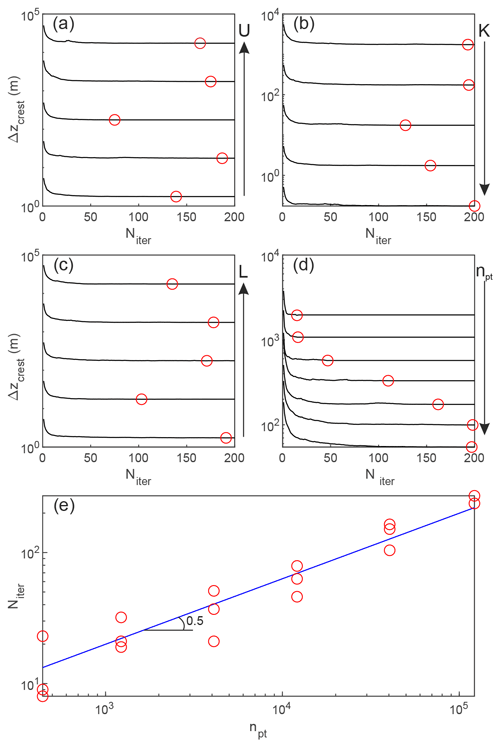
Figure 3Influence of model parameters and geometry on the convergence towards a steady-state landscape. (a) Uplift rate U was varied between 10−4 and 1 m yr−1. (b) Erodibility K was varied between and yr−1. (c) Model length L was varied between 0.1 and 100 km. (d) The number of model points npt was varied between 1.2×103 and 0.4×106. (e) The relationship between the number of iterations required to reach steady state and npt follows a power law with an exponent 0.5 (blue line).
The new algorithm developed in Salève presents significant advantages compared to finite-difference schemes, which are fundamentally limited by the time step Δt that must respect the Courant conditions , with k equal to ∼0.1 or to 100 for explicit or implicit schemes, respectively (e.g. Braun and Willett, 2013). Therefore, these finite-difference solutions are doomed to use shorter time steps and a larger number of iterations when considering finer resolutions. On the contrary, this analytical LEM converges towards steady state with roughly the same number of iterations, independently of the celerity C(l), which is set by K, A (i.e. L2) and m. The number of required iterations, however, increases with , which is equivalent to an increase with decreasing when L is constant, as in classical finite-difference schemes. Moreover, this steady-state modelling approach is compatible with spatially variable U, K and r.
I now explore the use of this analytical model in dynamic simulations with Salève (Fig. 1b). I first consider the case of potentially heterogeneous but constant uplift rate U(l). A transient solution for river elevation z(l,t) at a specific time t can be computed using Eqs. (4) or (5) by simply thresholding the response time so that for every node . It results in the following:
This solution therefore enables computation of the time evolution of a landscape under potentially heterogeneous erodibility, uplift and runoff (or precipitation) rates. Thresholding the response time enforces that the uplift rate is considered null before the beginning of the simulation. The limitation of non-optimality of the planar organization of flow network remains as in the steady-state solution. However, this limitation can be solved by simply updating the river network, the node order, the steepest slope and water discharge after each time step, as in any other LEMs. As the time step is not constrained by numerical stability issues, such as the Courant condition, it can be chosen only based on the rate of flow network reorganization linked to river capture and piracy. Note, however, that in the dynamic Salève models, flow network reorganization will lead to an immediate topographic reorganization, to respect Eq. (6). Indeed, time evolution of the elevation in Salève should not be seen as a continuous time evolution of a same topography, which would evolve by erosion under different time and space distributions of water discharge (e.g. as in other LEMs), but as a succession of topographic realizations which respect that the distribution of elevation is set by the flow network. In other words, Salève does not fully guarantee the time continuity of the topography through successive time steps, despite practically having a limited impact on model behaviour as I will demonstrate later.
I here run a simulation, using the same parameters as in the steady-state simulation, over a duration of 500 kyr (Fig. 4). The time steps Δt=2 and 0.2 kyr correspond to about 45 and 4.5 times the Courant condition, respectively. Because implicit finite-difference solutions to the SPIM also remain numerically stable for time steps longer than the one imposed by the Courant condition, I also run simulations using an implicit solution with the same parameters and time steps and compare them to the results of the Salève simulations. The implicit solution is computed following Eq. (22) in Braun and Willett (2013). I also compare Salève with results obtained with an implicit solution using a time step Δt=0.002 kyr, corresponding to a Courant condition of 0.45.
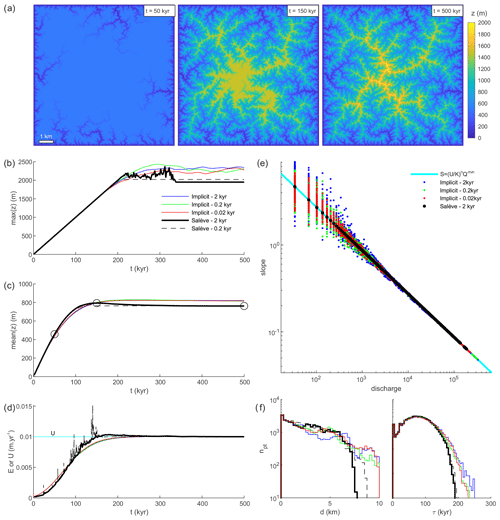
Figure 4Dynamic behaviour of the Salève model. (a) Time evolution of the modelled topography after 50 (left panel), 150 (middle panel) and 500 kyr (right panel). Time evolution of the (b) max elevation, (c) mean elevation and (d) mean erosion rate for Salève, using a time step of Δt=2 kyr (black line) and 0.2 kyr (dashed black line) and for the implicit solution with Δt=2 kyr (blue line), 0.2 kyr (green line) and 0.02 kyr (red line). The uplift rate U is shown in panel (d) with a cyan line. (e) Slope–discharge distributions at steady state (at 500 kyr) for the three models compared to the predicted relationship (cyan line). No binning is done, and all the model nodes are represented in panel (d). (f) Histograms of upstream distances d (left panel) and response times τ (right panel) for the different models at steady state.
The final topographies, i.e. at steady state, obtained with Salève or with the implicit solution share roughly the same statistical properties in terms of vertical and horizontal organization. The time evolution of the mean elevation (mean(z)) and maximum elevation (max(z)) is similar in all the models, even if the steady-state value is higher by ∼50 for mean(z) and ∼500 m for max(z), with the implicit solution (Fig. 4c). Moreover, the fluvial network and hence the topography modelled with Salève reach a stable configuration once at steady state, with no subsequent vertical or horizontal changes. Topographic stability occurs when the model time t becomes greater or equal to the response time τ(l) of all the model nodes, and in particular the ones located on crests (Fig. 4b). This is particularly true if Δt is small enough to allow the horizontal organization of the fluvial network to evolve concomitantly with its vertical component. On the contrary, the topography simulated by the finite-difference models continues to evolve after steady state, in particular the maximum elevation max(z), with larger variations for models with longer time steps, which occurs due to catchment reorganization and numerical noise.
Moreover, erosion rates E first increase more slowly and then more rapidly in Salève than with the implicit solutions before reaching steady state (Fig. 3d). In particular, the second phase is due to longer upstream distances and erosional response times in the topographies simulated with the implicit solution than with Salève (Fig. 3f). This is at least partly due to the dependency of the transient phase duration on Δt for finite-difference models (Braun and Willett, 2013). Geometrically, longer transient phases are associated with fluvial networks with longer upstream distances, i.e. distances to the outlet, in the implicit models with longer time steps compared to implicit models with shorter time steps or to Salève models (Fig. 3e). These results also show that the response time of the landscapes is shorter than with other 2D LEMs as it is equal to the 1D response time, based on the flow network length at steady state, when the time step used is sufficiently short to allow progressive reorganization of the fluvial network (e.g. model with Δt=0.2 kyr).
Erosion rates in Salève, calculated by differencing elevation between successive time steps and subtracting the contribution of uplift, are significantly more variable, in particular for the model with the shorter time step Δt=0.2 kyr than with the implicit solutions. This variability highlights phases of fluvial network reorganization which lead to immediate topographic reorganization, due to time discontinuity, and therefore to an immediate increase in erosion rates.
In terms of horizontal organization, all the Salève and implicit models lead to the same Hack's law (Hack, 1957), which relates, through a power-law relationship, the downstream maximum river length Lr with catchment area: Lr∝Ah. A least-square fitting gives an exponent h of 0.65±0.01 for Salève and the implicit models at steady state, with no dependency over Δt. In terms of vertical organization, the slope–discharge relationship obtained with Salève at steady state fits perfectly with the predicted one, , while the implicit solution shows a significant spread, in particular at low drainage area or discharge, which increases with Δt (Fig. 3d). Using Δt=0.02 instead of 2 kyr leads to a slightly better consistency between the implicit and Salève solution, including the slope–discharge relationship and the temporal evolution of elevation.
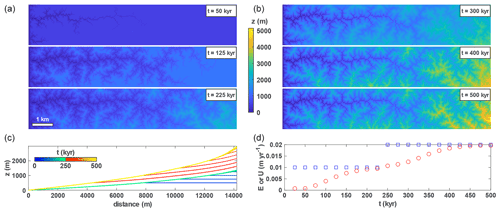
Figure 5Dynamic evolution of the topography and knickpoint migration over 500 kyr. The initial uplift rate U=10 mm yr−1 is doubled after 250 kyr. (a) Topography before the increase in uplift at 50 (top panel), 125 (middle panel) and 225 kyr (bottom panel). (b) Topography after the increase in uplift at 300 (top panel), 400 (middle panel) and 500 kyr (bottom panel). (c) Temporal evolution of the longest river profile shown at every time step (except the first one), with the “winter” and “autumn” colour map showing river profiles before and after the increase in uplift. (d) Temporal evolution of the uplift (blue squares) and erosion (red circles) rates.
I now investigate the case of time-variable but homogeneous uplift rate U(t). Following Royden and Taylor Perron (2013), this case leads to additional complexity as the uplift rate, when the slope patches were initiated, must be tracked during upstream migration. In a LEM, this is performed by computing, at the specific time t, what I refer to as the uplift memory map . It is not equivalent to a classical uplift map and corresponds to the uplift rate when the slope patches were formed. I remind the reader here that the response time is bounded by actual model time . The elevation at a time t is then simply computed in the upstream direction, starting with the river outlets, as
As in the heterogeneous uplift case, this solution is easily implemented in a LEM by updating the river network and its properties after each time step. I also emphasize here that the previous model example (Fig. 4) is already a specific case of a time-variable uplift rate, with a change in uplift rate which occurs at the beginning of the simulation, leading in turn to a simpler formalism (Eq. 6). In the following, I focus on demonstrating the ability of the model to simulate and track knickpoints.
Discrete temporal changes in uplift rates or in base-level elevation can lead to sharp ruptures in the slope of river profiles, generally referred to as knickpoints (e.g. Rosenbloom and Anderson, 1994; Whipple and Tucker, 1999; Steer et al., 2019). Finite-difference solutions to the stream power equation inherently lead to a progressive numerical diffusion of knickpoints during their migration, even with n=1, while the algorithm developed here preserves the shape of knickpoints. To illustrate this advantage, I run a simulation with the same parameters as in the steady-state case, except that U is raised from 10 to 20 mm yr−1 at 250 kyr for a total model duration of 500 kyr (Fig. 5). Compared to previous models, the model is here restricted to an extent of 10 km over 2 km, with only one boundary (left) that is considered as possible outlets for water. This setting limits fluvial network reorganization (or time discontinuity) and in turn allows for tracking geomorphological features during the evolution of the landscape. I use a time step of 25 kyr, which is about 500 times greater than the time step imposed by the Courant condition, clearly above the range of time steps compatible with numerical solutions. Despite this, the knickpoints formed at the outlets of the model at 250 kyr, at the onset of the increase in uplift rate, are accurately modelled, i.e. with analytical accuracy, throughout their propagation (Fig. 5c). The shape of the knickpoint is also kept throughout its migration. I also highlight here that, due to the model setting with only one outlet boundary, which limits river reorganization (and time discontinuity), erosion rates are smoother than in Fig. 4.
In previous sections, I have considered the steady-state and dynamic solutions of landscapes subjected only to river erosion following the SPIM. However, these analytical solutions can be extended to simulate the dynamics and morphology of colluvial valleys and hillslopes. Indeed, a power-law scaling for the slope–area relationship is observed in colluvial valleys, which suggest they could obey a similar erosion law as Eq. (1), but with different m and n exponents (Lague and Davy, 2003). A solution with m=0.24 and n=1, but considering a non-negligible incision threshold, was found to best explain the geometry of colluvial valleys in the Siwalik Hills of Nepal for drainage area between and 1 km2, representing the thresholds in drainage area between colluvial valleys and hillslopes or rivers, respectively (Lague and Davy, 2003). Below the area transition between colluvial valleys and hillslopes, the power-law scaling for the slope–area relationship becomes flat, due to landsliding and mass wasting processes, or reverts where hilltops are convex (Ijjasz-Vasquez and Bras, 1995; Tarolli and Dalla Fontana, 2009). Once again, this hillslope domain could be geometrically modelled using the SPIM with different m and n, e.g. with m=0 and n=1, to model hillslopes following a critical angle of repose Sc. I do not argue here that these laws necessarily encapsulate the processes controlling colluvial and hillslope erosion (e.g. Tucker and Bras, 1998; Densmore et al., 1998; Roering et al., 1999; Lague and Davy, 2013; Jeandet et al., 2019) but that this framework can approximate the observed geometrical relationships between slope and area.
Practically, considering three different erosion laws, for river, colluvial valleys and hillslopes, simply requires changing the value of K, m and n in the definition of celerity in the response time equation (Eq. 3) for each of the different domains, separated by thresholds in discharge or drainage area. Keeping n=1 for simplicity leads to the following set of response time equations:
where A(l1) and A(l2) are model parameters that define the threshold areas for river to colluvial valley and for colluvial valley to hillslope transitions, and (K1, m1), (K2, m2), and (K3, m3) are the K values and m exponents for rivers, colluvial valleys and hillslopes, respectively. I emphasize here that the colluvial law used here is only inspired from the colluvial law described in Lague and Davy (2003), as it neglects the incision threshold which lead to a non-linear behaviour. Figure 6 shows the steady-state topographies obtained when considering river, colluvial and hillslope erosion. Considering these additional erosion laws leads, as expected, to different scaling in the slope–discharge relationships, separated by thresholds in discharge or drainage area. These thresholds should be chosen to ensure (1) the continuity of the slope–discharge relationship and (2) the slope is equal to Sc when A≤A(l2). I emphasize, once again, that the models developed here lead to slope–discharge relationships with exact accuracy, at steady state, due to the use of analytical solutions. Other analytical solutions can be considered to account for hillslope processes such as the one developed in the DAC model (Goren et al., 2014b).
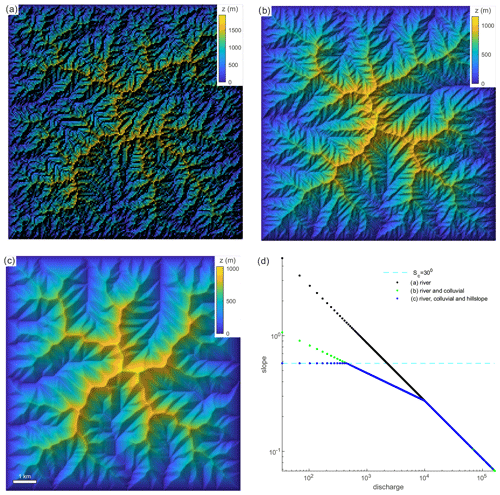
Figure 6Steady-state topographies obtained with Salève considering only (a) stream power incision (m=0.5) in rivers (like in Fig. 1), (b) stream power incision (m=0.5) in rivers and colluvial erosion (m=0.24), and (c) stream power incision in rivers (m=0.5), colluvial erosion (m=0.24), and hillslopes following a critical slope (m=0) of Sc=30∘. To better highlight relief, elevation is represented by transparency over the raster of hillshade. (d) Slope–discharge distributions for these three models.
Based on previous analytical developments (e.g. Royden and Taylor Perron, 2013), I have designed a new method to solve for the steady-state topography or the dynamic evolution of a landscape in 2D, following the SPIM, with analytical precision. The model can solve in a single time step, using an iterative scheme, the steady-state topography of a landscape under homogeneous or heterogenous conditions (i.e. uplift rate, erodibility and runoff). Iterations are required to optimize the planar organization of the river network and crest positions, starting from a random network. The number of iterations required for the convergence of the scheme only depends on the number of nodes discretizing the surface topography and only scales with , independently of other model parameters. Moreover, the model can also solve for the dynamic evolution of a landscape under either heterogeneous but constant or time-variable but homogeneous conditions. The dynamic and steady-state Salève models can solve for river, colluvial and hillslope erosion, if the associated erosion laws lead to slope–area (or discharge) relationships that can be modelled using a linear SPIM. The two main benefits of this new model are (1) its analytical accuracy that enables suppression of numerical diffusion and, for instance, the maintenance of the shape of knickpoints and (2) the absence of an upper bound for the time step that is not limited by the Courant condition. Contrary to any other state-of-the-art LEMs using the SPIM (e.g. Braun and Willett, 2013; Carretier et al., 2016; Campforts et al., 2017; Hobley et al., 2017; Salles, 2018), the time-stepping strategy in Salève can be chosen only based on physical considerations, such as the rate of river network reorganization, and not on numerical ones. All these advantages make Salève unique in its ability to efficiently model landscape evolution. In addition to its use in landscape evolution modelling, Salève could offer new opportunities to generate terrains for applications in computer graphics (e.g. Cordonnier et al., 2016); to infer the time and space evolution of uplift by inverting landscapes in 2D (e.g. Pritchard et al., 2009; Roberts and White, 2010; Goren et al., 2014a; Fox et al., 2014; Croissant and Braun, 2014) including river, colluvial valleys, and hillslopes; to predict thermochronological ages from landscape evolution (e.g. Braun et al., 2014); or to validate the accuracy of numerical schemes used in other LEMs. The model is fast as it makes use of the optimized flow routing algorithm provided by TopoToolbox (Schwanghart and Scherler, 2014).
The developed scheme, that uses 1D analytical solutions, is limited to flow networks that can be topologically classified as 1D node stacks or graphs (Braun and Willett, 2013), as resulting from a steepest slope flow routing algorithm. This excludes, for instance, recent models accounting for flow algorithms based on physical considerations (Davy et al., 2017). The main limitation of this new approach is that reorganizations of the river network, such as catchment piracy, will not lead to transient phases of erosion, as the river elevation is directly updated to its optimal elevation for each node where . The response time of the modelled landscapes is therefore shorter than with other 2D LEMs as it is equal to the 1D response time based on the flow network length at steady state. Moreover, the flow network topology is updated at every iteration or time step, in the steady-state or dynamic modes, respectively, while other strategies, based on physical criterion, could be adopted (Goren et al., 2014b). If many dynamic LEMs use the same approach (e.g. Braun and Willett, 2013), this is a critical aspect of the convergence speed and computational time in the steady-state mode, and future work should focus on accelerating it.
The Salève model is also not designed for horizontal tectonic displacement (e.g. Braun and Sambridge, 1997; Steer et al., 2011; Miller et al., 2007) that displaces nodes relative to the location of the base-level condition. Moreover, Salève is a purely detachment-limited model which does not consider the role of sediment transport and deposition in landscape dynamics. Only the linear SPIM with n=1 has been considered in this study, while some observations support non-linear models with greater values for n (e.g. Lague, 2014). These limitations also emphasize that analytical solutions to landscape dynamics, such as Salève, represent a complementary approach to other “numerical” LEMs, which are in essence more versatile and allow for tackling coupled or complex scientific problems which characterize geomorphological systems.
Extending the Salève algorithm to non-linear SPIMs represents a challenging and non-trivial perspective that requires accounting for more complex analytical solutions with overlapping or stretching river profiles for n>1 or n<1, respectively (Royden and Taylor Perron, 2013). Using Salève to simulate the impact of both a heterogeneous and time-variable uplift rate has not been attempted and might also result in convergence issues. Moreover, using an even more efficient algorithm to route water also represents a promising avenue (e.g. Barnes et al., 2014). This is critical for Salève that can use a time step much greater than the Courant condition and for which the main computational limit is the flow routing algorithm. Therefore, no computational time benchmark was done for this new model, as the computation of elevation changes, even on large grids, is negligible compared to flow routing. In turn, solving for individual time steps in this model takes a similar amount of computational time as in other similar LEMs using the same flow routing algorithm (e.g. Braun and Willett, 2013; Schwanghart and Scherler, 2014). Yet, the advantage of this new model is its ability to use longer time steps while preserving analytical accuracy and consistency. Lastly, Salève represents the first attempt to use analytical solutions to model the dynamics of landscapes in 2D using the SPIM. Because little modifications are required to implement this solution in other LEMs, I believe the strategy developed in this paper could be adapted and further developed to make LEMs more efficient and accurate.
A MATLAB version of the model can be accessed through a Zenodo repository: https://doi.org/10.5281/zenodo.4686733 (Steer, 2021). It is delivered with a routine to solve for the stream power law using an implicit finite-difference solution.
The author declares that there is no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The two reviewers, Liran Goren and Sébastien Carretier, as well as the editor, Joshua West, and associate editor, Greg Hancock, are acknowledged for their constructive comments that helped with improving this article. I am also grateful to Sean Willett for his insightful comments on an earlier version of this article. I thank Dimitri Lague, Philippe Davy, Jean Braun, Boris Gailleton, Joris Heyman, Alain Crave, Thomas Croissant and Edwin Baynes for their helpful comments and for discussions about this work.
This research has been supported by the H2020 European Research Council (grant no. 803721).
This paper was edited by Greg Hancock and reviewed by Sebastien Carretier and Liran Goren.
Barnes, R., Lehman, C., and Mulla, D.: Priority-flood: An optimal depression-filling and watershed-labeling algorithm for digital elevation models, Comput. Geosci., 62, 117–127, 2014.
Braun, J. and Sambridge, M.: Modelling landscape evolution on geological time scales: a new method based on irregular spatial discretization, Basin Res., 9, 27–52, 1997.
Braun, J. and Willett, S. D.: A very efficient O(n), implicit and parallel method to solve the stream power equation governing fluvial incision and landscape evolution, Geomorphology, 180, 170–179, 2013.
Braun, J., Simon-Labric, T., Murray, K. E., and Reiners, P. W.: Topographic relief driven by variations in surface rock density, Nat. Geosci., 7, 534–540, 2014.
Campforts, B. and Govers, G.: Keeping the edge: A numerical method that avoids knickpoint smearing when solving the stream power law, J. Geophys. Res.-Earth, 120, 1189–1205, 2015.
Campforts, B., Schwanghart, W., and Govers, G.: Accurate simulation of transient landscape evolution by eliminating numerical diffusion: the TTLEM 1.0 model, Earth Surf. Dynam., 5, 47–66, https://doi.org/10.5194/esurf-5-47-2017, 2017.
Carretier, S. and Lucazeau, F.: How does alluvial sedimentation at range fronts modify the erosional dynamics of mountain catchments?, Basin Res., 17, 361–381, 2005.
Carretier, S., Martinod, P., Reich, M., and Goddéris, Y.: Modelling sediment clasts transport during landscape evolution, Earth Surf. Dynam., 4, 237–251, 2016.
Cordonnier, G., Braun, J., Cani, M. P., Benes, B., Galin, E., Peytavie, A., and Guérin, E.: Large scale terrain generation from tectonic uplift and fluvial erosion, Comput. Graph. Forum, 35, 165–175, 2016.
Croissant, T. and Braun, J.: Constraining the stream power law: a novel approach combining a landscape evolution model and an inversion method, Earth Surf. Dynam., 2, 155–166, https://doi.org/10.5194/esurf-2-155-2014, 2014.
Croissant, T., Lague, D., Steer, P., and Davy, P.: Rapid post-seismic landslide evacuation boosted by dynamic river width, Nat. Geosci., 10, 680–684, 2017.
Croissant, T., Steer, P., Lague, D., Davy, P., Jeandet, L., and Hilton, R. G.: Seismic cycles, earthquakes, landslides and sediment fluxes: Linking tectonics to surface processes using a reduced-complexity model, Geomorphology, 339, 87–103, 2019.
Davy, P., Croissant, T., and Lague, D.: A precipiton method to calculate river hydrodynamics, with applications to flood prediction, landscape evolution models, and braiding instabilities, J. Geophys. Res.-Earth, 122, 1491–1512, 2017.
Densmore, A. L., Ellis, M. A., and Anderson, R. S.: Landsliding and the evolution of normal-fault-bounded mountains, J. Geophys. Res.-Solid, 103, 15203–15219, 1998.
Fox, M., Goren, L., May, D. A., and Willett, S. D.: Inversion of fluvial channels for paleorock uplift rates in Taiwan, J. Geophys. Res.-Earth, 119, 1853–1875, 2014.
Freeman, T. G.: Calculating catchment area with divergent flow based on a regular grid, Comput. Geosci., 17, 413–422, 1991.
Goren, L.: A theoretical model for fluvial channel response time during time-dependent climatic and tectonic forcing and its inverse applications, Geophys. Res. Lett., 43, 10753–10763, 2016.
Goren, L., Fox, M., and Willett, S. D.: Tectonics from fluvial topography using formal linear inversion: Theory and applications to the Inyo Mountains, California, J. Geophys. Res.-Earth, 119, 1651–1681, 2014a.
Goren, L., Willett, S. D., Herman, F., and Braun, J.: Coupled numerical–analytical approach to landscape evolution modeling, Earth Surf. Proc. Land., 39, 522–545, 2014b.
Hack, J. T.: Studies of longitudinal profiles in Virginia and Maryland, U.S. Geol. Surv. Prof. Pap., 294, 45–97, 1957.
Hobley, D. E. J., Adams, J. M., Nudurupati, S. S., Hutton, E. W. H., Gasparini, N. M., Istanbulluoglu, E., and Tucker, G. E.: Creative computing with Landlab: an open-source toolkit for building, coupling, and exploring two-dimensional numerical models of Earth-surface dynamics, Earth Surf. Dynam., 5, 21–46, https://doi.org/10.5194/esurf-5-21-2017, 2017.
Howard, A. D.: A detachment-limited model of drainage basin evolution, Water Resour. Res., 30, 2261–2285, 1994.
Howard, A. D. and Kerby, G.: Channel changes in badlands, Geol. Soc. Am. Bull., 94, 739–752, 1983.
Howard, A. D., Dietrich, W. E., and Seidl, M. A.: Modeling fluvial erosion on regional to continental scales, J. Geophys. Res.-Solid, 99, 13971–13986, 1994.
Ijjasz-Vasquez, E. J. and Bras, R. L.: Scaling regimes of local slope versus contributing area in digital elevation models, Geomorphology, 12, 299–311, 1995.
Jeandet, L., Steer, P., Lague, D., and Davy, P.: Coulomb mechanics and relief constraints explain landslide size distribution, Geophys. Res. Lett., 46, 4258–4266, 2019.
Lague, D.: The stream power river incision model: evidence, theory and beyond, Earth Surf. Proc. Land., 39, 38–61, 2014.
Lague, D. and Davy, P.: Constraints on the long-term colluvial erosion law by analyzing slope-area relationships at various tectonic uplift rates in the Siwaliks Hills (Nepal), J. Geophys. Res.-Solid, 108, 2129, https://doi.org/10.1029/2002JB001893, 2003.
Lavé, J.: Analytic solution of the mean elevation of a watershed dominated by fluvial incision and hillslope landslides, Geophys. Res. Lett., 32, L11403, https://doi.org/10.1029/2005GL022482, 2005.
Luke, J. C.: Mathematical models for landform evolution, J. Geophys. Res., 77, 2460–2464, 1972.
Luke, J. C.: Special solutions for nonlinear erosion problems, J. Geophys. Res., 79, 4035–4040, 1974.
Luke, J. C.: A note on the use of characteristics in slope evolution models, Z. Geomorph. Supp., 25, 114–119, 1976.
Miller, S. R., Slingerland, R. L., and Kirby, E.: Characteristics of steady state fluvial topography above fault-bend folds, J. Geophys. Res.-Earth, 112, F04004, https://doi.org/10.1029/2007JF000772, 2007.
Molnar, P. and England, P.: Late Cenozoic uplift of mountain ranges and global climate change: chicken or egg?, Nature, 346, 29–34, 1990.
O'Callaghan, J. F. and Mark, D. M.: The extraction of drainage networks from digital elevation data, Comput. Vis. Graph. Image Process., 28, 323–344, 1984.
Pelletier, J.: Quantitative modeling of earth surface processes, Cambridge University Press, Cambridge, 2008.
Phillips, J. D., Schwanghart, W., and Heckmann, T.: Graph theory in the geosciences, Earth-Sci. Rev., 143, 147–160, 2015.
Pritchard, D., Roberts, G. G., White, N. J., and Richardson, C. N.: Uplift histories from river profiles, Geophys. Res. Lett., 36, L24301, https://doi.org/10.1029/2009GL040928, 2009.
Quinn, P. F. B. J., Beven, K., Chevallier, P., and Planchon, O.: The prediction of hillslope flow paths for distributed hydrological modelling using digital terrain models, Hydrol. Process., 5, 59–79, 1991.
Roberts, G. G. and White, N.: Estimating uplift rate histories from river profiles using African examples, J. Geophys. Res.-Solid, 115, B02406, https://doi.org/10.1029/2009JB006692, 2010.
Roering, J. J., Kirchner, J. W., and Dietrich, W. E.: Evidence for nonlinear, diffusive sediment transport on hillslopes and implications for landscape morphology, Water Resour. Res., 35, 853–870, 1999.
Rosenbloom, N. A. and Anderson, R. S.: Hillslope and channel evolution in a marine terraced landscape, Santa Cruz, California, J. Geophys. Res.-Solid, 99, 14013–14029, 1994.
Royden, L. and Taylor Perron, J.: Solutions of the stream power equation and application to the evolution of river longitudinal profiles, J. Geophys. Res.-Earth, 118, 497–518, 2013.
Salles, T.: eSCAPE: parallel global-scale landscape evolution model, J. Open Source Softw., 3, 964, https://doi.org/10.21105/joss.00964, 2018.
Schwanghart, W. and Scherler, D.: Short Communication: TopoToolbox 2 – MATLAB-based software for topographic analysis and modeling in Earth surface sciences, Earth Surf. Dynam., 2, 1–7, https://doi.org/10.5194/esurf-2-1-2014, 2014.
Steer, P.: philippesteer/Saleve_regular: (Version v1), Zenodo [code], https://doi.org/10.5281/zenodo.4686733, 2021.
Steer, P., Cattin, R., Lavé, J., and Godard, V.: Surface Lagrangian Remeshing: A new tool for studying long term evolution of continental lithosphere from 2D numerical modelling, Comput. Geosci., 37, 1067–1074, 2011.
Steer, P., Simoes, M., Cattin, R., and Shyu, J. B. H.: Erosion influences the seismicity of active thrust faults, Nat. Commun., 5, 5564, https://doi.org/10.1038/ncomms6564, 2014.
Steer, P., Croissant, T., Baynes, E., and Lague, D.: Statistical modelling of co-seismic knickpoint formation and river response to fault slip, Earth Surf. Dynam., 7, 681–706, https://doi.org/10.5194/esurf-7-681-2019, 2019.
Tarolli, P. and Dalla Fontana, G.: Hillslope-to-valley transition morphology: New opportunities from high resolution DTMs, Geomorphology, 113, 47–56, 2009.
Thieulot, C., Steer, P., and Huismans, R. S.: Three-dimensional numerical simulations of crustal systems undergoing orogeny and subjected to surface processes, Geochem. Geophy. Geosy., 15, 4936–4957, 2014.
Tucker, G. E. and Bras, R. L.: Hillslope processes, drainage density, and landscape morphology, Water Resour. Res., 34, 2751–2764, 1998.
Tucker, G. E. and Whipple, K. X.: Topographic outcomes predicted by stream erosion models: Sensitivity analysis and intermodel comparison, J. Geophys. Res., 107, 2179, https://doi.org/10.1029/2001JB000162, 2002.
Weissel, J. K. and Seidl, M. A.: Inland propagation of erosional escarpments and river profile evolution across the southeast Australian passive continental margin, Geophys. Monogr., 107, 189–206, 1998.
Whipple, K. X. and Tucker, G. E.: Dynamics of the stream-power river incision model: Implications for height limits of mountain ranges, landscape response timescales, and research needs, J. Geophys. Res.-Solid, 104, 17661–17674, 1999.
Whipple, K. X.: The influence of climate on the tectonic evolution of mountain belts, Nat. Geosci., 2, 97–104, https://doi.org/10.1038/ngeo413, 2009.
Willett, S. D.: Orogeny and orography: The effects of erosion on the structure of mountain belts, J. Geophys. Res.-Solid, 104, 28957–28981, 1999.
- Abstract
- Introduction
- From a 1D to a 2D analytical solution to the stream power law
- A single time step iterative solution to topographic steady state in 2D
- A 2D dynamical model with analytical accuracy
- Application: time-variable uplift and knickpoint propagation
- Solving for river and hillslope dynamics
- Discussion and conclusion
- Code availability
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- From a 1D to a 2D analytical solution to the stream power law
- A single time step iterative solution to topographic steady state in 2D
- A 2D dynamical model with analytical accuracy
- Application: time-variable uplift and knickpoint propagation
- Solving for river and hillslope dynamics
- Discussion and conclusion
- Code availability
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References