the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Laboratory observations on meltwater meandering rivulets on ice
Gary Parker
We present a set of observations on meltwater meandering rivulets on ice and compare them (qualitatively and quantitatively) to morphologies commonly found in meandering channels in different media. The observations include data from planned centimeter-scale experiments and from incidental self-formed millimeter-scale rivulets. Our data show pulsed lateral migration features, undercut banks and overhangs, meander bend skewness, and meander bend cutoffs. The data also compare well with planform characteristics of alluvial meandering rivers (sinuosity, wavelength-to-width ratios, and meander bend fatness and skewness). We discuss the (ir)relevance of scale in our experiments, which, in spite of being in the laminar flow regime and likely affected by surface tension effects, are capable of shedding light into the processes driving formation and evolution of supraglacial meltwater meandering channels. Our observations suggest that sinuosity growth in meltwater meandering channels on ice is a function of flow velocity and the interplay between vertical and lateral incision driven by temperature differences between flow and ice. In the absence of recrystallization (depositional analog to alluvial rivers), bends are more likely to be downstream-skewed and channels show lower sinuosities.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(16087 KB)
- Corrigendum
-
Supplement
(4901 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(16087 KB) - Full-text XML
- Corrigendum
-
Supplement
(4901 KB) - BibTeX
- EndNote
Rivers and other channels containing liquid flow develop meandering patterns over different media and across a broad range of scales. The quintessential example of a meandering channel is the alluvial river, which forms and evolves by erosion and deposition of sediment (e.g., Fisk, 1944; Seminara, 2006) and interaction with riparian vegetation (e.g., Braudrick et al., 2009).
Meandering channels also form in bedrock where the driving processes include dissolution (e.g., Veress and Tóth, 2004; Allen, 1971; Zeller, 1967), abrasion by sediment particles (Sklar and Dietrich, 2004), plucking of bedrock (Chatanantavet and Parker, 2009; Whipple et al., 2000), slaking (Johnson and Finnegan, 2015), and weathering (Pelletier and Baker, 2011).
Rivulets on a plane can also meander due to an instability associated with surface tension (Le Grand Piteira et al., 2006; Davies and Tinker, 1984; Culkin and Davis, 1984; Gorycki, 1973), and channelized flows over ice surfaces also develop meandering patterns due to differential melting (e.g., Karlstrom et al., 2013; Parker, 1975; Ferguson, 1973; Zeller, 1967). Compared with the cases of alluvial and bedrock meandering channels, the study of meltwater meandering channels on ice has received little attention (Pitcher and Smith, 2019), and no experimental work has been reported to date.
We present a set of experimental observations that were motivated by the image in Fig. 1. It shows an ice island with melt ponds and meltwater meandering channels on its surface. It started as a very large iceberg that broke off Petermann Glacier and had been splitting into pieces as it drifted south over the Atlantic Ocean for more than a year. This led to our initial question: (i) can we produce meltwater meandering channels over ice in the laboratory? Simply put, the image shows an ice block with water flowing over it in a purely melting environment. Such conditions were easily reproduced in the laboratory.
We proceeded to work on answering the following: (ii) can we reproduce the observations made by previous researchers through field, theoretical, and high-resolution imagery-based analyses, albeit at a much smaller scale? (iii) How do small-scale laboratory meltwater meandering channels on ice compare to their supraglacial relatives and with meandering channels in other media?

Figure 1Ice island with melt ponds and meltwater channels on the Atlantic Ocean close to Newfoundland, Canada. Information: image of Petermann Ice Island A, fragment 2 captured by an astronaut from the International Space Station on 29 August 2011. Source: ISS Crew Earth Observations experiment and Image Science & Analysis Laboratory, Johnson Space Center.
1.1 Background
Interest in supraglacial meandering channels seems to have been triggered by Leopold and Wolman (1960), who described two meltwater meandering channels in the Dinwoody Glacier, Wyoming, and compared their planform and channel geometry to that of alluvial rivers. Similarities between alluvial meanders and supraglacial meltwater meandering channels were confirmed by other authors (Dahlin, 1974; Dozier, 1974; Ferguson, 1973; Knighton, 1972; Zeller, 1967). Notwithstanding these similarities, an important difference with alluvial meandering streams was observed. In these channels, the scale for the ratio of inertial forces to gravitational forces, given by the Froude number (, where U is the flow velocity, g is the acceleration of gravity, and H is flow depth), was greater than 1 (supercritical flow), whereas in alluvial meandering channels the value is typically smaller than 1 (subcritical flow). Supercritical flow conditions were documented by Dahlin (1974) and Knighton (1972), and a linear stability analysis of the problem suggested that they were necessary for meandering to occur in supraglacial streams (Parker, 1975). Nevertheless, sub- and supercritical flow conditions were observed in the Juneau Ice Field (Marston, 1983), and Karlstrom et al. (2013) presented a new theoretical model of meander formation in supraglacial streams in which, among other outcomes, they show that meltwater meandering can occur under both super- and subcritical flow conditions as long as the Froude number is greater than ∼0.4.
Recent research on supraglacial channels has not focused on the issue of meandering but rather on aspects such as channel inception (e.g., Mantelli and Camporeale, 2015), river networks (e.g., Yang et al., 2016), controls on drainage development and pathways (e.g., Banwell et al., 2016; Rippin et al., 2015), and supraglacial landscape evolution (e.g., Karlstrom and Yang, 2016). In their review of supraglacial streams and rivers, Pitcher and Smith (2019) discuss the issue of meandering briefly and note that in the past, the problem has been addressed with theoretical approaches (Karlstrom, 2013; Parker, 1975), field observations (Marston, 1983; Hambrey, 1977; Dozier, 1974, 1976; Ferguson, 1973; Knighton, 1972; Zeller, 1967; Leopold and Wolman, 1960), and, with the advent of high-resolution imagery, remote sensing (Rippin et al., 2015). This study, which focuses on fluvial aspects, represents the first step to establish an appropriate link between fluvial geomorphology and glaciology, where many challenges exist regarding glacier surface hydrology and the physical processes that govern the topology of supraglacial channel networks and their links to englacial and subglacial conduits. In this paper we (i) describe the experimental approach leading to the successful development of centimeter-scale and millimeter-scale meltwater meanders in the laboratory; (ii) present a qualitative and a simple quantitative comparison (including sinuosity, wavelength-to-width ratio, skewness, and fatness) of the small-scale meltwater meandering rivulets and meandering channels in other media; and (iii) interpret the differences and similarities observed in light of the different mechanisms driving the meandering processes.
This section provides a brief description of the methods used to conduct the experiments and process and analyze the data. A more comprehensive description is provided in the Supplement (Sect. S1) and is also available in Fernández (2018).
2.1 Centimeter-scale experiments
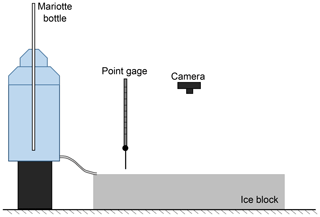
Experiments were conducted over 0.2 m thick ice blocks with a surface area of 0.96 m by 0.38 m. A rivulet was carved over the ice block with a chisel in all runs except Run 04 which was almost (but not precisely) a continuation of Run 03. After Run 03 finished, we put the ice block back in the freezer and attempted to add just enough water to cover the melt pond that formed upstream. In the process, some water made it into the channel and modified the shape and slope enough that we decided not to consider it the same run. Elevations along the carved rivulet and the ice surface were measured with a point gage. This was done before the run and at different times during the run to measure channel slope. A constant flow rate of 0.25 L min−1 (4.2 cm3 s−1) was used for all runs. Figure 2 shows the basic setup for the centimeter-scale experiments.
Planform evolution of the channel was documented with time-lapse imagery. Images were acquired at a constant frequency with typical time steps of 2–3 s depending on the experiment, although we report on a run that had a time step of 10 s. Inflow water temperature was measured with a common thermometer, and ice block temperatures were measured with a handheld infrared thermometer. Approximate flow depths were measured with a periodontal probe (a long, thin instrument with millimeter-scale markings used by dentists to measure the depth of the pocket between the gums and teeth) during the run and also estimated afterwards as follows: , where H is depth, Q is flow discharge, U is reach-averaged velocity, and B is reach-averaged channel width.
The experimental measurements were complemented with a mold of the channel made with room-temperature-vulcanizing (RTV) silicone. The silicone rubber was poured into the channel and allowed to harden while the ice block melted. The mold was recovered once the ice block melted completely.
2.2 Millimeter-scale experiments
The millimeter-scale experiments were, at first, an unexpected incidental byproduct of the centimeter-scale experiments. As the channel resulting from a centimeter-scale run was being molded, the millimeter-scale channels formed from thin meltwater flow generated on the surface of the ice block to either side of the mold by heat release from the molding material as it hardened. Figure 3 shows the first set of millimeter-scale channels that was observed. Following this discovery, the formative process was intentionally repeated to document the planform characteristics of the millimeter-scale channels.
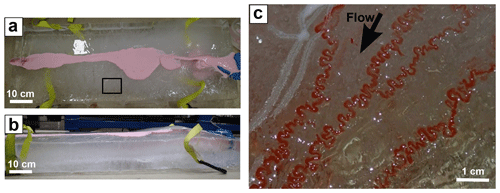
Figure 3(a) Top and (b) side view of an ice block over which (c) the first set of millimeter-scale self-formed meltwater meanders were observed. The area shown in (c) corresponds to region indicated in (a). Images in (a) and (b) were taken before adding dye.
Subsequent runs involved molding a centimeter-scale channel and letting the millimeter-scale channels form and evolve. The small size of the millimeter-scale channels only allows measuring planform morphology with the help of images. This was achieved by adding dye over the ice surface once the channels were formed.
2.3 Image analysis and planform characteristics
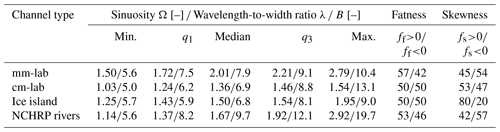
Channel centerlines were manually digitized in MATLAB and all length scales measured in the images were converted to real length units using the corresponding resolution. The analysis includes seven centerlines from the Petermann Ice Island, 17 millimeter-scale channels, and four centimeter-scale runs from which 26 centerlines were extracted as the channel evolved with time. The supplemental material includes images showing the millimeter-scale and ice island centerlines (Sect. S2) and videos showing two centimeter-scale runs are also available (video supplement). The parameters used to describe the planform characteristics of the meltwater meanders are channel sinuosity, wavelength-to-width ratio, coefficient of fatness, and coefficient of skewness (Vermeulen, 2016; Parker et al., 1982). Langbein and Leopold (1966) noted that meander bends sometimes possess double-valued planforms that make them look round and full, or as Parker et al. (1982) put it, “fat”. The coefficient of fatness is a measure of how round or angular a meander bend is. Skewness refers to the direction towards which a meander bend is pointing with respect to the direction of the flow. These terms come from the transformation of the Langbein and Leopold (1966) intrinsic coordinate meander equation to Cartesian coordinates. This transformation involves the generation of higher-order modes. The fatness and skewness coefficients are third-order modes. See Parker et al. (1982) for details. In this study, we use the forms derived from the wavelet analysis of Vermeulen et al. (2016).
Figure 4 shows a graphic description of these parameters using the Kinoshita meander equation (Parker et al., 1983; Kinoshita, 1961). In intrinsic coordinates, where s is the streamwise and n is the transverse direction, the relation is
Therein, θ is the direction (angle between the horizontal and the tangent to the curve), θ0 is the maximum angular amplitude, fs is the skewness coefficient, ff is the fatness coefficient, and λ is the meander wavelength.
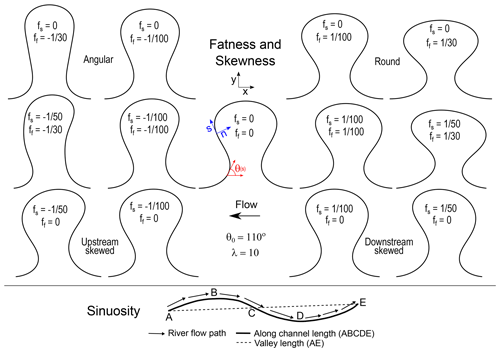
Figure 4Meander bend parameter definitions. The top panel shows the effect of the fatness and skewness coefficients in a Kinoshita meander curve (Eq. 1) and the bottom panel shows the definition of sinuosity.
The top row of the figure shows angular (ff<0) and round (ff>0) meanders with no skewness. The third row shows upstream- (fs<0) and downstream- (fs>0) skewed bends without fatness. Upstream skewness coefficients are negative because all channel centerline coordinates in this study were defined such that they are positive in the downstream direction. Figure 4 also shows a definition sketch for meander sinuosity. Sinuosity (Ω) is the ratio between the along-channel distance and the valley (straight) distance as follows:
Each channel centerline digitized in MATLAB was smoothed (Güneralp and Rhoads, 2008) and its direction (local angle) spatial series was standardized so that its average value over the entire reach was zero (Zolezzi and Güneralp, 2016). Details of the process are provided in the Supplement (Eqs. S1–S3 in Sect. S1). Meander bend wavelengths and coefficients of fatness and skewness were computed with “meanderscribe”, a set of MATLAB scripts developed by Vermeulen et al. (2016) to study the multiscale structure of meander bends. This procedure was also applied to rivers in the NCHRP database (Lagasse et al., 2004) so as to compare our results with the rivers therein. Specific details about the extraction and processing of the NCHRP data are included in the Supplement (Sect. S1).
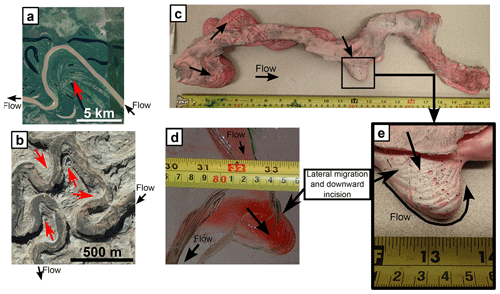
Figure 5Pulsed lateral migration features indicated by arrows in (a) an alluvial river (scroll bars), (b) a bedrock river, (c) the rubber mold of a meltwater laboratory channel, (d) a meltwater laboratory channel, and (e) a close-up of the bend in the rubber mold region indicated in (c). Image information: (a) Mamore river, Beni, Bolivia; Location: 255 863.55 E, 8 514 710.26 S; Source: © Google Earth 2020. (b) Tributary of the San Juan River; bedrock river in the Mogollon Rim, Utah, USA; Location: 574 447.88 E, 4 141 533.73 N; Source: © Google Earth 2020. (c–e) Source: this study.
The time-lapse images from the centimeter-scale runs were used to measure median channel widths, reach-averaged flow velocities, and lateral migration rates. Median channel widths were determined by measuring widths along the centerline at various locations and computing the median value. Reach-averaged velocities were determined by calculating the along-centerline distance traveled by injected dye fronts in subsequent images and dividing by the time between them. Lateral migration rates were determined by computing the displacement of the apex of a given meander bend at different times throughout the run and dividing by the corresponding time interval. Migration rates were made dimensionless with reach-averaged flow velocities.
3.1 Signatures of lateral migration and vertical incision
Pulsed lateral migration features (Fig. 5), undercut banks and overhangs (Fig. 6), meander bend skewness (Fig. 7), and meander bend cutoffs (Fig. 8) are common signatures of lateral migration in meandering channels. The timescales between formation and obliteration of these signatures are a function of channel medium and scale. All four signatures are present in our experimental observations. The figures in this section show a qualitative comparison with such signatures in other environments.

Figure 6Undercut bank in (a) an alluvial river, (b) a bedrock river, (c) a rubber mold of a laboratory meltwater channel, and (d) a schematic of the laboratory meltwater channel in (c). Image information: (a) Embarras River, Indiana, USA; picture by Gary Parker. (b) Turkey Run, Indiana, USA; picture by Gary Parker (c) Picture by Roberto Fernández.

Figure 7Bend skewness and terrace in (a) a bedrock river, (b) a supraglacial meltwater meandering channel, (c) a self-formed millimeter-scale laboratory meltwater meandering channel, and (d) soluble limestone (meanderkärren). Image information: (a) Horseshoe bend, Arizona; source: Hermans (2021). (b) Concordia, Pakistan; source: David Kaszlikowski. (c) Source: this study. (d) The Burren, Ireland; source: Stephen Marshak.

Figure 8Cutoffs in (a, b) an alluvial river, (c) a bedrock river, (d) a rubber mold of a laboratory melt water channel, (e, f) a supraglacial meltwater stream, and (g, h) self-formed meltwater laboratory channels. Image information: (a, b) chute cutoff in a bend of the Wabash River just upstream of the confluence with the Ohio River; location: 408 181.46 E, 4 186 022.16 N; source: © Google Earth 2020. (c) Bedrock tributary of the San Juan River; Mogollon Rim, Utah, USA; location: 574 447.88 E, 4 141 533.73 N; source: © Google Earth 2020. (d) Neck cutoff on rubber mold from a laboratory meltwater channel; source: this study. (e, f) Supraglacial meltwater stream in the Root Glacier, Alaska; location: 399 186.46 E, 6 831 268.59 N; source: © Google Earth 2020. (g, h) Neck and chute cutoffs on self-formed laboratory meltwater meandering channels; source: this study.
Skewed bends also appeared in both sets of experiments (Fig. 7c). Skewness direction (upstream or downstream) depends on local processes and conditions driving planform evolution. Figure 7 shows four examples of meandering channels with very different scales; all show skewed bends. Lateral migration promotes meander bend growth, thus increasing sinuosity. The process is, nevertheless, regulated by the occurrence of cutoffs (Fig. 8). Figure 8 shows examples of chute and neck cutoffs in alluvial, bedrock, supraglacial meltwater channels, and meltwater laboratory rivulets. An imminent neck cutoff in a millimeter-scale channel is also shown in Fig. 7c.
Figure 9 shows examples of knickpoints in the field and in the laboratory. Knickpoints are localized steps in the river profile. They do not represent a morphological feature specific to meandering streams, but their formation and upstream propagation in our centimeter-scale experiments are worth noting. Two knickpoints were observed during an experiment and were recorded in a mold (Fig. 9c). The knickpoints migrated upstream as the channel continued to incise vertically into the ice block (Fig. 9e). The neck cutoff shown in Fig. 8d is also shown in Fig. 9c. We believe that the most downstream knickpoint and the meander bend cutoff are related. It is likely that the neck cutoff produced a knickpoint, as has been observed in bedrock meandering rivers (e.g., Finnegan and Dietrich, 2011). The knickpoint height (Δh) in Fig. 9c and e is approximately 1 cm and the meander bend length before the cutoff (Lb) in Fig. 8d is approximately 14 cm long. These two variables are related via the channel slope as Δh=SLb. The slope for this run is not available but the knickpoint height divided by the meander bend length is equal to S=0.077, within the range of average slopes obtained in the centimeter-scale experiments (Table 2).
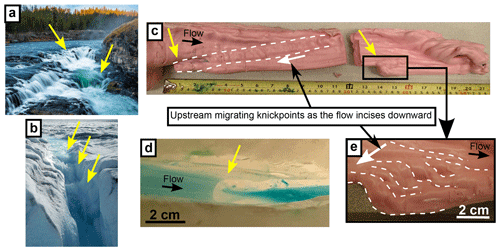
Figure 9Knickpoints indicated by yellow arrows on (a) mixed bedrock alluvial river, (b) supraglacial meltwater channel, (c) rubber mold of a laboratory meltwater channel, (d) laboratory meltwater channel and (e) close-up of rubber mold shown in (c). Image information: (a) Sheep Falls at Falls River, ID; source: Josh Packer. (b) Supraglacial meltwater channel flowing towards a moulin on the Greenland ice sheet; source: Jim Kastengren. (c–e) Source: this study.
3.2 Planform morphology and evolution
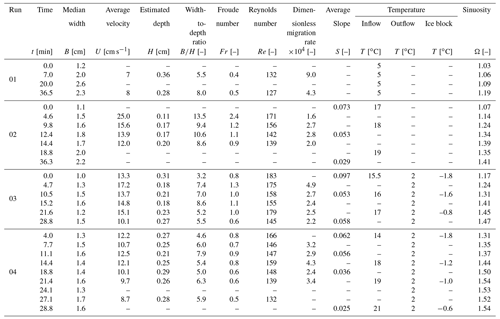
Planform morphology of the experimental rivulets was quantified with sinuosity (Ω), wavelength-to-width ratio (λB−1), coefficient of skewness (fs), and coefficient of fatness (ff). The results are compared with the seven centerlines extracted from the Petermann Ice Island (Fig. 1) and the alluvial meandering rivers in the NCHRP database (Lagasse et al., 2004). Figure 10 shows boxplots of the results and Table 1 summarizes the statistical values obtained. Figure 11 shows the planform evolution of four examples of centimeter-scale meandering channels. Table 2 summarizes measured and estimated hydraulic parameters for the four runs at different times during the experiments. It also shows width-to-depth ratios, measured lateral migration rates, and sinuosity values.
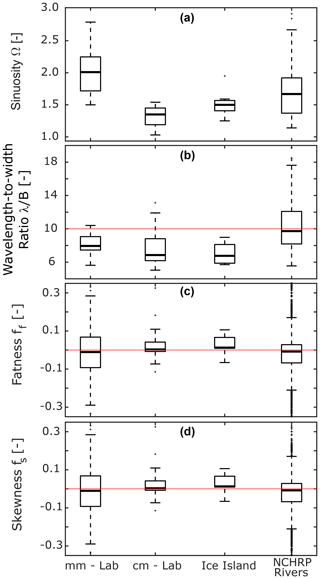
Figure 10(a) Sinuosity, (b) wavelength-to-width ratio, (c) fatness, and (d) skewness of meltwater meandering channels and the rivers in the NCHRP (see text) database.
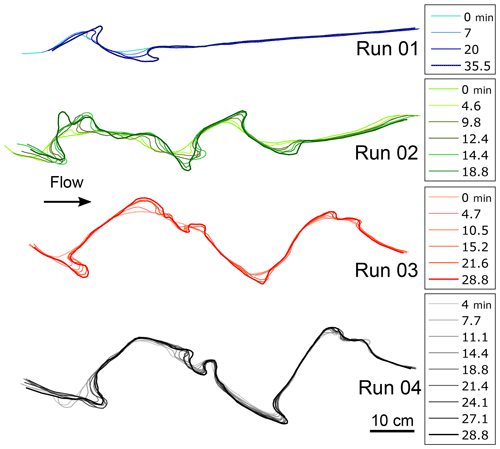
Figure 11Planform evolution for four different centimeter-scale laboratory meltwater meandering channel experiments.
In Fig. 10, the first and second boxes correspond to the millimeter- and centimeter-scale laboratory experiments, respectively. The third box corresponds to the channels extracted from the image of the Petermann Ice Island and the last box corresponds to the rivers in the NCHRP database. Boxes are plotted according to the following rules: the median value is shown as the horizontal line inside the box, and the top and lower edges of the box indicate the 75th and 25th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers. A value is considered an outlier if it is greater than or smaller than , where q3 is the 75th percentile (or third quartile) and q1 is the 25th percentile (or first quartile).
Logistical challenges render field research in glacial environments difficult. In spite of the advances in numerical models and remote sensing capabilities (Pitcher and Smith, 2019), laboratory experiments are a viable and exciting complementary path to better understand the processes driving supraglacial meltwater meandering channel hydro- and morphodynamics. We have presented an initial step along this path.
We have successfully produced meandering rivulets over an ice block in the laboratory. Observations on centimeter-scale channels developing from a set initial channel were complemented with observations on incidental self-formed millimeter-scale channels. Our experiments provide insight into the processes of formation and evolution of meltwater meandering channels on ice. Both sets show morphologies that are typically observed in meandering channels in other media and at larger scales (Sect. 4.1), but they also show differences (Sect. 4.2) worth discussing. Their significance, however, needs to be analyzed in light of the issue of scale (Sect. 4.3) before we can treat them as analogs of supraglacial meltwater channels instead of relatives.
4.1 Planform and channel morphologies
4.1.1 Signatures of lateral migration
Pulsed lateral migration episodes, analogous to those responsible for the formation of scroll bars and terraces, were recorded as streak lines on the overhangs on the outside of bends in the centimeter-scale experiments (Fig. 5c). Persistence of these features was a function of ice block melting rates and the depth within the ice block at which they formed. Smooth sloping terraces similar to alluvial point bars formed on the inner side of bends during the experiments (Figs. 6c, 7c).
In the case of alluvial rivers, scroll bars reflecting lateral migration pulses are found on the inner bank (Fig. 5a) (e.g., Strick et al., 2018). On the outer bank it is possible to observe undercut banks and overhangs (Fig. 6a) (e.g., Thorne and Tovey, 1981). Erosion of the bank toe leads to cantilever failure of the overhang and to the formation of slump blocks (e.g., Hackney et al., 2015). We did not observe overhang collapse due to thermal erosion at the toe of the outer bank in our experiments, but the uppermost layers of the overhangs melted away as the channel incised deeper into the ice block and the ice block surface melted.
In bedrock meandering rivers, lateral migration signatures are observed as terraces on the inner parts of bends (Figs. 5b, 7a) (e.g., Johnson and Finnegan, 2015; Finnegan and Dietrich, 2011) and undercuts and overhangs on the outer parts of bends (Fig. 6b) (e.g., Inoue et al., 2017). Terraces are also found in supraglacial meltwater meandering channels (Fig. 7b). In smaller scale channels, these terraces on the inner parts of bends melt according to the overall glacial surface ablation rates. In contrast with the bedrock case, their elevation with respect to the bed of the channel remains relatively constant (Karlstrom et al., 2013; Knighton, 1981). We presume this was also occurring in the millimeter-scale experiments since the elevation difference between channel thalweg and ice block surface did not seem to change with time. In the centimeter-scale experiments the terraces more closely resembled the case of bedrock meandering terraces (e.g., Fig. 7a, d). Vertical incision rates were much faster than ice block melting rates, thus leaving terraces high above the channel thalweg.
In alluvial meandering rivers, cutoffs leave abandoned bends whose inlet and outlet become plugged by sediment, preventing flow from entering the bend and forming an oxbow lake (e.g., Constantine and Dunne, 2008). These lakes can fill up with mud during floods and eventually become covered by vegetation (clay plug). In bedrock meandering rivers, abandoned bends might also be observed after cutoffs. Due to the limited sediment supply and continuous vertical incision of the channel itself, abandoned bends do not fill up and are found at higher elevations with respect to the active channel (Fig. 8c).
In supraglacial meandering channels, cutoffs also lead to the formation of abandoned bends (Rippin et al., 2015). As in the bedrock case, the bends do not become oxbow lakes and remain at a higher elevation than the active channel. Somewhat similar to the alluvial case, where sedimentation and vegetation growth might hide the abandoned bend from the naked eye, glacial surface ablation in the warm months and snowfall in the colder months might completely obliterate abandoned supraglacial meander bends (Rippin et al., 2015). In the millimeter-scale experiments, abandoned bends were not preserved due to melting of the ice block. In the centimeter-scale experiments, a neck cutoff was discovered after making the silicone mold of the channel (Fig. 8d). We did not observe the cutoff as it happened because it occurred approximately 0.10 m away from the ice block surface, and the channel had migrated laterally underneath an overhang.
4.1.2 Sinuosity
Sinuosity values measured in the millimeter-scale and centimeter-scale meandering channels show high variability (Fig. 10a). The former have a median value of 2.01, whereas the latter have a median value of 1.36 (Table 1), and the largest sinuosity measured for the centimeter-scale channels is similar to the smallest sinuosity measured for the millimeter-scale channels. The median sinuosity value measured for the channels over the Petermann Ice Island is 1.50, closer to the centimeter-scale channels. The median sinuosity obtained for the NCHRP rivers is 1.67, but the data spread in this case actually covers the ranges observed in the other three cases. In the case of alluvial rivers, different values have been reported depending on the geographic area being studied and the number of reaches included in the analysis. For example, MacDonald et al. (1991) report the sinuosity values of 16 reaches of meandering rivers in Minnesota. They observed values between 1.21 and 2.61 with a median value of 1.96, closer to the millimeter-scale meandering channels.
The low sinuosity values observed in the centimeter-scale channels are likely to be related to the initial planform conditions under which the experiments were conducted and the relatively small amount of time over which they were able to evolve (Fig. 11). These runs lasted approximately 30–35 min and were constrained by the time it took for the upstream pond to melt through the ice block until water came out the bottom. In spite of this, the behavior observed and values obtained are similar to those reported by other authors. In the case of Run 4 (Fig. 11, Table 2), sinuosity did not change significantly during the last 10 minutes of the run. Measured values varied between 1.50 and 1.54, suggesting that approximate equilibrium conditions had been reached.
Leopold and Wolman (1960) observed that meandering took some time to develop after an irregular sheet of water became channelized in the Dinwoody Glacier. Shallow channels had no well-developed meandering pattern, but deeper channels with a width similar to that of the shallow channels showed well-developed sinusoidal patterns. As the channels incised vertically, sinuosity increased. This behavior matches what was observed in the experiments (Fig. 11), and the range of values measured (1.03–1.54 with a median value of 1.36 (Table 1)) is similar to the 1.1–1.7 range reported by Zeller (1967) for meltwater streams in Swiss glaciers. The values measured on the Petermann Ice Island also match these observations. The range of values observed is 1.25–1.95, with a median value of 1.50.
We believe that the differences observed in the meltwater channels are related to the ratio between vertical incision rates and lateral migration rates. We discuss this issue in Sect. 4.2.
4.1.3 Wavelength-to-width ratio
The wavelength-to-width ratios measured for meltwater streams are shown in Fig. 10b and Table 1. The meltwater streams have values in the range of 5.0–13.1, with the smallest and largest values measured in the centimeter-scale runs (Table 1). The range of measured values lies between what has been observed in alluvial rivers and other meltwater channels.
Karlstrom et al. (2013) plotted a compilation of 61 wavelength vs. width pairs for meltwater meandering channels. Their values have the following statistics: min. = 5.4; q1=9.2, median = 10.8, q3=15.1, and max. = 37.6. The rivers in the NCHRP database have q1=8.2, median = 9.7, and q3=12.1. The median values for the millimeter-scale, centimeter-scale, and ice island vary between 6.8 and 7.9. Nevertheless, a larger sample would be needed to assess if the differences between the medians are significant. All previous data refer to meltwater channels with 10−1 m <B<101 m; we have extended this to include channels with widths as small as 10−3 m.
4.1.4 Fatness and skewness
Figure 10c and d show boxplots of the coefficients of fatness and skewness (Fig. 4), which were determined using the routines developed by Vermeulen et al. (2016). The method determined that 57 % of the bends in the millimeter-scale channels are round. In the case of the centimeter-scale and the ice island channels, half the bends were found to be round and half angular. The only meltwater channels showing preferential upstream skewness of their bends are the millimeter-scale ones, with 54 % having a negative skewness coefficient. The bends in the centimeter-scale and ice island channels show preferential downstream skewness.
Results for the NCHRP data show 53 % of the bends are round (ff>0) and 57 % are upstream-skewed (fs<0).
In the context of alluvial rivers and in the absence of other information, upstream skewness was thought to be predominant and therefore an indication of flow direction (Parker et al., 1982). The rivers in the NCHRP dataset show preference for upstream skewness, but the ratio is not so dominant as to indicate flow direction based uniquely on planform images of channels. Moreover, the results presented herein suggest that in environments where meandering is not caused by sediment erosion and deposition, downstream-skewed bends are more common. An example from a different environment where downstream-skewed bends might be more dominant is shown in Fig. 7d. It shows a short reach of a meandering channel in karst, created by bedrock dissolution. Almost all bends therein are downstream-skewed.
The results in Table 1 and Fig. 10 show that meltwater channels with lower sinuosity values have more downstream-skewed bends than otherwise and that round bends are as common as angular bends. These results might be related to the absence of sediment deposition, which has been inferred to contribute to the development of upstream skewness and roundness of bends (Parker et al., 1982).
4.1.5 Flow properties, migration rates, and downstream trends in the centimeter-scale rivulets
Flow properties for the centimeter-scale runs are summarized in Table 2. Reported depth values were estimated from other known variables assuming a rectangular cross section at the straighter portions of the reach. The median widths and estimated depths were used to compute width-to-depth ratios for all channels. The values obtained vary between 3.2 and 13.5 with a median value of 6.3. Parker (1975) included a set of seven channels from the Barnes Ice Cap with a median aspect ratio of 5.4, and Leopold and Wolman (1960) reported on two channels with an aspect ratio of ∼8.
Froude numbers were calculated as , where g is the acceleration of gravity (9.81 m s−2). Reynolds numbers were calculated as follows: , where is an estimate of the hydraulic radius and ν is the kinematic viscosity of water. Since the water temperature was changing from upstream to downstream, a value of m2 s−1, corresponding to a temperature of 7 ∘C, was used. The reach-averaged velocities reported for Run 01 are estimations of the minimum value that could have prevailed in each case. The time between images for this run was 10 s; therefore, velocities could not be calculated as in the other runs, where the position of an initial dye front was tracked in subsequent images. This affects the Froude and Reynolds numbers as well as the dimensionless migration rates. We decided to include these values in our compendium because they at least provide order of magnitude estimates.
The Froude numbers obtained at different times during Runs 02, 03, and 04 show both supercritical and subcritical flow conditions (Table 2). Karlstrom et al. (2013) show that meandering is possible when Fr≳0.4 and the channel aspect ratios are between 5 and 10. These conditions were also observed in our centimeter-scale experimental runs.
In all the centimeter-scale laboratory cases, the Froude numbers show a decreasing trend associated with a decrease in reach-averaged flow velocity, sinuosity growth, and decreasing channel slopes (Table 2). The decreasing trends observed in the downstream direction are related to the cooling of water as it flows downstream. As the temperature difference between flow and channel boundary decreases, thermal erosion is less effective. Also, the rubber molds (e.g., Fig. 9c) show larger vertical incision in the upstream portions than the downstream portions. We did not attempt to control this downstream reduction in temperature difference, which is likely difficult to do in the laboratory and might also exist in supraglacial channels.
Reynolds numbers () computed for the different runs are in the laminar (Re<575) regime. All values are below 200. Our laboratory observations on meltwater meandering channels provide one more set of examples of fluvial morphodynamic features that are possible by the interaction of purely laminar flow with an erodible bed (Lajeunesse et al., 2010), an issue we discuss in Sect. 4.3.
Measured dimensionless lateral migration values vary between and . In alluvial rivers, some lateral migration models compute bank erosion by using a dimensionless migration coefficient that varies between 10−6 and 10−8 (e.g., Motta et al., 2012). Our experiments show migration rates that are at least two orders of magnitude larger than typical values used in numerical models of alluvial river meandering. This result was expected and is thought to be dependent on the temperature difference between the flowing water and the ice boundary.
4.2 Planform and channel morphology differences
We have shown that the centimeter- and millimeter-scale meandering rivulets have features commonly observed in meandering channels in other media and at different scales. They also have some differences that raise an important question regarding our understanding of meandering channel processes and morphologies in ice. What variables exert control over sinuosity growth and bend skewness in meltwater meandering channels on ice?
Low sinuosity values measured in the centimeter-scale rivulets (compared to the millimeter-scale) are likely to be related to the ratio between vertical incision rate and lateral migration rate. In general, the more dominant lateral migration is with respect to vertical incision, the faster sinuosity is expected to grow. In addition, very high incision rates might suppress the formation of cutoffs by preventing two parts of a bend developing in 3D from intersecting each other. We infer that the ratio between vertical and lateral incision is a function of flow velocity and temperature difference between the flow and the ice.
Upstream skewness and roundness of bends is believed to be due to sediment deposition (e.g., Parker et al., 1982), and Marston (1983) observed differences in meander bend shapes when debris was present in the stream. In the absence of sediment, the analog to deposition in the meltwater channels would be recrystallization (freezing) of water back onto the ice surface. Based on the temperatures measured in the centimeter-scale experiments (Table 2) this was not occurring. Downstream skewness was preferentially observed in the centimeter-scale rivulets where no depositional analog was present. These conditions are also present in the image of meanderkärren (Fig. 7d), where bends grow by dissolution of karst and precipitation is either absent or not as dominant. In the case of the millimeter-scale, it is possible that recrystallization was occurring, thus creating conditions for bends to also show upstream skewness.
Daily temperature variations in glacial environments might provide sufficient conditions to create both erosional and depositional analogs, with melting being predominant during the day and recrystallization at night. Temperature gradients along the channels are a function of depth, solar radiation, and the presence or absence of sediment (Isenko et al., 2005). Conducting laboratory experiments with better temperature control might allow looking at these aspects in greater detail. In the context of climate change, where longer summer melt periods are expected and larger volumes of meltwater are expected to be transported by these channels (Irvine-Fynn et al., 2011), fieldwork will become even more difficult and thus experiments, coupled with numerical modeling and remote sensing, offer a unique opportunity to better understand these evolving landscapes.
4.3 Scaling (ir)relevance
Scaling is typically the first issue that comes to mind when trying to relate laboratory observations with field analogs. Depending on the problem at hand, dynamic similarity between model and prototype should be satisfied in order to relate the laboratory measurements to the field scale in a precise way. Nevertheless, in the case of earth surface processes, small-scale laboratory experiments have an “unreasonable effectiveness” (Paola et al., 2009) capable of providing valuable insights into the underlying physics, without necessarily matching all relevant dimensionless parameters. The main aspects related to the scale and setting of our experiments are flow regime, surface tension effects, and temperature.
4.3.1 Flow regime
Our experiments had Reynolds numbers well within the laminar regime, but this has been the case in many other studies looking at geomorphic processes. Examples include meandering channel processes (Smith, 1998), drainage basin evolution (Hasbargen and Paola, 2000), steady-state erosional landscapes (Bonnet and Crave, 2003), braided streams (Metivier and Meunier, 2003), and sand bedforms in open-channel flow (Coleman and Eling, 2000). Many more examples are discussed by Paola et al. (2009) and Lajeunesse et al. (2010). In spite of being in the laminar regime, our meltwater channels compare qualitatively and quantitatively very well with field cases, where flow regimes are turbulent.
Lajeunesse et al. (2010) and Malverti et al. (2008) show that turbulence is not necessary to create the morphologies themselves and that the most important aspect is the convergence of the underlying physics. The former authors suggest that “it is possible for a pair of flows to be simply two manifestations of the same phenomenon, both of which are described by a shared physical framework”. Similar findings are presented by Paola et al. (2009) who suggest that “unreasonable experimental effectiveness arises from natural scale independence”. The three studies provide convincing evidence that flow regime in and by itself is not an impediment to relate experimental observations to field analogs and that lessons learned at the small scale can be upscaled appropriately.
4.3.2 Surface tension
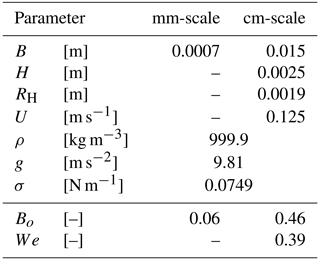
Malverti et al. (2008) also address the issue of surface tension. They conclude that surface tension is not an important aspect as long as the experimental scales are larger than the capillary length of the fluid (, where σ is surface tension, ρ is density, and g is gravitational acceleration) or as long as the channel Bond number (Eq. 3) is greater than unity. The Bond number is a measure of the ratio of gravity forces to surface tension force. Peakall and Warburton (1996) summarize some empirically suggested guidelines for critical Weber numbers (Eq. 4). The authors suggest values below which surface-tension induced distortion may be expected in experimental work involving small-scale channels. The Weber number is a measure of the relative importance of inertial forces to surface tension force. Based on their work, the minimum critical value of the Weber number may be 10. The value, however, is empirically based.
In Eqs. (3) and (4), L is a characteristic length scale of the flow. For water at 5 ∘C in air, the capillary length is 2.8 mm. It is readily seen that surface tension effects might have been present in our millimeter-scale channels. Bond and Weber dimensionless numbers were computed for the average channel characteristics in the centimeter-scale experiments, but only the former was computed for the millimeter-scale experiments due to the lack of flow velocity measurements. The hydraulic radius (RH) was the typical length scale used for the centimeter-scale channels, and the average channel width was used for the millimeter-scale channels.
Table 3 shows the parameters used to compute the dimensionless numbers and the results obtained. The results suggest that surface tension effects are present in both cases. The morphologies observed suggest they are not directly related to the process by which the meandering instability occurs.
Rivulets over a plane can meander due to an instability associated with surface tension (e.g., Le Grand-Piteira et al., 2006; Schmuki and Laso, 1990; Davies and Tinker, 1984; Goricky, 1973). All these studies acknowledge some planform similarities between surface tension generated meanders and those of alluvial rivers. Nevertheless, the meanders in these rivulets are fixed in space and time as long as the slope of the plane is constant and the input flow is steady. Once established, surface tension meandering channels display completely stationary paths (Le Grand-Piteira et al., 2006), i.e., bends do not migrate or change shape with time. Goricky (1973) observed that sinuosity values did not grow above 1.5 in their experiments; this led them to conclude that meander bend cutoffs and oxbow lakes could not be simulated on the surface tension stream plate. The signatures of lateral and vertical incision observed in our experiments suggest that additional dynamic processes occurred and that surface tension effects, although present, are not responsible for the meandering patterns observed.
4.3.3 Temperature
Lajeunesse et al. (2010) show a comparison between point-bar morphodynamics in bend flow in a river (turbulent regime) and a laboratory channel (laminar). They show that even though the morphologic signatures are comparable in both scenarios, the smaller channel required a higher Froude number and a much higher slope. In the laminar regime, a wide range of slope values are possible. For example, laminar river analogs have been observed to have 1.5–2.5 times higher slopes than their natural counterparts (Malverti et al., 2008) and others have also reported values such as 0.1 (Delorme et al., 2018) and (Abramian et al., 2020). In the context of our experiments, such analyses suggest that temperature gradients in laminar flows can have values that differ from the fully turbulent analogs but nevertheless still recreate specific morphologies.
All our observations were conducted in a purely melting environment with ambient temperatures well above the freezing point. We measured fluid and ice temperatures only during the centimeter-scale runs (Table 2). The temperature differences between water and ice were at least 17 ∘C at the inlet and between 2.5–4 ∘C at the outlet. It is likely that the centimeter-scale experiments had smaller Eckert and larger Stefan numbers than those in supraglacial streams. It is also likely that the millimeter-scale meanders did have similar values to those observed in the field since the water in the millimeter-scale channels was meltwater from the ice block and not inflow from an external source. Observed differences in planform characteristics between centimeter- and millimeter-scale rivulets (Table 1) could be related to the temperature differences prevalent in both sets of experiments.
Our experimental observations on centimeter- and millimeter-scale meltwater meandering channels in the laboratory lead to the following conclusions:
-
Small-scale laboratory experiments are capable of reproducing morphologies observed in natural-scale rivers even though dynamic similarity is not generally satisfied.
-
Specifically, small-scale laminar meltwater meandering rivulets have lateral migration signatures and planform morphologies also observed in meandering channels with turbulent flows.
-
Relatively slow sinuosity growth of meltwater meanders might be related to larger incision rates as compared to lateral migration rates. Channels that incise vertically at a faster rate have less time to migrate laterally, thus slowing down sinuosity growth in a relative sense.
-
Meltwater channels with larger temperature differences between the flow and the ice boundary showed preferentially downstream-skewed bends. In the absence of ice recrystallization (freezing), no sediment deposition analogs exist that would promote upstream bend skewness.
-
Ambient temperature control, which would lead to better constrained small-scale laboratory experiments, is necessary to assess the long-term equilibrium of meltwater channels. A key aspect for future research on meltwater rivulets is the relative importance of vertical vs. lateral incision rates and their effects on channel and planform morphologies.
All data used in preparation of this manuscript are available at https://doi.org/10.13012/B2IDB-4384362_V1 (Fernández et al., 2019).
Videos showing two centimeter-scale runs are available at: https://doi.org/10.5446/40431 (Fernández, 2019a) and https://doi.org/10.5446/40432 (Fernández, 2019b).
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-9-253-2021-supplement.
Experiments were designed by both authors. RF conducted the experiments, data analysis, and postprocessing. The manuscript was prepared and edited by both authors.
The authors declare that they have no conflict of interest.
We would like to thank Colin P. Stark for insightful discussions during the experiments and data processing, and for valuable feedback on a previous draft of this manuscript. We would like to thank Jaclyn Daum, Eduardo Hanon, and John Berens for their contributions to this study. We would like to thank David Kaszlikowski for his drone image of a supraglacial meander bend in Pakistan, Josh Packer for his image of Sheep Falls, and Jim Kastengren for his image of knickpoints on ice. We also thank Stephen Marshak for his image of meanderkärren and for copious insightful discussion. We also thank the associate editor Jens Turowski, Elisa Cantelli, and an anonymous reviewer for their feedback, which helped improve the clarity of the manuscript. Participation of both authors in this study was made possible thanks to funding provided by the US National Science Foundation [grant EAR1124482]. Participation of Roberto Fernández was also possible thanks to the Leverhulme Trust, Leverhulme Early Career Researcher Fellowship [grant ECF-2020-679] and the European Research Council under the European Union's Horizon 2020 research and innovation program [grant 725955].
This research has been supported by the US National Science Foundation (grant EAR1124482), the Leverhulme Trust, Leverhulme Early Career Researcher Fellowship (grant ECF-2020-679), and the European Research Council under the European Union's Horizon 2020 research and innovation program (grant 725955).
This paper was edited by Jens Turowski and reviewed by Elisa Mantelli and one anonymous referee.
Abramian, A., Devauchelle, O., and Lajeunesse, E.: Laboratory rivers adjust their shape to sediment transport, Phys. Rev. E, 102, 053101, https://doi.org/10.1103/PhysRevE.102.053101, 2020.
Allen, J. R. L.: Bed forms due to mass transfer in turbulent flows: a kaleidoscope of phenomena, J. Fluid Mech., 49, 49–63, https://doi.org/10.1017/S0022112071001927, 1971.
Banwell, A., Hewitt, I., Willis, I., and Arnold, N.: Moulin density controls drainage development beneath the Greenland ice sheet: Moulin Density and Subglacial Drainage, J. Geophys. Res.-Earth, 121, 2248–2269, https://doi.org/10.1002/2015JF003801, 2016.
Bonnet, S. and Crave, A.: Landscape response to climate change: Insights from experimental modeling and implications for tectonic versus climatic uplift of topography, Geology, 31, 123–126, https://doi.org/10.1130/0091-7613(2003)031<0123:LRTCCI>2.0.CO;2, 2003.
Braudrick, C. A., Dietrich, W. E., Leverich, G. T., and Sklar, L. S.: Experimental evidence for the conditions necessary to sustain meandering in coarse-bedded rivers, P. Natl. Acad. Sci. USA, 106, 16936–16941, https://doi.org/10.1073/pnas.0909417106, 2009.
Chatanantavet, P. and Parker, G.: Physically based modeling of bedrock incision by abrasion, plucking, and macroabrasion, J. Geophys. Res., 114, F04018, https://doi.org/10.1029/2008JF001044, 2009.
Coleman, S. E. and Eling, B.: Sand wavelets in laminar open-channel flows, J. Hydraul. Res., 38, 331–338, https://doi.org/10.1080/00221680009498314, 2000.
Constantine, J. A. and Dunne, T.: Meander cutoff and the controls on the production of oxbow lakes, Geology, 36, 23–26, https://doi.org/10.1130/G24130A.1, 2008.
Culkin, J. B. and Davis, S. H.: Meandering of water rivulets, Aiche J., 30, 263–267, https://doi.org/10.1002/aic.690300214, 1984.
Dahlin, B.: A contribution to the study of meandering, MSc thesis, Univeristy of Minnesota, Minnesota, 1974.
Davies, T. R. and Tinker, C. C.: Fundamental characteristics of stream meanders, Geol. Soc. Am. B., 5, 505–512, 1984.
Delorme, P., Devauchelle, O., Barrier, L., and Métivier, F.: Growth and shape of a laboratory alluvial fan, Phys. Rev. E, 98, 012907, https://doi.org/10.1103/PhysRevE.98.012907, 2018.
Dozier, J.: Channel adjustments in supraglacial streams, Icefield Ranges Res. Proj. Sci. Results, 4, 189–205, 1974.
Dozier, J.: An examination of the variance minimization tendencies of a supraglacial stream, J. Hydrol., 31, 359–380, https://doi.org/10.1016/0022-1694(76)90134-7, 1976.
Ferguson, R. I.: Sinuosity of supraglacial streams, Geol. Soc. Am. B., 84, 251–256, 1973.
Fernández, R.: Laboratory experiments on alluvial cover in mixed bedrock-alluvial meandering channels and on the formation and evolution of supraglacial meltwater meandering streams, PhD thesis, University of Illinois, Urbana, IL, USA, available at: http://hdl.handle.net/2142/101494 (last access: 29 March 2021), 2018.
Fernández, R.: Ice Meandering 01, Hydrosystems Laboratory, University of Illinois, Urbana-Champaign, https://doi.org/10.5446/40431, 2019a.
Fernández, R.: Ice Meandering 02, Hydrosystems Laboratory, University of Illinois, Urbana-Champaign, 2019b.
Fernández, R., Parker, G., and Stark, C. P.: Meltwater Meandering Channels on Ice: Centerlines and Images, University of Illinois at Urbana-Champaign, dataset, https://doi.org/10.13012/B2IDB-4384362_V1, 2019.
Finnegan, N. J. and Dietrich, W. E.: Episodic bedrock strath terrace formation due to meander migration and cutoff, Geology, 39, 143–146, https://doi.org/10.1130/G31716.1, 2011.
Fisk, H. N.: Geological investigation of the alluvial valley of the lower Mississippi River, US Department of the Army, Mississippi River Commission, Vicksburg, Mississippi, USA, 78 pp., 1944.
Gorycki, M. A.: Hydraulic Drag: A Meander-Initiating Mechanism, Geol. Soc. Am. B., 84, 175, https://doi.org/10.1130/0016-7606(1973)84<175:HDAMM>2.0.CO;2, 1973.
Güneralp, İ. and Rhoads, B. L.: Continuous Characterization of the Planform Geometry and Curvature of Meandering Rivers, Geogr. Anal., 4, 1–25, https://doi.org/10.1111/j.0016-7363.2007.00711.x, 2008.
Hackney, C., Best, J., Leyland, J., Darby, S. E., Parsons, D., Aalto, R., and Nicholas, A.: Modulation of outer bank erosion by slump blocks: Disentangling the protective and destructive role of failed material on the three-dimensional flow structure, Geophys. Res. Lett., 42, 10,663-10,670, https://doi.org/10.1002/2015GL066481, 2015.
Hambrey, M. J.: Supraglacial drainage and its relationship to structure, with particular reference to Charles Rabots Bre, Okstindan, Norway, Nor. Geogr. Tidsskr. – Nor. J. Geogr., 31, 69–77, https://doi.org/10.1080/00291957708545319, 1977.
Hasbargen, L. E. and Paola, C.: Landscape instability in an experimental drainage basin, Geology, 4, 1067–1070, 2000.
Hermans, P.: Horseshoe Bend TC 27-09-2012 15-34-14, available at: https://commons.wikimedia.org/wiki/File:Horseshoe_Bend_TC_27-09-2012_15-34-14.jpg, last access: 29 March 2021.
Inoue, T., Parker, G. and Stark, C. P.: Morphodynamics of a bedrock-alluvial meander bend that incises as it migrates outward: approximate solution of permanent form: Morphodynamics of a Bedrock-Alluvial Meander Bend, Earth Surf. Proc. Land., 42, 1342–1354, https://doi.org/10.1002/esp.4094, 2017.
Irvine-Fynn, T. D. L., Hodson, A. J., Moorman, B. J., Vatne, G., and Hubbard, A. L.: Polythermal Glacier Hydrology: A Review, Rev. Geophys., 49, RG4002, https://doi.org/10.1029/2010RG000350, 2011.
Isenko, E., Naruse, R., and Mavlyudov, B.: Water temperature in englacial and supraglacial channels: Change along the flow and contribution to ice melting on the channel wall, Cold Reg. Sci. Technol., 42, 53–62, https://doi.org/10.1016/j.coldregions.2004.12.003, 2005.
Johnson, K. N. and Finnegan, N. J.: A lithologic control on active meandering in bedrock channels, Geol. Soc. Am. B., 127, 1766–1776, https://doi.org/10.1130/B31184.1, 2015.
Karlstrom, L. and Yang, K.: Fluvial supraglacial landscape evolution on the Greenland Ice Sheet, Geophys. Res. Lett., 43, 2683–2692, https://doi.org/10.1002/2016GL067697, 2016.
Karlstrom, L., Gajjar, P., and Manga, M.: Meander formation in supraglacial streams, J. Geophys. Res. Earth Surf., 118, 1897–1907, https://doi.org/10.1002/jgrf.20135, 2013.
Kinoshita, R.: An investigation of channel deformation of the Ishikari River, Publication no. 36, Natural Resources Division, Ministry of Science and Technology of Japan, Tokyo, Japan , 139 pp., 1961.
Knighton, A. D.: Meandering Habit of Supraglacial Streams, Geol. Soc. Am. B., 83, 201, https://doi.org/10.1130/0016-7606(1972)83[201:MHOSS]2.0.CO;2, 1972.
Knighton, A. D.: Channel Form and Flow Characteristics of Supraglacial Streams, Austre Okstindbreen, Norway, Arct. Alp. Res., 13, 295, https://doi.org/10.2307/1551036, 1981.
Lagasse, P. F., Spitz, W. J., Zevenbergen, L. W., and Zachman, D. W.: Handbook for Predicting Stream Meander Migration and Supporting Software, Transportation Research Board, Washington, D.C., 2004.
Lajeunesse, E., Malverti, L., Lancien, P., Armstrong, L., Métivier, F., Coleman, S., Smith, C. E., Davies, T., Cantelli, A., and Parker, G.: Fluvial and submarine morphodynamics of laminar and near-laminar flows: a synthesis: Laminar fluvial and subaqueous morphodynamics, Sedimentology, 57, 1–26, https://doi.org/10.1111/j.1365-3091.2009.01109.x, 2010.
Langbein, W. B. and Leopold, L. B.: River Meanders- Theory of Minimum Variance, Geological Survey Professional Paper, United States Department of the Interior, Washington, D.C., 1966.
Le Grand-Piteira, N., Daerr, A., and Limat, L.: Meandering rivulets on a plane: a simple balance between inertia and capillarity?, Phys. Rev. Lett., 96, 254503, https://doi.org/10.1103/PhysRevLett.96.254503, 2006.
Leopold, L. B. and Wolman, M. G.: River Meanders, Geol. Soc. Am. B., 71, 769–794, 1960.
MacDonald, T., Parker, G., and Leuthe, D.: Inventory and analysis of stream meander problems in Minnesota, St. Anthony Falls Laboratory, University of Minnesota, Minnesota, 1991.
Malverti, L., Lajeunesse, E., and Métivier, F.: Small is beautiful: Upscaling from microscale laminar to natural turbulent rivers, J. Geophys. Res., 113, F04004, https://doi.org/10.1029/2007JF000974, 2008.
Mantelli, E., Camporeale, C., and Ridolfi, L.: Supraglacial channel inception: Modeling and processes, Water Resour. Res., 51, 7044–7063, https://doi.org/10.1002/2015WR017075, 2015.
Marston, R. A.: Supraglacial Stream Dynamics on the Juneau Icefield, Ann. Assoc. Am. Geogr., 73, 597–608, https://doi.org/10.1111/j.1467-8306.1983.tb01861.x, 1983.
Metivier, F., and Meunier, P.: Input and output flux correlations in an experimental braided stream. Implications on the dynamics of bed load transport, J. Hydrol., 271, 22–38, https://doi.org/10.1016/S0022-1694(02)00312-8, 2003.
Motta, D., Abad, J. D., Langendoen, E. J., and Garcia, M. H.: A simplified 2D model for meander migration with physically-based bank evolution, Geomorphology, 163–164, 10–25, https://doi.org/10.1016/j.geomorph.2011.06.036, 2012.
Paola, C., Straub, K., Mohrig, D., and Reinhardt, L.: The “unreasonable effectiveness” of stratigraphic and geomorphic experiments, Earth-Sci. Rev., 97, 1–43, https://doi.org/10.1016/j.earscirev.2009.05.003, 2009.
Parker, G.: Meandering of supraglacial meltwater streams, Water Resour. Res., 11, 551–552, 1975.
Parker, G., Sawai, K., and Ikeda, S.: Bend theory of river meanders. Part 2. Nonlinear deformation of finite-amplitude bends, J. Fluid Mech., 115, 303, https://doi.org/10.1017/S0022112082000767, 1982.
Parker, G., Diplas, P., and Akiyama, J.: Meander bends of high amplitude, J. Hydraul. Eng., 109, 1323–1337, https://doi.org/10.1061/(ASCE)0733-9429(1983)109:10(1323), 1983.
Peakall, J. and Warburton, J.: Surface tension in small hydraulic river models - the significance of the Weber number, J. Hydrol., 35, 199–212, 1996.
Pelletier, J. D. and Baker, V. R.: The role of weathering in the formation of bedrock valleys on Earth and Mars: A numerical modeling investigation, J. Geophys. Res., 116, E11007, https://doi.org/10.1029/2011JE003821, 2011.
Pitcher, L. H. and Smith, L. C.: Supraglacial Streams and Rivers, Annu. Rev. Earth Planet. Sci., 47, 421–452, https://doi.org/10.1146/annurev-earth-053018-060212, 2019.
Rippin, D. M., Pomfret, A., and King, N.: High resolution mapping of supra-glacial drainage pathways reveals link between micro-channel drainage density, surface roughness and surface reflectance: UAVs, SfM and Supra-Glacial Drainage, Earth Surf. Proc. Land., 40, 1279–1290, https://doi.org/10.1002/esp.3719, 2015.
Schmuki, P. and Laso, M.: On the stability of rivulet flow, J. Fluid Mech., 215, 125, https://doi.org/10.1017/S0022112090002580, 1990.
Seminara, G.: Meanders, J. Fluid Mech., 554, 271, https://doi.org/10.1017/S0022112006008925, 2006.
Sklar, L. S. and Dietrich, W. E.: A mechanistic model for river incision into bedrock by saltating bed load, Water Resour. Res., 40, W06301, https://doi.org/10.1029/2003WR002496, 2004.
Smith, C. E.: Modeling high sinuosity meanders in a small flume, Geomorphology, 25, 19–30, https://doi.org/10.1016/S0169-555X(98)00029-4, 1998.
Strick, R. J. P., Ashworth, P. J., Awcock, G., and Lewin, J.: Morphology and spacing of river meander scrolls, Geomorphology, 310, 57–68, https://doi.org/10.1016/j.geomorph.2018.03.005, 2018.
Thorne, C. R. and Tovey, N. K.: Stability of composite river banks, Earth Surf. Proc. Land., 6, 469–484, https://doi.org/10.1002/esp.3290060507, 1981.
Veress, M. and Tóth, G.: Types of meandering karren, Z. Geomorphol., 48, 53–77, 2004.
Vermeulen, B., Hoitink, A. J. F., Zolezzi, G., Abad, J. D., and Aalto, R.: Multiscale structure of meanders, Geophys. Res. Lett., 43, 3288–3297, https://doi.org/10.1002/2016GL068238, 2016.
Whipple, K. X., Hancock, G. S., and Anderson, R. S.: River incision into bedrock: Mechanics and relative efficacy of plucking, abrasion, and cavitation, Geol. Soc. Am. B., 112, 490–503, https://doi.org/10.1130/0016-7606(2000)112<490:RIIBMA>2.0.CO;2, 2000.
Yang, K., Smith, L. C., Chu, V. W., Pitcher, L. H., Gleason, C. J., Rennermalm, A. K., and Li, M.: Fluvial morphometry of supraglacial river networks on the southwest Greenland Ice Sheet, Gisci. Remote Sens., 53, 459–482, https://doi.org/10.1080/15481603.2016.1162345, 2016.
Zeller, J.: Meandering channels in Switzerland, Int. Assoc. Sci. Hydrol., 75, 174–186, 1967.
Zolezzi, G. and Güneralp, I.: Continuous wavelet characterization of the wavelengths and regularity of meandering rivers, Geomorphology, 252, 98–111, https://doi.org/10.1016/j.geomorph.2015.07.029, 2016.
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(16087 KB) - Full-text XML
- Corrigendum
-
Supplement
(4901 KB) - BibTeX
- EndNote