Short communication: Runout of rock avalanches limited by basal friction but controlled by fragmentation

Rock avalanches produce exceptionally long run-outs that correlate with their rock volume. This relationship has been attributed to the size-dependent dynamic lowering of the effective basal friction. However, it has also been observed that run-outs of rock avalanches with similar volumes can span several orders of magnitude, suggesting additional controlling factors. Here, we analyse analogue models of rock avalanches, with the experiments designed to test the role of dynamic fragmentation. We show that for a fixed low basal friction, the run-out of experimental rock avalanches varies over 2 orders of magnitude and is determined by their degree of fragmentation, while the basal friction acts only as an upper limit on run-out. We interpret the run-out's dependence on fragmentation as being controlled by the competition between mobility enhancing spreading and energy-consuming fragmentation limited by basal friction. We formalize this competition into a scaling law based on energy conservation, which shows that the variation in the degree of fragmentation can contribute to the large variation in run-out of rock avalanches seen in nature.

1 Introduction

With volumes larger than 10⁹ m³ and speeds reported at over 150 km/h (Campbell, 1989) and possibly up to 100 m/s (Legros, 2002), the destructive power of rock avalanches is unprecedented. They are exceptional hazards produced when very large rockslides disintegrate during transport (Hungr et al., 2013). The travel distance of the deposit front, or run-out, is an important measure for hazard assessment (Vaunat and Leroueil, 2002) and is generally found to be more than 10 times longer than the fall height (Hsü, 1975). This suggests low effective basal friction μ_eff, which is usually attributed to various dynamic weakening processes (e.g. Kent, 1966; Shreve, 1968; Hsü, 1975; Melosh, 1979; Campbell, 1989; Pudasaini and Miller, 2013; Legros, 2002; Lucas et al., 2014; Wang et al., 2017) or additional basal erosion processes (e.g. Hungr and Evans, 2004; Pudasaini and Fischer, 2020).

Field observations of the displacement of rock avalanches are typically given by the ratio of vertical (H) and horizontal (L) distance from the deposit's front to the top of the main scarp. The resulting ratio

$$\begin{array}{}\text{(1)}& {\mathit{\mu }}_{\mathrm{apparent}}={\displaystyle \frac{H}{L}},\end{array}$$

is known as the Heim's ratio (Heim, 1882, as cited in Hsü, 1975) and serves as a proxy for μ_eff, where it is called the “apparent” coefficient of friction (Manzella and Labiouse, 2012). One of the best established but perhaps least understood observations of rock avalanches is the dependence of the Heim's ratio on volume: rockslides below a size of approximately 10⁶ m³ all have a relatively constant Heim's ratio of ∼0.4–0.7, but for larger rockslides Heim's ratio decreases with volume, reaching values <0.1 for volumes larger than 10⁹ m³ (Pudasaini and Miller, 2013; Lucas et al., 2014). This suggests a scale-dependent mechanism of decreasing apparent friction with volume that becomes dominant at large volumes (Davies and McSaveney, 1999). Analytical modelling and numerical simulation involving lubrication mechanisms by Pudasaini and Miller (2013) and Lucas et al. (2014) provided mechanical explanations for this observation. Importantly, however, even within a narrow range of volumes, run-outs are seen to span orders of magnitude, suggesting additional controlling factors on run-out that are insensitive to size. Runout variability also lies in part in the fact that the run-out is defined by the front of the deposits, and it therefore contains the combined effect of both translation and spreading of the rock mass. The additional travel distance caused by spreading can have a profound effect on the run-out (Staron and Lajeunesse, 2009), especially if the effective basal friction is low.

Recently, the process of dynamic fragmentation has received increased attention from the research community, and much progress has been made in our understanding of its role in the dynamics of rock avalanches (Locat et al., 2006; Imre et al., 2010; Bowman et al., 2012; Pudasaini and Miller, 2013; De Blasio and Crosta, 2015; Haug et al., 2016; Zhao et al., 2017, 2018; Lin et al., 2020; Gao et al., 2020; Knapp and Krautblatter, 2020). Firstly, one may expect that the finer the material is, the more flow-like the behaviour will be, increasing its mobility and allowing the rock mass to spread more easily (Locat et al., 2006; Wang et al., 2017; Zhao et al., 2018). Secondly, models of fragmenting rockslides suggest that dynamic fragmentation actively increases the spreading (Bowman et al., 2012; De Blasio and Crosta, 2015; Lin et al., 2020). However, fragmentation has also been shown to consume energy (Haug et al., 2016; Zhao et al., 2017; Lin et al., 2020), potentially at a cost to the run-out length. Clearly, understanding the integrated effect of fragmentation on the run-out dynamics of rock avalanches requires more analysis.

To study the effects of friction and fragmentation on rock avalanche dynamics, here we analyse analogue models of dynamically fragmenting rockslides. We assume that there exists some mechanism (or a set of mechanisms) that causes a low effective coefficient of basal friction, which we set to 0.15–0.20 in our models. To isolate the scale-independent effect of fragmentation we keep both the volume and friction within a narrow range in our models compared to nature. Note that this approach explicitly excludes dynamic weakening mechanisms that are suspected in natural prototypes. Specifically, our models do not include fluids, and frictional heating is insignificant such that lubrication mechanisms (e.g. Pudasaini and Miller, 2013; Lucas et al., 2014) do not play a role. Granular pressurization (e.g. Imre et al., 2010) is also not considered significant in our experiments because of the low energy involved. Other potentially important mechanisms like bedrock erosion (e.g. Hungr and Evans, 2004; Pudasaini and Fischer, 2020) are excluded here for simplicity. The experimental design therefore means that the observed variation in Heim's ratio is due to fragmentation and dry friction. We describe the dependence observed between the run-out and the degree of fragmentation in the form of a scaling law. Finally, we compare our experimental results to a set of natural data and discuss their relevance to natural systems. All data underlying this study and additional relevant data are published as open access in Haug et al. (2021).

2 Experimental methods

In the experiments originally documented in Haug et al. (2016), a block of height h and length l₀ (width =l₀) of rock analogue material is gravitationally accelerated down a plate held at an angle of 45^∘ to the horizontal (Fig. 1). After 1 m of travel, the sample impacts a horizontal plate causing it to fragment. Once the sample fragments have slid onto the horizontal plane, they spread and decelerate due to the internal and basal frictional interaction before finally coming to rest. We use silicate glass as our substrate, upon which the basal friction coefficient is ca. 0.15–0.20 (Haug et al., 2016) – similar to the lowermost values found in natural prototypes (Pudasaini and Miller, 2013; Lucas et al., 2014). The analogue rock material is a cemented fluvial quartz sand. The sand is cemented by mixing it with water and gypsum or potato starch and is left to set for 2 d (for gypsum cement) or heated for 15 min in a 900 W microwave (for potato starch cement). The cohesion of the material can be controlled by the type and amount of cement added to the mixture, allowing control of the strength of the material over several orders of magnitude. The internal friction coefficient relevant for fragmenting intact material is 0.7 and reduces to 0.6 when fragments interact (see Haug et al., 2014, 2016, for details on the experimental setup).

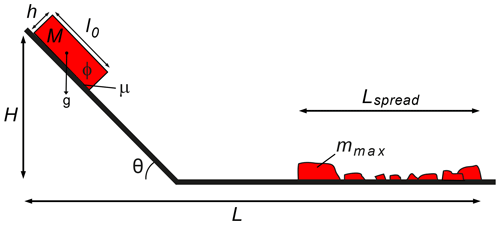
Figure 1 Sketch of the slope geometry of experiments, relevant parameters, and length scales (modified following Haug et al., 2016).

Figure 2 Snapshots from the experiments showing an (a) intermediate-strength sample (C=40 kPa) and a (b) low-strength sample (C=4 kPa).The red lines in the upper images indicate the geometry of the basal plates. Images are chosen to represent similar travel distances in (a) and (b). The time given above each image reflects the time since the first impact. The samples have dimensions $\mathrm{15}\times \mathrm{15}\times \mathrm{2}$ cm. Note that the stronger sample (a) breaks apart into six large fragments with a limited amount of fine material produced and moves apart with little interaction after breaking. In contrast, the weaker sample (b) fragments into many small pieces with a large fraction of fine material causing frictional interaction and that deposits relatively early. Movies of the experiments are available in Haug et al. (2021).

The three main observables from the experiments are (i) the degree of fragmentation (m_c), (ii) the Heim's ratio ($H/L$), and (iii) the normalized deposit length ($L_{\mathrm{spread}}/H$). We characterize the degree of fragmentation through the total mass of the sample divided by the mass of the largest fragment ($m_c=M/m_{\max }$). We choose this rather simple parameter, which has been validated and benchmarked against breakage parameters used by previous studies in Haug et al. (2016), as a tradeoff between capturing the process accurately in models and the accessibility of the equivalent information in nature. To define L_spread, we consider the mass-weighted average position of the most proximal and distal 5 % of the total mass. This defines a rim that is a more robust run-out estimate than using single fragment positions, as done by Haug et al. (2016), and is at the same time accessible both experimentally and empirically. We normalize L_spread by fall height H in order to have a parameter describing the conversion of potential energy into spreading that is equivalent to Heim's ratio.

The experimental data analysed here come from two series of experiments with varying degrees of fragmentation: (i) one series of experiments where the thickness-to-length ratio ($h/l_{\mathrm{0}}$) of the samples has been varied between 0.033 and 0.49 (corresponding to a 1 order of magnitude range in volume), while keeping the cohesion (C) constant at 14 kPa, and (ii) one series of experiments where the cohesion of the material is varied between 4 and 350 kPa, while keeping the thickness to length ratio constant at 0.13. In both series of experiments, the fall height (H) is kept constant at 0.71 m. Interested readers are referred to Haug et al. (2016) for details on the effect of cohesion and geometry on the degree of fragmentation. Additionally, two new experiments were performed to study the moment of fragmentation at high temporal resolution. For these experiments, the fragmentation of two samples with different cohesion but equal geometry (C=4 and 40 kPa, $h/l_{\mathrm{0}}=\mathrm{0.13}$) is considered. These two experiments have a fall height of 0.35 m, and data are captured by a camera with a frame rate of 500 Hz (see Haug et al., 2021, for movies of these experiments). Combining these sets of data from various experiments allows for covering a wide enough parameter space for the analysis in this study.

3 Results and discussion

3.1 Experimental observations and interpretation

Figure 2 presents snapshots from two representative experiments, one with an intermediate-strong sample and one with a low-strength sample, illustrating the process of fragmentation. The stronger sample (Fig. 2a) is observed to fragment less than the weaker one (Fig. 2b). Thereafter, fragments of the stronger sample spread with limited interaction, while the fragments from the weaker sample collide and/or slide next to each other and deposition starts relatively early. We infer at the first order that while mobility generally increases with fragmentation, a higher amount of internal deformation is experienced, along with increased fragmentation and increased deposition.

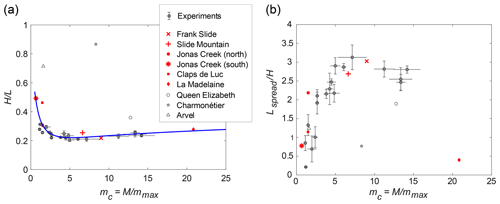
Figure 3 Heim's ratio and the deposit length of experiments (this study) and natural rock avalanches (from Locat et al., 2006). (a) The Heim's ratio of the analogue experiments (grey) and from the rock avalanches (red shows the selected set, and open shows discarded avalanches). The blue line represents the best fit of Eq. 8 to experimental and natural data with parameters $\mathit{\alpha }=-\mathrm{1.0}$, β=1.5, γ=0.11. (b) The deposit's lengths. In both panels, the grey circles represent the average value of a set of 4–15 experiments, and the error bars give the standard error of the set. Note the opposite trends of the two curves, suggesting an intrinsic relationship between spreading and run-out.

To quantitatively analyse the experiments, we focus on the correlation between run-out and fragmentation and neglect all other parameters. This is justified by the collapse of experimental and natural data when plotting Heim's ratio against fragmentation in Fig. 3a. Qualitatively, Heim's ratio decreases rapidly for low to intermediate degrees of fragmentation, reaching a minimum at m_c≈5 of about 0.2, and increases again slightly for higher degrees of fragmentation. A similar relation is observed between the length of the deposits (Fig. 3b), which increases with fragmentation until m_c≈5 and slightly decreases beyond.

The rapidly decreasing Heim's ratio for m_c<5 observed in Fig. 3a is likely linked to the increased spreading with fragmentation seen in Fig. 3b. A similar result was also obtained by previous analogue experiments (Bowman et al., 2012; Haug et al., 2016) and numerical models (De Blasio and Crosta, 2015; Zhao et al., 2017). However, here we show that the Heim's ratio is not simply decreasing with the degree of fragmentation but that it instead displays an optimum for m_c≈5. Importantly, the lowest apparent basal friction, equivalent to the lowest Heim's ratio, is close to the implemented basal friction (i.e. friction coefficient of 0.15–0.20 between samples and glass). Therefore, all processes operating in our models (e.g. fragmentation, internal friction between fragments, deposition) tend to consume energy and thereby reduce run-out from its optimum (Haug et al., 2016). Considering the increased internal deformation observed with the degree of fragmentation (Fig. 2), the reduction of run-out and spreading for m_c>5 appears to be the result of the increased energy dissipation through internal friction within the rock mass and an increase in basal friction as the sliding surface becomes rougher due to syn-sliding deposition (e.g. Pudasaini and Fischer, 2020). A loss of mass and therefore momentum due to deposition may additionally result in deceleration and reduced run-out as a function of m_c (e.g. Pudasaini and Fischer, 2020). Consequently, the minimum of the Heim's ratio observed in Fig. 3a appears as the result of a competition between the spreading enhancing mobility and the energy-consuming fragmentation process.

3.2 A scaling law for run-out

The interplay between fragmentation and friction in a dry environment can be formalized into a scaling law by considering the conservation of energy. Generally, the conservation of energy of a sliding mass M requires that

$$\begin{array}{}\text{(2)}& MgH=\mathit{\mu }Mg{L}_{\mathrm{p}}+W,\end{array}$$

where g is the gravitational acceleration, H is the vertical fall height, L_p is the entire travel path of the slide, and W is the sum of any other energy dissipating terms. Here, we have assumed a Coulomb friction coefficient μ at the base.

For the geometry of our experimental setup (see Fig. A1), as well as (roughly) for the set of selected rock avalanches, the L_p can be expressed in terms of the horizontal run-out L as

$$\begin{array}{}\text{(3)}& L_{\mathrm{p}}=L+L_{\mathrm{s}}(\mathrm{1}-\cos \mathit{\theta })-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{l}_{\mathrm{0}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{L}_{\mathrm{spread}},\end{array}$$

where L_s is the length and θ the angle of the slope, and l₀ is the initial length of the slide. It is assumed that the additional travel length due to spreading is equal to half the deposit length (L_spread). Since l₀ is expected to be very small compared to the other terms, it is neglected in further analysis. Inserting Eq. (3) into (2) and solving for L gives

$$\begin{array}{}\text{(4)}& L={\displaystyle \frac{H}{\mathit{\mu }}}-L_{\mathrm{s}}(\mathrm{1}-\cos \mathit{\theta })+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{L}_{\mathrm{spread}}-{\displaystyle \frac{\mathrm{1}}{\mathit{\mu }Mg}}W,\end{array}$$

where it is emphasized that both L_spread and W are expected to be functions of the basal friction, μ, internal friction, ϕ, and the degree of fragmentation, m_c, as well as a possible non-linear dependence between L_spread and W. Rearranging Eq. (4) yields the Heim's ratio in the form of

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{H}{L}}=\mathit{\mu }{\left(\mathrm{1}-{\displaystyle \frac{\mathit{\mu }}{\sin \mathit{\theta }}}\left(\mathrm{1}-\cos \mathit{\theta }\right)+{\displaystyle \frac{\mathit{\mu }}{\mathrm{2}H}}{L}_{\mathrm{spread}}-{\displaystyle \frac{\mathrm{1}}{MgH}}W\right)}^{-\mathrm{1}}.\end{array}$$

A direct determination of the two last terms in Eq. (5) is difficult. However, based on the shape of the function of both the Heim's ratio and the L_spread plotted in Fig. 3, it appears that it can be reasonably described by an exponential function of m_c:

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\mathit{\mu }}{\mathrm{2}H}}{L}_{\mathrm{spread}}=\mathit{\alpha }{e}^{-m_c/\mathit{\beta }}.\end{array}$$

Additionally, the experimental work by Haug et al. (2016) suggests that dissipative energy loss through fragmentation increases less for higher degrees of fragmentation and therefore can be described with a logarithmic function of m_c:

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{\mathrm{1}}{MgH}}W=\mathit{\gamma }\log \left(m_c\right).\end{array}$$

Using these approximations, Heim's ratio can be expressed as

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{H}{L}}=\mathit{\mu }{\left(\mathrm{1}-{\displaystyle \frac{\mathit{\mu }}{\sin \mathit{\theta }}}\left(\mathrm{1}-\cos \mathit{\theta }\right)+\mathit{\alpha }{e}^{-m_c/\mathit{\beta }}-\mathit{\gamma }\log \left(m_c\right)\right)}^{-\mathrm{1}},\end{array}$$

where α, β, and γ are constants to be empirically determined.

This equation describes the competition between spreading (proportional to $e^{-m_c/\mathit{\beta }}$) and the increasing energy dissipation (proportional to log (m_c)) with m_c and its relation to friction. A best fit of this function to the natural and experimental data is presented in Fig. 3a (blue line), where $\mathit{\alpha }=-\mathrm{1.0}$, β=1.5, and γ=0.11. A fit constrained only the experimental data yields very similar results ($\mathit{\alpha }=-\mathrm{0.68}$, β=2.0, γ=0.11; see Fig. B1). This suggests spreading dominates run-out for low degrees of fragmentation (i.e. m_c<5) but has little effect at high degrees of fragmentation as the exponential term approaches zero. At high degrees of fragmentation, the energy dissipation related to fragmentation therefore becomes increasingly relevant in controlling run-out. At m_c≈5, i.e. when about 80 %–85 % of the volume is fragmented, a state of optimal mobility is reached with a Heim's ratio limited by the basal friction coefficient suggesting that energy is consumed mainly by basal friction, which then is the limiting factor for run-out.

3.3 Application to a natural data set

We compare our experimental results in Fig. 3 with data from nine rock avalanches reported by Locat et al. (2006) that show no clear volume dependence of run-out. This feature makes this data set ideal for testing whether a scale-independent process is operating besides dynamic basal weakening. However, not all the rock avalanches reported in Locat et al. (2006) are comparable to our experimental setup concerning material properties and geometries (Fig. 1). Based on slope geometry, the Queen Elizabeth slide is discarded because of its run-up on the opposite valley wall. Also discarded is the Charmonétier slide because of the sudden free-fall stage at the end of its transport. Additionally, the Arvel slide was observed to bulldoze soft material in front of it, and as such complexities are not considered in our models, this one is also neglected. Note that in all three discarded cases, the late-stage processes tend to increase the expected Heim's ratio, and they consistently plot above the trend of the other data in Fig. 3b.

Figure 3 displays remarkably similar trends between the experimental and the selected natural data that all follow the proposed scaling law. The data points from Jonas Creek (north) and Claps de Luc are observed to extend the trend from the experiments to higher Heim's ratios for low degrees of fragmentation, while the La Madelaine slide is observed to extend the trend of the experimental results of Heim's ratio to higher degrees of fragmentation (Fig. 3a). Its low spreading value (Fig. 3b) suggests that the reduction of spreading indicated by the experiments for m_c>5 continues for even higher degrees of fragmentation. The agreement between these slide deposit lengths and the extrapolation of the experimental trend through Eq. (8) (Fig. 3b) supports the validity of our proposed scaling law. The Heim's ratios of the neglected slides are all, as expected, higher than the selected data set for their respective degrees of fragmentation, illustrating the importance of topography (e.g. opposite valley wall) and processes such as bulldozing.

The similarity seen between experimental and natural data suggests some universality concerning the empirical constants. Moreover, the similarity suggests that the rock avalanches considered here all have a close to constant effective basal friction of about 0.15–0.20. This implies that over the range of 2 orders of magnitude (from 2×10⁶ to 90×10⁶ m³) represented by this data set, the effective coefficient of friction of rock avalanches could be considered independent of volume. Consequently, our results suggest that the variation seen in Heim's ratio for these rock avalanches is not (only) caused by scale-dependent basal friction but instead by differing degrees of fragmentation. This shows that fragmentation plays a governing role in the run-out of rock avalanches and should be included in hazard assessments.

4 Conclusions

We studied the dynamics of fragmenting rock avalanches experimentally to unravel the control of basal friction versus fragmentation on run-out behaviour. We find that fragmentation causes both spreading and frictional interaction – competing processes that control the avalanche dynamics. Based on energy arguments we derive a scaling law with empirical constants that quantifies the relative importance of spreading and frictional interaction as a function of fragmentation. The scaling law approaches an extreme for which run-out is maximized and limited only by basal friction, which itself might be volume-dependent as suggested by earlier studies. The scaling law is validated against a natural data set verifying its applicability.

Appendix A: Definitions

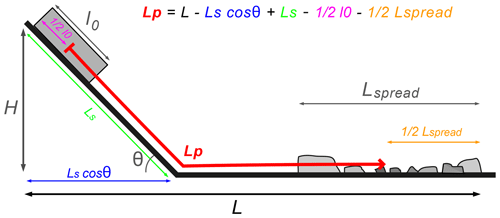
Figure A1 Definition of distances used in Eq. (3). L_p is the length of the travel path.

Appendix B: Scaling law fit to experimental data only

Figure B1 Heim's ratio and deposit length of experiments (this study) and natural rock avalanches (from Locat et al., 2006). The Heim's ratio of the analogue experiments (grey) and from the rock avalanches (red shows the selected set, and open shows the discarded avalanches). The blue line represents the best fit of Eq. (8) to experimental data with parameters α=0.11, β=0.68, and γ=2.0. Data shown and a MATLAB script to plot them are both available in Haug et al. (2021).