the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The rate and extent of wind-gap migration regulated by tributary confluences and avulsions
Eitan Shelef
Liran Goren
The location of drainage divides sets the distribution of discharge, erosion, and sediment flux between neighboring basins and may shift through time in response to changing tectonic and climatic conditions. Major divides commonly coincide with ridgelines, where the drainage area is small and increases gradually downstream. In such settings, divide migration is attributed to slope imbalance across the divide that induces erosion rate gradients. However, in some tectonically affected regions, low-relief divides, which are also called wind gaps, abound in elongated valleys whose drainage area distribution is set by the topology of large, potentially avulsing side tributaries. In this geometry, distinct dynamics and rates of along-valley wind-gap migration are expected, but this process remains largely unexplored. Inspired by field observations, we investigate along-valley wind-gap migration by simulating the evolution of synthetic and natural landscapes, and we show that confluences with large side tributaries influence migration rate and extent. Such confluences facilitate stable wind-gap locations that deviate from intuitive expectations based on symmetry considerations. Avulsions of side tributaries can perturb stable wind-gap positions, and avulsion frequency governs the velocity of wind-gap migration. Overall, our results suggest that tributaries and their avulsions may play a critical role in setting the rate and extent of wind-gap migration along valleys and thus the timescale of landscape adjustment to tectonic and climatic changes across some of the tectonically most affected regions of Earth, where wind gaps are common.
- Article
(17840 KB) - Full-text XML
-
Supplement
(738 KB) - BibTeX
- EndNote
Drainage divides play a pivotal role in controlling the geometry of fluvial landscapes and shaping their hydrologic and geomorphic functionality. Divide locations and, as a consequence, basin geometry are transient features of the landscape (e.g., Willett et al., 2014; Whipple et al., 2017) that respond to shifting boundary conditions. As early as the late 19th century, Gilbert (1877) and Davis (1889) described divide migration and drainage reorganization, and since then the geomorphology literature has documented many examples of such drainage network reorganization at both the local scale (e.g., Johnson, 1907; Woodruff, 1977; Nugent, 1990; Brocard et al., 2011; Prince et al., 2011; Yanites et al., 2013; Schmidt et al., 2015; Forte et al., 2015; Fan et al., 2018) and the regional scale (e.g., Ollier, 1995; Zelilidis, 2000; Shephard et al., 2010; Clark et al., 2004; Liu, 2014; Yang et al., 2020).
Whereas drainage divides could be breached abruptly via river capture events (e.g., Bishop, 1995; Prince et al., 2010; Willett et al., 2014), a possibly more common process involves long-lasting and continuous divide migration at basin headwaters, where the divides are located along ridgelines (e.g., Willett et al., 2014; Goren et al., 2014b; Shelef and Hilley, 2014; Whipple et al., 2017; Beeson et al., 2017; Braun, 2017). In these high-relief settings, divide migration is linked to an imbalance in erosion rate across the hillslopes that bound the divide (Forte and Whipple, 2018). Hillslope erosion and slope are linked to incision at the proximal channel head (the local base level for the hillslope). Given that channel erosion rate scales with channel gradient and drainage area (a proxy for discharge; e.g., Howard, 1994; Whipple and Tucker, 1999), small across-divide differences in these factors can lead to disparate channel incision rates across the divide and to a gradual divide migration directed from the rapidly eroding to the slowly eroding hillslope (Beeson et al., 2017; Braun, 2017).
Over long timescales, feedbacks might arise that promote a prolonged and gradually declining divide migration (Willett et al., 2014; Whipple et al., 2017). An area feedback occurs as the basin at the side of the rapidly eroding hillslope grows (hereafter the expanding basin), whereas its across-divide neighbor shrinks (hereafter the shrinking basin) (Willett et al., 2014; Yang et al., 2015; Whipple et al., 2017). An increase in the expanding basin drainage area increases its erosion rate and promotes further divide migration and area gain (Willett et al., 2014; Mudd and Furbish, 2005; Whipple et al., 2017; Goren et al., 2014b). The complementary process operates on the shrinking basin that loses drainage area and becomes susceptible to further area loss by continuous divide migration and side captures. Parallel to this area feedback, which furthers divide migration, a channel length feedback arises that gradually suppresses this migration. As the divide migrates, channels of the shrinking basin shorten and channels of the expanding basin lengthen, which increases the overall gradient of the shrinking basin compared to the expanding basin, eventually leading to a balance in erosion rate across the divide so the divide migration stops. The relative magnitude of these competing area and length feedbacks changes gradually through the migration process, and thus the velocity of divide migration typically declines smoothly through time (Braun, 2017). This gradual divide migration process is associated with settings in which the migrating divide is located along a ridgeline that is topographically higher than the tributaries draining to the shrinking basin. Migration then erases the morphology and topology of the shrinking basin and obliterates the antecedent course of its tributaries (Fig. 1a–b).
A distinctly different dynamic is expected to emerge when a drainage divide forms a deep saddle within a valley (a wind gap; e.g., Bishop, 1995). In such settings, the wind gap is lower than the ridges that bound the valley, and thus the morphology of the bounding ridgelines and the tributaries that drain them into the valley can be largely preserved as the wind gap migrates along the valley (e.g., Harel et al., 2019) (Fig. 1c–d). The preserved side tributaries can cause punctuated changes in drainage area through the divide migration process that distinctively differ from the aforementioned gradual exchange of drainage area. We thus intuit that the coupled dynamics of side tributaries draining close to a wind gap and wind-gap migration could be key in controlling wind-gap stability, migration velocity, and the evolution of valley topography.
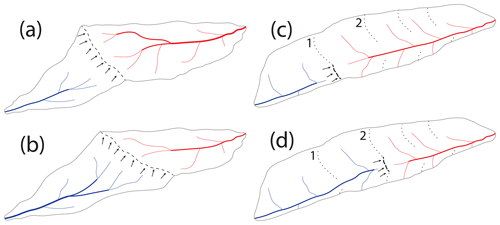
Figure 1Schematic illustration of a typical (a, b) vs. along-valley (c, d) divide migration. (a) Illustration of a typical divide migration process with the divide (dashed line) located along a ridgeline (after Whipple et al., 2017). (b) The same setting as in panel (a) after the divide migrated some distance. Note that as the ridgeline migrates it erases the tributaries of the shrinking basin. (c) Illustration of a wind-gap (dashed line) migration along a valley. Note that the tributaries that drain to the valley can be preserved through the migration process so that the migrating wind gap can traverse confluences with tributaries through its migration. (d) Same setting as in panel (c) after the wind gap migrated some distance. Low-order channels are marked with thinner lines. Note that the low-order drainage divides between tributaries (dotted lines) can merge with the migrating wind gap to form a high-order divide (for example, see the low-order divides marked 1 and 2 in panels c and d).
Wind-gap migration along a valley is likely common in tectonically active and/or structurally deformed areas where wind gaps are prevalent. Such migration is likely facilitated by relatively erodible bedrock or sediments within valleys (Harel et al., 2019), or it may be induced by tilting in tectonically active areas (Bishop, 1995; Clark et al., 2004). Wind gaps are found along longitudinal, structurally controlled valleys as well as in antecedent highland valleys truncated by cliffs or formed by large capture events (e.g., Haworth and Ollier, 1992; Bishop, 1995; Prince et al., 2010; Harel et al., 2019) (e.g., Fig. 2). The location and migration of wind gaps dictate the distribution of erosion, discharge, and sediment fluxes between diverging regional- to continental-scale drainage networks and sedimentary basins and may therefore set a primary control on the geologic evolution of some of the most active regions on Earth. Yet, the dynamics of wind-gap migration remain largely unexplored.
In this study we seek to identify and explore key aspects of the dynamics of wind-gap migration. In particular, we focus on the influence of confluences and avulsions of side tributaries on the rate and extent of wind-gap migration.
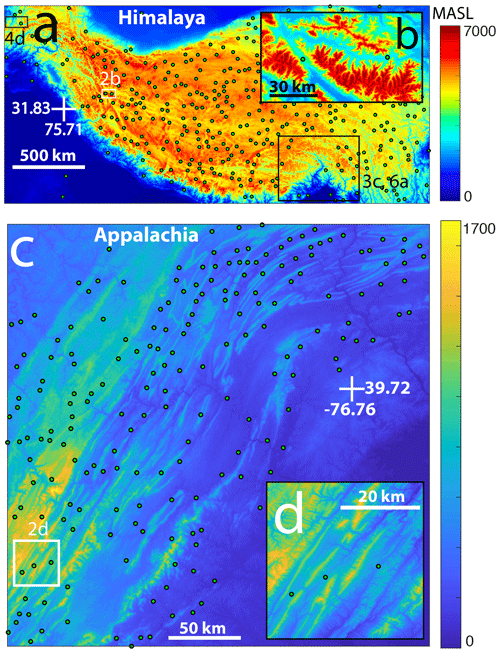
Figure 2Wind gaps in tectonically influenced areas. (a) A map of estimated wind-gap locations (yellow circles) in the Himalaya. Boxes mark the regions shown in other figures, and figure numbers are specified next to each box. (b) A zoom into the section of the map marked 2b in panel (a), showing a more detailed view (using an SRTM DEM; Farr et al., 2007) of wind-gap locations. Here, the color bar represents the range of elevations between 3500 and 6000 m. (c) A map of estimated wind-gap locations in the Appalachian fold-and-thrust belt. (d) A zoom into the section of the map marked 2d in panel (c), showing a more detailed view (using an SRTM DEM; Farr et al., 2007) of wind-gap locations. Here, the color bar represents the range of elevations between 450 and 1500 m. Color schemes were selected to highlight the specific topography of every region. Wind-gap locations were identified over GMTED DEMs (Danielson and Gesch, 2011) and are only a subset of all wind gaps in these regions. The procedure used for automated wind-gap identification is described in the Supplement.
This study is inspired by field observations of wind gaps that traversed confluences with side tributaries along their migration pathway. Along the Arava escarpment, Israel, antecedent valley systems were beheaded as part of a regional, long-lasting drainage reorganization associated with the escarpment's development (Ginat et al., 2000; Avni et al., 2000; Harel et al., 2019). Numerous wind gaps are aligned with the escarpment cliff, some of which migrated inland along antecedent valleys (Harel et al., 2019), traversing confluences with side tributaries. Observations from Wadi Grofit, for example, show that several confluences were traversed by a migrating wind gap, as seen by their barbed morphology (Fig. 3a–b). A similar setting, albeit at a much larger scale, is observed at the eastern syntaxis of the Himalaya. Here, the Parlung–Siang–Lohit river capture (Lang and Huntington, 2014; Schmidt et al., 2015; Govin et al., 2018; Zhang et al., 2019) (Fig. 3c) triggered a wind-gap migration of more than 200 km along the Parlung valley. Through its migration, the wind gap traversed confluences with side tributaries that may have influenced the migration dynamics.
This study is further motivated by field observations showing that avulsions of side tributaries can shift discharge across wind gaps. Such a setting is observed, for example, along an east–west-directed valley next to Mt. Berech on the highlands of the Arava escarpment. Here, avulsions occur at the head of an alluvial fan that is formed at the mouth of a side tributary, draining into a valley close to a wind gap. While most of the tributary discharge is still routed to the valley side that drains away from the escarpment, the avulsions route a fraction of the discharge across the wind gap to the escarpment side (Fig. 4a–c). A similar example of a somewhat larger scale is observed in the Hindu-Kush province of the Himalaya next to the Ishkashim Pass wind gap, Afghanistan. Here, a side tributary forms an alluvial fan as it drains into an east–west-directed valley, and avulsions at the apex of this fan route discharge across a wind gap (Fig. 4d–e). We intuit that such avulsions can modify the relative erosion rates across wind gaps and thus the rate and extent of wind-gap migration.
The observations described above (Figs. 3 and 4), and the realization that wind-gap migration may be a prominent mechanism of landscape development in tectonically active and structurally deformed regions (Fig. 2), inspired simulations that explored how the dynamics of wind-gap migration are influenced by (a) confluences with side tributaries and (b) avulsions of such side tributaries across wind gaps.
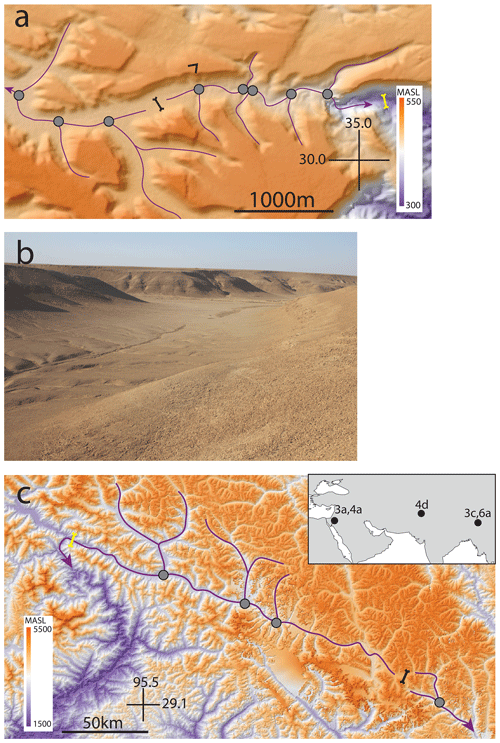
Figure 3Examples of valleys with wind gaps and major confluences with side tributaries (gray circles). Major channels are marked in purple, and their flow direction is marked with an arrow. (a) A map based on a TanDEM-X DEM (Krieger et al., 2007) showing an example from Wadi Grofit in the Negev highlands along the Arava escarpment, Israel. The current location of the wind gap is marked by a bold forked black line. The approximated initial location of the wind gap is marked with a forked yellow line (Harel et al., 2019). A black v-shaped symbol open to the southwest shows the locations from which the picture in panel (b) was taken. (b) A picture of the wind gap shown in panel (a). Note the low relief of the wind gap and a side tributary that joins the valley from the left-hand side of the picture. (c) A map based on a GMTED2010 DEM (Danielson and Gesch, 2011) showing the wind gap and confluences along the Parlung valley, China. Wind-gap symbols are as in panel (a). In both the Grofit and Parlung examples, the wind gap likely traversed confluences with side tributaries (gray circles), resulting in their barbed morphology. The inset map shows the general location of the field examples presented in this and other figures; figure numbers are specified next to each location.
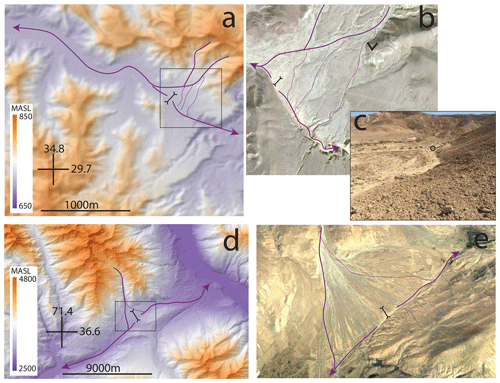
Figure 4Examples of avulsions across wind gaps (forked black line). Channels are marked in purple. (a) A map based on a TanDEM-X DEM (Krieger et al., 2007) of a wind gap next to Mt. Berech in the Negev highlands along the Arava escarpment, Israel. Note that although the side tributaries drain primarily northwest of the wind gap, a few bifurcating branches appear to route a fraction of the tributaries' discharge to the other side of the wind gap. The black box marks the area shown in panel (b). (b) An air photo (© Google Earth 2020) showing the main channels of the side tributaries as well as their bifurcating branches. A black v-shaped symbol open to the north shows the locations from which the picture in panel (c) were taken. (c) View of an avulsion point looking upstream (north) from the aforementioned v-shaped symbol. The circle marks a backpack for scale that is located at the bifurcation point. (d) A map based on a GMTED2010 DEM (Danielson and Gesch, 2011) of the Ishkashim Pass area in Afghanistan. Note that although the side tributary drains primarily southwest of the wind gap, a few bifurcating branches appear to route a fraction of its discharge to the other side of the wind gap. The black box marks the area shown in panel (e). (e) An air photo (© Google Earth 2020) showing the bifurcation of a side tributary across the wind gap.
To investigate the influence of side tributaries on the velocity and extent of wind-gap migration, we use a landscape evolution model (e.g., Tucker and Hancock, 2010; Perron et al., 2009):
In Eq. (1), , the change in elevation, z [L], through time, t [T], is a function of uplift rate, U [L T−1], channel incision through detachment-limited processes, KAmSn [L T−1], and changes in elevation due to diffusive sediment transport, D∇2z [L T−1], that likely dominates hillslope settings. In this model, channel incision is a function of drainage area, A [L2], and topographic gradient, S, as well as an erodibility coefficient, K [L1–2m T−1]. The two exponents m and n acknowledge that erosion may be a nonlinear function of drainage area and gradient, respectively (Howard and Kerby, 1983; Seidl and Dietrich, 1992; Howard, 1994). Sediment transport is modeled as a diffusive process, where D [L2 T−1] is a diffusion coefficient, and ∇2z [L−1] is the Laplacian of elevation (Culling, 1963; Howard, 1994). We use a finite-difference scheme, wherein drainage area is the summation of the area of all upstream nodes and the topographic gradient is computed via a forward-difference scheme in the downslope direction. The drainage area of the divide node is bifurcated between neighboring nodes according to the relative magnitude of the slope to each neighboring node (Freeman, 1991). This is a conservative choice that aims to minimize the influence of spatial discretization on wind-gap stability (Pelletier, 2004). The model integrates Eq. (1) through time using a fourth- to fifth-order explicit Runge–Kutta integration with time stepping constrained by the Courant criteria. The parameters K, m, and n are determined based on common values published in the literature, and D is scaled based on the values of K and m so that comparable models have the same length (Lp) associated with a Péclet value of unity (i.e., after Perron et al., 2008, 2009). We set this length to be relatively short (200–500 m) such that diffusive sediment transport is generally negligible within channels. The values of the parameters used in different simulations are reported in Table 1.
Table 1Table of model parameters. U: uplift rate; D: diffusion coefficient; K: erodibility coefficient; m and n: drainage area and slope exponents, respectively; Lc: distance to the center of model domain; L: distance between confluences; W: valley width; At: tributary area; Δx: node spacing; Δta: time between avulsions; a only for models with avulsions; b varying drainage area with the lowest value being the same as the drainage area of a single non-confluence node (i.e., W×Δx) and with all following values ranging from 2 to 20 segment areas (i.e., L×W) in steps of ; c varying time between avulsions (between 50 and 950 years in intervals of 100 years).

To explore how confluences with side tributaries influence the migration velocity and stable positions of wind gaps, we first simulate the evolution of a synthetic one-dimensional landscape with such confluences (hereafter “fixed confluence simulations”). The initial setting (Fig. 5a, b) is an elongated valley with the wind gap at the left edge of the valley bounded by a cliff to its left, and a trunk channel drains the valley to the right (Fig. 5b, case 1). The initial topography of the trunk channel is set to be at a topographic steady state (i.e., ) in accordance with Eq. (1). The boundary conditions are set to a constant and equal elevation at both ends of the model. The topology of the valley–tributary system is prescribed as a set of equally spaced trunk–tributary confluences along the valley with tributaries having the same drainage area (i.e., the drainage area added at the confluence) (Fig. 5a). The valley has a constant width, and thus non-confluence nodes are all assigned the same local drainage area. The deviation of this topology from a Hack scaling (Hack, 1957) is supported by field observations (i.e., Figs. 3, 4) and contributes to the simplicity of this synthetic model setting. We varied the tributary drainage areas between simulations and recorded the velocity of wind-gap migration and the location where the wind gap attains a stable position. A stable position is defined as where the wind-gap position is fixed and the elevation difference between consecutive time steps is zero everywhere for 100 consecutive time steps. Simulation results are compared to a reference simulation in which there are no confluences with side tributaries, and the total drainage area is equal to the equivalent simulation with trunk–tributary confluences and is distributed equally between all model nodes.
To study the influence of avulsions of side tributaries on the rate and extent of wind-gap migration, we simulated such avulsions by shifting the location of trunk–tributary confluences through time (hereafter, “avulsion simulations”). To achieve these dynamics, we randomly varied the confluence location within a prescribed distance from its initial position. The random distances are selected from a uniform distribution centered at the original location of each confluence, and the maximal distance is constrained to half the distance between the original locations of confluences (i.e., Fig. 5a). Avulsions occur in all tributaries regardless of their location relative to the wind gap. We explored the influence of the time span, Δta, between avulsions (i.e., shifts in confluence location) by varying it between simulations (from 50 to 950 years). We explored the influence of model parameters in all three versions of the simulations (reference, fixed confluence, and avulsions) with two different m values (m=0.45, m=0.55) for 11 different values of the tributary area segment area ratio in the fixed confluence simulations (Table 1). Simulation results of varying the slope exponent, n, are presented in the Supplement.
An independent set of simulations is dedicated to exploring the potential influence of tributary confluences on wind-gap migration in a natural setting. Here, the topology of the aforementioned Parlung–Siang–Lohit system is used as a template for the simulation, and we focus on the system dynamics following the Parlung–Siang–Lohit capture (Lang and Huntington, 2014; Schmidt et al., 2015; Govin et al., 2018; Zhang et al., 2019) (Fig. 6a–b). The initial conditions (Fig. 6d) replicate the inferred channel system topography and topology at the time of the capture. For this “natural” experiment, we assume that (a) the expanding (Siang river) and shrinking (Parlung river) basins were approximately at a topographic steady state at the time of capture, (b) the capture occurred at point d in Fig. 6a, (c) the channel profiles could be reconstructed based on Eq. (1), and (d) the location and drainage area of tributary confluences were similar to the present-day tributary confluence configuration. The confluence between the Siang and Lohit–Parlung (point f in Fig. 6a) is used as the boundary conditions for these simulations. We extract the drainage area along the rivers from a GMTED2010 digital elevation model (DEM) (Danielson and Gesch, 2011) with a resolution of 15 arcsec (approximately 500 m). We slightly modified the DEM to correct inaccuracies in basin boundaries close to the headwater of the Parlung river. The choice of model parameters (see Table 1) is coarsely guided by values suggested in the literature (Wang et al., 2017; Govin et al., 2018; Yang et al., 2018; Zhang et al., 2019) and adjusted to the present-day relief. Note that this simulation aims to demonstrate the potential influence of network topology on wind-gap migration in a natural setting and not to investigate the development of the Parlung–Siang–Lohit capture specifically.

Figure 5Simulations of along-valley wind-gap migration across confluences with tributaries. (a) Plan view schematic of a one-dimensional model domain that simulates a valley of constant width (w) that is drained by a trunk channel (dark line) with equally spaced (L) confluences with tributaries. The drainage area of nodes between confluences is fixed (Δx×w; see Table 1 for values of model parameters). The drainage area of a tributary is the local area that is added at each confluence (an example is represented here by a gray rectangle). Ld and Lc mark the distance from the left edge of the model domain to the location of a stable wind-gap position and to the center of the model domain, respectively. Confluences marked A–D are referred to in Fig. 7a. (b) An example of simulated topographic profiles along the trunk channel: (1) a topographic profile of the simulation's initial condition; (2) simulated steady-state topography that develops from the initial condition in profile no. 1 through a fixed confluence simulation. Note that the wind gap attains a stable position away from the center of the model domain (i.e., Ld<Lc). Also note that this steady position occurs adjacent to a trunk–tributary confluence on the shrinking side of the wind gap; (3) simulated steady-state topography with avulsions (light gray circles mark the mean location of trunk–tributary confluences, which is the same as that of the fixed confluence). The wind gap's stable position is at Lc. (c) Simulated wind-gap location vs. time for the simulations in panel (b). Note that the plot shows the model duration until the wind gap in the fixed confluence simulation attained a stable position (case 2 in panel b). (d) A χ–z plot (Perron and Royden, 2013) for case 2 in panel (b). Note that the relief from each channel head to the wind gap is also marked (see legend). The channel head is defined based on where the topographic profile shifts from concave to convex. The channel head to the right of the divide (a black filled circle in the χ–z plot) is at the adjacent tributary confluence. Model parameters are given in Table 1.
Fixed confluence simulations with synthetic topography show that trunk–tributary confluences affect the velocity of wind-gap migration. Analysis of the wind-gap location through time (Fig. 5c) shows that the velocity of wind-gap migration decreases as it approaches a trunk–tributary confluence at the shrinking side and increases as the wind gap migrates across a confluence. At a larger scale, the migration velocity decreases as the wind gap migrates further from its initial location and closer to the center of the model domain (Fig. 5a–d). Importantly, we observe that in cases in which the wind gaps do not reach the center of the model domain, they attain a stable position close to a confluence with a tributary that drains to the side of the shrinking basin.
The same simulations further show that the tributary drainage areas influence the location where the wind gap attains a stable position, as well as the mean wind-gap migration velocity (Fig. 7a, b). Figure 7a shows that as the relative drainage area of tributaries increases, the stable wind-gap position is farther away from the center of the model domain (i.e., closer to the left side of the model; Fig. 5). The figure also shows that this position is generally close to a confluence at the shrinking side of the wind gap (i.e., 7a). Importantly, a co-linear χ–z relation is observed for the expanding and shrinking basins even when the stable wind-gap position is not at the center of the model domain (Fig. 5a–d).
Figure 7a shows that, everything else being equal, the value of the area exponent m influences the position of stable wind gaps. More specifically, when changing the value of the exponent m from 0.55 to 0.45, wind gaps attain a stable position closer to the center of the model domain. The distance between stable wind-gap positions with m=0.55 and m=0.45 typically corresponds to the distance between successive confluences.
Fixed confluence simulations based on the Parlung–Siang–Lohit setting (Fig. 6), which were conducted to explore the effect of trunk–tributary confluences with a natural topology, show that the wind gap along the beheaded Parlung valley (with m=0.5, as in the simulations of Wang et al., 2017, and Yang et al., 2018, in the same area) migrated until attaining a stable position relatively close to the capture point and far from the observed location of the current wind gap (i.e., points d and e in Fig. 6, respectively). This stable wind-gap position is close to a trunk–tributary confluence on the shrinking side (tributary t1 and point 1 in Fig. 6b–c, about 150 km downstream of the observed wind-gap location). In contrast, in a similar experiment with a lower m value (m=0.45), the wind gap continued to migrate across this confluence and stopped approximately 30 km from the current natural wind-gap location.
Avulsion simulations show that avulsions influence the wind-gap migration velocity as well as its stable position. To compare wind-gap migration velocity between paired simulations with avulsions, without avulsions, and with a constant drainage area for each node, the mean wind-gap velocity in all models is computed up to the location where the wind gap reaches a stable position in the fixed confluence simulations. Figures 5c and 7b show that in synthetic settings, avulsions increase the mean velocity of wind-gap migration and that this velocity scales with the frequency of avulsions (Fig. 7c). For the Parlung–Siang–Lohit setting, we ran a simulation without avulsions (with m=0.5) until the wind gap attained the aforementioned stable position at point 1 (Fig. 6b) and then forced an avulsion by shifting the drainage area of this tributary to the expanding side of the wind gap. This caused the wind gap to migrate further east until it attained a stable position next to another large trunk–tributary confluence on the shrinking side (point 2, just west of the confluence with tributary t2 in Fig. 6b–c). Simulations with randomly occurring avulsions caused migration across these large trunk–tributary confluences and produced a final stable wind-gap location at point 3 (Fig. 6b–c), approximately 30 km from the current natural wind-gap location.
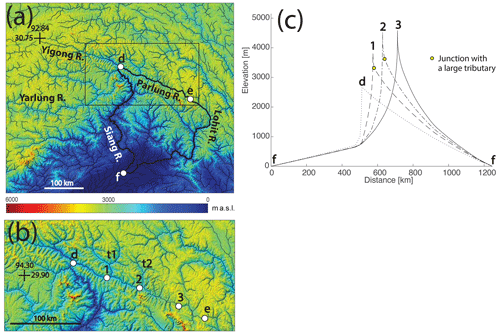
Figure 6Simulated wind-gap migration along the Parlung valley. (a) Regional map based on the 15 arcsec GMTED2010 DEM (approximately 500 m resolution; Danielson and Gesch, 2011) showing the Yigong, Parlung, Lohit, Siang, and Yarlung rivers (location is shown as a box in Fig. 2a). The approximate capture location of the Yarlung–Yigong by the Siang is marked by point d. Point e marks the current location of the wind gap between the northwest-flowing Parlung and southeast-flowing Lohit rivers. Point f marks the base level at the confluence of the Lohit and Siang rivers. Thin dark lines mark river systems with drainage area larger than 108 m2, and the bold dark lines mark the river system that is simulated in panel (c). A box marks the area shown in panel (b). (b) Map of the Parlung river basin. The Parlung reversed its flow direction following the capture, likely through wind-gap migration from the capture point (point d) to the current location of the wind gap (point e). Points 1, 2, and 3 mark simulated stable wind-gap locations in conjunction with panel (c). The labels t1 and t2 mark large tributaries of the Parlung river. (c) Profiles of simulated initial and steady-state topography. Curve d – a profile at the time of capture of the Yigong–Parlung by the Siang (the initial topography of the simulations); curve 1 – a profile of a simulated stable wind-gap position developed in a fixed confluence simulation. Note that this stable location is just west of a confluence with a large tributary (t1). Curve 2 – a stable wind-gap position that developed by simulating an avulsion of tributary t1 to the expanding side of the wind gap. This new stable wind-gap position is just west of a confluence with a large tributary t2. Curve 3 – a stable wind-gap position that is attained through an avulsion simulation in which tributaries with drainage area larger than 107 m2 are allowed to avulse. Model parameters are given in Table 1.
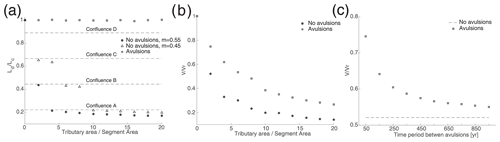
Figure 7e influence of tributary area and avulsion frequency on wind-gap migration. Note that every marker in panels (a–c) represents the results of a single simulation. (a) The influence of tributary area and the area exponent m on the position of the stable wind gap relative to the center of the model domain (i.e., , Fig. 5). When the stable position is closer to the center, the value is closer to unity. Tributary drainage area (At) is normalized by the area of the valley segment between tributaries. Note that stable wind-gap positions are typically next to a confluence on the shrinking valley side, whose location is marked by dashed horizontal lines. (b) The influence of tributary area (normalized as before) on the mean velocity of wind-gap migration. This velocity (V) is computed based on the location and time of where and when the wind gap reaches a stable position in the fixed confluence simulations and is normalized by the mean velocity (Vr) of the reference simulation with the same total drainage area. (c) The influence of time interval between avulsions on the mean velocity of wind-gap migration (computed with the same procedure described before) for the case in which the area of tributaries is twice the segment area. The dashed line marks the velocity of an equivalent fixed confluence simulation. Model parameters are given in Table 1.
Fixed confluence simulations indicate that a wind gap can attain a stable position that deviates from intuitive expectations. In synthetic simulations, wind gaps stabilize away from the center of the model domain, despite the asymmetry in drainage area and slope associated with this position (Fig. 5b). Similarly, in the natural topology simulation based on the Parlung–Siang–Lohit system, the simulated wind gaps stabilize away from the present-day location of the natural wind gap (Fig. 6). In these cases, the wind gap stabilizes close to a confluence draining to the shrinking side of the valley (Figs. 5b, 7a). From a dynamic perspective, this finding suggests that the erosion rate at this proximal confluence is approximately constant and largely independent of the wind-gap position. This large tributary confluence close to the wind gap counteracts the aforementioned area feedback by balancing the erosion rates across the wind gap, slowing the wind gap's migration rate, and in some cases stopping the migration process entirely and stabilizing the wind gap (Fig. 5c–d).
From a static perspective, stable wind-gap positions are possible as long as they conform to a restriction posed by a combination of channel and hillslope relief. In the context of Eq. (1), and assuming that D and K are spatially uniform and that the spatial transition between a hillslope and a channel is discrete (e.g., Goren et al., 2014a), a wind gap is stable as long as the steady-state elevation difference between the two channel heads that bound the wind gap is compensated for by the hillslope relief:
The distances between equi-elevation points along channels 1 and 2 (i.e., the location of the lower bounds of integration on the left-hand side – LHS) and the heads of these channels are described by Lch1 and Lch2, respectively, and the length of the corresponding hillslope is described by Lh1 and Lh2. x′ represents the position along-channel and recognizes that drainage area (A) varies with this position. The LHS describes the absolute difference in elevation gain along the channels on both sides of the wind gap (subscript 1 and 2) when the morphology of the channels is at topographic steady state and the elevation gain along each channel is integrated from the same elevation. The right-hand side (RHS) describes the maxima of the two hillslope reliefs between the wind gap and the channel heads at each of its sides. Note that this condition holds for drainage divides in general (i.e., not only for wind gaps) and that when the hillslope relief is negligible (i.e., the RHS ≃0), this condition for a stable divide simplifies to an equality in elevation gain along the two channels (Shelef and Hilley, 2014; Shelef, 2018).
An example of an asymmetric and stable wind gap is depicted as case 2 in Fig. 5b. The stability of this setting is verified by the co-linear χ–z relations of the channels that bound the wind gap, where (e.g., Perron and Royden, 2013) (Fig. 5d). The co-linearity of the χ–z profiles indicates that the two channels are at steady state and erode at the same rate. Here, the confluence adjacent to the wind gap forms a channel head that is approximately at the same elevation as that on the aggressor's side of the wind gap (channel heads were defined by the transition from a concave to convex profile). The hillslope relief is larger than the minute difference in elevation between the channel heads, and thus a stable wind-gap position is attained (see filled circles and bars in the χ–z plot). Generally, as long as Eq. (2) is satisfied, the same arrangement of confluences along a valley can produce different stable wind-gap positions such as those shown in Figs. 5b and 6b–c.
Fixed confluence simulations with synthetic topography (Figs. 5, 7a) show that the distance between stable wind-gap positions and the center of the model domain increases with the relative drainage area of tributaries (Figs. 5b, 7a). From the static perspective of Eq. (2), an increase in tributaries' drainage area reduces the elevation gain along the channels and is thus more likely to facilitate a situation in which the hillslope relief is larger than the difference in elevation gain between the channel heads (Eq. 2). From a dynamic perspective, and given that the simulation's initial condition is associated with high asymmetry in topographic gradient across the wind gap (i.e., case 1 in Fig. 5b), only confluences with relatively large tributaries are capable of balancing the shallower gradient along the shrinking side and ensuring equal erosion rates across the wind gap (i.e., Eq. 1), stopping its migration closer to the left model boundary. A similar pattern is observed in the simulations of the Parlung–Siang–Lohit capture, wherein the wind gap stabilizes just before it approaches confluences with large tributaries (points 1 and 2 in Fig. 6b). Tributaries of a relatively small drainage area are able to stop the migration process only when the wind gap is closer to the center of the model domain and the overall slope asymmetry across the wind gap is relatively small (Fig. 7a). Similarly, a lower value of the exponent m enables wind-gap migration closer to the center of the model domain because it decreases the dependency of (a) fluvial erosion (i.e., Eq. 1) and (b) the elevation gain along steady-state channels (i.e., Eq. 2) on the distribution of drainage area along the valley (Shelef and Hilley, 2014).
The velocity of wind-gap migration in fixed confluence simulations changes as confluences are being traversed, and the mean velocity decreases as the area of side tributaries increases (Figs. 5c, 7b). The decrease in wind-gap velocity as it approaches a confluence reflects an increased balance in erosion rate across the wind gap that stems from a relative increase in topographic gradient on the shrinking side of the wind gap between the migrating wind gap and the erosionally stable confluence. Once the wind gap traverses the confluence, the tributary's discharge shifts to the expanding basin. This amplifies the erosion rate at the expanding side of the wind gap compared to the shrinking side and increases the wind gap's velocity. The duration of decreased velocity can be prolonged (or even infinite if the wind gap attains a stable position) compared to the duration of increased velocity (Fig. 5c). Therefore, confluences generally decrease the mean migration velocity compared to reference simulations. This effect increases with the drainage area of side tributaries (Fig. 7b), which increases the erosional stability of the confluence. Overall, our results suggest that in regions where wind gaps are common, confluences with large side tributaries may be critical in setting the rate of landscape adjustment to changes.
The velocity and distance of wind-gap migration are influenced by the occurrence and frequency of avulsions. Stable wind-gap positions can be perturbed by avulsions that route discharge from the shrinking to the expanding basin, causing an increase in erosion rate of the expanding basin, a decrease in erosion rate of the shrinking basin, and further wind-gap migration (e.g., the migration of the wind gap from point 1 to 2 in Fig. 6b–c). The influence of avulsions on migration velocity is reflected in both the mean (Fig. 7c) and instantaneous (Fig. 5c) migration velocity: with everything else being equal, a higher avulsion frequency increases the velocity of wind-gap migration. Note that avulsions can effectively reduce or prevent wind-gap slowdown before large tributaries, reducing the temporal variability in migration velocity. The expression of avulsions in the time–location space in Fig. 5c therefore depends on the frequency of avulsion and the spatial resolution of the simulation. Overall, in settings in which wind-gap migration is common (e.g., Fig. 2), it is possible that the rate and pattern of landscape adjustment to changes in tectonic and climate depend not only on the drainage area of side tributaries, but also on the temporal frequency of avulsions in the alluvial fans at the mouth of the tributaries (e.g., Fig. 4).
Avulsions in natural alluvial fans typically occur on timescales of a few years to thousands of years (Field, 2001; Pelletier et al., 2005; Fuller, 2012). This is a relatively short timescale for large shifts in discharge across the divide given that ongoing shifts that occur through classic basin captures, as described by Bishop (1995), Clark et al. (2004), Prince et al. (2011), and Willett et al. (2014), are rarely observed (e.g., Fan et al., 2018; Stokes et al., 2018). Overall, basin captures that are triggered by avulsion are likely frequent, and focusing on such settings may provide ample field examples of recent fluvial response to basin capture (e.g., Fig. 4). Further, landscape evolution models tend to preserve antecedent patterns and show a relatively minor tendency for reorganization (Kwang and Parker, 2019). It could be that incorporating avulsion dynamics even in detachment-limited settings could reveal an important component that drives models toward more realistic outcomes. Given that the frequency of avulsions depends on the micro-topography of the system, sediment characteristics, and the magnitude, burstiness, and sequencing of floods (Field, 2001; Stock et al., 2008; de Haas et al., 2016; Leenman and Eaton, 2020), such modeling efforts may reveal new mechanisms through which climate, lithology, and tectonics influence the rate of landscape response.
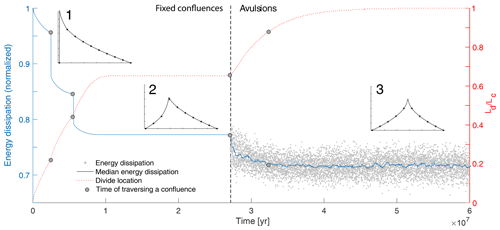
Figure 8The influence of avulsions on energy dissipation and wind-gap location. Model run time is shown on the x axis, energy dissipation (normalized by its maximal value) on the left y axis, and wind-gap location relative to the center of the model domain (i.e., , Fig. 5) on the right y axis. The plot shows the results of a fixed confluence simulation that produced a stable wind-gap position away from the center of the model domain at approximately 1×107 years. An avulsion simulation introduced at approximately 2.7 × 107 years perturbed this stable topography and triggered further divide migration to the center of the model domain. While avulsions can temporally increase the energy dissipation of the system, they lead to an abrupt decrease in energy dissipation as confluences (gray circles) are being traversed. Inset images 1–3 correspond to the topographic profiles in different stages in this experiment (similar to those in Fig. 5b) and show the initial topography (1), a stable asymmetric divide position attained with fixed confluence simulations (2), and a stable symmetric divide position attained with an avulsion simulation (3). Model parameters are given in Table 1. The calculation of energy dissipation, based on Sun et al. (1994a, b), is described in the Supplement.
Overall, our results demonstrate that although the same arrangement of trunk–tributary confluences along a valley can generate different stable wind-gap positions (Figs. 5, 6, 7), symmetric positions at the center of the model domain are more stable than others to perturbations caused by avulsions (Fig. 7). By analogy to optimal channel networks (OCNs) (e.g., Rinaldo et al., 1992; Sun et al., 1994a, b), stable wind-gap positions away from this favorable location represent a local energetic optimum that, once perturbed by avulsions, develops towards a global optimum in which the wind gap is close to the center of the model domain. This analogy is supported by tracking the energy dissipation over a fixed confluence simulation that produces a stable wind-gap position and then perturbing it by simulating avulsions (Fig. 8). From an OCN perspective, the perturbations introduced by avulsions enable the system to exit a local minimum by temporally increasing the energy dissipation of the system, which is analogous to an annealing procedure (Sun et al., 1994a; Colaiori et al., 1997) used in OCN simulations. Thus, avulsions may act as a natural annealing mechanism that shifts the landscape towards stable configurations that are energetically favorable.
Although our findings clearly demonstrate the influence of tributaries and their avulsions on wind-gap migration, they are based on a relatively simple set of assumptions and simulations as well as a limited number of field observations. For example, we use a detachment-limited model to simulate channel erosion, which was used before in similar settings (Yang et al., 2020) and is consistent with the incision into bedrock at sites such as the Parlung–Siang–Lohit capture and into cohesive sediments observed at the Negev field sites (e.g., Harel et al., 2019). However, given that alluvial fans are often associated with transport-limited conditions (at least periodically; Spelz et al., 2008) and that valleys are often filled with unconsolidated sediments, it is likely that a model that combines detachment- and transport-limited processes will more accurately describe such settings. Similarly, the hillslope processes in our simulations rely on a linear diffusion approach (Culling, 1963) and do not account for the potential influence of subsurface flow (e.g., seepage) and landsliding on the migrating wind gap (Brocard et al., 2011, 2012). The simulations further neglect variabilities in the base-level elevation, uplift rate, and lithology (Harel et al., 2019), and they do not account for flow bifurcations that can split a tributary's discharge into multiple confluences. We also did not attempt to explore the influence of vegetation (and by extension climate), which can have competing effects of stabilizing channel banks and reducing the frequency of avulsions (Tal and Paola, 2010) as well as obstructing flow and causing aggradation and avulsions (McCarthy et al., 1992; Jones and Schumm, 1999). We also note that processes such as valley damming by landslides or glaciers can cause overflow across wind gaps and perturb stable wind-gap positions. Finally, whereas our one-dimensional simulations likely capture the basic dynamics of wind-gap migration along valleys, they do not capture two-dimensional interactions such as drainage area exchange through divide migration along the ridgelines that bound the valley. Two-dimensional simulations might therefore reveal more detailed responses, which could depend on the 2D valley and confluence geometry.
In tectonically active and structurally deformed areas where elongated valleys are common, low-relief drainage divides, also called wind gaps, can migrate along such valleys and traverse confluences with side tributaries that drain into the valley. These confluences are stable with respect to wind-gap migration; namely, migration does not eradicate them and can thus influence the migration dynamics by (1) causing fluctuations in the velocity of wind-gap migration, with this velocity decreasing before the wind gap traverses a confluence and increasing right after it traverses the confluence; and (2) facilitating multiple configurations of stable wind-gap locations, aside from the perfectly symmetric configuration wherein the wind gap typically stabilizes close to a confluence in the shrinking valley. The location of these stable configurations is sensitive to the drainage area of side tributaries and the sensitivity of erosional processes to drainage area (i.e., the exponent m in Eq. 1).
Avulsions of tributaries can abruptly shift discharge across the wind gap and thus change the distribution of erosion across it. Such avulsions can perturb stable wind-gap positions and facilitate further wind-gap migration, whereby the velocity of wind-gap migration increases with the frequency of avulsions. From an energetic perspective, such avulsions may be analogous to a natural annealing mechanism that drives the channel system towards a global energetic optimum.
Overall, our results suggest that tributaries and their avulsions may play a critical role in determining the extent of river basins in tectonically active and/or structurally deformed areas where elongated valleys are common and thus the partitioning of discharge, erosion, and sediments between these basins. Further, the rate of landscape adjustment, even in bedrock-dominated mountainous regions, may be modulated by the frequency of such avulsions.
Related codes are available through the corresponding author's GitHub https://github.com/eshelef/WindgapMigration (eshelef, 2021). Other codes rely on TopoToolbox (https://topotoolbox.wordpress.com/download, Schwanghart and Scherler, 2014), which is freely available.
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-9-687-2021-supplement.
ES and LG conceptualized the project and designed the simulations. ES analyzed field examples, developed the code, ran the simulations and analyzed them, wrote the paper, and prepared the figures. LG contributed to simulation interpretation and code development as well as providing input on the paper text and figures.
The authors declare that there is no conflict of interest.
This research was supported by grant no. 2019656 from the United States–Israel Binational Science Foundation (BSF) and by grant no. 1946253 from the United States National Science Foundation (NSF-Geomorphology and Land-use Dynamics). We thank Onn Cruvi, Elhanan Harel, Tianyue Qu, Philip Prince, and Sean Gallen for valuable discussions. We also thank Helen Beeson and Fiona Clubb for insightful and constructive reviews that greatly improved this paper. TanDEM-X data were kindly provided by the German Aerospace Center (DLR) (project ID: DEM_GEOL1399).
This research has been supported by the National Science Foundation (grant no. 1946253) and the United States–Israel Binational Science Foundation (grant no. 2019656).
This paper was edited by Wolfgang Schwanghart and reviewed by Helen Beeson and Fiona Clubb.
Avni, Y., Bartov, Y., Garfunkel, Z., and Ginat, H.: Evolution of the Paran drainage basin and its relation to the Plio-Pleistocene history of the Arava Rift western margin, Israel, Israel J. Earth Sci., 49, 215–238, 2000. a
Beeson, H. W., McCoy, S. W., and Keen-Zebert, A.: Geometric disequilibrium of river basins produces long-lived transient landscapes, Earth Planet. Sc. Lett., 475, 34–43, 2017. a, b
Bishop, P.: Drainage rearrangement by river capture, beheading and diversion, Prog. Phys. Geogr., 19, 449–473, https://doi.org/10.1177/030913339501900402, 1995. a, b, c, d, e
Braun, J.: A review of numerical modeling studies of passive margin escarpments leading to a new analytical expression for the rate of escarpment migration velocity, Gondwana Res., 53, 209–224, https://doi.org/10.1016/j.gr.2017.04.012, 2017. a, b, c
Brocard, G., Teyssier, C., Dunlap, W. J., Authemayou, C., Simon-Labric, T., Cacao-Chiquín, E. N., Gutiérrez-Orrego, A., and Morán-Ical, S.: Reorganization of a deeply incised drainage: role of deformation, sedimentation and groundwater flow, Basin Res., 23, 631–651, https://doi.org/10.1111/j.1365-2117.2011.00510.x, 2011. a, b
Brocard, G., Willenbring, J., Suski, B., Audra, P., Authemayou, C., Cosenza-Muralles, B., Morán-Ical, S., Demory, F., Rochette, P., Vennemann, T., and Holliger, K.: Rate and processes of river network rearrangement during incipient faulting: The case of the Cahabón River, Guatemala, Am. J. Sci., 312, 449–507, 2012. a
Clark, M. K., Schoenbohm, L. M., Royden, L. H., Whipple, K. X., Burchfiel, B. C., Zhang, X., Tang, W., Wang, E., and Chen, L.: Surface uplift, tectonics, and erosion of eastern Tibet from large-scale drainage patterns, Tectonics, 23, TC1006, https://doi.org/10.1029/2002TC001402, 2004. a, b, c
Colaiori, F., Flammini, A., Maritan, A., and Banavar, J. R.: Analytical and numerical study of optimal channel networks, Phys. Rev. E, 55, 1298, 1298–1310, 1997. a
Culling, W.: Soil creep and the development of hillside slopes, J. Geol., 71, 127–161, 1963. a, b
Danielson, J. J. and Gesch, D. B.: Global multi-resolution terrain elevation data 2010 (GMTED2010), US Department of the Interior, US Geological Survey, Open-File Report 2011–1073, 2011. a, b, c, d, e
Davis, W. M.: A river-pirate, Science, 13, 108–109, 1889. a
de Haas, T., van den Berg, W., Braat, L., and Kleinhans, M. G.: Autogenic avulsion, channelization and backfilling dynamics of debris-flow fans, Sedimentology, 63, 1596–1619, 2016. a
eshelef: WindgapMigration, GitHub, available at: https://github.com/eshelef/WindgapMigration, last access: 25 June 2021. a
Fan, N., Chu, Z., Jiang, L., Hassan, M. A., Lamb, M. P., and Liu, X.: Abrupt drainage basin reorganization following a Pleistocene river capture, Nat. Commun., 9, 3756, https://doi.org/10.1038/s41467-018-06238-6, 2018. a, b
Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., Kobrick, M., Paller, M., Rodriguez, E., Roth, L., Seal, D., Shaffer, S., Shimada, J., Umland, J., Werner, M., Oskin, M., Burbank, D., and Alsdorf, D.: The shuttle radar topography mission, Rev. Geophys., 45, RG2004, https://doi.org/10.1029/2005RG000183, 2007. a, b
Field, J.: Channel avulsion on alluvial fans in southern Arizona, Geomorphology, 37, 93–104, 2001. a, b
Forte, A. M. and Whipple, K. X.: Criteria and tools for determining drainage divide stability, Earth Planet. Sc. Lett., 493, 102–117, https://doi.org/10.1016/j.epsl.2018.04.026, 2018. a
Forte, A. M., Whipple, K. X., and Cowgill, E.: Drainage network reveals patterns and history of active deformation in the eastern Greater Caucasus, Geosphere, 11, 1343–1364, https://doi.org/10.1130/GES01121.1, 2015. a
Freeman, T. G.: Calculating catchment area with divergent flow based on a regular grid, Comput. Geosci., 17, 413–422, 1991. a
Fuller, J. E.: Evaluation of avulsion potential on active alluvial fans in central and western Arizona, Arizona Geological Survey Contributed Report CR-12-D, Arizona Geological Survey, Tucson, Arizona, p. 83, 2012. a
Gilbert, G. K.: Report on the Geology of the Henry Mountains, US Government Printing Office, Washington, DC, 1877. a
Ginat, H., Zilberman, E., and Avni, Y.: Tectonic and paleogeographic significance of the Edom River, a Pliocene stream that crossed the Dead Sea Rift valley, Israel J. Earth Sci., 49, 159–178, 2000. a
Goren, L., Fox, M., and Willett, S. D.: Tectonics from fluvial topography using formal linear inversion: Theory and applications to the Inyo Mountains, California, J. Geophys. Res.-Earth, 119, 1651–1681, https://doi.org/10.1002/2014JF003079, 2014a. a
Goren, L., Willett, S. D., Herman, F., and Braun, J.: Coupled numerical–analytical approach to landscape evolution modeling, Earth Surf. Proc. Land., 39, 522–545, 2014b. a, b
Govin, G., Najman, Y., Dupont-Nivet, G., Millar, I., Van Der Beek, P., Huyghe, P., O'sullivan, P., Mark, C., and Vögeli, N.: The tectonics and paleo-drainage of the easternmost Himalaya (Arunachal Pradesh, India) recorded in the Siwalik rocks of the foreland basin, Am. J. Sci., 318, 764–798, 2018. a, b, c
Hack, J.: Studies of longitudinal profiles in Virginia and Maryland, no. 294-B in US Geol, Survey Prof. Papers, US Government Printing Office, Washington, DC, 690, 10, 1957. a
Harel, E., Goren, L., Shelef, E., and Ginat, H.: Drainage reversal toward cliffs induced by lateral lithologic differences, Geology, 47, 928–932, 2019. a, b, c, d, e, f, g, h
Haworth, R. and Ollier, C.: Continental rifting and drainage reversal: the Clarence River of eastern Australia, Earth Surf. Proc. Land., 17, 387–397, 1992. a
Howard, A. D.: A detachment-limited model of drainage basin evolution, Water Resour. Res., 30, 2261–2285, 1994. a, b, c
Howard, A. D. and Kerby, G.: Channel changes in badlands, Geol. Soc. Am. Bull., 94, 739–752, 1983. a
Johnson, D. W.: River capture in the Tallulah district, Georgia, Science, 25, 428–432, 1907. a
Jones, L. and Schumm, S.: Causes of avulsion: an overview, Int. As. Sed., 28, 171–178, 1999. a
Krieger, G., Moreira, A., Fiedler, H., Hajnsek, I., Werner, M., Younis, M., and Zink, M.: TanDEM-X: A satellite formation for high-resolution SAR interferometry, IEEE T. Geosci. Remote, 45, 3317–3341, 2007. a, b
Kwang, J. and Parker, G.: Extreme memory of initial conditions in numerical landscape evolution models, Geophys. Res. Lett., 46, 6563–6573, 2019. a
Lang, K. A. and Huntington, K. W.: Antecedence of the Yarlung–Siang–Brahmaputra River, eastern Himalaya, Earth Planet. Sc. Lett., 397, 145–158, 2014. a, b
Leenman, A. and Eaton, B.: Mechanisms for avulsion on alluvial fans: insights from high-frequency topographic data, Earth Surf. Proc. Land., 46, 1111–1127, 2020. a
Liu, L.: Rejuvenation of Appalachian topography caused by subsidence-induced differential erosion, Nat. Geosci., 7, 518–523, https://doi.org/10.1038/ngeo2187, 2014. a
McCarthy, T., Ellery, W., and Stanistreet, I.: Avulsion mechanisms on the Okavango fan, Botswana: the control of a fluvial system by vegetation, Sedimentology, 39, 779–795, 1992. a
Mudd, S. M. and Furbish, D. J.: Lateral migration of hillcrests in response to channel incision in soil-mantled landscapes, J. Geophys. Res.-Earth, 110, F04026, https://doi.org/10.1029/2005JF000313, 2005. a
Nugent, C.: The Zambezi River: tectonism, climatic change and drainage evolution, Palaeogeogr. Palaeocl., 78, 55–69, https://doi.org/10.1016/0031-0182(90)90204-K, 1990. a
Ollier, C. D.: Tectonics and landscape evolution in southeast Australia, Geomorphology, 12, 37–44, https://doi.org/10.1016/0169-555X(94)00075-3, 1995. a
Pelletier, J. D.: Persistent drainage migration in a numerical landscape evolution model, Geophys. Res. Lett., 31, L20501, https://doi.org/10.1029/2004GL020802, 2004. a
Pelletier, J. D., Mayer, L., Pearthree, P. A., House, P. K., Demsey, K. A., Klawon, J. E., and Vincent, K. R.: An integrated approach to flood hazard assessment on alluvial fans using numerical modeling, field mapping, and remote sensing, Geol. Soc. Am. Bull., 117, 1167–1180, 2005. a
Perron, J. T. and Royden, L.: An integral approach to bedrock river profile analysis, Earth Surf. Proc. Land., 38, 570–576, https://doi.org/10.1002/esp.3302, 2013. a, b
Perron, J. T., Dietrich, W. E., and Kirchner, J. W.: Controls on the spacing of first-order valleys, J. Geophys. Res.-Earth, 113, F04016, https://doi.org/10.1029/2007JF000977, 2008. a
Perron, J. T., Kirchner, J. W., and Dietrich, W. E.: Formation of evenly spaced ridges and valleys, Nature, 460, 502–505, 2009. a, b
Prince, P. S., Spotila, J. A., and Henika, W. S.: New physical evidence of the role of stream capture in active retreat of the Blue Ridge escarpment, southern Appalachians, Geomorphology, 123, 305–319, https://doi.org/10.1016/j.geomorph.2010.07.023, 2010. a, b
Prince, P. S., Spotila, J. A., and Henika, W. S.: Stream capture as driver of transient landscape evolution in a tectonically quiescent setting, Geology, 39, 823–826, https://doi.org/10.1130/G32008.1, 2011. a, b
Rinaldo, A., Rodriguez-Iturbe, I., Rigon, R., Bras, R. L., Ijjasz-Vasquez, E., and Marani, A.: Minimum energy and fractal structures of drainage networks, Water Resour. Res., 28, 2183–2195, 1992. a
Schmidt, J. L., Zeitler, P. K., Pazzaglia, F. J., Tremblay, M. M., Shuster, D. L., and Fox, M.: Knickpoint evolution on the Yarlung river: Evidence for late Cenozoic uplift of the southeastern Tibetan plateau margin, Earth Planet. Sc. Lett., 430, 448–457, https://doi.org/10.1016/j.epsl.2015.08.041, 2015. a, b, c
Schwanghart, W. and Scherler, D.: Short Communication: TopoToolbox 2 – MATLAB-based software for topographic analysis and modeling in Earth surface sciences, Earth Surf. Dynam., 2, 1–7, https://doi.org/10.5194/esurf-2-1-2014, 2014 (data available at: https://topotoolbox.wordpress.com/download, last access: 30 June 2021). a
Seidl, M. and Dietrich, W.: The problem of channel erosion into bedrock, Functional Geomorphology, 23, 101–124, 1992. a
Shelef, E.: Channel Profile and Plan-View Controls on the Aspect Ratio of River Basins, Geophys. Res. Lett., 45, 11–712, 2018. a
Shelef, E. and Hilley, G. E.: Symmetry, randomness, and process in the structure of branched channel networks, Geophys. Res. Lett., 41, 3485–3493, https://doi.org/10.1002/2014GL059816, 2014. a, b, c
Shephard, G. E., Muller, R. D., Liu, L., and Gurnis, M.: Miocene drainage reversal of the Amazon River driven by plate-mantle interaction, Nat. Geosci., 3, 870–875, https://doi.org/10.1038/ngeo1017, 2010. a
Spelz, R. M., Fletcher, J. M., Owen, L. A., and Caffee, M. W.: Quaternary alluvial-fan development, climate and morphologic dating of fault scarps in Laguna Salada, Baja California, Mexico, Geomorphology, 102, 578–594, 2008. a
Stock, J. D., Schmidt, K. M., and Miller, D. M.: Controls on alluvial fan long-profilesAlluvial fan long-profiles, GSA Bulletin, 120, 619–640, 2008. a
Stokes, M. F., Goldberg, S. L., and Perron, J. T.: Ongoing river capture in the Amazon, Geophys. Res. Let., 45, 5545–5552, https://doi.org/10.1029/2018GL078129, 2018. a
Sun, T., Meakin, P., and Jøssang, T.: Minimum energy dissipation model for river basin geometry, Phys. Rev. E, 49, 4865–4872, 1994a. a, b, c
Sun, T., Meakin, P., and Jøssang, T.: The topography of optimal drainage basins, Water Resour. Res., 30, 2599–2610, 1994b. a, b
Tal, M. and Paola, C.: Effects of vegetation on channel morphodynamics: results and insights from laboratory experiments, Earth Surf. Proc. Land., 35, 1014–1028, 2010. a
Tucker, G. E. and Hancock, G. R.: Modelling landscape evolution, Earth Surf. Proc. Land., 35, 28–50, 2010. a
Wang, Y., Zhang, H., Zheng, D., von Dassow, W., Zhang, Z., Yu, J., and Pang, J.: How a stationary knickpoint is sustained: New insights into the formation of the deep Yarlung Tsangpo Gorge, Geomorphology, 285, 28–43, 2017. a, b
Whipple, K. X. and Tucker, G. E.: Dynamics of the stream-power river incision model: Implications for height limits of mountain ranges, landscape response timescales, and research needs, J. Geophys. Res.-Sol. Ea., 104, 17661–17674, 1999. a
Whipple, K. X., Forte, A. M., DiBiase, R. A., Gasparini, N. M., and Ouimet, W. B.: Timescales of landscape response to divide migration and drainage capture: Implications for the role of divide mobility in landscape evolution, J. Geophys. Res.-Earth, 122, 248–273, https://doi.org/10.1002/2016JF003973, 2017. a, b, c, d, e, f
Willett, S. D., McCoy, S. W., Perron, J. T., Goren, L., and Chen, C.-Y.: Dynamic Reorganization of River Basins, Science, 343, 1248765, https://doi.org/10.1126/science.1248765, 2014. a, b, c, d, e, f, g
Woodruff, J. C. M.: Stream Piracy near the Balcones Fault Zone, Central Texas, J. Geol., 85, 483–490, https://doi.org/10.1086/628322, 1977. a
Yang, R., Willett, S. D., and Goren, L.: In situ low-relief landscape formation as a result of river network disruption, Nature, 520, 526–529, 2015. a
Yang, R., Herman, F., Fellin, M. G., and Maden, C.: Exhumation and topographic evolution of the Namche Barwa Syntaxis, eastern Himalaya, Tectonophysics, 722, 43–52, 2018. a, b
Yang, R., Suhail, H. A., Gourbet, L., Willett, S. D., Fellin, M. G., Lin, X., Gong, J., Wei, X., Maden, C., Jiao, R., and Chen, H.: Early Pleistocene drainage pattern changes in Eastern Tibet: Constraints from provenance analysis, thermochronometry, and numerical modeling, Earth Planet. Sci. Lett., 531, 115955, https://doi.org/10.1016/j.epsl.2019.115955, 2020. a, b
Yanites, B. J., Ehlers, T. A., Becker, J. K., Schnellmann, M., and Heuberger, S.: High magnitude and rapid incision from river capture: Rhine River, Switzerland, J. Geophys. Res.-Earth, 118, 1060–1084, https://doi.org/10.1002/jgrf.20056, 2013. a
Zelilidis, A.: Drainage evolution in a rifted basin, Corinth graben, Greece, Geomorphology, 35, 69–85, https://doi.org/10.1016/S0169-555X(00)00023-4, 2000. a
Zhang, P., Najman, Y., Mei, L., Millar, I., Sobel, E.R., Carter, A., Barfod, D., Dhuime, B., Garzanti, E., Govin, G., and Vezzoli, G.: Palaeodrainage evolution of the large rivers of East Asia, and Himalayan-Tibet tectonics, Earth-Sci. Rev., 192, 601–630, 2019. a, b, c





