Controls on the grain size distribution of landslides in Taiwan: the influence of drop height, scar depth and bedrock strength

The size of grains delivered to rivers by hillslope processes is thought to be a key factor controlling sediment transport, long-term erosion and the information recorded in sedimentary archives. Recently, models have been developed to estimate the grain size distribution produced in soil, but these models may not apply to active orogens where high erosion rates on hillslopes are driven by landsliding. To date, relatively few studies have focused on landslide grain size distributions. Here, we present grain size distributions (GSDs) obtained by grid-by-number sampling on 17 recent landslide deposits in Taiwan, and we compare these GSDs to the geometrical and physical properties of the landslides, such as their width, area, rock type, drop height and estimated scar depth. All slides occurred in slightly metamorphosed sedimentary units, except two, which occurred in younger unmetamorphosed shales, with a rock strength that is expected to be 3–10 times weaker than their metamorphosed counterparts. For 11 landslides, we did not observe substantial spatial variations in the GSD over the deposit. However, four landslides displayed a strong grain size segregation on their deposit, with the overall GSD of the downslope toe sectors being 3–10 times coarser than apex sectors. In three cases, we could also measure the GSD inside incised sectors of the landslides deposits, which presented percentiles that were 3–10 times finer than the surface of the deposit. Both observations could be due to either kinetic sieving or deposit reworking after the landslide failure, but we cannot explain why only some deposits had strong segregation. Averaging this spatial variability, we found the median grain size of the deposits to be strongly negatively correlated with drop height, scar width and depth. However, previous work suggests that regolith particles and bedrock blocks should coarsen with increasing depth, which is the inverse of our observations. Accounting for a model of regolith coarsening with depth, we found that the ratio of the estimated original bedrock block size to the deposit median grain size (D₅₀) of the deposit was proportional to the potential energy of the landslide normalized to its bedrock strength. Thus, the studied landslides agree well with a published, simple fragmentation model, even if that model was calibrated on rock avalanches with larger volume and stronger bedrock than those featured in our dataset. Therefore, this scaling may serve for future modeling of grain size transfer from hillslopes to rivers, with the aim to better understanding landslide sediment evacuation and coupling to river erosional dynamics.

1 Introduction

Grain size is an essential parameter for understanding sediment transport and associated processes in river evolution or in hazards related to sediment pulses. For geomorphologists, it is increasingly considered to be an important parameter for the long-term incision of bedrock streams (Sklar and Dietrich, 2001; Cook et al., 2013, 2014; Turowski, 2018), and it is an essential part of the sedimentological signal which is ultimately archived in stratigraphy (e.g., Armitage et al., 2011).

Nevertheless, there are many processes that control the grain size distribution (GSD) delivered to rivers, and they are poorly understood (Allen et al., 2015). In recent studies, models have been proposed that describe how weathering in the critical zone reduces the original size distribution of bedrock before the grains reach the surface (Marshall and Sklar, 2012; Riebe et al., 2015; Sklar et al., 2017). However, in active orogens with high erosion rates (>0.5 mm yr⁻¹), landslides are likely the main providers of sediments to rivers (Hovius et al., 1997; Struck et al., 2015; Marc et al., 2019), and a large fraction of sediment may reach the river only partially weathered. Indeed, the limits of models predicting soil GSD and the need to account for GSD derived from fractured bedrock was recently shown (Neely and DiBiase, 2020), although the role of mass wasting in delivering and further fragmenting bedrock particles was not explored. In those settings, understanding and modeling the controls on the landslide GSD should be an urgent goal, although, to date, it has only been addressed by a few studies. Indeed, in contrast to river sediments, for which many studies exist (e.g., Ibbeken, 1983; Whittaker et al., 2011; Chung and Chang, 2013; Guerit et al., 2014, 2018), landslide GSDs have rarely been measured; this is, in part, because the latter is considerably more difficult, time consuming and potentially dangerous than the former.

A few studies have measured and thoroughly discussed the GSDs of some large historical landslide or rock avalanches, often putting forward the various mechanisms of rock fragmentation and grain segregation to explain their data (see Crosta et al., 2007, and references therein). Although interesting for their discussion in terms of rock mechanics, such case studies do not allow us to understand the regional variability in landslide GSDs nor to derive physical scalings that could pave the way to model the GSDs of material delivered to river networks by landslides. To our knowledge, only seven studies have reported detailed GSD measurements from multiple landslide deposits. A pioneering study reported the GSDs from 42 landslide dams across the Apennines, with a discussion on the methods used to derive the GSD but none on the controls of the GSD variability (Casagli et al., 2003). Locat et al. (2006) presented GSDs from nine large (>100 Mm³) rock avalanches from Canada and the Alps, including various rock types, and analyzed these in terms of potential energy and fragmentation theories (Locat et al., 2006). They found that the ratio of bedrock initial median block size, D_i (estimated from fracture spacing), to the deposit median grain size, D₅₀, was proportional to the change in potential energy per unit of volume, ρgH (where H  is the drop height of the center of mass, ρ is the rock density and g is the gravitational acceleration), normalized by the point load strength of the bedrock, σ_c, measured with a point load test performed on rock sample from the sites. Specifically their nine rock avalanches were best fit by a relation that could be recast as follows:

$$\begin{array}{}\text{(1)}& D_{\mathrm{50}}={\displaystyle \frac{D_i}{k_{\mathrm{1}}}}{\displaystyle \frac{\mathit{\rho }gH}{{\mathit{\sigma }}_c-k_{\mathrm{2}}}},\end{array}$$

where k₂=0.5 is an empirical threshold for fragmentation, and k₁=83.3 is an empirical coefficient related to the conversion of potential energy into fragmentation energy and the effective breaking of particles. Thus, if the scaling is general for landslides, the deposit D₅₀ should increase with D_i and σ_c but decrease with H.

Subsequent studies often focused on the potential importance of landslide GSDs for understanding sediment transport dynamics and the expected GSDs at the outlet of basins, and they reported GSDs in Nepal, Japan, California and southern Italy (Attal and Lavé, 2006; Nishiguchi et al., 2012; Attal et al., 2015; Roda‐Boluda et al., 2018). Several of them qualitatively underlined the factors influencing GSDs, such as the different lithological units (Attal and Lavé, 2006; Roda‐Boluda et al., 2018) or the local hillslope gradient, as a control on the time spent in the weathering engine (Attal et al., 2015). Recently, a study presented the GSDs of seven medium-sized rockfalls in Spain, showing that the bedrock block size and the deposit GSD could be related through a fractal fragmentation model (Ruiz-Carulla and Corominas, 2020). They found that potential energy was a main control on the fragmentation, but no clear correlation with rock strength measures emerged. They did not compare their model and results to the simple scaling proposed by Locat et al. (2006). Thus, none of these more recent works have attempted to frame the landslide GSD in terms of the competition between fragmentation energy and source rock strength, and the scaling for large rock avalanches has not been reproduced on smaller, more frequent landslides.

Based on these studies, we formulate two hypotheses: first, we suggest that Eq. (1) could be generalized to landslides of intermediate size and depth and, thus, that the landslide deposit D₅₀ should increase with rock strength, σ_c, and the source material's median size, D_i, but decrease with drop height, H; second, we hypothesize that materials mobilized by shallow landslides coarsen with the landslide scar thickness, T (i.e., D_i increases with T), due to a reduction with depth of the fracture density of the bedrock (Clarke and Burbank, 2011) and/or of the degree of physical and chemical weathering experienced by particles (Cohen et al., 2010; Anderson et al., 2013; Sklar et al., 2017). Testing these hypotheses seems essential to pave the way towards geomorphic models accounting for the GSDs of sediments transferred from hillslopes to rivers and from rivers to sedimentary basins (Allen et al., 2015; Sklar et al., 2017).

With these goals, and given the sparse amount of data on landslide GSDs, we performed detailed measurements on 17 recent landslide deposits in Taiwan. Taiwan is a prime example of an active mountain belt where landslides are the main supplier of sediment to rivers (Hovius et al., 2000) and where reports of river GSDs exist in the literature (Chung and Chang, 2013; Lin et al., 2014). Nevertheless, to our knowledge, comprehensive landslide GSD measurements are still lacking in Taiwan. Below, we report our measurements and discuss the source of variability in the GSDs within given landslides and across the whole dataset. We then discuss the validity of the two hypotheses stated above based on the GSDs of these landslides. We end by discussing the implications in terms of caveats and opportunities for GSD sampling and implications for fluvial sediment transport.

2 Data and methods

In this study, we report original GSDs for 17 landslide deposits from Taiwan (Fig. 1) as well as basic landslide information that we use to discuss controls on the GSD (Table 1). We also detail how we constrained landslide characteristics and measured GSDs for each deposit. Note that there are two landslides at the same site named LS-9o (for “old”) and LS-9n (for “new”), as the latter appears to have happened after the former (see Fig. 1d).

Figure 1 (a) Hill-shaded elevation map of Taiwan, showing the main lithological units of the Central Range (based on the geological map of Taiwan available from the Taiwan Central Geological Survey) and the locations of the 17 sampled landslides deposits. (b–e) Pictures of some sampled landslides, where the yellow line is the approximate contour of the landslide (sometimes going beyond the pictures), and the dashed line indicates the transition from deposit to scar (it is only tentative when associated with “?”). In panels (b) and (e), the lead author is standing on the deposit for scale.

Table 1 Landslide characteristics for the 17 surveyed deposits. Asterisks indicate landslides for which the geometry was estimated in the field rather than from satellite imagery. Due to its complex displacement, LS-12 has large uncertainties regarding the displacement of its center of mass. The abbreviations used in the table are as follows: Bsc – black schist (Tananao Formation), Sl/Sd – slate/sandstone (Lushan Formation), Sh/Sd – shale/sandstone (Nanchuang Formation), Msd – metasandstone (Shipachungshi Formation), Sh – shale (Chinshui/Cholan Formation), U – up, M – mid, T – toe, I – in, C – channel and n/a – not applicable.

2.1 Landslide characteristics

To quantify the variability in landslide GSD and its controls, we have targeted landslides with a known triggering date and landslides covering a broad range of areas (40 m² to 0.1 km²) and lengths (10 to 400 m). Except for four small landslides (<1000 m²), which were opportunistically sampled close to larger neighboring ones, all landslides were targeted based on satellite imagery and chosen for the accessibility of their deposit.

Landslide type was difficult to assess, but most landslides could be called debris avalanches (Varnes, 1978), involving variable amounts of regolith and bedrock, although LS-13 and LS-14 could also be called rock falls. LS-12, the largest event, may rather be a deeper rock slump, with moderate displacement that is partly translational and partly rotational. Most landslides correspond to landslide polygons present in the Typhoon Morakot landslide inventory (Marc et al., 2018); thus, they occurred in August 2009, about 5.5 years before they were surveyed in March 2015. Other more recent landslides were dated based on the time series of images available in Google Earth (see Table 1).

To assess variability in the GSD independent of rock type, 13 out of 17 landslides were chosen in the same geographic area, on both sides of the southern section of the Taiwanese Central Range, in relatively homogeneous lithological units composed of slate and slightly metamorphosed sandstone (Fig. 1, Table 1). LS-1 and LS-15 also occurred on moderately metamorphosed units, on both sides of the northern part of the Central Range, in black schist and in metasandstone intercalated with slate, respectively. The two remaining landslides both occurred in unmetamorphosed units made of alternating sandstone and shale for LS-10, which occurred in the emergent topography of Taiwan's southern tip, and in shales of the northwestern foothills for LS-16. In LS-16, many coarse rock fragments (>10 cm) were crumbling when touched, highlighting the weakness of this rock compared with the other units.

In an effort to constrain the mechanical strength of these units, we refer to measurements reported for 128 samples from the Chenyoulan catchment, both for the Nanchuang/Nankang Formation, which extends to the southern tip of Taiwan and contains LS-10, and for the metasedimentary units of the Shipachungshi Formation, where LS-15 occurred (Lin et al., 2008). The unconfined compressive strength of Nanchuang sandstone ranged from 29 to 117 MPa (mean of 70 MPa), whereas the Shipachungshi metasandstone ranged from 45 to 179 MPa (mean of 100 MPa) (Lin et al., 2008). However, in the Nanchuang Formation, sandstones alternate with weak shale (strength below 10 MPa), with an equal proportion of each. In contrast, the Shipachungshi metasandstone is intercalated with less frequent slates, often stronger than the Nanchuang shales (Lin et al., 2008). These measurements clearly make the case for highly variable rock strength and are far from encompassing the potential diversity of the rock types sampled by the studied landslides. Our goal here is not primarily to constrain the rock strength of individual landslides but instead to estimate the relative strength of diverse units. Based on the measurements reported above, we make two assumptions: first, that the shales and sediments hosting LS-16 and LS-10 may be 7–13 times and 2–4 times weaker, respectively, than the metasediments hosting LS-15; and, second, that the slates and metasandstones in the Lushan Formation have similar strength to those in which LS-15, as well as LS-1, occurred and, thus, that these landslides can be compared without normalizing for strength.

Geometric landslide metrics were obtained from high-resolution satellite imagery available in Google Earth except for four deposits (LS-4, LS-9n, LS-13 and LS-14), which were too small to be clearly distinguished on the imagery, and which had their dimensions approximated from field observations only, using a laser rangefinder. Area was obtained by hand mapping the whole disturbed zone on the imagery. Length refers to the downslope length between the highest and lowest point of the polygon. The elevation difference between these two points, estimated from the elevation data of Google Earth (in Taiwan mostly the 30 m Digital Elevation Model, DEM, from the Shuttle Radar Topography Mission, SRTM, predating all of the studied landslides), defined the maximum drop height. Physically, the potential energy change in Eq. (1) is related to the displacement of the center of mass. Thus, we also estimate a length and drop height from the center of mass of the scar to that of the deposit, estimated from Google Earth imagery. An estimate of the pre-failure scar gradient could be derived from the scar's approximate length and height difference.

Beyond plan-view metrics, we must also estimate landslide scar volume in order to constrain the landslide scar depth. For a few landslides, the deposit volume could be approximated as a fraction (a quarter to a half) of a cone, for which a volume estimate could be obtained as $\mathit{\pi }{R}^{\mathrm{2}}h/\mathrm{3}$, where R and h are the respective approximate radius and height of the cone that were estimated in the field. This simplified geometry was only suitable for LS-3, LS-4, LS-7, LS-9n, LS-10, LS-11, LS-13 and LS-15, and yielded only a first-order “field volume” estimate (Table 1). For the other deposits, we had to rely on scaling relationships between the scar area and volume, with the additional complexity that the lower extent of the scar area could not be clearly assessed in most cases, even with high-resolution imagery. Thus, assuming the mean scar aspect ratio from a global database applies to the surveyed landslides (Domej et al., 2017), we estimated scar areas as A_s=1.5 $W_{\mathrm{s}}^{\mathrm{2}}$, where W_s is the scar width obtained by measuring the extent of the landslide in the direction orthogonal to flow, in the upper part of the failure only. With A_s, we estimated a maximum and minimum landslide volume using empirical scaling relationships of the form $V=\mathit{\alpha }{A}_{\mathrm{s}}^{\mathit{\gamma }}$, with different parameter values assuming the scar was mobilizing soil or bedrock, respectively. We used $\mathit{\gamma }=\mathrm{1.262}\pm \mathrm{0.009}$ and ${\log }_{\mathrm{10}}\left(\mathit{\alpha }\right)=\mathrm{-}\mathrm{0.649}\pm \mathrm{0.021}$ for landslides in soil, and $\mathit{\gamma }=\mathrm{1.41}\pm \mathrm{0.02}$ and ${\log }_{\mathrm{10}}\left(\mathit{\alpha }\right)=\mathrm{-}\mathrm{0.63}\pm \mathrm{0.06}$ for landslides in bedrock (Larsen et al., 2010). We then derived the upper and lower estimates of landslide mean scar depth as the ratio of volume to scar area for bedrock and soil, respectively. Although approximate, this scaling is still preferable to using total landslide area, as it removes bias in the volume estimates associated with variable runout length, which is difficult to constrain from field or satellite observations (e.g., Marc et al., 2019). Where available, the volumes estimated from the field mostly fall within the bracket of the volumes estimated from global scaling relationships (Fig. S1 in the Supplement), lending some support to this approach.

Nevertheless, for the deposits where we could not obtain a field estimate, a better constrained volume estimate could be obtained by choosing one of the two scaling relationships. We note that the field volume estimate of LS-3 and LS-4 is similar to the estimate from the soil scaling relationship (Fig. S1). This is consistent with the observation that they were composed of rock debris with a yellowish color that indicated advanced weathering, and contained fresh vegetation debris (see Fig. 1). For LS-7 and LS-11, which clearly involved mostly fresh bedrock, the field volume estimates match better with the bedrock scaling relationship (Fig. S1). Thus, where field volumes were lacking we used the bedrock estimate for the largest landslides (W_s>50) within which the rock looked mostly fresh (i.e., LS-1, LS-2, LS-8 and LS-12). Some other landslides (LS-5, LS-6, LS-9o and LS-16) featured a mixture of soil and rock material. Consequently, we used the average of the soil and bedrock scaling to estimate their volume. The best estimate for each landslide was divided by its scar area to obtain an estimate of scar thickness (Table 1).

2.2 Grain size count

GSDs were obtained using grid-by-number sampling, following established protocols developed for measuring riverine GSDs (see Kellerhals and Bray, 1971) and subsequently applied to landslide deposits (Casagli et al., 2003; Attal and Lavé, 2006). We extended survey tapes along an elevation contour over a substantial portion of the deposit width (10 to 50 m) and sampled grains along the tape at a constant interval, recording the size bin of the b axis, measured with rulers. We used bins following a half-phi scale (power of 2 by 0.5 increments) with the smallest bin encompassing all grains finer than 2 mm. When grains could not be moved, we considered the smallest of the two visible axes as the b axis. The sampling interval was 0.5 m in most cases but was adjusted to 1 m for deposits where many meter-scale boulders where present (LS-2s, LS-13 and LS-14) to avoid having to count many grains several times. We then moved the line in parallel, upslope by 1 to a few meters depending on the deposit's dimensions and local topography, and repeated the count. Most slides were sampled with 6–10 survey lines, allowing us to cover a substantial fraction of the deposit (often 30 % to 60 %), with total counts typically including 200–400 individual grains. This approach also allowed us to sample different sections of the deposit when a spatial segregation was visible (LS-3, LS-8, LS-9n and LS-10) and to quantitatively assess this spatial variability in grain size (see Ruiz-Carulla et al., 2015).

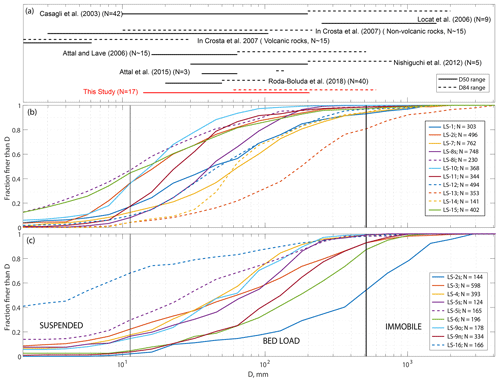
Figure 2 (a) Range of D₅₀ and D₈₄ for various studies, excluding the coarsest and finest distributions of each study. (b, c) Cumulative distribution function for the 17 sampled landslide deposits. Note that we show the surface and inner distributions for LS-5, LS-8 and LS-2; thus, 20 distributions are shown in total. For visibility, some lines are dashed and the distributions are shown in two panels. Vertical lines are the approximate boundary for grain transport by suspension and bed load, for a flood associated with a fluid shear stress of 220 Pa (see Sect. 4.3).

Specifically, we observed and measured spatial variations in the GSD on the surface deposit for four landslides (LS-3, LS-8, LS-9n and LS-10). In addition to the surface GSD, we also measured the GSD of a section of the deposit likely to represent the interior of the deposit for three of the landslides (LS-2, LS-5 and LS-8). Below, we explain how we could independently measure various GSDs on these landslide deposits. For LS-8 and LS-2, we counted grains on the vertical banks of a 2 m deep erosional gully incising the deposit, and on a debris fan next to and below the road that had been cleared from the deposit, respectively. Thus, the former case allowed us to survey the internal GSD in place, whereas the latter likely represents a remixing from surface and internal parts and, thus, must be closer to the inner GSD than what would be derived from surface measurements only. Note that the only undisturbed deposit for LS-2 was the one in the transport channel, where a carapace (a layer of very coarse grains, Crosta et al. (2007)) seems to have formed (Fig. S2). Finally, on LS-5, we separately measured a debris fan and the terminal section of a channelized deposit which was visibly coarser (Fig. S3). In this case, given the age of the deposit and its direct contact with the floodplain, it is plausible that the deposit was partly eroded and that the fan may be a mixture of internal and superficial material, whereas the higher up channel section may be more representative of the original surface of the deposit. This will be further discussed in the following during the examination of segregation. In any case, to differentiate between the GSD considered to represent the interior or surface of the deposit, we add the letter “i” or “s” after the name, respectively (Fig. 2).

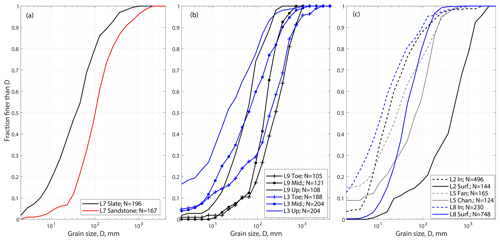
Figure 3 Examples of three types of heterogeneity in grain size distributions within the same landslide deposit: (a) lithological difference within the deposit of LS-7 with sandstone grains coarser than slate grains; (b) downslope differences between the upper, middle and lower part of the deposits of LS-3 and LS-9; (c) difference between the surface and inner part of the deposits of LS-2, LS-5 and LS-8.

Additionally, on the deposit of LS-7, we could distinguish (by visual inspection) grains made of slate, which were dark, elongated and without visible internal structure, from grains made of metasandstone, which were lighter, more cubic and with visible internal grains. We counted them separately as we found them over the deposit. In many other deposits, a large majority of grains either looked fairly homogeneous or, due to time constraints, a systematic count within different rock types could not be done. To study the variability between various landslides, we obtained an overall surface GSD by summing the grain counts from both lithologies of LS-7 and from the different sectors of the deposits with spatial segregation. For these cases, we did not use an area-weighted sum (Ruiz-Carulla et al., 2015) because the upper, middle (when differentiated) and lower sections of the deposits represented roughly similar proportions of the surface of the deposits, and we obtained count variations below 10 % from the different subsections (Table 1, Fig. 3). When we measured both internal and superficial GSDs, we had to select one of them as representative for the comparison to other landslide properties (see Sect. 3.2).

3 Results

3.1 Landslide grain size distributions and their internal variability

Before averaging the spatial variability, the landslide GSDs were found to have 50th and 84th percentiles ranging from about 15 to 200 mm and about 60 to 600 mm, respectively. This is consistent with the range of observations from previous studies, except the large rock avalanches from Locat et al. (2006) and the volcanic rock avalanches from Crosta et al. (2007), which were about 10 times coarser and finer, respectively, than all other studies. LS-2s and LS-16 are much coarser and finer than the rest of the studied landslides, respectively. Interquartile ratios vary between 3 and 15, but we note that 13 out of 20 GSDs have an interquartile ratio of 3 to 6, whereas only LS-1, LS-3, LS-5i, LS-5s, LS-8i, LS-15 and LS-16 have larger spreads (Fig. 2). All distributions seem unimodal except LS-16, which was found to have more than 40 % of the grains finer than 2 mm and likely contained a second, submillimetric mode that could not be constrained by our methods. Grain size distributions can often be well described by a Weibull or lognormal distribution (Ibbeken, 1983). For the studied landslides, eight GSDs are better fit (according to both Kolmogorov–Smirnov and Anderson–Darling statistics; Stephens, 1974) by a Weibull distribution (LS 2s, LS-3, LS-4, LS-5s, LS-5i, LS-6, LS-9n and LS-9o; Figs. 2b and S4), whereas all others are better fit by a lognormal distribution (Figs. 2a and S5). Note that LS-16 is poorly fit by both distributions. These two subgroups imply that we cannot prescribe a given distribution form to model landslide GSDs, and future work may aim at understanding why some landslide GSDs obey one or the other distribution. In any case, we refrain from using distribution parameters and will continue to discuss results based on empirical descriptors (i.e., median, interquartile ratio).

GSDs within a single landslide deposit were often heterogeneous: in one case, they were associated with differences between grains of different rock types (slate and sandstone in LS-7), whereas in seven other cases, they were associated with spatial variability across the landslide (Figs. 3 and S6). For LS-7, the slate pieces have grain sizes about three times smaller than the sandstone for a given quantile of the GSD, with a similar distribution shape. The slate grains were typically elongated platelets (i.e., with a axes about 3 times longer than the b axes, and c axes much smaller than the b axes), whereas the sandstone grains were cubic and slightly more abundant than the slate grains (N=196 vs. N=167). We observed (with the naked eye) downslope segregation, i.e., an increase in sediment coarseness from the apex to the toe of the deposits (Ruiz-Carulla et al., 2015), in four cases. The strongest segregation was found to occur in deposits LS-3 and LS-9n, where the upper part of the deposits have grains 5-10 times finer than the lower part of the deposit, without substantially changing the shape of the distribution. Deposits LS-8 and LS-10 were found to exhibit a more subtle segregation, with the upper part of the deposits having distributions that were a factor of 1.5–2 finer than the toe of the deposits (Fig. S6). The toe of LS-10 also displayed D₅₀ and D₈₄ values that were twice as coarse as at its apex, consistent with other cases, but also had more fine grains, with about 10 % of grains finer than 2 mm vs. less than 5 % at the apex.

In two cases, we could separately measure the superficial and internal GSD. For LS-8, we observed that the superficial GSD had D₁₆=20, D₅₀=40 and D₈₄=120 mm, whereas the internal GSD had D₁₆=3, D₅₀=10 and D₈₄=50 mm. At the abovementioned location, the superficial deposits had almost no fine sediment below 2 mm, whereas the internal body had more than 10 % of fine sediments. Thus, the internal GSD had quantiles that were 10 to 20 times finer than the channel carapace – the largest difference observed in terms of internal variability. Note that the carapace also had a coarser GSD than any other measured landslide deposit in our study. In spite of this large difference, we note that the internal GSD still only had about 3 % of grains finer than 2 mm. These two examples clearly show that the superficial GSD can be substantially different from the internal GSD, both in terms of fine grains (<2 mm) and for coarse to very coarse grains (10 to 100 mm).

Last, in the case of LS-5, it is not entirely clear if the two distributions represent vertical segregation or superficial spatial variability. Given that the fan has a D₁₆=4 and a D₅₀=20 mm, about 3 times finer than in the channel, but an almost identical D₈₄ of around 200 mm, we consider it to likely be an internal or mixed GSD.

3.2 Relationship with landslide properties

The percentiles of the GSDs are highly correlated with linear correlation coefficients of R²>0.9 between D₅₀ and D₁₆, D₂₅, D₇₅, D₈₄ and D₉₀ (Fig. S7). We note that more scatter is present for D₁₆ and D₉₀, suggesting that D₅₀ is a good proxy for the bulk of the distributions but does not completely capture the variability in their tails. The interquartile ratio (here $D_{\mathrm{75}}/D_{\mathrm{25}}$), which characterizes the span of grain size in the distribution, is also independent of the other percentiles (Fig. S8).

For comparison with landslide properties, we used a single GSD for each landslide. For lithological variations or spatial variability on the surface, we averaged the various GSDs from each landslide. For the three landslides for which we have both an internal and superficial grain count, we identified a single GSD that was most relevant for comparison with the other deposits. For LS-8, we considered the GSD at the surface, to be consistent with all other cases. For LS-5, we considered the coarser distribution from the channel as more representative of the surface deposit. If the fan of LS-5 is representative of the deposit and if the channel is coarser because of some spatial segregation, the percentiles of its GSD would be about 2–3 times finer than the ones that we have selected (Fig. 3). In contrast, for LS-2, we considered the internal GSD, as the superficial measurement recorded only what seems to be a carapace that overrepresents coarse grains. Indeed, with about half of the distribution made of boulders (>0.5 m), we consider that segregation to be exceptional within our dataset. Thus, in using LS-2i to study inter-event variability, we assume that none of the other landslides had a carapace with similar strong sorting. Nevertheless, LS-2i percentiles may be biased towards finer grains, when compared with surface deposits of the other landslides, and we assume the bias could be up to a factor of 2–3, based on LS-5 and LS-8 (Fig. 3).

According to Eq. (1) and assuming similar initial regolith material for all landslides, D₅₀ should decrease linearly with the ratio of drop height, H, to bedrock strength, σ_c. Indeed, log-transforming and fitting D₅₀ against H for the 15 deposits from the metasedimentary units, which we expect to have relatively similar strength, we obtain R²=0.71 and a power law exponent of −0.64 (Fig. 4). Including LS-10 and LS-16 from weaker units yields a substantially poorer fit (R²=0.31). Thus, to account for their weaker strength, we rescaled these two landslide drop heights by a factor of 3 and 10, respectively, reflecting the central values estimated from strength measurements (see Sect. 2). We then obtained a correlation coefficient for all of the landslides (R²=0.71; N=17) and a best fit power law exponent of −0.78. For landslides in metasedimentary units, D₅₀ is also negatively correlated (with a larger scatter R²=0.5–0.55) with landslide size metrics (area, width, volume and depth). However, we note that, for this dataset, these metrics are also strongly correlated with the drop height (R²=0.56–0.66; Fig. 5). Given that we would expect larger and deeper landslides to mobilize fresher and coarser grains and, thus, to have a positive correlation with D₅₀, these negative correlations may simply reflect the fact that deeper landslides have a larger drop height in our dataset, and that the effect of drop height on decreasing D₅₀ is more important than the effect of landslide size on sourcing coarser material.

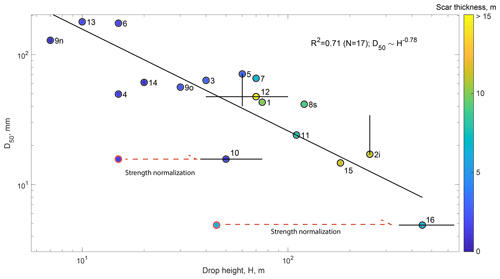
Figure 4 D₅₀ for the 17 landslides (color coded by scar thickness) in this study against the drop height of their center of mass. Results are similar for maximal drop height. The best fit (solid black line) and R² only consider the drop height rescaled by the landslide rock mass strength (black circles). The red circles show the original drop height for LS-10 and LS-16. Vertical bars show a factor of 2 uncertainty for LS-5s and LS-2i, for which there may be vertical segregation (see text). Horizontal error bars represent uncertainties in the drop height of LS-12 and the strength normalization of LS-10 and LS-16 (see Sect. 2).

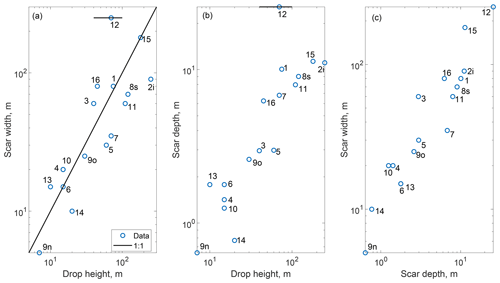
Figure 5 Correlation between the principal geometric dimensions of the surveyed landslides, drop height, scar width and scar depth. Note that scar depth is computed directly from scar width for all the landslides for which we do not have volume estimates from the field, i.e., all except LS 3, LS-4, LS-7, LS-9n, LS-10, LS-11, LS-13, LS-14 and LS-15 (see Sect. 2).

For the spread of the distribution, characterized by the interquartile ratio, we did not find any substantial correlation with any of the landslide variables. Even the rock type (or rock strength) does not seem to have an impact on the GSD spread, with several landslides in metasedimentary rocks with very large spreads (LS-3, LS-5 and LS-1), whereas the two landslides in unmetamorphosed units are on both ends of the spectrum. Thus, more data are needed to understand the spread of the landslide GSDs.

4 Discussion

In the following discussion, we propose that the variability in landslide D₅₀ can be reconciled with the fragmentation scaling of Locat et al. (2006) (i.e., D₅₀ decreases with the ratio of drop height to bedrock strength, as in Eq. 1), when accounting for regolith coarsening with depth (e.g., Cohen et al., 2010). We then detail processes that may lead to grain size segregation within a given deposit as well as practical implications for sampling. Last, we explore the implication of the measured GSD on sediment transport and evacuation from river channels.

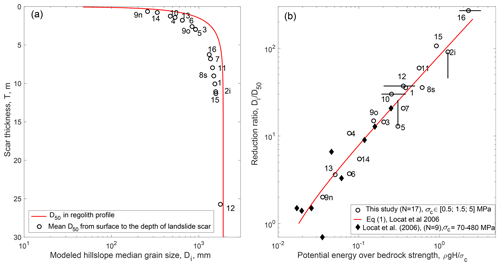
Figure 6 (a) Grain size as a function of depth in the regolith inspired by the weathering model of Cohen et al. (2010), used to estimate the original median grain size, D_i, mobilized by landslides with different thicknesses. (b) Reduction ratio, using the modeled D_i from panel (a), against the potential energy normalized by point load strength estimate for the 17 landslide deposits in this study. The error bars are the same as in Fig. 4.

Before turning to these points, we recall that some of our variables that are important for modeling landslide D₅₀ (Sect. 4.1) are only first-order estimates, if available at all. First, we rely on rough estimates of the landslide geometry (e.g., drop height, volume and depth). Better characterization in the field would have required more field work and was limited by accessibility or elaborate construction of DEM based on lidar or drone photogrammetry, which is difficult to perform and limited by the lack of accurate pre-failure DEMs. Thus, for the sake of this first study, we think that having consistent, first-order estimates of these metrics is sufficient to test the dependence of the D₅₀ on landslide geometry. The difficulty of accessing many scars as well as the mixed origin (i.e., weathered regolith and bedrock) of several landslide sources also meant that we could not practically measure the source materials' median grain size, D_i. Nevertheless, we propose below that variability in D_i may be captured with existing weathering models.

4.1 The importance of fragmentation and source material initial grain size

Here, we discuss the hypothesis that Eq. (1), proposed and validated by Locat et al. (2006) for large rock avalanches, can also be used for smaller, shallower landslides made of a mixture of regolith and bedrock. For the 17 Taiwanese landslide in our study, we found that, within a given lithology, drop height seems to be a first-order control on the landslide deposit median grain size (Fig. 4). We also found that by rescaling the drop heights by their weaker rock strength, LS-10 and LS-16 were consistent with the trend defined by the stronger metamorphosed units. These observations qualitatively agree with Eq. (1); however, quantitatively, the best fit between H and D₅₀ was not linear but a sublinear power law. Given that we observe that H and the landslide scar thickness, T, are correlated in our surveyed landslide (Fig. 5), this discrepancy with Eq. (1) could be resolved if D_i, which we could not measure, increases with T. Models describing the size of particles in a soil or regolith predict upwards fining of grains from the bedrock to the surface due to an increase in the degree of both physical and chemical weathering (Cohen et al., 2010; Anderson et al., 2013; Sklar et al., 2017). In bedrock, fracture density estimated from seismic wave refraction was also found to decrease nonlinearly from the surface to a depth of 5–10 m (Clarke and Burbank, 2011). Given that soils are often thin in Taiwan and represented a small proportion of the mobilized material, we consider that physical weathering is likely dominant. Here, we consider that the physical weathering rate (i.e., the rate of particle breakdown) can be modeled with an exponential decay from the surface, with a characteristic length scale of λ=2 m, consistent with previous modeling (Cohen et al., 2010; Anderson et al., 2013). Assuming the regolith median grain size at a depth z, D_r(z), to be proportional to the integral of the weathering rate, we modeled it as $D_{\mathrm{r}}=D_{\mathrm{b}}(\mathrm{1}-\exp (-z/\mathit{\lambda }\left)\right)$, where D_b is the unweathered bedrock block size, producing a rapid variation near the surface consistent with published models for physical weathering (Cohen et al., 2010; Anderson et al., 2013). Averaging D_r from 0 to T, the mean scar thickness, and choosing a value for D_b, we can obtain $D_i=D_{\mathrm{b}}(\mathrm{1}-\mathit{\lambda }/T(\mathrm{1}-e^{-T/\mathit{\lambda }}\left)\right)$ for each landslide (Fig. 6a).

For comparison with the prediction of Locat et al. (2006) (i.e., Eq. 1), we have to assume a value for D_b and use point load strength values (σ_c) of 0.5 MPa for LS-16, 1.5 MPa for LS-10 and 5 MPa for the other landslides in metasediments. These point load measurements are consistent with the typical unconfined compressive strength of intact rock (Lin et al., 2008) after dividing them by 20 (Chau and Wong, 1996). With these strength values and assuming D_b=1900 mm, the ratio of the modeled D_i to the measured D₅₀ agrees with Eq (1) (R²=0.9), even though its coefficients (k₁ and k₂) were calibrated on rock avalanches with rock strength and median grain size that were orders of magnitude larger than the ones in this study (Table 1, Figs. 2a and 6). All of the surveyed landslides are within a factor of 2 of the predictions from Eq. (1) – even LS-12, which likely had a different deformation style than the other landslides. This good agreement is not very sensitive to how we estimate landslide volume and scar thickness (Fig. S9). Note that by assuming D_b=1900 mm we have matched the D₅₀ of surface deposits, which may slightly overestimate the representative grain size relative to the whole landslide deposit, due to kinetic sieving or fine removal by surface runoff (Fig. 3c and discussion below). Based on LS-5 and LS-8, the inner D₅₀ may be 2–3 times finer than its surface counterpart; thus, field measurement of regolith and bedrock GSD may need to be compared to a model with D_b∼600–1000 mm, to which uncertainty in rock strength (i.e., probably a factor of 2) should also be added. Nevertheless, although uncertain, these latter values are intermediate between fracture measurement on surface outcrops in the US (Neely et al., 2019; Verdian et al., 2020), ranging from 10 to 400 mm, and the bedrock block size measured by Locat et al. (2006) on the scar of a large rock avalanche, ranging from 600 to more than 10 000 mm. D_b∼600–1000 mm also matches quite well with the range of D₅₀ to D₇₅ (450 to 900 mm) found in the carapace of LS-2 and may be a fair first-order estimate of the original bedrock block size (Crosta et al., 2007). We also note that LS-10 and LS-16, which occurred in weaker bedrock, may be expected to have a finer D_b than the other slides. We are not able to constrain this, but we note that even with a D_b 3 times finer, these two slides would only be a factor of 2 below the predicted D₅₀ (Fig. 6).

We conclude this section by underlining that more measurements, especially of source rock block size and strength, are needed to fully demonstrate the applicability of the fragmentation theory presented by Locat et al. (2006). Nevertheless, we suggest that such fragmentation theory is applicable to understand and predict landslide GSD in a wide range of contexts, at least for rock, soil, and mixed avalanches and generally disrupted slides, which are the most commonly triggered (Keefer, 1984). Further, our observations suggest that Eq. (1) can be generalized to account for an exponential reduction in regolith grain size towards the surface (Cohen et al., 2010; Anderson et al., 2013), yielding the following:

$$\begin{array}{}\text{(2)}& D_{\mathrm{50}}=\left(\mathrm{1}-{\displaystyle \frac{\mathit{\lambda }}{T}}(\mathrm{1}-e^{-T/\mathit{\lambda }})\right){\displaystyle \frac{D_{\mathrm{b}}}{k_{\mathrm{1}}\frac{\mathit{\rho }gH}{{\mathit{\sigma }}_c}-k_{\mathrm{2}}}},\end{array}$$

where D_i has been replaced by a term depending on the “fresh” bedrock median size (D_b), the length scale of weathering decay (λ) and the landslide thickness (T). In a sense, Eq. (2) supports previous qualitative statements on the importance of rock type (Attal and Lavé, 2006; Roda‐Boluda et al., 2018), which may physically relate to rock strength and regolith block size. Additionally, Eq. (2) combines the concept of physical weathering with the process of fragmentation, controlled by drop height, the latter of which is less often considered in the geomorphological community. Future studies should also clarify whether D_b is controlled by σ_c, which would make the equation more nonlinear but would reduce the number of parameters to constrain. More complex models of fragmentation have been used to predict landslide GSD (De Blasio and Crosta, 2014; Ruiz-Carulla and Corominas, 2020) and may be better suited to model the full GSD, but Eq. (2), provided it is further validated, opens various interesting perspectives. For example, it suggests that seismically triggered landslides, which occur more often near ridges than rainfall-triggered landslides (see Meunier et al., 2008; Rault et al., 2019) and are, thus, expected to have higher H, are more likely to deliver finer grains to the river systems, assuming they have a similar size and depth distributions (e.g., Marc et al., 2019). More generally it highlights the need for an investigation on how geomorphic factors (e.g., hillslope height, steepness and shape) modulate landslide runout, drop height and connectivity to channels. Comparing hillslopes in various landscapes could be easily attempted based on comprehensive landslide inventories (Tanyaš et al., 2017; Marc et al., 2018). Equation (2) would also be well-suited for landscape scale modeling of the input of various grain sizes into rivers (e.g., Benda and Dunne, 1997; Carretier et al., 2016; Neely and DiBiase, 2020) and, thus, for providing better coupling of landslide and river dynamics in landscape evolution models (Campforts et al., 2020; Egholm et al., 2013).

4.2 Controls on the internal variability in the GSD and implications for future sampling

We found three sources of internal variability in landslide GSD: one associated with the lithology of the individual grains, as reported for Himalayan landslides by Attal and Lavé (2006), and two related to the location of the grains on or in the deposit, as reported for various rock avalanches (Crosta et al., 2007; Ruiz-Carulla et al., 2015). We discuss these observations first in terms of implications for bias and sampling procedure, and second in terms of physical process causing them.

The lithological difference is not likely to be a bias as long as the grains of different lithologies are randomly distributed in the deposit: their sampling frequency should represent their relative abundance in the deposit. Spatial segregation on the surface of the deposit implies that – in order to ensure a representative GSD – the sampling method should ideally be performed across most of the deposit, or at least over the different subunits of the deposit, before doing a weighted average with their relative area of contribution. Measurement based on sieving at a single site or local grain counts along a line or over a fraction of the landslide area may misrepresent the GSD and should be avoided. For large deposits where access is difficult, the use of pictures from a drone may help with checking for segregation and potentially allow one to reproduce the grid-by-number counting method using image analysis (e.g., Casagli et al., 2003; Attal and Lavé, 2006). However, this requires the scaling of each drone picture and, thus, the deployment of reference objects across the deposit, which is not always practical; moreover, such sampling will be unable to resolve fine grains (<30–100 mm). In contrast, in the presence of a vertical segregation, where superficial and inner GSDs differ, it may be very difficult to estimate a GSD that is representative for the whole deposit. When possible, targeting the banks of incised gullies may offer a good opportunity to characterize the subsurface of the deposit. Some applications mainly require the subsurface GSD – for example, modeling the weathering of freshly fragmented bedrock in the landslide deposit and how they can contribute to solute fluxes (Emberson et al., 2016a, b). In contrast, the surface grains matter for sediment transport, and armoring may limit the mobilization of deeper finer grains. Additionally, in the case of a carapace, the question of how to combine the two end-member distributions would require an estimate of the relative thickness of the two end-member GSDs, which may be challenging. In the case of a less extreme segregation, as observed for LS-8 and probably LS-5, the proportion of coarse grains (>200 mm) was similar on the surface and inside the deposit, and only the medium and especially fine grains were more abundant inside the deposit.

The process of kinetic sieving (Savage and Lun, 1988; Gray, 2018) is expected to cause vertical segregation (i.e., a coarser surface and finer subsurface) in granular flows and a downslope segregation when shear is present, leading to boulder fronts as for LS-3. However, it should be noted that segregation is favored by transport along moderate slope gradients and tends to disappear for very steep chutes (Vallance and Savage, 2000). Although our gradient estimates are very rough, segregation mostly occurred for landslides with large transport distance, estimated as $\sqrt{L^{\mathrm{2}}+H^{\mathrm{2}}}$, and the least steep slopes (Table 1, Fig. S10). This excludes LS-12, which likely has complex displacement, and LS-16, for which the weak and clay-rich lithology, prone to form agglomerates, may not behave like a typical granular material. Nevertheless, it seems hard to use kinetic sieving to explain why LS-9n was so clearly segregated downslope, in spite of its very modest size and displacement. Instead, we could hypothesize that the episodic reactivation of the scar and channel chute may have sprayed the deposit with finer debris on some landslide deposits, depositing preferentially near the apex of the deposit. Such a mechanism might have happened on most of the landslides that we have sampled (given their ages), but we cannot currently constrain its relevance without repeated monitoring of the deposits, which is left for future studies. Alternatively, for old deposits, it is likely that fine materials could have been washed away by repeated storm events. This progressive washing of the fine grains would be consistent with the fact that the superficial deposits are very poor in fine materials but have a proportion of coarse blocks fairly similar to the internal part of the deposit (e.g., LS-5 and LS-8; Fig. 3). In these two cases, kinetic sieving may have been limited (although likely present in LS-8 to explain some downslope coarsening) and fines may have been preferentially washed out. On various parts of the LS-11 deposit we did find finer materials when scraping off the top layer of gravels, consistent with this hypothesis. If such a process is expected to happen on all landslide deposits, superficial measurements of very fresh landslides may represent the bulk of the material (e.g., LS-15 and LS-3, as they most recently failed and have a high proportion of fine grains), and older deposits may require some correction, as medium to fine grains may be underrepresented.

To conclude this discussion, it seems clear that several physical processes can add complexity to landslide deposit GSDs and that deconvolving them and applying a process-based correction is not straightforward. More datasets are needed to better understand these sources of variability in the GSDs – for example, with a more systematic sampling of very fresh landslides where fines should not have been washed out. Thus, we encourage that such issues are anticipated in future studies and that field work is performed in a way which allows the spatial variability to be recorded. This would also enable future studies to include various landslide GSDs based on different assumptions or corrections. In this sense, collecting more measurements of landslides with both internal and superficial GSDs seems essential, especially when comparing young landslides with similar characteristics (e.g., lithology and height drop).

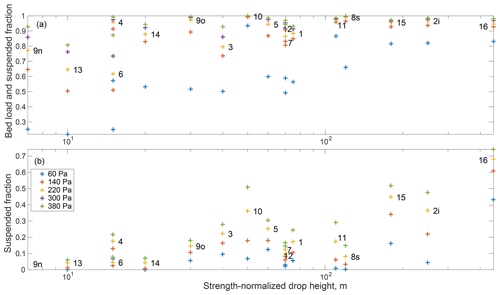
Figure 7 Fraction of the landslide GSD that could be transported as both bed load and suspended load (a) and only as suspended load (b) as a function of the strength-normalized landslide drop height (as in Fig. 4) and river shear stress during a 10-year return flood (illustrated using different colors). Note that the suspended fractions at 300 and 380 Pa are identical in panel (b).

4.3 Implications for sediment transport in Taiwan

The landslide GSDs that we report contain mainly gravel, but they also contain a substantial fraction of boulders, which suggests that, after reaching floodplains and channels, the transport and evacuation of the material will require large floods. To compare these GSDs to typical shear stresses occurring in Taiwanese rivers, we use the shear stress map derived by Yanites et al. (2010b) from detailed measurement of the width, discharge and slope along the Peikang River. For a 10-year return flood with a discharge of 1000 m³ s⁻¹, they found that shear stress, τ, mostly ranged from about 60 to about 380 Pa. For mountain channels with a typical gradient of about 2 % (Yanites et al., 2010b), these shear stresses correspond to flood heights of between 0.3 and 2 m. To assess a threshold for bed load transport, we computed the grain size D for which the Shields number $\mathit{\tau }/(\mathit{\rho }/{\mathit{\rho }}_{\mathrm{f}}-\mathrm{1})gD$, where ρ and ρ_f are the grain and fluid density, respectively, was above a transport threshold of 0.045 (Lamb et al., 2008). Similarly, for suspended load transport, we assessed the D value at which the shear velocity, estimated as $U_{*}=\sqrt{\mathit{\tau }/{\mathit{\rho }}_{\mathrm{f}}}$, was larger than the settling velocity of the grain U_s as defined and calibrated by Ferguson and Church (2004) (Figs. 2, 7). Even for an above average 10-year return flood, less than 25 % of most landslide deposits could be transported in suspension, except for LS-10 and LS-16 which had a suspended fraction of up to 50 %–70 %. When accounting for bed load transport, the largest shear stress of ∼380 Pa could not transport 5 %–25 % of the deposits for about half of the landslides, especially LS-6, LS-9n and LS-13. Considering smaller, but not uncommon, shear stresses (60–140 Pa) would result in an immobile fraction of 20 % to 40 % for most landslides, and up to 80 % for the three coarsest deposits.

Before discussing the implications of this, we highlight three main limitations that should be addressed by future work aiming at constraining the export of landslides deposits. First, the shear stress could not be adjusted to the local channel conditions in which the landslide occurred, neglecting specific width, discharge and gradient as well as relations between gradient and the critical Shields value (e.g., Lamb et al., 2008) or the influence of landsliding on the channel itself (e.g., Kuo and Brierley, 2014). Second, we ignored armoring effects, in which a superficial layer of coarse grains inhibits the mobility of finer grains (Parker and Sutherland, 1990). In our case, considering armoring could particularly reduce transport for deposits where coarse grains are segregated at the toe or surface of the deposit, such as for LS-2, LS-3 or LS-8. Third, we did not consider debris flows and hyperconcentrated flows, which are frequent in Taiwan and sometimes reach the ocean (Dadson et al., 2005; Lin et al., 2005; Hsu et al., 2010) and which would enhance sediment transport given their higher fluid density. Despite these sources of uncertainty, our results suggest that rapid evacuation of the sediment by suspension affects at most 30 % of most of the deposits in the relatively strong metasedimentary units, and most of the transport occurs as bed load. Further, only the largest (10-year return or more) floods will transport substantial parts of the deposit, meaning that large landslide events may load channels with a pulse of coarse sediments that require several decades to be evacuated. This is much longer than the transient pulse of enhanced landsliding (Marc et al., 2015) and suspended sediment transport (Hovius et al., 2011) observed after the Chi-Chi earthquake, which lasted less than 10 years, but is consistent with the ∼50-year timescales for enhanced lake sediment deposition (including bed load) after earthquakes observed in New Zealand (Howarth et al., 2012; Wang et al., 2020). This multidecadal timescale for sediment export seems consistent with the very large alluviation of river channels in southern Taiwan following intense flooding and landsliding triggered by Typhoon Morakot (Yanites et al., 2018), which was still visible in 2015 (e.g., Taimali River) and at the time of writing in satellite imagery. Substantial aggradation, suspected to be long term, was also observed after the Chi-Chi earthquake (Yanites et al., 2010a; Chen, 2009). More detailed modeling of the evacuation of landslide sediment (e.g., Yanites et al., 2010a; Croissant et al., 2017) could be combined with scenarios based on the detailed GSDs reported in this study to better quantify the dynamics and timescales of coarse sediment export after large landslides events.

5 Conclusions

We presented grain size distributions obtained from 17 landslide deposits in Taiwan. They have D₅₀ and D₈₄ values consistent with landslides reported in previous literature – between 15 and 200 mm and between 60 and 600 mm, respectively. We found that many deposits had significant spatial segregation in the downslope direction, with the lowest part of the deposits having 2–10 times coarser GSDs than the upper part of the deposits. For the three landslides in which we could sample the inner part of deposits, we also found that GSDs were 3–10 times finer than their surface counterparts. The presence and intensity of this segregation cannot be attributed to a single process, but kinetic sieving and deposit reworking are likely to play important roles. This internal variability could bias results obtained from local sampling of GSDs, such as sieve samples from a single pit.

Investigating the controls on landslide GSD variability, we observed a strong anticorrelation between the landslide drop height, width and inferred scar depth as well as the GSD percentiles for all of the landslides. Finer GSDs in the two landslides in unmetamorphosed, young sedimentary rocks can be well explained by normalizing the drop height by the rock strength. Further, modeling the source material median grain size with an exponential fining towards the surface, consistent with physical weathering models, we found that the reduction ratio from source material to landslide deposits matches the scaling proposed by Locat et al. (2006) and calibrated for rock avalanches with much larger volume and much higher point load strength than the ones we studied. Although future measurements on source rocks are needed for a complete demonstration, especially in terms of bedrock strength and fracture spacing, we suggest that simple geomorphic models coupling this fragmentation scaling with a model for regolith grain size (see Eq. 2) could provide a physically based first-order model for the GSD input to rivers by landslides in active orogens. Such an approach could be implemented into landscape evolution models accounting for sediment transport. Indeed, from our deposits, we also noted that even a 10-year flood may not be able to transport the coarsest fraction of many deposits, suggesting that floodplains and channels will likely need several decades to recover after large landslide events.