the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Quantifying the migration rate of drainage divides from high-resolution topographic data
Chao Zhou
Yiduo Liu
Feng Shi
The lateral movement of drainage divides is co-influenced by tectonics, lithology, and climate and therefore archives a wealth of geologic and climatic information. It also has wide-ranging implications for topography, the sedimentary record, and biological evolution and thus has drawn much attention in recent years. Several methods have been proposed to determine drainage divides' migration state (direction and rate), including geochronological approaches (e.g., 10Be) and topography-based approaches (e.g., χ plots or Gilbert metrics). A key object in these methods is the channel head, which separates the hillslope and channel. However, due to the limited resolution of topography data, the required channel-head parameters in the calculation often cannot be determined accurately, and empirical values are used in the calculation, which may induce uncertainties. Here, we propose two methods to calculate the migration rate of drainage divides based on the relatively accurate channel-head parameters derived from high-resolution topographic data. We then apply the methods to an active rift shoulder (Wutai Shan) in the Shanxi Rift and a tectonically stable area (Yingwang Shan) in the Loess Plateau, to illustrate how to calculate drainage-divide migration rates. Our results show that the Wutai Shan drainage divide is migrating northwestward at a rate between 0.21 and 0.27 mm yr−1, whereas the migration rates at the Yingwang Shan are approximately zero. This study indicates that the drainage-divide stability can be determined more accurately using high-resolution topographic data. Furthermore, this study takes the cross-divide differences in the uplift rate of channel heads into account in the measurement of drainage-divide migration rate for the first time.
- Article
(10049 KB) - Full-text XML
-
Supplement
(1359 KB) - BibTeX
- EndNote
The evolution of the Earth's surface is jointly controlled by tectonics, lithology, and climatic conditions (e.g., Molnar and England, 1990; Whipple, 2009; Gallen, 2018; Bernard et al., 2021; Hoskins et al., 2023), providing a basis for reconstructing the past tectonic (Pritchard et al., 2009; Kirby and Whipple, 2012; Shi et al., 2021) or climatic processes (Tucker an Slingerland, 1997; Hancock and Anderson, 2002; Schildgen et al., 2022) through topography. The evolution of unglaciated terrestrial terrains is fundamentally coupled with changes in drainage systems through a river's vertical (changes in river long profile) and lateral movements (drainage divide migration and river captures) (Whipple, 2001; Clark et al., 2004; Bonnet, 2009; Willett et al., 2014). Previous studies have extensively investigated how river channel profiles respond to tectonic uplift (Whipple, 2001; Crosby and Whipple, 2006; Kirby and Whipple, 2012), lithological differences (Duvall, 2004; Safran et al., 2005; Forte et al., 2016), and precipitation perturbations (Schlunegger et al., 2011; Bookhagen and Strecker, 2012). River long profiles have been used to study earthquake events (e.g., Burbank and Anderson, 2001; Wei et al., 2015) and the spatio-temporal variations in uplift (e.g., Whipple et al., 1999; Kirby et al., 2003; Pritchard et al., 2009; Goren et al., 2014). Recent studies show that the widespread lateral movement of river basins driven by geological and/or climatic disturbance (Yang et al., 2019; Zondervan et al., 2020; Zhou et al., 2022a; Bian et al., 2024) also interacts with the adjustment of channel profiles (Willett et al., 2014). Drainage-divide migration, one form of river lateral movement, may not only carry information on geological and/or climatic disturbance (Su et al., 2020; Zondervan et al., 2020; He et al., 2021; Shi et al., 2021; Zhou et al., 2022a; Zeng and Tan, 2023) but also influence the extraction of tectonic information from channel profiles (Goren et al., 2014; Ma et al., 2020; Jiao et al., 2022). Moreover, it has multi-facet consequences for landscape evolution (Scheingross et al., 2020; Stokes et al., 2023), sedimentary processes (Clift and Blusztajn, 2005; Willett et al., 2018; Deng et al., 2020; Zhao et al., 2021), and biological evolution (Waters et al., 2001; Zemlak et al., 2008; Hoorn et al., 2010; Musher et al., 2021). For this reason, the stability of drainage divides has drawn more and more attention in recent years (e.g., Authemayou et al., 2018; Vacherat et al., 2018; Chen et al., 2021; Shelef and Goren, 2021; Sakashita and Endo, 2023; Bian et al., 2024).
Drainage-divide migration is essentially controlled by the cross-divide difference in erosion and topographic slope (Beeson et al., 2017; Dahlquist et al., 2018; Chen et al., 2021; Zhou et al., 2022a). The erosion rates are routinely derived from geochronological techniques, such as cosmogenic nuclide (e.g., 10Be) concentration measurements (Mandal et al., 2015; Struth et al., 2017; Young and Hilley, 2018; Sassolas-Serrayet et al., 2019), which can be used to calculate the migration rates of drainage divides (Beeson et al., 2017; Godard et al., 2019; Hu et al., 2021). However, these techniques are usually based on samples collected from a catchment outlet that is several, or even tens of, kilometers away from the drainage divide and thus may not represent the erosion rates close to the drainage divide (Sassolas-Serrayet et al., 2019; Zhou et al., 2022a). Besides, the high cost of sample processing makes it challenging to determine the drainage divide's motion by measuring the erosion rates throughout the large landscapes. Hence, it would be ideal to find an accessible and efficient method that can be applied to the entire landscape and make full use of the 10Be-derived erosion rates.
The advancement of the digital elevation model (DEM) has promoted the development of geomorphic analysis, making it possible to determine the drainage divide's transient motion through topography analysis. For example, Willett et al. (2014) applied the χ method to map the dynamic state of river basins. Forte and Whipple (2018) proposed the cross-divide comparison of “Gilbert metrics” (including channel heads' relief, slope, and elevation) to determine a drainage divide's migration direction. Others adopted the comparison of slope angle or relief of the hillslopes across a drainage divide to deduce its stability (Scherler and Schwanghart, 2020; Ye et al., 2022; Zhou et al., 2022b). These geomorphic techniques, so far, have only been able to determine the migration direction of drainage divides. Braun (2018) provided an equation that considers both alluvial and fluvial areas to calculate the migration velocity of an escarpment (also a drainage divide). Zhou et al. (2022a) developed a technique to calculate the migration rate through the high base-level χ values on both sides of a drainage divide. These new approaches require channel-head parameters to calculate the migration rate. However, the location of the channel heads sometimes cannot be accurately identified because of the limitation in the resolution of DEMs in natural cases. For this reason, empirical values of channel-head parameters are used in these studies, which may induce uncertainties.
This study aims to establish an approach to derive the migration rate of drainage divides, at a high precision and low cost, based on topographic analysis. We chose a tectonically active area (i.e., the Wutai Shan in the Shanxi Rift) and a tectonically inactive area (i.e., the Yingwang Shan in the Loess Plateau) to demonstrate how to quantify drainage-divide migration rates (Fig. 1). We use the aerial photography acquired by unoccupied aerial vehicles (UAVs) and the Structure-from-Motion (SfM) technology to obtain the high-resolution DEM data of these two areas (0.67 and 0.84 m spatial resolution in the Wutai Shan and the Yingwang Shan, respectively). Benefiting from the high-resolution data, the location of channel heads can be identified more accurately. We then develop two methods to calculate the drainage-divide migration rates. One is based on the measured channel-head parameters, and the other is based on an improved method of Zhou et al. (2022a). Combining with the geological and low-temperature thermochronology studies of the Wutai Shan (Middleton et al., 2017; Clinkscales et al., 2020), we also quantify the cross-divide difference in uplift rates to improve the precision of drainage-divide migration rate.
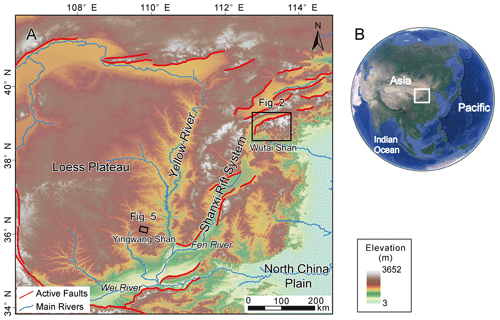
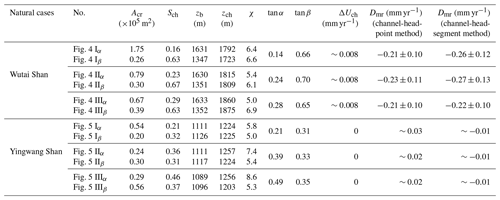
Figure 1Locations and tectonic background of the two nature cases in north China. The figure is modified from Fig. 7 in Shi et al. (2021). (a) Red lines represent the main active faults. Black rectangles show the locations of the two nature cases. The red curve denotes the active fault, sourced from https://www.activefault-datacenter.cn/ (last access: October 2023). The topography data (ALOS DEM) are downloaded from the Alaska Satellite Facility (ASF) data search (https://search.asf.alaska.edu/, last access: December 2011). (b) The satellite image downloaded from © Google Earth. White rectangles show the location of panel (a).
2.1 Channel-head-point method
According to the detachment-limited stream power model (Howard and Kerby, 1983; Howard et al., 1994), the channel's erosion rate (E) can be expressed as
where K is the erosion coefficient, A is the upstream drainage area, S is the gradient of the river channel, and m and n are empirical constants.
Because of thresholds such as erosion threshold (the shear stress of overland flow must exceed the threshold of the cohesion of bed material to generate river incision) (Howard and Kerby, 1983; Perron et al., 2008) or landslide threshold (landslides occur when the threshold of soil or rock strength is exceeded in a high relief region) (Burbank et al., 1996; Tucker and Bras, 1998), river channels (following Eq. 1) emerge at a certain distance from the drainage divide. The region between the channel head and the drainage divide is referred to as the hillslope area, where the erosion is controlled by landslide, collapse, and diffusion processes (Carson and Kirkby, 1972; Stock and Dietrich, 2006; Stark, 2010; Braun, 2018; Dahlquist et al., 2018). The channel-head point is the highest and the closest point to the drainage divide on a river channel (Clubb et al., 2014). Therefore, the erosion rate at channel-head points (Ech) can be described as
where Ech is the erosion rate at channel-head points, Acr is the critical upstream drainage area of a channel-head point (Duvall, 2004; Wobus et al., 2006), and Sch is the channel-head gradient measured along the channel near the channel-head point. Equation (2) indicates that the side of a drainage divide with a higher Acr or Sch can have a higher erosion rate than the other side and is more likely to pirate the opposite drainage basin. Besides, a high erosion coefficient can amplify the drainage basin's erosion rate.
Drainage-divide migration is essentially controlled by the cross-divide difference in erosion rates and topographic slope (Beeson et al., 2017; Dahlquist et al., 2018; Chen et al., 2021; Zhou et al., 2022a; Stokes et al., 2023). Furthermore, the differential uplift should also be considered when using the cross-divide erosion rates at the channel heads to calculate the erosion difference across the divide, especially in the case of tectonic tilting uplift (Zhou et al., 2022a). The drainage-divide migration rate (Dmr) can be obtained according to the cross-divide difference in erosion rate and uplift rate and the slopes across the divide (Zhou et al., 2022a):
where ΔEch is the difference in erosion rate between the two sides (annotated as α and β) of the drainage divide (). The choice of α or β is arbitrary, and the positive direction of the migration rate is assigned from the α to the β side, whereas the negative is the opposite. ΔUch is the cross-divide difference in uplift rate (), and tan α and tan β are the average gradients (along the normal-divide direction) upslope of the channel head (not including the hilltop part) on the α side and the β side, respectively. Assuming the erosion coefficient (K) is the same on both sides of a drainage divide, Eqs. (2) and (3) allow us to derive the equation of drainage divide's migration rate according to the parameters at the channel-head points:
If the exact value of K is unknown, the drainage divide's unilateral erosion rate can be used as a substitution:
or
Eα and Eβ are the erosion rates of the α and the β side of the drainage divide, respectively, which can be derived through cosmogenic nuclides (10Be) concentration measurements (Beeson et al., 2017; Godard et al., 2019; Hu et al., 2021). The regional average erosion rate () can also be used to calculate the migration rate:
Based on Eqs. (4)–(7), the migration rate of drainage divides can be estimated using channel-head parameters combined with one of the erosion-related parameters, erosion coefficient (K), erosion rate at one side of a drainage divide (Eα or Eβ), or regional average erosion rate ().
2.2 Channel-head-segment method
A channel-head segment is the channel segment just below the channel head (Zhou et al., 2022a). Zhou et al. (2022a) developed a method based on the cross-divide χ contrast of channel-head segments to calculate the migration rate of drainage divides. The essence of the method is the cross-divide comparison of the channel-head segments' normalized channel steepness (ksn) values. ksn is a widely used index (Whipple et al., 1999; Wobus et al., 2006; Hilley and Arrowsmith, 2008; Kirby and Whipple, 2012) that is quantitatively related to E and K (. χ is an integral function ( of a channel's upstream area (A) to horizontal distance x) (Royden et al., 2000; Perron and Royden, 2012), and A0 is an arbitrary scaling area to make the integrand dimensionless.
In the method of Zhou et al. (2022a), the location of channel heads cannot be accurately identified, because it is limited by the resolution of DEM. Therefore, an empirical value of Acr=105 m2 was used in the calculation. Benefiting from the high-resolution DEM in this study, we improve the method in Zhou et al. (2022a) and use the real location of channel heads to calculate the migration rate. When the regional erosion coefficient (K) is known and unchanged in the vicinity of the drainage divide, the drainage-divide migration rate can be estimated by the following equation:
where zch is the elevation of the channel head, zb is the elevation of catchment outlet (at the top part of the channel to make the elevation-χ profiles quasi-linear between the channel head and the outlet), and subscripts α and β denote the two rivers across a divide. The detailed derivation of Eq. (8) is in the Supplement. The drainage divide's unilateral erosion rate (Eα or E β) can also be used as a substitution for the K value:
or
Alternatively, one can use the regional average erosion rate () to calculate the migration rate:
Based on Eqs. (8)–(11), the drainage-divide migration rate can be estimated using the χ values of high-base-level channel segments combined with one of the erosion-related parameters, erosion coefficient (K), erosion rate at one side of a drainage divide (Eα or Eβ), or regional average erosion rate ().
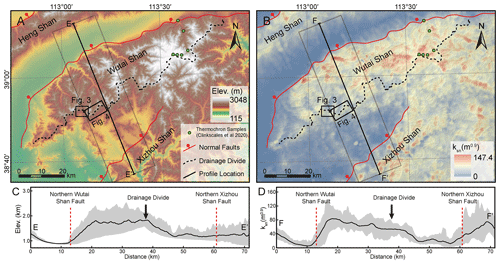
Figure 2Topography (a) and normalized channel steepness (ksn) (b) distribution of the Wutai Shan horst and surrounding area in the Shanxi Rift system. The dashed black line shows the location of the main drainage divide. Red lines show the main active faults. The black lines show the location of profiles E–E' and F–F'. Black rectangles show the area of Figs. 3b and 4a. Gray boxes show the area of the swath profiles in panels (c) and (d). Green dots denote the locations of the low-temperature thermochronology samples in Clinkscales et al. (2020). The ksn is calculated based on S and A extracted from ALOS DEM and a uniform (0.45) using TopoToolbox (Schwanghart and Scherler, 2014), and the interpolation uses the Kriging method on ArcGIS. (c) Topography swath profile along E–E'. See location in panel (a). (d) ksn swath profile along F–F'. See location in panel (b). The swath profiles are extracted using TopoToolbox (Schwanghart and Scherler, 2014). The dashed red lines show the location of the main active normal faults, and the black arrow shows the location of the main drainage divide. Both swath profiles are 20 km wide (10 km on each side).
2.3 Parameter extraction
In this study, we apply the equations (Eqs. 4 and 8) related to the erosion coefficient (K) to two natural examples in north China, the Wutai Shan in the Shanxi Rift and the Yingwang Shan in the Loess Plateau, to demonstrate how to calculate the drainage-divide migration rates (Fig. 1). We calculated the K according to the equation , the erosion rate obtained by chronological methods, the ksn, and the assumed slope exponent (n=1). The ksn is calculated based on S and A extracted from ALOS DEM (downloaded from https://search.asf.alaska.edu/, last access: December 2011) using TopoToolbox (Schwanghart and Scherler, 2014), and the interpolation uses the Kriging method on ArcGIS (Fig. 2). We use a small four-rotor unoccupied aerial vehicle (UAV), the DJI Phantom 4, to acquire stereo images of the areas. Based on the Structure-from-Motion (SfM) method and PhotoScan software, we obtained the DEMs with a spatial resolution of 0.67 m in the Wutai Shan and 0.84 m in the Yingwang Shan (can be download from https://doi.org/10.5069/G98C9TGT, Zhou, 2023). Both regions are semi-arid, and the vegetation is dominated by shrubs. We did not compare the elevations to the standard GPS points, which may introduce errors to the elevations.
Based on the high-resolution topography data, we first extract river channels and drainage divide, using a single-flow-direction algorithm (D8). Then we extract the relevant parameters and calculate the drainage-divide migration rate. Data analysis including slope–area plots, χ plots, the river's long profiles and topographic swath profiles, are based on the MATLAB toolbox TAK (Forte and Whipple, 2019) and TopoToolbox (Schwanghart and Scherler, 2014). According to the breaking point of the slope-area regression line, we obtain the value of the critical upstream drainage area (Acr) of each river channel (Duvall, 2004). According to these values, we mark the position (and its elevation, zch) of the channel heads on the χ plots and the topography map. An elevation of the catchment outlet (zb) can be assigned at the top part of the channel to make the elevation-χ profiles quasi-linear between the channel head and the outlet. The slope of the channel head (Sch) is calculated according to the 100 m long channel on the river's long profiles around the channel head (50 m upstream and downstream). Topographic gradient (tan α or tan β) is calculated through the average slope (in the normal-divide direction) of the hillslope segment (not including the hilltop part, because of its lower gradient). The cross-divide uplift difference in the channel-head points (ΔUch) is estimated according to the location of each channel head and the tectonic uplift trend.
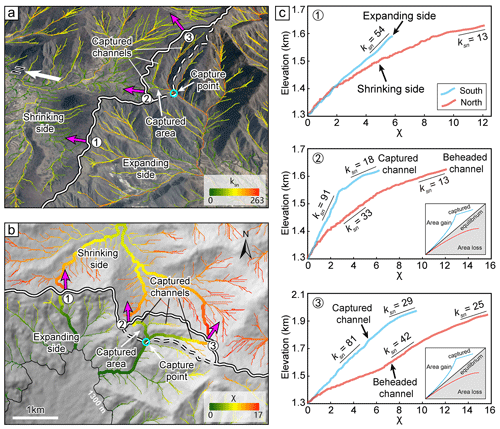
Figure 3Perspective views and χ map of the drainage divide in the Wutai Shan (see Fig. 2 for location). (a) Perspective views of a captured area and the channels mapped with ksn. The south side of the drainage divide has steeper channels and higher ksn than the north side. Magenta arrows show drainage divide migration directions. The satellite image is from © Google Earth. (b) χ map of this area with the outlet elevation of 1300 m. The south side of the drainage divide has lower χ values than the north side. It should be noted that the catchment outlet at the north side of the drainage basins (the 1300 m contour) is out of the map. The χ plots of the rivers in bold lines are shown in panel (c). (c) χ plots of the three paired rivers in panel (b). The blue and red curves correspond to the rivers on the south and north sides, respectively. The χ plot of river 1 is steeper on the south side, indicating that the river on the south side is expanding and the river on the north side is shrinking. The χ plots of rivers 2 and 3 in the captured area show obvious characteristics of the captured and beheaded rivers. The χ plot is extracted using TAK (Forte and Whipple, 2019) and TopoToolbox (Schwanghart and Scherler, 2014).
3.1 Wutai Shan
The Wutai Shan is a tilted fault block on the shoulder of the Shanxi Rift system located in the central north China craton (Fig. 1) (Xu et al., 1993; Su et al., 2021). The tilting uplift of the Wutai Shan is controlled by the North Wutai Shan Fault, and there is no active fault along the south edge of the Wutai Shan horst (Fig. 2). The bedrock of the Wutai Shan area consists mainly of metamorphic and igneous basement rocks (Clinkscales et al., 2020), and there is no obvious variation in rock erodibility and precipitation in this area (Figs. S2 and S3). Zhou et al. (2022b) reveal that the Wutai Shan drainage divide is migrating northwestward due to the tilting uplift and predicts the drainage divide will move ∼10 km to the northwest to achieve a steady state if all geological conditions remain. Geomorphic evidence also exhibits a northwestward migration of the drainage divide (Fig. 3). The plan and satellite views show several abnormally high junction angles around the Wutai Shan drainage divide, which indicate that the tributaries formerly part of the northern drainage have become part of the southern drainage (Fig. 3a and b). The χ plot analysis shows the southern side of the drainage divide has steeper channels, higher ksn, and lower χ. The χ plots of paired rivers illustrate obvious characteristics of shrinking–expanding and captured–beheaded rivers (Fig. 3c).
To derive the erosion coefficient of the Wutai Shan area, we calculate the channel steepness (ksn) of this region, assuming n = 1 and m=0.45 (Wobus et al., 2006; DiBiase et al., 2010; Perron and Royden, 2012; Wang et al., 2021). We then use the Kriging interpolation method to generate the ksn distribution map (Fig. 2b). In addition, results under the assumptions of m=0.35 and 0.55, respectively, are shown in the Supplement (Fig. S4). The average ksn value of the upthrown side near the North Wutai Shan Fault is ∼80 m0.9 (Fig. 2d). Middleton et al. (2017) showed that the Quaternary throw rates of the North Wutai Shan Fault are 0.8–1.6 mm yr−1. Clinkscales et al. (2020) showed, using low-temperature thermochronology, that the time-averaged long-term throw rates in the late Cenozoic period are about 0.25 mm yr−1, and there is accelerated activity in the Wutai Shan area. According to these studies, we assume a 0.50±0.25 mm yr−1 uplift/erosion rate in the northern margin of the Wutai Shan (in the footwall of the North Wutai Shan Fault). Combining with the equation, , and following the approach of previous studies (Kirby and Whipple, 2001; Kirkpatrick et al., 2020; Ma et al., 2020), the erosion coefficient (K) is calculated to be m0.1 yr−1 in this area. Because there is no obvious variation in rock erodibility and precipitation in this area (Figs. S2 and S3), we use this value as the erosion coefficient (K) of the Wutai Shan area.
We then apply the two new methods (Eqs. 4 and 8) to calculate the migration rate of the drainage divide in the Wutai Shan. We first choose three pairs of rivers (Fig. 4a) and acquire their slope–area plots (Fig. 4b, e, and h) and the χ plots (Fig. 4c, f, and i). According to the breaking point of the slope-area regression line (Duvall, 2004) (Fig. 4b, e and h), we obtain the values of the critical upstream drainage area (Acr). According to these values, we separate hillslope and channel areas and mark the position of the channel heads on the χ plots and the topography map (Fig. 4a). For the χ plots (Fig. 4c, f, and i), we obtain the elevations of channel heads (zch) and χ values based on the coordinates of the channel-head points. According to the location of the channel heads on the river's long profiles, we calculate the channel-head gradient (Sch). Topographic gradient (tan α or tan β) is calculated through the average slope (in the normal-divide direction) of the hillslope segment (not including the hilltop part, Fig. 4d, g, and j).
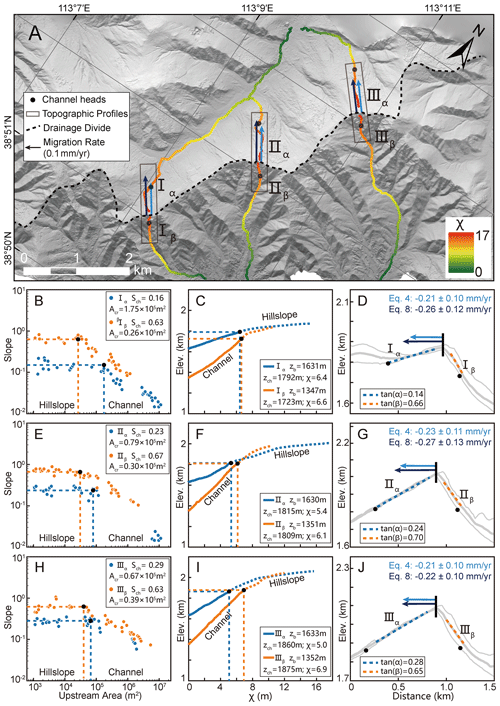
Figure 4Analytical results of the Wutai Shan drainage divide. (a) High-resolution hillshade map (0.67 m spatial resolution) of the Wutai Shan. The dashed black line shows the location of the main drainage divide. Colored lines show the three pairs of selected channels used for analysis. The black dots are the channel heads. Black rectangles show the location of the cross-divide topography swath profiles. The black arrows show the direction of drainage-divide migration. (b, e, h) Slope–area plots of the three pairs of selected channels. The blue and orange dots are the slope–area plots of the north (α) and south (β) sides of the drainage divide respectively. The black dots represent the channel heads. (c, f, i) χ plots of the selected channels. The blue and orange lines are the χ plots of the north (α) and south (β) sides of the drainage divide respectively. The black dots represent the channel heads. (d, g, j) Cross-divide topography swath profiles with the drainage-divide migration rates. The locations of the profiles are in panel (a). The light and dark blue arrows are the drainage-divide migration rates calculated by the channel-head-point (Eq. 4) and channel-head-segment (Eq. 8) methods, respectively.
According to the previous studies (Middleton et al., 2017; Clinkscales et al., 2020) and the ksn distribution (Fig. 2d), we assume the rock uplift rate decreases linearly from 0.5 to 0 mm yr−1 from northwest to southeast of the Wutai Shan horst (∼40 km wide). Then we can determine that the cross-divide uplift difference in the channel-head points (ΔUch) (the distance perpendicular to the direction of the boundary fault is ∼600 m) is ∼0.008 mm yr−1. After determining these parameters, we adopt the channel-head-point (Eq. 4) and channel-head-segment (Eq. 8) methods, respectively, to calculate the migration rates. The required data for calculation and the migration rates are shown in Table 1. The calculated results for and 0.55, respectively, are shown in the Supplement (Table S1). The migration rates are higher when and lower when , which indicates the value is sensitive to the result.
The rivers have different characteristics on both sides of the drainage divide, as illustrated on their slope–area plots (Fig. 4b, e and h) and the χ plots (Fig. 4c, f and i). For the first site (Fig. 4d), the migration rates calculated by the channel-head-point and channel-head-segment methods are 0.21 and 0.26 mm yr−1, respectively. For the second site (Fig. 4g), the migration rates are 0.23 and 0.27 mm yr−1, respectively. For the third site (Fig. 4j), 0.21 and 0.22 mm yr−1, respectively. The drainage divides of all three points are migrating northwestward, which is consistent with the previous result inferred by the cross-divide contrast of slopes in this area (Zhou et al., 2022b). Furthermore, the migration rates calculated by the two methods are comparable in all three sites.
3.2 Yingwang Shan
The Loess Plateau is hosted by the tectonically stable Ordos Block of the north China craton (Yin, 2010; Su et al., 2021). Over the past 2.6 million years, it has accumulated tens to hundreds of meters of eolian sediments (Yan et al., 2014), draping preexisting topography (Xiong et al., 2014). There is no active fault and little to no variation in rock erodibility and precipitation within the area (Shi et al., 2020; Zhou et al., 2022b).
We apply the two methods to the Yingwang Shan of the Loess Plateau to calculate the drainage-divide migration rate. Similar to the Wutai Shan site, we obtain the slope–area plots (Fig. 5b e and h) and the χ plots (Fig. 5c, f and i) and extract the values of Acr, Sch, zb, zch, χ, tan α, and tan β of the rivers. The rate of soil erosion in the study area is about 500 t km−2 yr−1 according to the distribution of silt discharge (Fu, 1989). Combining with the assumption of the density of loess, 1.65 t m−3, the present-day erosion rate in the study area is calculated to be 0.3 mm yr−1. Because there is no obvious unequal uplift in this region, we assign ΔUch to be zero. We also assume n=1 and m=0.45 in the calculation (Wobus et al., 2006; DiBiase et al., 2010; Perron and Royden, 2012; Wang et al., 2021). Then, we use the methods of channel-head parameters (Eq. 7) and channel segments (Eq. 11) to calculate the drainage-divide migration rates. The required data for calculation and the migration rates are shown in Table 1.
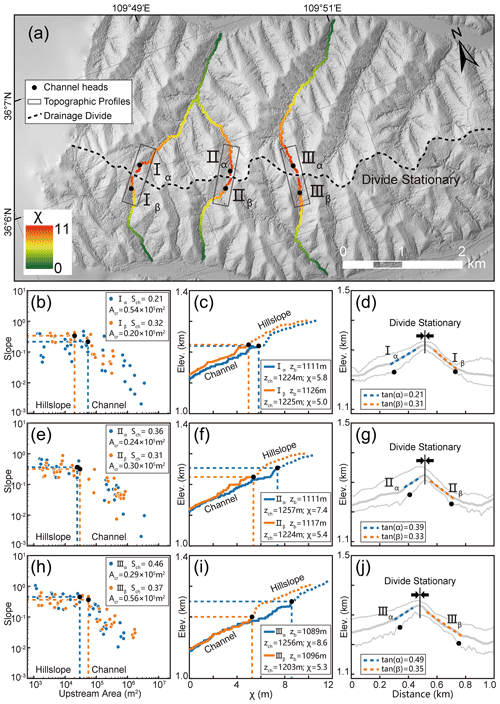
Figure 5Analytical results of the Yingwang Shan in the Loess Plateau. (a) High-resolution hillshade map (0.84 m spatial resolution). The dotted black line shows the location of the main drainage divide. Colored lines show the three pairs of selected channels used for analysis. The black dots represent the channel heads. Black rectangles show the location of the cross-divide topography swath profiles. (b, e, h) Slope–area plots of the three pairs of selected channels. The blue and orange dots are the data of the north (α) and south (β) sides of the drainage divide respectively. The black dots represent the channel heads. (c, f, i) χ plots of the selected channels. The blue and orange lines are the χ plots of the north (α) and south (β) sides of the drainage divide respectively. The black dots represent the channel heads. (d, g, j) The cross-divide topography swath profiles. The locations of the swath profiles are in panel (a).
All results of the three points show that the drainage-divide migration rate here is close to zero no matter which method is used in the calculation. The results show that the drainage divide of the study site is in topographical equilibrium, which is consistent with the inference in previous studies (Willett et al., 2014; Zhou et al., 2022b).
4.1 Location of channel heads
Willett et al. (2014) pioneered the use of cross-divide χ contrast to gauge the horizontal motion of drainage divides. According to their method, drainage divides are predicted to move toward the side with a higher χ value to achieve geomorphic equilibrium. However, in a region with spatially variable uplift rates, lithology, or precipitation, χ contrast may fail to reflect the drainage-divide migration (Willett et al., 2014; Whipple et al., 2017; Forte and Whipple, 2018; Wu et al., 2022; Zhou and Tan, 2023). In a tectonically active area, the cross-divide χ contrast can only be used in a small area where rock type, precipitation, and uplift rate are nearly uniform (Willett et al., 2014). Combining the advantages of the χ and Gilbert metrics methods, Zhou et al. (2022a) proposed to use the χ contrast with a high base level to calculate the ksn values at the channel heads on both sides of a drainage divide and quantified the migration rate of drainage divides at the eastern margin of Tibet.
To reduce the cross-divide difference in uplift rate, precipitation, and rock strength, the Gilbert metrics or χ-comparison method in Zhou et al. (2022a) should compare the parameters of points (slope, relief, elevation, and ksn) on both sides of the divide as closely as possible. As the hillslope area (above the channel head) does not follow Eq. (1) (Stock and Dietrich, 2006; Stark, 2010; Braun, 2018; Dahlquist et al., 2018), the channel heads are the closest point to the divide, following Eq. (1). Channel heads, therefore, are suitable for measuring the drainage-divide stability with parameters of the upstream drainage area and channel gradient (Forte and Whipple, 2018; Zhou et al., 2022a). However, limited by the resolution of DEM, the location of the channel heads cannot always be accurately identified. The channel-head parameters for calculating the migration rates are usually based on empirical values (both sides are the same value) in previous studies (e.g., Acr=105 m2 in Zhou et al., 2022a), which may induce uncertainties.
In this study, we advocate the use of a high-resolution DEM to determine a more accurate position and related parameters of the channel head. The use of UAVs to obtain the local DEM has become highly efficient. We advance the theory to calculate the drainage-divide migration rate based on the measured channel-head parameters. With the help of the aerial photography of UAVs and the SfM techniques, it is possible to obtain the high-resolution topography data of drainage divides (Figs. 4a and 5a) and get the required parameters through topography analysis. The key parameters include the exact locations (which usually have different Acr across the divides) and the gradients of the channel heads (Scr), which could improve the quantitative research on the drainage-divide migration. Furthermore, the method provides a new avenue to combine with catchment-wide 10Be erosion rate or low-temperature thermochronology data to calculate the migration rate, which has great potential for application in places where some variables are hard to be constrained.
4.2 Cross-divide difference in the uplift rate of the channel heads
Although the channel heads across the divide are very close on the spatial scale of an orogenic belt, differential uplift between the channel heads (ΔUch) could still exist, especially in a tilting horst, such as the Wutai Shan. The cross-divide difference in uplift rate could impact the calculation of the migration rate of drainage divides (Zhou et al., 2022a).
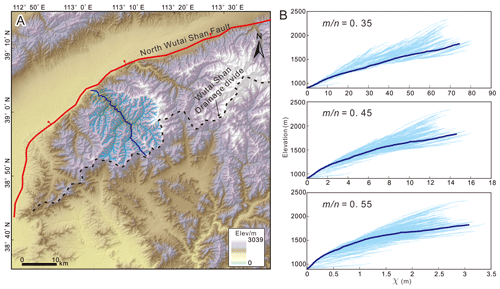
Figure 6(a) Drainage basin in the northern Wutai Shan. (b) χ plots of channel profiles in the drainage basin, using A0=1 m2 and , 0.45, and 0.55. The χ plots show the best choice of is 0.45, because the tributaries have systematically higher () or lower () elevations than the main stem for other values of (excluding the channels in the headwaters).
In this study, we quantify the influence of the cross-divide difference in rock uplift rate (ΔUch) on the calculation of the migration rate of drainage divides at the Wutai Shan, benefiting from the available tectonic and chronological research (Clinkscales et al., 2020) and the newly obtained high-resolution topographic data. In the Wutai Shan horst, ΔUch across the drainage divide is ∼0.008 mm yr−1. We estimate the influence of ΔUch on the drainage-divide migration rate in this case study, which can reduce the error theoretically. If ΔUch is ignored, the drainage-divide migration rate would decrease by ∼4 % in the Wutai Shan case. Although ∼4 % seems to be negligible, such a ratio will increase if the mountain belt is narrower, the tilting uplift is stronger, or the divide is closer to the steady state (i.e., the migration rate is lower) (Whipple et al., 2017; Ye et al., 2022). In other words, the differential uplift may play a significant influence on the measurement of drainage-divide stability in some situations. If we consider an extreme example where the main drainage divide of a tilting mountain range (relatively narrow in width) is at a steady state, the gradient, relief, and elevation of the channel heads (collectively called “Gilbert metrics”) (Forte and Whipple, 2018) will show a systematic cross-divide difference in theory. In this case, the drainage divide would be considered unstable if ΔUch were neglected. Therefore, this study highlights that ΔUch should be taken into account, either in a qualitative or a quantitative evaluation of the stability of drainage divides using the parameters on the channel heads.
4.3 Limitations and uncertainties
This study develops the method to calculate the drainage-divide migration rate based on the measured channel-head parameters. However, uncertainties still exist because of the limitations of this technique. First, we assume the erosion coefficient (K) is the same on both sides of a drainage divide in the derivation of the equations. If there are differences in rock erodibility or precipitation across the divide, uncertainties should exist in the results. Second, the calculation of migration rate is based on the erosion rates at the channel area in this study. However, the occurrence of drainage-divide migration is directly driven by the differential erosion of the hillslope area across the divide, mainly via the processes including landslide, collapse, and diffusion (Stock and Dietrich, 2006; Stark, 2010; Braun, 2018; Dahlquist et al., 2018). Such discontinuous processes in the hillslope area make it challenging to constrain erosion rates over such short timescales. Over a relatively longer period (i.e., spanning multiple seismic and climatic cycles), the erosion rate at the channel-head area in this study can be comparable with that at the hillslope area (Hurst et al., 2012; Godard et al., 2020).
The accuracy of the data and parameters can also impact the reliability of the results. First, we use the uniform values of n=1 and in the two natural cases to calculate the migration rate, because it is the best choice to align tributaries with the main stem on the χ plots in a drainage basin at the northern Wutai Shan (Fig. 6) (Perron and Royden, 2012). If the actual values deviate from the assumption, errors would be introduced into the results. For this reason, we have added the cases of and 0.55 in the Supplement. Further estimation of these values (Mudd et al., 2018) could improve the accuracy of the results. Second, in the case of the Wutai Shan, we refer to the geological and low-temperature thermochronology studies and assume a 0.50±0.25 mm yr−1 erosion rate at the northern margin of the Wutai Shan (i.e., the footwall of the North Wutai Shan Fault). Combining with the present-day ksn, we calculate the erosion coefficient (K) and derive the migration rates of the drainage divide. If the present-day erosion rate deviates from the assumption, errors would be inevitable in the results. Moreover, the horizontal and vertical errors in the DEM data, as well as the calculation errors in slope, upstream area, and channel steepness, can also affect the reliability of the results. In the case study of the Yingwang Shan, the lush vegetation may introduce errors to the DEM data based on the SfM technology. The application of airborne light detection and ranging (lidar) technology may help reduce this error. Future studies should take these challenges into account and overcome them.
We have developed a new method (called the “channel-head-point method”) to calculate the migration rate of drainage divides based on channel-head parameters. We have also improved the previously proposed “channel-head-segment method” (Zhou et al., 2022a) to adapt the theory to areas where the parameters of channel-heads can be accurately determined.
Using the new methods and high-resolution topographic data, we determined the exact locations of the channel heads on both sides of the drainage divide and quantified the drainage-divide migration rates in two natural cases in north China: Wutai Shan in the Shanxi Rift and Yingwang Shan in the Loess Plateau. The migration rates of the study sites in the Wutai Shan are 0.21–0.27 mm yr−1 (northwestward). The rates are close to zero in the Yingwang Shan.
Based on the locations of the channel heads and the uplift gradient of the Wutai Shan, we calculated the cross-divide difference in the uplift rate at the channel heads (ΔUch), which is taken into account in the calculation of the drainage-divide migration rate for the first time. If ΔUch is overlooked, the drainage-divide migration rate of the study sites in the Wutai Shan will be underestimated by ∼4 %. Our study highlights that ΔUch should be considered in the assessment of drainage divide stability based on the cross-divide difference in channel-head parameters.
The analysis of data is based on the MATLAB toolbox TAK (Forte and Whipple, 2019) and TopoToolbox (Schwanghart and Scherler, 2014). The topography data (ALOS DEM) are downloaded from the Alaska Satellite Facility (ASF) Data Search (https://search.asf.alaska.edu/, JAXA/METI, 2011). The high-resolution DEM of the two study areas, the Wutai Shan and the Yingwang Shan, can be downloaded from OpenTopography (https://doi.org/10.5069/G98C9TGT, Zhou, 2023).
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-12-433-2024-supplement.
XT and CZ contributed to the design of the research scheme. CZ performed the geomorphic analyses. CZ, XT, and FS carried out field data collection. CZ, XT, YL, and FS contributed to the text and reviewed the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We would like to thank the editor Simon Mudd, the reviewer Thomas Bernard, and an anonymous reviewer whose suggestions have greatly improved the paper.
This study is supported by the CAS Pioneer Hundred Talents Program (grant no. E2K2010010) and the Fundamental Research Funds for the State Key Laboratory of Earthquake Dynamics (grant no. LED2021A02).
This paper was edited by Simon Mudd and reviewed by Thomas Bernard and one anonymous referee.
Authemayou, C., Brocard, G., Delcaillau, B., Molliex, S., Pedoja, K., Husson, L., Aribowo, S., and Cahyarini, S. Y.: Unraveling the roles of asymmetric uplift, normal faulting and groundwater flow to drainage rearrangement in an emerging karstic landscape, Earth Surf. Proc. Land., 43, 1885–1898, https://doi.org/10.1002/esp.4363, 2018.
Beeson, H. W., McCoy, S. W., and Keen-Zebert, A.: Geometric disequilibrium of river basins produces long-lived transient landscapes, Earth Planet Sc. Lett., 475, 34–43, https://doi.org/10.1016/j.epsl.2017.07.010, 2017.
Bernard, T., Sinclair, H. D., Gailleton, B., and Fox, M.: Formation of Longitudinal River Valleys and the Fixing of Drainage Divides in Response to Exhumation of Crystalline Basement, Geophys. Res. Lett., 48, 1–9, https://doi.org/10.1029/2020gl092210, 2021.
Bian, S., Tan, X., Liu, Y., Fan, S., Gong, J., Zhou, C., Shi, F., and Murphy, M. A.: Orographic rainfall drives the Himalaya drainage divide to move north, Geomorphology, 444, 108952, https://doi.org/10.1016/j.geomorph.2023.108952, 2024.
Bonnet, S.: Shrinking and splitting of drainage basins in orogenic landscapes from the migration of the main drainage divide, Nat. Geosci., 2, 766–771, https://doi.org/10.1038/ngeo666, 2009.
Bookhagen, B. and Strecker, M. R.: Spatiotemporal trends in erosion rates across a pronounced rainfall gradient: Examples from the southern Central Andes, Earth Planet Sc. Lett., 327–328, 97–110, https://doi.org/10.1016/j.epsl.2012.02.005, 2012.
Braun, J.: A review of numerical modeling studies of passive margin escarpments leading to a new analytical expression for the rate of escarpment migration velocity, Gondwana Res., 53, 209–224, https://doi.org/10.1016/j.gr.2017.04.012, 2018.
Burbank, D. W. and Anderson, R. S.: Tectonic Geomorphology, Blackwell Science, Massachusetts, p. 274, ISBN 978-1-444-33887-4, 2001.
Burbank, D. W., Leland, J., Fielding, E., Anderson, R. S., Brozovic, N., Reid, M. R., and Duncan, C.: Bedrock incision, rock uplift and threshold hillslopes in the northwestern Himalayas, Nature, 379, 505–510, https://doi.org/10.1038/379505a0, 1996.
Carson, M. A. and Kirkby, M. J.: Hillslope form and process, Cambridge University Press, New York, p. 475, ISBN 052108234X, 1972.
Chen, C.-Y., Willett, S. D., Christl, M., and Shyu, J. B. H.: Drainage basin dynamics during the transition from early to mature orogeny in Southern Taiwan, Earth Planet Sc. Lett. 562, 116874, https://doi.org/10.1016/j.epsl.2021.116874, 2021.
Clark, M. K., Schoenbohm, L. M., Royden, L. H., Whipple, K. X., Burchfiel, B. C., Zhang, X., Tang, W., Wang, E., and Chen, L.: Surface uplift, tectonics, and erosion of eastern Tibet from large-scale drainage patterns, Tectonics, 23, 1–20, https://doi.org/10.1029/2002tc001402, 2004.
Clift, P. D. and Blusztajn, J.: Reorganization of the western Himalayan river system after five million years ago, Nature, 438, 1001–1003, https://doi.org/10.1038/nature04379, 2005.
Clinkscales, C., Kapp, P., and Wang, H.: Exhumation history of the north-central Shanxi Rift, North China, revealed by low-temperature thermochronology, Earth Planet. Sc. Lett., 536, 116146, https://doi.org/10.1016/j.epsl.2020.116146, 2020.
Clubb, F. J., Mudd, S. M., Milodowski, D. T., Hurst, M. D., and Slater, L. J.: Objective extraction of channel heads from high-resolution topographic data, Water Resour. Res., 50, 4283–4304, https://doi.org/10.1002/2013wr015167, 2014.
Crosby, B. T., and Whipple, K. X.: Knickpoint initiation and distribution within fluvial networks: 236 waterfalls in the Waipaoa River, North Island, New Zealand, Geomorphology, 82, 16–38, https://doi.org/10.1016/j.geomorph.2005.08.023, 2006.
Dahlquist, M. P., West, A. J., and Li, G.: Landslide-driven drainage divide migration, Geology, 46, 403-406, https://doi.org/10.1130/g39916.1, 2018.
Deng, B., Chew, D., Mark, C., Liu, S., Cogné, N., Jiang, L., O'Sullivan, G., Li, Z., and Li, J.: Late Cenozoic drainage reorganization of the paleo-Yangtze river constrained by multi-proxy provenance analysis of the Paleo-lake Xigeda, GSA Bull., 133, 199–211, https://doi.org/10.1130/b35579.1, 2020.
DiBiase, R. A., Whipple, K. X., Heimsath, A. M., Ouimet, W. B.: Landscape form and millennial erosion rates in the San Gabriel Mountains, CA, Earth Planet Sc. Lett., 289, 134–144, https://doi.org/10.1016/j.epsl.2009.10.036, 2010.
Duvall, A.: Tectonic and lithologic controls on bedrock channel profiles and processes in coastal California, J. Geophys. Res., 109, F03002, https://doi.org/10.1029/2003jf000086, 2004.
Forte, A. M. and Whipple, K. X.: Criteria and tools for determining drainage divide stability, Earth Planet Sc. Lett., 493, 102–117, https://doi.org/10.1016/j.epsl.2018.04.026, 2018.
Forte, A. M. and Whipple, K. X.: Short communication: The Topographic Analysis Kit (TAK) for TopoToolbox, Earth Surf. Dynam., 7, 87–95, https://doi.org/10.5194/esurf-7-87-2019, 2019.
Forte, A. M., Yanites, B. J., and Whipple, K. X.: Complexities of landscape evolution during incision through layered stratigraphy with contrasts in rock strength, Earth Surf. Proc. Land., 41, 1736–1757, https://doi.org/10.1002/esp.3947, 2016.
Fu, B.: Soil erosion and its control in the loess plateau of China, Soil Use Manage., 5, 76–82, https://doi.org/10.1111/j.1475-2743.1989.tb00765.x, 1989.
Gallen, S. F.: Lithologic controls on landscape dynamics and aquatic species evolution in post-orogenic mountains, Earth Planet Sc. Lett., 493, 150–160, https://doi.org/10.1016/j.epsl.2018.04.029, 2018.
Godard, V., Dosseto, A., Fleury, J., Bellier, O., and Siame, L.: Transient landscape dynamics across the Southeastern Australian Escarpment, Earth Planet Sc. Lett., 506, 397–406, https://doi.org/10.1016/j.epsl.2018.11.017, 2019.
Godard, V., Hippolyte, J.-C., Cushing, E., Espurt, N., Fleury, J., Bellier, O., and Ollivier, V.: Hillslope denudation and morphologic response to a rock uplift gradient, Earth Surf. Dynam., 8, 221–243, https://doi.org/10.5194/esurf-8-221-2020, 2020.
Goren, L., Fox, M., and Willett, S. D.: Tectonics from fluvial topography using formal linear inversion: Theory and applications to the Inyo Mountains, California, J. Geophys. Res.-Earth, 119, 1651–1681, https://doi.org/10.1002/2014jf003079, 2014.
Hancock, G. S. and Anderson, R. S.: Numerical modeling of fluvial strath-terrace formation in response to oscillating climate, GSA Bull., 114, 1131–1142, https://doi.org/10.1130/0016-7606(2002)114<1131:nmofst>2.0.co;2, 2002.
He, C., Yang, C. J., Turowski, J. M., Rao, G., Roda-Boluda, D. C., and Yuan, X. P.: Constraining tectonic uplift and advection from the main drainage divide of a mountain belt, Nat. Commun., 12, 544, https://doi.org/10.1038/s41467-020-20748-2, 2021.
Hilley, G. E. and Arrowsmith, J. R.: Geomorphic response to uplift along the Dragon's Back pressure ridge, Carrizo Plain, California, Geology, 36, 367–370, https://doi.org/10.1130/g24517a.1, 2008.
Hoorn, C., Wesselingh, F. P., Steege, H. T., Bermudez, M. A., and Antonelli, A.: Amazonia Through Time: Andean Uplift, Climate Change, Landscape Evolution, and Biodiversity, Science, 330, 927–931, https://doi.org/10.1126/science.1194585, 2010.
Hoskins, A. M., Attal, M., Mudd, S. M., and Castillo, M.: Topographic Response to Horizontal Advection in Normal Fault-Bound Mountain Ranges, J. Geophys. Res.-Earth, 128, e2023JF007126, https://doi.org/10.1029/2023jf007126, 2023.
Howard, A. D. and Kerby, G.: Channel changes in badlands, Geol. Soc. Am. Bull., 94, 739–752, https://doi.org/10.1130/0016-7606(1983)94<739:CCIB>2.0.CO;2, 1983.
Howard, A. D., Dietrich, W. E., and Seidl, M. A.: Modeling fluvial erosion on regional to continental scales, J. Geophys. Res.-Solid, 99, 13971–13986, https://doi.org/10.1029/94jb00744, 1994.
Hu, K., Fang, X., Ferrier, K. L., Granger, D. E., Zhao, Z., and Ruetenik, G. A.: Covariation of cross-divide differences in denudation rate and χ: Implications for drainage basin reorganization in the Qilian Shan, northeast Tibet, Earth Planet Sc. Lett., 562, 116812, https://doi.org/10.1016/j.epsl.2021.116812, 2021.
Hurst, M. D., Mudd, S. M., Walcott, R., Attal, M., and Yoo, K.: Using hilltop curvature to derive the spatial distribution of erosion rates, J. Geophys. Res.-Earth, 117, F02017, https://doi.org/10.1029/2011jf002057, 2012.
JAXA/METI: ALOS PALSAR Hi-Res Terrain Corrected, ASF Data Search, https://search.asf.alaska.edu/ (last access: December 2020), 2011.
Jiao, R., Fox, M., and Yang, R.: Late Cenozoic erosion pattern of the eastern margin of the Sichuan Basin: Implications for the drainage evolution of the Yangtze River, Geomorphology, 398, 108025, https://doi.org/10.1016/j.geomorph.2021.108025, 2022.
Kirby, E. and Whipple, K.: Quantifying differential rock-uplift rates via stream profile analysis, Geology, 29, 415-418, https://doi.org/10.1130/0091-7613(2001)029<0415:Qdrurv>2.0.Co;2, 2001.
Kirby, E. and Whipple, K. X.: Expression of active tectonics in erosional landscapes, J. Struct. Geol., 44, 54–75, https://doi.org/10.1016/j.jsg.2012.07.009, 2012.
Kirby, E., Whipple, K., Tang, W., and Chen, Z.: Distribution of active rock uplift along the eastern margin of the Tibetan Plateau: Inferences from bedrock channel longitudinal profiles, J. Geophys. Res., 108, 2217, https://doi.org/10.1029/2001JB000861, 2003.
Kirkpatrick, H. M., Moon, S., Yin, A., and Harrison, T. M.: Impact of fault damage on eastern Tibet topography, Geology, 49, 30–34, https://doi.org/10.1130/g48179.1, 2020.
Ma, Z., Zhang, H., Wang, Y., Tao, Y., and Li, X.: Inversion of Dadu River Bedrock Channels for the Late Cenozoic Uplift History of the Eastern Tibetan Plateau, Geophys. Res. Lett., 47, e2019GL086882, https://doi.org/10.1029/2019gl086882, 2020.
Mandal, S. K., Lupker, M., Burg, J.-P., Valla, P. G., Haghipour, N., and Christl, M.: Spatial variability of 10Be-derived erosion rates across the southern Peninsular Indian escarpment: A key to landscape evolution across passive margins, Earth Planet Sc. Lett., 425, 154–167, https://doi.org/10.1016/j.epsl.2015.05.050, 2015.
Middleton, T. A., Elliott, J. R., Rhodes, E. J., Sherlock, S., Walker, R. T., Wang, W., Yu, J., and Zhou, Y.: Extension rates across the northern Shanxi Grabens, China, from Quaternary geology, seismicity and geodesy, Geophys. J. Int., 209, 535–558, https://doi.org/10.1093/gji/ggx031, 2017.
Molnar, P. and England, P.: Late Cenozoic uplift of mountain ranges and global climate change: chicken or egg?, Nature, 346, 29–34, https://doi.org/10.1038/346029a0, 1990.
Mudd, S. M., Clubb, F. J., Gailleton, B., and Hurst, M. D.: How concave are river channels?, Earth Surf. Dynam., 6, 505–523, https://doi.org/10.5194/esurf-6-505-2018, 2018.
Musher, L. J., Giakoumis, M., Albert, J., Rio, G. D., Rego, M., Thom, G., Aleixo, A., Ribas, C. C., Brumfield, R. T., and Smith, B. T.: River network rearrangements promote speciation in lowland Amazonian birds, Cold Spring Harbor Laboratory, https://doi.org/10.1126/sciadv.abn1099, 2021.
Perron, J. T. and Royden, L.: An integral approach to bedrock river profile analysis, Earth Surf. Proc. Land., 38, 570–576, https://doi.org/10.1002/esp.3302, 2012.
Perron, J. T., Dietrich, W. E., and Kirchner, J. W.: Controls on the spacing of first-order valleys, J. Geophys. Res., 113, F04016, https://doi.org/10.1029/2007jf000977, 2008.
Pritchard, D., Roberts, G. G., White, N. J., and Richardson, C. N.: Uplift histories from river profiles, Geophys. Res. Lett., 36, L24301, https://doi.org/10.1029/2009gl040928, 2009.
Royden, L., Clark, M., and Whipple, K.: Evolution of river elevation profiles by bedrock incision: Analytical solutions for transient river profiles related to changing uplift and precipitation rates, in: Eos Trans AGU, 81, Fall Meet. Suppl., Abstract T62F-09, 2000.
Safran, E. B., Bierman, P. R., Aalto, R., Dunne, T., Whipple, K. X., and Caffee, M.: Erosion rates driven by channel network incision in the Bolivian Andes, Earth Surf. Proc. Land., 30, 1007–1024, https://doi.org/10.1002/esp.1259, 2005.
Sakashita, A. and Endo, N.: Mobility and Location of Drainage Divides Affected by Tilting Uplift in Sado Island, Japan, Remote Sens., 15, 729, https://doi.org/10.3390/rs15030729, 2023.
Sassolas-Serrayet, T., Cattin, R., Ferry, M., Godard, V., and Simoes, M.: Estimating the disequilibrium in denudation rates due to divide migration at the scale of river basins, Earth Surf. Dynam., 7, 1041–1057, https://doi.org/10.5194/esurf-7-1041-2019, 2019.
Scheingross, J. S., Limaye, A. B., McCoy, S. W., and Whittaker, A. C.: The shaping of erosional landscapes by internal dynamics, Nat. Rev. Earth Environ., 1, 661–676, https://doi.org/10.1038/s43017-020-0096-0, 2020.
Scherler, D. and Schwanghart, W.: Drainage divide networks – Part 2: Response to perturbations, Earth Surf. Dynam., 8, 261–274, https://doi.org/10.5194/esurf-8-261-2020, 2020.
Schildgen, T. F., van der Beek, P. A., D'Arcy, M., Roda-Boluda, D., Orr, E. N., and Wittmann, H.: Quantifying drainage-divide migration from orographic rainfall over geologic timescales: Sierra de Aconquija, southern Central Andes, Earth Planet Sc. Lett., 579, 117345, https://doi.org/10.1016/j.epsl.2021.117345, 2022.
Schlunegger, F., Norton, K. P., and Zeilinger, G.: Climatic Forcing on Channel Profiles in the Eastern Cordillera of the Coroico Region, Bolivia, J. Geology, 119, 97–107, https://doi.org/10.1086/657407, 2011.
Schwanghart, W. and Scherler. D.: Short Communication: TopoToolbox 2 – MATLAB-based software for topographic analysis and modeling in Earth surface sciences, Earth Surf. Dynam., 2, 1–7, https://doi.org/10.5194/esurf-2-1-2014, 2014.
Shelef, E. and Goren, L.: The rate and extent of wind-gap migration regulated by tributary confluences and avulsions, Earth Surf. Dynam., 9, 687–700, https://doi.org/10.5194/esurf-9-687-2021, 2021.
Shi, F., Tan, X., Zhou, C., and Liu, Y.: Impact of asymmetric uplift on mountain asymmetry: Analytical solution, numerical modeling, and natural examples, Geomorphology, 389, 107862, https://doi.org/10.1016/j.geomorph.2021.107862, 2021.
Shi, W., Dong, S., and Hu, J.: Neotectonics around the Ordos Block, North China: A review and new insights, Earth-Sci. Rev., 200, 102969, https://doi.org/10.1016/j.earscirev.2019.102969, 2020.
Stark, C. P.: Oscillatory motion of drainage divides, Geophys. Res. Lett., 37, L04401, https://doi.org/10.1029/2009gl040851, 2010.
Stock, J. D. and Dietrich, W. E.: Erosion of steepland valleys by debris flows, Geol. Soc. Am. Bull., 118, 1125–1148, https://doi.org/10.1130/b25902.1, 2006.
Stokes, M. F., Larsen, I. J., Goldberg, S. L., McCoy, S. W., Prince, P. P., and Perron, J. T.: The Erosional Signature of Drainage Divide Motion Along the Blue Ridge Escarpment, J. Geophys. Res.-Earth, 128, e2022JF006757, https://doi.org/10.1029/2022jf006757, 2023.
Struth, L., Teixell, A., Owen, L. A., and Babault, J.: Plateau reduction by drainage divide migration in the Eastern Cordillera of Colombia defined by morphometry and 10Be terrestrial cosmogenic nuclides, Earth Surf. Proc. Land., 42, 1155–1170, https://doi.org/10.1002/esp.4079, 2017.
Su, P., He, H., Tan, X., Liu, Y., Shi, F., and Kirby, E.: Initiation and Evolution of the Shanxi Rift System in North China: Evidence From Low-Temperature Thermochronology in a Plate Reconstruction Framework, Tectonics, 40, e2020TC006298, https://doi.org/10.1029/2020tc006298, 2021.
Su, Q., Wang, X., Lu, H., and Xie, H.: Dynamic Divide Migration as a Response to Asymmetric Uplift: An Example from the Zhongtiao Shan, North China, Remote Sens., 12, 4188, https://doi.org/10.3390/rs12244188, 2020.
Tucker, G. E. and Bras, R. L.: Hillslope processes, drainage density, and landscape morphology, Water Resour. Res., 34, 2751–2764, https://doi.org/10.1029/98wr01474, 1998.
Tucker, G. E. and Slingerland, R.: Drainage basin responses to climate change, Water Resour. Res., 33, 2031–2047, https://doi.org/10.1029/97wr00409, 1997.
Vacherat, A., Bonnet, S., and Mouthereau, F.: Drainage reorganization and divide migration induced by the excavation of the Ebro basin (NE Spain), Earth Surf. Dynam., 6, 369–387, https://doi.org/10.5194/esurf-6-369-2018, 2018.
Wang, Y., Liu, C., Zheng, D., Zhang, H., Yu, J., Pang, J., Li, C., and Hao, Y.: Multistage Exhumation in the Catchment of the Anninghe River in the SE Tibetan Plateau: Insights From Both Detrital Thermochronology and Topographic Analysis, Geophys. Res. Lett., 48, e2021GL092587, https://doi.org/10.1029/2021gl092587, 2021.
Waters, J. M., Craw, D., Youngson, J. H., and Wallis, G. P.: Genes meet geology: fish phylogeographic pattern reflects ancient, rather than modern, drainage connections, Evolution, 55, 1844–1851, https://doi.org/10.1111/j.0014-3820.2001.tb00833.x, 2001.
Wei, Z., Arrowsmith, J. R., and He, H.: Evaluating fluvial terrace riser degradation using LiDAR-derived topography: An example from the northern Tian Shan, China, J. Asian Earth Sci., 105, 430-442, https://doi.org/10.1016/j.jseaes.2015.02.016, 2015.
Whipple, K. X.: Fluvial landscape response time: how plausible is steady-state denudation?, Am. J. Sci., 301, 313–325, https://doi.org/10.2475/ajs.301.4-5.313, 2001.
Whipple, K. X.: The influence of climate on the tectonic evolution of mountain belts, Nat. Geosci., 2, 97–104, https://doi.org/10.1038/ngeo413, 2009.
Whipple, K. X., Kirby, E., and Brocklehurst, S. H.: Geomorphic limits to climate-induced increases in topographic relief, Nature, 401, 39–43, https://doi.org/10.1038/43375, 1999.
Whipple, K. X., Forte, A. M., DiBiase, R. A., Gasparini, N. M., and Ouimet, W. B.: Timescales of landscape response to divide migration and drainage capture: Implications for the role of divide mobility in landscape evolution, J. Geophys. Res.-Earth, 122, 248–273, https://doi.org/10.1002/2016JF003973, 2017.
Willett, S. D., McCoy, S. W., Perron, J. T., Goren, L., and Chen, C. Y.: Dynamic reorganization of river basins, Science, 343, 1248765, https://doi.org/10.1126/science.1248765, 2014.
Willett, S. D., McCoy, S. W., and Beeson, H. W.: Transience of the North American High Plains landscape and its impact on surface water, Nature, 561, 528–532, https://doi.org/10.1038/s41586-018-0532-1, 2018.
Wobus, C., Whipple, K. X., Kirby, E., Snyder, N., Johnson, J., Spyropolou, K., Crosby, B., and Sheehan, D.: Tectonics from topography: Procedures, promise, and pitfalls, in: Tectonics, Climate, and Landscape Evolution, edited by: Willett, S. D., Hovius, N., Brandon, M. T., and Fisher, D., Geological Society of America Special Paper 398, Geological Society of America, 5–74, https://doi.org/10.1130/2006.2398(04), 2006.
Wu, Y., Yang, R., He, C., and He, J.: Caution on determining divide migration from cross-divide contrast in χ, Geol. J., 57, 4090–4098, https://doi.org/10.1002/gj.4530, 2022.
Xiong, L.-Y., Tang, G.-A., Li, F.-Y., Yuan, B.-Y., and Lu, Z.-C.: Modeling the evolution of loess-covered landforms in the Loess Plateau of China using a DEM of underground bedrock surface, Geomorphology, 209, 18–26, https://doi.org/10.1016/j.geomorph.2013.12.009, 2014.
Xu, X., Ma, X., and Deng, Q.: Neotectonic activity along the Shanxi rift system, China, Tectonophysics, 219, 305–325, https://doi.org/10.1016/0040-1951(93)90180-R, 1993.
Yan, M.-J., He, Q.-Y., Yamanaka, N., and Du, S.: Location, Geology and Landforms of the Loess Plateau, in: Restoration and development of the degraded Loess Plateau, China, edited by: Tsunekawa, A., Liu, G., Yamanaka, N., Du, S., Springer, Japan, 3–22, https://doi.org/10.1007/978-4-431-54481-4, 2014.
Yang, R., Suhail, H. A., Gourbet, L., Willett, S. D., Fellin, M. G., Lin, X., Gong, J., Wei, X., Maden, C., Jiao, R., and Chen, H.: Early Pleistocene drainage pattern changes in Eastern Tibet: Constraints from provenance analysis, thermochronometry, and numerical modeling, Earth Planet Sc. Lett., 531, 1–10, https://doi.org/10.1016/j.epsl.2019.115955, 2019.
Ye, Y., Tan, X., and Zhou, C.: Initial topography matters in drainage divide migration analysis: Insights from numerical simulations and natural examples, Geomorphology, 409, 108266, https://doi.org/10.1016/j.geomorph.2022.108266, 2022.
Yin, A.: Cenozoic tectonic evolution of Asia: A preliminary synthesis, Tectonophysics, 488, 293–325, https://doi.org/10.1016/j.tecto.2009.06.002, 2010.
Young, H. H. and Hilley, G. E.: Millennial-scale denudation rates of the Santa Lucia Mountains, California: Implications for landscape evolution in steep, high-relief, coastal mountain ranges, GSA Bull., 130, 1809–1824, https://doi.org/10.1130/B31907.1, 2018.
Zemlak, T. S., Habit, E. M., Walde, S. J., Battini, M .A., Adams, E. D. M., and Ruzzante, D. E.: Across the southern Andes on fin: glacial refugia, drainage reversals and a secondary contact zone revealed by the phylogeographical signal of Galaxias platei in Patagonia, Molec. Ecol., 17, 5049–5061, https://doi.org/10.1111/j.1365-294X.2008.03987.x, 2008.
Zeng, X. and Tan, X.: Drainage divide migration in response to strike-slip faulting: An example from northern Longmen Shan, eastern Tibet, Tectonophysics, 848, 229720, https://doi.org/10.1016/j.tecto.2023.229720, 2023.
Zhao, X., Zhang, H., Hetzel, R., Kirby, E., Duvall, A. R., Whipple, K. X., Xiong, J., Li, Y., Pang, J., Wang, Y., Wang, P., Liu, K., Ma, P., Zhang, B., Li, X., Zhang, J., and Zhang, P.: Existence of a continental-scale river system in eastern Tibet during the late Cretaceous-early Palaeogene, Nat. Commun., 12, 7231, https://doi.org/10.1038/s41467-021-27587-9, 2021.
Zhou, C.: High Resolution Topography of Wutai Shan and Yingwang Shan, China, 2021, OpenTopography [data set], https://doi.org/10.5069/G98C9TGT, 2023.
Zhou, C. and Tan, X.: Quantifying the influence of asymmetric uplift, base level elevation, and erodibility on cross-divide χ difference, Geomorphology, 427, 108634, https://doi.org/10.1016/j.geomorph.2023.108634, 2023.
Zhou, C., Tan, X., Liu, Y., Lu, R., Murphy, M. A., He, H., Han, Z., and Xu, X.: Ongoing westward migration of drainage divides in eastern Tibet, quantified from topographic analysis, Geomorphology, 402, 108123, https://doi.org/10.1016/j.geomorph.2022.108123, 2022a.
Zhou, C., Tan, X., Liu, Y., and Shi, F.: A cross-divide contrast index (C) for assessing controls on the main drainage divide stability of a mountain belt, Geomorphology, 398, 108071, https://doi.org/10.1016/j.geomorph.2021.108071, 2022b.
Zondervan, J. R., Stokes, M., Boulton, S. J., Telfer, M. W., and Mather, A. E.: Rock strength and structural controls on fluvial erodibility: Implications for drainage divide mobility in a collisional mountain belt, Earth Planet Sc. Lett., 538, 116221, https://doi.org/10.1016/j.epsl.2020.116221, 2020.