Quantifying the migration rate of drainage divides from high-resolution topographic data

The lateral movement of drainage divides is co-influenced by tectonics, lithology, and climate and therefore archives a wealth of geologic and climatic information. It also has wide-ranging implications for topography, the sedimentary record, and biological evolution and thus has drawn much attention in recent years. Several methods have been proposed to determine drainage divides' migration state (direction and rate), including geochronological approaches (e.g., ¹⁰Be) and topography-based approaches (e.g., χ plots or Gilbert metrics). A key object in these methods is the channel head, which separates the hillslope and channel. However, due to the limited resolution of topography data, the required channel-head parameters in the calculation often cannot be determined accurately, and empirical values are used in the calculation, which may induce uncertainties. Here, we propose two methods to calculate the migration rate of drainage divides based on the relatively accurate channel-head parameters derived from high-resolution topographic data. We then apply the methods to an active rift shoulder (Wutai Shan) in the Shanxi Rift and a tectonically stable area (Yingwang Shan) in the Loess Plateau, to illustrate how to calculate drainage-divide migration rates. Our results show that the Wutai Shan drainage divide is migrating northwestward at a rate between 0.21 and 0.27 mm yr⁻¹, whereas the migration rates at the Yingwang Shan are approximately zero. This study indicates that the drainage-divide stability can be determined more accurately using high-resolution topographic data. Furthermore, this study takes the cross-divide differences in the uplift rate of channel heads into account in the measurement of drainage-divide migration rate for the first time.

1 Introduction

The evolution of the Earth's surface is jointly controlled by tectonics, lithology, and climatic conditions (e.g., Molnar and England, 1990; Whipple, 2009; Gallen, 2018; Bernard et al., 2021; Hoskins et al., 2023), providing a basis for reconstructing the past tectonic (Pritchard et al., 2009; Kirby and Whipple, 2012; Shi et al., 2021) or climatic processes (Tucker an Slingerland, 1997; Hancock and Anderson, 2002; Schildgen et al., 2022) through topography. The evolution of unglaciated terrestrial terrains is fundamentally coupled with changes in drainage systems through a river's vertical (changes in river long profile) and lateral movements (drainage divide migration and river captures) (Whipple, 2001; Clark et al., 2004; Bonnet, 2009; Willett et al., 2014). Previous studies have extensively investigated how river channel profiles respond to tectonic uplift (Whipple, 2001; Crosby and Whipple, 2006; Kirby and Whipple, 2012), lithological differences (Duvall, 2004; Safran et al., 2005; Forte et al., 2016), and precipitation perturbations (Schlunegger et al., 2011; Bookhagen and Strecker, 2012). River long profiles have been used to study earthquake events (e.g., Burbank and Anderson, 2001; Wei et al., 2015) and the spatio-temporal variations in uplift (e.g., Whipple et al., 1999; Kirby et al., 2003; Pritchard et al., 2009; Goren et al., 2014). Recent studies show that the widespread lateral movement of river basins driven by geological and/or climatic disturbance (Yang et al., 2019; Zondervan et al., 2020; Zhou et al., 2022a; Bian et al., 2024) also interacts with the adjustment of channel profiles (Willett et al., 2014). Drainage-divide migration, one form of river lateral movement, may not only carry information on geological and/or climatic disturbance (Su et al., 2020; Zondervan et al., 2020; He et al., 2021; Shi et al., 2021; Zhou et al., 2022a; Zeng and Tan, 2023) but also influence the extraction of tectonic information from channel profiles (Goren et al., 2014; Ma et al., 2020; Jiao et al., 2022). Moreover, it has multi-facet consequences for landscape evolution (Scheingross et al., 2020; Stokes et al., 2023), sedimentary processes (Clift and Blusztajn, 2005; Willett et al., 2018; Deng et al., 2020; Zhao et al., 2021), and biological evolution (Waters et al., 2001; Zemlak et al., 2008; Hoorn et al., 2010; Musher et al., 2021). For this reason, the stability of drainage divides has drawn more and more attention in recent years (e.g., Authemayou et al., 2018; Vacherat et al., 2018; Chen et al., 2021; Shelef and Goren, 2021; Sakashita and Endo, 2023; Bian et al., 2024).

Drainage-divide migration is essentially controlled by the cross-divide difference in erosion and topographic slope (Beeson et al., 2017; Dahlquist et al., 2018; Chen et al., 2021; Zhou et al., 2022a). The erosion rates are routinely derived from geochronological techniques, such as cosmogenic nuclide (e.g., ¹⁰Be) concentration measurements (Mandal et al., 2015; Struth et al., 2017; Young and Hilley, 2018; Sassolas-Serrayet et al., 2019), which can be used to calculate the migration rates of drainage divides (Beeson et al., 2017; Godard et al., 2019; Hu et al., 2021). However, these techniques are usually based on samples collected from a catchment outlet that is several, or even tens of, kilometers away from the drainage divide and thus may not represent the erosion rates close to the drainage divide (Sassolas-Serrayet et al., 2019; Zhou et al., 2022a). Besides, the high cost of sample processing makes it challenging to determine the drainage divide's motion by measuring the erosion rates throughout the large landscapes. Hence, it would be ideal to find an accessible and efficient method that can be applied to the entire landscape and make full use of the ¹⁰Be-derived erosion rates.

The advancement of the digital elevation model (DEM) has promoted the development of geomorphic analysis, making it possible to determine the drainage divide's transient motion through topography analysis. For example, Willett et al. (2014) applied the χ method to map the dynamic state of river basins. Forte and Whipple (2018) proposed the cross-divide comparison of “Gilbert metrics” (including channel heads' relief, slope, and elevation) to determine a drainage divide's migration direction. Others adopted the comparison of slope angle or relief of the hillslopes across a drainage divide to deduce its stability (Scherler and Schwanghart, 2020; Ye et al., 2022; Zhou et al., 2022b). These geomorphic techniques, so far, have only been able to determine the migration direction of drainage divides. Braun (2018) provided an equation that considers both alluvial and fluvial areas to calculate the migration velocity of an escarpment (also a drainage divide). Zhou et al. (2022a) developed a technique to calculate the migration rate through the high base-level χ values on both sides of a drainage divide. These new approaches require channel-head parameters to calculate the migration rate. However, the location of the channel heads sometimes cannot be accurately identified because of the limitation in the resolution of DEMs in natural cases. For this reason, empirical values of channel-head parameters are used in these studies, which may induce uncertainties.

This study aims to establish an approach to derive the migration rate of drainage divides, at a high precision and low cost, based on topographic analysis. We chose a tectonically active area (i.e., the Wutai Shan in the Shanxi Rift) and a tectonically inactive area (i.e., the Yingwang Shan in the Loess Plateau) to demonstrate how to quantify drainage-divide migration rates (Fig. 1). We use the aerial photography acquired by unoccupied aerial vehicles (UAVs) and the Structure-from-Motion (SfM) technology to obtain the high-resolution DEM data of these two areas (0.67 and 0.84 m spatial resolution in the Wutai Shan and the Yingwang Shan, respectively). Benefiting from the high-resolution data, the location of channel heads can be identified more accurately. We then develop two methods to calculate the drainage-divide migration rates. One is based on the measured channel-head parameters, and the other is based on an improved method of Zhou et al. (2022a). Combining with the geological and low-temperature thermochronology studies of the Wutai Shan (Middleton et al., 2017; Clinkscales et al., 2020), we also quantify the cross-divide difference in uplift rates to improve the precision of drainage-divide migration rate.

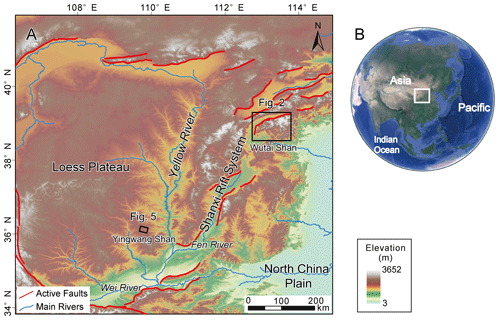
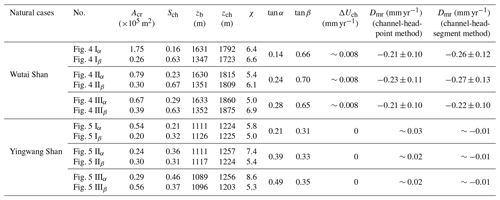
Figure 1 Locations and tectonic background of the two nature cases in north China. The figure is modified from Fig. 7 in Shi et al. (2021). (a) Red lines represent the main active faults. Black rectangles show the locations of the two nature cases. The red curve denotes the active fault, sourced from https://www.activefault-datacenter.cn/ (last access: October 2023). The topography data (ALOS DEM) are downloaded from the Alaska Satellite Facility (ASF) data search (https://search.asf.alaska.edu/, last access: December 2011). (b) The satellite image downloaded from © Google Earth. White rectangles show the location of panel (a).

2 Methods

2.1 Channel-head-point method

According to the detachment-limited stream power model (Howard and Kerby, 1983; Howard et al., 1994), the channel's erosion rate (E) can be expressed as

$$\begin{array}{}\text{(1)}& E=K{A}^m{S}^n,\end{array}$$

where K is the erosion coefficient, A is the upstream drainage area, S is the gradient of the river channel, and m and n are empirical constants.

Because of thresholds such as erosion threshold (the shear stress of overland flow must exceed the threshold of the cohesion of bed material to generate river incision) (Howard and Kerby, 1983; Perron et al., 2008) or landslide threshold (landslides occur when the threshold of soil or rock strength is exceeded in a high relief region) (Burbank et al., 1996; Tucker and Bras, 1998), river channels (following Eq. 1) emerge at a certain distance from the drainage divide. The region between the channel head and the drainage divide is referred to as the hillslope area, where the erosion is controlled by landslide, collapse, and diffusion processes (Carson and Kirkby, 1972; Stock and Dietrich, 2006; Stark, 2010; Braun, 2018; Dahlquist et al., 2018). The channel-head point is the highest and the closest point to the drainage divide on a river channel (Clubb et al., 2014). Therefore, the erosion rate at channel-head points (E_ch) can be described as

$$\begin{array}{}\text{(2)}& E_{\mathrm{ch}}=K{A}_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\end{array}$$

where E_ch is the erosion rate at channel-head points, A_cr is the critical upstream drainage area of a channel-head point (Duvall, 2004; Wobus et al., 2006), and S_ch is the channel-head gradient measured along the channel near the channel-head point. Equation (2) indicates that the side of a drainage divide with a higher A_cr or S_ch can have a higher erosion rate than the other side and is more likely to pirate the opposite drainage basin. Besides, a high erosion coefficient can amplify the drainage basin's erosion rate.

Drainage-divide migration is essentially controlled by the cross-divide difference in erosion rates and topographic slope (Beeson et al., 2017; Dahlquist et al., 2018; Chen et al., 2021; Zhou et al., 2022a; Stokes et al., 2023). Furthermore, the differential uplift should also be considered when using the cross-divide erosion rates at the channel heads to calculate the erosion difference across the divide, especially in the case of tectonic tilting uplift (Zhou et al., 2022a). The drainage-divide migration rate (D_mr) can be obtained according to the cross-divide difference in erosion rate and uplift rate and the slopes across the divide (Zhou et al., 2022a):

$$\begin{array}{}\text{(3)}& D_{\mathrm{mr}}={\displaystyle \frac{\mathrm{\Delta }{E}_{\mathrm{ch}}-\mathrm{\Delta }{U}_{\mathrm{ch}}}{\tan \mathit{\alpha }+\tan \mathit{\beta }}},\end{array}$$

where ΔE_ch is the difference in erosion rate between the two sides (annotated as α and β) of the drainage divide ($\mathrm{\Delta }{E}_{\mathrm{ch}}=E_{\mathrm{ch}\mathit{\alpha }}-E_{\mathrm{ch}\mathit{\beta }}$). The choice of α or β is arbitrary, and the positive direction of the migration rate is assigned from the α to the β side, whereas the negative is the opposite. ΔU_ch is the cross-divide difference in uplift rate ($\mathrm{\Delta }{U}_{\mathrm{ch}}=U_{\mathrm{ch}\mathit{\alpha }}-U_{\mathrm{ch}\mathit{\beta }}$), and tan α and tan β are the average gradients (along the normal-divide direction) upslope of the channel head (not including the hilltop part) on the α side and the β side, respectively. Assuming the erosion coefficient (K) is the same on both sides of a drainage divide, Eqs. (2) and (3) allow us to derive the equation of drainage divide's migration rate according to the parameters at the channel-head points:

$$\begin{array}{}\text{(4)}& D_{\mathrm{mr}}={\displaystyle \frac{K\left[{\left(A_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\right)}_{\mathit{\alpha }}-{\left(A_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\right)}_{\mathit{\beta }}\right]-\mathrm{\Delta }{U}_{\mathrm{ch}}}{\tan \mathit{\alpha }+\tan \mathit{\beta }}}.\end{array}$$

If the exact value of K is unknown, the drainage divide's unilateral erosion rate can be used as a substitution:

$$\begin{array}{}\text{(5)}& D_{\mathrm{mr}}={\displaystyle \frac{E_{\mathit{\alpha }}\left[\mathrm{1}-\frac{{\left(A_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\right)}_{\mathit{\beta }}}{{\left(A_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\right)}_{\mathit{\alpha }}}\right]-\mathrm{\Delta }{U}_{\mathrm{ch}}}{\tan \mathit{\alpha }+\tan \mathit{\beta }}}\end{array}$$

or

$$\begin{array}{}\text{(6)}& D_{\mathrm{mr}}={\displaystyle \frac{E_{\mathit{\beta }}\left[\frac{{\left(A_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\right)}_{\mathit{\alpha }}}{{\left(A_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\right)}_{\mathit{\beta }}}-\mathrm{1}\right]-\mathrm{\Delta }{U}_{\mathrm{ch}}}{\tan \mathit{\alpha }+\tan \mathit{\beta }}}.\end{array}$$

E_α and E_β are the erosion rates of the α and the β side of the drainage divide, respectively, which can be derived through cosmogenic nuclides (¹⁰Be) concentration measurements (Beeson et al., 2017; Godard et al., 2019; Hu et al., 2021). The regional average erosion rate ($\stackrel{\mathrm{‾}}{E}=\frac{E_{\mathit{\alpha }}+E_{\mathit{\beta }}}{\mathrm{2}}$) can also be used to calculate the migration rate:

$$\begin{array}{}\text{(7)}& D_{\mathrm{mr}}={\displaystyle \frac{\mathrm{2}\stackrel{\mathrm{‾}}{E}\left[\frac{{\left(A_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\right)}_{\mathit{\alpha }}-{\left(A_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\right)}_{\mathit{\beta }}}{{\left(A_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\right)}_{\mathit{\alpha }}+{\left(A_{\mathrm{cr}}^m{S}_{\mathrm{ch}}^n\right)}_{\mathit{\beta }}}\right]-\mathrm{\Delta }{U}_{\mathrm{ch}}}{\tan \mathit{\alpha }+\tan \mathit{\beta }}}.\end{array}$$

Based on Eqs. (4)–(7), the migration rate of drainage divides can be estimated using channel-head parameters combined with one of the erosion-related parameters, erosion coefficient (K), erosion rate at one side of a drainage divide (E_α or E_β), or regional average erosion rate ($\stackrel{\mathrm{‾}}{E}$).

2.2 Channel-head-segment method

A channel-head segment is the channel segment just below the channel head (Zhou et al., 2022a). Zhou et al. (2022a) developed a method based on the cross-divide χ contrast of channel-head segments to calculate the migration rate of drainage divides. The essence of the method is the cross-divide comparison of the channel-head segments' normalized channel steepness (k_sn) values. k_sn is a widely used index (Whipple et al., 1999; Wobus et al., 2006; Hilley and Arrowsmith, 2008; Kirby and Whipple, 2012) that is quantitatively related to E and K ($k_{\mathrm{sn}}={\left(\frac{E}{K}\right)}^{\frac{\mathrm{1}}{n}})$. χ is an integral function ($\mathit{\chi }=\underset{x_b}{\overset{x}{\int }}{\left(\frac{A_{\mathrm{0}}}{A\left(x\right)}\right)}^{\frac{m}{n}}\mathrm{d}x)$ of a channel's upstream area (A) to horizontal distance  x) (Royden et al., 2000; Perron and Royden, 2012), and A₀ is an arbitrary scaling area to make the integrand dimensionless.

In the method of Zhou et al. (2022a), the location of channel heads cannot be accurately identified, because it is limited by the resolution of DEM. Therefore, an empirical value of A_cr=10⁵ m² was used in the calculation. Benefiting from the high-resolution DEM in this study, we improve the method in Zhou et al. (2022a) and use the real location of channel heads to calculate the migration rate. When the regional erosion coefficient (K) is known and unchanged in the vicinity of the drainage divide, the drainage-divide migration rate can be estimated by the following equation:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{D}_{\mathrm{mr}}& ={\displaystyle \frac{K\left[k_{\mathrm{sn}\left(\mathit{\alpha }\right)}^n-k_{\mathrm{sn}\left(\mathit{\beta }\right)}^n\right]-\mathrm{\Delta }{U}_{\mathrm{ch}}}{\tan \mathit{\alpha }+\tan \mathit{\beta }}}\\ & ={\displaystyle \frac{K\left\{{\left[\frac{{\left(z_{\mathrm{ch}}-z_b\right)}_{\mathit{\alpha }}}{{\mathit{\chi }}_{\mathit{\alpha }}}\right]}^n-{\left[\frac{{\left(z_{\mathrm{ch}}-z_b\right)}_{\mathit{\beta }}}{{\mathit{\chi }}_{\mathit{\beta }}}\right]}^n\right\}-\mathrm{\Delta }{U}_{\mathrm{ch}}}{\tan \mathit{\alpha }+\tan \mathit{\beta }}},\end{array}\end{array}$$

where z_ch is the elevation of the channel head, z_b is the elevation of catchment outlet (at the top part of the channel to make the elevation-χ profiles quasi-linear between the channel head and the outlet), and subscripts α and β denote the two rivers across a divide. The detailed derivation of Eq. (8) is in the Supplement. The drainage divide's unilateral erosion rate (E_α or E β) can also be used as a substitution for the K value:

$$\begin{array}{}\text{(9)}& D_{\mathrm{mr}}={\displaystyle \frac{E_{\mathit{\alpha }}\left\{\mathrm{1}-{\left(\frac{{\mathit{\chi }}_{\mathit{\alpha }}}{{\mathit{\chi }}_{\mathit{\beta }}}\right)}^n{\left[\frac{{\left(z_{\mathrm{ch}}-z_b\right)}_{\mathit{\alpha }}}{{\left(z_{\mathrm{ch}}-z_b\right)}_{\mathit{\beta }}}\right]}^{-n}\right\}-\mathrm{\Delta }{U}_{\mathrm{ch}}}{\tan \mathit{\alpha }+\tan \mathit{\beta }}}\end{array}$$

or

$$\begin{array}{}\text{(10)}& D_{\mathrm{mr}}={\displaystyle \frac{E_{\mathit{\beta }}\left\{{\left(\frac{{\mathit{\chi }}_{\mathit{\alpha }}}{{\mathit{\chi }}_{\mathit{\beta }}}\right)}^{-n}{\left[\frac{{\left(z_{\mathrm{ch}}-z_b\right)}_{\mathit{\alpha }}}{{\left(z_{\mathrm{ch}}-z_b\right)}_{\mathit{\beta }}}\right]}^n-\mathrm{1}\right\}-\mathrm{\Delta }{U}_{\mathrm{ch}}}{\tan \mathit{\alpha }+\tan \mathit{\beta }}}.\end{array}$$

Alternatively, one can use the regional average erosion rate ($\stackrel{\mathrm{‾}}{E}$) to calculate the migration rate:

$$\begin{array}{}\text{(11)}& D_{\mathrm{mr}}={\displaystyle \frac{\mathrm{2}\stackrel{\mathrm{‾}}{E}\left\{\frac{{\left[\frac{{\left(z_{\mathrm{ch}}-z_b\right)}_{\mathit{\alpha }}}{{\left(z_{\mathrm{ch}}-z_b\right)}_{\mathit{\beta }}}\right]}^n-{\left(\frac{{\mathit{\chi }}_{\mathit{\alpha }}}{{\mathit{\chi }}_{\mathit{\beta }}}\right)}^n}{{\left[\frac{{\left(z_{\mathrm{ch}}-z_b\right)}_{\mathit{\alpha }}}{{\left(z_{\mathrm{ch}}-z_b\right)}_{\mathit{\beta }}}\right]}^n+{\left(\frac{{\mathit{\chi }}_{\mathit{\alpha }}}{{\mathit{\chi }}_{\mathit{\beta }}}\right)}^n}\right\}-\mathrm{\Delta }{U}_{\mathrm{ch}}}{\tan \mathit{\alpha }+\tan \mathit{\beta }}}.\end{array}$$

Based on Eqs. (8)–(11), the drainage-divide migration rate can be estimated using the χ values of high-base-level channel segments combined with one of the erosion-related parameters, erosion coefficient (K), erosion rate at one side of a drainage divide (E_α or E_β), or regional average erosion rate ($\stackrel{\mathrm{‾}}{E}$).

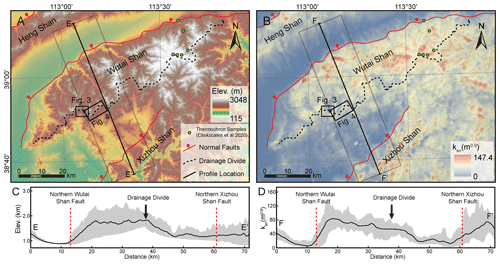
Figure 2 Topography (a) and normalized channel steepness (k_sn) (b) distribution of the Wutai Shan horst and surrounding area in the Shanxi Rift system. The dashed black line shows the location of the main drainage divide. Red lines show the main active faults. The black lines show the location of profiles E–E' and F–F'. Black rectangles show the area of Figs. 3b and 4a. Gray boxes show the area of the swath profiles in panels (c) and (d). Green dots denote the locations of the low-temperature thermochronology samples in Clinkscales et al. (2020). The k_sn is calculated based on S and A extracted from ALOS DEM $\left(k_{\mathrm{sn}}=S{A}^{\frac{m}{n}}\right)$ and a uniform $m/n$ (0.45) using TopoToolbox (Schwanghart and Scherler, 2014), and the interpolation uses the Kriging method on ArcGIS. (c) Topography swath profile along E–E'. See location in panel (a). (d) k_sn swath profile along F–F'. See location in panel (b). The swath profiles are extracted using TopoToolbox (Schwanghart and Scherler, 2014). The dashed red lines show the location of the main active normal faults, and the black arrow shows the location of the main drainage divide. Both swath profiles are 20 km wide (10 km on each side).

2.3 Parameter extraction

In this study, we apply the equations (Eqs. 4 and 8) related to the erosion coefficient (K) to two natural examples in north China, the Wutai Shan in the Shanxi Rift and the Yingwang Shan in the Loess Plateau, to demonstrate how to calculate the drainage-divide migration rates (Fig. 1). We calculated the K according to the equation $K=\frac{E}{k_{\mathrm{sn}}^n}$, the erosion rate obtained by chronological methods, the k_sn, and the assumed slope exponent (n=1). The k_sn is calculated based on S and A $\left(k_{\mathrm{sn}}=S{A}^{\frac{m}{n}}\right)$ extracted from ALOS DEM (downloaded from https://search.asf.alaska.edu/, last access: December 2011) using TopoToolbox (Schwanghart and Scherler, 2014), and the interpolation uses the Kriging method on ArcGIS (Fig. 2). We use a small four-rotor unoccupied aerial vehicle (UAV), the DJI Phantom 4, to acquire stereo images of the areas. Based on the Structure-from-Motion (SfM) method and PhotoScan software, we obtained the DEMs with a spatial resolution of 0.67 m in the Wutai Shan and 0.84 m in the Yingwang Shan (can be download from https://doi.org/10.5069/G98C9TGT, Zhou, 2023). Both regions are semi-arid, and the vegetation is dominated by shrubs. We did not compare the elevations to the standard GPS points, which may introduce errors to the elevations.

Based on the high-resolution topography data, we first extract river channels and drainage divide, using a single-flow-direction algorithm (D8). Then we extract the relevant parameters and calculate the drainage-divide migration rate. Data analysis including slope–area plots, χ plots, the river's long profiles and topographic swath profiles, are based on the MATLAB toolbox TAK (Forte and Whipple, 2019) and TopoToolbox (Schwanghart and Scherler, 2014). According to the breaking point of the slope-area regression line, we obtain the value of the critical upstream drainage area (A_cr) of each river channel (Duvall, 2004). According to these values, we mark the position (and its elevation, z_ch) of the channel heads on the χ plots and the topography map. An elevation of the catchment outlet (z_b) can be assigned at the top part of the channel to make the elevation-χ profiles quasi-linear between the channel head and the outlet. The slope of the channel head (S_ch) is calculated according to the 100 m long channel on the river's long profiles around the channel head (50 m upstream and downstream). Topographic gradient (tan α or tan β) is calculated through the average slope (in the normal-divide direction) of the hillslope segment (not including the hilltop part, because of its lower gradient). The cross-divide uplift difference in the channel-head points (ΔU_ch) is estimated according to the location of each channel head and the tectonic uplift trend.

Figure 3 Perspective views and χ map of the drainage divide in the Wutai Shan (see Fig. 2 for location). (a) Perspective views of a captured area and the channels mapped with k_sn. The south side of the drainage divide has steeper channels and higher k_sn than the north side. Magenta arrows show drainage divide migration directions. The satellite image is from © Google Earth. (b) χ map of this area with the outlet elevation of 1300 m. The south side of the drainage divide has lower χ values than the north side. It should be noted that the catchment outlet at the north side of the drainage basins (the 1300 m contour) is out of the map. The χ plots of the rivers in bold lines are shown in panel (c). (c) χ plots of the three paired rivers in panel (b). The blue and red curves correspond to the rivers on the south and north sides, respectively. The χ plot of river 1 is steeper on the south side, indicating that the river on the south side is expanding and the river on the north side is shrinking. The χ plots of rivers 2 and 3 in the captured area show obvious characteristics of the captured and beheaded rivers. The χ plot is extracted using TAK (Forte and Whipple, 2019) and TopoToolbox (Schwanghart and Scherler, 2014).

3 Applications to natural cases

3.1 Wutai Shan

The Wutai Shan is a tilted fault block on the shoulder of the Shanxi Rift system located in the central north China craton (Fig. 1) (Xu et al., 1993; Su et al., 2021). The tilting uplift of the Wutai Shan is controlled by the North Wutai Shan Fault, and there is no active fault along the south edge of the Wutai Shan horst (Fig. 2). The bedrock of the Wutai Shan area consists mainly of metamorphic and igneous basement rocks (Clinkscales et al., 2020), and there is no obvious variation in rock erodibility and precipitation in this area (Figs. S2 and S3). Zhou et al. (2022b) reveal that the Wutai Shan drainage divide is migrating northwestward due to the tilting uplift and predicts the drainage divide will move ∼10 km to the northwest to achieve a steady state if all geological conditions remain. Geomorphic evidence also exhibits a northwestward migration of the drainage divide (Fig. 3). The plan and satellite views show several abnormally high junction angles around the Wutai Shan drainage divide, which indicate that the tributaries formerly part of the northern drainage have become part of the southern drainage (Fig. 3a and b). The χ plot analysis shows the southern side of the drainage divide has steeper channels, higher k_sn, and lower χ. The χ plots of paired rivers illustrate obvious characteristics of shrinking–expanding and captured–beheaded rivers (Fig. 3c).

To derive the erosion coefficient of the Wutai Shan area, we calculate the channel steepness (k_sn) of this region, assuming n = 1 and m=0.45 (Wobus et al., 2006; DiBiase et al., 2010; Perron and Royden, 2012; Wang et al., 2021). We then use the Kriging interpolation method to generate the k_sn distribution map (Fig. 2b). In addition, results under the assumptions of m=0.35 and 0.55, respectively, are shown in the Supplement (Fig. S4). The average k_sn value of the upthrown side near the North Wutai Shan Fault is ∼80 m^0.9 (Fig. 2d). Middleton et al. (2017) showed that the Quaternary throw rates of the North Wutai Shan Fault are 0.8–1.6 mm yr⁻¹. Clinkscales et al. (2020) showed, using low-temperature thermochronology, that the time-averaged long-term throw rates in the late Cenozoic period are about 0.25 mm yr⁻¹, and there is accelerated activity in the Wutai Shan area. According to these studies, we assume a 0.50±0.25 mm yr⁻¹ uplift/erosion rate in the northern margin of the Wutai Shan (in the footwall of the North Wutai Shan Fault). Combining with the equation, $K=\frac{E}{k_{\mathrm{sn}}^n}$, and following the approach of previous studies (Kirby and Whipple, 2001; Kirkpatrick et al., 2020; Ma et al., 2020), the erosion coefficient (K) is calculated to be $(\mathrm{6.25}\pm \mathrm{3.13})\times {\mathrm{10}}^{-\mathrm{6}}$ m^0.1 yr⁻¹ in this area. Because there is no obvious variation in rock erodibility and precipitation in this area (Figs. S2 and S3), we use this value as the erosion coefficient (K) of the Wutai Shan area.

We then apply the two new methods (Eqs. 4 and 8) to calculate the migration rate of the drainage divide in the Wutai Shan. We first choose three pairs of rivers (Fig. 4a) and acquire their slope–area plots (Fig. 4b, e, and h) and the χ plots (Fig. 4c, f, and i). According to the breaking point of the slope-area regression line (Duvall, 2004) (Fig. 4b, e and h), we obtain the values of the critical upstream drainage area (A_cr). According to these values, we separate hillslope and channel areas and mark the position of the channel heads on the χ plots and the topography map (Fig. 4a). For the χ plots (Fig. 4c, f, and i), we obtain the elevations of channel heads (z_ch) and χ values based on the coordinates of the channel-head points. According to the location of the channel heads on the river's long profiles, we calculate the channel-head gradient (S_ch). Topographic gradient (tan α or tan β) is calculated through the average slope (in the normal-divide direction) of the hillslope segment (not including the hilltop part, Fig. 4d, g, and j).

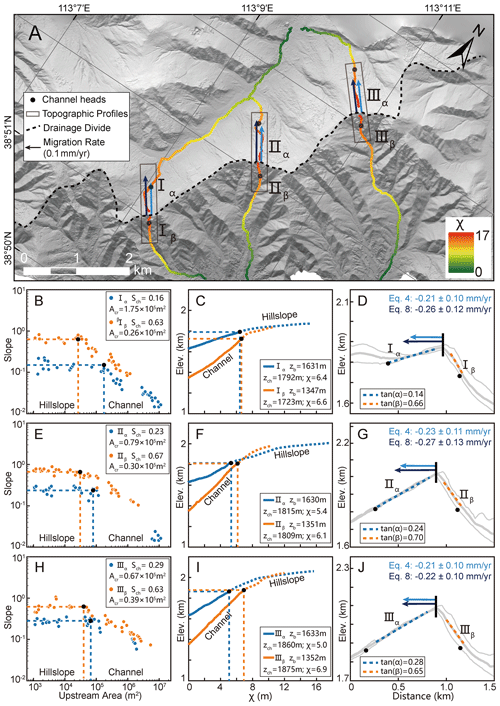
Figure 4 Analytical results of the Wutai Shan drainage divide. (a) High-resolution hillshade map (0.67 m spatial resolution) of the Wutai Shan. The dashed black line shows the location of the main drainage divide. Colored lines show the three pairs of selected channels used for analysis. The black dots are the channel heads. Black rectangles show the location of the cross-divide topography swath profiles. The black arrows show the direction of drainage-divide migration. (b, e, h) Slope–area plots of the three pairs of selected channels. The blue and orange dots are the slope–area plots of the north (α) and south (β) sides of the drainage divide respectively. The black dots represent the channel heads. (c, f, i) χ plots of the selected channels. The blue and orange lines are the χ plots of the north (α) and south (β) sides of the drainage divide respectively. The black dots represent the channel heads. (d, g, j) Cross-divide topography swath profiles with the drainage-divide migration rates. The locations of the profiles are in panel (a). The light and dark blue arrows are the drainage-divide migration rates calculated by the channel-head-point (Eq. 4) and channel-head-segment (Eq. 8) methods, respectively.

According to the previous studies (Middleton et al., 2017; Clinkscales et al., 2020) and the k_sn distribution (Fig. 2d), we assume the rock uplift rate decreases linearly from 0.5 to 0 mm yr⁻¹ from northwest to southeast of the Wutai Shan horst (∼40 km wide). Then we can determine that the cross-divide uplift difference in the channel-head points (ΔU_ch) (the distance perpendicular to the direction of the boundary fault is ∼600 m) is ∼0.008 mm yr⁻¹. After determining these parameters, we adopt the channel-head-point (Eq. 4) and channel-head-segment (Eq. 8) methods, respectively, to calculate the migration rates. The required data for calculation and the migration rates are shown in Table 1. The calculated results for $m/n=\mathrm{0.35}$ and 0.55, respectively, are shown in the Supplement (Table S1). The migration rates are higher when $m/n=\mathrm{0.35}$ and lower when $m/n=\mathrm{0.55}$, which indicates the $m/n$ value is sensitive to the result.

Table 1 Channel parameters and migration rates of drainage divides in two field cases.

The rivers have different characteristics on both sides of the drainage divide, as illustrated on their slope–area plots (Fig. 4b, e and h) and the χ plots (Fig. 4c, f and i). For the first site (Fig. 4d), the migration rates calculated by the channel-head-point and channel-head-segment methods are 0.21 and 0.26 mm yr⁻¹, respectively. For the second site (Fig. 4g), the migration rates are 0.23 and 0.27 mm yr⁻¹, respectively. For the third site (Fig. 4j), 0.21 and 0.22 mm yr⁻¹, respectively. The drainage divides of all three points are migrating northwestward, which is consistent with the previous result inferred by the cross-divide contrast of slopes in this area (Zhou et al., 2022b). Furthermore, the migration rates calculated by the two methods are comparable in all three sites.

3.2 Yingwang Shan

The Loess Plateau is hosted by the tectonically stable Ordos Block of the north China craton (Yin, 2010; Su et al., 2021). Over the past 2.6 million years, it has accumulated tens to hundreds of meters of eolian sediments (Yan et al., 2014), draping preexisting topography (Xiong et al., 2014). There is no active fault and little to no variation in rock erodibility and precipitation within the area (Shi et al., 2020; Zhou et al., 2022b).

We apply the two methods to the Yingwang Shan of the Loess Plateau to calculate the drainage-divide migration rate. Similar to the Wutai Shan site, we obtain the slope–area plots (Fig. 5b e and h) and the χ plots (Fig. 5c, f and i) and extract the values of A_cr, S_ch, z_b, z_ch, χ, tan α, and tan β of the rivers. The rate of soil erosion in the study area is about 500 t km⁻² yr⁻¹ according to the distribution of silt discharge (Fu, 1989). Combining with the assumption of the density of loess, 1.65 t m⁻³, the present-day erosion rate in the study area is calculated to be 0.3 mm yr⁻¹. Because there is no obvious unequal uplift in this region, we assign ΔU_ch to be zero. We also assume n=1 and m=0.45 in the calculation (Wobus et al., 2006; DiBiase et al., 2010; Perron and Royden, 2012; Wang et al., 2021). Then, we use the methods of channel-head parameters (Eq. 7) and channel segments (Eq. 11) to calculate the drainage-divide migration rates. The required data for calculation and the migration rates are shown in Table 1.

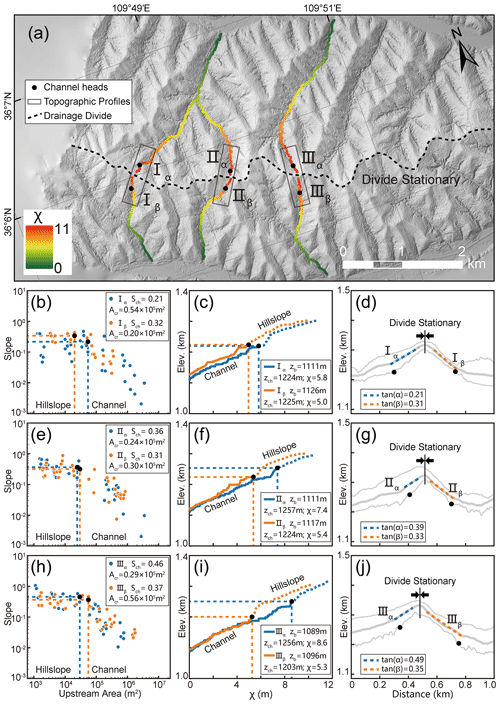
Figure 5 Analytical results of the Yingwang Shan in the Loess Plateau. (a) High-resolution hillshade map (0.84 m spatial resolution). The dotted black line shows the location of the main drainage divide. Colored lines show the three pairs of selected channels used for analysis. The black dots represent the channel heads. Black rectangles show the location of the cross-divide topography swath profiles. (b, e, h) Slope–area plots of the three pairs of selected channels. The blue and orange dots are the data of the north (α) and south (β) sides of the drainage divide respectively. The black dots represent the channel heads. (c, f, i) χ plots of the selected channels. The blue and orange lines are the χ plots of the north (α) and south (β) sides of the drainage divide respectively. The black dots represent the channel heads. (d, g, j) The cross-divide topography swath profiles. The locations of the swath profiles are in panel (a).

All results of the three points show that the drainage-divide migration rate here is close to zero no matter which method is used in the calculation. The results show that the drainage divide of the study site is in topographical equilibrium, which is consistent with the inference in previous studies (Willett et al., 2014; Zhou et al., 2022b).

4 Discussion

4.1 Location of channel heads

Willett et al. (2014) pioneered the use of cross-divide χ contrast to gauge the horizontal motion of drainage divides. According to their method, drainage divides are predicted to move toward the side with a higher χ value to achieve geomorphic equilibrium. However, in a region with spatially variable uplift rates, lithology, or precipitation, χ contrast may fail to reflect the drainage-divide migration (Willett et al., 2014; Whipple et al., 2017; Forte and Whipple, 2018; Wu et al., 2022; Zhou and Tan, 2023). In a tectonically active area, the cross-divide χ contrast can only be used in a small area where rock type, precipitation, and uplift rate are nearly uniform (Willett et al., 2014). Combining the advantages of the χ and Gilbert metrics methods, Zhou et al. (2022a) proposed to use the χ contrast with a high base level to calculate the k_sn values at the channel heads on both sides of a drainage divide and quantified the migration rate of drainage divides at the eastern margin of Tibet.

To reduce the cross-divide difference in uplift rate, precipitation, and rock strength, the Gilbert metrics or χ-comparison method in Zhou et al. (2022a) should compare the parameters of points (slope, relief, elevation, and k_sn) on both sides of the divide as closely as possible. As the hillslope area (above the channel head) does not follow Eq. (1) (Stock and Dietrich, 2006; Stark, 2010; Braun, 2018; Dahlquist et al., 2018), the channel heads are the closest point to the divide, following Eq. (1). Channel heads, therefore, are suitable for measuring the drainage-divide stability with parameters of the upstream drainage area and channel gradient (Forte and Whipple, 2018; Zhou et al., 2022a). However, limited by the resolution of DEM, the location of the channel heads cannot always be accurately identified. The channel-head parameters for calculating the migration rates are usually based on empirical values (both sides are the same value) in previous studies (e.g., A_cr=10⁵ m² in Zhou et al., 2022a), which may induce uncertainties.

In this study, we advocate the use of a high-resolution DEM to determine a more accurate position and related parameters of the channel head. The use of UAVs to obtain the local DEM has become highly efficient. We advance the theory to calculate the drainage-divide migration rate based on the measured channel-head parameters. With the help of the aerial photography of UAVs and the SfM techniques, it is possible to obtain the high-resolution topography data of drainage divides (Figs. 4a and 5a) and get the required parameters through topography analysis. The key parameters include the exact locations (which usually have different A_cr across the divides) and the gradients of the channel heads (S_cr), which could improve the quantitative research on the drainage-divide migration. Furthermore, the method provides a new avenue to combine with catchment-wide ¹⁰Be erosion rate or low-temperature thermochronology data to calculate the migration rate, which has great potential for application in places where some variables are hard to be constrained.

4.2 Cross-divide difference in the uplift rate of the channel heads

Although the channel heads across the divide are very close on the spatial scale of an orogenic belt, differential uplift between the channel heads (ΔU_ch) could still exist, especially in a tilting horst, such as the Wutai Shan. The cross-divide difference in uplift rate could impact the calculation of the migration rate of drainage divides (Zhou et al., 2022a).

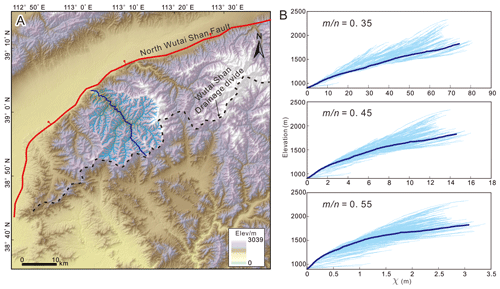
Figure 6 (a) Drainage basin in the northern Wutai Shan. (b) χ plots of channel profiles in the drainage basin, using A₀=1 m² and $m/n=\mathrm{0.35}$, 0.45, and 0.55. The χ plots show the best choice of $m/n$ is 0.45, because the tributaries have systematically higher ($m/n=\mathrm{0.35}$) or lower ($m/n=\mathrm{0.55}$) elevations than the main stem for other values of $m/n$ (excluding the channels in the headwaters).

In this study, we quantify the influence of the cross-divide difference in rock uplift rate (ΔU_ch) on the calculation of the migration rate of drainage divides at the Wutai Shan, benefiting from the available tectonic and chronological research (Clinkscales et al., 2020) and the newly obtained high-resolution topographic data. In the Wutai Shan horst, ΔU_ch across the drainage divide is ∼0.008 mm yr⁻¹. We estimate the influence of ΔU_ch on the drainage-divide migration rate in this case study, which can reduce the error theoretically. If ΔU_ch is ignored, the drainage-divide migration rate would decrease by ∼4 % in the Wutai Shan case. Although ∼4 % seems to be negligible, such a ratio will increase if the mountain belt is narrower, the tilting uplift is stronger, or the divide is closer to the steady state (i.e., the migration rate is lower) (Whipple et al., 2017; Ye et al., 2022). In other words, the differential uplift may play a significant influence on the measurement of drainage-divide stability in some situations. If we consider an extreme example where the main drainage divide of a tilting mountain range (relatively narrow in width) is at a steady state, the gradient, relief, and elevation of the channel heads (collectively called “Gilbert metrics”) (Forte and Whipple, 2018) will show a systematic cross-divide difference in theory. In this case, the drainage divide would be considered unstable if ΔU_ch were neglected. Therefore, this study highlights that ΔU_ch should be taken into account, either in a qualitative or a quantitative evaluation of the stability of drainage divides using the parameters on the channel heads.

4.3 Limitations and uncertainties

This study develops the method to calculate the drainage-divide migration rate based on the measured channel-head parameters. However, uncertainties still exist because of the limitations of this technique. First, we assume the erosion coefficient (K) is the same on both sides of a drainage divide in the derivation of the equations. If there are differences in rock erodibility or precipitation across the divide, uncertainties should exist in the results. Second, the calculation of migration rate is based on the erosion rates at the channel area in this study. However, the occurrence of drainage-divide migration is directly driven by the differential erosion of the hillslope area across the divide, mainly via the processes including landslide, collapse, and diffusion (Stock and Dietrich, 2006; Stark, 2010; Braun, 2018; Dahlquist et al., 2018). Such discontinuous processes in the hillslope area make it challenging to constrain erosion rates over such short timescales. Over a relatively longer period (i.e., spanning multiple seismic and climatic cycles), the erosion rate at the channel-head area in this study can be comparable with that at the hillslope area (Hurst et al., 2012; Godard et al., 2020).

The accuracy of the data and parameters can also impact the reliability of the results. First, we use the uniform values of n=1 and $m/n=\mathrm{0.45}$ in the two natural cases to calculate the migration rate, because it is the best choice to align tributaries with the main stem on the χ plots in a drainage basin at the northern Wutai Shan (Fig. 6) (Perron and Royden, 2012). If the actual values deviate from the assumption, errors would be introduced into the results. For this reason, we have added the cases of $m/n=\mathrm{0.35}$ and 0.55 in the Supplement. Further estimation of these values (Mudd et al., 2018) could improve the accuracy of the results. Second, in the case of the Wutai Shan, we refer to the geological and low-temperature thermochronology studies and assume a 0.50±0.25 mm yr⁻¹ erosion rate at the northern margin of the Wutai Shan (i.e., the footwall of the North Wutai Shan Fault). Combining with the present-day k_sn, we calculate the erosion coefficient (K) and derive the migration rates of the drainage divide. If the present-day erosion rate deviates from the assumption, errors would be inevitable in the results. Moreover, the horizontal and vertical errors in the DEM data, as well as the calculation errors in slope, upstream area, and channel steepness, can also affect the reliability of the results. In the case study of the Yingwang Shan, the lush vegetation may introduce errors to the DEM data based on the SfM technology. The application of airborne light detection and ranging (lidar) technology may help reduce this error. Future studies should take these challenges into account and overcome them.

5 Conclusions

We have developed a new method (called the “channel-head-point method”) to calculate the migration rate of drainage divides based on channel-head parameters. We have also improved the previously proposed “channel-head-segment method” (Zhou et al., 2022a) to adapt the theory to areas where the parameters of channel-heads can be accurately determined.

Using the new methods and high-resolution topographic data, we determined the exact locations of the channel heads on both sides of the drainage divide and quantified the drainage-divide migration rates in two natural cases in north China: Wutai Shan in the Shanxi Rift and Yingwang Shan in the Loess Plateau. The migration rates of the study sites in the Wutai Shan are 0.21–0.27 mm yr⁻¹ (northwestward). The rates are close to zero in the Yingwang Shan.

Based on the locations of the channel heads and the uplift gradient of the Wutai Shan, we calculated the cross-divide difference in the uplift rate at the channel heads (ΔU_ch), which is taken into account in the calculation of the drainage-divide migration rate for the first time. If ΔU_ch is overlooked, the drainage-divide migration rate of the study sites in the Wutai Shan will be underestimated by ∼4 %. Our study highlights that ΔU_ch should be considered in the assessment of drainage divide stability based on the cross-divide difference in channel-head parameters.