the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Time-varying drainage basin development and erosion on volcanic edifices
Liran Goren
Roos M. J. van Wees
Benjamin Campforts
Pablo Grosse
Pierre Lahitte
Gabor Kereszturi
Matthieu Kervyn
The erosional state of a landscape is often assessed through a series of metrics that quantify the morphology of drainage basins and divides. Such metrics have been well explored in tectonically active environments to evaluate the role of different processes in sculpting topography, yet relatively few works have applied these analyses to radial landforms such as volcanoes. We quantify drainage basin geometries on volcanic edifices of varying ages using common metrics (e.g., Hack's law, drainage density, and number of basins that reach the edifice summit, as well as basin hypsometry integral, length, width, relief, and average topographic slope). Relating these measurements to the log-mean age of activity for each edifice, we find that drainage density, basin hypsometry, basin length, and basin width quantify the degree of erosional maturity for these landforms. We also explore edifice drainage basin growth and competition by conducting a divide mobility analysis on the volcanoes, finding that young volcanoes are characterized by nearly uniform fluvial basins within unstable configurations that are more prone to divide migration. As basins on young volcanoes erode, they become less uniform but adapt to a more stable configuration with less divide migration. Finally, we analyze basin spatial geometries and outlet spacing on edifices, discovering an evolution in radial basin configurations that differ from typical linear mountain ranges. From these, we present a novel conceptual model for edifice degradation that allows new interpretations of composite volcano histories and provides predictive quantities for edifice morphologic evolution.
- Article
(8687 KB) - Full-text XML
-
Supplement
(2868 KB) - BibTeX
- EndNote
Understanding how drainage basins on eroding landforms develop and evolve is a fundamental principle of geomorphology. Over regional scales, basin geometry, structure, and spacing evolve in response to both external (e.g., climate and tectonics; Castelltort et al., 2012; Duvall and Tucker, 2015; Han et al., 2015; Yang et al., 2015) and internal (e.g., channel piracy; Bishop, 1995; Whipple et al., 2016) forcing as topographic slopes adjust to develop and maintain an equilibrium between erosion and uplift (e.g., Willett et al., 2001; Castelltort et al., 2009). As these landscapes adjust, transient signals within basins propagate upstream to surrounding channel heads, where opposing signals between adjacent basins drive divide migration that modifies the available area for overland flow (e.g., Willett et al., 2014; O'Hara et al., 2019).
Work in the 20th century established foundational relationships between basin drainage areas, lengths, and slopes (e.g., Horton, 1945; Strahler, 1952; Hack, 1957; Flint, 1974), providing the basis for analyzing landscape disequilibrium and evolution in both tectonically active (e.g., Kirby and Whipple, 2012; Fox et al., 2014) and passive (Prince and Spotila, 2013; Willett et al., 2014; Braun, 2018) regions. These relationships are built on the assumption of a dominantly dendritic fluvial network existing on a near-linear primary landform (e.g., a mountain range; Castelltort and Simpson, 2006). Furthermore, basin competition is often considered in the simplified configuration of a binary drainage system, where a divide supports only two opposing basins that compete across it (e.g., Gilbert, 1909; Mudd and Furbish, 2007).
Although dendritic channel networks are most prevalent on Earth, they are not the only type of configuration. Trellis, rectangular, parallel, and radial drainages also occur (Howard, 1967). The formation of these other drainages often relate to the region's tectonic, volcanic, or glacial history; subsurface structure; or geometry of the primary landform that they erode (Zernitz, 1932). However, compared to dendritic basins, studies that explore the geometries and evolution of other drainage settings are scarce (e.g., Mejía and Niemann, 2008; Becerril et al., 2021; Hamawi et al., 2022).
Volcanic edifices are characterized by radial drainages. In these settings, quantifying drainage evolution can be challenging as these landforms experience interspersed, short-term eruptive episodes superimposed onto the long-term degradation record (e.g., Thouret et al., 2014). These stochastic volcanic events often produce spatially varying excess sediment supply in the form of pyroclasts with varying grain properties that significantly alter fluvial transport on decadal scales (e.g., Major et al., 2018; Hayes et al., 2002). Additionally, drainage formation can lag behind surfacing by volcanic deposits over 1–100 kyr timescales due to transmission losses associated with permeable volcanic material (e.g., lava flows and pyroclasts; Lohse and Dietrich, 2005; Jefferson et al., 2010; Sweeney and Roering, 2017). Finally, the more symmetric drainage divide configuration typical of linear mountain ranges breaks down on volcanic edifices due to their radial nature, with multiple catchments constrained to the conical structure of the volcano and converging towards one or a few main summits. Despite these challenges, volcanic edifices represent ideal primary landforms to investigate drainage evolution due to their well-defined conical initial conditions, datable surfaces, and scarce inheritance from regional tectonics. Furthermore, quantifying the relationships between edifice construction and drainage basin morphology provides new insight for investigating edifices remotely and can thus expand our understanding of basin dynamics while also complementing field-based surveys to resolve volcano edifice histories.
Here, we explore the development of drainage basins and topography on stratovolcanoes from Indonesia, Papua New Guinea, Aotearoa / New Zealand, and Guatemala (Fig. 1). Using common hydrographic metrics and broad volcanic histories, we determine stages of maturation during basin evolution and derive a new generalized model for stratovolcano degradation that builds on previous studies (Ollier, 1988). We then quantify divide mobility on radial structures within the context of our conceptual model and discuss the applicability of our analyses to characterize an edifice's history.
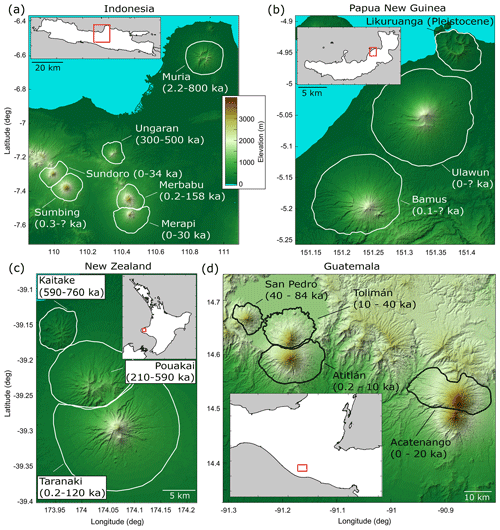
Figure 1Regional hillshaded relief maps of 16 analyzed edifices from (a) Indonesia, (b) Papua New Guinea, (c) Aotearoa / New Zealand, and (d) Guatemala. Maps are projected to 30 m UTM and use the same color scale. Solid white lines in panels (a)–(c) and solid black lines in panel (d) represent edifice boundaries (boundary definition described in Sect. 2). The text describes volcano names and the known ages of activity (Table S2). Insets are larger-scale regional maps for reference; gray areas represent the ocean, white areas are land, and red squares are the bounds of hillshaded maps.
To constrain the temporal evolution of stratovolcano morphologies, we focus on closely spaced volcano sets (Fig. 1). The advantages of this approach are that within each respective region (1) volcanoes were likely fed by similar magma sources (e.g., Locke and Cassidy, 1997; Haapala et al., 2006; Mulyaningsih and Shaban, 2020), constructed by similar volcanic deposits, and thus had similar volcanic shapes; (2) edifices experienced similar climate conditions; (3) volcano sets have radiometric ages related to their initiation and most recent eruption that are comparable, providing constraints on their overall lifespan; and (4) volcanoes within the same set were active over different time intervals, thus showing contrasting time-dependent degrees of dismantling within a short (tens of kilometers) distance. In order to consider drainage basin evolution through fluvial erosion from the perspective of radial landforms, we exclude volcano massifs from our analysis, as well as any volcano with recognizable collapse scars, and only consider volcanoes that do not have an extensive glacial history. All analyzed volcanoes are classified as stratovolcanoes by the Smithsonian Global Volcanism Program (Global Volcanism Program, 2024).
2.1 Edifice delineation
Although automated algorithms exist to generate volcano edifice boundaries (e.g., Bohnenstiehl et al., 2012; Euillades et al., 2013), these often create conservative limits around the edifice that ignore lower flanks and volcanic sedimentary aprons (e.g., O'Hara et al., 2020). We thus follow the method suggested by van Wees et al. (2021) to delineate edifice boundaries from surrounding topography. Using 30 m Shuttle Radar Topography Mission (SRTM) digital elevation models (DEMs) (Farr et al., 2007), projected in the Universal Transverse Mercator (UTM) with the World Geodetic System (WGS 84), we first generate hillshade, aspect, and local slope rasters of the raw topography. Lower-edifice flanks are generally characterized by slope angles greater than some threshold value (Karátson et al., 2012); we therefore remove short-wavelength variations in the slope raster by filtering it over a 300 m wavelength (O'Hara et al., 2020) and contour regions that surpass a 3° slope threshold (van Wees et al., 2021). Using these maps as visual aids, we then hand-draw boundaries that separate the edifice from surrounding terrain. Afterwards, the DEMs are clipped using these boundaries to isolate the edifices for morphometric analysis. The planform areas of edifice boundaries derived using this method range from 30.2 km2 (Kaitake, Aotearoa / New Zealand) to 432.7 km2 (Mount Muria, Indonesia).
2.2 Edifice basin morphology
We analyze edifice basin morphologies with DrainageVolc, a series of scripts modified from TopoToolbox (Schwanghart and Scherler, 2014), which is designed to investigate volcanic topography through a set of topography-, drainage-, and channel-based analyses. The metrics considered here are commonly used within tectonic settings but have not previously been applied to radial drainages. Figure 2 displays an example of our methods using the Mount Ungaran volcano in Indonesia.

Figure 2Analyzed basin metrics. (a) Example from the map of the Mount Ungaran volcano (Indonesia); colored lines are defined in the legend. (b) Hack's law relationship between basin areas and lengths. Black circles are basins used in the power law analysis, and black dots are excluded basins; the dashed blue line is the drainage area threshold (AT; 1.0 km2) for channelization. (c) Scaled edifice metrics. Red line shows the normalized number of basins along elevation contours. Black lines are summit basin hypsometry curves. (d) Local slope and geometry values of the representative basin (thick black line in panel a). Gray double arrow represents the cross-basin direction (i.e., the extent of the basin) perpendicular to the Euclidean basin length. (e) Cross-basin values along the basin shown in panel (d). Black line is the relief along the flowpath; blue line is the cross-valley width.
We first fill sinks in the DEM through TopoToolbox's preprocessing algorithm (Schwanghart and Scherler, 2014) to ensure continuous flow to the edifice boundary and extract drainage basins from topography using the steepest-descent flow routing (Fig. 2a). We then perform a series of analyses related to basin geometry. The lengths (L) of all basins draining to the edifice boundaries are calculated by determining mid-point paths between basin divides perpendicular to the Euclidean distance between the highest and lowest reaches of the basin, irrespective of whether there is an actual flow channel in this path (Fig. 2d). Assuming basins with total drainage areas (A) greater than some threshold (AT) support overland flow, we explore the correlation between the lengths and drainage areas of these basins through a power law regression to derive the Hack's law relationship (Fig. 2b) for the edifice as
where ka and H are Hack's coefficient and exponent, respectively (Hack, 1957). H values are compared across edifices, as this exponent describes general basin geometry, with values of ∼0.47–0.6 typically attributed to dendritic systems (Hack, 1957; Mueller, 1972). Our Hack's law derivation uses basin lengths as opposed to typical flow path lengths to remove the effects of channel sinuosity and focus explicitly on basin geometry; however, within the context of our edifice basins, this derivation does not significantly alter our results, and values are thus comparable to those of previous studies (Fig. S1 in the Supplement). We also analyze the density of the edifice's channel network by extracting flow paths with drainage areas greater than AT from the landform and calculate the edifice-scale drainage density as
where ∑Lc is the cumulative sum of all channel lengths, and AE is the planform area of the edifice's boundary (Fig. 2a) (Horton, 1945). Using an automated slope–area analysis of basins to determine the drainage area threshold that best corresponds with the power law decrease in slope (Montgomery and Dietrich, 1994) for each edifice (Supplemental text; Fig. S2), we find AT ranges between 0.32–1.62 km2, with a mean threshold of 0.85 km2 (Table S1 in the Supplement). For consistency across all edifices, we assume a constant drainage area threshold of 1.0 km2 to delineate networks. A sensitivity analysis (Fig. S3) demonstrates that although the selection of AT does not significantly impact the general behavior of drainage density results, Hack's law exponent is more sensitive to this choice.
Afterwards, we calculate mean values of basin geometries on each edifice. Rather than analyzing the geometry of all basins that exist on a volcano, we limit our analysis to larger basins that best characterize the edifice's drainage and thus its dismantling. These large characteristic basins may be determined using a variety of methods, such as through an arbitrary number or percentage of basin sizes, using the basins that are within some radial distance of the edifice's peak, or determining basins that extend to some portion of the edifice's height. Determining characteristic basins by an arbitrary number or percentage of basin sizes may introduce bias as the population of basins drastically varies between edifices (Fig. 8a), whereas determining characteristic basins by radial distance from the edifice's peak introduces geometric constraints as edifice shapes often deviate from the textbook symmetric, single-peaked edifice; instead, there is the development of large, irregular summit regions that are defined by high topography and multiple peaks (e.g., Karátson et al., 1999; Grosse et al., 2012). As slope (and thus elevation) is an essential component of erosion and basin development (Hack, 1957; Flint, 1974), we define characteristic basins as those that reach the edifice's summit region. However, we note that defining characteristic basins based on radial distance can produce different trends (Fig. S4) and may be more appropriate for some of our analyzed metrics (Sect. 5.3).
Generating a series of elevation contours along the edifice at intervals of 2.5 % of the edifice's relief, we calculate the number of basins that intersect each contour, normalized by the contour's length (Fig. 2c; red line). For all edifices, we define the edifice's summit as the upper 30 % of the edifice's relief and thus consider the basins that reach this summit region (referred to here as summit basins) as those that best characterize the edifice's drainage development. We then determine summit basin numbers, mean basin slopes (Fig. 2d), basin lengths (LB; Fig. 2d, red line), basin reliefs (Fig. 2e, black line), and maximum cross-basin widths (WB; Fig. 2e, blue line). To compare values across edifices of varying sizes, summit basin numbers are normalized by the length of the summit contour (Fig. 2c), and basin reliefs are normalized by the relief of the entire edifice. We also utilize the radial nature of edifices to generate normalized values of basin length () and width () as
and
respectively, where LE is the edifice's effective radius, defined as the radius of the circle with the same planform area (AE) as the edifice's boundary (). is the distance from the highest point within a basin to where the basin is widest. thus converts basin widths into an angle relative to the summit (Fig. 2d, light blue lines). Mean values of these quantities are then calculated for each edifice.
We also calculate mean summit basin hypsometry integrals for each edifice (Strahler, 1952; Fig. 2c, black lines). Individual basin hypsometry curves (HC) are derived by counting the number of basin pixels at or above normalized elevation values (, ranging from 0 to 1); afterwards, these values are normalized by the total number of basin pixels () as
where I is a counter over normalized elevation values from 0 to 1. Hypsometry integrals of each basin are calculated as the positive integration over the curves from Eq. (5). These are also averaged for each edifice.
2.3 Edifice landform morphology
As well as studying the temporal evolution of drainages on edifices, we also consider the broad geometry of the volcanoes. Grosse et al. (2009, 2012) developed the initial MORVOLC algorithm in Interactive Data Language (IDL), which quantifies edifice morphologies through a series of size, shape, slope, orientation, peak, and summit parameters. Using the same framework as DrainageVolc, we redeveloped the IDL code in MATLAB, also utilizing the TopoToolbox DEM analysis package (Schwanghart and Scherler, 2014). Both DrainageVolc and the updated MORVOLC scripts are available for use on GitHub (https://github.com/danjohara/Volc_Packages, last access: 12 March 2024).
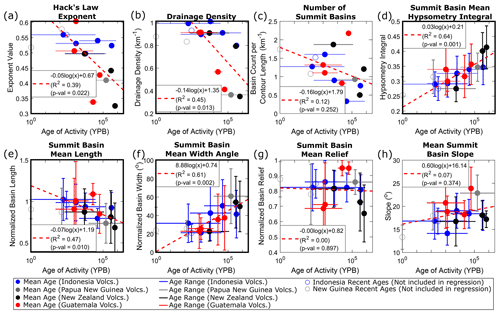
Figure 3Temporal relationships of drainage basin morphology metrics: (a) Hack's law exponent, (b) drainage density, (c) number of summit basins, (d) summit basin mean hypsometry integral, (e) summit basin mean length, (f) summit basin mean width, (g) summit basin mean relief, and (h) summit basin mean slope. Colors correspond to volcanic region. Horizontal lines are edifice age ranges of activity, with filled circles representing log-mean age. Vertical lines represent 1 standard deviation of values (where appropriate). Dashed red lines and equations characterize logarithmic regressions; open circles are excluded from the regression due to age constraints. The thick black border highlights relationships with R2>0.35.
We analyze simple edifice geometry measurements with this updated version of MORVOLC, including effective radius, height, height–radius ratio, and mean slope of the main flank (edifice region between the lowest closed contour that encompasses the edifice and the summit contour; Fig. 2a). We also quantify the mean contour ellipticity and irregularity indices of the main flank from the previously computed contours. The ellipticity index (EI) describes the elliptical nature of the edifice elevation contours and is defined as
where LM is the length of the major axis of a best-fitting ellipse through the contour, and AC is the area enclosed by the contour (Grosse et al., 2012). The irregularity index (II) describes divergence of the contour from a smooth ellipse as
where “di” is the dissection index, defined as
with PC and AC being the perimeter and area of the contour, respectively (Grosse et al., 2012). Finally, we also incorporate new measurements within MORVOLC, including the slope variance of the entire edifice (standard deviation of all slope values divided by the mean slope, similar to roughness), as well as a minimum eroded volume estimate. Eroded volume is estimated from a convex hull reconstruction of the edifice, using the methodology described in O'Hara and Karlstrom (2023), in which the footprints of individual elevation contours along the edifice are altered to remove concave regions (assuming they represent incised topography), thus creating convex polygons. Polygons are then interpolated in three dimensions to create a simplified, reconstructed edifice. Afterwards, the current topography is subtracted from the reconstructed edifice, and positive values (i.e., areas having been eroded) are integrated to estimate the volume of eroded material. Finally, eroded volume is normalized as a percent relative to the total reconstructed volume.
Edifice landform and basin metrics that are based on average values (main flank mean slope, mean contour irregularity index, and mean contour ellipticity index, as well as mean summit basin hypsometry, length, width, relief, and slope) have standard deviations of the sampled population that are presented as vertical bars in Figs. 3 and 4. Other metrics (edifice height, radius, height–radius ratio, slope variance, normalized eroded volume, Hack's law exponent, drainage density, and normalized number of summit basins) are singular values for each edifice and thus do not have associated standard deviations. Potential deviations of these values relate to the edifice's boundary, summit designation, DEM source, or imposed drainage area threshold (Grosse et al., 2012; O'Hara et al., 2020; van Wees et al., 2024; see the Supplement).
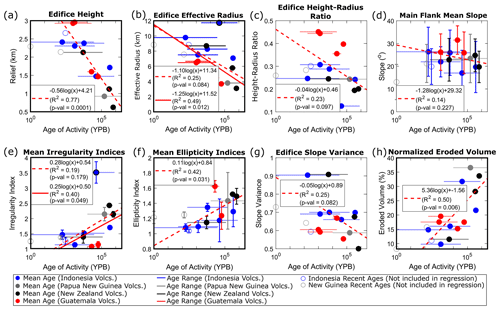
Figure 4Temporal relationships of landform morphology metrics: (a) edifice height, (b) edifice effective radius, (c) edifice height–radius ratio, (d) main flank mean slope, (e) mean irregularity index, (f) mean ellipticity index, (g) edifice slope variance, and (h) normalized eroded volume. Colors and symbols are same as those described in Fig. 3. Solid red lines in panels (b) and (e) are secondary regressions with the outlier (Mount Muria) excluded. The thick black border highlights relationships with R2>0.35.
2.4 Edifice ages
To explore morphological evolution through time, we correlate edifice landform and drainage basin metrics to volcano ages of activity. We thus compile known eruption records of each volcano, with ages ranging from present to early Pleistocene (Table S2). Volcanoes often have complex surface evolutions, with lifespans of activity that range 100–1000 kyr and are characterized by episodes of stochastic growth interspersed with periods of erosion during quiescence (e.g., Karátson et al., 1999; Lahitte et al., 2012). Furthermore, episodes of activity are often constrained to localized regions of the edifice and thus do not fully resurface the entire landform (e.g., Civico et al., 2022). Similarly, erosion across the edifice is typically non-uniform as local conditions are dependent on the age and type of activity, as well as microclimates (e.g., Ferrier et al., 2013; Pierson and Major, 2014; Thouret et al., 2014; Ricci et al., 2015).
Despite the spatial and temporal heterogeneities of activity and erosion, we argue that a generalized morphologic age of an edifice may be derived that quantifies the erosional state of the landform and relates to the edifice's lithologic age. To account for the time differences between short-term events and the cumulative long-term history on morphology, we define an edifice's age as a single value using the log-mean between the most recent eruption and the oldest date of activity. This definition thus accounts for the span of temporal magnitudes; however, we note that using linear mean ages produces similar results (Fig. S5) and recognize that other definitions of an edifice's morphologic age are plausible (e.g., the time since the last eruption; Fig. S6). Afterwards, we analyze the temporal evolution of edifice morphologies by fitting logarithmic relationships between edifice age and morphometric parameters. Some volcanoes (Sumbing, Bamus, and Ulawun) have poorly documented histories (only the most recent eruption has been dated) and are therefore excluded from the regression. Conversely, Likuruanga is known to have erupted only during the Pleistocene and is incorporated in the analysis.
We find trends between stratovolcano age and our morphometry metrics through time (Figs. 3 and 4; Table S3). Considering all metrics, we find that edifice height, mean ellipticity index, normalized eroded volume, Hack's law exponent, drainage density, mean summit basin hypsometry integral, normalized basin length, and normalized basin width have R2 values ranging 0.39–0.77 and correlating p values ≤ 0.05. This list expands to include effective edifice radius and mean irregularity index by removing a notable outlier (Mount Muria, Indonesia; Fig. 4b and e), suggesting that all of these metrics provide quantitative measures to characterize the overall maturity of the edifice. Other metrics have weaker correlation values (0–0.25) and are statistically insignificant (p values > 0.1) and thus may be more sensitive to the initial edifice geometry or other processes that alter edifice morphology or that age is not a significant factor for these metrics. Mount Muria (the noted outlier for effective edifice radius and irregularity index) has an extensive volcanic history (from ∼800 to 2 ka; McBirney et al., 2003; Global Volcanism Program, 2024) and a morphology characterized by two broad fluvial networks on opposite flanks that are deeply incised into the landform and may be associated with breached craters or flank collapses (Fig. 1a), suggesting that this edifice may not fit into the simple radial volcano expectation of our dataset. We also note that due to the geometries that Acatenango and Atitlán share with their sister volcanoes (Fuego and Tolimán, respectively; Fig. 1d), and our imposed definition of an edifice's main flank (region between the lowest closed contour and upper 30 % of the edifice's height), irregularity and ellipticity values could not be derived for these volcanoes.
Of the statistically significant metrics related to edifice drainage morphology, mean summit basin hypsometry integral and normalized width increase through time, whereas Hack's law exponent, drainage density, and mean summit basin normalized length decrease (Fig. 3). Similarly, considering statistically significant metrics related to the edifice as a primary landform, mean irregularity index, mean ellipticity index, and convex-hull-based eroded volumes increase with age, while edifice height and effective radius decrease with age (Fig. 4).
4.1 Generalized model for edifice degradation
The evolution of stratovolcanoes as primary landforms and the drainage basins that erode them are inextricably linked. Our results thus establish a new framework for evaluating volcanic edifices by considering both the landform and its drainage systems. This evolutionary model expands on stages previously defined qualitatively (Ollier, 1988) and follows similar drainage evolution to that observed in badlands (Schumm, 1956).
The erosion of a stratovolcano can be described within the context of our metrics by considering a simplified conical edifice (Fig. 5). In the initial stages of erosion (Fig. 5a; equivalent to ∼10 % normalized eroded volume in Fig. 4h), narrow (∼20° normalized width angle) and uniform (normalized mean length near 1) drainages form that extend from the summit region to the lower flanks (i.e., “parasol ribbing”; Ollier, 1988), giving a high drainage density (∼1 km−1) and Hack's law exponent (∼0.6).

Figure 5Conceptual model of edifice dissection based on interpretation of temporal morphologic trends shown in Figs. 3 and 4. Thin black lines represent drainage systems.
As the edifice degrades to 30 %–40 % normalized eroded volume (Fig. 4h) on 10–100 kyr timescales (Fig. 5b and c), both its height and area decrease; however, height decreases faster, leading to a decrease in height–radius ratios. The erosion of the edifice is accompanied by drainage basin growth, with summit basins expanding azimuthally along the edifice to normalized basin widths of 40–60°, pushing the headwaters of other basins down the edifice flanks. Furthermore, as summit basins expand, they incise into the edifice flanks and develop a more dendritic structure associated with lower drainage density (∼0.5 km−1) and Hack's law exponent (∼0.4). This is accompanied by non-uniform summit basin growth that causes normalized basin lengths to decrease below 1.
As the edifice erodes, processes occur over varying scales to alter general edifice morphology: (1) over the entire edifice, erosion-driven topographic lowering occurs faster than horizontal areal loss of the edifice, creating a flatter landform; and (2) at the scale of a basin, incision carves into the initially planar flanks of the edifice, steepening surrounding valley walls and increasing contour irregularity. The relationship between basin-scale incision and edifice-scale flattening is recorded through summit basin hypsometry integrals, with increasing values suggesting that edifice-scale flattening is the dominant process. This leads to a scale-dependent behavior in edifice morphology – although the edifice as a landform is becoming flatter, incision causes topography to steepen locally. Previous studies (e.g., Karátson et al., 2012; Dibacto et al., 2020; Ollier, 1988) suggest that this simultaneous behavior causes the edifice to lose its conical single-peaked nature over longer (>1 Myr) timescales, developing high-relief drainage divides over an extended summit region that support binary basin competition as the edifice erodes to the same relief as the surrounding terrain. Furthermore, we note that the decrease in edifice area through time differs from the expectation of a sedimentary apron around the edifice that increases in area as the edifice erodes. Since edifice boundaries are consistently defined, in part by a 3° topographic slope threshold, this suggests that on the 100 kyr scale, sediment is not depositing at the edifice's base but is being evacuated from the vicinity of the edifice, likely through fluvial transport. The loss of sedimentary apron and the overall decrease in the edifice planform area was also suggested by Ollier (1988), as an edifice transitions from its intact stage to the planèzes stage.
This conceptual model represents a generalized view of edifice degradation, as a variety of processes (both volcanic and erosional) can impact an edifice's morphology throughout its lifespan. Furthermore, other climate conditions not considered here (e.g., glaciers and arid environments) are expected to alter the patterns and rates of basin evolution. Nonetheless, we propose that, barring major events that significantly alter topography, stratovolcano degradation by fluvial processes generally follows the model presented here.
4.2 How do basins compete on radial structures?
Our results suggest that drainages on radial structures are highly dynamic. From initially uniform basin geometries, preferential erosion causes basins near the summit to become more dominant and expand, forcing other basins down-flank and generating a “topographic hierarchy”, with higher-order basins spanning the entire flank of the edifice and lower-order basins occurring on lower sections, analogous to inferred basin evolution on linear fault blocks (Talling et al., 1997). This hierarchy of basin ordering is a direct product of non-uniform basin development over the edifice that contributes to the preservation of less eroded portions of the lower flanks (i.e., planèzes; Ollier, 1988).
Non-uniform basin development and transience is a natural component of landscape evolution (e.g., Hasbargen and Paola, 2000); however, various factors (both volcanic and non-volcanic) can influence erosional patterns and accentuate basin growth across volcanic edifices. These may include (1) local slope changes associated with magmatic intrusions (e.g., Wicks et al., 2002; Biggs et al., 2010; Castro et al., 2016) or mass wasting (e.g., Ui and Glicken, 1986; Shea and van Wyk de Vries, 2008); (2) variable volcanic eruption activity that increases sediment loads (Hayes et al., 2002; Pierson and Major, 2014), alters infiltration and rock erodibility (e.g., Wells et al., 1985; Sklar and Dietrich, 2001; Jefferson et al., 2010), or removes bedrock through scouring by pyroclasts (Gase et al., 2017) or melting by lava flows (i.e., thermal erosion; Kerr, 2001) during deposition; (3) non-uniform changes in overland flow and stream power associated with breached craters (e.g., Karátson et al., 1999) or edifice-scale precipitation gradients (e.g., Ferrier et al., 2013); and (4) downstream alterations to drainage channels that migrate upstream as a propagating incision wave (i.e., knickpoints; Kirby et al., 2003; Cook et al., 2013; Perron and Royden, 2013). The long-term compilation of such processes helps drive non-uniform erosion across the edifice, which in turn encourages divide migrations and changes in basin size and geometry. More specifically, basins that exhibit higher erosion rates would tend to expand at the expense of their neighboring basins and potentially become the dominant basins, while lower erosion rates will cause other basins to shrink and their boundaries to migrate further down the edifice's flank.
The morphology of drainage divides is sensitive to differences in erosion between neighboring basins and can thus be used to characterize basin competition. We quantify basin geometry unsteadiness through an exploration of divide stability using the divide asymmetry index (DAI; Forte and Whipple, 2018; Scherler and Schwanghart, 2020), calculated as the positive difference in hillslope relief (vertical distance between the ridge and nearest channel) across a divide and normalized by the sum of hillslope reliefs, ranging between 0 (symmetric) and 1 (asymmetric). We limit our analysis to only consider divides that correspond to fluvial basins (i.e., have drainage areas > 1.0 km2 (Scherler and Schwanghart, 2020).
Divide mobility is expressed using probability density functions (PDFs) of DAI for all volcanoes (Fig. 6a). A clear temporal trend emerges: older volcanoes have larger distributions clustered around a lower (<0.4) DAI that rapidly decrease with increasing DAI, while younger volcanoes show monotonically decreasing distributions with fewer normalized populations of low-DAI values and greater normalized populations of high-DAI values compared to older volcanoes. Integrating these PDFs into single values (referred to here as Γ; Fig. 6b) shows a moderate correlation with age (R2=0.38) with the removal of Likuruanga (Papua New Guinea) as an outlier, which may be associated with a breached crater (Fig. 1b).
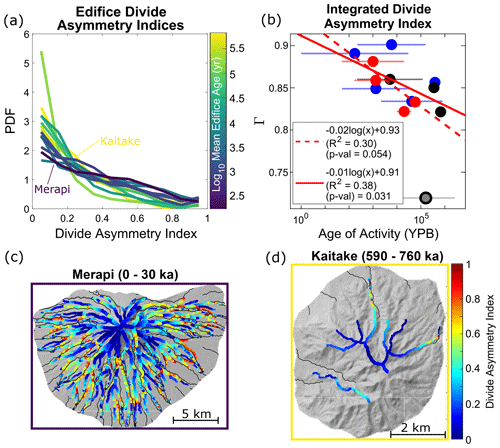
Figure 6(a) Probability density functions (PDFs) of volcano divide asymmetry indices (DAIs); colors correspond to log-mean edifice ages. (b) Integral of PDFs (Γ) compared to edifice age. Colors and symbols are the same as Fig. 4. (c, d) DAI values for (c) Merapi (Fig. 1a) and (d) Kaitake (Fig. 1c) at the divides. Background images are hillshades of topography; black lines are edifice channel network. Borders are colored with respect to the panel (a) color scale.
Combined with basin morphology trends (Fig. 3), this suggests younger volcanoes have basins with more uniform planform geometries and less stable basin configurations. As the edifice erodes, basin planform geometries become less uniform but develop more stable configurations, as evidenced by the greater symmetry of hillslope relief across divides. The relationship between basin non-uniformity and stability can be observed spatially by comparing DAI values between Merapi (youngest) and Kaitake (oldest) volcanoes (Fig. 6c and d). Highest DAI values on both volcanoes generally occur at the mid- and lower flanks of the volcano, suggesting basin expansion occurs mainly azimuthally along edifice flanks rather than across the edifice summit. This spatial analysis highlights the process that generates topographic hierarchy: by expanding azimuthally, basin growth drives less dominant basins down-flank through a zippering process, creating drainages with tapered geometries along the lower flanks.
4.3 Edifice basin widths and spacing
Our results show that edifices experience the same morphologic trends when considering the number of basins along edifice relief (Fig. 7a); lower flanks are characterized by normalized basin numbers between 2–5 km−1, main flanks are characterized by relatively consistent normalized basin numbers < 2 km−1, while the normalized basin numbers increase near the summit (upper 30 % of the edifice). This trend appears to occur largely independent of age, even within the upper flank (as demonstrated by a low R2 value of 0.12 at the summit contour; Fig. 3c), suggesting that this morphologic trend is a direct consequence of the conical nature of volcanoes. Furthermore, non-normalized summit basin numbers also demonstrate a weak temporal trend, both at the upper 30 % height designation (Fig. 7b) and other percentages (Fig. S7). This suggests that basins that initially form on the summit region may retain their topographic position as the edifice erodes. However, Fig. 3f demonstrates that these basins still widen through time to a width angle of ∼60°, though further analysis on older volcanoes is needed to explore whether this persists on the million-year timescale.
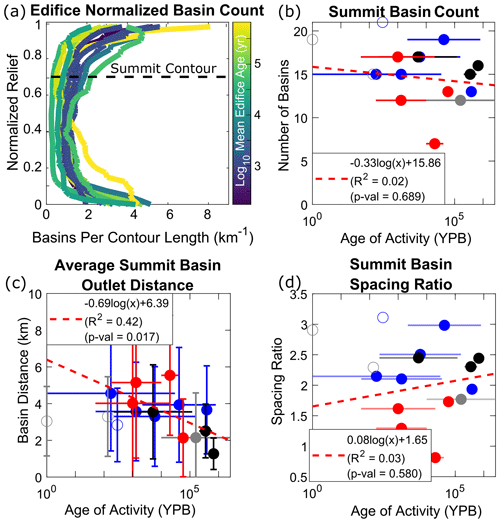
Figure 7(a) Normalized number of basins along normalized relief for each volcano; colors are the log-mean edifice age. (b) Non-normalized number of summit basins (defined by the upper 30 % of the edifice's height; dashed black line in panel a) compared to log-mean edifice age. (c) Average along-perimeter summit basin distance compared to edifice age. (d) Summit basin spacing ratio (data from Fig. 4b divided by data from panel c) compared to edifice age. Colors and symbols in panels (b)–(d) are the same as Fig. 3.
An apparent contradiction occurs when comparing the mean summit basin width angles to the number of summit basins. If all summit basins reached a width angle of ∼60°, it would be expected that only ∼6 basins would exist at the summit; however, Fig. 7b shows that the number of basins that reach the summit on most edifices is greater than 10. This difference is a consequence of radial drainage basins achieving their maximum widths at different heights relative to the height of the edifice, such that basin widths are normalized by different distances from the summit. Indeed, as discussed in Sect. 4.2, divide asymmetry is most frequent in the mid- and lower flanks of the edifice (Fig. 6), thus accommodating largest basin widths at different sections of the flank.
If the number of basins that reach the summit is time invariant, how does this translate to the circumferential spacing of their outlets at the base of the edifice? Hovius (1996) compiled the ratio between mountain belt half-widths (distance between the major divide and mountain front, WM, and distances, s) in 11 mountain ranges globally and determined a globally averaged spacing ratio () of ∼2–3. We perform a similar analysis by dividing effective edifice radii by the average along-perimeter spacing between summit basin outlets. Figures 4b and 7c show that while effective edifice radii decrease through time, so does the average perimeter distance between summit basin outlets. These behaviors thus combine to produce summit basin spacing ratios of ∼1–3 (Fig. 7d), consistent with Hovius (1996) and modeling studies of drainage patterns (Habousha et al., 2023). This suggests that while summit basins azimuthally expand their widths, the edifice is also decreasing in area as the landform erodes, thus decreasing the distances between summit basin outlets.
However, a different behavior emerges when considering basins by their radial distance relative to the edifice's peak (Fig. 8), which is more sensitive to the areal expansion of basins along the edifice's flank. Plotting the non-normalized number of basins as a function of radial distance (normalized by maximum radius for each edifice) and time shows a clear temporal trend (Fig. 8a), with younger edifices having more basins along all sections of the volcano (as schematized in Fig. 5). This trend becomes more apparent through the logarithmic regression between edifice age and the number of basins that exist at 30 % radial distance from the peak (Fig. 8b), with other normalized distances showing the same behavior (Fig. S8). Conducting a similar outlet perimeter distance analysis on these basins shows that the average distance between basin outlets is relatively constant at ∼2 km (Fig. 8c), giving a temporal decrease in basin spacing ratios (R2=0.35; Fig. 8d). This relationship suggests a dynamic in radial drainage evolution related to landform geometry. Combined with other metrics, our results suggest that as the edifice erodes and loses planform area through time, very small basins on the edifice's lower flanks likely become erased while more dominant basins widen on the mid-flank, thus causing basins that exist within 30 % radial distance of the edifice's summit to retain an approximately constant outlet distance along the shrinking perimeter.

Figure 8(a) Non-normalized number of basins as a function of normalized distance from the edifice's peak; colors are the log-mean edifice age, and the dashed black line represents 30 % normalized radial distance from the edifice's peak (basins used for plots in panels b–d). (b) Non-normalized number of basins compared to log-mean edifice age. (c) Average along-perimeter basin distance compared to edifice age. (d) Basin spacing ratio (data from Fig. 4b divided by data from panel c) compared to edifice age. Colors and symbols in panels (b)–(d) are the same as Fig. 3.
4.4 Radial drainage basin area–length relationship
As a final observation for volcanic edifice drainage basins, we consider basin geometries with reference to Hack's power law relationships between basin areas and lengths (Hack, 1957). Analyzing Hack's law regressions for Merapi and Kaitake (Fig. 9), the relationships between spatial location and basin geometries become apparent. On Merapi, basins smaller than 105 m2 do not conform to the same power law trend as those greater than 105 m2, whereas on Kaitake this break occurs at 106 m2. These smaller basins are constrained to the lowest regions of the flanks of the edifices and likely correspond to non-channeled surfaces. Of those considered for the Hack's law regression, the log10 basin length deviation (DL) from the power law is calculated as
where LH is the basin length of the Hack's law regression from a given basin's area (A), and L is the basin's length. As expected from the geometric relationship, basins that fall below the power law regression (DL<0) are wider, and those that are above the power law regression (DL>0) are narrower.
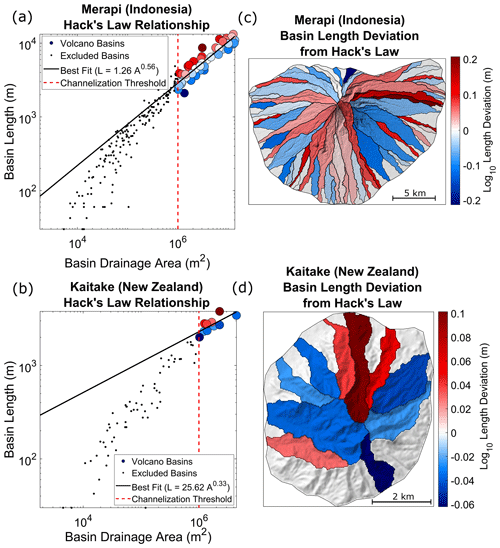
Figure 9Hack's law analysis of (a, c) Merapi and (b, d) Kaitake. (a, b) Basin drainage area–length relationships. Black lines represent Hack's law regressions. Colored circles correspond to the deviation from the regression trend (Eq. 9) and are associated with the color bars in panels (c) and (d). Dashed red line is the imposed 1.0 km2 channelization threshold; black dots are basins smaller than the threshold and are excluded from the regression. (c, d) Semi-transparent hillshaded relief maps showing the deviation of each basin from the best-fit power law regression.
When calculating DL for basins with areas greater than our imposed channelization threshold (1.0 km2), one clear observation is the presence of highly elongated basins on Merapi that exist on the mid- to upper flanks and have DL values > 0.15 (Fig. 9c). These basins appear wedged or pinched between larger basins and would be expected to not have as much growth potential compared to their wider neighbors. Elongated basins also exist on Kaitake; however, they do not have as high of a deviation (maximum DL≈0.1; Fig. 9d). This may be a product of the lower number of basins that exist on Kaitake, the overall lower amount of drainage area occupied by that Kaitake basins, or an evolution of basins towards more consistent patterns, thus decreasing the amount of variability from the power law relationship. On both Merapi and Kaitake, these elongated basins may further highlight the dynamics of basin competition on radial structures; through drainage divide migration and areal loss (likely influenced by edifice-scale sector collapses or regrowth events; Gertisser et al., 2023), less erosive drainages become passive players to more dominant basins and adopt non-standard geometries, becoming narrow, chute-like basins on the mid- and upper flanks.
4.5 How do radial drainages compare to other settings?
Thus far, our discussion has focused on deriving a foundational understanding of how radial drainages on volcanic edifices evolve and compete. However, we note similarities between our interpretation and those from previous studies in other drainage settings. This leads to a simple question: is there a significant difference between radial and dendritic drainage development and evolution?
Our results show that basin formation on volcanic edifices follows the development of rills and gullies within badlands (Schumm, 1956). As radial drainages evolve and certain basins expand to become dominant features on the edifice, less dominant basins become passive and are pushed down-flank, often adhering to non-standard geometries as imposed by their more dominant neighbors (Habousha et al., 2023; Beeson and McCoy, 2022). The dynamics of this basin competition and formation of passive basins are demonstrated by edifice basin spacing ratios. Summit basins on edifices have spacing ratios that appear time-independent and fit within the range of values observed in linear mountain ranges globally (Hovius, 1996) (Fig. 7), suggesting that this ratio is set during the initial stages of basin formation – an attribute of basin evolution that has been shown to occur on linear fault blocks (Talling et al., 1997; Habousha et al., 2023). However, basins that are within a radial distance from the summit that is 30 % of the edifice's maximum radius do experience a temporally decreasing spacing ratio and constant distance between outlets (Fig. 8), capturing the development of a basin topographic hierarchy along the edifice – a behavior not previously observed. Finally, our drainage divide analysis on volcanic edifices suggest that radial drainage basins evolve towards a stable basin configuration as topography matures towards a dynamic equilibrium, similar to regional landscape evolution globally (e.g., Perron and Royden, 2013; Willett et al., 2014).
This comparison suggests that drainage development and evolution on radial structures are largely similar to those occurring within linear mountain settings. However, some differences still occur, particularly in relation to basin geometries imposed by the larger-scale, radial primary landform. Dendritic drainages in linear mountain belts and fault blocks are characterized by their leaf-like geometries (e.g., Zernitz, 1932; Strahler, 1952; Talling et al., 1997) having a broad headwater region that decreases towards the outlet to a tapered point. Although radial drainages also have tapered outlets and basin widths increase upstream, these widths are hindered by the conical geometry of the primary landform and convergence of multiple basins towards the summit, leading to a tapered headwater and a tapered outlet. This geometric constraint is well demonstrated by the drainages on Merapi (Fig. 9c), where summit basins are generally widest on the lower or mid-flanks; however, this trend is not as obvious on Kaitake (Fig. 9d), where erosion has dissected the landform and weakened the conical influence of the edifice on basin geometries. Furthermore, as edifice drainages are limited to a conical landform, their evolution and configuration are constrained by a cumulative areal limit. As opposed to linear mountain ranges (where a morphologic change in one basin impacts its neighbors, which then impacts their neighbors as a cascading chain across the landscape), on volcanic edifices, a morphologic change in one basin (particularly a dominant basin) may directly impact the erosional state and morphology of most other basins on the landform due to the high number of basins that may share a divide with this basin. This areal effect on radial basin evolution may be further augmented by the higher diversity of underlying host rocks between edifice basins associated with magmatic and volcanic products (e.g., tephra deposits, lava flows, and intrusions) that is not as prevalent within linear mountain ranges.
Despite the differences in basin geometries and interactions discussed above, edifice-averaged morphometric values (e.g., Hack's law exponent, drainage density, mean basin hypsometry, and mean basin slopes) are similar to those of other settings (Hack, 1957; Strahler, 1952; Horton, 1945). This suggests that although radial drainages experience phenomena that differ from those typically experienced in dendritic settings, drainage development, geometries, and competition largely follow those of dendritic patterns. As volcanic surfaces are easily datable and their ages can often vary by orders magnitude on a single edifice, volcanoes thus represent ideal locations for studying terrain evolution over varying temporal scales within a general framework.
4.6 Basin morphology capturing volcanic processes
In this study, we considered edifice morphologies using mean values over the entire edifice. However, our metrics also allow for the comparison of basin morphologies on a single edifice. Variations associated with these metrics would likely relate to spatially localized attributes of aggradation, degradation, and climate and would thus provide a quantitative method to disentangle these signals using topography. For example, edifice flanks that have been resurfaced by large volcanic deposits or destroyed by sector collapses should exhibit younger drainage networks, according to the metrics explored here, and are expected to differ from other parts of the volcano. Furthermore, alterations to the erosional efficiency of a basin by tephra accumulation or lava flow emplacement should create spatial variability that can be quantified by similar analyses. These concepts should be tested over well-constrained cases and would be beneficial for both preliminary fieldwork and to approximate relative volcanic chronologies remotely. Our model for edifice degradation, radial drainage evolution, and divide stability thus provides a first step to deconvolving the various signals that relate to edifice morphology. This presents new avenues of exploration for the volcanology community to interrogate volcanic histories from topography and for the geomorphic community to investigate surface evolution on landforms that often fall outside standard tectonic studies.
Volcanic edifices represent a class of primary landforms whose erosion remains relatively unexplored. We analyzed the degradational histories of stratovolcanoes using a set of metrics that have not previously been considered for radial drainage networks. We show that these metrics relate to the overall age of a volcano and propose a new general model for the temporal evolution of edifice drainage morphology. Divide stability analysis underscores the dynamic nature of basin evolution and suggests that radial drainage networks initiate with nearly uniform geometries and unstable configurations that evolve towards non-uniform basin geometries and more stable configurations to generate a basin topographic hierarchy on volcanoes. Finally, comparing basin geometries, configurations, and outlet spacing between basins that exist on volcanic edifices to those that exist on linear mountain ranges highlights the similarities and differences between radial and dendritic drainage basins.
DrainageVolc and MORVOLC codes are available at https://doi.org/10.5281/zenodo.10906553 (O'Hara, 2024).
Collected edifice data are included in the Supplement as both an Excel file and shapefile.
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-12-709-2024-supplement.
All authors provided editorial advice on the paper. DO wrote DrainageVolc and updated the MORVOLC codes, conducted the morphology analyses, and wrote the paper. RMJvW assisted with data collection, determined edifice boundaries from topography, and tested DrainageVolc/MORVOLC. LG and BC gave advice on drainage basin morphology and evolution, while PG, PL, and GK provided insight into volcanic edifice morphology, evolution, and general volcano ages. MK secured funds and coordinated the project, giving advice on the research direction, analyses, and interpretation.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
This research has been funded through the EVoLvE project and Junior FWO project (grant no. G029820N) of the Fonds Wetenschappelijke Onderzoek – Vlaanderen.
This research has been supported by the Fonds Wetenschappelijk Onderzoek – Vlaaneren (FWO) (grant no. G029820N).
This paper was edited by Susan Conway and reviewed by Karen G. Bemis and one anonymous referee.
Becerril, L., Lara, L. E., and Astudillo, V. I.: The strong competition between growth and erosive processes on the Juan Fernández Archipelago (SE Pacific, Chile), Geomorphology, 373, 107513, https://doi.org/10.1016/j.geomorph.2020.107513, 2021.
Beeson, H. W. and McCoy, S. W.: Disequilibrium river networks dissecting the western slope of the Sierra Nevada, California, USA, record significant late Cenozoic tilting and associated surface uplift, Bull. Geol. Soc. Am., 134, 2809–2853, https://doi.org/10.1130/B36517.1, 2022.
Biggs, J., Mothes, P., Ruiz, M., Amelung, F., Dixon, T. H., Baker, S., and Hong, S. H.: Stratovolcano growth by co-eruptive intrusion: The 2008 eruption of Tungurahua Ecuador, Geophys. Res. Lett., 37, L21302, https://doi.org/10.1029/2010GL044942, 2010.
Bishop, P.: Drainage rearrangement by river capture, beheading and diversion, Prog. Phys. Geogr., 19, 449–473, 1995.
Bohnenstiehl, D. W. R., Howell, J. K., White, S. M., and Hey, R. N.: A modified basal outlining algorithm for identifying topographic highs from gridded elevation data, Part 1: Motivation and methods, Comput. Geosci., 49, 308–314, https://doi.org/10.1016/j.cageo.2012.04.024, 2012.
Braun, J.: A review of numerical modeling studies of passive margin escarpments leading to a new analytical expression for the rate of escarpment migration velocity, Gondwana Res., 53, 209–224, https://doi.org/10.1016/j.gr.2017.04.012, 2018.
Castelltort, S. and Simpson, G.: River spacing and drainage network growth in widening mountain ranges, Basin Res., 18, 267–276, https://doi.org/10.1111/j.1365-2117.2006.00293.x, 2006.
Castelltort, S., Simpson, G., and Darrioulat, A.: Slope-control on the aspect ratio of river basins, Terra Nov., 21, 265–270, https://doi.org/10.1111/j.1365-3121.2009.00880.x, 2009.
Castelltort, S., Goren, L., Willett, S. D., Champagnac, J. D., Herman, F., and Braun, J.: River drainage patterns in the New Zealand Alps primarily controlled by plate tectonic strain, Nat. Geosci., 5, 744–748, https://doi.org/10.1038/ngeo1582, 2012.
Castro, J. M., Cordonnier, B., Schipper, C. I., Tuffen, H., Baumann, T. S., and Feisel, Y.: Rapid laccolith intrusion driven by explosive volcanic eruption, Nat. Commun., 7, 1–7, https://doi.org/10.1038/ncomms13585, 2016.
Civico, R., Ricci, T., Scarlato, P., Taddeucci, J., Andronico, D., Del Bello, E., D'Auria, L., Hernández, P. A., and Pérez, N. M.: High-resolution Digital Surface Model of the 2021 eruption deposit of Cumbre Vieja volcano, La Palma, Spain, Sci. Data, 9, 1–7, https://doi.org/10.1038/s41597-022-01551-8, 2022.
Cook, K. L., Turowski, J. M., and Hovius, N.: A demonstration of the importance of bedload transport for fluvial bedrock erosion and knickpoint propagation, Earth Surf. Proce. Land., 38, 683–695, https://doi.org/10.1002/esp.3313, 2013.
Dibacto, S., Lahitte, P., Karátson, D., Hencz, M., Szakács, A., Biró, T., Kovács, I., and Veres, D.: Growth and erosion rates of the East Carpathians volcanoes constrained by numerical models: Tectonic and climatic implications, Geomorphology, 368, 107352, https://doi.org/10.1016/j.geomorph.2020.107352, 2020.
Duvall, A. R. and Tucker, G. E.: Dynamic Ridges and Valleys in a Strike-Slip Environment, J. Geophys. Res.-Earth, 120, 2016–2026, https://doi.org/10.1002/2015JF003618, 2015.
Euillades, L. D., Grosse, P., and Euillades, P. A.: NETVOLC: An algorithm for automatic delimitation of volcano edifice boundaries using DEMs, Comput. Geosci., 56, 151–160, https://doi.org/10.1016/j.cageo.2013.03.011, 2013.
Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., Kobrick, M., Paller, M., Rodriguez, E., Roth, L., Seal, D., Shaffer, S., Shimada, J., Umland, J., Werner, M., Oskin, M., Burbank, D., and Alsdorf, D.: The Shuttle Radar Topography Mission, Rev. Geophys., 45, 1–43, 2007.
Ferrier, K. L., Huppert, K. L., and Perron, J. T.: Climatic control of bedrock river incision, Nature, 496, 206–209, https://doi.org/10.1038/nature11982, 2013.
Flint, J. J.: Stream gradient as a function of order, magnitude, and discharge, Water Resour. Res., 10, 969–973, https://doi.org/10.1029/WR010i005p00969, 1974.
Forte, A. M. and Whipple, K. X.: Criteria and tools for determining drainage divide stability, Earth Planet. Sc. Lett., 493, 102–117, https://doi.org/10.1016/j.epsl.2018.04.026, 2018.
Fox, M., Goren, L., May, D. A., and Willett, S. D.: Inversion of fluvial channels for paleorock uplift rates in Taiwan, J. Geophys. Res.-Earth, 119, 1853–1875, https://doi.org/10.1002/2014JF003196, 2014.
Gase, A. C., Brand, B. D., and Bradford, J. H.: Evidence of erosional self-channelization of pyroclastic density currents revealed by ground-penetrating radar imaging at Mount St. Helens, Washington (USA), Geophys. Res. Lett., 44, 2220–2228, https://doi.org/10.1002/2016GL072178, 2017.
Gertisser, R., Troll, V. R., Walter, T. R., Nandaka, I. G. M. A., and Ratdomopurbo, A.: Merapi Volcano: Geology, Eruptive Activity, and Monitoring of a High-Risk Volcano, Springer Nature, https://doi.org/10.1007/978-3-031-15040-1, 2023.
Gilbert, G. K.: The Convexity of Hilltops, J. Geol., 17, 344–350, 1909.
Global Volcanism Program: [Database] Volcanoes of the World (v. 5.1.7; 26 Apr 2024), compiled by: Venzke, E., Smithsonian Institution, https://doi.org/10.5479/si.GVP.VOTW5-2023.5.1, 2024.
Grosse, P., van Wyk de Vries, B., Petrinovic, I. A., Euillades, P. A., and Alvarado, G. E.: Morphometry and evolution of arc volcanoes, Geology, 37, 651–654, https://doi.org/10.1130/G25734A.1, 2009.
Grosse, P., van Wyk de Vries, B., Euillades, P. A., Kervyn, M., and Petrinovic, I. A.: Systematic morphometric characterization of volcanic edifices using digital elevation models, Geomorphology, 136, 114–131, https://doi.org/10.1016/j.geomorph.2011.06.001, 2012.
Haapala, J. M., Wolf, R. E., Vallance, J. W., Rose Jr., W. I., Griswold, J. P., Schilling, S. P., Ewert, J. W., and Mota, M.: Volcanic hazards at Atitlan volcano, Guatemala, US Geological Survey Open-File Report 2005-1403, S Geological Survey, https://doi.org/10.3133/ofr20051403, 2006.
Habousha, K., Goren, L., Nativ, R., and Gruber, C.: Plan-Form Evolution of Drainage Basins in Response to Tectonic Changes: Insights From Experimental and Numerical Landscapes, J. Geophys. Res.-Earth, 128, 1–24, https://doi.org/10.1029/2022jf006876, 2023.
Hack, J. T.: Studies of longitudinal stream profiles in Virginia and Maryland, in: Vol. 294, US Government Printing Office, https://doi.org/10.3133/pp294B, 1957.
Hamawi, M., Goren, L., Mushkin, A., and Levi, T.: Rectangular drainage pattern evolution controlled by pipe cave collapse along clastic dikes, the Dead Sea Basin, Israel, Earth Surf. Proc. Land., 47, 936–954, https://doi.org/10.1002/esp.5295, 2022.
Han, J., Gasparini, N. M., and Johnson, J. P. L.: Measuring the imprint of orographic rainfall gradients on the morphology of steady-state numerical fluvial landscapes, Earth Surf. Proc. Land., 40, 1334–1350, https://doi.org/10.1002/esp.3723, 2015.
Hasbargen, L. E. and Paola, C.: Landscape instability in an experimental drainage basin, Geology, 28, 1067–1070, https://doi.org/10.1130/0091-7613(2000)28<1067:LIIAED>2.0.CO, 2000.
Hayes, S. K., Montgomery, D. R., and Newhall, C. G.: Fluvial sediment transport and deposition following the 1991 eruption of Mount Pinatubo, Geomorphology, 45, 211–224, https://doi.org/10.1016/S0169-555X(01)00155-6, 2002.
Horton, R. E.: Erosional development of streams and their drainage basins; hydrological approach to quantative morphology, Geol. Soc. Am. Bull., 56, 275–370, https://doi.org/10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2, 1945.
Hovius, N.: Regular spacing of drainage outlets from linear mountain belts, Basin Res., 8, 29–44, https://doi.org/10.1111/j.1365-2117.1996.tb00113.x, 1996.
Howard, A. D.: Drainage Analysis in Geologic Interpretation: A Summation, Am. Assoc. Petrol. Geol. Bull., 51, 2246–2259, https://doi.org/10.1306/5d25c26d-16c1-11d7-8645000102c1865d, 1967.
Jefferson, A., Grant, G. E., Lewis, S. L., and Lancaster, S. T.: Coevolution of hydrology and topography on a basalt landscape in the Oregon Cascade Range, USA, Earth Surf. Proc. Land., 35, 803–816, https://doi.org/10.1002/esp.1976, 2010.
Karátson, D., Thouret, J. C., Moriya, I., and Lomoschitz, A.: Erosion calderas: Origins, processes, structural and climatic control, Bull. Volcanol., 61, 174–193, https://doi.org/10.1007/s004450050270, 1999.
Karátson, D., Telbisz, T., and Wörner, G.: Erosion rates and erosion patterns of Neogene to Quaternary stratovolcanoes in the Western Cordillera of the Central Andes: An SRTM DEM based analysis, Geomorphology, 139–140, 122–135, https://doi.org/10.1016/j.geomorph.2011.10.010, 2012.
Kerr, R. C.: Thermal erosion by laminar lava flows, J. Geophys. Res.-Solid, 106, 453–465, https://doi.org/10.1029/2001JB000227, 2001.
Kirby, E. and Whipple, K. X.: Expression of active tectonics in erosional landscapes, J. Struct. Geol., 44, 54–75, https://doi.org/10.1016/j.jsg.2012.07.009, 2012.
Kirby, E., Whipple, K. X., Tang, W., and Chen, Z.: Distribution of active rock uplift along the eastern margin of the Tibetan Plateau: Inferences from bedrock channel longitudinal profiles, J. Geophys. Res.-Solid, 108, 2217, https://doi.org/10.1029/2001JB000861, 2003.
Lahitte, P., Samper, A., and Quidelleur, X.: DEM-based reconstruction of southern Basse-Terre volcanoes (Guadeloupe archipelago, FWI): Contribution to the Lesser Antilles Arc construction rates and magma production, Geomorphology, 136, 148–164, https://doi.org/10.1016/j.geomorph.2011.04.008, 2012.
Locke, C. A. and Cassidy, J.: Egmont Volcano, New Zealand: Three-dimensional structure and its implications for evolution, J. Volcanol. Geoth. Res., 76, 149–161, https://doi.org/10.1016/S0377-0273(96)00074-1, 1997.
Lohse, K. A. and Dietrich, W. E.: Contrasting effects of soil development on hydrological properties and flow paths, Water Resour. Res., 41, 1–17, https://doi.org/10.1029/2004WR003403, 2005.
Major, J. J., Mosbrucker, A. R., and Spicer, K. R.: Sediment erosion and delivery from Toutle River basin after the 1980 eruption of Mount St. Helens: A 30-year perspective, Ecol. Responses Mt. St. Helens Revisit. 35 years after 1980 Erupt., Springer, 19–44, https://doi.org/10.1007/978-1-4939-7451-1_2, 2018.
McBirney, A. R., Serva, L., Guerra, M., and Connor, C. B.: Volcanic and seismic hazards at a proposed nuclear power site in central Java, J. Volcanol. Geoth. Res., 126, 11–30, https://doi.org/10.1016/S0377-0273(03)00114-8, 2003.
Mejía, A. I. and Niemann, J. D.: Identification and characterization of dendritic, parallel, pinnate, rectangular, and trellis networks based on deviations from planform self-similarity, J. Geophys. Res.-Earth, 113, 1–21, https://doi.org/10.1029/2007JF000781, 2008.
Montgomery, D. R. and Dietrich, W. E.: Landscape dissection and drainage area-slope thresholds, in: Process Models and Theoretical Geomorphology, Chap. 11, edited by: Kirkby, M. J., John Wiley and Sons, https://docubase.berkeley.edu/cgi-bin/pl_dochome?query_src=pl_search&format=pdf&collection=Dietrich&id=82&show_doc=yes (last access: 6 May 2024). 1994.
Mudd, S. M. and Furbish, D. J.: Responses of soil-mantled hillslopes to transient channel incision rates, J. Geophys. Res.-Earth, 112, 1–12, https://doi.org/10.1029/2006JF000516, 2007.
Mueller, J. E.: Re-evaluation of the relationship of master streams and drainage basins, Bull. Geol. Soc. Am., 83, 3471–3474, https://doi.org/10.1130/0016-7606(1972)83[3471:ROTROM]2.0.CO;2, 1972.
Mulyaningsih, S. and Shaban, G.: Geochemistry of basaltic Merbabu volcanic rocks, Central Java, Indonesia, Indones. J. Geosci., 7, 161–178, https://doi.org/10.17014/ijog.7.2.161-178, 2020.
O'Hara, D.: danjohara/Volc_Packages: Volc_Packages (v3.0.0), Zenodo [code], https://doi.org/10.5281/zenodo.10906553, 2024.
O'Hara, D. and Karlstrom, L.: The arc-scale spatial distribution of volcano erosion implies coupled magmatism and regional climate in the Cascades arc, United States, Front. Earth Sci., 11, 1–15, https://doi.org/10.3389/feart.2023.1150760, 2023.
O'Hara, D., Karlstrom, L., and Roering, J. J.: Distributed landscape response to localized uplift and the fragility of steady states, Earth Planet. Sc. Lett., 506, 243–254, https://doi.org/10.1016/j.epsl.2018.11.006, 2019.
O'Hara, D., Karlstrom, L., and Ramsey, D. W.: Time-evolving surface and subsurface signatures of Quaternary volcanism in the Cascades arc, Geology, 49, e526, https://doi.org/10.1130/g47706.1, 2020.
Ollier, C.: Volcanoes, Blackwell, Oxford, 288 pp., ISBN 13 9780631156642, 1988.
Perron, J. T. and Royden, L.: An integral approach to bedrock river profile analysis, Earth Surf. Proc. Land., 38, 570–576, https://doi.org/10.1002/esp.3302, 2013.
Pierson, T. C. and Major, J. J.: Hydrogeomorphic effects of explosive volcanic eruptions on drainage basins, Annu. Rev. Earth Planet. Sci., 42, 469–507, https://doi.org/10.1146/annurev-earth-060313-054913, 2014.
Prince, P. S. and Spotila, J. A.: Evidence of transient topographic disequilibrium in a landward passive margin river system: Knickpoints and paleo-landscapes of the New River basin, southern Appalachians, Earth Surf. Proc. Land., 38, 1685–1699, https://doi.org/10.1002/esp.3406, 2013.
Ricci, J., Lahitte, P., and Quidelleur, X.: Construction and destruction rates of volcanoes within tropical environment: Examples from the Basse-Terre Island (Guadeloupe, Lesser Antilles), Geomorphology, 228, 597–607, https://doi.org/10.1016/j.geomorph.2014.10.002, 2015.
Scherler, D. and Schwanghart, W.: Drainage divide networks – Part 1: Identification and ordering in digital elevation models, Earth Surf. Dynam., 8, 245–259, https://doi.org/10.5194/esurf-8-245-2020, 2020.
Schumm, S. A.: Evolution of drainage systems and slopes in badlands at Perth Amboy, New Jersey, Bull. Geol. Soc. Am., 67, 597–646, https://doi.org/10.1130/0016-7606(1956)67[597:EODSAS]2.0.CO;2, 1956.
Schwanghart, W. and Scherler, D.: Short Communication: TopoToolbox 2 – MATLAB-based software for topographic analysis and modeling in Earth surface sciences, Earth Surf. Dynam., 2, 1–7, https://doi.org/10.5194/esurf-2-1-2014, 2014.
Shea, T. and van Wyk de Vries, B.: Structural analysis and analogue modeling of the kinematics and dynamics of rockslide avalanches, Geosphere, 4, 657–686, https://doi.org/10.1130/GES00131.1, 2008.
Sklar, L. S. and Dietrich, W. E.: Sediment and rock strength controls on river incision into bedrock, Geology, 29, 1087–1090, https://doi.org/10.1130/0091-7613(2001)029<1087:SARSCO>2.0.CO;2, 2001.
Strahler, A. N.: Hypsometric (area-altitude) analysis of erosional topography, Bull. Geol. Soc. Am., 63, 1117–1142, https://doi.org/10.1128/AAC.03728-14, 1952.
Sweeney, K. E. and Roering, J. J.: Rapid fluvial incision of a late Holocene lava flow: Insights from LiDAR, alluvial stratigraphy, and numerical modeling, Bull. Geol. Soc. Am., 129, 500–512, https://doi.org/10.1130/B31537.1, 2017.
Talling, P. J., Stewart, M. D., Stark, C. P., Gupta, S., and Vincent, S. J.: Regular spacing of drainage outlets from linear fault blocks, Basin Res., 9, 275–302, https://doi.org/10.1046/j.1365-2117.1997.00048.x, 1997.
Thouret, J. C., Oehler, J. F., Gupta, A., Solikhin, A., and Procter, J. N.: Erosion and aggradation on persistently active volcanoes – a case study from Semeru Volcano, Indonesia, Bull. Volcanol., 76, 857, https://doi.org/10.1007/s00445-014-0857-z, 2014.
Ui, T. and Glicken, H.: Internal structural variations in a debris-avalanche deposit from ancestral Mount Shasta, California, USA, Bull. Volcanol., 48, 189–194, https://doi.org/10.1007/BF01087673, 1986.
van Wees, R., Tournigand, P.-Y., O'Hara, D., Grosse, P., Kereszturi, G., Campforts, B., Lahitte, P., and Kervyn, M.: The role of erosion in the morphometry of composite volcanoes, EGU General Assembly 2021, online, 19–30 April 2021, EGU21-14500, https://doi.org/10.5194/egusphere-egu21-14500, 2021.
van Wees, R. M. J., O'Hara, D., Kereszturi, G., Grosse, P., Lahitte, P., Tourniganda, P.-Y., and Kervyn, M.: Towards more consistent volcano morphometry datasets: Assessing boundary delineation and DEM impact on geometric and drainage parameters, Geomorphology, in review, 2024.
Wells, S. G., Dohrenwend, J. C., McFadden, L. D., Turrin, B. D., and Mahrer, K. D.: Late Cenozoic landscape evolution on lava flow surfaces of the Cima volcanic field, Mojave Desert, California, Geol. Soc. Am. Bull., 96, 1518–1529, https://doi.org/10.1130/0016-7606(1985)96<1518:LCLEOL>2.0.CO;2, 1985.
Whipple, K. X., DiBiase, R. A., Ouimet, W. B., and Forte, A. M.: Preservation or piracy: Diagnosing low-relief, high-elevation surface formation mechanisms, Geology, 45, 91–94, https://doi.org/10.1130/G32501Y.1, 2016.
Wicks, C. W., Dzurisin, D., Ingebritsen, S., Thatcher, W., Lu, Z., and Iverson, J.: Magmatic activity beneath the quiescent Three Sisters volcanic center, central Oregon Cascade Range, USA, Geophys. Res. Lett., 29, 26-1–26-4, https://doi.org/10.1029/2001GL014205, 2002.
Willett, S. D., Slingerland, R., and Hovius, N.: Uplift, shortening, and steady state topography in active mountain belts, Am. J. Sci., 301, 455–485, https://doi.org/10.2475/ajs.301.4-5.455, 2001.
Willett, S. D., McCoy, S. W., Perron, T. J., Goren, L., and Chen, C. Y.: Dynamic reorganization of River Basins, Science, 343, 1248765, https://doi.org/10.1126/science.1248765, 2014.
Yang, R., Willett, S. D., and Goren, L.: In situ low-relief landscape formation as a result of river network disruption, Nature, 520, 526–529, https://doi.org/10.1038/nature14354, 2015.
Zernitz, E. R.: Drainage Patterns and Their Significance, J. Geol., 40, 498–521, https://doi.org/10.1086/623976, 1932.




