Improving a multi-grain-size total sediment load model through a new standardized reference shear stress for incipient motion and an adjusted saltation height description

Modelling sediment transport is important to understand how fluvial systems respond to climatic change or other transient conditions such as catastrophic sediment release. In natural rivers, heterogeneity of sediment properties and variability of the flow regime result in different modes of transport that all contribute to the total sediment load. Le Minor et al. (2022) presented a sediment transport law for rivers that extends from bed load to suspended load while being relevant for a wide range of grain sizes but not specifically addressing the case of a distribution of grain sizes, which must also consider the interactions between grain classes that are mainly important during the sediment erosion phase. If these interactions are not properly considered, the model overestimates transport rates compared to measured ones. We present a new formalism for the reference shear stress of multiple-size sediments, a parameter governing the onset of transport. We show that using a reference shear stress standardized across datasets improves transport rate predictions made with the model of Le Minor et al. (2022). We show that considering the bed roughness length as a reference transport height for single- and multiple-size sediments significantly improves transport rate predictions. We also suggest that, for multiple-size sediments where the bed surface is not fully mobile, the entrainment coefficient should include a dependency on the fraction of mobile grain sizes at the bed surface, although data are insufficient to add this effect in a definite parameterization. Therefore, a standardized reference shear stress and a transport length adjusted with a common reference height across all sizes appear to be two critical ingredients of a fully functional multi-grain-size total sediment load model based on the disequilibrium length. This adjusted model offers the potential to quantify grain-size-specific sediment fluxes when different modes of transport may be observed simultaneously, paving the way for more informed numerical modelling of fluvial morphodynamics and sediment transfers.

1 Introduction

Transport over riverbeds made from sediment composed of heterogeneous grain sizes is complex due to concomitant bed load and suspended load transport. Capturing grain-size-specific transport modes simultaneously is relevant for a variety of phenomena such as the total load partitioning under a wide range of water discharge (Turowski et al., 2010), sorting patterns at the bed surface, e.g. armouring and downstream fining (Paola et al., 1992; Powell, 1998; Viparelli et al., 2017), and gravel–sand transitions (Blom et al., 2017; Dingle and Venditti, 2023; Venditti and Church, 2014). These phenomena and being able to model them accurately are important when investigating fluvial system response to climatic change or other transient conditions, such as the response to catastrophic sediment delivery from landsliding (De Haas et al., 2015; Tunnicliffe et al., 2024). A universal total sediment transport load model suitable for extremely wide grain size distributions and hydraulic conditions would help to better understand the controls on sediment dynamics from mountain slopes to river valleys and fluvial plains.

To predict fractional transport rates of mixed-size sediments, i.e. for each grain size, it is important to account for grain size heterogeneity and grain size interactions, such as hiding-exposure effects that make the entrainment of fine fractions harder (increased threshold of motion) and the entrainment of coarse fractions easier (lowered threshold of motion). Although sediment transport has been studied at grain scale and reach scale (e.g. Charru et al., 2004; Engelund and Hansen, 1967; Houssais and Lajeunesse, 2012; Lajeunesse et al., 2010; Meyer-Peter and Müller, 1948; van Rijn, 1984a, b), there has been, to our knowledge, only a few attempts at a continuous transport law that extends from bed load to suspended load for a wide range of flow strengths and sediment grain size distributions introduced. Most of these continuous total load transport laws have been established by summing up contributions of bed load and suspended load calculated using separate formalisms (Dade and Friend, 1998; van Rijn, 1984b). A more recent attempt by Le Minor et al. (2022; model referred to as LM2022 in this study) differs conceptually from this approach. Instead of discriminating between bed load and suspended load, LM2022 introduced a single formalism that brings both contributions together by describing the portion of the water column where most sediment transport occurs, i.e. the characteristic sediment transport height. The advantage of LM2022's model is that it is relevant to studying catastrophic sediment delivery to fluvial systems, as it applies to a wide range of grain size distributions and hydraulic conditions.

LM2022 is a multi-grain-size total load sediment transport model that applies to various transport modes in both non-stationary and stationary regimes. It is based on the erosion–deposition formalism using a transport length, resulting in a spatial lag to reach transport saturation, which depends on flow condition and grain size (Charru, 2006; Daubert and Lebreton, 1967; Davy and Lague, 2009; El Kadi Abderrezzak and Paquier, 2009; Jain, 1992; Kooi and Beaumont, 1994; Lajeunesse et al., 2010; Lamb et al., 2008; Le Minor et al., 2022; Sklar and Dietrich, 2004). At equilibrium, i.e. when there are neither spatial nor temporal changes, the transport length equals the ratio of the sediment transport rate per unit width to the entrainment rate. The transport length increases with excess shear stress and gives its scaling with shear stress to the transport rate such that $q_{\mathrm{s}}\propto {\left(\mathit{\tau }-{\mathit{\tau }}_{\mathrm{r}}\right)}^{\mathrm{1}+a}$, where a is the scaling exponent of the transport length with shear stress, q_s is the sediment transport rate per unit width, and τ and τ_r are the bed and reference shear stress, respectively. LM2022 succeeded in predicting the scaling between transport rate and excess shear stress for various transport modes, using two key elements: transport height and entrainment rate. Although the model succeeded in describing a continuum of transport rates from bed to suspended load for a given size, LM2022 had some limitations when the model predictions were compared to a variety of experimental datasets for single- and multiple-size bed load and total load transport. First, it tended to predict larger transport rates compared to measured ones for single- and multiple-size sediment. The magnitude of this overestimation decreased for low shear stress but increased for high shear stress. This suggests that the transport length, entrainment rate, or both may not be parameterized correctly because these two parameters set the magnitude and scaling of modelled transport rates with shear stress. Second, Le Minor et al. (2022) showed that the single-size erosion–deposition formulation based on the disequilibrium length was not directly applicable to multiple-size sediments, as the reference transport height was too dependent on individual grain sizes and not on the interactions between different grain sizes. They propose to use a common reference transport height at the base of the transport layer. Preliminary results using the median grain size as this common reference transport height showed an improvement for multiple grain sizes.

Another explanation for the discrepancies in model predictions may be that input model parameters are not actually comparable between the experimental datasets, in particular when it comes to characterizing the incipient motion of sediment mixtures. Le Minor et al. (2022) use a critical shear stress formalism to characterize incipient motion in the entrainment rate. Critical shear stress means that for bed shear stress values lower than or equal to the critical value, there is no transport. Experimentally measuring the critical shear stress is very difficult due to the very low transport rates. An alternative approach is commonly used instead, known as a reference shear stress (e.g. Shvidchenko et al., 2001; Wilcock and Crowe, 2003). The reference shear stress differs from the critical shear stress in that it is defined as the bed shear stress required to produce a given transport rate, and hence, for bed shear stress values lower than or equal to the reference value, there may be a very low non-zero transport rate. However, methods and estimates of the reference shear stress values vary between studies, resulting in a lack of consistency across the datasets used to evaluate the model in Le Minor et al. (2022). Indeed, in Le Minor et al. (2022), reference shear stress values and the empirical formulations derived from them were taken directly from the literature with no consideration of how they were measured (e.g. “by-eye” observations) or for which reference transport rate they were established. For instance, the reference transport rate considered by Wilcock and Crowe (2003) for mixed-size sediment was related to different entrainment probabilities from one grain size to another. This model contrasts with Shvidchenko et al. (2001), whose reference shear stress model relies on a unique entrainment probability. Another issue is that the reference shear stress measurement relates to a specific bed surface grain size composition and hydraulic conditions. Studies suggest that the reference shear stress relates to the grain size distribution of the final bed surface rather than the one of the bulk sediment (initial bed surface) when both hiding-exposure effects and surface armouring occur (Parker and Klingeman, 1982; Parker and Wilcock, 1993). The main limitations of existing definitions stem from two approaches. First, some definitions are based on the grain size distribution of the initial bed surface, with the assumption that the surface composition remains relatively constant between the initial and final states (Shvidchenko et al., 2001). Second, other definitions rely on the grain size distribution of the final bed surface, which is averaged over several runs with similar initial bulk sediment. This method also assumes that the surface composition does not change significantly with variations in water discharge and sediment transport rates, meaning there is a similar degree of kinetic sorting (Wilcock and Crowe, 2003). These may not be comparable and could introduce inconsistencies in model calibration or validation using different datasets, especially for bed load transport predictions.

In this study, we seek to improve on LM2022's model by (i) applying a standardized approach to determine the reference shear stress for incipient motion of single- and multiple-size sediments, (ii) introducing a new formalism for the reference shear stress of individual fractions of multiple-size sediments based on the work by Shvidchenko et al. (2001) and Wilcock and Crowe (2003), and (iii) presenting improvements to the entrainment rate and the transport length – two key model elements. In doing so, we seek to balance the objectives of accurately predicting single- and multiple-grain size bed load and total sediment load and developing a parsimonious model that is relatively easy to parameterize. In Sect. 2, we present the empirical equations of reference shear for incipient motion used in Le Minor et al. (2022), the key elements of LM2022's model, and improvements to its entrainment rate and transport length. In Sect. 3, we describe the datasets used for model calibration and validation and the procedure to establish a new model of reference shear stress. In Sect. 4, we present results for the new model of reference shear stress and transport rate predictions made considering the standardized threshold of motion and the modifications of the transport length. In Sect. 5, we discuss our findings and identify the key adjustments required to produce a multi-grain-size total sediment load model that applies to single- and multiple-size sediments.

2 Model description and adjustment

2.1 Standardization of reference shear stress for incipient motion

In Le Minor et al. (2022), reference shear stress values used as model input were inconsistent across datasets because the methods used by the original authors were measured or calculated in different ways for single- and multi-grain-size sediments (Table 1). We detail these differences below. As is usual, all equations are based on the dimensionless form of shear stress, i.e. the Shields stress θ_i [–]:

$$\begin{array}{}\text{(1)}& {\mathit{\theta }}_i={\displaystyle \frac{\mathit{\tau }}{\mathit{\rho }{R}_{i}g{d}_i}},\end{array}$$

where $R_i={\mathit{\rho }}_{\mathrm{s},i}/\mathit{\rho }-\mathrm{1}$ [–] is the sediment specific gravity, with ρ_s,i and ρ [kg m⁻³] being the sediment and water densities, respectively, g [m s⁻²] is the gravitational constant, d_i [m] is the sediment diameter, and τ [Pa] is the bed shear stress. Note that the subscript “c” is added when referring to the critical Shields stress θ_c,i and that the subscript “r” is added when referring to the reference Shields stress θ_r,i. We also refer to grain-size-specific parameters using the “i” subscript for the ith size.

Table 1 Summary of datasets and methods employed to obtain values of the Shields stress for the reference shear stress in Le Minor et al. (2022). Two datasets were added in this study (Shvidchenko et al., 2001; Shvidchenko and Pender, 2000a). The choice of various methods to determine the bed roughness depends on the information provided for each dataset or the lack thereof. In the latter case, the use of Nielsen's equation (1992) results from a sensitivity analysis of LM2022's model with respect to the roughness formulation (Le Minor et al., 2022).

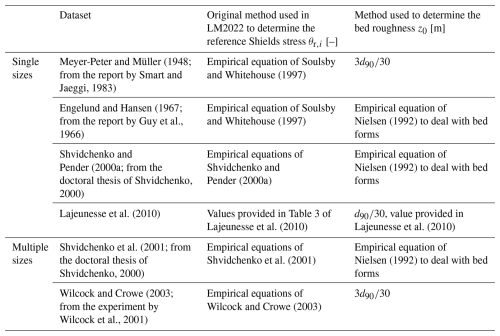
For single-size sediments (Table 1), Le Minor et al. (2022) used critical Shields stress values published in the original studies or calculated using the modified form of the Shield's curve (Shields, 1936) by Soulsby and Whitehouse (1997):

$$\begin{array}{}\text{(2)}& {\mathit{\theta }}_{\mathrm{c},i}={\displaystyle \frac{\mathrm{0.3}}{\mathrm{1}+\mathrm{1.2}{d}_i^{\ast }}}+\mathrm{0.055}\left(\mathrm{1}-\exp \left(-\mathrm{0.02}{d}_i^{\ast }\right)\right),\end{array}$$

where $d_i^{\ast }=\sqrt[\mathrm{3}]{\frac{R_{i}g{d}_i^{\mathrm{3}}}{{\mathit{\nu }}^{\mathrm{2}}}}$ [–] is the non-dimensional grain diameter (ν [Pa s] is the kinematic viscosity of water).

For multiple-size sediments (Table 1), Le Minor et al. (2022) used critical shear stress values published in the original studies or reference Shields stress values calculated from empirical equations.

Note that we included two new datasets for our analysis compared to Le Minor et al. (2022): Shvidchenko and Pender (2000a) for single-size sediments and Shvidchenko et al. (2001) for multiple-size sediments. Both provide empirical equations of the reference Shields stress that we used to predict transport rates, with LM2022 as a reference case (Sect. 4).

In turn, two formalisms were used in this study for the multiple-size sediment datasets: Wilcock and Crowe (2003; model referred to as WC2003 in this study), which is the most widely used when it comes to sediment mixtures, and Shvidchenko et al. (2001; model referred to as S2001 in this study). Each formalism consists of two equations: one for the reference Shields stress of the median size and one for the hiding function characterizing grain size interactions on a rough bed. They differ significantly in their approach to estimating the reference shear stress:

1. S2001's estimate is based on the incipient motion criterion (Shvidchenko et al., 2001; Shvidchenko and Pender, 2000a):

   $$\begin{array}{}\text{(3)}& q_{\mathrm{s},i}^{\ast }={\displaystyle \frac{q_{\mathrm{s},i}}{F_i{\sqrt{R_{i}g{d}_i}}^{\mathrm{3}}}},\end{array}$$

   where $q_{\mathrm{s},i}^{\ast }$ [–] is the dimensionless transport rate per unit width or Einstein number (Einstein, 1950), q_s,i [m³ s⁻¹] is the transport rate per unit width, and F_i [–] is the fraction on the bed surface. The incipient motion criterion relies on the 1:1 correlation between $q_{\mathrm{s},i}^{\ast }$ and the transport intensity I_i [s⁻¹], which is the fraction of mobile grains at the bed surface per unit time.

2. WC2003's estimate is based on the reference transport criterion $W_i^{\ast }$ [–] (Parker et al., 1982b, a; Wilcock, 1988; Wilcock and Crowe, 2003):

   $$\begin{array}{}\text{(4)}& W_i^{\ast }={\displaystyle \frac{R_{i}g{q}_{\mathrm{s},i}}{F_i{u}_{\ast }^{\mathrm{3}}}},\end{array}$$

   where u_∗ [m s⁻¹] is the shear velocity.

Empirical equations of the reference Shields stress have been established for sand–gravel mixtures using both the incipient motion criterion (Shvidchenko et al., 2001) and the reference transport criterion (Wilcock and Crowe, 2003) with reference values such as $q_{\mathrm{s},\mathrm{ref}}^{\ast }={\mathrm{10}}^{-\mathrm{4}}$ (correlated to $I_{\mathrm{ref}}={\mathrm{10}}^{-\mathrm{4}}$ s⁻¹) and $W_{\mathrm{ref}}^{\ast }={\mathrm{2.10}}^{-\mathrm{3}}$, respectively.

The reference transport criterion of Parker et al. (1982a) was defined with no dependency on grain size for the purpose of a similarity collapse, meaning that transport rate data for individual fractions fall on the same curve and are not affected by grain size. This contrasts with the incipient motion criterion of Shvidchenko and Pender (2000a) that included a dependency on grain size because the transport intensity was defined as the ratio of the number of grain displacements to the number of grains available on the bed surface per unit time. Hence, it may be interpreted as a measure of grain mobilization (ratio of mobilized grains to immobile grains) or a probability of entrainment (Shvidchenko et al., 2001; Shvidchenko and Pender, 2000a). Comparisons of these two criteria by Shvidchenko et al. (2001) reveal that the incipient motion criterion scaled by grain diameter results in similar mobilization rates across grain sizes, contrary to the transport criterion. Consequently, the incipient motion criterion is better suited for developing a universal transport law applicable to single- and multiple-size sediments.

Recalling that the reference Shields stress is not defined in the same way in S2001 and WC2003, it is important to note that the authors both observe a dependency of θ_r,i with the heterogeneity of the grain size distribution at the surface of the bed. However, they measure this heterogeneity differently and obtain different empirical relationships that we describe below.

Shvidchenko et al. (2001) found a dependency of θ_r,i on median grain size d₅₀ [m], the grain size to median size ratio $d_i/d_{\mathrm{50}}$ [–], and the mixture geometric log-standard deviation σ_g [–]; i.e. ${\mathit{\sigma }}_{\mathrm{g}}=\sqrt{d_{\mathrm{84}}/d_{\mathrm{16}}}$ (Nakagawa et al., 1982), where d₁₆ [m] and d₈₄ [m] are the grain diameters of the 16th and 84th percentile. For simplification, in this study, we refer to the mixture geometric log-standard deviation as the grain size sorting. In S2001, the grain-size-specific reference Shields stress is written as

$$\begin{array}{}\text{(5)}& {\mathit{\theta }}_{\mathrm{r},i}={\mathit{ϵ}}_i{\displaystyle \frac{\mathrm{0.60}}{a}}{s}^{\mathrm{0.278}},\end{array}$$

where $a=-\mathrm{1.1}{\left({\log }_{\mathrm{10}}\left(\mathrm{1000}{d}_{\mathrm{50}}\right)\right)}^{\mathrm{3}}+\mathrm{4.8}{\left({\log }_{\mathrm{10}}\left(\mathrm{1000}{d}_{\mathrm{50}}\right)\right)}^{\mathrm{2}}-\mathrm{5.0}{\log }_{\mathrm{10}}\left(\mathrm{1000}{d}_{\mathrm{50}}\right)+\mathrm{4.6}$ [–] is the mobility factor, ϵ_i [–] is the hiding function, and s [–] is the channel-bed slope. Equation (5) was first established for the incipient motion of coarse single-size sediments by Shvidchenko and Pender (2000b). Parameter a decreases from about 4.5 to 3 for grain sizes between 1 and 5 mm and increases from about 3 to 5 for grain sizes between 5 and 100 mm.

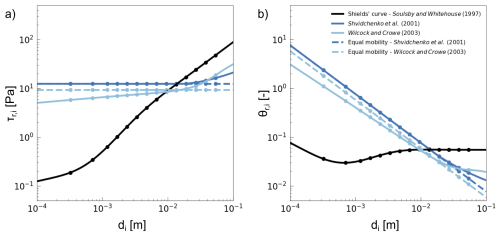
Figure 1 Comparison of the S2001 and WC2003 formalisms. (a) Reference shear stress as a function of grain size. (b) Reference Shields stress as a function of grain size. The Shields's curve is included as well as the curves corresponding to equal mobility conditions. Dots correspond to grain size classes of WC2003's dataset for the grain size distribution with the lowest sand fraction.

The hiding function that corrects the reference Shields stress of the median size θ_r,50 [–] from hiding-exposure effects is written as

$$\begin{array}{}\text{(6)}& \begin{array}{l}{\mathit{ϵ}}_i=\frac{{\mathit{\theta }}_{\mathrm{r},i}}{{\mathit{\theta }}_{\mathrm{r},\mathrm{50}}}=\left\{\begin{array}{l}{\left(\frac{d_i}{d_{\mathrm{50}}}\right)}^{-e}\mathrm{if}\frac{d_i}{d_{\mathrm{50}}}\le \mathrm{1}\\ {\log }_{\mathrm{10}}{\left(\mathrm{10}\frac{d_i}{d_{\mathrm{50}}}\right)}^{-\mathrm{2.2}}\mathrm{if}\frac{d_i}{d_{\mathrm{50}}}\ge \mathrm{1}\end{array}\right.,\end{array}\end{array}$$

where

$$\begin{array}{rl}e& =\mathrm{2.0}{\mathit{\sigma }}_{\mathrm{g}}^{-\mathrm{0.10}}\left(\mathrm{0.049}{\left({\log }_{\mathrm{10}}\left(\mathrm{1000}{d}_{\mathrm{50}}\right)\right)}^{\mathrm{3}}\right.\\ & \left.-\mathrm{0.26}{\left({\log }_{\mathrm{10}}\left(\mathrm{1000}{d}_{\mathrm{50}}\right)\right)}^{\mathrm{2}}+\mathrm{0.33}{\log }_{\mathrm{10}}\left(\mathrm{1000}{d}_{\mathrm{50}}\right)+\mathrm{1.20}\right)\\ & -\mathrm{1.4}\end{array}$$

[–] is the hiding exponent. Parameter e decreases for grain sizes between 1 and 5 mm and increases for grain sizes between 5 and 100 mm. The magnitude of parameter e decreases with grain size sorting σ_g. Figure 1 illustrates, for a range of grain sizes, the difference between the Shields curve and S2001's model with and without hiding effects.

Wilcock and Crowe (2003) found a dependency of θ_r,i on the sand fraction F_sand [–] and $d_i/d_{\mathrm{50}}$. The grain-size-specific reference Shields stress is written as

$$\begin{array}{}\text{(7)}& {\mathit{\theta }}_{\mathrm{r},i}={\left({\displaystyle \frac{d_i}{d_{\mathrm{50}}}}\right)}^{-\left(\mathrm{1}-b_i\right)}{\mathit{\theta }}_{\mathrm{r},\mathrm{50}},\end{array}$$

where b_i [–] is the grain-size-specific hiding exponent.

The reference Shields stress of median grain size is written as

$$\begin{array}{}\text{(8)}& {\mathit{\theta }}_{\mathrm{r},\mathrm{50}}=\mathrm{0.021}+\mathrm{0.015}\exp \left(-\mathrm{20}{F}_{\mathrm{sand}}\right).\end{array}$$

This equation means that the reference Shield stress starts at 0.036 for gravels and decreases down to 0.021 when the sand fraction is above 0.05.

The hiding exponent is as follows:

$$\begin{array}{}\text{(9)}& b_i={\displaystyle \frac{\mathrm{0.67}}{\mathrm{1}+\exp \left(\mathrm{1.5}-\frac{d_i}{d_{\mathrm{50}}}\right)}}.\end{array}$$

Figure 1 illustrates, for a range of grain sizes, the difference between the Shields curve and WC2003's model with and without hiding effects.

We note that both models are rather complicated, include a dependency on $d_i/d_{\mathrm{50}}$, and express bed heterogeneity as dependent on either $d_{\mathrm{84}}/d_{\mathrm{16}}$ (S2001), which does not depend on a fixed grain size, or the sand fraction (WC2003), which is based on a specific grain size cutoff (2 mm). Moreover, S2001's reference Shields stress depends on the bed slope to account for effects of relative depth (Shvidchenko and Pender, 2000a), but WC2003 does not. Relative depth is expected to alter turbulence, velocity fields, and thus transport intensity in the vicinity of incipient motion (Lamb et al., 2008; Prancevic and Lamb, 2015; Shvidchenko and Pender, 2000a). S2001 assumed that the reference shear stress increases with the channel-bed slope, which is negatively correlated to the relative depth. Another difference pertains to the bed surface composition: S2001 was established using the bed surface composition at the initial state. In contrast, WC2003 considered the bed surface composition at the final state and averaged over runs with a similar initial sediment mixture. WC2003 was calibrated using grain size distributions that are of about 1 order of magnitude wider than S2001: 0.1–64 mm (14 size classes) compared to 1–14 mm (eight size classes), respectively. The grain size sorting of the datasets used to establish the two formalisms overlap: 2.2–7.3 for WC2003 compared to 1.3–6.0 for S2001 (combination of datasets they used; 1.3–2.2 for their own data).

To resolve the inconsistency between the reference shear stress models in Le Minor et al. (2022), we have reanalysed two of the most complete multi-grain-size sediment transport datasets (Shvidchenko et al., 2001; Wilcock and Crowe, 2003), as well as single-grain-size datasets (Engelund and Hansen, 1967; Lajeunesse et al., 2010; Meyer-Peter and Müller, 1948; Shvidchenko and Pender, 2000a). In doing so, our objectives were

• to estimate reference shear stresses for each dataset using a standardized approach so that they are comparable;

• to derive a new empirical model for the reference shear stress for multiple-size sediments that includes a hiding-exposure function with parameters describing the bed heterogeneity;

• to evaluate LM2022's model predictions using sediment transport datasets standardized by applying a common approach to calculate the reference shear stress.

Section 3 describes the detailed processing of the datasets that allow these three steps to be performed.

2.2 Key aspects of Le Minor et al. (2022)'s model

The erosion–deposition model is defined by two elements: the entrainment rate ${\dot{e}}_i$ [m s⁻¹] and the transport length ξ_i [m] (Davy and Lague, 2009). This model has been extended to a spectrum of transport modes as well as to a spectrum of sediment grain sizes (Le Minor et al., 2022). Model elements relevant for this study are briefly described below, and more details are given in Sect. S1 in the Supplement and in Le Minor et al. (2022).

According to Davy and Lague (2009), the transport length that links erosion and deposition may be parameterized with the thickness of the layer where most of the grains are transported, their transport velocity, and their settling velocity. Le Minor et al. (2022) thus assume that the transport length can be written as

$$\begin{array}{}\text{(10)}& {\mathit{\xi }}_i={\displaystyle \frac{h_{\mathrm{s},i}{\stackrel{\mathrm{‾}}{v}}_{\mathrm{s},i}}{w_{\mathrm{s},i}}},\end{array}$$

where h_s,i [m] is the sediment transport height, $\stackrel{\mathrm{‾}}{v_{\mathrm{s},i}}$ [m s⁻¹] is the depth-averaged sediment transport velocity, and w_s,i [m s⁻¹] is the sediment settling velocity. The magnitude of the settling velocity is assumed to be equal to the terminal settling velocity calculated using the empirical equation of Ferguson and Church (2004) because it covers a wide spectrum of grain sizes.

The sediment transport length corresponds to the height reached by a grain after its ejection or detachment from the bed. Le Minor et al. (2022) write the transport height as

$$\begin{array}{}\text{(11)}& \begin{array}{l}{h}_{\mathrm{s},i}=\left\{\begin{array}{l}{h}_{\mathrm{salt},i}+\frac{h-h_{\mathrm{salt},i}}{r_{\mathrm{0},i}}\mathrm{if}{T}_i^{\ast }>\mathrm{0}\\ \mathrm{0}\mathrm{otherwise}\end{array}\right.,\end{array}\end{array}$$

where h_salt,i [m] is the saltation height, r_0,i [–] is the gradient of the vertical sediment distribution, and $T_i^{\ast }=\mathit{\tau }/{\mathit{\tau }}_{\mathrm{r},i}-\mathrm{1}$ [–] is the transport stage, with τ_r,i [Pa] being the sediment reference shear stress. The saltation height can be written as

$$\begin{array}{}\text{(12)}& \begin{array}{l}{h}_{\mathrm{salt},i}=\left\{\begin{array}{l}min\left(\mathrm{0.6}{d}_i+\mathrm{0.025}{d}_i{T}_i^{\ast },h\right)\mathrm{if}{T}_i^{\ast }>\mathrm{0}\\ \mathrm{0}\mathrm{otherwise}\end{array}\right..\end{array}\end{array}$$

To improve upon Le Minor et al. (2022), we propose a simplified formulation of the transport velocity assuming a logarithmic water velocity profile (law of the wall) and that sediment grains travel as fast as the water velocity averaged over the thickness of the layer where most transport occurs regardless of the transport mode, i.e. bed load or suspended load:

$$\begin{array}{}\text{(13)}& \begin{array}{l}{\stackrel{\mathrm{‾}}{v}}_{\mathrm{s},i}=\left\{\begin{array}{l}min\left(\frac{u_{\ast }}{\mathit{\kappa }}\left(\ln \left(\frac{h_{\mathrm{s},i}}{z_{\mathrm{0}}}\right)-\mathrm{1}+\frac{z_{\mathrm{0}}}{h_{\mathrm{s},i}}\right),\stackrel{\mathrm{‾}}{u}\right)\mathrm{if}{T}_i^{\ast }>\mathrm{0}\\ \mathrm{0}\mathrm{otherwise}\end{array}\right.,\end{array}\end{array}$$

where κ [–] is the von Kármán constant, $\stackrel{\mathrm{‾}}{u}$ [m s⁻¹] is the depth-averaged water velocity, and u_∗ [m s⁻¹] is the shear velocity. We observed that this simplified transport velocity formulation degrades neither the magnitude nor the scaling with the excess shear stress of single- and multiple-size transport rate predictions (see Fig. S1 in the Supplement). Maintaining the predictive power of the model with a simpler formulation is desirable because it makes the model easier to parameterize. We thus use Eq. (13) to calculate the transport velocity from now on in this study.

Based on grain-scale dynamic studies (Charru et al., 2004; Lajeunesse et al., 2010), Le Minor et al. (2022) assume that the entrainment rate can be written as

$$\begin{array}{}\text{(14)}& \begin{array}{l}{\dot{e}}_i=F_i{k}_{\mathrm{e},i}\left(\mathit{\tau }-{\mathit{\tau }}_{\mathrm{c},i}\right),\end{array}\end{array}$$

where k_e,i [m² s kg⁻¹] is the entrainment coefficient. Here, we adjust LM2022 by replacing the critical shear stress by the reference shear stress:

$$\begin{array}{}\text{(15)}& {\dot{e}}_i=F_i{k}_{\mathrm{e},i}\left(\mathit{\tau }-{\mathit{\tau }}_{\mathrm{r},i}\right).\end{array}$$

For multiple-size sediments, Le Minor et al. (2022) used Eqs. (7)–(9) (Wilcock and Crowe, 2003) to calculate the critical shear stress. In this study, we propose a new model for the reference shear stress for individual grain sizes in sediment mixtures and use that instead (see Sect. 4.1).

In the erosion–deposition model, the entrainment coefficient has the following form (Lajeunesse et al., 2010; Le Minor et al., 2022):

$$\begin{array}{}\text{(16)}& k_{\mathrm{e},i}={\displaystyle \frac{\mathit{\alpha }}{{\mathit{\rho }}_{\mathrm{s},i}{w}_{\mathrm{e},i}}},\end{array}$$

where α [–] is an entrainment factor and w_e,i [m s⁻¹] is the sediment ejection velocity. In Le Minor et al. (2022), the magnitude of the ejection velocity is assumed to be equal to the terminal settling velocity.

When there is no more spatial nor temporal variations of sediment load in the water column, the sediment load is at equilibrium and can be expressed as

$$\begin{array}{}\text{(17)}& q_{\mathrm{s},i}^{\mathrm{eq}}={\mathit{\xi }}_i{e}_i=F_i{\displaystyle \frac{h_{\mathrm{s},i}\stackrel{\mathrm{‾}}{v_{\mathrm{s},i}}}{w_{\mathrm{s},i}}}{\displaystyle \frac{\mathit{\alpha }}{{\mathit{\rho }}_{\mathrm{s},i}{w}_{\mathrm{s},i}}}\left(\mathit{\tau }-{\mathit{\tau }}_{\mathrm{r},i}\right).\end{array}$$

In this formulation, τ_r,i replaces τ_c,i, which was used in the original LM2022 model.

The dimensionless form of this transport law (Einstein number) can be written as

$$\begin{array}{}\text{(18)}& q_{\mathrm{s},i}^{\mathrm{eq}\ast }={\displaystyle \frac{q_{\mathrm{s},i}}{F_i\sqrt{R_{i}g{d}_i^{\mathrm{3}}}}}=\mathit{\alpha }{\displaystyle \frac{\mathit{\rho }}{{\mathit{\rho }}_{\mathrm{s},i}}}{\displaystyle \frac{h_{\mathrm{s},i}}{d_i}}{\displaystyle \frac{\stackrel{\mathrm{‾}}{v_{\mathrm{s},i}}\sqrt{R_{i}g{d}_i}}{w_{\mathrm{s},i}^{\mathrm{2}}}}\left({\mathit{\theta }}_i-{\mathit{\theta }}_{\mathrm{r},i}\right).\end{array}$$

When the reference shear stress is not exceeded, we assume that the transport rate is so small that it can be neglected, and thus the transport rate equals 0. This is a conceptual difference from empirical equations such as the one of Wilcock and Crowe (2003) that predicts non-zero but weak transport for bed shear stress below the reference shear stress.

2.3 LM2022 model adjustment and calibration

As suggested by Le Minor et al. (2022), we modify the saltation height with an identical reference height for all sizes instead of a grain-size-specific one. This is important because the higher the saltation height, the higher the grain velocity and, thus, the transport fluxes. Because the bed roughness z₀ plays a critical role in flow hydraulics and may be seen as the lower vertical limit of transport, we test the following modification of the saltation height:

$$\begin{array}{}\text{(19)}& \begin{array}{l}{h}_{\mathrm{salt},i}=\left\{\begin{array}{l}min\left(z_{\mathrm{0}}+\mathrm{0.6}{d}_i+\mathrm{0.025}{d}_i{T}_i^{\ast },h\right)\mathrm{if}{T}_i^{\ast }>\mathrm{0}\\ \mathrm{0}\mathrm{otherwise}\end{array}\right..\end{array}\end{array}$$

In Le Minor et al. (2022), the measured density of moving sediment grains at the bed surface and the ratio of deposition to erosion time from Lajeunesse et al. (2010) and Houssais and Lajeunesse (2012) were used to obtain a value of the entrainment factor that was assumed to be constant. This allowed direct evaluation of model performance against experimental datasets without any prior calibration. However, this procedure is not applied in this study for two reasons: (i) the density of moving sediment grains at the bed surface is not a parameter that is commonly measured in flume experiments and thus is lacking in most of the datasets used in this study, and (ii) the narrow range of hydraulic conditions and sediment properties explored by Lajeunesse et al. (2010) and Houssais and Lajeunesse (2012) does not provide us with a sufficiently broad dataset for testing our hypotheses and highlighting phenomena potentially missing in the LM2022 model. Hence, as a first approach, we evaluate the effect of the standardized reference shear stress and new transport length using the original mobility factor of LM2022's model: $\mathit{\alpha }=\frac{\mathit{\pi }}{\mathrm{6}}\mathrm{37.64}=\mathrm{19.71}$. In a second step, we re-calibrate the model by estimating an empirical value of α in response to model adjustments. We calculate it as the median value of the population of values of α for each measured transport rates as follows:

$$\begin{array}{}\text{(20)}& \mathit{\alpha }={\displaystyle \frac{q_{\mathrm{s},i,\mathrm{measured}}^{\mathrm{eq}}}{F_i{\mathit{\xi }}_{\mathrm{s},i,\mathrm{predicted}}\frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{s},i}{w}_{\mathrm{e},i}}\left(\mathit{\tau }-{\mathit{\tau }}_{\mathrm{r},i}\right)}}.\end{array}$$

3 Data and methods

3.1 Datasets

Six datasets from flume experiments on single- and multiple-size sediments were used in this study (Table 1) for (i) model comparison of the original LM2022 model, (ii) calibration of the new reference shear stress, and (iii) calibration of the new version of LM2022's model, specifically the new reference shear stress for incipient motion and the entrainment factor α. See Sect. S2 for details on the range of values tested for each dataset.

Contrary to Le Minor et al. (2022), the dataset of Houssais and Lajeunesse (2012) was not considered in this study because values of depth-averaged water velocity used to calculate the transport length are lacking. For the dataset of Meyer-Peter and Müller (1948), only the data where the median size d₅₀ [m] is the same as the 90th-percentile size d₉₀ [m] were used, i.e. with a single grain size (5.21 and 28.65 mm).

In Le Minor et al. (2022), the sensitivity analysis revealed that the transport rate predictions were affected by the bed roughness z₀ fed to the model and hence that the impact of bed forms on the bed roughness should be accounted for. Details on the bed roughness considered for each dataset are given in Table 1.

3.2 Dataset processing to estimate the reference shear stress

As in Le Minor et al. (2022), for all the datasets, the same method as the one mentioned in Wilcock and Crowe (2003) was applied to calculate values of the bed shear stress corrected for sidewall effects (Chiew and Parker, 1994; Vanoni and Brooks, 1957). In the following work, we hypothesize that the reference Shields stress corresponds to the bed shear stress that produces a reference transport intensity of 10⁻⁴ s⁻¹ and, thus, an Einstein number of 10⁻⁴ (Shvidchenko and Pender, 2000a). This value corresponds to only rare movements of grains at the bed surface (Kramer, 1935), and transport is considered negligible below it. Reference Shields stress values are obtained by plotting the transport intensity data as a function of the grain-size-specific Shields stress. We then use an empirical fit such as $\log \left(q_{\mathrm{s},i}^{\ast }\right)=a+\frac{b}{{\mathit{\theta }}_i}$, where a and b are two constants (Fig. 2) instead of a power law $\log \left(q_{\mathrm{s},i}^{\ast }\right)=a+b\log \left({\mathit{\theta }}_i\right)$. The power law is suitable for constant scaling of the dimensionless transport rate (Einstein number) with the Shields stress. However, this scaling is not constant for all the datasets we use, especially for the finer grain sizes, where it varies from about 1.5 for bed load transport to 2.5 for suspended load. Applying an exponential fit better captures this varying scaling. With the above equation, the reference Shields stress is

$$\begin{array}{}\text{(21)}& {\mathit{\theta }}_{\mathrm{r},i}={\displaystyle \frac{b}{\log \left(q_{\mathrm{s},\mathrm{ref}}^{\ast }\right)-a}}.\end{array}$$

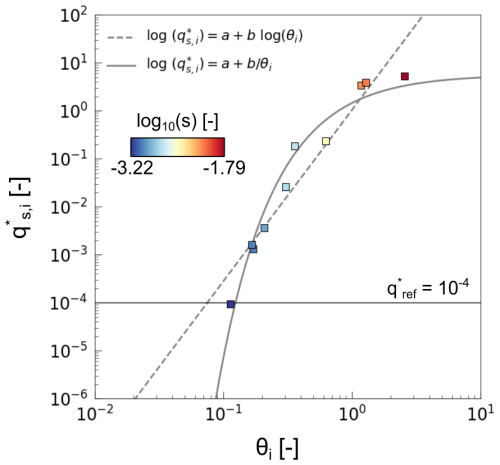
Figure 2 Example of fitting to data points using two interpolation methods. Dimensionless transport rates, i.e. values of the Einstein parameter, for the data of Wilcock and Crowe (2003) (finest grain size: 210–500 µm; highest initial sand fraction: 34 %) are plotted as a function of the Shields stress. While the linear fit has a correlation coefficient of 0.92, the more complex fit used in this study has a correlation coefficient of 0.96.

The automatic fitting procedure requires at least three data points and that the resulting fit has a trend similar to the one expected (increasing trend in the Einstein number with increasing Shields stress). Otherwise, the reference shear stress is considered as unknown, and the corresponding measurements, as unexploitable. Ultimately, we obtained 40 estimates of the reference shear stress out of 52 for single-size sediments and 182 out of 240 for multiple-size sediments.

For the single-size data, one value of the reference shear stress was calculated per grain size. For the multiple-size data, one value of the reference shear stress was calculated per grain size and per mixture (initial state). For the single-size data of Shvidchenko and Pender (2000a) and the multiple-size data of Shvidchenko et al. (2001), several runs were carried out for a constant channel-bed slope as well, and hence we calculated one value of the reference shear stress per channel-bed slope to evaluate its influence.

3.3 Procedure to establish a new formalism of the reference shear stress for multiple-size sediments

For the multiple-size sediments, we went one step beyond the measurements of the reference shear stress by building a new model of incipient motion of individual sizes that combines the formalisms of Shvidchenko et al. (2001) and Wilcock and Crowe (2003).

A preparation of the data was needed to extract the necessary parameters from the two datasets:

1. Each dataset was subdivided according to the grain size, initial sediment mixture, and channel-bed slope when applicable (single-size data of Shvidchenko and Pender, 2000a, and multiple-size data of Shvidchenko et al., 2001).

2. Final surface properties (d₅₀, σ_g, and F_sand) were averaged over the runs carried out for a given initial sediment mixture and channel-bed slope (when applicable).

3. For each initial sediment mixture and channel-bed slope (when applicable), we had a series of grain sizes with their calculated reference Shields stress and corresponding final surface properties. Linear interpolations were conducted over this series of grain sizes in log-scale to determine the reference Shields stress θ_r,50 of the median size d₅₀ estimated in step 2.

Once we had the standardized datasets, we proceeded in developing an empirical model for θ_r,50 as a function of bed heterogeneity, exploring the potential influence of d₅₀, σ_g and F_sand, and we then developed a new hiding-exposure model.

4 Results

4.1 Standardized reference shear stress for incipient motion

Figure 3a shows that θ_r,50 decreases significantly with final surface grain size sorting, ranging from ∼ 0.03 for very large grain size heterogeneity and converging to values ranging between 0.05 and 0.06 for nearly uniform grain size mixtures (σ_g≈1). This is consistent with the expected trend that was reported for non-uniform sediments using the transport rate criterion by Patel and Ranga Raju (1999) and Patel et al. (2010), but the magnitude is slightly larger.

We found that the reference Shields stress of the median grain size in the mixture can be expressed as (Fig. 3a)

$$\begin{array}{}\text{(22)}& {\mathit{\theta }}_{\mathrm{r},\mathrm{50}}=\mathrm{0.060}{\mathit{\sigma }}_{\mathrm{g}}^{-\mathrm{0.469}}(R^{\mathrm{2}}=\mathrm{0.69}).\end{array}$$

The high sigma values associated with WC2003's data significantly affect the scaling exponent of the reference Shields stress for the median grain size with the sorting. More data with high sorting would help to better constrain our new model of the reference Shields stress for wide grain size distributions.

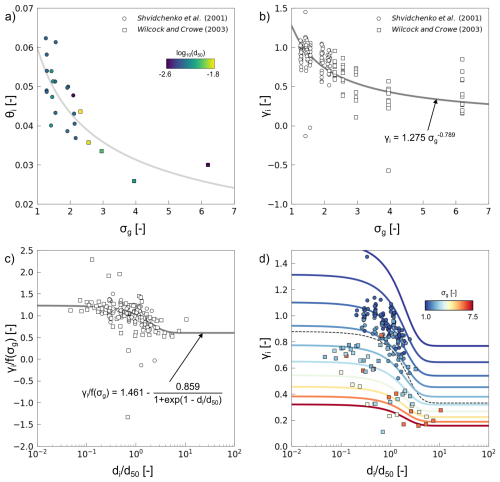
Figure 3 New formalism of the reference shear stress for incipient motion of multiple-size sediments. (a) Variations of the reference Shields stress of the median size as a function of the final surface grain size sorting. The grey line corresponds to Eq. (22) (R²=0.69). Markers are coloured according to the median grain size. (b) Variations of the exponent in the hiding function as a function of grain size sorting. (c) Variations of the exponent in the hiding function without the effect of the grain size sorting as a function of the grain size to median grain size ratio. (d) Variations of the exponent in the hiding function as a function of the grain size to median size ratio. Markers are coloured according to the final surface grain size sorting. Equation (24) (R²=0.74) is plotted for 10 values of the final surface grain size sorting. The dashed line corresponds to the equation of Wilcock and Crowe (2003).

Figure 3a shows that there is no clear influence of d₅₀ on θ_r,50 and that Eq. (22) holds for S2001 and WC2003. Using a functional relationship similar to WC2003, we found that the correlation between θ_r,50 and the sand fraction was weaker (${\mathit{\theta }}_{\mathrm{r},\mathrm{50}}=\mathrm{0.049}\exp \left(-\mathrm{0.97}{F}_{\mathrm{sand}}\right)$, R²=0.30), so we do not use F_sand subsequently.

We seek to develop a simple hiding function following previous studies (e.g. Parker and Klingeman, 1982; Wilcock and Crowe, 2003):

$$\begin{array}{}\text{(23)}& {\mathit{\theta }}_{\mathrm{r},i}={\left({\displaystyle \frac{d_i}{d_{\mathrm{50}}}}\right)}^{-{\mathit{\gamma }}_i}{\mathit{\theta }}_{\mathrm{r},\mathrm{50}},\end{array}$$

in which γ_i could depend on $d_i/d_{\mathrm{50}}$ as in WC2003 or on grain size sorting σ_g as in S2001. For this, we compute individual values of γ_i, calculated as ${\mathit{\gamma }}_i=-\log \left({\mathit{\theta }}_{\mathrm{r},i}/{\mathit{\theta }}_{\mathrm{r},\mathrm{50}}\right)/\log \left(d_i/d_{\mathrm{50}}\right)$, for all experimental data. Figure 3d shows the variation of γ_i as a function of $d_i/d_{\mathrm{50}}$ and σ_g. The range of γ_i obtained varies between 0.1 and 1.2. Three negative points are ignored. Recall that γ_i=1 means perfect equal mobility, as the reference shear stress is identical for all size classes. If γ_i<1, the reference shear stress increases with grain size, resulting in classical size selective entrainment, while γ_i>1 predicts that the reference shear stress decreases with grain size. Figure 3b shows that γ_i decreases significantly with the grain size sorting, leading to a pronounced size selective entrainment, while as the final surface tends to a uniform grain size (σ_g≈1), equal mobility conditions dominate. We fit a power law to account for this dependency (Fig. 3b–c). The residuals show a dependency with $d_i/d_{\mathrm{50}}$ (Fig. 3c) that we adjust with a function similar to that of Wilcock and Crowe (2003) (Eq. 9). This leads to a new formulation of γ_i:

$$\begin{array}{}\text{(24)}& \begin{array}{rl}{\mathit{\gamma }}_i& =\mathrm{1.275}{\mathit{\sigma }}_{\mathrm{g}}^{-\mathrm{0.789}}\left(\mathrm{1.461}-{\displaystyle \frac{\mathrm{0.859}}{\mathrm{1}+\exp \left(\mathrm{1}-\frac{d_i}{d_{\mathrm{50}}}\right)}}\right)\\ & (R^{\mathrm{2}}=\mathrm{0.74}\mathrm{and}p=\mathrm{0.00}).\end{array}\end{array}$$

We propose a hiding function formulation that combines both versions of the Shvidchenko et al. (2001) and Wilcock and Crowe (2003) empirical models and parameters: the variations of the hiding-exposure exponent with both the grain size sorting and the grain size to median size ratio are shown in Fig. 3d.

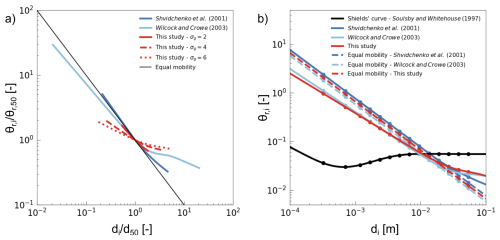
Figure 4 Comparison between our new model and the S2001 and WC2003 formalisms. (a) Hiding functions as well as equal mobility curve. (b) Reference Shields stress curves as a function of grain size. The Shields's curve is included, as well as the curves corresponding to equal mobility conditions. Dots correspond to grain size classes of WC2003's dataset for the grain size distribution with the lowest sand fraction.

The former two formalisms of Shvidchenko et al. (2001) and Wilcock and Crowe (2003) and the new hiding function (Eqs. 23 and 24) are plotted in Fig. 4. Figure 5 compares the modelled reference shear stress values calculated using Eqs. (22) and (24) and the interpolated ones obtained using the approach shown in Fig. 1. Our approach manages to predict both the values we have interpolated with the method presented in Sect. 3.2 for the Shvidchenko et al. (2001) and Wilcock and Crowe (2003) data better (R²=0.92 and p=0.00) than the equations of Shvidchenko et al. (2001; R²=0.69 and p=0.00) and Wilcock and Crowe (2003; R²=0.64 and p=0.00), although there is a significant correlation between the interpolated and predicted reference Shields stress for all three equations.

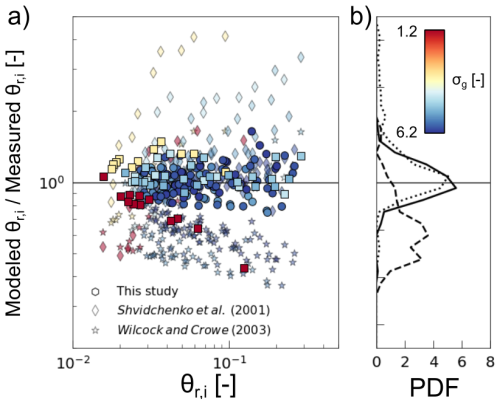
Figure 5 Comparison between our new formalism and the ones of Shvidchenko et al. (2001) and Wilcock and Crowe (2003). (a) Comparison of the predicted and measured values of the reference Shields stress. (b) PDF of the residuals. The solid, dashed, and dotted lines correspond to the PDF of residuals obtained with the set of equations from this study, Shvidchenko et al. (2001), and Wilcock and Crowe (2003), respectively.

4.2 Impact of model changes on transport rate predictions

4.2.1 Original model parameterization of Le Minor et al. (2022)

We use the Le Minor et al. (2022) model results as a reference case against which we compare new model adjustments (Fig. 6a to d). The original value for the entrainment factor in LM2022's model was α=19.71. This model parameterization produced transport rate predictions that had residuals (ratio of transport rate predictions to flume observations) that exhibit a decreasing trend with the excess of Shields stress between 10⁻³ and 10⁻¹ and a slightly increasing trend below 10⁻³ and above 10⁻¹. Also, 53 % and 65 % of the single-size experimental data were predicted within a factor of 5 and 10, respectively. In addition, 36 % and 51 % of the multiple-size experimental data were predicted by our model within a factor of 5 and 10, respectively.

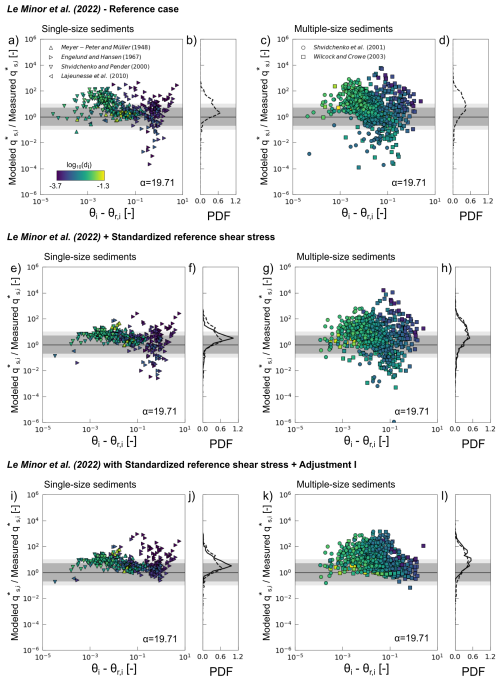
Figure 6 Effects of standardized incipient motion and adjusted transport height on predictions of total load transport rates at equilibrium using the original entrainment factor of LM2022's model. (a–d) Predictions with the same critical shear stress values as those of Le Minor et al. (2022) and the original parameterization of LM2022's model. (e–h) Predictions with the original parameterization of LM2022's model and the standardized reference shear stress values. (i–l) Predictions with LM2022's model adjusted with the bed roughness length as the reference height across all grain sizes and the standardized reference shear stress values. The ratio of model predictions to flume observations is plotted against the dimensionless excess of shear stress (Shields stress) along with the probability density function (PDF) of the residuals for single-size sediments (a–b, e–f, i–j) and multiple-size sediments (c–d, g–h, k–l). For the PDF, the dashed and solid lines correspond to predictions with the original LM2022 model and the adjusted model, respectively. The dark- and light-grey areas correspond to measured values that are predicted within a factor of 5 and 10, respectively.

4.2.2 Standardized reference shear stress for incipient motion

We predict transport rates with interpolated values of the reference shear stress for single-size sediments (procedure described in Sect. 3.2) and calculated values of the reference shear stress for multiple-size sediment due to changes in bed composition (Eqs. 22 and 24).

First, we do not adjust α (Fig. 6e to h). Compared to Le Minor et al. (2022), for the single-size sediments, the decreasing trend with the excess of Shields stress between 10⁻³ and 10⁻¹ is considerably attenuated, while the increasing trend below 10⁻³ and above 10⁻¹ remains (Fig. 6e). For the multiple-size sediments, the decreasing trend is slightly attenuated (Fig. 6g). The scattering of residuals is reduced for the single-size sediments, while it does not change for multiple-size sediments (Fig. 6e–h). In addition, 59 % and 80 % of the single-size experimental data are predicted by our model within a factor of 5 and 10, respectively. Meanwhile, 39 % and 55 % of the multiple-size experimental data are predicted by our model within a factor of 5 and 10, respectively. Note that the residuals are not centred on one when considering the original entrainment factor of LM2022's model, and thus a re-calibration of this factor is required to improve the magnitude of the predicted transport rates.

Re-calibrating the entrainment factor for single- and multiple-size sediments using the approach described in Sect. 2.3 gives an entrainment factor α=4.61. In this case, 81 % and 89 % of the single-size experimental data (∼ 20 % improvement compared to Le Minor et al. (2022) are predicted within a factor of 5 and 10, respectively, while 54 % and 73 % of the multiple-size experimental data (∼ 15 % improvement) are predicted within a factor of 5 and 10, respectively. Hence, the standardization of the threshold of motion enhances both single- and multiple-size sediment transport predictions once the entrainment coefficient is readjusted.

4.2.3 Standardized reference shear stress and common reference transport height

Here, we first keep the original parameterization of Le Minor et al. (2022) (α=19.71) but use the new reference shear stress and set the bed roughness as the minimum saltation height across all grain sizes (Eq. 19). Figure 6i shows that for the single-size sediments, the decreasing trend with the excess of dimensionless shear stress between 10⁻³ and 10⁻¹ remains, as does the increasing trends below 10⁻³ and above 10⁻¹ (Fig. 6i). For the multiple-size sediments, the decreasing trend is attenuated (Fig. 6k). Scattering of residuals is reduced for both single- and multiple-size sediments (Fig. 6i–l). In addition, 56 % and 76 % of the single-size experimental data are predicted by our model within a factor of 5 and 10, respectively. This is a marginal improvement. Meanwhile, 32 % and 48 % of the multiple-size experimental data are predicted by our model within a factor of 5 and 10, respectively, which is worse than the original model. The residuals are not centred on one when considering the original entrainment factor of LM2022's model, similar to the outcome of the step above.

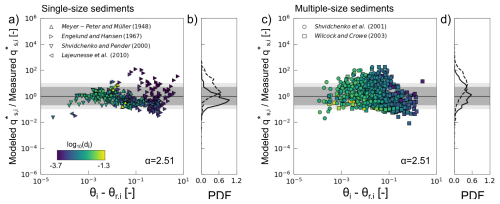
Figure 7 Effects of standardized incipient motion and adjusted transport height on predictions of the total load transport rates at equilibrium using the re-calibrated entrainment factor. Predictions with the LM2022 model adjusted with the bed roughness length as the reference height across all grain sizes and the standardized reference shear stress values for single- (a–b) and multiple-size sediments (c–d). The ratio of model predictions to flume observations is plotted against the dimensionless excess of shear stress (Shields stress) along with the probability density function (PDF) of the residuals for single-size sediments (a–b) and multiple-size sediments (c–d). For the PDF, the dashed and solid lines correspond to predictions with the original LM2022 model and the adjusted model, respectively. The dark- and light-grey areas correspond to measured values that are predicted within a factor of 5 and 10, respectively.

Re-calibrating the entrainment factor for single- and multiple-size sediments at the same time as described in Sect. 2.3 gives an entrainment factor $\mathit{\alpha }=\mathrm{2.51}\pm \mathrm{28.92}$ and results in the best predictions of the transport rate magnitudes (Fig. 7): 79 % and 92 % of the single-size experimental data (∼ 25 % improvement compared to Le Minor et al., 2022) are predicted by our model within a factor of 5 and 10, respectively, and 62 % and 81 % of the multiple-size experimental data (∼ 20 % improvement compared to Le Minor et al., 2022) are predicted by our model within a factor of 5 and 10, respectively. The combination of the standardized reference shear stress, common reference height, and re-calibrated entrainment factor thus gives substantial improvements for both single- and multiple-size sediment transport compared to the original LM2022 model version.

5 Discussion

5.1 Reference shear stress for incipient motion

To improve on the inconsistency of reference shear stress estimates in Le Minor et al. (2022), we present a reanalysis of two of the largest and well-documented surface-based multiple-size transport datasets: Shvidchenko et al. (2001) and Wilcock and Crowe (2003).

We show that θ_r,50 decreases as a power law with the final surface grain size sorting (Eq. 22). This dependency was not shown by Shvidchenko et al. (2001) or Wilcock and Crowe (2003), although they considered narrow and wide as well as skewed grain size distributions. Shvidchenko et al. (2001) expressed the reference Shields stress of the median size as the one for a uniform coarse sediment that varies with grain size and channel-bed slope (Shvidchenko and Pender, 2000a). As for Wilcock and Crowe (2003), the Shields stress of the median size depends only on the sand fraction on the bed surface. Although sorting is a less direct way to quantify the pore-filling size and account for near-bed hydraulic effects, we believe that it allows wider applications of the model and not only application to sand–gravel mixtures. The dependency on channel-bed slope introduced by Shvidchenko and Pender (2000a) is a proxy for the relative depth. We explored the potential effect of relative depth on θ_r,50 and found that it was of lower magnitude than the final surface grain size sorting (${\mathit{\theta }}_{\mathrm{r},\mathrm{50}}=\mathrm{0.046}{\mathit{\sigma }}_g^{-\mathrm{0.471}}{\left(h/d_{\mathrm{50}}\right)}^{\mathrm{0.089}}$, R²=0.72, p=0.131, and ${\mathit{\theta }}_{\mathrm{r},\mathrm{50}}=\mathrm{0.108}{\mathit{\sigma }}_{\mathrm{g}}^{-\mathrm{0.446}}{s}^{\mathrm{0.122}}$, R²=0.74, p=0.057). Combining the final surface grain size sorting and relative depth with the same hiding function (Eq. 24) does not improve significantly the quality of the predictions (R²=0.92 when comparing modelled and interpolated values of the reference shear stress). More data are needed to distinguish the role played by each parameter. Note that the new formalism presented in this study has been established for sand–gravel mixtures with grain sizes ranging from 0.1 to 64 mm. Equation (22) for the reference shear stress of the median size applies to mixtures with gravel as the median size (surface final median size between 2.5 and 16.4 mm).

The hiding-exposure function (Eq. 24) is a key component of multiple-size sediment transport because it quantifies how interactions between grain sizes, such as sheltering of fine grains and exposure of coarse grains, increase and decrease the reference shear stress, respectively. It quantifies the changes in the boundary layer structure (near the bed), as angularity differences exist between grain sizes, and the turbulence forces on the different grain sizes, as pressure fluctuations penetrate through the porous bed and may entrain preferentially fine grains lying between coarse ones (Kleinhans and van Rijn, 2002; Vollmer and Kleinhans, 2007). Our empirical equation for the hiding exponent shows a dependency on both the grain size sorting and grain size to median size ratio (Eq. 24). Our new formalism is similar to Shvidchenko et al. (2001) because it relies on the incipient motion criterion but differs from it because it is based on the final bed composition instead of the initial one. Our new formalism is similar to Wilcock and Crowe (2003) because it is based on the final bed surface composition but differs from it because it relies on the reference transport criterion. The final bed surface properties were averaged over runs with similar initial bulk mixture and channel-bed slope. This averaging procedure smooths the surface properties at the final state of experimental runs characterized by variable hydraulic conditions with the same initial sediment mixture. The smoothing is more important for large initial grain size sorting (increasing values of σ_g) because the range of surface properties at the final state is wider. Although our new model for reference shear stress does not account for this (intra-subset) heterogeneity, the averaging procedure seems sufficient to link bed surface composition at the final state and sediment transport at equilibrium, as shown by the quality of the residuals (Fig. 5). In addition, we propose a formalism of intermediate complexity between Wilcock and Crowe (2003) and Shvidchenko et al. (2001) while covering a broader range of grain sizes than each study taken individually. Our model is slightly more complex than Wilcock and Crowe (2003) but has lower residuals and explicitly includes grain sorting as an important controlling factor (Fig. 3). At the same time, our model is much simpler than Shvidchenko et al. (2001) but also has lower residuals. On balance, we argue that our model is the best model because it provides intermediate complexity with better predictive power over a wider parameter space.

While our new model offers some advantages over existing formulations, there are several areas where improvements could be made. Considering the skewness of the grain size distribution could improve the hiding function, as different grain sizes sit at different elevations within the flow and thus are subject to different forcing (Vollmer and Kleinhans, 2007). Another aspect that would need further consideration is the preparation of the bed surface before conducting flume experiments, as it has been shown that initial conditions affect the evolution of bed surface grain size distribution and transport (Parker and Wilcock, 1993). Data used to establish S2001's and WC2003's formalisms were obtained from experiments where the bed surface had been screeded flat with a blade and thus imbrication of sediment grains was forced. As the duration of experiments was short and the transport rates were very low for S2001 compared to WC2003, the initial bed surface had more influence on the measurements. The sensitivity to the initial bed surface may explain the larger reference Shields stress values for S2001 than for WC2003.

As LM2025's and WC2003's models do not define the reference shear stress using the same criterion (incipient motion versus reference transport), here are some differences between the two that are worth noting:

1. WC2003's model uses the reference transport criterion, and thus all reference shear stress values relate to a single transport function, as grain size does not appear in Eq. (4). By contrast, LM2025's model uses the incipient motion criterion, and thus reference shear stress values relate to as many transport functions as the number of grain sizes, as grain size appears in Eq. (3).

2. The reference shear stress values obtained with the incipient motion criterion ($q_{\mathrm{s},i}*={\mathrm{10}}^{-\mathrm{4}}$) are lower and higher for the fine and coarse grain sizes, respectively, compared to the ones obtained with the reference transport criterion ($W_i*=\mathrm{0.002}$).

3. LM2022's model and its adjusted version LM2025 presented in this paper do not provide a link between excess of shear stress and transport rate as direct as the similarity collapse used to establish WC2003. However, LM2022's and LM2025's model include a more detailed description of processes driving sediment transport, as they are physics-based. Also, LM2022 is (i) a non-steady-state model and (ii) describes the full range of sediment transport from bed load to suspended load. It can resolve transient behaviours or bed load and suspended load that WC2003 alone – a steady-state multi-grain-size bed load model – cannot. In the end, while being not as parsimonious as WC2003, it has a broader scope of application.

4. LM2025's model does not directly account for the effect of sand on gravel transport. However, it includes the effects of sorting, which is another way to look at the ratio of fine to coarse sizes and thus pore filling. In addition to the statistical significance of sorting compared to sand fraction, LM2025's model does not aim only at sand and gravel mixtures but also at wider grain size distributions, and thus sorting instead of sand fraction seems more appropriate to broader applications.

5.2 Bridging the gap between the reference shear stress of single- and multiple-grain-size transport

Based on our new formalism (Eq. 22), the reference Shields stress of median size tends towards 0.06 for nearly uniform grain size mixtures (σ_g≈1). The reference Shields stress values determined with the method presented in Fig. 1 for single-size datasets used in this paper range from about 0.01 to 0.1. A reference Shields stress of 0.06 is consistent with values obtained for gravel for the dataset of Shvidchenko and Pender (2000b, a). Thus, our new formalism bridges the gap between the reference shear stress of single-size gravel and multiple-size sediments. However, it overestimates by up to a factor of 6 the values reported for medium and coarse sand for the dataset of Lajeunesse et al. (2010) and underestimates by a factor of 2 the values reported for fine sand for the dataset of Engelund and Hansen (1967). Expressing the reference Shields stress of median size as a function of the sand fraction as in Wilcock and Crowe (2003), i.e. ${\mathit{\theta }}_{\mathrm{r},\mathrm{50}}=\mathrm{0.049}\exp \left(-\mathrm{0.97}{F}_{\mathrm{sand}}\right)$ (R²=0.30), could improve its suitability for single-size sediments because it tends towards 0.018 for sand mixtures. However, this formulation was not as statistically significant as the grain size sorting, so further investigations are required to explore this option.

Some studies have pointed out the potential role of the slope dependency on incipient motion (Lamb et al., 2008; Recking, 2008; Shvidchenko and Pender, 2000a) and found that the reference shear stress increases with the channel-bed slope due to a concomitant decrease in the water depth to grain size ratio, i.e. relative depth. This trend stems from grains that occupy a large portion of the water column and, in turn, have a larger resistance to the flow (Ferguson, 2007, 2012).

More sediment mixtures should be tested to find out how the reference shear stress of the median size varies when the median size becomes finer (finer than gravel), when the grain size sorting is higher, and for a wider range of channel-bed slopes. The dependence of the hiding function on the relative depth and the properties of the grain size distribution should also be investigated.

5.3 LM2022 model adjustment

Our results show that standardizing the reference shear stress for incipient motion has a positive impact on transport rate predictions, especially after re-calibration of the entrainment factor. Our study supports the fact that the original ingredients of LM2022's model hold because it is able to predict the magnitude and scaling of transport rates when the reference shear stress is properly standardized.

As suggested in Le Minor et al. (2022), our results show that a key adjustment of LM2022's model is the addition of the bed roughness length as the minimum transport height (Eq. 19). We assume that the bed roughness length is a hydraulic boundary that has meaning for single- and multiple-size sediment transport, i.e. negligible transport below, and all the entrained grains leave the bed from this height, whatever their size. This is important because it impacts the calculation within LM2022 of the mean flow velocity experienced by a grain.

Assumptions made in parameterization have effects that propagate through our model and are ultimately accounted for in the entrainment coefficient, which is the only parameter that needs calibration against observations. Two assumptions made on the transport velocity (Eq. 13) may lead to overestimation/underestimation of the entrainment coefficient: the law of the wall that differs from the observed linear velocity profile in gravel beds (Vollmer and Kleinhans, 2007) and the saltation layer thickness that is not included in the bed roughness (Kleinhans et al., 2017). As for the adjustment made on the transport height (Eq. 19), it may be necessitated by model assumptions such as the ones made on the transport velocity or the fact that the effect of grain arrangement (three-dimensional structure) at the bed surface on the reference shear stress is not included in the hiding function, although studies report on its significant effect (Kirchner et al., 1990; Vollmer and Kleinhans, 2007).

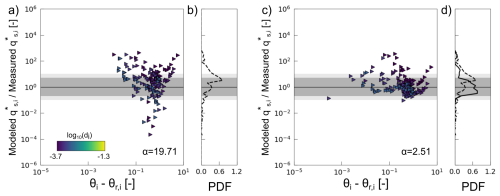
Figure 8 Effects of standardized incipient motion and adjusted transport height on predictions of total load transport rates at equilibrium for Engelund and Hansen (1967). (a–b) Predictions with the same critical shear stress values as those of Le Minor et al. (2022) and the original parameterization of LM2022's model (α=19.71). (c–d) Predictions with LM2022's model adjusted with the bed roughness length as the reference height across all grain sizes, a bed roughness of $\mathrm{3}{d}_{\mathrm{90}}/\mathrm{30}$ (no bed forms), and the standardized reference shear stress values after re-calibration (α=2.51). The ratio of model predictions to flume observations is plotted against the dimensionless excess of shear stress (Shields stress) along with the probability density function (PDF) of the residuals. For the PDF, the dashed line corresponds to predictions with the original LM2022 model. The solid line in (d) corresponds to predictions with the adjusted model. The dark- and light-grey areas correspond to measured values that are predicted within a factor of 5 and 10, respectively.

Here, we explore how LM2022's improvements impact the predictions for suspended and total load, using the dataset by Engelund and Hansen (1967). The comparison between the performance of LM2022's model and our adjusted model shows that the modifications presented in this study improve total load predictions as well (Fig. 8). As discussed in Le Minor et al. (2022), bed forms likely affect the bed roughness, which is a model input for the transport height and transport velocity and consequently may impact the transport rate predictions. To account for bed forms, as in LM2022's model, we used the equation of Nielsen (1992) to calculate the bed roughness for the experiments of Engelund and Hansen (1967), Shvidchenko and Pender (2000a), and Shvidchenko et al. (2001), where bed form development was identified on the bed. Only averaged bed form dimensions have been reported for the first two studies, while for the latter, they were lacking for some runs. Considering no bed forms in the case of Engelund and Hansen (1967), i.e. a bed roughness of $\mathrm{3}{d}_{\mathrm{90}}/\mathrm{30}$, reduces residual scattering and improves transport rate predictions for the total sediment load (Fig. 8). It is likely that better knowledge of the bed roughness would increase model performance, although this parameter is difficult to measure due to its spatiotemporal variations. Near-bed turbulence may also drop due to sediment-induced density stratification, and thus the entrainment rate is reduced (Winterwerp, 2001; Wright and Parker, 2004). Large density effects (van Maren et al., 2009; van Rijn, 2007) may be of relevance when looking at catastrophic sediment release and overloading of rivers.

5.4 Potential parameters that could improve the model

Despite significant improvements in model predictions, the multiple-size transport rates measured by Shvidchenko et al. (2001) are slightly overestimated compared to the ones of Wilcock and Crowe (2003), suggesting that second-order physical processes are not considered. Here, we explore some of these by examining the effect of the Froude number, the relative depth (ratio between the grain size or the water depth) or the relative roughness (ratio between a characteristic length scale of the bed surface and the grain size), the particle Reynolds number, and the fraction of mobile sediment.

Vanoni (1974) found that the strong correlation of the entrainment coefficient with the Froude number is due to the definition of the Froude number, which includes the depth-averaged flow velocity and the water depth, two key determinants of sediment concentration in the bed load layer. Thus, the Froude number, which represents turbulent flow properties (Cheng et al., 2020), indirectly characterizes sediment transport and grain mobility. For a low relative depth and thus a high friction coefficient, near-bed turbulence is reduced, and consequently sediment transport rates are lowered (Lamb et al., 2017b). For Froude numbers of 1 or above, surface waves cause turbulence that reaches the sediment bed and increases sediment mobility and, thus, entrainment. Furthermore, the relative roughness characterizes the grain protrusion through the bed surface. The bed roughness affects the flow features and the near-bed turbulence intensity due to grains that protrude through the bed (Vollmer and Kleinhans, 2007).

Tables S2 and S3 in the Supplement explore the effect of including these factors individually or combined in the entrainment factor and the corresponding model prediction quality for single- and multiple-size datasets. However, we found no clear evidence that the entrainment factor varies with dimensionless parameters such as the Froude number, the relative roughness, or the Reynolds number. The fact that we do not find a strong correlation between these parameters and the entrainment factor may stem from the concomitance of their effects or simply the considerable dispersion in the data, which may mask weak trends.

For multiple-size sediments, Yager et al. (2007) suggested considering the limited availability of mobile sediment. To determine the effect of sediment availability on bed load transport in steep boulder bed channels where gravel grains are mobile, contrary to boulders that rarely are, they carried out flume experiments with sediment beds consisting of mobile natural gravel grains and spheres mimicking immobile boulders. They showed that the less mobile the bed surface is, the lower the quantity of sediment available for transport, hindering the mobility of the mobile grains. Several studies have considered partial transport, i.e. a partially mobile bed surface (Kleinhans et al., 2017; Wilcock and McArdell, 1993; Yager et al., 2007). This phenomenon has been accounted for using a hindering factor in transport laws (e.g. Kleinhans and van Rijn, 2002). However, to our knowledge, none of the published entrainment relations demonstrate a dependency on the immobile fraction at the bed surface in the context of sediment mixtures. While not explicitly considered in existing entrainment relations, existing research attempts to unravel the potential importance of the immobile fraction by looking at shear stress partitioning (e.g. Gilbert and Wilcox, 2024; Nativ et al., 2022).

We tested the effect of an adjusted entrainment factor that varies with the mobile fraction on the bed surface rather than being constant. The mobile fraction was calculated as the sum of surface fractions of mobile grain sizes, i.e. reference shear stress exceeded. Surface fractions of grain size, regardless of their reference shear stress, were included in the mobile fraction if they had a non-zero measured transport rate. We forced the entrainment factor to be equal to the one calibrated using the single-size data and the multiple-size data when the bed surface was fully mobile, which resulted in an empirically fitted entrainment factor $\mathit{\alpha }=\mathrm{2.51}{F}_{\mathrm{mobile}}^{\mathrm{2.24}}=\mathrm{2.51}{\left(\mathrm{1}-F_{\mathrm{immobile}}\right)}^{\mathrm{2.24}}$. However, the low correlation coefficient (R²=0.07), which may be due to the data dispersion, does not allow us to draw any conclusion about the role played by the mobile surface fraction in the entrainment rate.

Another important aspect to consider is the dispersion of the sediment transport data, especially for mixed-size sediment, which makes finding strong correlations challenging. More data are needed to better calibrate the model and to identify the contribution of experimental conditions on the entrainment factor (especially for grain size sorting above 4). As the multiple-size sediment data used in this study either are entirely bed load or include low-flying suspended sand (Wilcock et al., 2001), we tested our adjusted model for suspended and total load transport against single-size sediment data only, i.e. Engelund and Hansen's dataset (1967). Thus, a next step could be testing our model against more robust suspended transport of multiple-size sediment. There also could be additional physical complexity such as grain protrusion through the bed surface (Dey and Ali, 2019; Dwivedi et al., 2011; Lamb et al., 2017a; Lee and Balachandar, 2017; Papanicolaou et al., 2002; Xie et al., 2023), grain packing density in the bed (Cheng and Chiew, 1998; Lamb et al., 2017a), and grain shape (Schmeeckle et al., 2007), but our current objective is to have a parsimonious model capturing first-order phenomena, which we believe is the case.

6 Conclusions

We explored several improvements to the model by Le Minor et al. (2022). First, we introduce a new formalism for the reference shear stress of multiple-size sediments that successfully combines the approaches of Shvidchenko et al. (2001) and Wilcock and Crowe (2003). With a model formulation of intermediate complexity, the reference shear stress model applies to a large range of sediment mixtures and contributes to a significant improvement of LM2022's model when applied to both single- and multiple-size datasets. Another important improvement is the definition of a reference transport length set by the bed roughness length. When accounting for these two factors, and by adjusting the mobility factor of the model ($\mathit{\alpha }=\mathrm{2.51}\pm \mathrm{28.92}$), LM2022 provides greatly improved model predictions for both single- and multiple-grain size transport in the bed load regime and for single-grain-size suspended load. Further testing of the model is limited by the availability of flume or field data suitable to test it beyond the range of grain sizes, slope, and transport stages explored here.

To ensure the quality of predictions with this model, we recommended the use of

• a reference shear stress determined with the incipient motion criterion and a reference value of 10⁻⁴;

• the transport height adjusted with the bed roughness as the reference height across all sizes (Eq. 19);

• the simplified version of the transport velocity because it does not degrade the transport rate predictions (Eq. 13).

Seeking a transport model that is as universal as possible while remaining relatively parsimonious is a matter of compromise. While additional model complexity could certainly be brought into the model to account for effects of partially mobile bed or bed form developments, we consider that, at this stage of development, the model is already usable to explore sediment transport and the resulting morphodynamics of rivers under a wide range of hydraulic forcing, median grain sizes, and grain size heterogeneity. In particular, using it in a fully coupled morphodynamics model to compare with flume experiments studying grain size sorting will provide another range of tests to evaluate its performance.