the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Scaling and similarity of a stream-power incision and linear diffusion landscape evolution model
Nikos Theodoratos
Hansjörg Seybold
James W. Kirchner
The scaling and similarity of fluvial landscapes can reveal fundamental aspects of the physics driving their evolution. Here, we perform a dimensional analysis of the governing equation of a widely used landscape evolution model (LEM) that combines stream-power incision and linear diffusion laws. Our analysis assumes that length and height are conceptually distinct dimensions and uses characteristic scales that depend only on the model parameters (incision coefficient, diffusion coefficient, and uplift rate) rather than on the size of the domain or of landscape features. We use previously defined characteristic scales of length, height, and time, but, for the first time, we combine all three in a single analysis. Using these characteristic scales, we non-dimensionalize the LEM such that it includes only dimensionless variables and no parameters. This significantly simplifies the LEM by removing all parameter-related degrees of freedom. The only remaining degrees of freedom are in the boundary and initial conditions. Thus, for any given set of dimensionless boundary and initial conditions, all simulations, regardless of parameters, are just rescaled copies of each other, both in steady state and throughout their evolution. Therefore, the entire model parameter space can be explored by temporally and spatially rescaling a single simulation. This is orders of magnitude faster than performing multiple simulations to span multidimensional parameter spaces.
The characteristic scales of length, height and time are geomorphologically interpretable; they define relationships between topography and the relative strengths of landscape-forming processes. The characteristic height scale specifies how drainage areas and slopes must be related to curvatures for a landscape to be in steady state and leads to methods for defining valleys, estimating model parameters, and testing whether real topography follows the LEM. The characteristic length scale is roughly equal to the scale of the transition from diffusion-dominated to advection-dominated propagation of topographic perturbations (e.g., knickpoints). We introduce a modified definition of the landscape Péclet number, which quantifies the relative influence of advective versus diffusive propagation of perturbations. Our Péclet number definition can account for the scaling of basin length with basin area, which depends on topographic convergence versus divergence.
- Article
(5122 KB) - Full-text XML
- BibTeX
- EndNote
Hillslopes and river valleys are organized in striking patterns that appear to be repeated across landscapes and scales. Furthermore, within each landscape the transition from hillslopes to valleys seems to occur at a characteristic scale. These two properties have captivated scientists from the early days of geomorphology (e.g., Gilbert, 1877; Davis, 1892). Both properties are thought to be related to the scaling of processes that shape fluvial landscapes (e.g., Perron et al., 2008, 2012; Paola et al., 2009).
Scaling problems are often studied with the aid of dimensional analysis (e.g., Sonin, 2001; Bear and Cheng, 2010), which stems from Fourier's principle that all terms of physically meaningful equations should have consistent dimensions (Huntley, 1967). Dimensional analyses of landscape evolution models (LEMs) have been used to describe how the relative strengths of landscape-forming processes control properties of ridge and valley topography, such as drainage density (Willgoose et al., 1991), shapes of basins (Howard, 1994), the fluvial relief of mountains (Whipple and Tucker, 1999), topographic roughness (Simpson and Schlunegger, 2003), valley spacing (Perron et al., 2008, 2009), and drainage areas of first- and second-order valleys (Perron et al., 2012). The aforementioned studies used LEMs that, while differing in details, all assumed that fluvial landscapes are shaped by a combination of advective and diffusive erosion, with the former dominating valleys and the latter dominating hillslopes.
Here, we present a dimensional analysis of the governing equation of a simple, widely used LEM (see Eq. 1 below). Our work is based on two key premises. First, we define characteristic scales from the model parameters, rather than from extrinsic properties of the simulated landscape, such as the domain size or relief. Characteristic scales defined in this way are intrinsic to each landscape and its parameters (and thus to its underlying properties and to the strengths of the processes that shape it), and are independent of the initial and boundary conditions of any simulation. Second, in our approach we distinguish between the dimensions of horizontal length and vertical height. These two premises are not new (e.g., Willgoose et al., 1991; Whipple and Tucker, 1999; Perron et al., 2008; Robl et al., 2017), but here, for the first time, we apply them jointly to define and interpret all of the characteristic scales in this LEM. In so doing, we obtain three characteristic scales – a characteristic length, height, and time – that significantly simplify the model's governing equation. These characteristic scales are also geomorphologically interpretable, linking competition between processes to the scales of the features that emerge from these processes.
Our specific results directly apply only to the LEM that we dimensionally analyzed and to the landscapes that we can assume to be described by this LEM. However, our work illustrates an approach for the definition and interpretation of characteristic scales that could potentially be employed in dimensional analyses of other LEMs as well.
2.1 Landscape evolution model
We perform a dimensional analysis of a simple, widely used model that describes the evolution of landscapes under the influence of stream-power incision, linear diffusion, and uplift, according to the governing equation
(e.g., Howard, 1994; Dietrich et al., 2003), where z(x, y) is the elevation of a point with horizontal coordinates (x, y), t is time and is the rate of change of elevation; K is the coefficient of incision, A is the drainage area (per unit contour width) at the point (x, y), |∇z| is the norm of the gradient of z (i.e., the topographic slope in the direction of steepest descent, to which the gradient vector points by definition); D is the coefficient of diffusion, ∇2z is the Laplacian of z (i.e., the topographic curvature, here assumed to be positive in concave-up areas, e.g., valleys, and negative in concave-down areas, e.g., hillslopes); and U is the uplift rate. The dimensions of the variables and parameters of Eq. (1) are discussed in the following subsection, which focuses on dimensional analysis.
The incision term gives the rate of change of elevation due to detachment-limited sediment transport by flowing water, assumed to be proportional to stream power, i.e., the work performed by water per unit time per unit streambed area (Dietrich et al., 2003). The incision term of Eq. (1) is a specific case of the more general incision term −KAm(∇z)n, which can take on different drainage area and slope exponents m and n in order to express more general incision behavior (e.g., Dietrich et al., 2003). Here, we assume m=0.5 and n=1, in keeping with the stream-power law and with the common assumptions that discharge scales linearly with drainage area and that channel width scales with the square root of drainage area, but in Appendix A we present results from a dimensional analysis of the same LEM with generic exponents m and n (Eq. A1). We show that all the results and interpretations that we derived from the simplified LEM (Eq. 1), which we present in the main text, can be recovered from results of the generic LEM (Eq. A1) by setting m=0.5 and n=1. We do not present any results or interpretations that do not satisfy this condition. In other words, our results are not merely properties of a special case; we just describe them by simpler formulas whose presentation and interpretation is straightforward. Additionally, the incision term could include a threshold, below which no incision occurs (e.g., Dietrich et al., 2003; Perron et al., 2008). We investigate the scaling behavior of an LEM with an incision term with a non-zero incision threshold in other work, to be published separately.
The diffusion term D∇2z gives the rate of change of elevation due to diffusive sediment transport processes, such as soil creep due to bioturbation and freeze–thaw cycles. The diffusion term is linear and assumes that the flux of sediment is proportional to the topographic slope (Fernandes and Dietrich, 1997). Depending on the sign of the curvature, this term can be either negative or positive, corresponding to erosional diffusion on ridges and hillslopes or depositional diffusion in valleys.
The term U gives the rate of increase of elevation relative to the boundary due to either a falling base level or tectonic uplift of the domain's interior. Throughout this paper, we refer to both effects as uplift since they are mathematically indistinguishable.
If a landscape evolves to a condition in which, at every point, the three terms of the right-hand side of Eq. (1) cancel each other out, then everywhere; this condition is termed steady state or dynamic equilibrium. Numerical simulations are typically assumed to have converged to steady state when the rate of elevation change is smaller than an arbitrary, small threshold ε:
Equation (1) is presumed to describe soil-mantled landscapes with sufficiently cohesive soils and gentle slopes, where we can assume that incision is detachment-limited and diffusion is linear (e.g., Perron et al., 2008). Other types of landscapes are shaped by processes that cannot be described by Eq. (1). For example, diffusive processes on steep soil-mantled hillslopes are better described by a nonlinear diffusion term (e.g., Roering et al., 1999, 2007).
Equation (1) assumes that all three processes act at all points of the landscape, without distinguishing between channels or hillslopes (e.g., Howard, 1994; Simpson and Schlunegger, 2003). All three terms are needed to model fluvial landscapes. Uplift fulfills the role of the source term, forcing the evolution of the landscape (e.g., Tucker and Hancock, 2010). Without it, the landscape would decay to a flat surface of zero elevation. The combination of the incision and diffusion terms is necessary for the emergence of ridges and valleys. Whereas the incision term amplifies topographic perturbations, setting in motion a positive feedback, the diffusion term dampens them, leading to a negative feedback (e.g., Smith and Bretherton, 1972; Perron et al., 2012). Both types of feedback are needed for the synthesis of surfaces with complex structures that resemble ridge and valley topography; therefore, the incision and diffusion terms of Eq. (1), or other terms with equivalent properties, represent the simplest combination of processes that can model landscapes characterized by ridge and valley topography (e.g., Smith and Bretherton, 1972; Howard, 1994). Because different points have different topographic properties (drainage area, slope, and curvature), the modeled incision and diffusion processes have different relative strengths across the landscape. Thus, even though distinct convergent (channel) and divergent (hillslope) landforms are not specified a priori, they can emerge from Eq. (1) (e.g., Howard, 1994), at scales that can be explored using dimensional analysis (e.g., Perron et al., 2008, 2009, 2012).
2.2 Dimensional analysis
Our dimensional analysis of Eq. (1) begins by specifying the dimensions of its various variables. We will rescale Eq. (1) in the horizontal direction separately from the vertical direction so that we can study scaling of lengths and reliefs separately (e.g., Dietrich and Montgomery, 1998). Therefore, we must assume that the coordinates of points (x, y) have dimensions of length (L), while elevation z has an equivalent, but conceptually distinct, dimension of height (H). Huntley (1967) outlined a theoretical justification for distinct dimensions for quantities with identical units and presented examples demonstrating the benefits of this approach. Distinct dimensions of length and height have been adopted by some previous studies of scaling of landscapes (e.g., Willgoose et al., 1991) but using different approaches than the one outlined below. The three fundamental dimensions in this model are length (L), height (H), and time (T), and all variables of Eq. (1) have dimensions that are powers, products, or ratios of L, H, and T. Specifically, the rate of elevation change and, thus, also the incision, diffusion, and uplift terms of Eq. (1) have dimensions of H T−1. Given that the gradient |∇z| and the curvature ∇2z have dimensions of H L−1 and H L−2, respectively, the parameters K, D, and U must have dimensions of T−1, L2 T−1, and H T−1, respectively.
Because the dimensions of all variables of Eq. (1) can be expressed in terms of L, H, and T, we can non-dimensionalize Eq. (1) using a characteristic length lc, a characteristic height hc, a characteristic time tc, and combinations thereof. For important reasons that are discussed throughout this study, we choose to define lc, hc, and tc as intrinsic scales, i.e., in terms of the model's parameters K, D, and U, not in terms of sizes of geomorphic features, such as basin length (e.g., Willgoose et al., 1991; Whipple and Tucker, 1999) or total relief (e.g., Whipple and Tucker, 1999; Perron et al., 2008), or in terms of the extent of the solution domain (e.g., Simpson and Schlunegger, 2003).
We define the characteristic length scale as
which has dimensions of length. Perron et al. (2008) showed that is related to the competition between incision and diffusion and that it controls the scales of valley spacing (Perron et al., 2009) and valley-network branching (Perron et al., 2012). The quantity has also previously been used to non-dimensionalize LEMs (e.g., Duvall and Tucker, 2015).
We introduce a characteristic height scale
which has dimensions of height, and a characteristic timescale
which has dimensions of time (these characteristic scales are equivalent to those presented by Robl et al. (2017) using a somewhat different formulation). The U∕K ratio has been previously used in several different contexts. For instance, , where n is the slope exponent, is the steady-state value (e.g., Moglen and Bras, 1995; Sklar and Dietrich, 1998) of the steepness index (e.g., Whipple, 2001), which has been used to analyze river profiles and predict ridge migration dynamics (e.g., Wobus et al., 2006; Harkins et al., 2007; Whipple et al., 2017). It has also been previously noted that the U∕K ratio scales relief (e.g., Sklar and Dietrich, 1998; Perron and Royden, 2013; Willett et al., 2014). To the best of our knowledge, however, previous dimensional analyses have not used U∕K as a characteristic height scale to non-dimensionalize landscape evolution equations.
The characteristic scales of length, height, and time lc, hc, and tc, as defined above (Eqs. 3–5), have not been previously combined to non-dimensionalize landscape evolution equations. Here, we adopt them as a group on purely dimensional grounds because Eqs. (3), (4), and (5) define the only combinations of D, K, and U that yield dimensions of L, H, and T, respectively. However, in Sect. 4 we also show that these characteristic scales have interesting geomorphological properties that further justify defining them according to Eqs. (3)–(5).
In Appendix A, we define analogous characteristic scales for an LEM with generic exponents m and n. In this more general case, each of the three characteristic scales depends on all three parameters K, D, and U.
Using the characteristic scales lc, hc, and tc, we can express length, height, and time in equivalent dimensionless forms:
where the starred variables are dimensionless. Likewise, we can express each term of Eq. (1) as a corresponding dimensionless term multiplied by characteristic scales (or their products and ratios) which carry the corresponding dimensions.
Specifically, each differential (here using dz as an example) can be re-expressed as
Consequently, we can express the rate of elevation change as
which suggests that we can view the uplift rate U as a characteristic rate of elevation change. Furthermore, we can express the gradient operator as
where i and j are the unit vectors in the direction of the x and y coordinates and ∇∗ is the gradient operator in dimensionless coordinates. Therefore, we can express topographic slope as
where Gc is a characteristic gradient defined as
Our characteristic gradient Gc should not be confused with the critical slope Sc used in a nonlinear diffusion law (e.g., Roering et al., 1999). Likewise, we can express topographic curvature as
where κc is a characteristic curvature defined as
Our characteristic curvature should not be confused with the contour curvature, also denoted as κc elsewhere (e.g., Perron et al., 2012). The negative of U∕D has been previously shown to describe the steady-state curvature of hilltops and drainage divides (e.g., Roering et al., 2007; Perron et al., 2009). Finally, given that areas scale as the square of lengths, we can express drainage area as (e.g., Perron et al. 2008, 2012)
where Ac is a characteristic area, defined as
Substituting Eqs. (6), (8), (10), (12), and (14) into the governing equation (Eq. 1) yields
which can be simplified to the dimensionless form
Equation (16) includes only dimensionless variables and no parameters. Because Eq. (16) has no parameters to be adjusted, for a given set of boundary and initial conditions, it will have only one steady-state solution, which will be arrived at via only one path of evolution. This implies that all simulated landscapes with any parameters (but properly rescaled domains, boundary conditions, and initial conditions) will evolve as rescaled replicas of each other because they can all be reduced to Eq. (16) through rescaling by the characteristic scales lc, hc, and tc. We explore this rescaling property in length in Sect. 3 and in Appendix B.
Alternative dimensionless forms of Eq. (1) can reveal properties of the LEM that are not revealed by Eq. (16). For example, Perron et al.'s (2008) Eq. (19) was derived using the domain half width as a characteristic length and the steady-state maximum relief as a characteristic height. In this way, Perron et al.'s (2008) dimensionless equation includes information about the domain size and the initial conditions (which influence the final relief; e.g., Howard, 1994); therefore, that equation highlights the dependence of its solutions on the domain size and the initial conditions. Perron et al.'s (2008) Eq. (19) is equivalent to our Eq. (16) if one can express the domain size and relief in terms of lc and hc, but the relationships between these two different pairs of scales will vary for different landscape configurations arising from different initial and boundary conditions.
Likewise, Eq. (16) does not reveal that flow-routing algorithms, and thus LEM solutions, can be resolution-dependent if the channel width w is smaller than the mesh resolution δ (e.g., Pelletier, 2010). This dependence can be minimized by including the factor δ∕w in the diffusion term (e.g., Pelletier, 2010) or the factor w∕δ in the incision term (e.g., Perron et al., 2008). Equation (16) does not include such factors. However, the rescaling of domains (detailed in Sect. 3) guarantees that both w and δ scale with lc; this guarantees that the resolution dependence of model solutions is consistent across rescaled landscapes.
The fact that Eq. (16) includes no parameters has an additional important implication. One can use the factors that appear in front of terms of a dimensionless equation to infer the relative importance of each term (e.g., Huntley, 1967). In the case of Eq. (16), all such factors are equal to 1, which implies that none of the terms of this LEM (Eq. 1) is negligible everywhere across a landscape. In other words, each term may be dominant at some points of a landscape, depending on the local values of drainage area A, slope |∇z|, and curvature ∇2z, even if it is negligible elsewhere. Therefore, none of the terms of Eq. (1) can be dropped purely on grounds of process dominance.
We can rewrite Eq. (16) in a form that reveals what controls the relative dominance of each process across a landscape. Specifically, the dimensionless quantities of Eq. (16) are equal to the ratio of the corresponding dimensional quantities over appropriate characteristic scales (Eqs. 8, 10, 12, and 14). Therefore, we can rewrite Eq. (16) as
Equation (17) is exactly equivalent to Eq. (16) but helps illuminate different properties of the model. Specifically, Eq. (17) shows that the relative contributions of each of the topographic properties A, |∇z|, and ∇2z are equal to their ratios over the corresponding characteristic scales Ac, Gc, and κc. The ratios in Eq. (17), or other, equivalent groupings of variables and parameters, could be defined as dimensionless numbers. Often, dimensional analyses use dimensionless numbers to express the relative contributions of processes. In the case of landscape evolution models, examples of such dimensionless numbers are uplift numbers (e.g., Whipple and Tucker, 1999) and Péclet numbers (e.g., Perron et al., 2008). Equation (17) expresses how such dimensionless numbers emerge from the dimensionless governing equation.
Table 2Parameters and resulting characteristic scales of the three landscapes presented in Figs. 1–5. Landscape B, the baseline landscape, has parameters with typical values (e.g., Perron et al., 2008; Tucker, 2009; Clubb et al., 2016). We use the baseline landscape to demonstrate properties of height and length scales in Figs. 7–10.

The dimensionless form of the governing equation (Eq. 16) implies that landscapes with any parameters but with properly rescaled boundary and initial conditions (see immediately below what we term as “proper” rescaling) will evolve in such a way that snapshots of these landscapes at properly rescaled moments in time will be (horizontally and vertically) rescaled copies of each other. In other words, the evolution of these landscapes will obey temporal and geometric similarity. This, in turn, implies that such landscapes will reach geometrically similar steady states.
We consider domains, elevations, and time to be properly rescaled if they are equivalent when normalized by the characteristic scales of length, height, and time lc, hc, and tc, respectively. For instance, let a landscape have parameters K, D, and U, and a second landscape have parameters K′, D′, and U′. Variables and characteristic scales of the second landscape are primed to match the notation of its parameters. Domains are properly rescaled when pairs of points with dimensional coordinates (x, y) and (x′, y′) correspond to the same point with dimensionless coordinates (x∗, y∗). Thus,
and, likewise,
Likewise, elevations are properly rescaled when dimensional elevations z and z′ at equivalent points (x, y) and (x′, y′) correspond to the same dimensionless elevation z∗ at (x∗, y∗), such that
and two moments in time t and t′ are properly rescaled when they correspond to the same moment in dimensionless time t∗ such that
We should point out that simulations of these two landscapes will reach geometrically similar steady states only if we rescale the threshold ε in the steady-state criterion of Eq. (2). Specifically, we assume that the two landscapes have reached numerical steady states that satisfy the criteria and . Using Eq. (8) we see that in the dimensionless coordinate system of Eq. (16) these criteria become and, likewise, . If the two numerical steady states are geometrically similar, then they must be satisfying the same dimensionless criterion, i.e., , which leads to a steady-state threshold rescaling formula:
In the following subsections we use a numerical model to demonstrate the temporal and geometric similarity of rescaled landscapes that is implied by the dimensionless governing equation (Eq. 16). In addition, in Appendix B we outline a simple analytical proof of this similarity property. That proof suggests that rescaling works only if we rescale initial conditions (elevations) by hc. This implies that rescaling works only if lc and hc are defined separately, i.e., only if we assume distinct dimensions for lengths and heights.

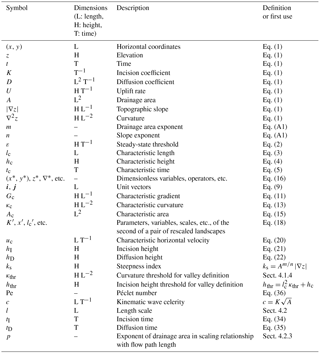
Figure 1Horizontal similarity of rescaled landscapes. Steady-state shaded relief maps demonstrate the horizontal geometric similarity of three landscapes with widely varying parameters but properly rescaled domains (see Eq. 18 for definition of proper rescaling). We label axes in units of each landscape's characteristic length lc (on the bottom axis and on the right axis, in normal fonts) and in kilometers (on the top axis and on the left axis, in bold fonts) to highlight the similarity of the three landscapes despite their very different sizes. The landscapes are shown in order of increasing lc from left to right. Notice that the sizes of the three simulated domains differ by factors of 10 in units of kilometers but are identical in units of lc. Lengths and heights scale separately. This leads to different characteristic gradients Gc across landscapes, manifested as varying grayscale intensity ranges. Despite these pronounced differences in gradients, the three landscapes are geometrically similar in plan view.
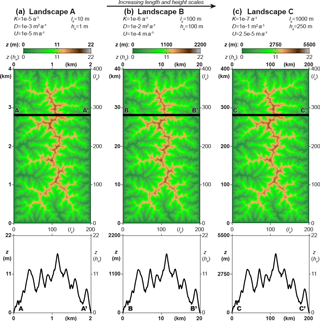
Figure 2Vertical similarity of rescaled landscapes. Steady-state elevation maps and transects demonstrate the vertical geometric similarity of the three landscapes of Fig. 1. We color the maps by elevation with color scales that are rescaled by each landscape's characteristic height hc using a color map distributed with the SIGNUM model (Refice et al., 2012). Notice that across color scales, each color corresponds to the same elevation value in units of hc but to different elevation values in meters. Therefore, the fact that the color patterns are identical reveals the vertical similarity of the landscapes. Transects corroborate the vertical similarity. Transects pass through the highest peak of the landscapes and are marked on the maps with thick black lines. Note that elevations measured in units of hc (in normal fonts) are the same, while elevations measured in meters (in bold fonts) are different. The landscapes are shown in order of increasing lc from left to right. (The ranges of elevation in map color scales and transect z axes match those of Figs. 4 and 5.)
3.1 Numerical demonstration
3.1.1 Model setup
We used the Channel-Hillslope Integrated Landscape Development (CHILD) model (Tucker et al., 2001) to numerically demonstrate the similarity property revealed by the dimensionless governing equation (Eq. 16). We chose CHILD due to its wide use by the geomorphologic community and due to the fact that it uses triangular irregular networks (TINs), which avoid the geometric bias of regular grids (e.g., Braun and Sambridge, 1997). We selected CHILD modules and parameters such that CHILD would simulate Eq. (1). Specifically, we selected CHILD's detachment-limited incision module, with constant, uniform precipitation, along with linear diffusion and uniform uplift (see Tucker et al., 2001, and Tucker, 2010, for definitions of CHILD's assumptions, modules, and parameters). In Appendix C we present in more detail how we set up our CHILD simulations and how we retrieved our results from CHILD's output files.

Figure 3Temporal similarity of evolving, rescaled landscapes. We compare the evolution of the three landscapes of Fig. 1 using shaded relief maps drawn at four properly rescaled moments in time (see Eq. 18d for definition of proper rescaling of time). The comparison shows that, at rescaled moments in time, the horizontal patterns of the landscapes are geometrically similar (and geometrically identical in units of lc). Each row shows four snapshots of a given landscape. The fourth column shows steady-state landscapes, i.e., those of Fig. 1. The snapshots that appear in each vertical column correspond to the same moment in rescaled time. Values of time in units of tc are the same along each column (labels in normal fonts), while the values of time in years vary (labels in bold fonts). Time increases from left to right, and horizontal scale increases from top to bottom. Lengths and heights scale separately; this leads to different characteristic gradients Gc across landscapes, manifested as varying grayscale intensity ranges across rows.
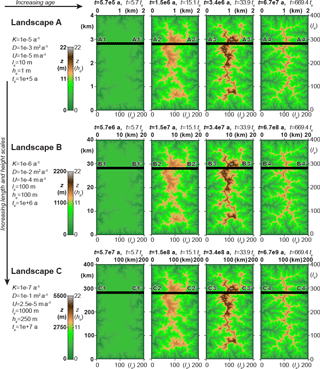
Figure 4Temporal, horizontal, and vertical similarity of evolving, rescaled landscapes. We compare elevation maps of the three evolving landscapes of Fig. 2, using the same snapshots as in Fig. 3 and the same layout (i.e., landscapes sorted by row, rescaled times sorted by column). Color maps are rescaled by each landscape's characteristic height, hc. The comparison illustrates the horizontal and vertical geometric similarity of the landscapes at rescaled moments in time. For each landscape (i.e., across each row), we use a single color scale, constant in time, to show how elevations (rescaled by each landscape's characteristic height hc) evolve. The fact that the color patterns are identical within each column reveals the vertical component of the temporal and geometric similarity of the landscapes. Thick black lines mark the transects shown in Fig. 5. The fourth column shows steady-state landscapes, i.e., those of Fig. 2.
We ran simulations using multiple combinations of the model parameters K, D, and U. We chose baseline parameter values of , , and , which are typical in the literature (e.g., Perron et al., 2008; Tucker, 2009; Clubb et al., 2016), and we varied each parameter by 2 orders of magnitude around its baseline value in a total of 34 parameter combinations.
We applied these parameter combinations on rescaled copies of two random, dimensional TINs. In Appendix C1.2 we describe how we prepared the rescaled TINs. Domain size was 200 lc by 400 lc with an average mesh edge of 0.8 lc, resulting in approximately 150 000 TIN vertices. Initial elevations were a uniform white noise, ranging between 0 and 0.1 hc. For each simulation we calculated lc and hc according to Eqs. (3) and (4), respectively. We rescaled the horizontal TIN coordinates and initial elevations according to Eqs. (18a–c).
Simulation time step lengths were not explicitly rescaled. Rather, we defined simulation time step lengths using Courant–Friedrichs–Lewy criteria (Refice et al., 2012) as described in Appendix C (Eq. C3). As seen in Eq. (C4), it turns out that the resulting time step lengths were in effect rescaled by tc due to the dependence of the Courant–Friedrichs–Lewy criteria on rescaled variables.
We ran simulations until they reached numerical steady states, which we defined using rescaled steady-state thresholds according to Eq. (19). We compared the resulting landscapes during their evolution and at their steady states.
3.1.2 Numerical results
The numerical results confirmed the rescaling properties of the dimensionless governing equation (Eq. 16). Simulations which were run on rescaled versions of the same random TIN evolved similarly in space and time. Specifically, at time steps rescaled by tc (Eq. 18d), elevations of corresponding points across simulations could be rescaled by hc (Eq. 18c) Furthermore, if steady-state criteria were rescaled according to Eq. (19), then simulations reached geometrically similar steady states.
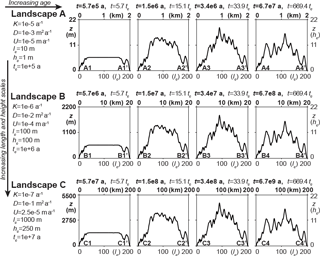
Figure 5Temporal and vertical similarity of evolving, rescaled landscapes. Transects of the three evolving landscapes of Fig. 2 corroborate the vertical component of their temporal and geometric similarity. We use the same snapshots as in Figs. 3 and 4 with the same layout (i.e., landscapes sorted by row, rescaled times sorted by column). The rescaled transects are identical along each column, demonstrating the exact temporal and geometric similarity of the rescaled landscapes. Transects pass through the highest peak of the steady-state landscapes and are marked on the maps of Fig. 4 with thick black lines. The fourth column shows steady-state transects, i.e., those of Fig. 2.
In Figs. 1 and 2 we present steady-state results for three landscapes (our baseline and two alternatives), and in Figs. 3–5 we present transient results during their evolution. These figures illustrate the geometric and temporal similarity of these landscapes. The parameter combinations of these three landscapes are a subset of all the combinations that we used; their values can be seen in Table 2. We are presenting these specific combinations for demonstration purposes as they lead to wide ranges of lc and hc. However, all the other parameter combinations that we tested also yielded landscapes that exhibited temporal and geometric similarity.
In Fig. 1 we show steady-state shaded relief maps, and in Fig. 2 we show elevation maps and transects. In both figures, lc and hc increase from left to right. We vary lc and hc separately; thus, the characteristic gradient Gc does not vary monotonically from left to right. In Fig. 2, the thick black lines in the top panels mark transects corresponding to the elevation profiles in the bottom panels and pass through the highest peaks of the simulated landscapes. The coloring and labeling of Figs. 1 and 2 highlight both the large differences of scale and the geometric similarity of the three rescaled landscapes. For comparison, lengths and elevations on axes and color bars are shown both in units of kilometers or meters using bold fonts and in units of lc or hc using normal fonts. Note that the lc and hc values for different landscapes are different as they depend on the model parameters. Color scales of elevation maps in Fig. 2 are rescaled by hc to assist with comparing the elevations of features.
In the shaded relief maps of Fig. 1, the spatial pattern of ridges and valleys is identical across the three landscapes, illustrating their horizontal geometric similarity, although their shaded relief contrast varies, reflecting their different characteristic gradients Gc. Likewise, in the elevation maps of Fig. 2, the spatial pattern of colors is identical across the three landscapes. This illustrates that the three landscapes are geometrically similar both horizontally and vertically because the color scales are rescaled by hc. Finally, the horizontal and vertical geometric similarity of the three landscapes is illustrated also by the shapes of the transects of Fig. 2.
The geometric similarity of the three steady-state landscapes is exact, not just visually convincing. Our domain rescaling procedure does not affect the point IDs of the TIN vertices, so we can directly compare corresponding points using their IDs. In these simulated landscapes, the maximum absolute difference in dimensionless elevations z∗ of corresponding points was less than 10−9 units of hc.
Figures 3–5 show shaded relief maps, elevation maps, and transects for four snapshots in time during the evolution of the three landscapes. Each column shows snapshots of the three landscapes that correspond to the same moment in dimensionless time (but different moments in dimensional time), with time increasing from left to right. Each row shows the evolution of one landscape, with one set of model parameters. As in Figs. 1 and 2, lengths and elevations on axes and color bars in units of kilometers or meters are shown in bold, and the corresponding values in units of lc or hc are shown in normal font for comparison. Labels above each snapshot show time in millions of years (in bold fonts) and in units of tc (in normal fonts). Color scales of elevation maps in Fig. 4 are rescaled by hc to assist with comparing the elevations of features. For each landscape, we use one color scale that remains constant in time to highlight how relief evolves. Each landscape's color scale is set to match the highest elevation among the four snapshots. We use different color scales for different landscapes and rescale them by hc to facilitate comparison of features across landscapes. Visual comparison shows the three landscapes to be temporally similar, since at the same moments in properly rescaled time they are in geometrically similar transient states. Note that lc and hc are different across landscapes, but for each landscape, they are constant in time. Note also that the snapshots that we present are not equally spaced in time because these landscapes evolve rapidly at first and much more slowly later.
As in the case of steady-state landscapes, the temporal and geometric similarity of the three evolving landscapes is exact, not just visually convincing. Throughout the evolution of the three landscapes, the maximum absolute difference in dimensionless elevations z∗ of corresponding points at corresponding moments of dimensionless time is less than 10−7 units of hc.
3.2 Implications of temporal and geometric similarity
3.2.1 Deducing how model parameters control landscape metrics
The geometric similarity of rescaled landscapes implies that all horizontal coordinates (x, y) and elevations z, and thus all lengths and heights, will be rescaled by the characteristic length and height scales lc and hc, respectively, according to Eq. (18a–c). Likewise, the temporal similarity of the evolution of rescaled landscapes implies that all time intervals will be rescaled by the characteristic timescale tc according to Eq. (18d). Thus, any variables that combine the dimensions of length L, height H, and/or time T will be rescaled by the corresponding combinations of lc, hc, and tc. For example, as we showed in Sect. 2.2, drainage areas, slopes, curvatures, and rates of elevation change are rescaled by the characteristic area , characteristic gradient , characteristic curvature , and uplift rate (we showed that U can be viewed as a characteristic rate of elevation change; Eq. 8).
The characteristic scales of length, height, and time lc, hc, and tc depend only on the model parameters K, D, and U (Eqs. 3–5). Therefore, we can infer how any variable scales with K, D, and U based on how its corresponding characteristic scale combines lc, hc, and tc (which we can infer from how the variable's dimensions combine L, H, and T). For example, from the definitions of lc, Gc, hc, tc, Ac, κc, and U (Eqs. 3, 11, 4, 5, 15, 13, 8), we infer that if we change the incision coefficient by a factor k, i.e., if we change it from K to kK, then all distances and slopes will change by , all reliefs, durations, and drainage areas will change by 1∕k, and all (Laplacian) curvatures and rates of elevation change will remain the same.
As an additional example, the ratio of the characteristic length lc to the characteristic time tc defines a characteristic horizontal velocity
We can, thus, deduce that horizontal velocities of drainage divide migration must scale by uc, i.e., by . This does not imply that all drainage divides move with velocity uc. Rather, it implies that any formula describing drainage divide migration must scale as and cannot include any other terms that depend on the model parameters K, D, and U. Such a formula will also depend on factors that vary locally across the landscape (such as, for example, divide asymmetry) and which must be derived separately for specific cases; they cannot be derived by scaling considerations. These principles provide a plausibility check for theoretical predictions of drainage divide migration in landscapes that follow Eq. (1). The same general approach may also be applicable in landscapes that follow other governing equations if one can define a characteristic velocity (which may scale differently than the example shown in Eq. 20).
3.2.2 Improving modeling efficiency
The temporal and geometric similarity of our rescaled simulations (Sect. 3.1) implies that we can explore the entire K, D, and U parameter space by rescaling a single simulation. For instance, if we are interested in how the slope–area curve depends on these three parameters, we can run one simulation with one combination of K, D, and U and plot its slope–area curve. To obtain the slope–area curve for any other combination of parameters K′, D′, and U′, we can simply rescale slopes by the characteristic gradient and drainage areas by the characteristic area, i.e., we can multiply slopes by and drainage areas by (see Eqs. 11 and 15). The resulting rescaled drainage areas and slopes will be exactly equal to the drainage areas and slopes of a simulation with parameters K′, D′, and U′, and with domain size, resolution, and initial conditions that are rescaled as described in Sect. 3.1.
Exploring a parameter space by rescaling can be orders of magnitude more efficient than running multiple simulations for multiple parameter combinations. For example, consider a numerical experiment exploring 10 values for each of the three parameters K, D, and U, in all possible combinations. Exploring this parameter space by brute force would require 1000 simulations versus just one simulation with the rescaling approach.
Inferring the results of a simulation by rescaling the results of another simulation assumes that the sizes of the simulation domains are equal in units of characteristic length lc (i.e., domain sizes are rescaled by lc); this may often be physically unrealistic. For example, if the simulation domain represents an island, increasing lc (e.g., by increasing the diffusion coefficient D) will make the island less dissected (i.e., will increase the spacing of valleys) but will not make the island bigger as would be required to keep the domain size constant in units of lc. Consequently, the original island will look rougher than the island with increased lc and the two islands, overall, will not be geometrically similar, even in a statistical sense. Locally, however, features that are much smaller than both islands, and sufficiently far from the coastlines, will be insensitive to whether the coastlines are rescaled or not; thus, these features may be statistically similar (even if their exact spatial patterns differ). Therefore, our rescaling approach may give us insight into how model parameters control the behavior of sufficiently small features, regardless of whether domain rescaling is assumed.
However, if we vary the model parameters such that the features of interest are no longer small with respect to the domain, then these features will be influenced by boundary effects and may not be able to express their intrinsic shapes or behaviors, i.e., the shapes or behaviors that they would have if they were small relative to the domain. On the other hand, if we vary the parameters such that features of interest are not sufficiently large with respect to the resolution, then these features may be influenced by resolution effects because they may be insufficiently resolved. In both of these cases, we can no longer reasonably assume that we can study the features of interest with a rescaling approach.
To be able to assess which combinations of domain sizes and resolutions and model parameters K, D, and U could result in boundary or resolution effects, one should consider domain sizes and resolutions in units of characteristic length lc. For example, the regime transition from dominant diffusion to dominant incision occurs at length scales of the order of lc as shown by Perron et al. (2008, 2009); see also Sect. 4.2.2 below. Thus, if we want to study this regime transition, we should vary the model parameters such that lc remains sufficiently small compared to the domain size and sufficiently large compared to the resolution. How small is sufficiently small (and, likewise, how large is sufficiently large) will not be known a priori. However, if, within a range of values of lc, a feature's properties and behavior scale according to lc, hc, and tc as described in Sect. 3.2.1 (e.g., if drainage divide migration velocity follows Eq. 20), then we can infer a posteriori that it can be studied with a rescaling approach over that range of lc.
In general, one should consider all the specifications of simulations not only in units of meters and years but also in units of lc, hc, and tc (amplitudes of initial conditions in units of hc, rates of elevation change in units of , etc.). Likewise, we recommend converting simulation results into units of lc, hc, and tc (drainage densities in units of , drainage areas of valley heads in units of , response times in units of tc, etc.). This can be helpful in comparing seemingly disparate model results and identifying which metrics and features can be studied with a rescaling approach.
The values of the characteristic scales depend on the relative magnitudes of the model parameters K, D, and U and thus on the relative strengths of incision, diffusion, and uplift. In the present section, we show that the characteristic scales can link the relative strengths of these processes with topographic properties of the landscape. Thus, they can aid the study of process competition and regime transitions.
4.1 Height scales
4.1.1 Using height scales to quantify the vertical influence of incision, diffusion, and uplift
The incision, diffusion, and uplift terms of the governing equation (Eq. 1) give the rates of change of elevation due to the respective processes. We can scale these rates using the characteristic time tc along with the characteristic height hc and two additional height scales that we introduce in this section.
The definitions of the characteristic height (; Eq. 4) and the characteristic time (; Eq. 5) show that hc is the elevation uplifted per unit of tc, i.e., hc=U tc. Therefore, we can view hc as a scale that measures the contribution of uplift to elevation change per unit of tc. We extend this notion to the incision and diffusion terms of the governing equation (Eq. 1) and define an incision height scale as the erosion due to incision per unit of tc,
and a diffusion height scale as the elevation change due to diffusion per unit of tc,
Intuitive interpretations of hI, hD, and hc are schematically illustrated in Fig. (6), which is described in more detail in the following subsection (Sect. 4.1.2). The incision height is defined as a positive quantity, but because it measures erosion we should remember that it is pointing in a downward direction. The diffusion height is negative for erosive diffusion and positive for depositional diffusion. We observe that, for the case of Eq. (1), which has drainage area and slope exponents m=0.5 and n=1, hI is equal to the steepness index, defined as (e.g., Whipple, 2001). For slope exponents n≠1, however, ks and hI are not equal; ks is proportional to (Eq. A19).
In geometrically similar landscapes, the incision and diffusion heights of corresponding points will be rescaled by the characteristic height hc in the same way as all other variables with dimensions of height (elevations, reliefs, etc.). Specifically, assume that two geometrically similar landscapes have parameters K, D, and U and K′, D′, and U′ (and thus have characteristic scales lc, hc, and tc and lc′, hc′, and tc′; note that primed variables refer to the second landscape, whose parameters are also primed). As we explain in Sect. 3 and Appendix B, corresponding points in these landscapes, i.e., points with coordinates such that and (Eqs. 18a, b), will have drainage areas and slopes such that and . Therefore, they will have incision heights that are related according to
Likewise, one can show that they will have diffusion heights that are related according to
Equation (23a, b) are examples of the ability of a characteristic scale to rescale variables with which it has the same dimensions – in this case the characteristic height hc rescales hI and hD even though they are not physical heights (they just have dimensions of height).
Note that Eq. (23a) shows that, if we define a dimensionless incision height as the ratio of the incision height hI to the characteristic height hc, then it will be equal to the dimensionless incision terms of Eqs. (16) and (17), i.e.,
Likewise, one can show that an analogously defined dimensionless diffusion height will be equal to the dimensionless diffusion terms of Eqs. (16) and (17), i.e.,
Equation (24a, b) highlight that the three terms of the dimensionless Eqs. (16) and (17) quantify the relative contributions of incision, diffusion, and uplift to elevation change.
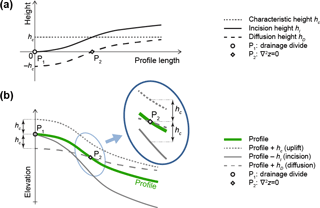
Figure 6Schematic illustration of height scales. Profiling the incision, diffusion, and characteristic height scales hI, hD, and hc along a flow path allows visualizing their properties as described by Eqs. (27)–(29). Panel (a) shows the height scales of incision, diffusion, and uplift (hI, hD, and hc, corresponding to the solid, dashed, and dotted black lines, respectively) along a flow path from the drainage divide to a valley. Panel (b) shows these height scales as changes in elevation along a steady-state elevation profile (thick green line). Subtracting hI from the elevations along the profile, or adding hD or hc to them, shows the change in elevation per unit of characteristic time tc that would result from incision, diffusion, and uplift (the solid, dashed, and dotted gray lines, respectively). At the divide (point P1), incision is ineffective and diffusion balances uplift (hI=0 and ; Eq. 28). At the point where curvature is zero (point P2), net diffusion is zero and incision balances uplift (hD=0 and hI=hc; Eq. 27). (Note that P2, where ∇2z=0, generally is not the same as the inflection point of the profile line.) Along the entire profile, the combination of incision and diffusion balances uplift; thus, the distance between the hI and hD lines in (a) (solid and dashed black lines) is constant and equal to hc (; Eq. 29).
4.1.2 Properties of the incision, diffusion, and characteristic height scales hI, hD, and hc
We can express the governing equation Eq. (1) in terms of the incision, diffusion, and characteristic height scales hI, hD, and hc if we multiply it by the characteristic time tc:
In steady state (, Eq. (25) yields
which we can manipulate in various ways to reveal useful properties of the three height scales hI, hD, and hc.
First, we focus on points that have zero curvature (∇2z=0). At these points, the net effect of diffusion on elevation is zero; thus, incision and uplift must be in balance with each other in steady state. Setting hD=0 in Eq. (26), we can mathematically express the incision–uplift balance at these points in two equivalent ways:
These expressions show that the characteristic height hc determines the steady-state value of the incision height hI at points with zero curvature so that incision and uplift are in balance with each other (since diffusion has a zero net contribution to elevation change at these points). Points with zero curvature represent a regime transition between concave-down hillslopes, characterized by net erosion by diffusive transport, and concave-up valleys, characterized by net deposition by diffusive transport (e.g., Howard, 1994). Thus, a notable implication of Eq. (27) is that points with hI=hc will map out this important topography- and process-related regime transition in steady state. Equation (27) is reminiscent of a bedrock river steady-state slope–area relation, and we discuss the similarities and differences between them in Sect. 4.1.3.
Second, we focus on drainage divides, where the drainage area A is zero and there is no incision. At drainage divides, diffusion and uplift must be in balance with each other in steady state. Setting hI=0 in Eq. (26), we express the diffusion–uplift balance on drainage divides as . Substituting the definitions of hD and the characteristic curvature κc and rearranging yields the steady-state value of drainage divide curvature (e.g., Roering et al., 2007; Perron et al., 2009):
This relation shows that we can view the characteristic height hc and length lc as two distinct components (one vertical, the other horizontal) that jointly determine the steady-state curvature of drainage divides so that diffusion and uplift are in balance.
Equations (27) and (28) refer to special points where incision or diffusion is zero. These are special cases of a general steady-state property of hc that is valid at all points; rearranging Eq. (26) yields
which shows that the difference hI−hD is constant and equal to hc across steady-state landscapes.
Figure 6 schematically illustrates how the incision, diffusion, and characteristic height scales hI, hD, and hc vary along a steady-state profile. In Fig. 6b, the green line shows a steady-state profile that traces a flow path from the drainage divide to a point in a valley. Subtracting hI from the elevations along the profile, or adding hD or hc to them, yields three gray lines (one solid, one dashed, and one dotted) that, respectively, show the individual contributions of incision, diffusion, and uplift to elevation change per unit of tc. (These contributions are equivalent to how the profile would change if only incision, diffusion, or uplift operated on it, at their equilibrium rates, for one unit of tc.) The three contributions must sum to 0 at all points along this equilibrium profile. Whereas Fig. 6b shows elevations and elevation changes, Fig. 6a shows the values of hI, hD, and hc along the profile, using black lines that have the same shapes as the corresponding gray lines of Fig. 6b. Figure 6a schematically illustrates the relationships described by Eqs. (27), (28), and (29). Specifically, at the divide (point P1), hI is 0 and hc and hD are equal and opposite; at the point of zero curvature (point P2; also shown magnified in Fig. 6b), hD is 0 and hI equals hc; and over the entire profile, (the spacing between the dashed and solid black lines is constant and equal to hc).
Substituting the definitions of hI and hD (Eqs. 21, 22) into Eq. (29) yields
which shows that the constant difference hI−hD implies that, in steady state, drainage areas A, slopes |∇z|, and curvatures ∇2z are constrained by a relationship that is constant across the landscape and is parameterized by hc (along with lc).
In this sense, we can interpret the characteristic height hc as a parameter that constrains the steady-state values of the drainage area A, slope |∇z|, and curvature ∇2z across the landscape so that incision, diffusion, and uplift are in balance.
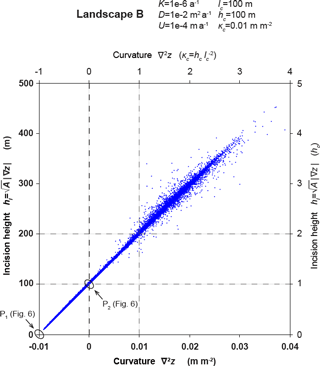
Figure 7Steady-state relationship between drainage areas, slopes, and curvatures, parameterized by characteristic length and height scales lc and hc. Plotting incision height data ( versus curvature data (∇2z) from the simulated steady-state landscape B (shown in Figs. 1–5) shows that these data followed a linear trend consistent with the relation (Eq. 31). We label incision height and curvature axes in units of meters and m m−2, respectively, in bold fonts, and in units of characteristic height hc and characteristic curvature κc, respectively, in normal fonts. Vertical and horizontal dashed lines facilitate the calculation of the slope and intercept of this trend. For every unit of κc of curvature increase, the product increases by a unit of hc; thus, the trend's slope is . The value corresponds to the curvature value ∇2z=0; thus, the trend's intercept is hc. The linear relationship illustrated here shows that we can view the characteristic length and height lc and hc as parameters of a steady-state relationship that constrains the topographic properties A, |∇z|, and ∇2z. This relationship must be satisfied so that incision, diffusion, and uplift are in equilibrium. Thus, we can view hc as a scale that expresses the competition between these three processes. (Note the two arrows that mark where data from points P1 and P2 of Fig. 6 would plot.)
For drainage area and slope exponents m and n such that 2m≠n (Eq. A1), hc depends on all three parameters K, D, and U (Eq. A9). Therefore, we should not interpret the characteristic height hc as a scale that expresses the relative strength of uplift versus incision (as the definition (Eq. 4) may seem to suggest) but rather interpret it as expressing the relative strengths of all three processes. Thus, the aforementioned interpretation that hc constrains steady-state topography so that all three processes are in balance is in line with the definition of hc for generic exponents m and n.
Given that Eq. (30) can be rewritten as
if we plot the product versus the curvature ∇2z we can graphically illustrate how hc and lc constrain A, |∇z|, and ∇2z in a steady-state landscape. Additionally, we can graphically illustrate the special cases on points with zero curvature and on drainage divides described by Eqs. (27) and (28), respectively. We show such a plot in Fig. 7 using data from the simulated equilibrium landscape B (shown in Figs. 1 and 2). Figure 7 shows that versus ∇2z plots on a straight line, as demanded by Eq. (31). In Fig. 7, the vertical dashed lines show the values ∇2z=0 and ∇2z=κc; the horizontal dashed lines show the values and . Therefore, these dashed lines illustrate that the straight line on which the data points plot has an intercept equal to the characteristic height hc and a slope equal to hc∕κc, i.e., equal to , the square of the characteristic length, as demanded by Eq. (31).
4.1.3 Quantitative predictions
Equations (30) and (31), the relationships that constrain steady-state topography, are testable predictions. They imply that we can test whether the governing equation Eq. (1) describes a given, presumably steady-state, real-world landscape by plotting estimates of the product versus estimates of the curvature ∇2z from across this landscape. These estimates should plot on a straight line, as shown in Fig. 7 for our simulated landscape. (Note that our analysis only shows that Eqs. (30) and (31) must hold for a steady-state landscape governed by Eq. (1); we have not shown that a landscape that conforms to Eqs. (30) and (31) is necessarily governed by Eq. (1) or in steady state. Although it seems unlikely that data from a non-steady-state landscape that follows different geomorphic transport laws would happen to plot according to Eqs. (30) and (31), this premise should be tested using numerical experiments.)

Figure 8Steady-state valley networks visualized by incision height hI. The simulated equilibrium landscape B (shown in Figs. 1–5) is shown here with each pixel colored by the incision height . In steady state, this incision height is linearly related to topographic curvature (Eq. 33, Fig. 7), with values of hI<hc corresponding to convex topography (ridgelines) and values of hI>hc corresponding to concave topography (valleys). Thus, high values of hI reveal the dendritic valley network.
Equation (31) can be used to estimate model parameters. Specifically, we can estimate (i.e., the D∕K ratio) from the slope of plots of the product versus the curvature ∇2z and estimate hc (i.e., the U∕K ratio) from the intercept of these plots. Alternatively, given that (Eq. 13), we can rewrite Eq. (31) as
and estimate hc as the slope of plots of the product versus the quantity . To apply Eq. (32) to real-world data we would need to estimate κc, e.g., as discussed above from steady-state drainage-divide curvature (e.g., Perron et al., 2009). Note that Eqs. (30)–(32) are equivalent to Eq. (5) of Perron et al. (2009), which they used to estimate lc and which they recognized as a test for model validity. For instance, dividing Eq. (32) by κc yields Eq. (5) of Perron et al. (2009).
Another equation that could hypothetically be used to estimate model parameters is Eq. (27), which is reminiscent of the steepness-index formula that has been used to estimate model parameters from steady-state profiles of bedrock rivers (e.g., Sklar and Dietrich, 1998; Whipple, 2001). Although the two equations are similar in form, they apply to different points on the landscape. Equation (27) describes points of zero curvature, where diffusive transport is negligible, whereas the steepness-index formula is applied to bedrock rivers, where curvature is clearly not zero but diffusive transport is nonetheless assumed to be zero (and thus Eq. (1) does not apply). To estimate hc, Eq. (27) can only use the relatively few points with zero curvature, whereas Eq. (32) can use data from the whole landscape and, thus, would presumably yield more robust estimates of hc.
Figure 9Prediction of ridge migration by differences of incision height hI across ridges. These maps show that migrating ridges move toward the side with relatively smaller hI values. Panel (a) shows four snapshots during the early phase of the evolution of landscape B (also shown in Figs. 1–5). The red squares seen in (a) are focused on a ridge that migrates from left to right; they are also shown magnified in (b). The dashed black lines inside the red squares are fixed at the initial position of the migrating ridge to illustrate its movement more clearly. The black arrows in (b) point to the direction toward which the ridge will migrate. In all maps, each pixel is colored by the incision height . Darker colors correspond to higher values of hI. These maps show that drainage basins expanded at the expense of neighboring drainage basins with lighter colors, i.e., with relatively lower hI values. For the case of Eq. (1), the incision height hI is equal to the steepness index ks, which was among the metrics used by Whipple et al. (2017) to quantify erosion rates. Therefore, these maps confirm Whipple et al.'s (2017) finding that the direction of ridge migration can be predicted by erosion rate differences across migrating ridges.
4.1.4 Valley definition
Valleys have been defined as areas where the quantity A(∇z)2 exceeds some threshold value (e.g., Montgomery and Dietrich, 1992; Orlandini et al., 2011; Clubb et al., 2014). This quantity is equal to , the square of the incision height. Montgomery and Dietrich (1992) used thresholds of A(∇z)2 as criteria for defining channels and valleys, concluding that channelization and valley incision are controlled by the same topographic properties. Other authors have used curvature ∇2z to define valleys; specifically, valleys have been defined as regions with curvature above some threshold, i.e., ∇2z≥κthr, where the threshold curvature κthr is assumed to be zero (e.g., Howard, 1994) or a small positive value (e.g., Lashermes et al., 2007; Pelletier, 2013). Here, we demonstrate that these seemingly disparate criteria are closely related in steady-state landscapes that follow Eq. (1).
Equations (26) and (31) can be combined as
which shows that, in steady state, – the square root of Montgomery and Dietrich's valley criterion – is linearly related to topographic curvature ∇2z. Equation (33) shows that points with ∇2z ≥ κthr will be identical to points whose incision heights exceed a corresponding threshold value hthr. Figure 8 graphically illustrates the property of hI to define valleys. It shows that coloring the simulated equilibrium landscape B (shown in Figs. 1 and 2) using the hI value of each pixel reveals a dendritic pattern. Given that hI and ∇2z are linearly related, they have identical spatial patterns; thus, the dendritic pattern of Fig. 8 shows the valley network defined by either criterion.
Given that one is a linear function of the other, are there practical reasons to prefer A(∇z)2 or ∇2z as a valley definition criterion? The first criterion requires computing drainage areas to each point on the landscape, which can be computationally tedious, whereas the second criterion requires estimating curvatures, which can be sensitive to topographic noise. Note, however, that thresholds of the quantity A(∇z)2 correspond to curvature thresholds only if 2m=n. In the more general case of 2m≠n (Eq. A1), curvature thresholds will correspond to thresholds of the quantity A(∇z)n∕m (Eq. A26), rather than A(∇z)2 (e.g., Ijjasz-Vasquez and Bras, 1995).
4.1.5 Divide migration dynamics
Equation (33) holds only in steady state; its counterpart in transient states would be , as implied by Eq. (25). In transient states, the term varies across the landscape. Thus, the incision height hI is not linearly related with curvature ∇2z, but nonetheless it remains a useful quantity. For instance, it reproduces Whipple et al.'s (2017) finding that erosion rate differences across drainage divides can predict the direction of divide migration. In Fig. 9 we show four snapshots of the simulated evolving landscape B (shown in Figs. 3 and 4), which we colored using the hI value of each pixel. This coloring revealed that hI's spatial distribution followed dendritic patterns. Furthermore, it revealed that dendritic patterns across migrating drainage divides had different colors, i.e., different hI values. Finally, it revealed that drainage basins overwhelmingly tended to expand at the expense of neighbors with dendritic patterns with relatively lower hI values. Figure 9 suggests that hI predicts the direction of divide migration. This property characterized the entire evolution of landscape B, but was more evident during the early phases from which we chose the four snapshots of Fig. 9. For the case of Eq. (1), hI is equal to the steepness index ks, which was one of the metrics that Whipple et al. (2017) used to measure erosion rates; thus, Fig. 9 also illustrates the use of ks to predict divide migration dynamics.
4.2 Scales of length and time
Perron et al. (2008, 2009, 2012) expressed the competition between diffusion, which smooths landscapes, and incision, which dissects them, in terms of a Péclet number , where l is a length scale that characterizes landscape features of interest. Their analysis implied that incision and diffusion should be equally effective when the Péclet number is roughly equal to 1, and thus the length scale is roughly equal to , i.e., to the characteristic length lc. They showed that distances between equally spaced valleys scale with lc, while drainage areas of first-order valley heads and of second- to first-order valley branching scale with , i.e., with the characteristic area Ac. Here, we introduce a related, but different, definition of the Péclet number and explore its implications. One such implication is that we can use this Péclet number to interpret the characteristic scales of length and time lc and tc as scales that characterize a transition between regimes of dominant diffusion and dominant incision.
4.2.1 Quantifying the horizontal influence of incision and diffusion
To examine the properties of lc, we focus on the horizontal effects of incision, diffusion, and uplift. This approach is in line with our goal to study horizontal and vertical scaling separately and with the assumption that the dimensions of length and height are distinct. Equation (1) explicitly defines rates of elevation change, i.e., effects of processes in the vertical direction. However, the incision and diffusion terms have additional, implicit horizontal effects. Specifically, incision advects topographic perturbations, such as knickpoints, and diffusion smooths them (e.g., Whipple and Tucker, 1999; Perron et al., 2008). We can quantify the strength of these effects using timescales that characterize incision and diffusion.
The incision term of Eq. (1) has the form of a kinematic wave and advects perturbations at a rate equal to the kinematic wave celerity (e.g., Whipple and Tucker, 1999). The time needed to advect perturbations over some distance l gives an appropriate measure of incision's horizontal influence; thus, we define an incision timescale as
A small tI value corresponds to a strong horizontal influence of incision (the stronger the incision, the less time is needed for advection over a given distance l).
The diffusion term of Eq. (1) smooths elevation differences by redistributing them over an expanding region of neighboring points. For example, an elevation difference that is initially concentrated at a single point will evolve as a Gaussian function, centered around this point and with a standard deviation that grows proportionally to . In general, all elevation perturbations will spread proportionally to regardless of their initial shape because the diffusion term of Eq. (1) is linear and thus the superposition principle applies (e.g., Balluffi et al., 2005). Thus, the quantity is a length scale that characterizes how far diffusion can spread elevation perturbations during some time t. Consequently, the diffusion timescale (e.g., Perron et al., 2008, 2012)
which is equal to the time needed for the quantity to reach some value l, is an appropriate measure of diffusion's horizontal influence. Analogously to tI, a small tD value corresponds to a strong horizontal influence of diffusion.
Following Perron et al. (2008, 2009, 2012), we quantify the relative horizontal influence of incision versus diffusion across a landscape by the ratio of the diffusion time tD to the incision time tI. Using the definitions in Eqs. (34) and (35) leads to the following definition of the Péclet number Pe:
Given that small tD or tI values correspond to strong influences of the respective process, small Pe values correspond to hillslopes, where diffusion is horizontally dominant, and large Pe values correspond to valleys, where incision is horizontally dominant.
The transition between the regimes of horizontally dominant diffusion and incision can be assumed to occur where the incision and diffusion timescales are roughly equal, i.e., where tI≈tD or, equivalently, where Pe≈1. Substituting this value into the definition of the Péclet number (Eq. 36) yields
As mentioned above, Perron et al.'s (2008) Péclet number is equal to 1 for a length scale equal to lc. In contrast, Eq. (37) shows that our Péclet number is equal to 1 not for specific values of the length scale l or the drainage area A but rather for all combinations of values for which is equal to . Note that ; thus, if both l≈lc and A≈Ac, then Pe≈1. Furthermore, note that for l≈lc and A≈Ac, the incision and diffusion times are both roughly equal to the characteristic time, i.e., tI≈tc and tD≈tc. Thus, the characteristic scales of length, area, and time can be interpreted as characterizing the regime transition from dominant diffusion to dominant incision.
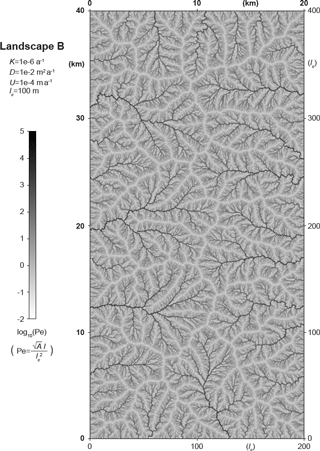
Figure 10Steady-state valley networks visualized by Péclet number Pe. The simulated equilibrium landscape B (shown in Figs. 1–5) is shown here with each pixel colored by the logarithm of (Eq. 36), where l is the flow path length (the maximum distance along flow paths from each pixel to the drainage divide). The Péclet number quantifies the relative horizontal influence of incision versus diffusion. Thus, dark pixels in this map are horizontally dominated by incision (i.e., valleys) and light pixels by diffusion (i.e., ridgelines).
4.2.2 Spatial distribution of the Péclet number across a landscape
To calculate values of the Péclet number Pe across a landscape, we must specify what the length scale l is. In this study, we define l as the maximum distance along flow paths from a point to the drainage divide and refer to it as the point's flow path length. Because the incision term has the form of a kinematic wave (and kinematic waves propagate only in the direction of the gradient; Lighthill and Whitham, 1955), perturbations are advected only in the uphill direction along flow paths. Thus, it is reasonable to quantify advection's influence using a length scale that is measured along flow paths and points in the uphill direction; the flow path length is such a length scale. Because the diffusion term spreads out elevation differences in all directions (uphill and downhill along flow paths and laterally across flow paths), its influence could be quantified using several length scales, including the flow path length. Because the flow path length is the natural length scale for the incision term and one of several possible length scales for the diffusion term, it is a reasonable length scale for calculating the Péclet number, which measures the relative influence of advection versus diffusion.
Figure 10 shows how the Péclet number Pe varies across a landscape. We calculated Pe according to Eq. (36), assuming that l is the flow path length and using data from the simulated equilibrium landscape B (as shown in Figs. 1, 2, and 8). Each pixel in Fig. 10 is colored by log10Pe. We used the logarithm to visualize values of Pe that are both much smaller and much larger than 1. Figure 10 shows that the highest values of Pe follow the dendritic valley network, similar to the highest values of the incision height hI (see Fig. 8). Diffusion and incision are horizontally dominant on hillslopes and in valleys, respectively. Therefore, the dendritic patterns in Fig. 10 suggest that our Péclet number (defined by Eq. (36) and calculated using the flow path length) is a reasonable measure of the relative horizontal influence of incision versus diffusion.
Just as the incision and diffusion heights hI and hD can be rescaled by the characteristic height hc (Eq. 23a, b), one can show that, at corresponding points in geometrically similar landscapes, the incision and diffusion times tI and tD can be rescaled by the characteristic time tc; i.e.,
Furthermore, one can show that, at corresponding points in geometrically similar landscapes, Péclet numbers are equal; i.e.,
In other words, if we plotted maps of Pe using data from the simulated landscapes A and C, then we would obtain rescaled copies of the map of Pe derived from landscape B (as seen in Fig. 10).
4.2.3 Implications of the new Péclet number definition
In this subsection, we discuss the differences between the Péclet number defined in this study and the Péclet number defined by Perron et al. (2008, 2009, 2012). Our definition (Eq. 36) includes both the drainage area A and the length scale l, whereas theirs included only l. Specifically, our Péclet number is defined as , whereas theirs was defined as (for drainage area and slope exponents m=0.5 and n=1). To introduce their Péclet number, Perron et al. (2008) defined an incision-term celerity that implicitly assumed that , and in this way they substituted l2 for . In contrast, we defined the incision and diffusion timescales and the Péclet number (Eqs. 34–36) using an abstract length scale l, and we calculated values of the Péclet number assuming that l is the flow path length.
To determine how our Péclet number scales with the flow path length l or the drainage area A, we first need to explore the scaling relationship between l and A. The flow path length l scales as a power law of the drainage area A, i.e., as Ap, with an exponent p that depends on how convergent or divergent the topography is. (Here, we refer to horizontal topographic convergence or divergence, as measured, for example, by the contour curvature.) In convergent contributing areas, the scaling exponent is p=0.5 (i.e., l scales as ; e.g., Montgomery and Dietrich, 1992), in planar contributing areas, it is p=1 (i.e., l scales linearly with A; e.g., Pelletier, 2010), and in divergent topography, it is p>1. In general, the topography of contributing areas is not purely convergent, planar, or divergent; it is a mixture of these three types. In such cases, the scaling exponent p will be somewhere between the values of the three types of topography, depending on how they are mixed. At large scales, l will generally scale as (e.g., Mueller, 1972), which corresponds to convergent topography.
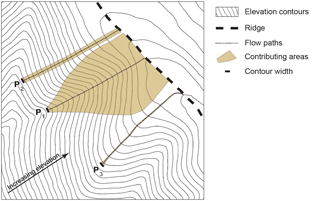
Figure 11Dependence of drainage area on flow path length and convergence or divergence of topography. Three points that have equal flow path lengths can have very different drainage areas. Elevation contours (gray lines) reveal that point P1 is in a valley with convergent topography, P2 on a hillslope with planar topography, and P3 on an interfluve with divergent topography. The thick dashed line shows the ridge line, and the three dotted lines show flow paths from the ridge to the points P1, P2, and P3. The three flow paths have equal lengths l. The three brown polygons show the contributing areas that correspond to a given contour width (thick black bars) centered at the three points. Point P1 has a much larger drainage area A than points P2 and P3. Note the topography of the contributing area of point P1; it tends to become planar near the ridge. Specifically, the lateral boundaries of the contributing area tend to become parallel, and the curvature of the contour lines decreases. This example highlights that, in general, contributing areas have mixed topographies.
Figure 11 schematically illustrates how the scaling relationship between flow path length l and drainage area A depends on the topography of contributing areas. It shows a point inside a valley (P1) that has convergent contributing topography, a point on a hillslope (P2) that has planar contributing topography, and a point on an interfluve (P3) that has divergent contributing topography. Figure 11 shows that, even though the three points have equal flow path lengths, they have different drainage areas, and those drainage areas scale differently with flow path length. Additionally, Fig. 11 illustrates how contributing areas can have mixed topographies; for example, the contributing area of P1 becomes less convergent and more planar near the ridge.
Given that the Péclet number Pe is proportional to (Eq. 36) and that l scales as Ap, the Péclet number will scale as or . The values of the exponents and are determined by the value of p, which depends on topography as described above. Therefore, in convergent topography, and at large scales, Pe will scale as l2 or A. At small scales in non-convergent or mixed topography, Pe will scale with l raised to a power less than 2 or with A raised to a power greater than 1.
Perron et al.'s (2008, 2009, 2012) Péclet number scales as l2. To calculate Pe across real-world landscapes, Perron et al. (2012) defined the length scale l as the length of basins and calculated it from drainage area data according to ; in this case their Péclet number scales as A. Consequently, in convergent topography, and at large scales, both their Péclet number and ours scale as l2 or as A. In contrast, at small scales in non-convergent or mixed topography, the two Péclet numbers scale differently from each other with l and A.
In this study, we perform a dimensional analysis of an LEM that includes terms for stream-power incision, linear diffusion, and uplift (Eq. 1; e.g., Howard, 1994; Dietrich et al., 2003). The governing equation that we analyze in the main text (Eq. 1) includes the relatively simple incision term , which is a special case of the more general incision law KAm(∇z)n (Eq. A1). As we demonstrate in Appendix A, results obtained from a dimensional analysis of the LEM with the general incision law (Eq. A1) are equivalent to results obtained from the LEM with the simple incision law (Eq. 1), but the latter have much simpler forms and, thus, are more suitable for presentation in the main text.
Our dimensional analysis is based on two key premises. First, we assume that the dimensions of length and height are conceptually distinct. Second, we use only intrinsic characteristic scales, i.e., scales that depend only on the parameters of the model (the incision coefficient K, the diffusion coefficient D, and the uplift rate U), not on sizes of the domain or of landscape features. We use the characteristic scale lc (Eq. 3) previously defined by Perron et al. (2008), and we introduce new characteristic scales of height and time hc and tc. (Eqs. 4 and 5). The use of these three characteristic scales allows us to obtain three main results.
First, rescaling the governing equation (Eq. 1) by lc, hc, and tc yields a dimensionless form (Eq. 16) that includes only variables and no parameters. Because it has no parameters that can be adjusted, this dimensionless equation has only one solution for any given set of (dimensionless) boundary and initial conditions. This result means that landscapes that are rescaled horizontally by lc (Eq. 18a, b) and whose initial conditions are rescaled vertically by hc (Eq. 18c) will follow temporally and geometrically similar evolutions; i.e., if we compare these landscapes at times that are rescaled by tc (Eq. 18d), then they will be copies of each other (rescaled horizontally by lc and vertically by hc). We demonstrate the temporal and geometric similarity of rescaled landscapes theoretically (Appendix B) and numerically (Sect. 3.1, Figs. 1–5).
Second, lc, hc, and tc can be combined to define other characteristic scales (e.g., characteristic velocities, slopes, and curvatures), which rescale variables whose dimensions combine L, H, and T in the same way. Based on these definitions of characteristic scales, we can straightforwardly deduce scaling relations between any landscape metric and the model parameters K, D, and U because all of our scales are defined to depend only on parameters. As an example, we present a characteristic horizontal velocity that must rescale the migration velocity of drainage divides (Eq. 20).
The temporal and geometric similarity of rescaled landscapes implies that we can explore all combinations of the model parameters K, D, and U by simulating a single combination of parameters for any given dimensionless domain size, resolution, and initial conditions. We can then simply rescale the results of this simulation to obtain any results for any other combinations of parameters, which is significantly more efficient than running multiple simulations for multiple parameter combinations.
Such a modeling approach assumes that simulation domains are rescaled, but this is not always physically realistic (e.g., if a domain represents an island, changing model parameters may change the sizes of ridges and valleys on the island, but not the size of the island itself). Nonetheless, as we explain in Sect. 3.2.2, landscape features that are sufficiently small with respect to the domain size may locally remain statistically similar, even if the landscapes globally are not similar. Therefore, the rescaling approach may offer insights into how such features depend on model parameters, even if the domain is not rescaled.
However, if landscapes are not rescaled and model parameters are varied too widely, then boundary or resolution effects may arise. These boundary and resolution effects will be minimized if the domain size is much larger than lc and the resolution is much smaller than lc. More generally, we recommend performing model simulations in units of the characteristic scales (i.e., in dimensionless terms) instead of in conventional dimensional units. This should be helpful in comparing disparate model results and identifying which features can be rescaled.
Third, lc, hc, and tc can be interpreted as expressing the competition between incision, diffusion, and uplift and as linking the relative strengths of these processes to topographic properties of the landscape (Sects. 4.1, 4.2). This interpretation is facilitated by introducing process-specific scales of height and time hI, hD, tI, and tD (Eqs. 21, 22, 34, and 35) that measure the vertical and horizontal influences of incision and diffusion. The incision and diffusion heights quantify the contribution of these processes to the total elevation change per unit tc. The incision and diffusion timescales quantify how long it takes for these processes to propagate elevation perturbations over some horizontal length scale (i.e., the stronger a process, the smaller its timescale).
In steady-state landscapes, the characteristic height hc is everywhere equal to the difference between the incision and diffusion height scales, i.e., (Eq. 29), and in this way hc expresses the balance between incision, diffusion, and uplift. Given that we define hI as a function of drainage area and slope and hD as a function of curvature, expresses how steady-state topography is linked to the balance between incision, diffusion, and uplift (Eq. 30, Figs. 6, 7). Equations (29) and (30) show that hc expresses the balance between all three processes, not only between incision and uplift as the definition (Eq. 4) seemingly suggests. This can also be seen by the fact that, for the case of the LEM with the general incision law (Eq. A1), the definition of hc includes all three parameters (Eq. A9).
Equation (30) is a testable prediction that can discriminate between landscapes that are in steady state and follow the governing equation (Eq. 1), and those that do not. Furthermore, it can be rearranged to estimate lc and hc, i.e., the parameter ratios D∕K and U∕K. Finally, it implies that the incision height hI is linearly related to curvature (Eq. 33). Thus, the spatial distribution of hI follows the valley network (Fig. 8), and hI can be used as a proxy for curvature to define the hillslope–valley transition.
The characteristic scales of length and time lc and tc characterize the regime transition from diffusion-dominated to incision-dominated propagation of topographic perturbations. Following Perron et al. (2008, 2009, 2012), we quantify the relative influence of incision versus diffusion by the ratio of the diffusion timescale tD to the incision timescale tI. This leads to a new definition of the Péclet number (specifically, , where l is the flow path length to the divide; Eq. 36). The spatial distribution of this Péclet number follows the valley network (Fig. 10), with small Pe values corresponding to diffusion-dominated features (ridges and hillslopes) and large Pe values corresponding to incision-dominated features (valleys). The transition occurs where Pe is roughly equal to 1 (i.e., where tI and tD are roughly equal). This condition is satisfied by combinations of length scale l and drainage area A for which (Eq. 37). One such combination is l≈lc and , in which case tI and tD are both also roughly equal to tc.
Our definition of the Péclet number differs from that in Perron et al. (2008, 2009, 2012) in that ours includes both the length scale l and the drainage area A, while theirs includes only l. Perron et al.'s definition implicitly assumes that . We assume that l is the flow path length, i.e., the maximum distance along the flow paths from a point to the divide. In this way our Pe expresses how topographic convergence and divergence control the relative importance of incision versus diffusion across the landscape (Sect. 4.2.3, Fig. 11). In convergent topography, the two Pe definitions (ours and Perron et al.'s) both scale as l2. However, in planar or divergent topographies, Perron et al.'s Pe still scales as l2, whereas ours scales as lp with
To summarize, lc, hc, and tc lead to a dimensionless form of the governing equation that significantly simplifies the model. Additionally, they can be combined to rescale any variables with dimensions in L, H, and T. Finally, they express process competitions and link them to topographic properties. The ability of lc, hc, and tc to perform all of these tasks is a direct consequence of the two key premises underlying our dimensional analysis (characteristic scales are intrinsic, and horizontal lengths and vertical heights are dimensionally distinct). Our analysis suggests that lc, hc, and tc, as a group, are fundamental properties of landscapes that follow equations such as Eqs. (1) or (A1). This in turn suggests that lc, hc, and tc or their combinations may explain additional properties of ridge and valley topography beyond those that we briefly mention here for demonstration purposes. Therefore, it may be illuminating to estimate lc, hc, and tc in future landscape studies, whether in the field, in laboratory experiments, or in computer simulations.
A1 Generic governing equation
We perform a dimensional analysis of an LEM with an incision term with generic drainage area and slope exponents m and n that follows the governing equation
A2 Dimensions and characteristic scales
The variables and parameters of Eq. (A1) have the following dimensions. Coordinates of points (x, y) have dimensions of L, elevation z has dimensions of H, and time t has dimensions of T. Therefore, using square brackets to denote the dimensions of quantities, we obtain H T−1, [A]= L2, [∇z]= H L−1, [∇2z]= H L−2. Consequently, the coefficient of incision K has dimensions of
Likewise, the coefficient of diffusion and the uplift rate have dimensions of
All terms of Eq. (A1) have dimensions that can be expressed in terms of L, H, and T. Therefore, we can non-dimensionalize Eq. (A1) using a characteristic length lc, a characteristic height hc, a characteristic time tc, and combinations thereof. We wish to define lc, hc, and tc as functions of only the parameters K, D, and U and the exponents m and n. We can utilize Eqs. (A2)–(A4) to derive these functions. Below, we present how the definition of lc is obtained. The definitions of hc and tc can be obtained analogously.
We assume that lc will be the product of three power laws of the three parameters K, D, and U, i.e., lc=KkDdUu, where k, d, and u are unknown exponents that we seek to determine. The two sides of this definition of lc must have the same dimensions, i.e., [lc]=[KkDdUu], which implies, in combination with Eqs. (A2)–(A4), that
We can find the exponents k, d, and u by requiring that in the right-hand side of Eq. (A5), the exponent of L is equal to 1 and the exponents of H and T are equal to 0, i.e., by solving the system
The solution of this system is
i.e., L .
Therefore, the characteristic length can be defined as
Following the same procedure, we find definitions of the characteristic scales of height and time:
For m=0.5 and n=1, Eqs. (A8)–(A10) yield the corresponding Eqs. (3)–(5) in the main text.
Note the exponents of the parameters K, D, and U in the definitions of lc, hc, and tc (Eqs. A8–A10). The following observations can be made:
-
For n=1, the definitions of lc and tc are simplified because U drops out.
-
For n=2m, the definitions of hc and tc are simplified because D drops out.
-
D would drop out of lc's definition if n=0 and U would drop out of hc's definition if . Such exponents would not yield physically meaningful stream-power or shear-stress incision laws.
-
K never drops out of any of the three definitions.
-
Therefore, eliminating U from lc's and tc's definitions (for n=1) or eliminating D from hc's and tc's definitions (for n=2m) are the only simplifications of the definitions of characteristic scales that correspond to meaningful stream-power or shear-stress incision laws.
-
Equation (1) satisfies both n=1 and n=2m; therefore, it results in the simplest set of characteristic scales that are physically meaningful.
Based on the definitions of lc, hc, and tc we define a characteristic area
a characteristic gradient
and a characteristic curvature
Note that the uplift rate can be viewed as a characteristic rate of elevation change because
We define a characteristic horizontal velocity as
We have shown that the characteristic scales of the governing equation in the main text, Eq. (1), are consistent with the characteristic scales of Eq. (A1). Below we confirm that all results and interpretations that refer to Eq. (1) and were presented in the main text are also consistent with Eq. (A1).
A3 Dimensionless governing equation
We define dimensionless variables according to Eqs. (6, 8, 10, 12, and 14) (using the characteristic scales defined by Eqs. A8–A13) and substitute into Eq. (A1):
A4 Height scales
We define an incision height as the erosion due to incision during one unit of tc:
Note that the dimensionless incision height is
The incision height hI is related with the steepness index ks according to
We define a diffusion height as the elevation change due to diffusion per unit of tc:
Note that the dimensionless diffusion height is
Multiplying Eq. (A1) by tc and substituting from Eqs. (A14), (A17), and (A20), we obtain
which in steady state becomes
At points of zero curvature (∇2z=0), Eq. (A23) becomes
Therefore, hc and U∕K are the steady-state values of hI and Am(∇z)n, respectively, at points of zero curvature. For m=0.5 and n=1, i.e., for the governing equation in the main text (Eq. 1), these two relations coincide.
At drainage divides (A=0), Eq. (A23) becomes
Substituting the definition of hD (Eq. A20) into Eq. (A23) yields
i.e., hI remains a linear function of curvature in steady state. Thus, hI can be used for valley definition for the generic model in the same way that it can be used for the simplified model.
A5 Scales of length and time
The celerity of the incision term is
Therefore, the time needed to advect perturbations over some distance l defines an incision timescale:
The diffusion timescale of Eq. (A1) is the same as in the case of Eq. (1); i.e., according to Eq. (35), it is .
Therefore, the Péclet number is defined as
We observe that . Therefore, the Péclet number definition becomes
The condition Pe≈1 is satisfied at points with length scale l, drainage area A, and slope |∇z| such that
One combination of length scales, drainage areas, and slopes that satisfies this condition is l≈lc, A≈Ac, and |∇z|≈Gc. Substituting these values into the definitions of tI and tD yields tI≈tc and tD≈tc.
We outline an analytical proof of the rescaling property implied by the dimensionless governing equation (Eq. 16), namely that landscapes with any parameters will evolve temporally and geometrically similarly and will reach geometrically similar steady states provided that we properly rescale their boundary and initial conditions. Equation (18a–d) defines what we term as proper rescaling.
A simple way to demonstrate this property is to explore the necessary conditions for the dimensionless governing equation (Eq. 16) to describe two different landscapes and then show that the same conditions lead to a temporally and geometrically similar evolution of these two landscapes. Let a landscape have parameters K, D, and U and a second landscape have parameters , , and , where k, d, and u are positive real numbers, and let both landscapes satisfy Eq. (16). In what follows, we denote variables and scales of the second landscape as primed to match the notation of its parameters.
First, we derive rescaling relationships between characteristic scales of the two landscapes as functions of k, d, and u. The second landscape's characteristic length scale, lc′, will be
Likewise, its remaining characteristic scales will be
Second, we derive relationships between coordinates of the landscapes and between moments in time during their evolution. We substitute Eq. (B1a) into Eq. (18a) and obtain
Likewise, we can obtain
and
We consider the two landscapes to be temporally and geometrically similar if the points (x, y) and (x′, y′) have elevations z and z′ at moments in time t and t′, respectively, such that
Third, one can show that drainage areas, time derivatives, and differential operators of the two landscapes will be related according to
Fourth, we can retrieve the following dimensional governing equation for the second landscape if we start from the dimensionless Eq. (16) and use the rescaling formulas of Eq. (18):
We can retrieve Eq. (1), the first landscape's dimensional governing equation, by reversing the derivation of Eq. (16) presented in Sect. 2.2. In Eq. (B3) it is important to note that we use primed elevations, time, drainage areas, and differential operators. This is the necessary condition for the dimensionless Eq. (16) to describe both landscapes, and we found it by using Eqs. (B2a–h) to rescale variables between the two landscapes.
Fifth, we can now show that rescaling according to Eqs. (B2a–h) additionally leads to temporal and geometric similarity. Specifically, we can show that if the two landscapes are geometrically similar (i.e., they obey Eq. B2d) at any moments in time t and t′ that are rescaled according to Eq. (B2c), then they will remain geometrically similar for all later moments in time. To show this we compare the left-hand side and the incision, diffusion, and uplift terms of the right-hand side of the dimensional governing equations of the two landscapes. These terms have dimensions of H T−1, i.e., dimensions of a vertical velocity. Thus, to simplify notation, we denote them here as v, vI, vD, and vU, respectively. The comparisons show that
likewise,
and, therefore, also
Thus, after a time interval dt′, the second landscape will have elevation equal to
i.e., the two landscapes will continue obeying Eq. (B2d) and thus remain geometrically similar.
Therefore, we can conclude that if the two landscapes have geometrically similar initial conditions, then they will evolve temporally and geometrically similarly and will reach geometrically similar steady states.
C1 Inputs
C1.1 Calculation of CHILD parameters
To simulate the governing equation (Eq. 1) with CHILD we used the detachment-limited module; constant, uniform, and continuous precipitation; zero infiltration; hydraulic geometry scaling exponents ωb and ωs equal to 0.5; and detachment capacity exponents mb, nb, and Pb equal to 1 (see Tucker et al., 2001, and Tucker, 2010, for definitions of CHILD's assumptions, modules, and parameters).
For this choice of exponents, the rate of elevation change due to incision is calculated by CHILD from the following equations (in CHILD notation):
where Dc is the maximum detachment capacity in ma−1, τ is stream power per unit bed area in Wm−2, kb is a detachment rate coefficient in m a−1 (W m−2)−1 (i.e., kb is the rate of elevation change per each unit of stream power per unit bed area), kt is the specific weight of water in N m−3, P is the precipitation intensity in m a−1, kw is bankfull width per unit scaled discharge in s0.5 m−0.5, and S is slope (Tucker et al., 2001; Tucker, 2010).
Equating the incision term of Eq. (1) to Dc, we can relate the incision coefficient, K, with CHILD's parameters according to
CHILD input files use a mixed system of units which includes both years and seconds, and the program converts variables to a single system of units. Therefore, to calculate the values of parameters entered into CHILD's input files, we must include the unit conversion factor seen in Eq. (C2).
We varied the values of K by varying the value of kb according to Eq. (C2), while we used constant values of , , and .
We defined combinations of the parameters K, D, and U, each ranging by 2 orders of magnitude around arbitrary baseline values. The baseline values were found to be used frequently in the literature (e.g., Perron et al., 2008; Tucker, 2009; Clubb et al., 2016). Table 2 shows values of parameters, characteristic scales, and simulation properties of the three landscapes presented in Figs. 1–5 and 7–10, including the baseline landscape (landscape B).
C1.2 Simulation domain and mesh
We synthesized two random TINs by randomly perturbing a deterministic TIN generated by the geometry definition module of MATLAB's PDE toolbox. We used MATLAB to better control the rescaling procedure that we describe below. We exported the rescaled TINs of simulations as text files. Using the coordinates of TIN points included in these files, CHILD calculated the corresponding Delaunay triangulation using its own, built-in modules. We set all four domain boundaries to be open (see Tucker, 2010).
To prepare rescaled TINs, we followed the following procedure. First, we synthesized two random TINs on rectangular domains with x coordinates between 0 and 200 and y coordinates between 0 and 400; the average triangle edge length was 0.8, and the z coordinates were drawn from a uniform distribution between 0 and 0.1. By assuming that the aforementioned values are unitless, we can consider the resulting TINs to be dimensionless. Second, using Eqs. (3) and (4), we calculated the characteristic length and height scales lc and hc that correspond to the parameter combination of each simulation. Third, using Eq. (6), we multiplied the x, y, and z coordinates of the points of the dimensionless TINs by the lc and hc of each simulation. This yielded each simulation's dimensional TINs with size of 200 lc by 400 lc, an average triangle edge of 0.8 lc, and initial elevations between 0 and 0.1 hc. CHILD assumes that x, y, and z are in units of meters; therefore, we calculated lc and hc in units of meters as well. The above procedure resulted in dimensional TINs that are rescaled copies of each other according to Eqs. (18a–c).
C1.3 Time steps
We defined the time step length Δt using Courant–Friedrichs–Lewy criteria for the incision and diffusion terms of Eq. (1) according to the following formulas (Refice et al., 2012):
with
where Lij is the length of the TIN edge connecting points i and j and Ai is the drainage area of point i. Normalizing lengths and drainage areas in Eqs. (C3 b, c) by lc and , respectively, yields
Therefore, both the incision and diffusion time step limits are in effect rescaled by tc, even though we do not explicitly impose such scaling.
CHILD allows the definition of a single time step length, which is used throughout the entire simulation. However, since Ai evolves during simulations, we do not know a priori which combination of Lij and Ai will yield the smallest ΔtInc.. Therefore, to be on the safe side, we calculate ΔtInc. using the domain-wide minimum of Lij and an Ai equal to 0.5(100lc)2, which is the area of a square whose diagonal spans the domain's half width. We assume that this square has a similar area as the largest basins to be formed. To avoid very small Lij, which would result in very short Δt, we do not allow TIN perturbation during the synthesis of random TINs (described above) to result in Lij shorter than one-third of the average TIN length of 0.8lc.
C1.4 Steady state
We assume that in Eq. (19); i.e., we assume that a steady state has been reached when
where Δzi is the elevation change in point i during a time step Δt.
C2 Outputs
CHILD produces output files with various variables. Relevant to our model are those with data of elevation zi, drainage area Ai, slope |∇zi|, and stream power per unit streambed area τi, at every point i, the point IDs of TIN triangle and edge vertices, and the ID of the neighbor to which each point drains.
Using the triangle and edge output data, we define the Voronoi polygon associated with a point i and calculate this point's curvature ∇2zi and elevation change rate due to diffusion vD i according to the following formulas (Tucker et al., 2001):
where Λi is the area of the Voronoi polygon of point i, j is neighbors of i, Mi is the number of these neighbors, zi and zj are elevations of points i and j, λij is the distance between i and j, and wij is the length of the Voronoi polygon edge shared between i and j.
Our study used numerical data produced by the CHILD model (Tucker et al., 2001). All CHILD input files needed to reproduce these numerical data are available from the corresponding author upon request.
NT derived analytical results, and NT and JWK interpreted them. NT designed, performed, and analyzed numerical simulations, and NT, HS, and JWK interpreted them. NT drafted the paper, and NT, HS, and JWK edited it.
The authors declare that they have no conflict of interest.
This study was made possible by financial support from ETH Zurich. We thank
Taylor Perron and Sean Willett for helpful discussions and Greg Tucker and
an anonymous referee for their feedback, which helped improve our
paper.
Edited by: Jean Braun
Reviewed by: Gregory Tucker and one anonymous referee
Balluffi, R. W., Allen, S., and Carter, W. C.: Kinetics of materials, John Wiley & Sons, New Jersey, USA, 2005.
Bear, J. and Cheng, A. H.-D.: Modeling Groundwater Flow and Contaminant Transport, in: Theory and Applications of Transport in Porous Media, Vol. 23, edited by: Bear, J., Springer Netherlands, Dordrecht, Netherlands, 2010.
Braun, J. and Sambridge, M.: Modelling landscape evolution on geological time scales: a new method based on irregular spatial discretization, Basin Res., 9, 27–52, 1997.
Clubb, F. J., Mudd, S. M., Milodowski, D. T., Hurst, M. D., and Slater, L. J.: Objective extraction of channel heads from high-resolution topographic data, Water Resour. Res., 50, 4283–4304, https://doi.org/10.1002/2013WR015167, 2014.
Clubb, F. J., Mudd, S. M., Attal, M., Milodowski, D. T., and Grieve, S. W. D.: The relationship between drainage density, erosion rate, and hilltop curvature: Implications for sediment transport processes, J. Geophys. Res.-Earth Surf., 121, 1724–1745, https://doi.org/10.1002/2015JF003747, 2016.
Davis, W. M.: The convex profile of bad-land divides, Science, 20, 245–245, 1892.
Dietrich, W. E. and Montgomery, D. R.: Hillslopes, Channels, and Landscape Scale, in: Scale Dependence and Scale Invariance in Hydrology, edited by: Sposito, G., 30–60, Cambridge University Press, Cambridge, UK, 1998.
Dietrich, W. E., Bellugi, D. G., Sklar, L. S., Stock, J. D., Heimsath, A. M., and Roering, J. J.: Geomorphic Transport Laws for Predicting Landscape form and Dynamics, in: Prediction in Geomorphology, Geophysical Monograph Series, 135, edited by: Wilcock, P. R., and Iverson, R. M., 103–132, American Geophysical Union, Washington, D. C., USA, https://doi.org/10.1029/135GM09, 2003.
Duvall, A. R. and Tucker, G. E.: Dynamic Ridges and Valleys in a Strike-Slip Environment, J. Geophys. Res. Earth Surf., 120, 2016–2026, https://doi.org/10.1002/2015JF003618, 2015.
Fernandes, N. F. and Dietrich, W. E.: Hillslope evolution by diffusive processes: The timescale for equilibrium adjustments, Water Resour. Res., 33, 1307–1318, 1997.
Gilbert, G. K.: Report on the Geology of the Henry Mountains, US Govt. Print. Off., Washington, D. C., USA, 1877.
Harkins, N., Kirby, E., Heimsath, A., Robinson, R., and Reiser, U.: Transient fluvial incision in the headwaters of the Yellow River, northeastern Tibet, China, J. Geophys. Res., 112, F03S04, https://doi.org/10.1029/2006JF000570, 2007.
Howard, A. D.: A detachment-limited model of drainage basin evolution, Water Resour. Res., 30, 2261–2285, 1994.
Huntley, H. E.: Dimensional analysis, Dover publications, New York, USA, 1967.
Ijjasz-Vasquez, E. J. and Bras, R. L.: Scaling regimes of local slope versus contributing area in digital elevation models, Geomorphology, 12, 299–311, 1995.
Lashermes, B., Foufoula-Georgiou, E., and Dietrich, W. E.: Channel network extraction from high resolution topography using wavelets, Geophys. Res. Lett., 34, L23S04, https://doi.org/10.1029/2007GL031140, 2007.
Lighthill, M. J. and Whitham, G. B.: On kinematic waves. I. Flood movement in long rivers, Proc. R. Soc. Lond. Ser. Math. Phys. Sci., 281–316, 1955.
Moglen, G. E. and Bras, R. L.: The effect of spatial heterogeneities on geomorphic expression in a model of basin evolution, Water Resour. Res., 31, 2613–2623, 1995.
Montgomery, D. R. and Dietrich, W. E.: Channel Initiation and the Problem of Landscape Scale, Science, 255, 826–830, 1992.
Mueller, J. E.: Re-evaluation of the Relationship of Master Streams and Drainage Basins, Geol. Soc. Am. Bull., 83, 3471–3474, 1972.
Orlandini, S., Tarolli, P., Moretti, G., and Dalla Fontana, G.: On the prediction of channel heads in a complex alpine terrain using gridded elevation data, Water Resour. Res., 47, W02538, https://doi.org/10.1029/2010WR009648, 2011.
Paola, C., Straub, K., Mohrig, D., and Reinhardt, L.: The “unreasonable effectiveness” of stratigraphic and geomorphic experiments, Earth-Sci. Rev., 97, 1–43, https://doi.org/10.1016/j.earscirev.2009.05.003, 2009.
Pelletier, J. D.: Minimizing the grid-resolution dependence of flow-routing algorithms for geomorphic applications, Geomorphology, 122, 91–98, https://doi.org/10.1016/j.geomorph.2010.06.001, 2010.
Pelletier, J. D.: A robust, two-parameter method for the extraction of drainage networks from high-resolution digital elevation models (DEMs): Evaluation using synthetic and real-world DEMs, Water Resour. Res., 49, 75–89, https://doi.org/10.1029/2012WR012452, 2013.
Perron, J. T. and Royden, L.: An integral approach to bedrock river profile analysis, Earth Surf. Process. Landf., 38, 570–576, https://doi.org/10.1002/esp.3302, 2013.
Perron, J. T., Dietrich, W. E., and Kirchner, J. W.: Controls on the spacing of first-order valleys, J. Geophys. Res., 113, F04016, https://doi.org/10.1029/2007JF000977, 2008.
Perron, J. T., Kirchner, J. W., and Dietrich, W. E.: Formation of evenly spaced ridges and valleys, Nature, 460, 502–505, https://doi.org/10.1038/nature08174, 2009.
Perron, J. T., Richardson, P. W., Ferrier, K. L., and Lapôtre, M.: The root of branching river networks, Nature, 492, 100–103, https://doi.org/10.1038/nature11672, 2012.
Refice, A., Giachetta, E., and Capolongo, D.: SIGNUM: A Matlab, TIN-based landscape evolution model, Comput. Geosci., 45, 293–303, https://doi.org/10.1016/j.cageo.2011.11.013, 2012.
Robl, J., Hergarten, S., and Prasicek, G.: The topographic state of fluvially conditioned mountain ranges, Earth-Sci. Rev., 168, 190–217, https://doi.org/10.1016/j.earscirev.2017.03.007, 2017.
Roering, J. J., Kirchner, J. W., and Dietrich, W. E.: Evidence for nonlinear, diffusive sediment transport on hillslopes and implications for landscape morphology, Water Resour. Res., 35, 853–870, https://doi.org/10.1029/1998WR900090, 1999.
Roering, J. J., Perron, J. T., and Kirchner, J. W.: Functional relationships between denudation and hillslope form and relief, Earth Planet. Sci. Lett., 264, 245–258, https://doi.org/10.1016/j.epsl.2007.09.035, 2007.
Simpson, G. and Schlunegger, F.: Topographic evolution and morphology of surfaces evolving in response to coupled fluvial and hillslope sediment transport, J. Geophys. Res. Solid-Ea., 108, 2300, https://doi.org/10.1029/2002JB002162, 2003.
Sklar, L. and Dietrich, W. E.: River longitudinal profiles and bedrock incision models: Stream power and the influence of sediment supply, in: Rivers Over Rock: Fluvial Processes in Bedrock Channels, Geophys. Monogr. Ser., Vol. 107, edited by: Tinkler, K. and Wohl, E., 237–260, AGU, Washington, D. C., USA, 1998.
Smith, T. R. and Bretherton, F. P.: Stability and the conservation of mass in drainage basin evolution, Water Resour. Res., 8, 1506–1529, 1972.
Sonin, A. A.: The Physical Basis of Dimensional Analysis, 2nd edition, Department of Mechanical Engineering, MIT, Cambridge, MA, USA, available at: http://web.mit.edu/2.25/www/pdf/DA_unified.pdf (last access: 30 March 2018), 2001.
Tucker, G. E.: Natural experiments in landscape evolution, Earth Surf. Process. Landf., 34, 1450–1460, https://doi.org/10.1002/esp.1833, 2009.
Tucker, G. E.: CHILD Users Guide for version R9.4.1, Coop. Inst. Res. Environ. Sci. (CIRES) and Dep. Geol. Sci., Univ. Colo., Boulder, CO, USA, available at: http://csdms.colorado.edu/mediawiki/images/Child_users_guide.pdf, last access: 30 March 2018, 2010.
Tucker, G. E. and Hancock, G. R.: Modelling landscape evolution, Earth Surf. Process. Landf., 35, 28–50, https://doi.org/10.1002/esp.1952, 2010.
Tucker, G., Lancaster, S., Gasparini, N., and Bras, R.: The channel-hillslope integrated landscape development model (CHILD), in: Landscape erosion and evolution modeling, edited by: Harmon, R. S. and Doe III, W. W., 349–388, Kluwer Academic/Plenum Publishers, New York, USA, 2001.
Whipple, K. X.: Fluvial landscape response time: How plausible is steady-state denudation?, Am. J. Sci., 301, 313–325, 2001.
Whipple, K. X. and Tucker, G. E.: Dynamics of the stream-power river incision model: Implications for height limits of mountain ranges, landscape response timescales, and research needs, J. Geophys. Res.-Solid Ea., 104, 17661–17674, https://doi.org/10.1029/1999JB900120, 1999.
Whipple, K. X., Forte, A. M., DiBiase, R. A., Gasparini, N. M., and Ouimet, W. B.: Timescales of landscape response to divide migration and drainage capture: Implications for the role of divide mobility in landscape evolution, J. Geophys. Res.-Earth Surf., 122, 248–273, https://doi.org/10.1002/2016JF003973, 2017.
Willett, S. D., McCoy, S. W., Perron, J. T., Goren, L., and Chen, C.-Y.: Dynamic Reorganization of River Basins, Science, 343, 1248765, https://doi.org/10.1126/science.1248765, 2014.
Willgoose, G., Bras, R. L., and Rodriguez-Iturbe, I.: A coupled channel network growth and hillslope evolution model: 2. Nondimensionalization and applications, Water Resour. Res., 27, 1685–1696, https://doi.org/10.1029/91WR00936, 1991.
Wobus, C., Whipple, K. X., Kirby, E., Snyder, N., Johnson, J., Spyropolou, K., Crosby, B., and Sheehan, D.: Tectonics from topography: Procedures, promise, and pitfalls, in: Tectonics, Climate, and Landscape Evolution: Geological Society of America Special Paper 398, Penrose Conference Series, edited by: Willett, S. D., Hovius, N., Brandon, M. T., and Fisher, D. M., Geological Society of America, Boulder, CO, USA, 55–74, https://doi.org/10.1130/2006.2398(04), 2006.
- Abstract
- Introduction
- Theory
- Scaling and similarity of landscapes
- Interpretations of the characteristic scales
- Summary and conclusions
- Dimensional analysis of LEM with generic slope and area exponents m, n
- Appendix B: Rescaling of landscapes
- Appendix C: Numerical simulation setup
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- Theory
- Scaling and similarity of landscapes
- Interpretations of the characteristic scales
- Summary and conclusions
- Dimensional analysis of LEM with generic slope and area exponents m, n
- Appendix B: Rescaling of landscapes
- Appendix C: Numerical simulation setup
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- References