the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Colluvial deposits as a possible weathering reservoir in uplifting mountains
Sébastien Carretier
Yves Goddéris
Javier Martinez
Martin Reich
Pierre Martinod
The role of mountain uplift in the evolution of the global climate over geological times is controversial. At the heart of this debate is the capacity of rapid denudation to drive silicate weathering, which consumes CO2. Here we present the results of a 3-D model that couples erosion and weathering during mountain uplift, in which, for the first time, the weathered material is traced during its stochastic transport from the hillslopes to the mountain outlet. To explore the response of weathering fluxes to progressively cooler and drier climatic conditions, we run model simulations accounting for a decrease in temperature with or without modifications in the rainfall pattern based on a simple orographic model. At this stage, the model does not simulate the deep water circulation, the precipitation of secondary minerals, variations in the pH, below-ground pCO2, and the chemical affinity of the water in contact with minerals. Consequently, the predicted silicate weathering fluxes probably represent a maximum, although the predicted silicate weathering rates are within the range of silicate and total weathering rates estimated from field data. In all cases, the erosion rate increases during mountain uplift, which thins the regolith and produces a hump in the weathering rate evolution. This model thus predicts that the weathering outflux reaches a peak and then falls, consistent with predictions of previous 1-D models. By tracking the pathways of particles, the model can also consider how lateral river erosion drives mass wasting and the temporary storage of colluvial deposits on the valley sides. This reservoir is comprised of fresh material that has a residence time ranging from several years up to several thousand years. During this period, the weathering of colluvium appears to sustain the mountain weathering flux. The relative weathering contribution of colluvium depends on the area covered by regolith on the hillslopes. For mountains sparsely covered by regolith during cold periods, colluvium produces most of the simulated weathering flux for a large range of erosion parameters and precipitation rate patterns. In addition to other reservoirs such as deep fractured bedrock, colluvial deposits may help to maintain a substantial and constant weathering flux in rapidly uplifting mountains during cooling periods.
- Article
(37783 KB) - Full-text XML
-
Supplement
(16303 KB) - BibTeX
- EndNote
Since the contribution of Walker et al. (1981), the chemical weathering of continental silicate rock is known to be at the heart of the geological regulation of the carbon cycle and climate, through the existence of a negative feedback between climate and silicate weathering (Berner et al., 1983; François and Walker, 1992). The associated consumption of atmospheric carbon indeed depends on the air temperature and continental run-off (Brady, 1991). Since the pioneering work of Walker et al. (1981), numerous studies have investigated the role of parameters other than climate on the silicate weathering efficiency. Those parameters include the key role of the vegetation cover (Berner, 1994; Drever, 1994; Le Hir et al., 2011), of the lithology (Bluth and Kump, 1994; Caves et al., 2016; Dessert et al., 2003; Ibarra et al., 2016), and of the paleogeography (Donnadieu et al., 2006; Gibbs et al., 1999; Goddéris et al., 2014; Kent and Muttoni, 2013; Marshall et al., 1988). But the most debated issue remains the link existing between chemical weathering and physical erosion. Raymo et al. (1988) proposed that the uplift of major mountain ranges over the course of the Cenozoic triggered the global climatic cooling, assuming that enhanced physical erosion promotes CO2 consumption by chemical weathering. Soil column models have challenged this theory by predicting that above a certain erosion rate value, minerals do not stay in the regolith long enough to significantly weather, producing a hump in the weathering–erosion relationship (Dixon et al., 2009b; Ferrier and Kirchner, 2008; Gabet and Mudd, 2009; Hilley et al., 2010). Other models argue that when the regolith vanishes at large erosion rates, weathering becomes significant in the fractured bedrock (Calmels et al., 2011; Maher, 2011; West, 2012), or that high reliefs consume more CO2 than low reliefs during wetter periods (Maher and Chamberlain, 2014). Datasets from soil pits and riverine fluxes show a monotonic relationship between both the denudation rate and weathering rate in some cases (Dixon et al., 2009b; Millot et al., 2002; West et al., 2005), but they also evidence a possible maximum erosion rate above which the soil weathering rate decreases (Dixon and von Blanckenburg, 2012). Recent data from the Southern Alps in New Zealand have challenged the existence of this erosion rate limit by demonstrating that soil production rate was able to continue increasing at the highest erosion rates when rainfall is abundant (Larsen et al., 2014). In such regions, landslides constitute a significant weathering reservoir (Emberson et al., 2016a, b). In large orogenic belts such as the Andes and Himalayas, transported minerals may continue to weather significantly in the floodplain (Bouchez et al., 2012; Lupker et al., 2012; Moquet et al., 2016). As a result, the debate on the locus of weathering in mountains is still open and different weathering reservoirs from the hillslopes to plains may dominate at different stages of the mountain evolution. Until now, four main weathering reservoirs have been identified: soils (Dixon et al., 2009b); fractured bedrock (Calmels et al., 2011; Schopka and Derry, 2012); basins (Bouchez et al., 2012), which also trap a considerable amount of organic carbon (France-Lanord and Derry, 1997; Galy et al., 2015); and oceans (Oelkers et al., 2011). In this paper, we address the particular question of the relative contributions of regolith and colluvial deposits produced in situ in the weathering outflux of an uplifting mountain under a cooling climate.
None of the available models are able to discriminate between these weathering reservoirs. Moreover, few models (Braun et al., 2016; Vanwalleghem et al., 2013) account for the heterogeneity of erosion and weathering during relief adaptation to uplift which may control the overall evolution of the weathering rate of a rising mountain range (Anderson et al., 2012; Carretier et al., 2014; Cohen et al., 2013). None of these models can be used to trace the weathered material through its stochastic displacement from hillslopes to basins.
We therefore developed a dynamical model (CIDRE) that accounts for the heterogeneity of the erosion and weathering evolution under during different uplift and climate scenarios. This model uses a novel approach that couples the landscape evolution with moving clasts, which can be used to follow the weathered material through different weathering reservoirs. By linking weathering processes on the mineral, hillslope, and river scales, we provide new insights into the effect of valley widening and the associated colluvial deposits (unconsolidated sediment that has been deposited at the base of hillslopes or colluvium) on weathering rates in uplifted areas.
In the following, we define “regolith” as loose material produced in situ by the conversion of fresh bedrock into weathered material.
2.1 Erosion–deposition model
CIDRE is a c++ code that models the topography dynamics on a regular grid of square cells. Precipitation falls on the grid at a rate P (L T−1) and a multiple-flow algorithm propagates the water flux Q (L3 T−1) toward all downstream cells in proportion to the slope in each direction. Note that we do not include evapotranspiration in our simulations. Thus P is actually the net precipitation (run-off) although we call it rainfall or precipitation in the following for simplicity. A detailed description of the erosion–deposition model is given in Carretier et al. (2016) and Mouchene et al. (2017). We recall here the main parameters.
The elevation z (river bed or hillslope surface) changes in each cell (size dx) according to the balance between erosion ϵ (L T−1), deposition D (L T−1), sediment discharge per unit length from lateral (bank) erosion qsl (L2 T−1), and uplift U (L T−1) (Davy and Lague, 2009):
and we define (Carretier et al., 2016; Davy and Lague, 2009)
where K (T−0.5) and κ (L T−1) are lithology-dependent (different for bedrock or regolith or sediment) erosion parameters, S is the slope, q (L3 T−1) is the water discharge per stream unit width, m and n are positive exponents, and
where qsr and qsh are the incoming river and hillslope sediment fluxes (total ) per unit width (L2 T−1), ξ is river transport length parameter (T L−1), and Sc is a slope threshold. These fluxes are the sum of sediment fluxes leaving upstream neighbour cells. The deposition fluxes on a cell are a fraction of the incoming sediment. When the local q and S values are larger, less sediment eroded from upstream will deposit on the cell. The sediment leaving a cell is spread in the same way as water, i.e. proportional to the downstream slopes. Note that the erosion–deposition hillslope model leads to similar solutions (Carretier et al., 2016) as the critical slope-dependent hillslope model studied for example by Roering et al. (1999).
Flowing water in each direction can erode lateral cells perpendicular to that direction. The lateral sediment flux per unit length qsl (L2 T−1) eroded from a lateral cell is defined as a fraction of the river sediment flux qsr (L2 T−1) in the considered direction (Murray and Paola, 1997; Nicholas and Quine, 2007):
where α is a bank erodibility coefficient. α is specified for loose material (regolith or sediment) and is implicitly determined for bedrock layers proportional to their “fluvial” erodibility such that (K from Eq. 2). If a regolith or sediment covers the bedrock of a lateral cell, α is weighted by its respective thickness above the target cell.
Following several authors, we assume that the regolith production rate follows a humped law, so that there is an optimum thickness at which the regolith production rate is at its maximum (Strudley et al., 2006; Wilkinson et al., 2005):
where wo (L T−1) is the regolith production rate for the exposed bedrock, d1 and d2 (L) are the attenuation depths, k1 is a non-dimensional coefficient, and B (L) is the regolith thickness.
We also let wo depend on temperature T and precipitation rate P, following White and Blum (1995) and Dixon et al. (2009a) among others:
where kw is a factor with the dimension of a weathering rate (L T−1), P (L T−1) is the amount of water entering the regolith (equal here to the rainfall rate), Po is the water flow reference value (1 m a−1 in this study), Ea is the activation energy corresponding to the mineral that controls the weathering front advance, To is a reference temperature (298.15 K), T is the local temperature expressed in Kelvin, and R is the gas constant.
Equations 7 and 8 are similar to the regolith production model tested by Norton et al. (2014) and were also used in Carretier et al. (2014). Nevertheless, except in rare studies (Heimsath et al., 2001; Wilkinson et al., 2005), no data fully support (or exclude) the humped function in Eq. (7), and there is no direct evidence that it applies to chemical weathering. The existence of an optimum regolith thickness has been conceptually justified as resulting from water pumping by plants, or an optimum residence time of water within a porous soil to dissolve minerals (Gilbert, 1877). The exponential decrease in Eq. (8) emerges from a reactive-transport model when diffusion dominates (Lebedeva et al., 2010). However, for thick regoliths (≫1 m), their thickening may mainly depend on groundwater discharge (Hilley et al., 2010; Maher, 2010; Maher and Chamberlain, 2014; Rempe and Dietrich, 2014). Lebedeva et al. (2010) and Braun et al. (2016) showed that in the absence of uplift and erosion, this type of model predicts that the regolith thickens as and also that the regolith production rate varies inversely with soil thickness (). Compared with the exponential trend of Eq. (7), this 1∕B trend predicts a much slower attenuation of the regolith development when it thickens. This allows very thick (>100 m) regoliths to develop within a realistic period of time (Braun et al., 2016). Alternatively, if the weathering front advance is controlled by the rate of mineral fracturing, then the regolith production rate is predicted to be constant (Fletcher et al., 2006). Because we are analysing the effect of erosion on weathering, the 1∕B depth attenuation for thick regoliths is not considered here. Nevertheless, we show one experiment that uses this 1∕B attenuation to illustrate that the particular model for local regolith development is not crucial for our conclusions.
Studies of silicate weathering fluxes on both the soil and catchment scales suggest that local regolith production depends on both temperature and precipitation rate (Brantley et al., 2008; Dupré et al., 2003; Gaillardet et al., 1999; Oliva et al., 2003; Riebe et al., 2004; West, 2012; White and Blum, 1995). Dixon et al. (2009a) showed that Eq. (8) fits saprolite data in the western Sierra Nevada Mountains in California. Nevertheless, Maher (2010, 2011) and Maher and Chamberlain (2014) argued that in many mountainous situations, the weathering rate should essentially and linearly depend on the water flow in the soil, with a minor effect from temperature. In Eq. (8), the linear dependency between the regolith production rate and run-off and the weaker dependence on temperature are consistent with that view, although our model does not account for the partitioning of water between the surface and ground (Braun et al., 2016; Maher and Chamberlain, 2014; Rempe and Dietrich, 2014; Schoonejans et al., 2016). The drawback of Eqs. 7 and 8 is that they are parametric and not truly physically based. Nevertheless, given the lack of consensus, we assume the form of these laws and test the effect of varying their parameters. In particular, we test the difference between the humped form and the exponential form (k1=0) of this law (Heimsath et al., 1997).
2.2 Clast weathering
The previous regolith production model allows the dynamic coupling between denudation and weatherable material production, but it is not used to model the weathering flux. This flux is calculated by tracing clasts that dissolve.
In our model, a clast has a specified radius r, with no particular limitation, between the size of a small mineral and a large cobble. Its probability to be detached, deposited, or to pass through a cell depends on its size and on the associated fluxes calculated by CIDRE for each cell Carretier et al. (2016). With this algorithm, the spreading of the different clasts depends on the relative magnitude of diffusive and advective transport (Eqs. 2 to 5), while the mean population transport rate is determined by the transport discharge qs calculated in CIDRE (Carretier et al., 2016). This model generates a clast residence time distribution that evolves from the soil to the valley.
Clast weathering is a new feature of our model. Compared to previous versions, clast dissolution allows us to model a weathering flux and not only a mean bedrock-to-regolith conversion rate (Carretier et al., 2014). The weathering of the clast begins when the clast enters the regolith or when it is detached from the bedrock. For a clast made up of only one mineral, the volumetric dissolution rate wm (L3 T−1) is
where Vm is the molar volume [L3 𝒩−1], λ is a non-dimensional roughness coefficient defined by White and Brantley (2003) (White et al., 2008), and km is a dissolution parameter depending on each mineral (𝒩 ) (Brantley et al., 2008). The other parameters are defined in Eq. (8). The product is the reactive surface (Brantley et al., 2008; Goddéris et al., 2006; Maher et al., 2009; Navarre-Sitchler et al., 2011). The second part of this equation comes from experimental laws of mineral dissolution (Brantley et al., 2008). The first part, with the run-off dependence (), accounts for the linear increase in the dissolution rate with water discharge (Maher, 2010). As for the regolith production law, we acknowledge that it is a simplification to assume a linear correlation between groundwater discharge in the soil and run-off.
If a clast is made up of different minerals, their proportions are specified at the beginning (χmo) and then evolve during their lifetime (χm). Modelling a complex mineralogical texture with a subdivision into different grains would be intractable in practice. In a simplified model, the main issue is to define a reactive surface for each mineral type. Given that minerals are spread into different grains within the clast, this surface is larger than the surface of a simple sphere made up of a particular mineral (White and Brantley, 2003).
In order to take this reactive surface into account in the simplest manner, each mineral type is converted to an “equivalent” sphere with radius rm including the mineral and “virtual” vacuum. In addition, this sphere surface is multiplied by the roughness coefficient λ to define the reactive surface (Fig. 1). The sphere geometry is chosen for its simplicity. The virtual vacuum implies that the reactive surface of each mineral is larger than the surface of a “solid” sphere made up of this mineral only (even if λ=1). λ is an adjusted factor that may account for the complex geometry of the crystals within the clast. This formulation also respects the fact that when smaller proportions of a mineral occur within the clast, its specific surface is larger (reactive surface over mineral mass).
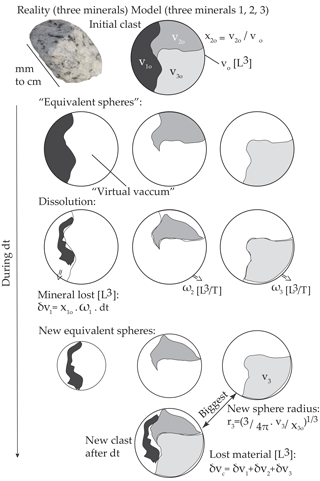
Figure 1The dissolution model for a clast made up of three different mineral types. The sequence from top to bottom illustrates the mineral dissolution and the resulting clast size decrease during a time step.
At the beginning of the process, each equivalent sphere has the same radius as the clast (Fig. 1).
The total dissolution rate for the clast wc (L3 T−1) is then
Over a time step, the volume δvm (L3) lost by one particular mineral is
and the total volume lost by the clast δvc (L3) is
The solid (real) volume lost by each mineral δvm is subtracted from its previous volume to calculate the new mineral volume vm. The new mineral radius rm is then calculated considering an equivalent sphere incorporating the solid and virtual vacuum of volume :
The sum of the new solid mineral volumes vm is the new solid clast volume. The new clast radius is the radius of the largest equivalent sphere of its constitutive minerals (Fig. 1). Doing this, we assume that the largest mineral forms a mass that includes the other minerals.
This formulation was also designed to respect a basic mass balance: a clast of a given size constituted initially of one mineral (for example 100 % of albite) evolves exactly in the same way as if it were constituted of different proportions of the same mineral (for example 40 % of albite + 50 % of albite + 10 % of albite). This equivalence is achieved by using the initial mineral fraction χmo in Eq. (13) to define each equivalent sphere.
If a clast includes minerals of contrasting weathering rates, for example albite and quartz, the rapid dissolution of albite ends up with a porous clast made up of a vacuum within the quartz. The true clast volume is therefore larger than the solid sphere corresponding to the mass of the quartz only, which is reproduced well by Eq. (13). The porosity increases in these clasts, consistent with reality. Obviously this approach supposes that the initial clast does not lose its cohesion and is not divided into different mineral grains, which can occur in nature. Thus particle size evolution is controlled entirely by chemical processes.
This approach is probably less realistic when the clast size exceeds several centimetres. In that case, the advance of the annular weathering front may control the clast volume that is effectively being weathered (Lebedeva et al., 2010). This type of front could be simply introduced into the model in the future based on the results of Lebedeva et al. (2010). In the present form, the predicted dissolved volume of such large clasts is therefore probably a maximum volume.
The weathering rate of the clasts does not depend on the depth in the regolith in the present version. The removal of water by plants, changes in the regolith porosity, pCO2, groundwater flow velocity, pH, sensitivity of the surface temperature variations, clay precipitation, etc. can modify the weathering rate according to the depth. In particular, the precipitation of secondary phases is known to strongly modulate the weathering front advance (Navarre-Sitchler et al., 2011; Oelkers et al., 1994), soil weathering rate (Maher et al., 2009; Vazquez et al., 2016), and catchment-scale weathering rate (Bouchez and Gaillardet, 2014; Buss et al., 2017). Consequently, neglecting the precipitation of secondary phases overestimates the weathering outflux. In the future, this could be accounted for by, for example, modulating the weathering rate by the same humped law (Eq. 7) used for regolith production (Vanwalleghem et al., 2013) and allowing the precipitation of secondary phases within the pores of clasts.
Nevertheless, to validate our approach in a simple case, we simulated weathering on marine terraces in Santa Cruz, California, and found that the results agree with empirical observations (Supplement).
2.3 Integration on the cell and grid scales
CIDRE use the available limited information provided by the clasts present on some of the cells to estimate the chemical weathering outflux of the landscape. Weathering first occurs in the regolith and then during clast transport on the hillslopes and in rivers. Whereas the weathering of all clasts is calculated at each time step, integrated weathering on the model scale can be calculated at a lower frequency (for example every 10 ka). Cells are treated sequentially and we test whether they contain clasts in the regolith. In that case, the regolith is subdivided into layers around each clast. The border between two layers is set midway between the clasts (Fig. 2). As a result, the number of layers and their size depend on the number and spacing of the clasts present in the regolith and can vary at each time step. Their number and depth depend either on the initial clasts seeded in the parent rock or on the erosion–sedimentation processes affecting the regolith. The dissolution rate of the clasts is integrated within the corresponding layers, and their sum provides an estimate of the dissolved flux per cell (Fig. 2). The vertical meshing evolves through time, and adapts itself to the changing clast distribution according to the available clasts within each cell.

Figure 2Calculation of the weathering outflux by integrating clast weathering on the cell and mountain scales. (a) A regolith + bedrock soil column containing three clasts in the regolith at a particular time step. Three layers were defined with a size depending on the spacing between the clasts, which itself results either from an initial disposition in the bedrock or from the erosion–deposition history. The equations indicate how the integration on the layer and regolith scales proceeds. The same operation is performed for deposits. wc: clast weathering rate; wl: layer weathering rate; wcell: cell weathering rate; all (L3 T−1). (b) Once the calculation of all wcell values is completed, the mountain-scale weathering rate W (L3 T−1) is estimated by taking into account the spatial distribution of the clasts. (c) Example of the reference experiment WARM at 15 Ma where the clasts in green are actively dissolving, and the clasts in red are still in the fresh bedrock. Only half of the clasts (5000) are plotted here.
The dissolved chemical flux per layer wl (L3 T−1) is the clast dissolution rate per clast volume , multiplied by the layer volume vl. This value is also weighted by the ratio between the current and initial clast volumes in order to take into account the fact that the volume of weathering material decreases within the layer:
namely,
The corresponding dissolved flux is also calculated for each mineral constituting the clasts, as well as for some of their elements according to their stoichiometric proportions in the minerals. If a clast is completely dissolved, it remains in the regolith or in the deposit where it is trapped so that there is an integration layer around it that produces zero chemical flux. This allows us to account for the depleted layers of the soil. A totally dissolved clast is killed as soon as it is detached from the regolith. The dissolved chemical flux of the entire cell wcell is obtained by summing wl (Fig. 2). Finally, the total weathering outflux W (L3 T−1) integrated over the model grid is weighted by the relative proportion of regolith or sediment that contains clasts:
2.4 Clast revival
A clast is killed when detached after complete dissolution, or if it simply goes out of the model grid. In both cases, the model offers the possibility to recycle the clast. A recycled clast is put back into the same cell in which it was initially seeded, with the same characteristics, at a random depth between 0 and B (regolith thickness) within the parent rock below the regolith (except if B=0 in which case the revival depth is set at 10 m to avoid the handling of numerous clasts for which weathering is null). The maximum depth B at which the clasts are repositioned is optimal in order to favour an equidistance between the clasts within the regolith. Recycling a dead clast to its initial location also permits the densification of the number of clasts for which the exhumation is faster. By this approach, a limited number of clasts are handled, while optimising their distribution at depth to obtain the best estimate of the chemical outflux.
2.5 Non-dimensionalisation
Assuming m=0.5 and n=1 (Whipple and Tucker, 1999) and using the scaling factors H for mountain height, L for mountain width, P for effective precipitation rate (run-off), and U uplift rate, we obtain the non-dimensional form (∗) of the mass balance Eq. (1):
where
These numbers affect the morphology of the resulting topography at steady state. Smaller Nriv and Ndepo values and larger Nhill and Sc values yield topographies that are increasingly dominated by (diffusive) smooth and rounded hillslopes.
Following the same approach, the non-dimensional form of the regolith thickness variation (Supplement) yields the number . This non-dimensional number determines whether or not regolith exists at dynamic equilibrium. Nreg>1 produces a regolith-covered mountain, whereas Nreg<1 leads to a bare-bedrock mountain (Carretier et al., 2014).
Finally, the dimensional analysis of the clast dissolution rate leads to a non-dimensional number , where τr is a clast's residence time in the regolith at steady state () and τm is the characteristic dissolution time of the main mineral (here albite) defined as the time necessary to decrease the initial clast volume by a factor of e1 (see the Supplement for the full expression including the model parameters). This number includes the clast size and the kinetic parameters associated with the particular mineral m. Nclast is actually the Damköhler number (Hilley et al., 2010; White and Brantley, 2003). This number indicates the weathering grade of a clast leaving the hillslopes. When Nclast is large, a clast leaving the regolith is very depleted, whereas it remains fresh if Nclast is small. The first situation has been called supply-, transport-, or erosion-limited weathering (Dixon et al., 2009a). The second situation has been called a “kinetically” limited regime (Ferrier and Kirchner, 2008). Hilley et al. (2010) identified Nreg (“ϵ∗” for them) and Nclast (“Di” for them) as key parameters controlling the weathering flux on the scale of a soil column.
It is worth noting that experiments sharing different model parameters but the same non-dimensional numbers give similar results (Supplement Fig. S1). For fixed values of temperature and precipitations, the complexity of this model is actually reduced to seven non-dimensional numbers reflecting a great diversity of precipitation, uplift, and weathering rates. Nevertheless, there are limitations to this similarity in some of the following experiments that use elevation-dependent temperatures and precipitations. For example, the cooling of the surface temperature imposed by a mountain uplift decreases the regolith production rate through time. This decrease will be more pronounced in high mountains than in low mountains. During the rise of high mountains, the initial regolith that formed at low (warm) elevations may rapidly disappear. On the contrary it may continue to cover the low mountains. The weathering outflux will evolve differently in both cases. In these cases, Nclast and Nreg are given for the temperature and precipitation at base level of the final topography.
2.6 Model parameters that matter
The number of parameters that matter in this contribution can be reduced to three, namely the valley widening parameter α, the Damköhler number Nclast, and the uplift-to-weathering number Nreg. The other four non-dimensional numbers Sc, Nriv, Ndepo, and Nhill affect the final relief, drainage density, hillslope roundness, and the response time for denudation to reach the uplift rate value. Nevertheless, whatever the value of these four parameters in the following experiments in which the climate cools, the weathering outflux follows the same evolution characterised by a period of increase followed by a period of decrease. This evolution is primarily controlled by the evolution of the regolith layer, itself mainly controlled by the decrease in temperature and precipitation rate and by the increase in erosion rate, but not by Sc, Nriv, Ndepo, and Nhill (Supplement Figs. S3, S4, and S5). Thus, the main results of this contribution do not crucially depend on these four parameters. Conversely, α, Nclast, and Nreg determine the regolith thickness evolution and the time spent by the clasts in the different weathering reservoirs (regolith, colluvium, valley). Thus, we primarily vary the parameters included in these numbers to study the different behaviours of the model with regards to the long-term trend of the weathering outflux.
2.7 Description of experiments
The following set of experiments is intended to analyse the contribution of the regolith covering the hillslopes and of the sediment trapped in the valleys to the weathering outflux under a cooling climate. In order to evaluate the influence of this cooling on the weathering outflux, we first design a reference and control experiment, WARM, corresponding to a warm, wet, and constant climate (Table 1). An initial horizontal rough surface (σ=0.5 m) is uplifted. Sediment can leave the southern boundary but not the northern one (equivalent to a divide), and the two other sides are linked by periodic boundary conditions. The resulting half mountain is 100 km wide and 150 km long (dx=500 m), an order of magnitude of catchment size that can be found for example in the Himalayas or Andes. Rivers do not erode laterally (α=0); uplift rate U (1 mm a−1), precipitation rate P (1 m a−1), and temperature T (25 ∘C for all z values) are kept constant. We fix the erodibility parameters (K and κ) so that the maximum elevation at steady state reaches a reasonable height of ∼7000 m consistent with the Andes and Himalayas, on a timescale of ∼15 Myr: a−0.5 (bedrock) and a−0.5 (regolith or sediment) are within the range of previous estimates (Giachetta et al., 2015), m a−1 and Sc=0.84 (=tan40) for both bedrock and loose material, and ξ=0.1 a m−1 (Table 1).
Table 1Parameters for the main simulations (OROGR. stands for OROGRAPHIC). Other common parameters include the following: U=1 mm a−1. r=1 mm. Ea=66 000 J mol−1 (albite), 85 000 (quartz), and 35 000 (biotite). (albite), 10−13.39 (quartz), and 10−10.88 (biotite). m3 mol−1 (albite), (quartz), and (biotite). Sc=0.84. k1=0.8. d1=0.5 m. d2=0.1 m. For experiments with lateral erosion for loose material except in “OROGRAPHIC_dx=20m” where . ξ=0.1 a m−1. The values of P and T, as well as the non-dimensional numbers, are given for z=0 m at the end of the simulation. n.d.: not defined.
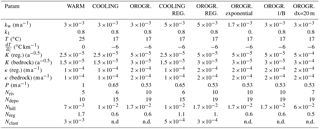
In the regolith production law (Eq. 8), Ea=48 kJ mol−1 is intermediate between albite and biotite, the minerals that control the weathering front advance. The reference temperature To is 298.15 K. The humped attenuation parameters are from Strudley et al. (2006), with d1=0.5 m, d2=0.1 m, and k1=0.8. We acknowledge that these parameters are empirical and are not necessarily representative of chemical weathering. We come back to this point later. With these values, the regolith production rate w is optimal (wop) for B=0.17 m. The parameter kw=0.003 m a−1 is chosen so that Nreg=1.7; a value >1 implies that the hillslopes are mantled by a 0.55 m thick regolith at dynamic equilibrium.
The reference model uses 10 000 clasts spread randomly in the bedrock between 0 and 4 m below the initial surface (Fig. 2c). Each clast mixes albite (55 %), quartz (30 %), and biotite (15 %) with a 1 mm radius and a roughness factor λ=1. The dissolution parameters of these minerals are from experimental studies (Brantley et al., 2008): Ea=66 000 J mol−1 (albite), 85 000 (quartz), and 35 000 (biotite). (albite), 10−13.39 (quartz), and 10−10.88 (biotite). m3 mol−1 (albite), (quartz), and (biotite). With these parameters, Nclast=0.003, a value that indicates that the weathering is mainly kinetically limited when the denudation rate equals the uplift rate at dynamic equilibrium.
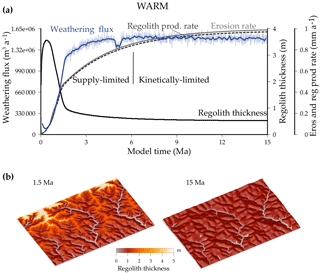
Figure 3(a) Topography, regolith thickness, erosion, and weathering flux evolutions averaged over the domain in the reference experiment WARM. The thick weathering curve corresponds to a 0.1 Myr sliding window averaging. Variations in the weathering curve are mainly due to the stochastic transport of clasts. More clasts decrease this variability but do not change the mean values. The decrease near 5 Ma is due to a local hillslope collapse (Eq. 5). Weathering becomes kinetically limited after ∼6 Ma when the erosion rate is too rapid to allow clasts to stay in the regolith for a long time (low Damköhler number Nclast = 0.003). (b) Topography and regolith thickness at 1.5 and 15 Ma.
In order to illustrate the sensitivity of the model to the different parameters, we perform additional simulations in which some of the WARM experiment parameters are varied but lead to mountains mantled by regolith.
Then, we design a series of experiments with a cooling and drying climate. In a first set of experiments (COOLING and OROGRAPHIC – Table 1), the hillslopes become entirely bedrock at the end of the cooling period. These experiments represent an end-member model as pure bare-bedrock mountains do not exist (Heimsath et al., 2012). Nevertheless, this case will be useful to quantify the effect of sediment temporally stored in valleys. The COOLING simulation, uses the same set of parameters as the WARM simulation but the climate cools. The modelled cooling operates through a decrease in temperature at the mountain foot in four arbitrary steps of −2 ∘C at 3, 6, 9, and 12 Ma of the model time. Furthermore, an altitudinal temperature gradient of −6 is prescribed. Moreover, in order to account for the drying potentially associated with global cooling, we add a rainfall decrease of −5 % per degree of cooling (Labat et al., 2004; Manabe et al., 2004), following Maher and Chamberlain (2014). As the rainfall pattern may influence the regolith pattern and thickness, and thus the weathering outflux evolution, we also add orographic precipitations in experiment OROGRAPHIC. The orographic precipitation patterns are obtained by prescribing a Gaussian relationship between rainfall and elevation (Colberg and Anders, 2014). The rainfall peak is centred at 1300 m or 2000 as it is in the case of the Andes or Himalaya (Bookhagen and Burbank, 2006; Bookhagen and Strecker, 2008).
We explore more realistic situations for which the mountain is partially covered by a regolith at the end of the cooling process at low elevations. These simulations (COOLING REG. and OROGRAPHIC REG.) are built on the COOLING and OROGRAPHIC experiments but use higher weatherability coefficient kw in Eq. (8), so that the regolith production rate exceeds the denudation rate at low elevations (Table 1).
Then, we test wether our results significantly depend on the regolith production law. We run experiment OROGRAPHIC_Exponential built on the previous OROGRAPHIC simulation but using an exponential dependance of the regolith production rate instead of the humped law. We do this by setting k1=0 in Eq. (7). In order to compare experiments, we also decrease kw (Eq. 8) so that the maximum regolith production rate for bare bedrock equals the optimum regolith production rate calculated using the humped version of the law (same Nreg at z=0 m – Table 1). We also test the effect of a regolith production rate inversely proportional to the regolith thickness B in experiment OROGRAPHIC_1/B. Finally, in order to test the robustness of our conclusion regarding the model and pixel size, we run OROGRAPHIC_dx=20 m that uses a pixel size of 20 m instead of 500 m. In this experiment, we increase the erodibility parameters K and κ to obtain a maximum elevation of 1200 m (Table 1).
In cases using a cooling climate, we compare simulations without lateral erosion and simulations that include this process. This comparison highlights the contribution of sediment temporarily stored in widened valleys to the weathering outflux. A total of 44 simulations are presented in this contribution.
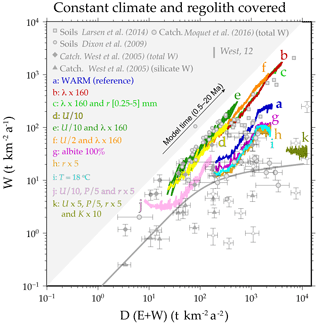
Figure 4Comparison of the total denudation rate (physical erosion + weathering) in CIDRE vs. the weathering rate with data and the model of West (2012). Grey symbols correspond to cratons and submontane domains covered by regolith (West et al., 2005). White symbols correspond to the bedrock-dominated alpine domains of West et al. (2005). The data of Moquet et al. (2016) are in the Andes and Amazon basin. Data from Dixon et al. (2009b) are from Sierra Nevada, California. Data from Larsen et al. (2014) are from New Zealand. Data from Dixon et al. (2009) and Larsen et al. (2014) correspond to local soil production rates in rapidly eroding settings. They thus represent some maximum weathering rates, to which it is useful to compare our model results. Note that CIDRE results correspond to silicate weathering rates, not total weathering rate. We show both sets of data to emphasise that the modelled silicate weathering rate is probably overestimated but remains in the range of measured total weathering rates. The CIDRE simulations correspond to regolith-covered mountains (Nreg>1). In order to convert the CIDRE weathering and erosion rates into , a density of 2.6 t m−3 (albite) was used. There is no lateral erosion (α=0). (a) Reference WARM model with uplift U=1 mm a−1; precipitation P=1 m a−1; temperature T=25 ∘C; clast radius r=1 mm; albite (55 %), quartz (30 %), and biotite (15 %); and mineral roughness λ=1. Consequently Nclast=0.003 and Nreg= 1.7. (b) Nclast=0.45 and Nreg= 1.7. (c) Random initial distribution of r between 0.25 and 5 mm following a power law with exponent −3 and a mean of 1 mm. Nclast= 0.45 and Nreg = 1.7. (d) Nclast= 0.09 and Nreg = 17. (e) Nclast= 14 and Nreg = 17. (f) Nclast= 1.5 and Nreg = 3.4. (g) Nclast= 0.003 and Nreg = 1.7. (h) Nclast= 0.0009 and Nreg = 1.1. (i) Nclast= 0.0006 and Nreg=1.7. (j) Nclast= 0.002 and Nreg=3.4. (k) Nclast= 0.00001 and Nreg=1.1. The weathering rate is smaller for pure albite (g) than for a granitoid composition (a) because the reactive specific surface of the albite minerals (clast surface divided by mineral volume) is smaller in (g) than in (a).
3.1 Regolith-covered mountains under constant and homogeneous climate
We run the simulation WARM until erosion balances uplift, which occurs when the maximum elevation is ∼7000 m after ∼15 Myr of simulation. Figure 3 shows that during the adaptation of the topography and erosion to the imposed uplift, the mean regolith production rate increases. As predicted by the value of Nreg>1 (=1.7), the mountain is covered by a ∼0.5 m thick regolith at dynamic equilibrium. The mean regolith thickness reaches a maximum in the early stages of the surface uplift when erosion is still low on average. Then the regolith thickness decreases as the drainage network invades the uplifting surface and the hillslopes steepen. The weathering flux increases during this process because increasing erosion removes depleted clasts from the regolith, fosters the descent of the weathering front, and thus supplies fresh clasts to the regolith. On average, the weathering is supply limited during this period. Near 6 Ma, the erosion becomes too large and the regolith too thin for clasts to have time to significantly weather in the regolith. The weathering flux reaches a steady state and the weathering becomes kinetically limited, which is consistent with the small Damköhler number (Nclast=0.003) of this experiment.
The weathering rate is also plotted against the total denudation rate and compared to data in Fig. 4, as well as the model of West (2012). Other experiments are plotted, in which we vary the uplift (U∕10 and U×5), temperature (T∕1.4), precipitation (P∕5), clast size (r=0.25–5 mm), and mineral roughness (λ×160) and mineralogy (granitoid or pure albite). For experiments with larger Nclast values than the reference experiment (mainly supply limited), the denudation and weathering rates fit the linear relationship observed for regolith-covered landscapes characterised by supply-limited weathering (Dixon et al., 2009a). For experiments with a smaller Nclast value, the weathering becomes progressively kinetically limited as in the reference experiment, and thus saturates at high denudation rates (Fig. 4). Overall, Fig. 4 shows that the range of weathering and denudation rates predicted by these different simulations through time fits a large range of data for regolith-covered mountains.
3.2 Cooling and bedrock mountains
Figure 5 shows the response to the climate cooling for the COOLING experiment. During the mountain rise, progressive cooling and drying decreases the regolith production rate and the clast weathering rate. Moreover, the erosion rate increases. During the first several millions of years, the weathering flux increases because there is a sufficient landscape area covered by regolith characterised by supply-limited weathering. Then the regolith cover decreases dramatically and the weathering flux falls to zero everywhere in the bedrock mountain (Fig. 5).
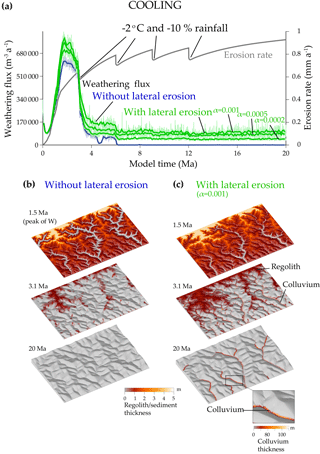
Figure 5The COOLING experiment uses the same parameters as the reference experiment, WARM, but the climate is now cooling. The temperature decreases with elevation (−6 ), the sea level temperature T decreases by 8 ∘C in four steps, and the rainfall decreases by −5 % per degree of cooling. (a) Weathering flux evolution without lateral erosion and with lateral erosion for the reference model with uplift U= 1 mm a−1; precipitation P= 1 m a−1; initial temperature 25 ∘C; clast radius r= 1 mm; albite (55 %), quartz (30 %), and biotite (15 %); and mineral roughness λ= 1. α is the lateral erosion parameter. Panels (b) and (c) show topographic and regolith thickness evolutions at 1.5, 3.1, and 20 Ma. In (c), note the progressive transfer from the regolith reservoir on the hillslopes to the colluvium reservoir in the valleys, responsible for the constant weathering flux after 6 Ma in the case including lateral erosion.
We now allow valleys to widen by lateral erosion for the same experiment (Table 1). The factor α controlling the widening rate of the valleys is poorly constrained. Nicholas (2013) used a slightly different equation for lateral erosion: qsl=(ESl)qsr, where Sl is the lateral slope. He calibrated E between 1 and 10 in large alluvial rivers. With lateral slopes Sl on the order of 0.01, α ranges between 0.01 and 0.1 for sediment. We use a lower reference value α=0.001 for regolith or sediment, probably better adapted to large pixels. Allowing rivers to erode laterally, the weathering rate follows the same initial evolution but then it does not fall to zero (Fig. 5). Valley widening steepens the foot of the hillslopes on the borders of the valleys, which generates mass wasting and the deposition of fresh material on the valley borders (Fig. 5c). These fresh minerals weather before being removed by rivers. Colluvium resides long enough in valleys (99 % of the clast residence times are smaller than 1500 years in the COOLING experiment with lateral erosion – Fig. 6) to generate a significant and nearly constant weathering rate. As there is no remaining regolith on the hillslopes even at low elevations (erosion exceeds the regolith production rate), colluvium is the only loose material producing a weathering flux. The prescribed drops in rainfall have a limited impact on the weathering flux of the colluvium (Fig. 5). Indeed, a decrease in water discharge increases the colluvium residence time (Fig. 6), which counterbalances their lower weathering rate. Consequently, the weathering flux reaches a steady state when an equilibrium is reached between the rate of colluvium removal and the weathering rate. Dividing the lateral erosion parameter α by 2 and 5 only decreases the weathering flux by a quarter and a half, respectively (Fig. 5a). As soon as α is large enough for the valleys to widen and to drive mass wasting, the volume of the colluvial deposits depends weakly on α. The lower weathering rate for narrower valleys is due to the smaller residence times of colluvial deposits in the mountain.
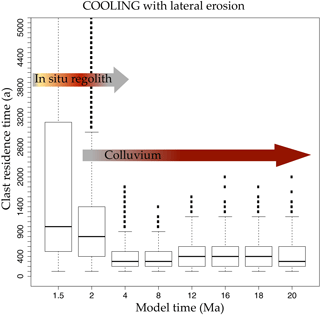
Figure 6Distribution of the residence times for the clasts at different steps of the evolution in the COOLING experiment with lateral erosion (Fig. 5a and c). The clast residence time is defined as the time during which a clast weathers (Dosseto et al., 2006; Mudd and Yoo, 2010), either in the regolith on the hillslopes, or in the colluvium. Note that the distribution is cut at 5 ka, but residence times of several tens of thousands of years are present at 1.5 Ma, although they constitute much less than 1 % of the clasts. After 6 Ma, the regolith has completely disappeared, so that the residence times represent the time spent after their detachment from the bedrock, i.e. primarily within the colluvium and possibly sediment temporarily deposited by the rivers. This distribution of the residence times gives an estimate of the colluvium residence times along the valleys. Of the residence times, 99 % are smaller than 1.5 kyr after 4 Ma. This distribution increases slightly after 6 Ma because the rainfall decreases. The increase in residence time compensates for the rainfall decrease to produce the nearly constant weathering outflux seen in Fig. 5.
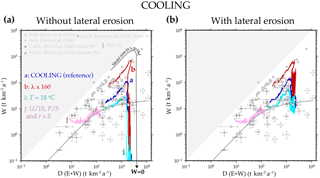
Figure 7Different experiments with cooling climate. The temperature decreases with elevation (−6 ), the sea level temperature T decreases by 8 ∘C in four steps, and the rainfall decreases −5 % per degree of cooling. Experiments a (COOLING), b, i, and j use the same parameters as in Fig. 4 but with a cooling climate. Without (a) and with (α= 0.001) (b) lateral erosion.
Figure 7 illustrates the effect of colluvium weathering for several experiments using different model parameters. In all cases but one, colluvium associated with valley widening sustains the weathering rate for large denudation rates. The exception corresponds to a slowly uplifting domain with arid climate in which weathering clasts are coarse (U∕10, P∕5, and r×5 compared to the COOLING experiment). In this case, the removal of the regolith is slow. After 20 Ma, a large portion of the domain is still covered by regolith, which remains the main weathering reservoir.
Prescribing a orographic-like distribution of rainfall with a rainfall peak centred at 1300 m or 2000 (OROGRAPHIC experiments) has a limited effect compared to previous cooling experiments (Fig. 8). Colluvium mainly forms along valley floors at elevations at which the rainfall is higher, which promotes their weathering but decreases their residence time. The weathering steady state occurs earlier with the orographic peak at 2000 m because the regolith is removed faster and thus colluvium dominates earlier in the weathering evolution.
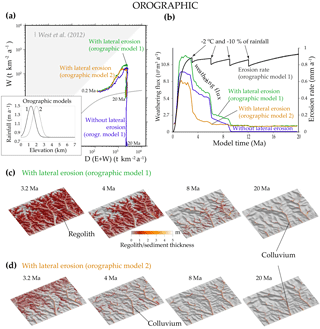
Figure 8OROGRAPHIC experiment. A orographic-like precipitation peak is considered in addition to the parameters of the previous COOLING experiment. The erodibility coefficients are doubled in order to obtain comparable maximum elevations (K and κ in Eq. 2). (a) Denudation–weathering evolution with and without lateral erosion for two orographic models with peaks at 1300 or 2000 m of elevation. (b) Erosion and weathering flux through time for the two orographic models. (c) Elevation and regolith or sediment cover evolution for the orographic model 1 with lateral erosion (α= 0.001). (d) The same for orographic model 2. The regolith legend applies to (c) and (d).
3.3 Cooling and mountains partially covered by regolith
Previous cooling models led to bare-bedrock mountains. Nevertheless, soils almost always cover the bedrock at low elevations. In order to generate a more realistic regolith distribution, we only increase the bedrock weatherability kw (Eq. 8, Table 1). In the resulting COOLING REG. experiments, a regolith persists at low elevations (<1500 m) when the climate is cooler and drier. In this case, the persistent regolith is able to sustain the weathering rate of the whole mountain at a significant value (Fig. 9). Adding valley widening (α=0.001) does not significantly modify the weathering flux evolution during the last 10 Myr. Nevertheless, colluvium still plays a role in that case. Because the hillslopes steepen near valley borders, the area covered by regolith is reduced by half compared to the case without lateral erosion. However, the weathering flux is similar with and without lateral erosion, which shows that colluvium accounts for half the weathering flux. This fraction is also observed for the OROGRAPHIC REG. experiments that use a Gaussian rainfall–elevation relationship (Fig. 10).
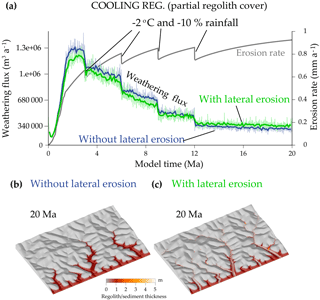
Figure 9Experiments ending with a regolith covering the low elevations (<1500 m) and corresponding to a cooling climate. (a) Erosion and weathering flux through time for the models without and with lateral erosion. Panels (b) and (c) show corresponding topography and regolith or sediment thickness at 20 Ma for the model with and without lateral erosion.
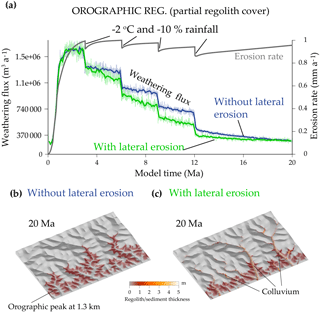
Figure 10Same as Fig. 9 (cooling ending with a regolith at elevations <1500 m), but the precipitations vary with elevation according to a Gaussian curve with an elevation peak at 1300 m (orographic model 1 illustrated in Fig. 8). The erodibility parameters (Eq. 2) are also doubled to compensate for the smaller precipitation rate at high elevations and thus to obtain comparable maximum elevations.
3.4 Other regolith production laws and pixel size
We made assumptions about the regolith production law. However, the form of the production law controls the spatial distribution of the regolith thickness and production rate in a mountain (Braun et al., 2016; Carretier et al., 2014). We thus test the robustness of our main result by assuming an exponential regolith production rather than a humped law. Figure 11 compares the OROGRAPHIC experiments using the humped law with the same experiments using the exponential law (OROGRAPHIC_Exponential, Table 1). For regolith thickness larger than the optimum thickness, the regolith production is faster for the humped law. Consequently, the total volume of regolith produced with this law is larger. The weathering flux is thus greater with the humped law while some regolith remains.
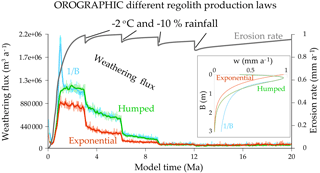
Figure 11Effect of changing the regolith production law (inset diagram) in the OROGRAPHIC experiment with lateral erosion (Table 1).
We now assume that the regolith thickness decreases as 1∕B for thicknesses larger than the optimum thickness (0.17 m), instead of exponentially (Braun et al., 2016) (OROGRAPHIC_1/B, Table 1). This different law produces a much thicker regolith of several tens of metres in the early stage (∼1 Ma) of the mountain erosion. This rapid regolith thickening generates a weathering peak, but which is only twice that produced with the humped law (Fig. 11). Indeed, the thick regolith is rapidly depleted, so that only the weathering of its deeper layer feeds the weathering outflux after several hundreds of thousands of years. Then, the weathering flux follows the same evolution as with the humped law.
Finally, in order to test the influence of mountain size and model resolution, we reduce the pixel size to 20 m (Fig. 12 – Table 1). The widening parameter α is multiplied by 5 in order to have a valley width larger than 1 pixel. The final weathering rate, totally produced by colluvium, is about 2 times larger than in the OROGRAPHIC experiment because elevations are lower and more located around the precipitation maximum, so that total precipitation rate and temperature are larger. Thus, the significant weathering of colluvium seems not to depend on the simulated system size.
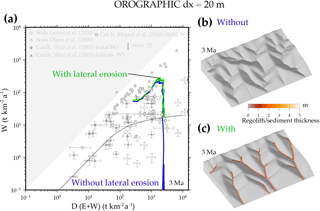
Figure 12OROGRAPHIC experiments using a smaller cell size of 20 m (mountain size∕25) (Table 1). The mountain erosion increases faster than in other experiments. Thus the cooling and drying steps are applied at 0.5, 1, 1.5, and 2 Ma. The final maximum elevation at 3 Ma is 1200 m. The precipitation rate is thus maximum at mountaintop (orographic model 1 illustrated in Fig. 8). (a) Weathering rate for the experiment with and without lateral erosion. (b) Topography and regolith or sediment thickness at 3 Ma in the case without lateral erosion. (c) The same for the case with lateral erosion, showing the colluvium in valleys. Relief×2.
CIDRE does not model the precipitation of secondary minerals or variations in the pH, pCO2, and changes in the chemical equilibrium related to the water–rock interaction (Brantley et al., 2008; Lebedeva et al., 2010; Maher et al., 2009; Oelkers et al., 1994). Neglecting chemical equilibrium and the precipitation of secondary phases overestimates the predicted dissolved fluxes. Predicting the effect of pH variations is difficult because it could increase the weathering rate (pH decrease by sulfide mineral oxidation for example) or decrease it (pH increase by carbonate dissolution for example). Accounting for pCO2 would require modelling soil–vegetation interactions, which remains a challenge on the mountain scale. The effect of neglecting pCO2 is not easy to predict. The groundwater circulation is also neglected, although it can contribute significantly to the weathering outflux (Calmels et al., 2011; Maher, 2011; Schopka and Derry, 2012). Allowing water to infiltrate would probably increase the predicted weathering outflux. We also acknowledge that the elevation-dependent rainfall and temperature models used here are simplified. The feedback between relief growth and the evolution of precipitation and temperature patterns may be much more complicated. Even using a simplified orographic model, CIDRE produces different and complex responses in terms of regolith, relief, and weathering evolutions (Fig. 8). More complex elevation–rainfall–temperature relationships may have significant implications for the evolution towards steady-state topography. Glacier erosion and associated physical weathering is not modelled. Glaciers would provide fresh sediment eroded from high elevations to the fluvial system. This is already the case in our simulations with cold climate but glaciers may generate more and finer sediment. In addition, frost-cracking at high elevations produces sediment. Both phenomena should increase the weathering contribution of sediment stored in valleys. We also neglected the fragmentation of clasts during hillslope and river transport by physical weathering and crushing. We propose that this fragmentation should increase the weathering contribution of sediment trapped in the valleys as smaller grains weather faster.
Nevertheless, our modelling approach presents several advantages: the model is on the scale of the whole landscape but also on the pedon scale (a denser clast distribution can be set in specific areas of interest); any mineralogical assemblage and clast size distribution can be studied; and there is no need to calculate the mountain weathering outflux W at each time step. If only a long-term trend of W is studied, it can be calculated at a low frequency, which is computationally efficient and allows this 3-D approach to be applied to long time periods. Most importantly, (1) weathered material can be followed from the source to the sink and (2) the weathering outflux results from the stochastic residence times of the clasts in the hillslopes and in rivers. These two last points constitute the main differences of our approach compared to previous pedon and landscape weathering models Braun et al. (2016); Ferrier and Kirchner (2008); Vanwalleghem et al. (2013).
All previous models founded on clast residence time in the regolith predict that weathering should be zero when the regolith disappears (Ferrier and Kirchner, 2008). However, documented catchment weathering rates are significantly larger than zero (Dixon and von Blanckenburg, 2012). A simple explanation may be that there is always a sufficient fraction of hillslopes covered by soils to produce a significant weathering flux, even in fast-eroding mountains (Heimsath et al., 2012; Larsen et al., 2014). Alternatively, deep-weathering within fractured bedrock may account for this difference. Calmels et al. (2011) showed that this deep weathering reservoir accounts for more than 1/3 of the silicate weathering flux of a catchment in Taiwan. Schopka and Derry (2012) also showed a major contribution of this deep reservoir in Hawaii. The significant contribution of deep groundwater weathering echoes the model proposed by Maher (2010). In this model, this is the ratio between the fluid residence time and the characteristic mineral dissolution time (our τm), which controls the weathering flux, rather than the ratio Nclast between the clast's residence time and τm. West (2012) also argued for a monotonic increase in chemical weathering with erosion due to water circulation in the fractured bedrock, so that the weathering would not critically depend on the regolith thickness. If alternatively the weathering layer corresponds to the vadose zone, then this layer may thicken and sustain the weathering flux in rapidly eroding hillslopes (Braun et al., 2016; Maher and Chamberlain, 2014; Rempe and Dietrich, 2014).
Our model points to another possible reservoir: the colluvium temporarily stored along valley borders. When the regolith thins, colluvium becomes the main locus of weathering, which prevents the weathering outflux of the catchment from dropping to very low values. This finding is supported by the correlation between the weathering rate and the volume of the landslides present in catchments in southwestern New Zealand (Emberson et al., 2016a). In another catchment in New Zealand, Emberson et al. (2016b) monitored a recent landslide and demonstrated that landslides can generate extremely high and local weathering flux. In this case, the weathering flux results mainly from the oxidation of pyrite and the dissolution of carbonate. Although these phases and the pH effect were not included in our simulations, the underlying process by which landslides sustain the catchment weathering is the same as in our simulations. Landslides and colluvium both rapidly exhume fresh minerals that reside long enough in the catchment to boost its weathering outflux. As stated by Emberson et al. (2016b), the cumulative contribution of landslides to the catchment weathering should depend on the landslide storage duration and the characteristic dissolution time of the most labile phases. In our simulations, the most labile phases are albite and biotite with a characteristic dissolution time of several thousand years. The clast residence time distribution provides a direct estimate of the colluvium residence times of several thousand years (Fig. 6). These durations are consistent with residence times in the Andes for example, as determined from U series (Dosseto et al., 2008). Thus, grains stay in the catchments long enough to yield a significant weathering flux. Nevertheless, our model does not account for the full stochasticity of landslides documented by Emberson et al. (2016a). In our model, colluvium is produced relatively continuously, so that differences in clast residence times are mainly due to progressive colluvium removal and differences in the initial distance from the outlet. In real landscapes, even those without significant lateral river erosion, there will still be colluvium storage on the hillslopes because the sediment production is stochastic. Thus, a better description should include the stochastic production of landslides (Gabet, 2007). Despite these limitations, our results extend the findings of Emberson et al. (2016a) and Emberson et al. (2016b) by showing that the weathering of such collapsed material covering a very limited catchment area may control the weathering evolution of mountains over millions of years, even if their residence time in the catchment is not longer than several centuries or millennia. The impact of colluvium does not contradict weathering models based on the fluid residence time. The porosity increase in colluvium should increase the groundwater velocity in colluvium and thus the weathering flux (Emberson et al., 2016b; Maher, 2011).
Despite its limitations, our model predicts weathering–erosion rates within the range of existing data (Figs. 3 and 8) and may explain this range in terms of topographic evolution. In cooling experiments, our model predicts weathering rates that initially increase with time due to supply-limited conditions and increasing erosion but then decline because the regolith is progressively stripped off. This hump evolution is consistent with previous 1-D models (Dixon and von Blanckenburg, 2012; Gabet and Mudd, 2009). This is a remarkable similarity given the heterogeneity of the regolith thickness and denudation rate in the simulated landscapes during the relief growth. In our results, the hump in the weathering evolution results from the progressive stripping of the regolith via an increasing erosion rate and cooling climate, whatever the form of the regolith production law. The peak occurs due to the competing factors of the area covered by regolith and its thickness distribution (Carretier et al., 2014). When accounting for colluvium, the weathering peak is followed by a nearly constant weathering flux in agreement with models assuming a constant weathering layer (West, 2012) or based on the residence time of water in the weathering zone to the river (Maher and Chamberlain, 2014). However, in our model, this sustained weathering rate does not result from a constant weathering layer but rather from a change in the weathering reservoir.
Note that the duration of the weathering peak may depend on the choice of n=1 in Eq. (2). The n exponent is known to control the response time of the topography to uplift (Tucker and Whipple, 2002) and the time required to develop the drainage network on the initial uplifted surface (Carretier et al., 2009). In regions where detachment threshold is significant, n>1 (Lague, 2014). Using n>1 would thus lengthen the period during which a thick regolith covers the initial uplifted surface. It would thus probably affect the duration of the weathering peak, but not the contribution of colluvial deposit once this regolith has been eroded.
The contribution of colluvium to the weathering flux should depend on the ratio of river width to valley width, which itself depends on the lithology, uplift rate, or flood distribution (Brocard and van der Beek, 2006). Thus, the colluvium reservoir cannot be considered as a general model for all catchments. Nevertheless, colluvium contributes significantly in all our cooling simulations, regardless of the rainfall pattern or catchment size. This suggests that fresh sediment that is temporarily stored along valleys, irrespective of the cause of their width (uplift variations, glaciations, etc.), may contribute to the long-term weathering fluxes trend. In particular, the weathering of these sediments may be only slightly dependent on climate variations. An increase in water discharge fosters mineral weathering but at the same time decreases mineral residence times, so that the net weathering variation is negligible (Fig. 6). The same balance may operate in foreland basins and may take part in the weathering stability over the last 12 Myr observed in the offshore sediment record (Willenbring and von Blanckenburg, 2010; von Blanckenburg et al., 2015).
In cooling experiments (Fig. 7), the short weathering time of the grains implies that they are only partially weathered when they leave the mountain, so that their weathering in adjacent basins could also contribute to the total weathering outflux. At present, there are few studies that explore weathering fluxes of materials in sedimentary basins after they have left their source areas (Bouchez et al., 2012; Lupker et al., 2012; Moquet et al., 2016). The contribution of the basin still needs to be analysed through the stochastic dynamics of the grains in the alluvial plain, a study within the scope of our model.
We designed a new model on the landscape scale that takes the weathering of distinct clasts in the regolith, colluvium, and rivers into account. This model accounts for part of the stochasticity of sediment transport, which is reflected by the distribution of the clast residence times in an uplifting mountain. The weathering model has limitations (no groundwater model; no dependence on PH, pCO2, or water–rock chemical disequilibrium; no precipitation of secondary phases). Nevertheless the model predicts a range of weathering rates consistent with the available data for a wide range of climatic and tectonic contexts. During the rising of a mountain and as the climate cools, the weathering flux increases and then decreases, which is consistent with previous models. In addition, the dynamic adjustment of the topography, the tracing of weathered material, and the stochastic transport of grains point to a possible significant contribution from colluvial deposits during cold periods. This weathering reservoir may contribute to a high and constant weathering flux in rapidly eroding mountains under cold conditions, in addition to deep weathering in fractured bedrock and other potential reservoirs. The model predicts that the contribution of colluvial deposits should vary according to valley width, latitude (temperature), and elevation. The model also predicts the mineral and elementary depletion of clasts. In order to test these outcomes, we need systematic measurements of weathering outflux (Emberson et al., 2016b) and weathering grade of hillslope regolith, colluvium, and river terraces within different catchments. In addition, proxies of paleo-denudation and paleo-weathering rates in foreland basin deposits are still needed to validate or not the humped evolution of the weathering outflux during the growth of a mountain range. Meanwhile, this new model opens perspectives to study the weathering contribution of foreland basins during mountain growth and decline and the response of these reservoirs to cyclic climatic variations.
The source codes of CIDRE are available on request to Sébastien Carretier.
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-6-217-2018-supplement.
The authors declare that they have no conflict of interest.
This paper is a contribution to the LMI COPEDIM (funding from
IRD). Martin Reich acknowledges funding by the MSI grant “Millennium
Nucleus for Metal Tracing Along Subduction
(NC130065)”. Constructive comments on a previous
version from two reviewers and from Robert Hilton (associated editor), Simon Mudd,
Jeremy Caves, and the anonymous reviewer were highly
appreciated. Sara Mullin edited the English on a previous version of the paper.
Edited by: Robert Hilton
Reviewed by: Simon Mudd, Jeremy Caves Rugenstein, and one anonymous referee
Anderson, S., Anderson, R., and Tucker, G.: Landscape scale linkages in critical zone evolution, CR Geosci., 344, 586–596, 2012. a
Berner, R.: 3GEOCARB-II – A Revised Model Of Atmospheric CO2 Over Phanerozoic Time, Am. J. Sci., 294, 56–91, https://doi.org/10.2475/ajs.294.1.56, 1994. a
Berner, R., Lasaga, A., and Garrels, R.: The carbonate-silicate geochemical cycle and its effect on atmospheric carbon-dioxide over the past 100 million years, Am. J. Sci., 283, 641–683, https://doi.org/10.2475/ajs.283.7.641, 1983. a
von Blanckenburg, F., Bouchez, J., Ibarra, D., and Maher, K.: Stable runoff and weathering fluxes into the oceans over Quaternary climate cycles, Nat. Geosci., 8, 538–U146, https://doi.org/10.1038/NGEO2452, 2015. a
Bluth, G. and Kump, L.: Lithologic and climatologic controls of river chemistry, Geochim. Cosmochim. Ac., 58, 2341–2359, https://doi.org/10.1016/0016-7037(94)90015-9, 1994. a
Bookhagen, B. and Burbank, D.: Topography, relief, and TRMM-derived rainfall variations along the Himalaya, Geophys. Res. Lett., 33, L08405, https://doi.org/10.1029/2006GL026037, 2006. a
Bookhagen, B. and Strecker, M. R.: Orographic barriers, high-resolution TRMM rainfall, and relief variations along the eastern Andes, Geophys. Res. Lett., 35, L06403, https://doi.org/10.1029/2007GL032011, 2008. a
Bouchez, J. and Gaillardet, J.: How accurate are rivers as gauges of chemical denudation of the Earth surface?, Geology, 42, 171–174, https://doi.org/10.1130/G34934.1, 2014. a
Bouchez, J., Gaillardet, J., Lupker, M., Louvat, P., France-Lanord, C., Maurice, L., Armijos, E., and Moquet, J.-S.: Floodplains of large rivers: Weathering reactors or simple silos?, Chem. Geol., 332, 166–184, https://doi.org/10.1016/j.chemgeo.2012.09.032, 2012. a, b, c
Brady, P. V.: The effect of silicate weathering on global temperature and atmospheric CO2, J. Geophys. Res., 96, 18101–18106, 1991. a
Brantley, S., Bandstra, J., Moore, J., and White, A.: Modelling chemical depletion profiles in regolith, Geoderma, 145, 494–504, 2008. a, b, c, d, e, f
Braun, J., Mercier, J., Guillocheau, F., and Robin, C.: A simple model for regolith formation by chemical weathering, J. Geophys. Res.-Earth, 121, 2140–2171, https://doi.org/10.1002/2016JF003914, 2016. a, b, c, d, e, f, g, h
Brocard, G. and van der Beek, P.: Influence of incision rate, rock strength and bedload supply on bedrock river gradients and valley-flat widths: Field-based evidence and calibrations from western Alpine rivers (SE France), in: Tectonics, Climate and Landscape Evolution, edited by: Willett, S. D., Hovius, N., Brandon, M. T., and Fisher, D., Geol. Soc. Am. Spec. Publ., 101–126, 2006. a
Buss, H. L., Lara, M. C., Moore, O. W., Kurtz, A. C., Schulz, M. S., and White, A. F.: Lithological influences on contemporary and long-term regolith weathering at the Luquillo Critical Zone Observatory, Geochim. Cosmochim. Ac., 196, 224–251, https://doi.org/10.1016/j.gca.2016.09.038, 2017. a
Calmels, D., Galy, A., Hovius, N., Bickle, M., West, A. J., Chen, M.-C., and Chapman, H.: Contribution of deep groundwater to the weathering budget in a rapidly eroding mountain belt, Taiwan, Earth Planet. Sc. Lett., 303, 48–58, https://doi.org/10.1016/j.epsl.2010.12.032, 2011. a, b, c, d
Carretier, S., Poisson, B., Vassallo, R., Pepin, E., and Farías, M.: Tectonic interpretation of erosion rates at different spatial scales in an uplifting block, J. Geophys. Res., 114, F02003, https://doi.org/10.1029/2008JF001080, 2009. a
Carretier, S., Goddéris, Y., Delannoy, T., and Rouby, D.: Mean bedrock-to-saprolite conversion and erosion rates during mountain growth and decline, Geomorphology, 209, 29–52, https://doi.org/10.1016/j.geomorph.2013.11.025, 2014. a, b, c, d, e, f
Carretier, S., Martinod, P., Reich, M., and Goddéris, Y.: Modelling sediment clasts transport during landscape evolution, Earth Surf. Dynam., 4, 237–251, https://doi.org/10.5194/esurf-4-237-2016, 2016. a, b, c, d
Caves, J. K., Jost, A. B., Lau, K. V., and Maher, K.: Cenozoic carbon cycle imbalances and a variable weathering feedback, Earth Planet. Sc. Lett., 450, 152–163, https://doi.org/10.1016/j.epsl.2016.06.035, 2016. a
Cohen, S., Willgoose, G., and Hancock, G.: Soil-landscape response to mid and late Quaternary climate fluctuations based on numerical simulations, Quaternary Res., 79, 452–457, https://doi.org/10.1016/j.yqres.2013.01.001, 2013. a
Colberg, J. S. and Anders, A. M.: Numerical modeling of spatially-variable precipitation and passive margin escarpment evolution, Geomorphology, 207, 203–212, https://doi.org/10.1016/j.geomorph.2013.11.006, 2014. a
Davy, P. and Lague, D.: The erosion/transport equation of landscape evolution models revisited, J. Geophys. Res., 114, F03007, https://doi.org/10.1029/2008JF001146, 2009. a, b
Dessert, C., Dupré, B., Gaillardet, J., François, L., and Allègre, C.: Basalt weathering laws and the impact of basalt weathering on the global carbon cycle, Chem. Geol., 202, 257–273, 2003. a
Dixon, J. and von Blanckenburg, F.: Soils as pacemakers and limiters of global silicate weathering, CR Geosci., 344, 597–609, https://doi.org/10.1016/j.crte.2012.10.012, 2012. a, b, c
Dixon, J., Heimsath, A., and Amundson, R.: The critical role of climate and saprolite weathering in landscape evolution, Earth Surf. Proc. Land., 34, 1507–1521, https://doi.org/10.1002/esp.1836, 2009a. a, b, c, d
Dixon, J., Heimsath, A., Kaste, J., and Amundson, R.: Climate-driven processes of hillslope weathering, Geology, 37, 975–978, https://doi.org/10.1130/G30045A.1, 2009b. a, b, c, d
Donnadieu, Y., Goddéris, Y., Pierrehumbert, R., Dromart, G., Fluteau, F., and Jacob, R.: A GEOCLIM simulation of climatic and biogeochemical consequences of Pangea breakup, Geochem. Geophy. Geosy., 7, Q11019, https://doi.org/10.1029/2006GC001278, 2006. a
Dosseto, A., Bourdon, B., Gaillardet, J., Maurice-Bourgoin, L., and Allègre, C.: Weathering and transport of sediments in the Bolivian Andes: Time constraints from uranium-series isotopes, Earth Planet. Sc. Lett., 248, 759–771, 2006. a
Dosseto, A., Turner, S., and Chappell, J.: The evolution of weathering profiles through time: new insights from uranium-series isotopes., Earth Planet. Sc. Lett., 274, 359–371, 2008. a
Drever, J.: The effect of land plants on weathering rates of silicate minerals, Geochim. Cosmochim. Ac., 58, 2325–2332, https://doi.org/10.1016/0016-7037(94)90013-2, 1994. a
Dupré, B., Dessert, C., Oliva, P., Goddéris, Y., Viers, J., François, L., Millot, R., and Gaillardet, J.: Rivers, chemical weathering and Earth's climate, Compt. R. Acad. Sci., 335, 1141–1160, 2003. a
Emberson, R., Hovius, N., Galy, A., and Marc, O.: Chemical weathering in active mountain belts controlled by stochastic bedrock landsliding, Nat. Geosci., 9, 42, https://doi.org/10.1038/NGEO2600, 2016a. a, b, c, d
Emberson, R., Hovius, N., Galy, A., and Marc, O.: Oxidation of sulfides and rapid weathering in recent landslides, Earth Surf. Dynam., 4, 727–742, https://doi.org/10.5194/esurf-4-727-2016, 2016b. a, b, c, d, e, f
Ferrier, K. and Kirchner, J.: Effects of physical erosion on chemical denudation rates: A numerical modeling study of soil-mantled hillslopes, Earth Planet. Sc. Lett., 272, 591–599, 2008. a, b, c, d
Fletcher, R., Buss, H., and Brantley, S.: A spheroidal weathering model coupling porewater chemistry to soil thicknesses during steady-state denudation, Earth Planet. Sc. Lett., 244, 444–457, https://doi.org/10.1016/j.epsl.2006.01.055, 2006. a
France-Lanord, C. and Derry, L. A.: Organic carbon burial forcing of the carbon cycle from Himalaya erosion, Nature, 390, 65–67, 1997. a
François, L. and Walker, J.: Modeling the phanerozoic carbon-cycle and climate – constraints from the Sr-87–Sr-86 isotopic ratio of seawater, Am. J. Sci., 292, 81–135, https://doi.org/10.2475/ajs.292.2.81, 1992. a
Gabet, E. J.: A theoretical model coupling chemical weathering and physical erosion in landslide-dominated landscapes, Earth Planet. Sc. Lett., 264, 259–265, https://doi.org/10.1016/j.epsl.2007.09.028, 2007. a
Gabet, E. and Mudd, S.: A theoretical model coupling chemical weathering rates with denudation rates, Geology, 37, 151–154, 2009. a, b
Gaillardet, J., Dupré, B., Louvat, P., and Allègre, C.: Global silicate weathering and CO2 consumption rates deduced from the chemistry of the large rivers, Chem. Geol., 159, 3–30, 1999. a
Galy, V., Peucker-Ehrenbrink, B., and Eglinton, T.: Global carbon export from the terrestrial biosphere controlled by erosion, Nature, 521, 204, https://doi.org/10.1038/nature14400, 2015. a
Giachetta, E., Molin, P., Scotti, V. N., and Faccenna, C.: Plio-Quaternary uplift of the Iberian Chain (central-eastern Spain) from landscape evolution experiments and river profile modeling, Geomorphology, 246, 48–67, https://doi.org/10.1016/j.geomorph.2015.06.005, 2015. a
Gibbs, M., Bluth, G., Fawcett, P., and Kump, L.: Global chemical erosion over the last 250 my: Variations due to changes in paleogeography, paleoclimate, and paleogeology, Am. J. Sci., 299, 611–651, https://doi.org/10.2475/ajs.299.7-9.611, 1999. a
Gilbert, G.: Report on the Geology of the Henry Mountains U. S. Geographical and Geological Survey of the Rocky Mountain Region Washington D.C, Tech. rep., 1877. a
Goddéris, Y., Francois, L., Probst, A., Schott, J., Moncoulon, D., Labat, D., and Viville, D.: Modelling weathering processes at the catchment scale: The WITCH numerical model, Geochim. Cosmochim. Ac., 1128–1147, https://doi.org/10.1016/j.gca.2005.11.018, 2006. a
Goddéris, Y., Donnadieu, Y., Le Hir, G., Lefebvre, V., and Nardin, E.: The role of palaeogeography in the Phanerozoic history of atmospheric CO2 and climate, Earth-Sci. Rev., 128, 122–138, https://doi.org/10.1016/j.earscirev.2013.11.004, 2014. a
Heimsath, A. M., Dietrich, W. E., Nishiizumi, K., and Finkel, R. C.: The soil production function and landscape equilibrium, Nature, 388, 358–361, 1997. a
Heimsath, A., Dietrich, W., Nishiizumi, K., and Finkel, R.: Stochastic processes of soil production and transport: Erosion rates, topographic variation and cosmogenic nuclides in the Oregon Coast Range, Earth Surf. Proc. Land., 26, 531–552, https://doi.org/10.1002/esp.209, 2001. a
Heimsath, A. M., DiBiase, R., and Whipple, K.: Soil production limits and the transition to bedrock-dominated landscapes, Nat. Geosci., 5, 1–4, https://doi.org/10.1038/NGEO1380, 2012. a, b
Hilley, G., Chamberlain, C., Moon, S., Porder, S., and Willett, S.: Competition between erosion and reaction kinetics in controlling silicate-weathering rates, Earth Planet. Sc. Lett., 293, 191–199, 2010. a, b, c, d
Ibarra, D. E., Caves, J. K., Moon, S., Thomas, D. L., Hartmann, J., Chamberlain, C. P., and Maher, K.: Differential weathering of basaltic and granitic catchments from concentration-discharge relationships, Geochim. Cosmochim. Ac., 190, 265–293, https://doi.org/10.1016/j.gca.2016.07.006, 2016. a
Kent, D. V. and Muttoni, G.: Modulation of Late Cretaceous and Cenozoic climate by variable drawdown of atmospheric pCO2 from weathering of basaltic provinces on continents drifting through the equatorial humid belt, Clim. Past, 9, 525–546, https://doi.org/10.5194/cp-9-525-2013, 2013. a
Labat, D., Goddéris, Y., Probst, J., and Guyot, J.: Evidence for global runoff increase related to climate warming, Adv. Water Resour., 27, 631–642, 2004. a
Lague, D.: The stream power river incision model: evidence, theory and beyond, Earth Surf. Proc. Land., 39, 38–61, https://doi.org/10.1002/esp.3462, 2014. a
Larsen, I., Almond, P., Eger, A., Stone, J., Montgomery, D., and Malcolm, B.: Rapid Soil Production and Weathering in the Southern Alps, New Zealand, Science, 343, 637–640, https://doi.org/10.1126/Science.1244908, 2014. a, b, c
Lebedeva, M., Fletcher, R., and Brantley, S.: A mathematical model for steady-state regolith production at constant erosion rate, Earth Surf. Proc. Land., 35, 508–524, https://doi.org/10.1002/esp.1954, 2010. a, b, c, d, e
Le Hir, G., Donnadieu, Y., Goddéris, Y., Meyer-Berthaud, B., Ramstein, G., and Blakey, R. C.: The climate change caused by the land plant invasion in the Devonian, Earth Planet. Sc. Lett., 310, 203–212, https://doi.org/10.1016/j.epsl.2011.08.042, 2011. a
Lupker, M., France-Lanord, C., Galy, V., Lave, J., Gaillardet, J., Gajurel, A., Guilmette, C., Rahman, M., Singh, S., and Sinha, R.: Predominant floodplain over mountain weathering of Himalayan sediments (Ganga basin), Geochem. Cosmochem. Ac., 84, 410–432, https://doi.org/10.1016/j.gca.2012.02.001, 2012. a, b
Maher, K.: The dependence of chemical weathering rates on fluid residence time, Earth Planet. Sc. Lett., 294, 101–110, https://doi.org/10.1016/j.epsl.2010.03.010, 2010. a, b, c, d
Maher, K.: The role of fluid residence time and topographic scales in determining chemical fluxes from landscapes, Earth Planet. Sc. Lett., 312, 48–58, 2011. a, b, c, d
Maher, K. and Chamberlain, C. P.: Hydrologic Regulation of Chemical Weathering and the Geologic Carbon Cycle, Science, 343, 1502–1504, https://doi.org/10.1126/Science.1250770, 2014. a, b, c, d, e, f, g
Maher, K., Steefel, C. I., White, A. F., and Stonestrom, D. A.: The role of reaction affinity and secondary minerals in regulating chemical weathering rates at the Santa Cruz Soil Chronosequence, California, Geochim. Cosmochim. Ac., 73, 2804–2831, https://doi.org/10.1016/j.gca.2009.01.030, 2009. a, b, c
Manabe, S., Wetherald, R., Milly, P., Delworth, T., and Stouffer, R.: Century-scale change in water availability: CO2-quadrupling experiment, Climatic Change, 64, 59–76, https://doi.org/10.1023/B:CLIM.0000024674.37725.ca, 2004. a
Marshall, H., Walker, J., and Kuhn, W.: Long-term climate change and the geochemical cycle of carbon, J. Geophys. Res.-Atmos., 93, 791–801, https://doi.org/10.1029/JD093iD01p00791, 1988. a
Millot, R., Gaillardet, J., Dupre, B., and Allègre, C.: The global control of silicate weathering rates and the coupling with physical erosion: new insights from rivers of the Canadian Shield, EPSL, 196, 83–98, 2002. a
Moquet, J.-S., Guyot, J.-L., Crave, A., Viers, J., Filizola, N., Martinez, J.-M., Oliveira, T. C., Hidalgo Sanchez, L. S., Lagane, C., Lavado Casimiro, W. S., Noriega, L., and Pombosa, R.: Amazon River dissolved load: temporal dynamics and annual budget from the Andes to the ocean, Environ. Sci. Pollut. R., 23, 11405–11429, https://doi.org/10.1007/s11356-015-5503-6, 2016. a, b, c
Mouchené, M., van der Beek, P., Carretier, S., and Mouthereau, F.: Autogenic versus allogenic controls on the evolution of a coupled fluvial megafan–mountainous catchment system: numerical modelling and comparison with the Lannemezan megafan system (northern Pyrenees, France), Earth Surf. Dynam., 5, 125–143, https://doi.org/10.5194/esurf-5-125-2017, 2017. a
Mudd, S. and Yoo, K.: Reservoir theory for studying the geochemical evolution of soils, J. Geophys. Res., 115, F03030, https://doi.org/10.1029/2009JF001591, 2010. a
Murray, A. B. and Paola, C.: Properties of a cellular braided-stream model, Earth Surf. Proc. Land., 22, 1001–1025, 1997. a
Navarre-Sitchler, A., Steefel, C. I., Sak, P. B., and Brantley, S. L.: A reactive-transport model for weathering rind formation on basalt, Geochim. Cosmochim. Ac., 75, 7644–7667, https://doi.org/10.1016/j.gca.2011.09.033, 2011. a, b
Nicholas, A.: Morphodynamic diversity of the world's largest rivers, Geology, 41, 475–478, https://doi.org/10.1130/G34016.1, 2013. a
Nicholas, A. and Quine, T.: Modeling alluvial landform change in the absence of external environmental forcing, Geology, 35, 527–530, https://doi.org/10.1130/G23377A.1, 2007. a
Norton, K. P., Molnar, P., and Schlunegger, F.: The role of climate-driven chemical weathering on soil production, Geomorphology, 204, 510–517, https://doi.org/10.1016/j.geomorph.2013.08.030, 2014. a
Oelkers, E., Schott, J., and Devidal, J.: The effect of aluminium, pH, and chemical affinity on the rates of aluminosilicate dissulution reactions, Geochim. Cosmochim. Ac., 58, 2011–2024, https://doi.org/10.1016/0016-7037(94)90281-X, 1994. a, b
Oelkers, E. H., Gislason, S. R., Eiriksdottir, E. S., Jones, M., Pearce, C. R., and Jeandel, C.: The role of riverine particulate material on the global cycles of the elements, Appl. Geochem., 26, S365–S369, https://doi.org/10.1016/j.apgeochem.2011.03.062, 2011. a
Oliva, P., Viers, J., and Dupré, B.: Chemical weathering in granitic environments, Chem. Geol., 202, 225–256, 2003. a
Raymo, M., Ruddiman, W., and Froelich, P.: Influence of late Cenozoic mountain building on ocean geochemical cycles, Geology, 14, 649–653, 1988. a
Rempe, D. and Dietrich, B.: A bottom-up control on fresh-bedrock topography under landscapes, P. Natl. Acad. Sci. USA, 111, 6576–6581, https://doi.org/10.1073/pnas.1404763111, 2014. a, b, c
Riebe, C., Kirchner, J., and Finkel, R.: Erosional and climatic effects on long-term chemical weathering rates in granitic landscapes spanning diverse climate regimes, Earth Planet. Sc. Lett., 224, 547–562, 2004. a
Roering, J. J., Kirchner, J. W., and Dietrich, W. E.: Evidence for nonlinear, diffusive sediment transport on hillslopes and implications for landscape morphology, Water Resour. Res., 35, 853–870, 1999.
Schoonejans, J., Vanacker, V., Opfergelt, S., Ameijeiras-Marino, Y., and Christl, M.: Kinetically limited weathering at low denudation rates in semiarid climatic conditions, J. Geophys. Res.-Earth, 121, 336–350, https://doi.org/10.1002/2015JF003626, 2016. a
Schopka, H. H. and Derry, L. A.: Chemical weathering fluxes from volcanic islands and the importance of groundwater: The Hawaiian example, Earth Planet. Sc. Lett., 339, 67–78, https://doi.org/10.1016/j.epsl.2012.05.028, 2012. a, b, c
Strudley, M., Murray, A., and Haff, P.: Emergence of pediments, tors, and piedmont junctions from a bedrock weathering-regolith thickness feedback, Geology, 34, 805–808, https://doi.org/10.1130/G22482.1, 2006. a, b
Tucker, G. and Whipple, K.: Topographic outcomes predicted by stream erosion models: Sensitivity analysis and intermodel comparison, J. Geophys. Res., 107-B9, 2179, https://doi.org/10.1029/2001JB000162, 2002. a
Vanwalleghem, T., Stockmann, U., Minasny, B., and McBratney, A.: A quantitative model for integrating landscape evolution and soil formation, J. Geophys. Res.-Earth, 118, 331–347, https://doi.org/10.1029/2011JF002296, 2013. a, b, c
Vazquez, M., Ramirez, S., Morata, D., Reich, M., Braun, J.-J., and Carretier, S.: Regolith production and chemical weathering of granitic rocks in central Chile, Chem. Geol., 446, 87–98, https://doi.org/10.1016/j.chemgeo.2016.09.023, 2016. a
Walker, J., Hays, P., and Kasting, J.: A negative feedback mechanism for the long-term stabilization of Earth's surface temperature, J. Geophys. Res., 86, 9776–9782, 1981. a
West, A.: Thickness of the chemical weathering zone and implications for erosional and climatic drivers of weathering and for carbon-cycle feedbacks, Geology, 40, 811–814, 2012. a, b, c, d, e, f
West, A., Galy, A., and Bickle, M.: Tectonic and climatic controls on silicate weathering, Earth Planet. Sc. Lett., 235, 211–228, 2005. a, b, c
Whipple, K. X. and Tucker, G. E.: Dynamics of the stream-power incision model: implication for heigth limits of mountain ranges, landscape response timescales, and research needs, J. Geophys. Res., 104, 17661–17674, 1999. a
White, A. and Blum, A.: Effects of climate on chemical weathering rates in watersheds, Geochim. Cosmochim. Ac., 59, 1729–1747, 1995. a, b
White, A. and Brantley, S.: The effect of time on the weathering of silicate minerals: why do weathering rates differ in the laboratory and field?, Chem. Geol., 202, 479–506, https://doi.org/10.1016/j.chemgeo.2003.03.001, 2003. a, b, c
White, A., Schulz, M., Vivit, D., Blum, A., Stonestrom, D., and Anderson, S.: Chemical weathering of a marine terrace chronosequence, Santa Cruz, California. I: Interpreting rates and controls based on soil concentration-depth profiles, Geochim. Cosmochim. Ac., 72, 36–68, 2008. a
Wilkinson, M., Chappell, J., Humphreys, G., Fifield, K., Smith, B., and Hesse, P.: Soil production in heath and forest, Blue Mountains, Australia: influence of lithology and palaeoclimate, Earth Surf. Proc. Land., 30, 923–934, 2005. a, b
Willenbring, J. and von Blanckenburg, F.: Long-term stability of global erosion rates and weathering during late-Cenozoic cooling, Nature, 465, 211–214, https://doi.org/10.1038/nature09044, 2010. a





