Evaluating post-glacial bedrock erosion and surface exposure duration by coupling in situ optically stimulated luminescence and ¹⁰Be dating

Assessing the impact of Quaternary glaciation at the Earth's surface implies an understanding of the long-term evolution of alpine landscapes. In particular, it requires simultaneous quantification of the impact of climate variability on past glacier fluctuations and on bedrock erosion. Here we present a new approach for evaluating post-glacial bedrock surface erosion in mountainous environments by combining terrestrial cosmogenic nuclide ¹⁰Be (TCN) and optically stimulated luminescence (OSL) surface exposure dating. Using a numerical approach, we show how it is possible to simultaneously invert bedrock OSL signals and ¹⁰Be concentrations into quantitative estimates of post-glacial exposure duration and bedrock surface erosion. By exploiting the fact that OSL and TCN data are integrated over different timescales, this approach can be used to estimate how bedrock erosion rates vary spatially and temporally since glacier retreat in an alpine environment.

1 Introduction

During the last few million years of the Earth's history, the global climate cooled and evolved towards cyclic glaciations in high-latitude and high-altitude regions (e.g. Miller et al., 1987; Zachos et al., 2001; Lisiecki and Raymo, 2005, 2007). It has been suggested that rates of erosion varied during these multiple cycles and that such variations could in turn feed back into climate (e.g. Molnar and England, 1990; Raymo and Ruddiman, 1992; Champagnac et al., 2007; Herman and Champagnac, 2016). Such erosion rate variations are most expressed in alpine environments, wherein the main erosion agents vary from ice to water and landslides during glacial and interglacial periods, respectively. However, quantifying how their respective contributions in sediment production have varied remains challenging because both ice-extent fluctuations and associated bedrock surface erosion must be reconstructed simultaneously.

Glacially polished bedrock offers the possibility to reconstruct past ice extents and quantify concomitant bedrock surface erosion. These landforms are smooth and glossy, resulting from glacial abrasion, quarrying and meltwater erosion during glacial periods (e.g. Bennett and Glasser, 2009; Siman-Tov, 2017). Following ice retreat, they are exposed to post-glacial erosion, which results in the transition from a well-preserved glacially polished surface (Fig. 1a and b) to a coarse-grained rough surface (Fig. 1c and d). Post-glacial bedrock surface erosion is due to the alteration of rock surfaces exposed to atmospheric conditions. Rock alteration can occur in different ways, involving physical (e.g. frost cracking), chemical and biological processes that weaken and modify the rock surface and ultimately result in its progressive erosion (e.g. Łoziński, 1909; Anderson and Anderson, 2010; Hall et al., 2012; Moses et al., 2014). Because we are concerned with the removal of bedrock surface material since exposure to the atmosphere following glacial retreat, rather than the modification of its physical and chemical characteristics caused by weathering, we hereafter use the term “erosion”. Our objective is to develop an approach that may be used to address the following questions: how fast is the transition from a polished bedrock to a coarse-grained surface (Fig. 1)? How much information about post-glacial exposure is preserved on weathered rock surfaces? What analytical tools or approaches can we use to quantify this morphological transition?

Analytical methods to quantify erosion of rock surfaces differ depending on the timescale of interest (see Moses et al., 2014, for a complete review). Over short timescales (from a few seconds to decades) erosion can be quantified through remote sensing (e.g. photogrammetric methods, terrestrial laser scanner; Armesto-Gonzàlez et al., 2010; Duffy et al., 2013) or measured relative to anthropogenic reference features (historic or experimental; e.g. Nicholson, 2008; Häuselmann, 2008; Stephenson and Finlayson, 2009). Over longer timescales (10³–10⁷ years), erosion can be measured relative to a natural reference feature (e.g. resistant mineral veins such as quartz or a surface of known age) or quantified using surface exposure dating with terrestrial cosmogenic nuclides (TCNs; Lal, 1991; Balco et al., 2008; Bierman and Nichols, 2004; Brandmeier et al. 2011; Liu and Broecker, 2007). TCN methods rely on the production of specific isotopes in terrestrial material by cosmic rays at or near the Earth's surface (Gosse and Philips, 2001), such as minerals located in the top few metres of soil or bedrock (Lal and Peters, 1967). In glacial and paraglacial environments, the formation of glacial landforms can be directly dated over timescales of 10³ to 10⁶ years with TCN surface exposure dating (Ivy-Ochs and Briner, 2014). However, TCN concentrations must also be corrected for surface erosion, which would otherwise lead to an underestimation of the exposure age (Gosse and Phillips, 2001). The combination of short-lived radionuclides such as ¹⁴C with long-lived radionuclides (i.e. ¹⁰Be, ²⁶Al, ³⁶Cl) can be used to resolve and quantify complex exposure histories with burial episodes, but this approach does not allow for the quantification of erosion during exposure (Hippe, 2017).

Consequently, complementary approaches are still needed to quantify bedrock erosion over multiple timescales, more specifically methods that can bridge short and long timescales. In this study, we couple TCN with optically stimulated luminescence (OSL) dating. Rock surface exposure dating using optically stimulated luminescence (named hereafter as OSL surface exposure dating) has recently shown promising potential (e.g. Sohbati et al., 2012a; 2018; King et al., 2019). Luminescence dating is based on the accumulation of trapped electrons through time in the crystalline lattice of specific minerals (e.g. quartz or feldspar), which are sensitive to daylight (Aitken, 1985; Huntley et al., 1985). In addition to its common application to dating sediment burial in a range of geomorphological environments (e.g. Duller, 2008; Rhodes, 2011; Fuchs and Owen, 2008), luminescence dating can also be used to determine the exposure of both naturally formed and anthropogenically formed rock surfaces (e.g. Polikreti et al., 2003; Sohbati et al., 2011; Gliganic et al., 2018; Lehmann et al., 2018). This latter application is based on the principle that when a rock surface is exposed to daylight, the luminescence signal, which is initially homogenous within the rock, will progressively decrease at depth until completely zeroed, a phenomenon called “bleaching” (Aitken, 1998). The assumption is that the longer a surface has been exposed to daylight, the deeper the OSL signal bleaching will be (Polikreti et al., 2002). In granitic and gneissic rocks, bleaching through time has been shown to occur over the first few millimetres to centimetres below the rock surface (Vafiadou et al., 2007; Sohbati et al., 2011; Freiesleben et al., 2015). Due to the attenuation of daylight, the bleaching rate decreases exponentially with depth. It becomes negligible at depth where the luminescence signal is effectively unbleached and remains in field saturation. For long timescales, trapping due to ionizing radiation will compete with detrapping due to daylight exposure at all depths (after ∼ 10⁴ years in Fig. A1), ultimately resulting in an equilibrium bleaching profile (after ∼ 10⁶ years in Fig. A1; Sohbati et al., 2012a).

For a bedrock OSL profile which is not in equilibrium, measuring and calibrating the depth-dependent luminescence signal beneath the exposed surface by generating multiple luminescence depth profiles enables the estimation of an apparent exposure age. OSL surface exposure dating is thus presented as a relatively new surface exposure dating method and has already been applied on both geological and archaeological rock surfaces (Polikreti, 2007; Sohbati et al., 2012a; Freiesleben et al., 2015; Lehmann et al., 2018; Meyer et al., 2018; Gliganic et al., 2018). Sohbati et al. (2012c) were able to quantify the exposure age of historic rock art from the Great Gallery rock art panel in Canyonlands National Park (southeastern Utah, USA). Some of the paintings were damaged by a rockfall event, and conventional luminescence was applied on a rockfall boulder and buried sediments (Chapot et al., 2012). This provided a minimum age for the event. Using a road cut of known age to constrain the bleaching rate for this specific site and lithology, Sohbati et al. (2012c) were able to quantify the exposure age of both the modern analogue (∼ 130 years) and the rock art (∼ 700 years). In a periglacial environment, Lehmann et al. (2018) showed that infrared stimulated luminescence at 50 ^∘C (IRSL50) signals from crystalline bedrock slices exhibits increasingly deep bleaching profiles with elevation and thus exposure age, which is consistent with progressive glacier thinning since the Little Ice Age (LIA; 10¹–10² years). Note that several signals can be targeted in the same rock slice depending on the mineral (e.g. Sohbati et al., 2015; Jenkins et al., 2018). OSL is usually used to analysed the luminescence of quartz (Murray and Wintle, 2000) and IRSL for the potassium-rich feldspar signal (both at 50 and 225 ^∘C; Buylart et al., 2009).

Recently, Sohbati et al. (2018) showed that surface erosion has to be taken into consideration when OSL surface exposure dating is applied to natural bedrock surfaces. Indeed, removal of material would bring the bleaching front towards the surface, which may lead to a considerable underestimation of the OSL surface exposure age if not accounted for. When bedrock surface erosion is high (> 10⁻² mm a⁻¹), the competition between bleaching and surface removal will potentially prevent the use of OSL surface exposure dating as a chronometer for bedrock surface exposure (Sohbati et al., 2018). In practice, when erosion is maintained long enough, an equilibrium between trapping, bleaching (i.e. detrapping) and erosion is reached, and consequently the bleaching profile reaches steady state. Sohbati et al. (2018) explained that the sensitivity difference to erosion between TCN and OSL surface exposure dating can be exploited to calculate the erosion rate experienced by rock surfaces. Indeed, TCN dating is mainly sensitive to cosmic rays over the top ∼ 50–60 cm below the exposed bedrock surface (depending on rock density; Lal et al., 1991), while OSL surface exposure dating is sensitive to light penetration of only millimetres to centimetres (Sohbati et al., 2011, 2012a, b). Thus, using both OSL surface exposure dating and TCN methods, it is possible in theory to quantify surface erosion over different timescales (i.e. 10²–10⁴ years).

Here we couple TCN and OSL surface exposure dating to quantify post-glacial erosion in paraglacial environments. To achieve this, we developed a new model which depends on the exposure age, the surface erosion, the trapping and detrapping (bleaching) rates, and the athermal loss (see Eq. 1, Sect. 2.1). Using this model, we then investigate different synthetic scenarios in which erosion rates follow a series of step functions in time. After this synthetic experiment, the model is used to invert OSL surface exposure data from two glacially polished bedrock surfaces sampled along the Mer de Glace glacier (Mont Blanc massif, European Alps). We find that the relationships between the depth of luminescence bleaching, the exposure age and the surface erosion allow for discrimination between transient and steady-state regimes. Finally, we discuss our findings regarding post-glacial surface erosion in paraglacial environments and the benefits of OSL surface exposure dating combined with TCN surface exposure dating.

Figure 1 Granitic bedrock surfaces along the Mer de Glace glacier (Mont Blanc massif, European Alps). Surfaces (a) and (b) present well-preserved glacial morphologies exposed for only a few years (striations). Surfaces with longer aerial exposure (Late Glacial to Holocene timescales) show glacially abraded surfaces at the macro-scale (c), but at the centimetre scale they reveal a coarse-grained rough surface (d).

2 Methodology: combining TCN and OSL surface exposure dating

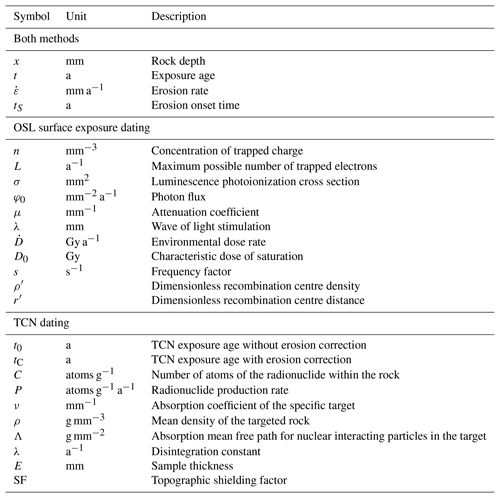
In the following, we focus on the theoretical aspects of both OSL and TCN surface exposure dating methods. We show how different time-dependent exposure and erosion histories are recorded by each technique. Finally, we combine OSL surface exposure and TCN dating to constrain erosion rate and exposure duration simultaneously. Note that all the symbols used below are defined in Table 1.

2.1 OSL surface exposure dating

2.1.1 The bleaching model

The intensity of a luminescence signal reflects the number of trapped electrons (Aitken, 1985). For a rock surface exposed to daylight, the luminescence signal intensity, i.e. the trapped electron concentration, is controlled by the competing processes of electron trapping in response to ambient radiation and electron detrapping due to daylight exposure combined with anomalous fading for feldspar IRSL (Habermann et al., 2000; Polikreti et al., 2003; Sohbati et al., 2011). Sohbati et al. (2011, 2012a, b) introduced a mathematical model that describes the process of luminescence bleaching with depth in a homogeneous lithology, enabling the quantification of rock surface exposure duration. Here we propose a new model describing the evolution of luminescence in rock surface as a function of different parameters characterizing the probability of charge trapping, the wavelength-specific photon flux (φ), the mineral- and wavelength-specific photoionization cross section (σ), and the lithology-specific light attenuation factor (μ) (Eq. 1). Thus, the measured luminescence signal $L(x,t,r^{\prime })$ (dimensionless) at a given depth x (mm), time t (year) and recombination centre distance r^′ (dimensionless) can be described by the following differential equation:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle \frac{\text{d}L(x,t,r^{\prime })}{\text{d}t}}=& {\displaystyle \frac{\dot{D}}{D_{\mathrm{0}}}}[\mathrm{1}-L(x,t,r^{\prime }\left)\right]-L(x,t,r^{\prime })\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}{e}^{-\mathit{\mu }x}\\ & -L(x,t,r^{\prime }){\text{se}}^{-{{\mathit{\rho }}^{\prime }}^{-\frac{\mathrm{1}}{\mathrm{3}}}{r}^{\prime }}+\dot{\mathit{\epsilon }}\left(t\right){\displaystyle \frac{\text{d}L(x,t,r^{\prime })}{\text{d}x}}.\end{array}\end{array}$$

The first term on the right-hand side of Eq. (1) describes the electron-trapping rate in response to ambient radiation with $\dot{D}\left(x\right)$ the environmental dose rate (Gy a⁻¹) at depth x (m) and D₀ the characteristic dose (Gy). In the context of bedrock surface exposure dating, the dose rate can be approximated as a depth-independent constant in the case of homogeneous lithology, i.e. $\dot{D}\left(x\right)=\text{const}$ (e.g. Sohbati et al., 2018).

The second term describes the electron detrapping or bleaching rate due to daylight exposure, where σ(λ) is the luminescence photoionization cross section (mm²) defining the probability of a specific trap being excited by light stimulation. φ₀(λ,x) is the photon flux (mm⁻² a⁻¹) as a function of wavelength at the rock surface (x=0) and describes the rate of incoming photons that can bleach the trap of interest. Here we assume that the photon flux does not fluctuate through time (Sohbati et al., 2011). We are only concerned with $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}$ (a⁻¹), which is the effective decay rate of luminescence at the rock surface following exposure to a particular light spectrum (Sohbati et al., 2011). The light attenuation coefficient μ (mm⁻¹) describes how deep into the rock a photon will penetrate and affect the luminescence signal. μ is assumed to be independent of wavelength in the spectral range of interest (Sohbati et al., 2011).

The third term on the right-hand side of Eq. (1) represents the athermal loss of the IRSL signal of feldspar thought to be due to quantum mechanical tunnelling of trapped electrons (Wintle, 1973; Visocekas et al., 1998) to the nearest available recombination centres (Huntley, 2006). s is the frequency factor equal to 3×10¹⁵ s⁻¹, and ρ^′ is the dimensionless recombination centre density (Tachiya and Mozumder, 1974; Huntley, 2006).

The fourth term describes the advection of the luminescence signal in response to erosion $\dot{\mathit{\epsilon }}\left(t\right)=\text{d}x/\text{d}t$ (mm a⁻¹) on the propagation of the luminescence bleaching front into the rock using an Eulerian system of reference. Equation (1) is solved using the finite-difference method including a second-order upwind scheme for the advection term. This approach is different to the one recently proposed by Sohbati et al. (2018), who used an analytical solution that is based on a confluent hypergeometric function and that requires steady erosion rates. We benchmarked our approach against that of Sohbati et al. (2018), and we obtain results which are similar to their results calculated using their analytical solution (Fig. A3).

Ou et al. (2018) experimentally derived μ for different rock types (greywacke, sandstone, granite and quartzite) using both direct measurements with a spectrometer and bleaching experiments. They showed that the attenuation coefficients are different according the energy of stimulation (e.g. IRSL measured at 50 ^∘C and the post-IR IRSL signal measured at 225 ^∘C). Meyer et al. (2018) and Gliganic et al. (2018) have shown that the distribution of opaque minerals between rock slices can significantly affect the reproducibility of luminescence–depth profiles. The conclude of the need for close petrographic analysis of luminescence–depth profile samples to ensure that the rock cores from calibration and application sites have a similar mineralogical composition and therefore share a similar μ parameter. In this study, we refer to Sohbati et al. (2011, 2012a) for a complete description of $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}$ and μ parameters and their control on the penetration of the bleaching front into a rock surface.

Alternatively, $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}$ and μ can be determined from a known-age rock surface with no erosion ($\dot{\mathit{\epsilon }}\left(t\right)=\mathrm{0}$) with a uniform lithology (Sohbati et al., 2012a; Lehmann et al., 2018; Meyer et al., 2018) and a negligible contribution of athermal loss (as presented in Fig. A2). Under these conditions, Sohbati et al. (2012a) proposed the following analytical solution for Eq. (1), neglecting the athermal loss:

$$\begin{array}{}\text{(2)}& L(x,t)={\displaystyle \frac{\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}{e}^{-\mathit{\mu }x}{e}^{-t\left(\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}{e}^{-\mathit{\mu }x}+\frac{\dot{D}}{D_{\mathrm{0}}}\right)}+\frac{\dot{D}}{D_{\mathrm{0}}}}{\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}{e}^{-\mathit{\mu }x}+\frac{\dot{D}}{D_{\mathrm{0}}}}}.\end{array}$$

For non-eroding surfaces, OSL surface exposure dating can theoretically be used for a broad range of timescales from 0.01 to 10⁵ years (Fig. A1; and Sohbati et al., 2012a, b, 2018). Under these geomorphic conditions for natural rock surfaces (e.g. glacially polished bedrock), OSL surface exposure dating has been successfully applied by solving Eq. (2) over 10¹–10²-year timescales (Lehmann et al., 2018; Gliganic et al., 2018). At longer timescales and/or for rock surfaces affected by erosion, the measured OSL signals reflect not only the exposure age.

2.1.2 Sensitivity analysis to model parameters

In this section, we investigate the respective contribution of the different terms in Eq. (1) for the interpretation of a measured OSL bleaching profile. We investigate the sensitivity of the model to athermal loss, trapping rate and erosion. We use $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}=\mathrm{129}$ a⁻¹ and μ=0.596 mm⁻¹ that were determined from two calibration rock surfaces of similar granitic lithology from the Mont Blanc massif, with no erosion and known exposure age (Fig. A2). The values $\dot{D}=\mathrm{8}$ Gy ka⁻¹ (Table 2) and D₀=500 Gy were selected as they are comparable to the average values for samples used in this study.

Athermal loss

In this section, we investigate the role of athermal loss when constant erosion rates are low (i.e. 10⁻⁵ mm a⁻¹) and high (i.e. 10¹ mm a⁻¹). In Eq. (1), ρ^′ is varied between 10⁻¹⁰ and 10⁻⁵ (natural values vary between 10^−6.5 and 10^−5.1; Valla et al., 2016; King et al., 2018) and is integrated over dimensionless distances, r^′, ranging from 0 to 2.5 (Kars et al., 2008) in all cases. Four model runs were done to test whether the shape of the bleaching profile (i.e. luminescence signal vs. depth) changes with different athermal loss rates, rather than the absolute luminescence signal intensity level which reduces as ρ^′ increases. To remove this effect, the luminescence signals were normalized using the steady-state luminescence plateau as unity (NLS for normalized luminescence signal; Figs. 2 and A2a). Figure 2 shows that the shape of the IRSL profiles would be indistinguishable within uncertainties for the two endmember athermal fading rates. We thus find that athermal loss is negligible, and it is not included in the following calculations or considered further.

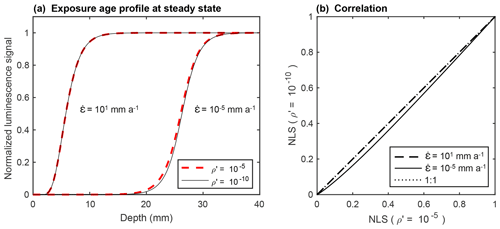
Figure 2 (a) Synthetic luminescence profiles predicted by Eq. (1) for two dimensionless recombination centre densities ρ^′ (10⁻¹⁰ and 10⁻⁵) and two erosion rates $\dot{\mathit{\epsilon }}$ (10⁻¹⁰ and 10⁻⁵ mm a⁻¹). (b) Comparison of the normalized luminescence signal (NLS) for the different values of ρ^′ and $\dot{\mathit{\epsilon }}$. Values for the different parameters $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}$, μ, $\dot{D}$ and D₀ are described in Sect. 2.1.2.

Trapping

Here we illustrate the importance of the trapping term and the effect of the different trapping parameters, i.e. the environmental dose rate ($\dot{D}$) and the characteristic dose of saturation (D₀), on OSL surface exposure dating. Assuming a non-eroding rock surface, the bleaching front will keep propagating with time if trapping is not accounted for (Fig. A1 of Sohbati et al., 2012). In contrast, a secular equilibrium (Sohbati et al., 2018) defined by the steady state between trapping and light-stimulated detrapping at depth can be reached when trapping is considered. In this case, the depth and the time at which the secular equilibrium occurs depend only on the $\dot{D}$, D₀, $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}$ and μ parameters. Using the parameters mentioned in Sect. 2.1.2 and solving Eq. (1) without considering athermal loss, our simulations show that for typical granitic rocks (i.e. $\dot{D}$ between 2 and 8 Gy ka⁻¹) the bleaching front stabilizes at around 20–25 mm of depth after an exposure duration of 10⁵–10⁶ years (Fig. 3).

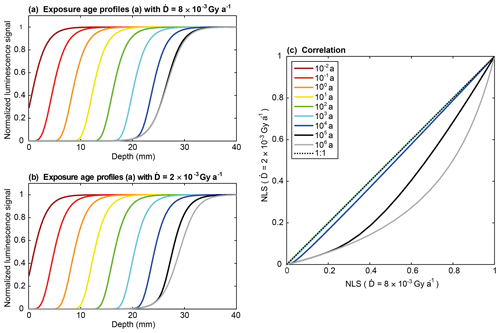
Figure 3 Synthetic luminescence profiles for bleaching models with exposure ages from 10⁻² to 10⁻⁶ years and considering trapping rates of (a) $\mathrm{8}\times {\mathrm{10}}^{-\mathrm{3}}$ and (b) $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹. Panel (c) shows the comparison of the normalized luminescence signal (NLS) for both models after the different exposure ages. As there is no difference between the modelled profiles for both scenarios between 10⁻² and 10⁻³ years, the curves are overlying each other. The choice of parameters $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}$, μ, $\dot{D}$ and D₀ is described in Sect. 2.1.2.

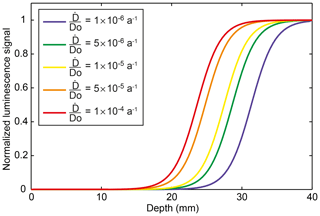
In Fig. 4 we investigate the effects of $\dot{D}/D_{\mathrm{0}}$ on setting the depth of the bleaching front. We use extreme values of D₀ of 100 and 2000 Gy and $\dot{D}$ of $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{3}}$ and 10⁻² Gy a⁻¹ (King et al., 2016; Jenkins et al., 2018; Biswas et al., 2018), resulting in $\dot{D}/D_{\mathrm{0}}$ from 10⁻⁶ to 10⁻⁴ a⁻¹. Our simulations show that the higher the $\dot{D}/D_{\mathrm{0}}$, the closer to the surface the steady-state bleaching profile, which is a consequence of the more rapid saturation of the sample luminescence signal. The steady-state bleaching depth varies between around 22 and 31 mm (measured at the inflection point) for our endmember simulations (Fig. 4). The influence of $\dot{D}/D_{\mathrm{0}}$ on the bleaching profile is minor relative to the other parameters (μ, $\dot{\mathit{\epsilon }}$); however, dose rate can vary by an order of magnitude between rock slices and may possibly explain part of the noise observed in reported experimental data (Meyer et al., 2018).

Figure 4 Synthetic luminescence profiles predicted by Eq. (1) for different values of the ratio $\dot{D}/D_{\mathrm{0}}$ (10⁻⁶, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{6}}$, 10⁻⁵, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ and 10⁻⁴ a⁻¹) and assuming no erosion. The choice of parameters $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}$, μ, $\dot{D}$ and D₀ is described in Sect. 2.1.2.

Erosion

The effect of surface erosion on the luminescence signal has recently been highlighted by Sohbati et al. (2018), who proposed an analytical solution to account for this process. In this section, we numerically solve Eq. (1), neglecting athermal loss, and test the effect of different erosion rates on luminescence profiles. Figure 5a shows the resulting synthetic luminescence profiles at steady state with erosion rates from 0 to 10² mm a⁻¹. Under these synthetic conditions, the effect of surface erosion starts to be noticeable from around 10⁻⁴ mm a⁻¹; for an erosion rate of 10² mm a⁻¹, the steady-state bleaching front is brought forward to 2 mm below the exposed surface. Indeed, surface erosion advects the luminescence signal closer to the surface (Fig. 5). As a result, rock luminescence profiles reflect a competition through time between erosion, trapping and detrapping. When the effects of the three processes are in disequilibrium, such as following initial bedrock surface exposure or the onset of surface erosion, a transient state occurs during which the luminescence signal continues to evolve. After prolonged exposure and assuming constant erosion, the competing effects equilibrate, leading to a steady state at which the bleaching profile is no longer propagating into the rock. In Fig. 5b, we evaluate the evolution of the luminescence profiles from transient to steady state using a dimensionless parameter calculated from the product of the profile depth in which luminescence reaches 50 % of its saturation value (x_50 %), defined as the inflection point NLS(x_50 %=0.5) and the light attenuation coefficient μ (Sohbati et al., 2018). We see that the higher the erosion rate, the faster the system reaches steady state. Consequently, to characterize how a surface is affected by erosion through time, an independent temporal framework is needed to determine the duration of rock surface exposure. This can be achieved by combining OSL surface exposure with TCN dating, which is briefly introduced in the following section.

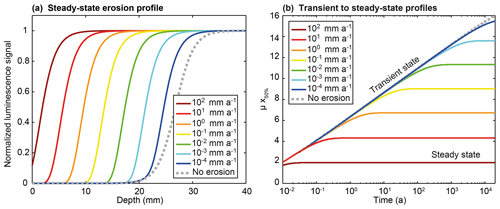
Figure 5 Sensitivity of luminescence–depth profiles with erosion. (a) Synthetic luminescence profiles at steady state with erosion rates from 0 to 10² mm a⁻¹. (b) Transient to steady-state profile for erosion rates from 0 to 10² mm a⁻¹ as a function of time (a) and as the product of the attenuation factor μ (mm⁻¹) and the depth x_50 % defined as NLS(x_50 %=0.5). The choice of parameters $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}$, μ, $\dot{D}$ and D₀ is described in Sect. 2.1.2.

2.2 Terrestrial cosmogenic nuclide (TCN) dating

TCN dating is based on the observation that when cosmic rays reach Earth's surface, they produce cosmogenic isotopes in specific targets, such as the production of ¹⁰Be in quartz (e.g. Gosse and Philips, 2001; Dunai, 2010). The in situ production of quartz ¹⁰Be occurs predominantly within a few metres of Earth's surface and decreases exponentially with depth (Fig. A4a; Portenga and Bierman, 2011, and references therein). The evolution of cosmogenic nuclide C (atoms g⁻¹) in time t (year) and rock depth x (mm) is a function of the disintegration constant λ (a⁻¹), the production rate of a radionuclide P (atoms g⁻¹ a⁻¹) and the erosion $\dot{\mathit{\epsilon }}$ and can be described by the following equation (Gosse and Phillips, 2001):

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\text{d}C(x,t)}{\text{d}t}}=-C(x,t)\mathit{\lambda }+P(\mathrm{0},t)e^{-\mathit{\nu }x}+\dot{\mathit{\epsilon }}\left(t\right){\displaystyle \frac{\text{d}C(x,t)}{\text{d}x}}.\end{array}$$

P(0) is the production rate of the radionuclide at the target surface. The symbol ν defines the absorption coefficient (mm⁻¹) of the target: $\mathit{\nu }=\frac{\mathit{\rho }}{\mathrm{\Lambda }}$. Λ is the mean attenuation length for nuclear particles interacting within the target (g mm⁻²). If the radionuclide concentration at the surface represents the last exposure event, assuming there is no inheritance from a potential previous exposure and that the erosion rate is constant, Eq. (3) can be solved analytically (Lal, 1991), which gives

$$\begin{array}{}\text{(4)}& C(x,t)={\displaystyle \frac{P\left(\mathrm{0}\right)}{\mathit{\lambda }+\mathit{\nu }\dot{\mathit{\epsilon }}}}{e}^{-\mathit{\nu }x}[\mathrm{1}-e^{-(\mathit{\lambda }+\mathit{\nu }\dot{\mathit{\epsilon }})t}].\end{array}$$

When $t\gg \mathrm{1}/(\mathit{\lambda }+\mathit{\nu }\dot{\mathit{\epsilon }}$) the radionuclide concentration reaches a steady state; i.e. a secular equilibrium is reached (Lal, 1991). Under these circumstances, a measured cosmogenic nuclide concentration can be interpreted in terms of a maximum steady-state erosion rate. Here we solve Eq. (3) numerically using the finite-difference method and use the analytical solution to estimate the maximum possible erosion rate. The general behaviour of the quartz ¹⁰Be concentration with erosion and exposure age is well documented in the literature (e.g. Lal, 1991), and we illustrate it in Fig. A4 for comparison with OSL surface exposure dating (Fig. 5). Note that for solving Eq. (3), the experimental measurement of ¹⁰Be concentration C_exp must first be corrected by the depth normalization factor f_E and by the topographic shielding factor (SF) of the surface following the equation (Martin et al., 2017)

$$\begin{array}{}\text{(5)}& C_{\text{corr}}={\displaystyle \frac{C_{\text{exp}}}{f_{\text{E}}\times \text{SF}}},\end{array}$$

with f_E computed by integrating average production over the sample thickness using a single exponential spallation attenuation equation (Balco et al., 2008):

$$\begin{array}{}\text{(6)}& f_{\text{E}}={\displaystyle \frac{\mathrm{\Lambda }}{\mathit{\rho }\times E}}\left[\mathrm{1}-{\displaystyle \frac{-\mathit{\rho }\times E}{\mathrm{\Lambda }}}\right],\end{array}$$

where ρ is the mean density of the targeted rock (g mm⁻³) and E the sample thickness (mm). As we discussed previously, OSL surface exposure and TCN dating both depend on the timing of surface exposure and erosion. These two processes are recorded at different depths into the rock surface: centimetre scale for OSL surface exposure dating and metre scale for TCN; therefore, OSL surface exposure dating is potentially sensitive to surface erosion over shorter timescales than TCN dating. To combine the two methods, one needs to solve Eqs. (1) and (3) simultaneously, for which the two unknowns are the exposure age t and the erosion rate $\dot{\mathit{\epsilon }}$.

Table 1 Symbol table.

3 Inversion approach for synthetic erosion rates

In this section, we generate a series of forward and inverse models. The forward model calculates a luminescence signal and a ¹⁰Be concentration from synthetic erosion and exposure histories. The goal of the inverse model is to constrain the model parameters (i.e. erosion and exposure histories) using the data (i.e. IRSL signal and ¹⁰Be concentration). To validate the inversion procedure, we use the forward model to create synthetic data, which we then recover using the inverse model. For these tests, we use the same OSL surface exposure dating parameters explored in the previous sections: $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}=\mathrm{129}$ a⁻¹ and μ=0.596 mm⁻¹. The value $\dot{D}=\mathrm{8}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹ was selected as an average value obtained for samples used in this study ($\dot{D}=\mathrm{7.4}$ and $\mathrm{8.4}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹ in Table 2). D₀=500 Gy was selected as a representative value for IRSL50 signals from granite. The ¹⁰Be exposure age is estimated using the measured quartz ¹⁰Be concentration of sample MBTP1 collected on a polished granitic bedrock surface at 2545 m a.s.l. from the Tête de Trélaporte located on the left bank of the Mer de Glace glacier (Mont Blanc massif, European Alps). Note that the lithology of this sample is similar to that of the OSL surface exposure dating calibration site from which the model parameters are taken (Fig. A2; Lehmann et al., 2018). The sample was located on a surface presenting a shielding factor 0.963 and has a thickness of 8 cm (Table 2). Its non-corrected ¹⁰Be concentration is equal to 47 4750±17 530 atoms g${}_{\mathrm{qtz}}^{-\mathrm{1}}$ using the sea level high latitude (SLHL) rescaled local production rate of the Chironico landslide: 4.16±0.10 atoms g${}_{\mathrm{qtz}}^{-\mathrm{1}}$ a⁻¹ (Claude et al., 2014). This is corrected for the sample longitude, latitude and elevation considering no erosion correction and the ERA40 atmospheric model (Uppala et al. 2005). We use a disintegration constant λ of $\mathrm{4.9}\times {\mathrm{10}}^{-\mathrm{7}}$ a⁻¹ and a mean attenuation length for nuclear interacting particles in the target Λ of 1.6×10³ g mm⁻² (Gosse and Phillips, 2001; Nishiizumi et al., 2007). The density of the Mont Blanc granite is measured at around $\mathrm{2.55}\times {\mathrm{10}}^{-\mathrm{3}}$ g mm⁻³.

3.1 Forward modelling experiments

In the first scenario, a series of synthetic luminescence profiles were generated using Eq. (1) in a forward model, together with erosion rates of $\dot{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{2}}$ mm a⁻¹ and $\dot{\mathit{\epsilon }}=\mathrm{1}$ mm a⁻¹. This range of values is based on the results of the numerical experiment reported in Sect. 2.1.2. For this scenario, erosion rates are assumed to be constant over the TCN exposure age t_s =t₀, with t_s being the onset time of erosion (dashed lines in Fig. 7a–d). A reference luminescence profile is also calculated, assuming no erosion, using t₀ and Eq. (2) (black dot in Fig. 6b and black lines in Figs. 6c and 7a–d). In the third scenario, another set of synthetic luminescence profiles was again generated using Eq. (1) in a forward model, but the erosion rate was allowed to vary with time (Fig. 6 and green dots in Fig. 7a–d). The assumption made here is that the evolution of erosion in time can follow a step function (Fig. 6a and b). Our objective is explore the effect of a non-constant erosion rate in time on both the luminescence signal and ¹⁰Be concentration. This is the simplest possible time-varying erosion rate history. The erosion is initially equal to zero, i.e. between the corrected exposure age t_c and an onset time of erosion t_s, and increases to a fixed rate between t_s and today (Fig. 6a). Note that more sophisticated erosion rate histories could be tested with the same approach, which is beyond the scope of the current study. Figure 6 illustrates the schematic representation of four different erosion scenarios through time (Fig. 6a and b) and their resulting luminescence signal (Fig. 6c). Note that the corrected exposure age t_c is part of the calculation obtained by solving Eq. (3) using the nuclide concentration and an entire erosion rate history. We report the four model outputs calculated using t_s between 1 and 100 years and erosion rates $\dot{\mathit{\epsilon }}$ between 10⁻² and 1 mm a⁻¹ (green dots in Fig. 7a–d). Note that we added 10 % white noise to the predicted OSL surface exposure dating profiles (used for the inversion approach in Sect. 2).

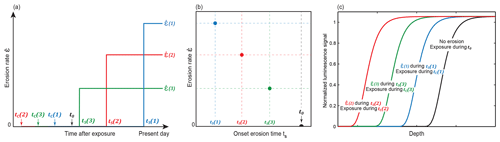
Figure 6 Schematic representation of four different erosion scenarios through time (a, b) and their resulting luminescence signal (c). t₀ is the uncorrected ¹⁰Be exposure age, t_s the onset times of erosion, t_c the corrected exposure ages and $\dot{\mathit{\epsilon }}$ the erosion rate. Note that the luminescence plots in (c) are not model outputs but drawings, with the aim of conceptualizing how the experiments are designed.

By applying a constant erosion rate of 10⁻² mm a⁻¹ to a rock surface exposed since t₀ (16 428 ± 707 years), the luminescence signal is brought 7.8 mm closer to the surface (i.e. 17 mm deep from the surface) compared to the reference signal (luminescence signal exposed since t₀ and not affected by erosion; black line in Fig. 7a–d at 24.8 mm deep from the surface). For a constant erosion rate of 1 mm a⁻¹, the luminescence signal is brought 15.4 mm closer to the surface (i.e. 9.4 mm deep from the surface) compared to the reference signal (difference between black lines and dashed lines measured at NLS = 0.5 in Fig. 7a–d).

If an erosion rate of 10⁻² mm a⁻¹ is applied for a duration of 1 year before sampling and integrated over its specific corrected exposure age (since $t_{\text{c}}=\mathrm{16}\mathrm{428}\pm \mathrm{707}$ years), the luminescence signal is brought 0.4 mm closer to the surface compared to the reference signal (green dots in Fig. 7a) and 1.2 mm if the same erosion rate is applied for 100 years before sampling and integrated over its specific t_c (16 455±713 years; green dots in Fig. 7b). In both scenarios, the predicted luminescence profiles do not overlap the luminescence profile predicted for a constant erosion rate, indicating that the system is in a transient state.

For an erosion rate of 1 mm a⁻¹ applied during 1 year before sampling and for an exposure time corrected with its specific erosion history t_c (16 455±713 years), the luminescence profile (green dots in Fig. 7c) is brought 1.2 mm closer to the surface compared to the reference signal (black line in Fig. 7c). In this case, the luminescence profile is in a transient state with erosion because it is not overlapping the luminescence profile produced by applying the same erosion rate for an infinite time (dashed line in Fig. 7c). Interestingly, the same effect on the luminescence signal is produced by applying an erosion rate of 1 mm a⁻¹ during 1 year (green dots in Fig. 7c) and an erosion rate 10⁻² mm a⁻¹ during 100 years before sampling (green dots in Fig. 7b). For an erosion rate of 1 mm a⁻¹ applied during 100 years before sampling and for an exposure time corrected with its specific erosion history t_c (16 945±722 years), the luminescence signal is brought 15.4 mm closer to the surface (green dots in Fig. 7d) compared to the reference signal (black lines in Fig. 7d). A similar result is obtained when the erosion rate is applied for an infinite time (dashed line in Fig. 7d): in this scenario, the steady state with erosion is reached.

3.2 Inverse modelling experiments

The synthetic data are now inverted to assess the extent to which it is possible to recover the values of $\dot{\mathit{\epsilon }}$ and t_s. Ultimately, our objective is to establish and validate a numerical protocol that enables erosion rate histories to be estimated from paired OSL surface exposure and TCN dating measurements on bedrock surfaces. To find the most likely solutions, we test 10⁴ pairs of both $\dot{\mathit{\epsilon }}$ and t_s (combination of 100 values of both parameters) in log space. The range of possible erosion rates $\dot{\mathit{\epsilon }}$ varies between 10⁻⁵ and 10¹ mm a⁻¹. These endmember values were selected from the erosion sensitivity test performed in Sect. 2.1.5. The erosion onset times t_s range between $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{1}}$ years and 3×10⁴ years, with this range being arbitrarily decided with the upper boundary set to approximately twice the initial TCN age.

As mentioned above, the measured ¹⁰Be concentration has be to corrected for erosion. If the applied erosion rate is too high, the duration is too long or both, the ¹⁰Be concentration must remain small (Fig. A4). On that basis, there is a range of solutions with high erosion rates and durations which is unable to predict the observed ¹⁰Be concentration (Lal, 1991). We call this the “forbidden zone” and exclude it from the parameter search. Expressed differently, for each $\dot{\mathit{\epsilon }}$ and t_s pair, Eq. (3) is first solved and a first estimate of the corrected exposure age t_c is calculated. However, Eq. (3) does not yield a solution for a range of values that produce too much erosion and thus a ¹⁰Be concentration loss that is too high to fit the measured sample concentration. In the studied cases, the forbidden zone is defined by the values between the pairs $\dot{\mathit{\epsilon }}=\mathrm{10}$ mm a⁻¹, t_s∼110 years and $\dot{\mathit{\epsilon }}\sim \mathrm{5}\times {\mathrm{10}}^{-\mathrm{1}}$ mm a⁻¹, t_s=29 210 years.

For all the other pairs of $\dot{\mathit{\epsilon }}$ and t_s, the corrected exposure age t_c is subsequently used to predict luminescence profiles (NLS_inverse) that are compared to the synthetic luminescence profiles (NLS_forward) presented in the previous section (green dots in Fig. 7a–d). The quality of these fits is evaluated using a misfit function, and the inversion results are converted into probability density functions using a likelihood function (Eq. 7). The least-squares deviation regression method minimizes the sum of the square differences between the forward NLS_forward and the inverted values NLS_inverse, giving

$$\begin{array}{}\text{(7)}& \mathcal{L}=\exp \left(-{\displaystyle \frac{\mathrm{1}}{{\mathit{\sigma }}^{\mathrm{2}}}}\sum _{i=\mathrm{1}}^n{\left[{\text{NLS}}_{\text{forward}}^{\left(i\right)}-{\text{NLS}}_{\text{inverse}}^{\left(i\right)}\right]}^{\mathrm{2}}\right),\end{array}$$

where n is the number of rock slices per sample and σ is the standard deviation of the normalized saturated luminescence signal intensities that form the plateau at depth (0.053 ⩽ σ ⩽ 0.059 for our samples).

The results of these inversions are shown in Fig. 7e–h with the parameter space for erosion rate and time as well as the resulting likelihood. The green circles depict the synthetic forward-modelled pair of $\dot{\mathit{\epsilon }}$ and t_s (NLS_forward), which should be recovered in the inversion (green dots in Fig. 7a–d), and the black circles show the $\dot{\mathit{\epsilon }}-t_{\mathrm{0}}$ pair used to produce the model assuming erosion is constant (dashed lines in Fig. 7a–d). We then select the pairs of $\dot{\mathit{\epsilon }}$ and t_s leading to the maximum 5 % likelihood values that fit the synthetic data (the threshold of 5 % is arbitrarily chosen) and plot their corresponding luminescence profile values (red lines in Fig. 7a–d).

The first noticeable observation is that the erosion rate $\dot{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{2}}$ mm a⁻¹ could be applied over every time period below $\sim \mathrm{3}\times {\mathrm{10}}^{-\mathrm{3}}$ years. The numerical solutions for both constant and non-constant erosion rate are outside the forbidden zone (black and green circles, respectively, in Fig. 7e–f). As another example, an erosion rate equal to $\dot{\mathit{\epsilon }}=\mathrm{1}$ mm a⁻¹ could also be applied for any time lower than 1200 years. Indeed, it is not possible to apply an erosion $\dot{\mathit{\epsilon }}=\mathrm{1}$ mm a⁻¹ during t₀ as this pair of values would lie in the forbidden zone (Fig. 7g, h) since such a high erosion rate would imply a ¹⁰Be concentration loss that is too high to fit the measured sample concentration.

For the first scenario, the synthetic luminescence profile produced by applying an erosion rate $\dot{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{2}}$ mm a⁻¹ during time period t_s=1 year has a great number of possible pairs of $\dot{\mathit{\epsilon }}$ and t_s that would reproduce this specific luminescence signal (normalized likelihood > 0.9; yellow area in Fig. 7e). The acceptable solutions range between pairs of values below $\dot{\mathit{\epsilon }}\sim \mathrm{2}\times {\mathrm{10}}^{-\mathrm{2}}$ mm a⁻¹ with $t_{\text{s}}=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{1}}$ years and $\dot{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{5}}$ mm a⁻¹ with t_s=10³ years. These low values do not produce enough erosion to significantly alter the TCN exposure age (t_c∼t₀).

In the second scenario, the erosion rate is $\dot{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{2}}$ mm a⁻¹ during a time period t_s = 100 years, and the forward model pair values can be successfully recovered from the inversion with a more restrained range of numerical solutions (Fig. 7f). The transient state with erosion is well illustrated by trade-offs between erosion rate and time. To fit the forward luminescence profile, low erosion rates should be associated with long time periods following the trend from $\dot{\mathit{\epsilon }}\sim \mathrm{2}$ mm a⁻¹ with $t_{\text{s}}=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{1}}$ years to $\dot{\mathit{\epsilon }}\sim \mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{4}}$ mm a⁻¹ with $t_{\text{s}}=\mathrm{1.2}\times {\mathrm{10}}^{\mathrm{4}}$ years. When the erosion rate of $\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{4}}$ mm a⁻¹ is applied longer than 1.2×10⁴ years, a steady state with erosion is reached and this specific erosion rate could be applied for an infinite time. The highest correction of the TCN exposure age possible with these solutions is of the order of 0.1 % ($t_{\mathrm{0}}=\mathrm{16}\mathrm{428}\pm \mathrm{707}$ years and $t_{\text{c}}=\mathrm{16}\mathrm{455}\pm \mathrm{713}$ years), which is insignificant compared to the 3.6 % uncertainties on t₀.

The third scenario, in which the erosion rate is $\dot{\mathit{\epsilon }}=\mathrm{1}$ mm a⁻¹ during time period t_s=1 year, shares the exact same solution as the second case ($\dot{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{2}}$ mm a⁻¹ with t_s=100 years). This confirms the observation made with the forward modelling whereby both scenarios predicted similar luminescence profile depths. This can be explained because both pairs of $\dot{\mathit{\epsilon }}-t_{\text{s}}$ lie on the trend from $\dot{\mathit{\epsilon }}\sim \mathrm{2}$ mm a⁻¹ with $t_{\text{s}}=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{1}}$ years and $\dot{\mathit{\epsilon }}\sim \mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{4}}$ mm a⁻¹ with $t_{\text{s}}=\mathrm{1.2}\times {\mathrm{10}}^{\mathrm{4}}$ years.

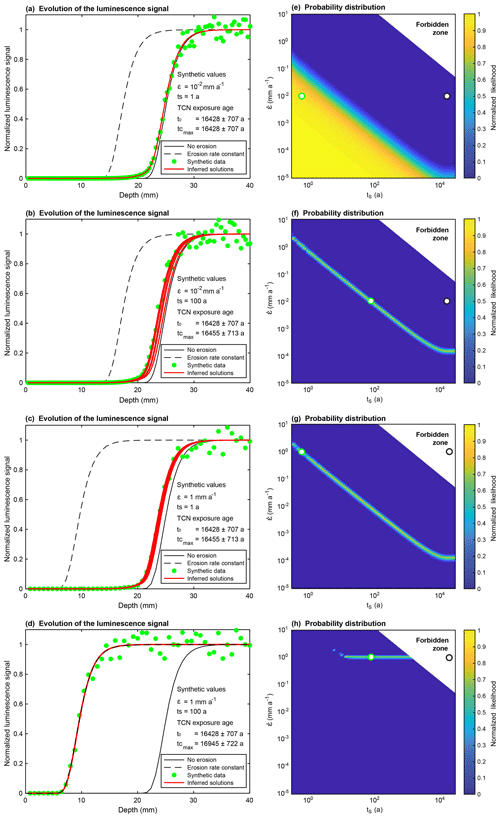
Figure 7 Results of forward and inverse modelling experiments. Green dots represent the simulated luminescence profiles for rock surfaces exposed to (a) an erosion rate of $\dot{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{2}}$ mm a⁻¹ during time t_s=1 year, (b) an erosion rate of $\dot{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{2}}$ mm a⁻¹ during time t_s=100 years, (c) an erosion rate of $\dot{\mathit{\epsilon }}$ = 1 mm a⁻¹ during time t_s=1 year and (d) an erosion rate of $\dot{\mathit{\epsilon }}=\mathrm{1}$ mm a⁻¹ during time t_s=100 years. Black lines represent the reference luminescence profiles for a surface exposed since $t_{\mathrm{0}}=\mathrm{16}\mathrm{428}\pm \mathrm{707}$ years with no erosion. Dashed lines show the luminescence profiles produced by applying constant erosion rates of (a, b) $\dot{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{2}}$ mm a⁻¹ and (c, d) $\dot{\mathit{\epsilon }}=\mathrm{1}$ mm a⁻¹ during t₀. Red lines represent the best-fitting profiles inverted for all numerical solutions with likelihood > 5 %. $t_{{\text{c}}_{\max }}$ represents the maximum corrected TCN exposure age using the forward modelled values of $\dot{\mathit{\epsilon }}$ and t_s. (e–h) The probability distributions inverted from the synthetic luminescence profiles, respectively, in (a–d). Green open circles represent the pairs of values of $\dot{\mathit{\epsilon }}$ and t_s used in the forward model to produce the profiles, and the black open circles represent the values $\dot{\mathit{\epsilon }}$ and t₀ used to predict luminescence profiles with constant erosion (dashed line insets, a–d). All models were performed by solving Eq. (1) using the following parameters: $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}=\mathrm{129}$ a⁻¹, μ=0.596 mm⁻¹, $\dot{D}=\mathrm{8}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹ and D₀=500 Gy. TCN ages were calculated by solving Eq. (3) for the ¹⁰Be concentration of sample MBTP1 presented in the following section.

In the fourth scenario, the erosion rate $\dot{\mathit{\epsilon }}=\mathrm{1}$ mm a⁻¹ is applied during time t_s=100 years, and the range of solutions is much more restrained than for the other scenarios. The synthetic luminescence profile is at steady state with erosion, wherein the erosion rate $\dot{\mathit{\epsilon }}=\mathrm{1}$ mm a⁻¹ can be applied from 18 to 1200 years. For a longer time of erosion, the pairs of $\dot{\mathit{\epsilon }}-t_{\text{s}}$ lie within the forbidden zone regarding the TCN concentration. In this case, the maximum correction of the TCN exposure age is around 3.1 % ($t_{\mathrm{0}}=\mathrm{16}\mathrm{428}\pm \mathrm{707}$ years and $t_{{\text{c}}_{\max }}=\mathrm{16}\mathrm{945}\pm \mathrm{722}$ years), which is comparable to the initial uncertainty on t₀.

4 Application to natural samples

In this section, we apply the method presented above on two natural rock surfaces. Samples MBTP1 and MBTP6 were collected from glacially polished bedrock surfaces at 2545 and 2084 m a.s.l., respectively, from the Tête de Trélaporte located on the left bank of the Mer de Glace glacier (Mont Blanc massif, European Alps). Rock surfaces were collected for the application of both the TCN and OSL surface exposure dating methods (Fig. 9 and Tables 2 and 3.3). Both samples are from the same phenocrystalline granitic lithology of the Mont Blanc massif (Fig. 8).

Figure 8 Locations and sample pictures of MBTP1 and MBTP6, both located on the Tête de Trélaporte along the Mer de Glace glacier (Mont Blanc massif, European Alps).

4.1 Sample preparation, measurement and age calculation

The ¹⁰Be sample preparation method is comprehensively described in the literature (e.g. Kohl and Nishiizumi, 1992; Ivy-Ochs, 1996). We used quartz separates from grain sizes between 250 µm and 1 mm. The addition of a commercial ⁹Be carrier was followed by quartz dissolution in HF and Be purification using ion-exchange columns and selective precipitation. The ¹⁰Be ∕ ⁹Be ratio was measured by accelerator mass spectrometry (AMS) on the 600 KV TANDY system at the Laboratory of Ion Beam Physics (LIP) at ETH Zürich (Switzerland) against the standard S2007N (Christl et al., 2013) that is calibrated against the 07KNSTD standard (Nishiizumi et al., 2007). We correct for a long-term average full chemistry procedural blank of ¹⁰Be ∕ ⁹Be $(\mathrm{3.7}\pm \mathrm{2.2})\times {\mathrm{10}}^{-\mathrm{15}}$ . Ages are calculated using the SLHL rescaled local production rate of the Chironico landslide, 4.16±0.10 atoms g${}_{\mathrm{qtz}}^{-\mathrm{1}}$ a⁻¹(Claude et al., 2014), corrected for the sample longitude, latitude and elevation considering no erosion correction, with the Lifton–Sato–Dunai (LSD) scaling scheme (Lifton et al., 2014), the ERA40 atmospheric model (Uppala et al., 2005) and the Lifton VDM 2016 geomagnetic database (for ages between 0 and 14 ka, Pavon-Carrasco et al., 2014, and for ages between 14 and 75 ka, GLOPIS-75, Laj et al., 2004) with a modified version of the CREp online calculator to process non-linear erosion rate correction by solving Eq. (3) (Martin et al., 2017). The reported errors propagate uncertainties from AMS standard reproducibility, counting statistics, the standard mean error of the samples, blank correction and the local production rate. These external errors are used to compare absolute ages to independent chronologies. All errors are reported at 1σ.

For luminescence analysis we followed the methodology of Lehmann et al. (2018). The bedrock samples were cored down to 30 mm of depth using a Husqvarna DM220 drill with a 10 mm diameter. Cores were then sliced into 0.7 mm thick rock slices with a Buehler IsoMet low-speed saw equipped with a 0.3 mm thick diamond blade. The samples were drilled and sliced under wet conditions (water and lubricant, respectively) to avoid any heating that could potentially reset the OSL signal. Sample preparation was done under subdued red-light conditions. The thickness of each rock slice was measured to determine the precise depth of each luminescence measurement. Luminescence measurements were performed using Risø TL-DA 20 TL–OSL readers (Bøtter-Jensen et al., 2010) equipped with ⁹⁰Sr beta sources at the University of Lausanne (Switzerland). We performed a preheat at 250 ^∘C before giving infrared (IR) stimulation (870 nm, full width at half-maximum (FWHM) 40 nm) at 50 ^∘C analysis are described in further detail in the Figs. A2 and A5). The calculation of $\dot{D}$ was achieved through the measurement of the concentrations of U, Th, K and Rb of the bulk rock sample and the use of the DRAC online calculator (Table 2 and details in Table A1; Durcan et al., 2015). The determination of D₀ was done by constructing a dose-response curve (DRC) of the IRSL signal measured at 50 ^∘C using a single-aliquot regenerative dose (SAR) protocol (Murray and Wintle, 2000; Wallinga et al., 2000) and fitting the DRC with a single saturating exponential. The validity of the measurement protocol was confirmed using a dose-recovery experiment (Wallinga et al., 2000). Recovered doses were within 10 % of unity.

Table 2 Sample list and measurements.

^a Measured against standard 07KNSTD (Nishiizumi et al., 2007), corrected for full process blank of $(\mathrm{3.7}\pm \mathrm{2.2})\times {\mathrm{10}}^{-\mathrm{15}}$ ¹⁰Be ∕ ⁹Be. ^b Local production rate using the sea level high latitude (SLHL) rescaled local production rate of the Chironico landslide, 4.16 ± 0.10 atoms g${}_{\mathrm{qtz}}^{-\mathrm{1}}$ a⁻¹ (Claude et al., 2014), corrected for the sample longitude, latitude and elevation considering no erosion correction, with the LSD scaling scheme (Lifton et al., 2014), the ERA40 atmospheric model (Uppala et al., 2005) and the Lifton VDM 2016 geomagnetic database (for ages between 0 and 14 ka, Pavon-Carrasco et al., 2014, and for ages between 14 and 75 ka, GLOPIS-75, Laj et al., 2004). ^c Dose rates were calculated using the concentrations of U, Th and K of the bulk rock sample and the DRAC online calculator (details in Table A1; Durcan et al., 2015).

4.2 Experimental results

Sample MBTP1 provided a ¹⁰Be concentration of 474 750 ± 17 530 atoms g${}_{\mathrm{qtz}}^{-\mathrm{1}}$. The solution of Eq. (3) gives an apparent ¹⁰Be age for sample MBTP1 of $t_{\mathrm{0}}=\mathrm{16}\mathrm{428}\pm \mathrm{707}$ years, assuming a sample thickness of 8 cm and a shielding factor of 0.963 (Tables 2 and 3). In the same way, the measured ¹⁰Be concentration of 84 100±13 060 atoms g${}_{\mathrm{qtz}}^{-\mathrm{1}}$ for sample MBTP6 gives a ¹⁰Be age of $t_{\mathrm{0}}=\mathrm{6667}\pm \mathrm{965}$ years, assuming a sample thickness of 7 cm and a shielding factor of 0.594 (Tables 2 and 3). Apparent ¹⁰Be ages were calculated as described in Sect. 4.1, assuming no erosion.

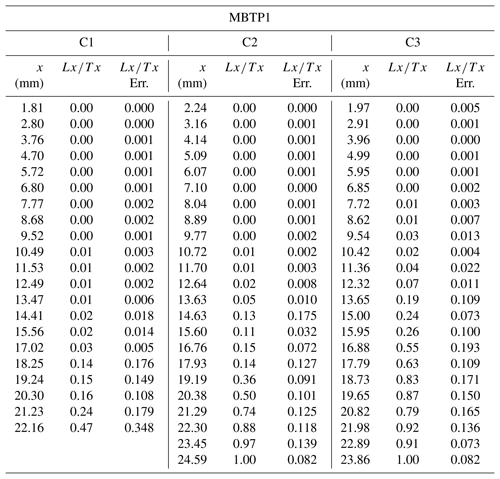
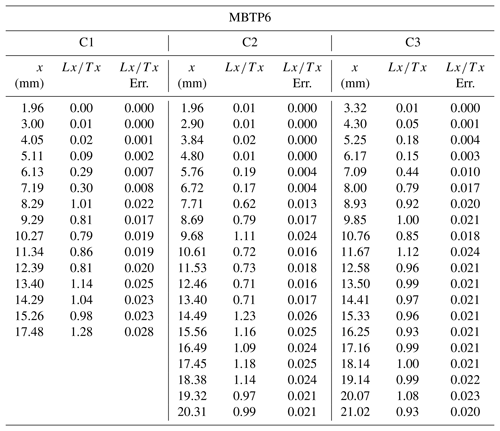
Figure 9 shows the infrared stimulated luminescence at 50 ^∘C (IRSL50, normalized signal) measurements for samples MBTP1 and MBTP6. Three replicates (i.e. individual cores) per sample were sliced in a way that a depth and an IRSL50 signal can be attributed to each rock slice (Tables A2 and A3). The IRSL50 signal is bleached near the surface and reaches a plateau at depth (even for sample MBTP1 for which the plateau is poorly defined). The scattering of the measurements between rock slices is probably due to the granitic nature of the samples. Indeed, the phenocryst lithology can cause heterogeneity in the resulting IRSL50 signals (Meyer et al., 2018) caused by differential bleaching and possibly variations in the environmental dose rate, mainly beta dose heterogeneity (Morthekai et al., 2006), and thus the rate of electron trapping.

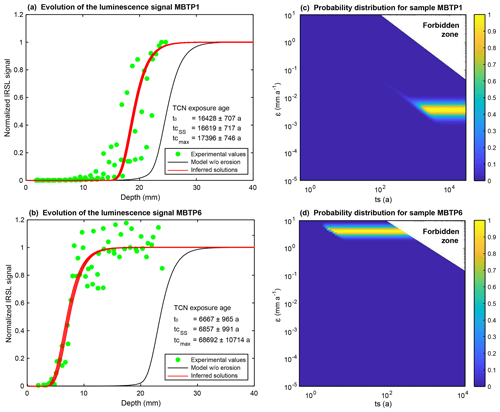
Figure 9 IRSL50 profiles and inversion results for samples MBTP1 and MBTP6. (a, b) Green dots represent the measured IRSL50 profiles for samples MBTP1 and MBTP6. Black lines represent the reference profiles calculated using Eq. (2) and taking the TCN exposure age with no erosion correction (t₀). Red lines represent inferred fits where the likelihood is greater than 0.95. $t_{{\text{c}}_{\text{ss}}}$ represents the corrected TCN exposure age calculated at steady state. $t_{{\text{c}}_{\max }}$ represents the maximum corrected TCN exposure age. (c, d) The probability distributions inverted from the respective insets in (a) and (b). All models were computed by solving Eq. (1) and using the following parameters: $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}=\mathrm{129}$ a⁻¹, μ=0.596 mm⁻¹, D₀=500 Gy, $\dot{D}=\mathrm{7.4}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹ and $\dot{D}=\mathrm{8.4}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹ for samples MBTP1 and MBTP6. Dose rates were calculated using the concentrations of U, Th, K and Rb of the bulk rock sample and the DRAC online calculator (details in Table A1; Durcan et al., 2015).

As a reference profile, a model is computed by solving Eq. (2) using t₀ considering no erosion (black line in Fig. 9a) and lies at 25 mm below the rock surface. The bleaching front measured from the IRSL50 signal of sample MBTP1 (green dots in Fig. 9a) is located 4 mm closer to the surface compared to the reference profile (21 mm from the surface). The IRSL50 profile considering no erosion correction gives an apparent age about 2 orders of magnitude lower compared to t₀: about 642±160 years (1σ; Table 3 and Fig. A5).

For sample MBTP6, the reference profile is 23.5 mm below the surface (black line in Fig. 9b). The measured IRSL50 profile (green dots in Fig. 9b) is approximately 16.5 mm closer to the surface in comparison to the reference profile (7 mm from the surface). The OSL surface exposure apparent age for sample MBTP6 is about 0.39±0.02 years (1σ; Table 3 and Fig. A5).

4.3 Inversion results

In this section, we report the results from the inversion of $\dot{\mathit{\epsilon }}$ and t_s for the IRSL50 profiles of samples MBTP1 and MBTP6 following the procedure presented in Sect. 2. For both samples, the corrected ¹⁰Be ages are calculated using Eq. (3) with a range of erosion rates from 10⁻⁵ to 10¹ mm a⁻¹ and t_s ranging from $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{1}}$ years to ${\mathrm{10}}^{\log \left(t_{\mathrm{0}}\right)+\mathrm{0.25}}$ years (this formula limits the search to ∼ 30 ka because these surfaces are known to be post-LGM (Last Glacial Maximum); Coutterand and Buoncristiani, 2006).

The resulting forbidden zone for sample MBTP1 lies between the erosion rate–time pairs of $\dot{\mathit{\epsilon }}=\mathrm{10}$ mm a⁻¹, t_s∼ 110 years and $\dot{\mathit{\epsilon }}\sim \mathrm{5}\times {\mathrm{10}}^{-\mathrm{1}}$ mm a⁻¹, t_s=29 210 years (already discussed in Sect. 3.2). The inversion results indicate that sample MBTP1 reached a steady state with erosion characterized by an erosion rate of $\dot{\mathit{\epsilon }}=(\mathrm{3.5}\pm \mathrm{1.2})\times {\mathrm{10}}^{-\mathrm{3}}$ (1σ) mm a⁻¹ applied during a minimum duration of 2300 years (Fig. 9c). In these conditions, the corrected TCN age is $t_{{\text{c}}_{\text{ss}}}=\mathrm{16}\mathrm{647}\pm \mathrm{593}$ years (1.1 % of correction). The maximum corrected TCN age $t_{{\text{c}}_{\max }}=\mathrm{17}\mathrm{396}\pm \mathrm{746}$ years is obtained by using $\dot{\mathit{\epsilon }}=(\mathrm{3.5}\pm \mathrm{1.2})\times {\mathrm{10}}^{-\mathrm{3}}$ (1σ) mm a⁻¹ and the maximum t_s possible (29 214 years); this comprises a correction of about 5.8 %.

For sample MBTP6, the forbidden zone lies between the erosion rate–time pairs of $\dot{\mathit{\epsilon }}$ = 10 mm a⁻¹, t_s∼150 years and $\dot{\mathit{\epsilon }}\sim \mathrm{1}\times {\mathrm{10}}^{-\mathrm{10}}$ mm a⁻¹, t_s=11 860 years. The inversion results show that the IRSL50 profile of sample MBTP6 reaches steady state with erosion for an erosion rate $\dot{\mathit{\epsilon }}=\mathrm{4.3}\pm \mathrm{0.56}$ mm a⁻¹ (1σ) applied since at least 4 years. In these conditions, the corrected TCN age is $t_{{\text{c}}_{\text{ss}}}=\mathrm{6857}\pm \mathrm{991}$ years (2.8 % of correction). This steady state cannot be maintained for longer than 344 years because further values correspond to the forbidden zone (Fig. 9d). The maximum corrected TCN age $t_{{\text{c}}_{\max }}=\mathrm{68}\mathrm{692}\pm \mathrm{10}\mathrm{714}$ years would represent a significant correction of 930 %.

At steady state, the surfaces MBTP1 and MBTP6 would have lost 8.05 mm and 17.2 mm, respectively. These values seem realistic regarding the natural surface textures observed on site: no smooth surface or striations are preserved on the roches moutonnées (Fig. 8). By taking the endmember hypothetical erosion values, the surfaces MBTP1 and MBTP6 would have lost a maximum of 102 and 1479 mm, respectively.

Table 3 TCN and OSL surface ages and inversion results for samples MBTP1 and MBTP6.

Ages are calculated using the sea level high latitude (SLHL) rescaled local production rate of the Chironico landslide, 4.15 ± 0.10 atoms g⁻¹ a⁻¹, rescaled for every longitude (Claude et al., 2014), latitude and elevation considering no erosion correction, with the LSD scaling scheme (Lifton et al., 2014), the ERA40 atmospheric model (Uppala et al., 2005) and the Lifton VDM 2016 geomagnetic database (for ages between 0 and 14 ka, Pavon-Carrasco et al., 2014, and for ages between 14 and 75 ka, GLOPIS-75, Laj et al., 2004) by solving Eq. (3). (2) TCN age corr. $t_{{\text{c}}_{\max }}$ corresponds to the maximum corrected TCN exposure ages calculating from the best maximum 5 % solution. For (1) and (2) the errors represent the internal errors. (3) Ages were inverted (Fig. A5) using Eq. (2) and prescribing 10⁶ solutions for a range of time from 0 to t₀ (TCN age calculated using the ¹⁰Be concentration of each sample and solving Eq. (3) without erosion correction). All models were calculated using the following parameters: $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}=\mathrm{129}$ a⁻¹, μ=0.596 mm⁻¹, D₀=500 Gy, $\dot{D}=\mathrm{7.4}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹ and $\dot{D}=\mathrm{8.4}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹ for sample MBTP1 and sample MBTP6. The uncertainties represent 1σ of the distribution presented in Fig. A5. ^* SS means steady state.

5 Discussion

The mismatch between OSL surface exposure and TCN ages presented in this study clearly shows how significant the impact of erosion for OSL surface exposure dating is. If the luminescence bleaching front is interpreted without considering erosion, the resulting exposure age will be strongly underestimated (Figs. 5, 7 and 9). For samples MBTP1 and MBTP6 the apparent OSL surface exposure ages are 642±160 years and 0.32±0.02 years, respectively, while apparent TCN exposure ages are 16 428±707 and 6667±965 years, respectively. We demonstrated in Sect. 2.1 that OSL surface exposure dating is hardly applicable to natural rock surfaces that experience even a minimal erosion rate of about 10⁻⁴ mm a⁻¹. Our models and results show that the position of the bleaching front is highly sensitive to the erosion rate history. Recent studies (e.g. Freiesleben et al., 2015; Sohbati et al., 2012a, 2015; Rades el al., 2018) showed very convincingly that OSL rock surface dating can be used to identify multiple burial and exposure events in the history of a single clast. However, our results imply that erosion cannot be neglected. We show in this study that this high sensitivity to erosion can instead be used to estimate the erosion history of such rock surfaces.

To do so, we have numerically solved the equation describing the evolution of the luminescence signal of a rock surface exposed to light and erosion (Eqs. 1 and 3). The validation of the model was tested on synthetic data and applied to two different glacially polished bedrock surfaces. We assumed a simple erosion rate history following a step function. However, it is very likely that rock surfaces are subject to stochastic erosion processes (e.g. Ganti et al., 2016). These stochastic processes potentially cover temperature, moisture, snow cover or wind fluctuations along the year. The numerical approach adopted here would potentially enable us to consider any type of erosion history (inverse exponential, stochastic distribution, etc.). We considered the erosion rate to be non-constant in time but to follow a step function which changes from zero to a constant erosion rate at certain times in the exposure history. We observed that the resulting erosion histories can follow two states: a transient state or a steady state. Indeed, an experimental luminescence signal can be either at steady or transient state with erosion. To identify at which state the signal is, a model using Eq. (1) should try to fit the experimental luminescence signal considering a range of constant erosion rates applied over the TCN exposure age t₀ of the specific surface. If one specific erosion rate enables the model to fit the experimental luminescence signal, the system is at steady state with this specific erosion rate. If there is no unique solution, the system is at transient state with erosion. Note that some erosion rates cannot be applied for long durations. Indeed, the quantity of material removed and the concentration of cosmogenic nuclides in the rock surface would not match the measured nuclide concentrations. To avoid that, we have defined a forbidden zone which characterized the range of pairs $\dot{\mathit{\epsilon }}$ and t_s for which Eq. (3) could not be solved.

When a luminescence profile is derived from multiple erosion rate $\dot{\mathit{\epsilon }}$ and time t_s pairs, the system is experiencing a transient state with erosion. This situation is characterized by a trade-off between erosion rate and the time of erosion. During this state, the luminescence signal does not evolve with depth if an increase in the erosion time is compensated for by a decrease in the erosion rate. On the other hand, when a luminescence signal is derived from an erosion rate applied across a range of times t_s, the system can be considered at steady state regarding the luminescence profile. In this case, the erosion rate can be considered constant in time over the entire exposure age given by TCN dating, providing that this solution falls outside the forbidden zone. At steady state, the time during which the erosion rate is applied is always lower than or equal to the maximum corrected TCN age (i.e. $t_{\text{s}}\le t_{{\text{c}}_{\max }}$).

The luminescence profile from a given rock surface is able to give information about the erosion history of this surface at both transient and steady state with erosion. The coupling with TCN dating allows for the determination of a limit in time of the steady state with erosion, which cannot tend to infinity as discussed above (i.e. the forbidden zone). According to the inverse modelling of sample MBTP1, the total erosion experienced by the rock surface is about 8.05 mm when the system reached steady state with erosion ($\dot{\mathit{\epsilon }}=\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{3}}$ mm a⁻¹ during t_s=2300 years) and 17.2 mm for sample MBTP6 ($\dot{\mathit{\epsilon }}=\mathrm{4.3}$ mm a⁻¹ during t_s=4 years). This quantity of material removal is plausible given field observations, wherein the micro-structures of striations (coated layer and glacial polish) are not preserved but the macro-patterns of glacial erosion can still be observed (moulded forms, whalebacks, grooves). By taking the endmembers authorized by our model, we explore the limit of our method. The maximum total erosion is about 102 mm for MBTP1 ($\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{3}}$ mm a⁻¹ during 29 214 years) and about 1479 mm for MBTP6 (4.3 mm a⁻¹ during 344 years). Such a high difference in erosion between two locations of the same vertical profile could be explained by the local topographic and environmental conditions, such as slope surface and snow cover, controlling the efficiency of frost cracking.

The quantification of the erosion rate distribution provides the opportunity to quantitatively correct TCN ages. These corrections can be minor but significant: for example, about 1.1 % for MBTP1 by taking the steady-state values and about 5.8 % using the endmember values. For sample MBTP6, the correction is about 2.8 % by taking the steady-state values. Using the endmember values, the maximum corrected TCN age for the highest sample is $t_{{\text{c}}_{\max }}$(MBTP1) = 17 396 ± 746 years and the lowest sample is $t_{{\text{c}}_{\max }}$(MBTP6) = 68 692 ± 10 714 years (representing a maximum correction of about 930 %). The assumption that a surface at 2094 m a.s.l. (surface MBTP6) was exposed almost 50 kyr longer than a surface located 451 m higher (surface MBTP1 at 2545 m a.s.l.) on the same vertical profile in the context of glacial thinning is hardly acceptable. According to the known glaciological evolution of the western Alps during the LGM, exposure ages of > 25 ka are simply not possible. Surfaces at 2600 m a.s.l. located in accumulation zones of former glaciated areas were covered by ice at least until the LGM (e.g. Penck and Brückner, 1909; Bini et al., 2009; Coutterand, 2010; Seguinot et al., 2018), which implies that the age estimates must be treated with caution. However, our results imply that the uncertainty of the exposure age could be large. A correction of the exposure age of a few thousand years would have significant implications when investigating how post-LGM climate variability regionally impacted past ice extent.

We have presented the results using one luminescence signal only (IRSL50). Jenkins et al. (2018) and Sohbati et al. (2015) showed that multiple luminescence signals can be exploited. Since bleaching propagates at different rates within rocks (see Ou et al., 2018), using multiple signals (e.g. pIR225 and OSL125) should enable us to better assess whether the position of the bleaching front is steady or not and thus to further constrain the erosion history (both erosion rate and duration).

Our results confirm the results of Sohbati et al. (2018), who derived an analytical solution assuming steady erosion and using a confluent hypergeometric function. Here we solve the transient solution of Eq. (1) using the finite-difference method. An important difference to the earlier study of Sohbati et al. (2018) is that here the system is fully coupled between OSL and TCN surface exposure dating. OSL dating provides information about the evolution of the erosion rate in time, and TCN dating gives a realistic time frame for this evolution by setting a forbidden zone.

The most striking outcome of this new approach is the ability to quantify surface erosion rates over timescales from 10 to 10⁴ years. The quantification of erosion rates using TCN concentration is limited (expressed in Sect. 2) with the minimum time given by $t\gg \mathrm{1}/(\mathit{\lambda }+\mathit{\nu }\dot{\mathit{\epsilon }}$). By taking the two endmembers of erosion in this study, $\dot{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{5}}$ mm a⁻¹ and $\dot{\mathit{\epsilon }}=\mathrm{10}$ mm a⁻¹, the time limits are respectively 2×10⁶ and 6×10⁴ years, which means that one cannot use TCN to constrain the erosion history of post-LGM surfaces. Consequently, the coupling of OSL and TCN surface exposure dating makes the quantification of bare bedrock surface erosion possible at the timescale of a single interglacial event and might provide insight into the processes of topographic evolution in alpine environments.

6 Conclusions

In this study, we couple OSL and TCN surface exposure dating to constrain post-glacial bedrock erosion and surface exposure duration. We numerically solve the equation describing the evolution of luminescence signals in rock surfaces considering exposure age, bedrock surface erosion, and trapping and detrapping rates due to bleaching and athermal losses. We show that it is critical to account for bedrock surface erosion while interpreting luminescence bleaching profiles. Even at low erosion rates (10⁻⁴ mm a⁻¹) for periglacial environments, only a few years are needed to affect the luminescence profile of a rock surface.

We were able to discriminate between two regimes characterizing the relationships between the depth of the luminescence bleaching, the exposure age and the bedrock surface erosion. The transient state describes a rock surface with a luminescence profile in disequilibrium. In contrast, a rock surface in steady state is produced when the influence of bedrock surface erosion, exposure age and trapping rate compensate for one another. If the system is maintained under these conditions, the luminescence signal no longer evolves with time. Indeed, the determination of the time at which the steady state with erosion occurs is critical. For the two natural surfaces we analysed here, this time can range from 4 years (at an erosion rate of 4.3 mm a⁻¹) to 2300 years (at an erosion rate of $\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{3}}$ mm a⁻¹). The approach developed in this study thus represents a new asset to directly quantify an erosion correction for TCN dating. We see that this correction can range from 1.2 % to 930 % for natural surfaces, although one must keep in mind that the exposure age may be overestimated if not compared to independent observations. Finally, this new approach enables the quantification of erosion rates over surfaces exposed for 10–10⁴ years, filling a methodological gap between short timescales (from a few seconds to decades) and long timescales (>10⁵ years). The contribution of this approach will allow for the quantification of the contribution of bare bedrock surface in sediment production and the topographic evolution of alpine environments over glacial–interglacial cycles. Measurements at locations where bedrock surface erosion is very low (e.g. polar areas, high mountains) need to be investigated to check if OSL surface exposure is potentially applicable to timescales >10² years without accounting for the effect of erosion rates. Another perspective is to investigate the control of temperature and climate on erosion rate evolution in time along an elevation transect. Using this approach, the contribution of post-glacial bedrock erosion can be quantified and the feedback between erosion and climate evaluated.

Appendix A

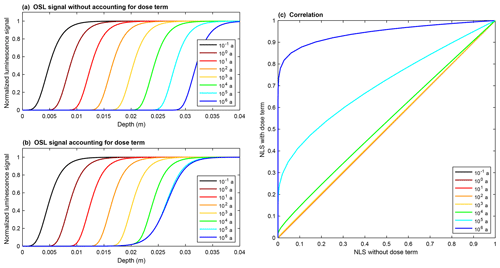
Figure A1 Modelled luminescence–depth profiles as predicted by Eq. (1) accounting for neither fading nor erosion, (a) without the trapping term and (b) with the trapping term, respectively. The selected parameter values are $\dot{D}=\mathrm{8}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹, D₀=500 Gy, $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}=\mathrm{129}$ a⁻¹ and μ=0.596 mm⁻¹. (c) Comparison between the normalized luminescence (NLS) signal for both scenarios shown in (a) and (b).

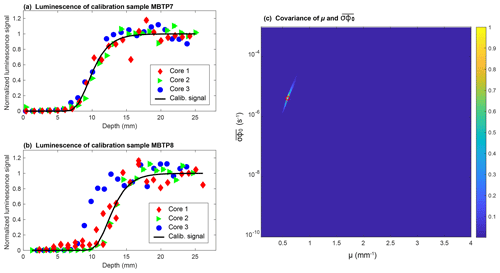
Figure A2 Calibration of the parameters μ and $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}$ using two calibration samples, MBTP7 (1936 m a.s.l.) and MBPT8 (1995 m a.s.l.), with exposure ages of 2±2 years and 11±2 years, respectively. These samples were at the bottom of the Trélaporte vertical profiles in 2016. The surfaces are located between the present-day position of the glacier and the Little Ice Age maximal elevation. These ages were determined using the reconstruction from Vincent et al. (2014). The calibration is made through an inversion protocol by prediction 10⁸ luminescence signals corresponding to the combinations of 10⁴ values of $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}$ in the logarithmic space and 10⁴ values of μ. The inversed solutions are inferred using a least absolute deviation regression as described in Lehmann et al. (2018).

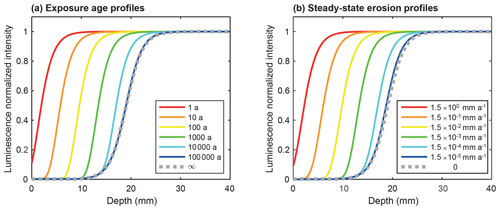
Figure A3 Modelled luminescence–depth profiles as predicted by Eq. (1) for a (a) non-eroding and (b) eroding rock surface, respectively. The selected parameter values are $\dot{D}=\mathrm{6}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹, D₀=250 Gy, $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}=\mathrm{2200}$ ka⁻¹ and μ=0.6 mm⁻¹, similar to Sohbati et al. (2018).

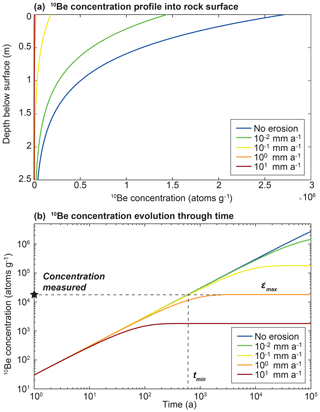
Figure A4 Evolution of the ¹⁰Be production of a rock surface affected by different rates of erosion as a function of (a) the rock depth and (b) the exposure age calculated using a modified version of the CREp online calculator to process the non-linear erosion rate correction by solving Eq. (3) (Martin et al., 2017) as a modelling exercise and for comparison with OSL surface exposure curves in Fig. 5.

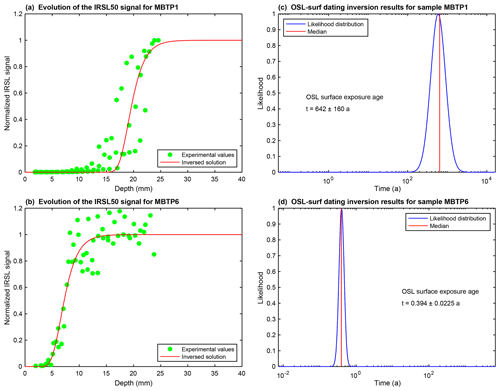
Figure A5 Determination of the apparent OSL surface exposure ages for samples MBTP1 and MBTP6. Experimental values in (a) and (b) correspond to the value measured for three cores per sample. The likelihood was determined using a probability density function following a least-squares deviation regression method minimizing the sum of the square differences between the experimental and the inverted values. Red lines in (c) and (d) represent the median value of the distribution. Apparent ages were inverted using Eq. (2) and prescribing 10⁶ solutions for a range of time from 0 to t₀ (TCN age calculated using the nuclide concentration of each sample and solving Eq. (3) without erosion correction). All models were calculated using the following parameters: $\stackrel{\mathrm{‾}}{\mathit{\sigma }{\mathit{\phi }}_{\mathrm{0}}}=\mathrm{129}$ a⁻¹, μ=0.596 mm⁻¹, D₀=500 Gy, $\dot{D}=\mathrm{7.4}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹ and $\dot{D}=\mathrm{8.4}\times {\mathrm{10}}^{-\mathrm{3}}$ Gy a⁻¹ for sample MBTP1 and sample MBTP6 (see main text for details).

Table A1 Dosimetry calculations for the feldspar samples analysed. Conversion factors have been chosen after Adamiec and Aitken (1998). Alpha-particle attenuation and beta-particle attenuation factors have been chosen after Bell (1980) and Mejdahl (1979), respectively. Cosmic dose rates have been calculated using the method of Prescott and Hutton (1994), assuming an overburden density of 2.7±0.1 g cm⁻³. Internal K concentration is assumed to be 12±0.5 % for both samples. Environmental dose rates were calculated using the DRAC online calculator (Durcan et al., 2015), assuming a grain size between 750 and 1000 µm and water content of 2 %.

Table A2 Infrared stimulated luminescence at 50 ^∘C (IRSL50) experimental values for sample MBTP1.

Table A3 Infrared stimulated luminescence at 50 ^∘C (IRSL50) experimental values for sample MBTP6.